Abstract
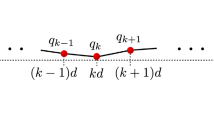
We present a generating-function representation of a vector defined in either Euclidean or Hilbert space with arbitrary dimensions. The generating function is constructed as a power series in a complex variable whose coefficients are the components of a vector. As an application, we employ the generating-function formalism to solve the eigenproblem of a vibrating string loaded with identical beads. The corresponding generating function is an entire function. The requirement of the analyticity of the generating function determines the eigenspectrum all at once. Every component of the eigenvector of the normal mode can be easily extracted from the generating function by making use of the Schläfli integral. This is a unique pedagogical example with which students can have a practical contact with the generating function, contour integration, and normal modes of classical mechanics at the same time. Our formalism can be applied to a physical system involving any eigenvalue problem, especially one having many components, including infinite-dimensional eigenstates.

Similar content being viewed by others
References
D.E. Knuth, The Art of Computer Programming, vol. 1. Fundamental Algorithms, 3rd edn. (Addison-Wesley, Boston, 1997) (Section 1.2.9)
H.S. Wilf, Generatingfunctionology, 3rd edn. (A. K. Peters/CRC Press, Natick, 2005)
W.A. Schwalm, M.K. Schwalm, Am. J. Phys. 51, 230 (1983)
G.N. Watson, J. Lond. Math. Soc. S1–8, 189 (1933)
G.N. Watson, J. Lond. Math. Soc. S1–8, 194 (1933)
G.B. Arfken, H.-J. Weber, F.E. Harris, Mathematical Methods for Physicists, 7th edn. (Academic Press, Oxford, 2012)
L.M. Narducci, M. Orszag, Am. J. Phys. 40, 1811 (1972)
J.B. Marion, Classical Dynamics of Particles and Systems, 2nd edn. (Academic Press, Oxford, 1970)
A.L. Fetter, J.D. Walecka, Theoretical Mechanics of Particles and Continua (McGraw-Hill, New York, 1980) (Chapter 24)
R.A. Matzner, L.C. Shepley, Classical Mechanics (Prentice-Hall, Hoboken, 1991), pp. 232–239
P.D. Ritger, N.J. Rose, Differential Equations with Applications (McGraw-Hill, New York, 1968), pp. 367–372
J.W. Brown, R.V. Churchill, Complex Variables and Applications, 8th edn. (McGraw-Hill, New York, 2009)
S. Ponnusamy, H. Silverman, Complex Variables with Applications (Birkhäuser, Boston, 2006)
R.E. Greene, S.G. Krantz, Function Theory of One Complex Variable, 3rd edn. (American Mathematical Society, Providence, 2006)
D.G. Zill, W.S. Wright, Advanced Engineering Mathematics, 10th edn. (Wiley, Hoboken, 2011)
D.-W. Jung, U-R. Kim, J. Lee, C. Yu, Lagrange-multiplier regularization of eigenproblem for \(J_x\). KPOP\({\mathscr {E}}\)-2021-01
D.-W. Jung, W. Han, U-R. Kim, J. Lee, C. Yu, Finding normal modes of loaded string with Lagrange multipliers. KPOP\({\mathscr {E}}\)-2020-08
J.-H. Ee, D.-W. Jung, U-R. Kim, D. Kim, J. Lee, Three-body inertia tensor. Eur. J. Phys. https://doi.org/10.1088/1361-6404/abf8c6 (in press)
W. Han, D.-W. Jung, J. Lee, C. Yu, Determination of eigenvectors with Lagrange multiplier. J. Korean Phys. Soc. https://doi.org/10.1007/s40042-021-00112-3 (in press)
F.W. Byron, Jr., R.W. Fuller, Mathematics of Classical and Quantum Mechanics, vol. II (Addison-Wesley, Reading, 1970), pp. 371–378 (Section 6.9)
Acknowledgements
As members of the Korea Pragmatist Organization for Physics Education (KPOP\({\mathscr {E}}\)), the authors thank the remaining members of KPOP\({\mathscr {E}}\) for useful discussions. The work is supported in part by the National Research Foundation of Korea (NRF) under the BK21 FOUR program at Korea University, Initiative for science frontiers on upcoming challenges. The work of JL, URK, and DK is supported in part by grants funded by the Korea government (MSIT) under Contract No. NRF-2020R1A2C3009918. The work of DWJ and CY is supported in part by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education 2018R1D1A1B07047812 (DWJ) and 2020R1I1A1A01073770 (CY), respectively.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to this work.
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Kim, UR., Jung, DW., Kim, D. et al. Solving an eigenproblem with analyticity of the generating function. J. Korean Phys. Soc. 79, 113–124 (2021). https://doi.org/10.1007/s40042-021-00201-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40042-021-00201-3