Treatments of Micro-channel Flows Revisited: Continuum Versus Rarified Gas Considerations

Abstract

There are numerous treatments of micro-channel flows available that point out the breakdown of the Navier–Stokes equations under molecular flow conditions when continuum conditions should still apply. The wrong conclusion regarding the validity of the Navier–Stokes equations comes about from the missing mass diffusion terms in the continuity equation. This term also affects the Navier–Stokes equations and yields improved theoretical results for flows with strong pressure and temperature gradients. Rarified gas treatments are often applied, although the fluid mechanics conditions are still such, that continuum equations should work. In the paper, the missing mass diffusion term is added, and it is shown that those extended fluid mechanics equation (EFME) allows micro-channel flows to be treated in the so-called slip regime. Hence, the continuum approach for flow treatment holds in micro-channel flows, in the flow regimes where modeling of wall interactions is applied these days. The paper also describes the treatments of micro-channel flows in the slip-flow regime by the rarified gas flow treatment method of Shapiro and Seleznev, and the results are compared with the corresponding results of the EFME. Good agreement was obtained, but differences exist regarding the wall interactions, which are explained, and suggested to use both methods to obtain a deeper insight into molecule–wall interactions in micro-channel flows. The EFME claim that large pressure and temperature gradients are the reasons for the differences between experimental and theoretical results of micro-channel flows. Such differences also exist in other fluid flows with strong property gradients, e.g., in shock waves. Flows of this kind are also treated in this paper in a way to show that the EFME have a wide range of applications.

Introduction and Aims of Work

It can be observed in the literature that for gaseous flows through micro-channels and micro-capillaries, under some conditions (Harley et al. [1], Arkilic et al. [2], Errol et al. [3], Maurer et al. [4], Yang and Garimella [5]), the measured mass flow rates can be higher than those obtained by solving the classical fluid flow equations, i.e., by solving the Navier–Stokes equations with no-slip boundary conditions at the wall and for the same given inlet and outlet pressure conditions. The observed increase in mass flow rate in experiments is usually referred to as a “micro-channel phenomenon,” which has puzzled fluid flow researchers. In order to bridge the gap between the experimental results and the theoretical predictions, various first- or second-order Maxwellian slip velocity models have been introduced at the channel walls as boundary conditions. A good summary of research along this line is given by Karniadakis et al. [6].

From the book of Karniadakis et al. [6] and from review papers like that of Sharipov and Seleznev [7], one can see that there are numerous papers available that treat micro-channel gaseous flows by methods usually applied to treatments of rarified gas flows. This treatment is applied although the molecular motion still shows properties that obey continuum requirements. In spite of this, the existing literature claims in most papers that micro-channel flows require methods of rarified gas flows to be applied to yield agreement between theoretical results and corresponding experimental data. A very good summary of this kind of treatment is provided in Karniadakis et al. [6]. Such a treatment of micro-channel flows readily suggests that these flows cannot be treated by using the Navier–Stokes equation.

Through these observations in published papers, it is indirectly suggested that the continuum approach, to treat micro-channel flows theoretically, fails already in the flow region, usually referred to as slip-flow region as mentioned in Hadjiaconstantinou [8]. There is, however, the possibility that the conventional Navier–Stokes equations miss a transport term which is not important for macro-channel flows, but becomes relevant for gaseous flows in micro-channels stated in Dongari et al. [9] and Durst et al. [10]. The present paper revisits this work and stresses again that the incorporation of the missing terms in the continuity and the corresponding terms in the Navier–Stokes equations permit typical micro-channel flows to be treated by the continuum equations of fluid mechanics, but they need to be extended by the missing mass diffusion terms in the continuity and the Navier–Stokes equations.

The paper also refers to the work carried out to treat micro-channel flows by the theory of rarified gases. A good review about this field of micro-channel flow research is given by Sharipov and Saliznev [7]. These authors derive equations for the mass flow rate through micro-channels of the kind experimentally investigated by the authors given in the first sentence of this introduction. Treatments by verified gas theory were employed by the authors, and the results derived on the basis of rarified gas flow considerations are compared with results based on the extended Navier–Stokes equations. The latter results are provided numerically and analytically, and the comparison turns out to agree well with the experimental data of Maurer et al. [4]. Agreement is also obtained by the results of Sharipov and Seleznev [7], but remaining differences indicated that the RGT modeling is not capturing the “micro-channel” effect very well. Furthermore, the results show that the solutions, based on the extended fluid mechanics equation (EFME) predict the transition from the macro-channel regime to the micro-channel regime very well without any special modeling of molecular wall interactions. The results of Maurer et al. [4] lie very well in this transition regime and can therefore be compared with the theoretical results of continuum and rarified gas flow treatments, as done in this paper.

A summary of the treatment of micro-channel flow by the extended Navier–Stokes equation is given in this paper. Although these derivations have been shown in Sambasivam and Durst [11], a summary is given again for completeness of the present work. The numerical solutions of the corresponding extended channel flow equations are shown to fit well with the experimental data of Maurer et al. [4].

The treatment of internal rarified gas flows is summarized, and results of the final equations are shown in later part of this paper. This part of the authors’ work is entirely based on the publication of Sharipov and Seleznev [7] using their final equations for the mass flow rate computations. Adopting their result, the diffusion term in the authors’ mass flow rate equation is explained in this work. Results have been presented that suggest that the additional diffusion transport term needs to be included in the governing equations to get good agreements with the experimental data of Maurer et al. [4]. The rarified gas considerations of Sharipov and Seleznev [7] describe micro-channel data only well at very small values of the difference of the square of the inlet and outlet pressures. The authors suggest looking into this finding more closely in future work on this subject.

To demonstrate that it is the missing diffusion mass transport term in the fluid mechanics equations which causes the difference between experimental and theoretical fluid flows, the treatment of shock waves is considered. Such flows are not influenced by flow wall interactions. However, they process the regions of high pressure and temperature gradients. Using the EFME to predict shock wave flows, improved results are obtained as per Greenshields and Reese [12]. This is taken as an additional proof that the EFME needs to be employed to treat flows with strong pressure and temperature gradients.

Micro-channel Flow Treatment by Extended Fluid Mechanics Equations

Self-diffusion in Ideal Gas Flows

Sambasivam and Durst [11] published the numerical results for micro-channel flows based on the full set of the “Extended Fluid Mechanics Equations” (EFME). These can be written, for example, in rectangular coordinates, as follows:

$$ \frac{\partial \rho }{\partial t} + \frac{{\partial \left( {\rho U_{i}^{T} } \right)}}{{\partial x_{i} }} = 0; $$

(1)

$$ \rho \left( {\frac{{\partial U_{j}^{T} }}{\partial T} + U_{i}^{T} \frac{{\partial U_{j}^{T} }}{{\partial x_{i} }}} \right) = - \frac{\partial P}{{\partial x_{j} }} - \frac{{\partial t_{ij}^{T} }}{{\partial x_{i} }} + \rho g_{j} $$

(2)

containing the following term:

$$ \tau_{ij}^{T} = \left[ {\frac{{\partial U_{j}^{T} }}{{\partial x_{i} }} + \frac{{\partial U_{i}^{T} }}{{\partial x_{j} }}} \right] + \frac{2}{3}\delta_{ij} \mu \frac{{\partial U_{k}^{T} }}{{\partial x_{k} }} $$

(3)

where ρ is the density of the fluid, $t$ is the time, μ is the viscosity, $\tau_{ij}$ is the molecular momentum transport, $\delta_{ij}$ is the Kronecker delta and $U_{i}^{T} , U_{j}^{T} , U_{k}^{T} ,$ are the total velocity components in the $x_{i}$-, $x_{j}$-, $x_{k}$-direction, respectively. These equations contain the total velocity $U_{i}^{T}$ rather than the convective velocity $U_{i}^{C}$ in all corresponding terms as:

$$ U_{i}^{T} = U_{i}^{C} + U_{i}^{D} $$

(4)

where $U_{i}^{D}$ is the diffusive velocity. Durst et al. [10] claimed in their paper that the usually employed conventional Navier–Stokes equations are valid only when the diffusive local mass flux is zero. In that case, the continuity and the Navier–Stokes equations contain the same terms as Eqs. (1)–(5), but they are expressed for the convective velocity rather than the total velocity in the equations for mass and momentum conservation.

From the authors’ work, the following considerations are summarized below. From the derivations of mass diffusion (see Durst et al. [10]), the following equations can be used for the mass flow rate caused by diffusion:

$$ \dot{M}_{i}^{D} = \rho U_{i}^{D} = - \rho D\left( {\frac{1}{\rho }\frac{\partial \rho }{{\partial x_{i} }} - \frac{1}{2 T}\frac{\partial T}{{\partial x_{i} }}} \right) $$

(5)

where $D$ is the coefficient of mass diffusion and the two terms represent:

$$ \left( {\dot{M}_{i}^{D} } \right)^{\text{F}} = - \,D\frac{\partial \rho }{{\partial x_{i} }} = {\hbox{Fick'}}\,{\text{s diffusion term}}; $$

(6)

$$ \left( {\dot{M}_{i}^{D} } \right)^{S} = \frac{\rho D}{2T}\frac{\partial T}{{\partial x_{i} }}\quad {\hbox{Soret'}}\,{\text{s diffusion term:}} $$

(7)

Both of these mass fluxes are those for self-diffusion in ideal gases, driven by density and temperature gradients. The simple derivations by Durst et al. [10] yield the Soret diffusion term to read:

$$ D_{{\mathrm{S}}} = \frac{\rho D}{2T}. $$

Considering the ideal gas equation $P = \rho RT$, one can derive:

$$ \frac{ 1}{P}\frac{\partial \rho }{{\partial x_{i} }} = \frac{ 1}{\rho }\frac{\partial \rho }{{\partial x_{i} }} + \frac{ 1}{T}\frac{\partial \rho }{{\partial x_{i} }} $$

(8)

Replacing the density term in Eq. (5) by the terms in Eq. (8) yields

$$ \dot{M}_{i}^{D} = - \, \rho D\left( {\frac{1}{P}\frac{\partial P}{{\partial x_{i} }} - \frac{1}{2 T}\frac{\partial T}{{{\text{d}}x_{i} }}} \right) $$

(9)

Hence, the local mass flux for self-diffusion can also be expressed in terms of pressure and temperature gradients. For isothermal flows through micro-channels, the local diffusive mass flux is driven by a pressure gradient only and can be written as follows since $\rho D = \mu$ for ideal gases:

$$ \rho U_{i}^{D} = - \frac{\mu }{P}\frac{\partial P}{{\partial x_{i} }} \to R_{e}^{D} = \frac{{\rho U_{i}^{D} h}}{\mu } = \left( {\frac{h}{P}} \right)\left( {\frac{\partial P}{{\partial x_{i} }}} \right) $$

(10)

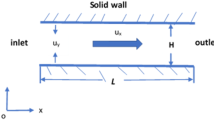
For micro-channel flows, the imposed pressure gradient in the $x_{i}$-direction also results in a convective part of the flow, for which the following differential equation holds:

$$ \frac{ 1}{\rho }\frac{{{\mathrm{d}}P}}{{{\mathrm{d}}x_{i} }} = \left( {\frac{\mu }{\rho }} \right)\left( {\frac{{{\text{d}}^{2} U_{1}^{C} }}{{{\text{d}}^{2} x_{2} }}} \right) $$

(11)

The flow described by Eq. (11) is usually only considered when plane channel flows are treated theoretically. The diffusive mass flux, expressed by Eq. (9), is usually neglected in fluid mechanical treatments of channel flows, since it is small for ${\text{Re}} > 1$. For micro-channel flows, the diffusive mass flux needs to be taken into account, since it is not negligible for certain imposed flow conditions, i.e., for certain micro-channel flow parameters. At the walls of micro-channels, the total velocity takes on the value of the diffusion velocity and, hence, a “slip velocity” of nonzero value is expected. Unlike the convection velocity, the diffusion velocity is constant through the cross section of the channel and, hence, it will be nonzero in the vicinity of the wall. For more detailed discussions on this topic, the authors refer to the work of Sambasivam and Durst [11]. In their work, these authors show that the nonzero velocities close to the walls in micro-channel flows are caused by mass diffusion, driven by pressure gradients and can be computed if Eq. (5) is taken into account. It is not necessary to model the resultant “slip velocity” as the result of wall–fluid flow interactions to predict micro-channel flows.

In Fig. 1, the mass flow rates through a straight micro-channel measured experimentally by Maurer et al. [4] are compared with the numerically obtained flow rates employing the extended Navier–Stokes equations, i.e., the EFME summarized above.

Fig. 1

Comparison of numerical solutions with the classical and extended Navier–Stokes equations with the experimental results of Maurer et al. [4] for an outlet pressure of 0.12 bar

The mass flow rates predicted by the classical equations with no-slip boundary conditions are also shown in Fig. 1, for comparison. One can easily deduce that the average Knudsen number increases with a decrease in $\frac{1}{2}\left( {P_{\text{in}}^{2} - P_{\text{out}}^{2} } \right)$ in parts of the flow, where $P_{\text{in}}^{2}$ is the inlet pressure and $P_{\text{out}}^{2}$ is the outlet pressure of a corresponding micro-channel test section.

The numerical results given in the above diagram also led to the insight that the additional mass flow, measured and predicted in the micro-channels, is completely governed by the pressure gradient in Eq. (10). The acceleration terms on the left-hand side of the “Extended Basic Fluid Mechanics Equations” (see Eqs. 1–3) are either zero for the time derivative term or very small for the advection terms. Hence, it was concluded that an analytical solution for the ideal gas flows through micro-channels, deducible from Eqs. (1)–(5), resulting in Eqs. (10) and (11) appears feasible. This conclusion led to the work of the first author and various of his co-workers, summarized in the following sections.

Analytical Treatments

It was stressed in several papers, published by Durst et al. [10] and also Sambasivam and Durst [11] that the velocities of fluid flows consist of convective and diffusive components:

$$ U_{i}^{T} = U_{i}^{C} + U_{i}^{D} $$

(12)

Hence, the fluid mechanics equations must be written in terms of total velocity when diffusive transports are not negligible, as in micro-channel flows, as shown by, e.g., Sambasivam and Durst [11]. For analytical treatments of micro-channel flows, one needs to solve the following equations:

$$ 0 = - \frac{\partial P}{\partial x} + \mu \frac{{\partial^{2} U_{i}^{T} }}{{\partial x_{l}^{2} }} $$

(13)

Solving this equation, one obtains:

$$ U_{i}^{T} = \frac{1}{2\mu }\left( {\frac{{{\text{d}}P}}{{{\text{d}}x}}} \right)x_{2} + C_{1} x_{2} + C_{2} $$

(14)

Applying the boundary conditions:

$$ x_{2} = 0:\quad \left( {\frac{{\partial U_{i}^{T} }}{{\partial x_{2} }}} \right) = 0\quad \left( {\text{axis of the flow}} \right) \, \to C_{1} = 0; $$

(15)

$$ x_{2} = h:\quad U_{1}^{T} = - \frac{\mu }{\rho }\frac{1}{P}\frac{\partial P}{{\partial x_{i} }}\quad \left( {\text{wall of the flow}} \right) $$

(16)

Hence, one obtains for channel flows the following equation for the fully developed fluid velocity distribution in the $x_{2}$ direction:

(17)

In all macro-channel flows, the above given diffusion term for the velocity is very small in comparison with the convective term. This is, however, not the case for micro-channel flows. For these flows, the second term is not negligible and contributes, under certain pressure and temperature conditions and channel heights, considerably to the flow in the x-direction. This contribution to the total flow is the so-called wall-slip flow observed in micro-channel flows, i.e., the slip-flow results from the pressure diffusion in micro-channels. Hence, when micro-channel flows are treated by the “Extended Basic Fluid Mechanics Equations” (EFME), this slip-flow needs not to be modeled by Maxwell’s diffuse and discrete wall reflections of gas molecules, but physically it represents the additional mass flow due to diffusion.

From Eq. (17), one can derive the relation for the total mass flow rate by integrating Eq. (17) first in the cross-flow direction, yielding:

$$ \begin{aligned} \dot{M}^{T} & = \mathop \int \limits_{ - h}^{h} \left( {\rho U} \right){\text{d}}y = - w\mathop \int \limits_{ - h}^{h} \left\{ {\frac{\rho }{2\mu }\left( {h^{2} - y^{2} } \right)\frac{{{\text{d}}P}}{{{\text{d}}x}} + \frac{\mu }{P}\frac{{{\text{d}}P}}{{{\text{d}}x}}} \right\}{\text{d}}y \\ & = - 2hw\left( {\frac{{h^{2} P}}{3\mu RT} + \frac{\mu }{P}} \right)\frac{{{\text{d}}P}}{{{\text{d}}x}} \\ \end{aligned} $$

(18)

where $w$ is the width of the considered micro-channel.

Integrating Eq. (18) from the inlet ($x = 0$) to the outlet ($x = L$), one can derive:

$$ \dot{M}^{T} = \frac{{h^{3} wP_{\text{out}}^{2} }}{3\mu LRT}\left\{ {\left( {\frac{{P_{\text{in}} }}{{P_{\text{out}} }}} \right)^{2} - 1} \right\} + \frac{2\mu hw}{L}\ln \left( {\frac{{P_{\text{in}} }}{{P_{\text{out}} }}} \right) $$

(19)

Therefore, the total mass flow rate $M^{T}$ can be expressed as a function of the pressure ratio $P_{\text{in}} /P_{\text{out}}$. As the given result in Fig. 2 below shows, the pressure at the inlet and at the outlet of a two-dimensional micro-channel flow yields a mass flow rate that is higher than the part only caused by convection. The additional mass flow rate depends on the channel height h and the channel length $L$, the channel width $w$, the viscosity $\mu$ and the specific gas constant $R$, as well as the inlet and outlet pressures.

Fig. 2

The total mass flow rate as a function of the difference of squares of pressure at the inlet and outlet together with experimental data of Maurer et al. [4]

Utilizing the above equations, one can calculate the total mass flow rates of a helium gas flow in a micro-channel with boundary conditions, corresponding to the experiments of Maurer et al. [4], which are tabulated in Table 1. The total mass flow rates $\dot{M}^{T}$, for the outlet pressure $P_{\text{out}}$ changing from 0.012 to 0.1 MPa, are shown in Fig. 2 together with experimental results of Maurer et al. [4], where the abscissa is expressed as $0.5\left( {P_{\text{in}}^{2} - P_{\text{out}}^{2} } \right)$ according to the notation of Maurer et al. [4]. Figure 2 shows that the choice of the outlet pressure conditions is relevant to obtain the typical micro-channel effects on the gas flow. It can be seen that, as the outlet pressure is decreased, the total mass flow rate deviates from that of the classical Navier–Stokes equations. The difference increases with decreasing outlet pressure, as known from the experiments of Maurer et al. [4]. Figure 2 shows that good agreement between the theoretical results of Eq. (19), and the experimental data are obtained.

Table 1 Experimental conditions of Maurer et al. [4] and Arkilic et al. [2]

The total mass flow rate, especially for $P_{\text{out}} = 0.012\,{\text{MPa}}$, shows considerable deviations from predictions based on the Navier–Stokes equations with no-slip wall conditions. The present analytical result of $P_{\text{out}} = 0.012\,{\text{MPa}}$ shows good agreement with the experimental results of Maurer et al. [4], and the analytically deduced solution follows the micro-channel deviation that occurred in their experiment. This finding is a good proof that the equation for the total velocity, see Eq. (14), describes physically correct the flow in micro-channels, without modeling wall–fluid interactions.

Furthermore, one can proceed with the theoretical considerations of micro-channel flows to obtain a universal relationship between the total mass flow rate and the applied pressure, as well as the pressure gradient. Therefore, Eq. (19) can be rewritten as:

$$ \dot{M}^{T} = - \,2hw\frac{\mu }{P}\frac{{{\text{d}}P}}{{{\text{d}}x}}\left( {\frac{{h^{2} P^{2} }}{{3\mu^{2} RT}} + 1} \right) $$

(20)

Since for micro-channel flows the pressure $P$ is constant in the $y$-direction, the diffusive mass flow rate $M^{D}$ can be expressed by integrating Eq. (11) over a cross-sectional area to obtain:

$$ \dot{M}^{D} = - \,2hw\frac{\mu }{P}\frac{{{\text{d}}P}}{{{\text{d}}x}}. $$

(21)

Hence, the diffusive mass flow increases in the direction of the channel outlet. Combining Eq. (20) with (21) yields for the ratio of local diffusive and total mass flow rates:

$$ \frac{{\dot{M}^{D} }}{{\dot{M}^{T} }} = \frac{1}{{\frac{{h^{2} P^{2} }}{{3\mu^{2} RT}} + 1}} $$

(22)

Defining the characteristic pressure of a micro-channel gas flow as $P_{{\mathrm{c}}} = \mu \sqrt {3RT} /h$, one can rewrite Eq. (23) as follows:

$$ \frac{{\dot{M}^{D} }}{{\dot{M}^{T} }} = \frac{1}{{\left( {\frac{P}{{P_{{\mathrm{c}}} }}} \right)^{2} + 1}} $$

(23)

The above final equation is a universal relation between the local diffusive mass flow rate and the normalized local pressure. It varies in the flow direction, and it is lowest at the micro-channel exit.

Utilizing the derived analytical solutions, one can understand why the deviation between the mass flow rates, obtained from the extended Navier–Stokes equations and the classical theory, decreases as $P_{\text{in}} /P_{\text{out}}$ is increased. The reason is that the increase in the pressure ratio $P_{\text{in}} /P_{\text{out}}$ reduces the deviation between the measured and predicted mass flow rates. This behavior can be explained by Eq. (23). Namely, a significant deviation from the classical theory appears at lower pressure ratios for a given inlet pressure $P_{\text{in}}$, because the diffusion effect is proportional to the term ln ($P_{\text{in}} /P_{\text{out}} )$. The order of the magnitude of this term is comparable to that of $\left( {P_{\text{in}} /P_{\text{out}} } \right)^{2}$ only for smaller pressure ratios. This implies that diffusion is only effective for the micro-channel flows if the pressure P is small and the pressure ratio $P_{\text{in}} /P_{\text{out}}$ between the inlet and outlet is also small.

The relation expressed by Eq. (23) is shown in Fig. 3. In this diagram, the ranges of the experimental data of Maurer et al. [4], Arkilic et al. [2] and Colin et al. [13] are shown. Comparing the ranges makes clear, why Maurer et al. [4] showed the higher “micro-channel effect” in their measured mass flow rates.

Fig. 3

Ratio of the diffusive mass flow rate to the total mass flow rate versus ratio of the pressure to the characteristic pressure with ranges of the experimental data of (I) Maurer et al. [4], (II) Arkilic et al. [2] and (III) Colin et al. [13]

It is interesting that the derived analytical solution of the flow through micro-channels also provides the explanations of other experimental findings available in the literature. Hence, the analytically derived results are very useful to fully understand experimental findings for micro-channel flows available in the literature. To measure typical “micro-channel effects,” the pressure range of experiments should be chosen to lie close to the characteristic pressure of the experimental setup, as the data of Maurer et al. [4] show.

The authors show through their analytical work that micro-channel flows do not require Maxwell’s molecular reflection model to be applied to yield good theoretical solutions for micro-channel flows. The present results can even be used to deduce the ratio of discrete and diffusive reflection employed by Maxwell. Hence, the provided analytical treatment can be employed to yield a deeper insight into the physics of micro-channel flows.

From the provided analytical treatment of micro-channel flows, a characteristic pressure resulted, $P_{{\mathrm{c}}} = \mu \sqrt {3 RT} /h$ that allows the experimental conditions to be chosen:

$$ P_{\text{in}} \gtrsim P_{{\mathrm{c}}} \gtrsim P_{\text{out}} $$

(24)

This means that the channel height should be chosen as follows, to get easy measurable “micro-channel effects”:

$$ h = \frac{\mu }{{P_{{\mathrm{c}}} }}\sqrt {3 RT} \to \quad {\text{with}}\quad P_{\text{out}} \lesssim P_{{\mathrm{c}}} $$

(25)

Taking into account that experimental pressure can be achieved to set $P_{{\mathrm{c}}} \approx 500\,{\text{Pa}}$, one can deduce from Eq. (25) that $h\lesssim 20\,\upmu{\text{m}}$. For $P_{{\mathrm{c}}} \approx 1000$, $P_{\text{out}} = 10\,{\text{mbar}}$, the size h is $10\,\upmu{\text{m}}$. Channels with very small dimensions must be chosen to measure the higher mass flows in micro-channels reported in the literature. This can be seen by comparing the results of the investigations by Maurer et al. [4] with those of Arkilic et al. [2] and Collin et al. [13]. This comparison led to pressure range information shown in Fig. 3.

Similar to the derivations in this paper for micro-channel flows, treatments of micro-capillary flows yield similar results.

Pressure Gradient Versus Wall Reflection Effects

It is well known that the so-called micro-channel flow effects, of the kind measured by Maurer et al. [4], exist already at flow length scales much larger than the molecular length scale of the employed gases. In spite of this, most theoretical treatments of micro-channel flows employ methods of rarefied gas flows to treat micro-channel flows, e.g., see Karniadakis et al. [6] for a good summary of this kind of work. In other flow cases of this kind, theoretical treatments are still carried out, using continuum-based equations (see Durst and co-workers). To overcome this discrepancy between physical facts and methods of theoretical treatments of micro-channel flows, some publications refer to small scale hydromechanics as the method to treat these flows, e.g., see Karniadakis et al. [6], Hadjiconstantinou [8], Gad-el-Hak [14]. In this paper and in previous publications of the authors Durst et al. [10], Dongari et al. [15], Sambasivam and Durst [11], it was claimed that the “micro-channel flow effect” was caused by the pressure gradient and the related “pressure diffusion”-driven mass flux in micro-channels. The small dimensions of the channels cause high velocity gradients in the cross-flow directions and correspondingly resulting high viscous forces, and these give rise to high pressure gradients in the flow direction. The latter cause an “additional mass flow” due to diffusion that is constant over the channel cross section and acts like a wall-slip flow. The pressure-driven diffusion is not of importance in most flows, since the diffusion term is small in comparison with the convection term in the Navier–Stokes equations. As shown in the previous sections, the derivation does not require the theoretical treatments based on Maxwell-like wall reflections. It is sufficient to solve the “Extended Basic Equations of Fluid Mechanics” taking mass diffusion into account, also see refs. Durst et al. [10], Sambasivam and Durst [11] to yield agreement with corresponding mass flux measurements.

The derivations of Durst et al. [10] suggest that pressure gradient-driven mass flow rates, that are remarkable in comparison with “convectively driven” values, occur not only in micro-channels, but in all isothermal flows with high pressure gradients. If high temperature gradients exist, a mass transport term due to the temperature gradients comes also into play. In isothermal micro-channel flows, high velocity gradients are caused by the small dimensions of the channels in the cross-flow direction. The cause of high pressure gradients, in the flow directions, to drive the flow in supersonic flows, similarly high pressure gradients can be caused by both high pressure and small dimensions, e.g., consider the pressure gradients across a plane shock wave. Hence, if the conventional basic equations of fluid mechanics are employed to solve the shock wave flow problem, deviations to the real flow through shock waves arise. This is indicated in Fig. 4 below, showing experimental density-results [Rho_Expt] across a shock wave in comparison with corresponding computational results using the conventional Navier–Stokes equations. Results are also obtained by numerically solving the extended Navier–Stokes equations [Rho_EFME] and simulation using EFME [RHO_MBNSE]. Hence, shock waves in gas flows require the “Extended Basic Equations of Fluid Mechanics” to be employed for their correct theoretical treatments.

Fig. 4

Comparison of experimental and computational results of the pressure variation across a shock wave

It was found by Greenshields and Reese [12], who numerically investigated shock wave flows that they had to add into their continuity equation a diffusive mass flow term to get converged numerical solutions for their investigation of shock wave flows. To remove the discrepancy of the numerical results in Fig. 4, i.e., between DSMB and Navier–Stokes solutions. The mass diffusion terms, see Eq. (9), was needed to get any sensible results of shock wave computations. The last author of this paper treated the shock wave flow by solving the extended flow equation, see Sambasivam [16]. The results obtained in this way are given in Figs. 4 and 5. From these figures, it can be seen clearly that good agreement between the computational results of Sambasivam [16] and DSMS-results is obtained. Hence, the extended Navier–Stokes equations need to be solved to get good agreement between experimental data and corresponding theoretical results.

Fig. 5

Results of the solution of extended flow equations agree well with experiments for shock flows

The above considerations show that the discrepancy between experimental findings and theoretical treatments for micro-channel flows is not a particularly micro-channel phenomenon. It is not caused by features of rarified gas flows in small channels. The discrepancies come from a “defect of the basic equations of fluid mechanics,” when applied in their conventional form to flows with high pressure or/and high temperature gradients, e.g., see Eq. (9). These basic equations need to be extended to take mass diffusion into account in the continuity equation. This introduced mass diffusion term also yields additional transport terms in the momentum and the energy equations. Introducing all these terms, differential equations result for the total velocity $U_{{\dot{i}}}^{T} = U_{i}^{c} + U_{i}^{D}$, consisting of the convection and the diffusion velocity, e.g., see Eqs. (1)–(4). The diffusion velocity turns up as slip velocity in micro-channel flows, as said above.

There is an additional conclusion to be drawn from the present work. Rarified gas flow treatments of micro-channel flows, considering two ways of molecular wall reflections, should be in very close agreement with the results presented in this paper. To investigate this, the extended work of Sharipov and Seleznev [7] was taken into account by the present authors. In Ref. [7], Sharipova nd Seleznev presented a study of rarified gas flows in various regimes of micro-channel flows, including the free molecular regime. Using the BGK-model to treat the molecular motion, Shapirov and Seleznev [7] derived for the mass flow rate in a micro-channel, under isothermal flow conditions and exposed to a given pressure gradient, the mass flow rate can be computed as:

$$ \dot{M}_{ch} = \left( {\frac{m}{2\pi k}} \right)^{1/2} W\left[ {\frac{{P_{\text{in}} - P_{\text{out}} }}{\sqrt T }} \right]; $$

(26)

where in this equation:$\dot{M} =$ mass flow rate of the gas molecules (helium atoms for Maurer’s data), $k =$ Boltzmann constant, $P_{\text{in}} =$ Inlet pressure, $P_{\text{out}} =$ Outlet pressure, $T =$ Temperature (isothermal case), $W =$ transmission probability.

The transmission probability $W$ can be calculated analytically, based on the principles of diffuse and discrete scattering and was given by Shapirov and Seleznev [7]:

$$ W = \frac{1}{2}\left[ {1 + \left( {1 + L^{2} } \right)^{1/2} - L} \right] - \frac{{1,5 \left\{ {L - \ln \left[ {L + \left( {1 + L^{2} } \right)^{1/2} } \right]} \right\}^{2} }}{{L^{3} + 3 L^{2} + 4 - \left( {L^{2} + 4} \right)\left( {1 + L^{2} } \right)^{1/2} }}; $$

(27)

where $x = L/\left( {2h} \right)$, i.e., ratio of channel length to channel height. Here, $x = 7837$ and, hence, the transmission probability comes out to be as low as $W = 0.00115$. Using this value for $W$ and calculating the mass flow rate by Eq. (26) yields the results given in Fig. 6.

Fig. 6

Mass flow rate vs. P_avg*ΔP using ENSE, FMP and experimental data of Maurer et al. [4]

The above figure suggests that Eq. (26) yields, for small values of $\left( {P_{\text{in}}^{2} - P_{\text{out}}^{2} } \right) = \left( {P_{\text{in}} - P_{\text{out}} } \right)\left( {P_{\text{in}} - P_{\text{out}} } \right)$ too high values for the computed mass flow rate in micro-channels. If one changes the $W$ value to $W = 0.004$, the computed mass flow rate, using Eq. (26), results in the data presented in Fig. 7. These show very good agreement with the authors’ results, for low values of $\left( {P_{\text{in}}^{2} - P_{\text{out}}^{2} } \right)$. However, in the region where Maurer’s data lie, the rarified gas considerations yield too high values for the computed mass flow rates.

Fig. 7

Replot of data in Fig. 6, but FMP-Data plotted for W = 0.0004

The data in Fig. 7 show also that the authors’ analytical results show good agreement with the experimental findings. This readily suggests that micro-channel flows should be treated by the “Extended Basic Equations of Fluid Mechanics” rather than rarified gas flow equations. This is also suggested by the findings that “micro-channel flow effects” occur already at flow length scales much larger than corresponding molecular length scales.

The EFME-results plotted in Fig. 7 suggest that the conventional Navier–Stokes equations describe two-dimensional channel flows for the range $\left( {P_{\text{in}}^{2} - P_{\text{out}}^{2} } \right) \ge 5$. The application of the extended Navier–Stokes equations allows these continuum equations to be successfully applied down to the pressure difference region to be applied where the RGT-Rarified Gas Theory starts to yield good results for micro-channel flows.

Last, but not least, the present authors would like to stress that the “Extended Basic Equations of Fluid Mechanics” also allow micro-channel flows to be numerical treated that have arbitrary channel geometrics. This was successfully demonstrated by Sambasivam et al. [17], who obtained numerically the results shown in Table 2 and in Fig. 8 below:

Table 2 Summary of experimental conditions used in the published literature for the case of micro-channel with a backward facing step

Fig. 8

Comparison of local Mach number along the streamwise distance at different cross-stream locations; inlet Mach number 0.45; outlet Knudsen number 0.018; channel height 1.25 µm. The symbols represent the simulation data of Beskok [18], and the lines show the results obtained with extended Navier–Stokes equations, through numerical predictions

Comparisons of the results Table 2 and in Fig. 8 show that the results of numerical computations, using the extended Navier–Stokes equations, yield good agreement with the DSMC results of Beskok [18] and Celik and Edis [19]. Hence, the EFME can be applied to micro-channel flows of arbitrary geometries and for different flow situations. This is considered to be a great advantage to study flows as they occur in MEMS-channels. The lay-out of such channels can therefore be based on numerical flow prediction using CFD-methods for EFME.

Conclusions, Final Remarks and Outlook

The present paper stresses that the “Conventional Basic Equations of Fluid Mechanics” are only applicable to fluid flows when mass diffusion, driven by pressure and temperature gradients, is negligible in comparison with convection see Durst [20]. This is not the case for micro-channel flows, and this is the reason why there exist discrepancies between the predicted and measured mass flow rates in such channels. Taking mass diffusion into account yields the “Extended Basic Equations of Fluid Mechanics.” These equations allow numerical and analytical solution to micro-channel flows that agree well with corresponding experimental data. This is shown in Figs. 1 and 2.

Some publications claim that the validity of the Navier–Stokes equations breaks down when applied to micro-channel flows. Hence, continuum-based equations become invalid for such flows, in spite of the fact that characteristic length scales of the flow are still much larger than the characteristic length sales of the molecular motion. The present paper shows that the considered continuum equations—the conventional continuity and the Navier–Stokes equations—miss the mass diffusion term. If this is added, i.e., if the “Extended Basic Equation of Fluid Mechanics” are employed, the continuum-based equations hold and yield correct solutions for micro-channel flows. This means that solutions based on the Extended Equation of fluid mechanics can be applied to micro-channel flows, as length scale considerations suggest. Good agreements with experimental results are obtained.

The present paper also suggests that the observed discrepancy between experimental results of the mass flow rate through micro-channels is due to the high pressure gradients occurring in the mass diffusion equation:

$$ \dot{m}_{i}^{D} = - \rho D\left[ {\frac{1}{P}\frac{\partial P}{{\partial x_{1} }} - \frac{1}{2T}\frac{\partial T}{{\partial x_{2} }}} \right] $$

(28)

It is not the small dimension of micro-channels that yield the discrepancies between experimental and theoretical results, but the occurring pressure gradients. Hence, differences between experimental results and corresponding theoretical findings of flows with high pressure (and temperature) gradients can also be eliminated by employment of the EFME. This has been demonstrated for flows with shock waves, e.g., see Fig. 5.

Last, but not least, the “Extended Basic Equations of Fluid Mechanics” can also be applied to micro-channel flows with strong temperature gradients in the flow direction. If applied, they will yield good agreement with the experimentally obtained mass flow rates driven by pressure and temperature gradients. Indirectly, this is demonstrated by the results in Fig. 8, showing high Mach-number flow results and their agreement with DSMG-data. This figure also demonstrates that theoretical treatments of flows by the EFME allow the treatment of micro-channel flows of arbitrary geometries.

When the present publication was already written, the paper by A. Jaishankar and G. H. McKinley was mentioned to the authors, entitled: “An exact analytical solution to the extended Navier–Stokes equations using the Lambert W function”, see ref. [21].

In this paper, the micro-channel flow was also treated by the extended Navier–Stokes equations and, in the conclusions, the authors pointed out that the extended Navier–Stokes equations cover a large range of flows. Their diagram is presented as Fig. 9. This diagram summarizes nicely the findings the authors obtained by re-visiting methods of treatment of micro-channel flows.

Fig. 9

The different flow regimes for micro-channel gas flows [21]