Galerkin Analysis of Effect of Dead Load on Natural Frequencies of Box Beam

Abstract

Based on Hamilton’s principle, a nonlinear differential equation considering the effect of dead loads is formulated for box beams. By using Galerkin method, the effect of dead load on the natural frequencies of box beams with various restraint conditions being simply supported, fixed at both ends, cantilevered and fixed at one end and simply supported at the other end is studied. The effects of major physical parameters, including the magnitude of dead load, sectional inertia moment and inertia radius, span length, and restraint conditions are discussed, and the natural frequencies are presented for these box beams, with the nonlinear effect of dead load taken into account. The results show that the deterrent effect of dead loads has significant effect on the increase of the natural frequencies of box beams. It is further observed that this behavior is more apparent at lower-order natural frequencies; the varying deterrent effect of dead loads relates to the stiffness of structures and is more significant for more flexible structures.

Introduction

In general, engineering structures and components are mostly subjected to a combination of constant initial loads and variable additional loads [1]. The combination of these loads can be considered as live loads and is found to have significant effect on the sustainability and durability of the structures. When the structure bears these live loads, its deformation starts from the reference state of constant initial loads that mainly contain the initial stress which causes the subsequent deformation. The stress generated by constant initial load will produce deterrent effect, which will change the internal force and deformation of the structure under live loads. The deterrent effect is not only caused by the initial middle surface tension, but also induced by the initial bending. Brunelle [2] demonstrates the effect caused on structures due to the influence of initial middle surface tension. However, studies regarding the effect due to initial bending are found scarce. The stiffening effect caused by the initial bending stress of dead load is called dead load effect according to Takabatake [3].

Takabatake [3] considered the effects of dead loads on the static characteristics of beam for the first time and derived the static force differential equation of uniform beam under dead loads. He also studied the response under the dead loads of simply supported beam and clamped–clamped beam in addition. He reported the effect of dead loads on the dynamic characteristics of beams and plates [4, 5]. Zhou and Zhu [6,7,8,9] analyzed the effect of dead loads on the natural frequencies of beams and plates by means of finite element method. Zhang et al. [10,11,12,13,14,15] have studied the influence of dead loads effect on static and dynamic characteristics of arch beams. At this end, most of the studies and their findings are primarily based on solid beam. However, these studies did not involve the impact on the thin-walled box structures.

In this paper, the effect of dead loads on the thin-walled boxes structure is analyzed. A nonlinear differential equation considering the effect of dead loads is formulated for box beams, based on Hamilton’s principle. By using Galerkin method, the effect of dead load on the natural frequencies of box beams with various restraint conditions being simply supported, fixed at both ends, cantilevered and fixed at one end and simply supported at the other end. The effects of key physical parameters mainly, magnitude of dead load, sectional inertia moment and inertia radius, span length, and restraint conditions are subsequently discussed as a function of natural frequencies by taking into account the nonlinear effect of dead load.

Establishment of Differential Equation

Basic Assumption

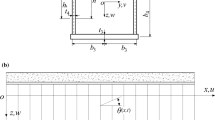
The cross section and coordinate system which are used for deriving basic are shown in Figs. 1 and 2. Figure 2 represents the formula and force–deformation conditions of the beam when $\hat{v}$ represents the deflection of beam under dead loads ($\hat{p}$); $\bar{v}$ represents the deflection of beam under live loads ($\bar{p}$). The deflection state of beam under dead loads is used as the reference state, and $\bar{v}$ is derived from this reference state.

Fig. 1

Cross section

Fig. 2

Coordinate system and loads distribution

At the assumption of the deformation of beam obeying the hypothesis of Bernoulli–Euler beam equation,the linear strain–displacement relationship can be written as [16],

$$\varepsilon_{x} = - yv^{\prime\prime}$$

(1)

where top slab

$$\varepsilon_{xu} = h_{u} v^{\prime\prime}$$

(2)

Bottom slab

$$\varepsilon_{xb} = - h_{b} v^{\prime\prime}$$

(3)

Web slab

$$\varepsilon_{xw} = - yv^{\prime\prime}$$

(4)

The nonlinear strain–displacement relationship can be written as

$$\varepsilon_{x} = - yv^{\prime\prime} + \frac{1}{2}\left( {v^{\prime}} \right)^{2}$$

(5)

where top slab

$$\varepsilon_{xu} = h_{u} v^{\prime\prime} + \frac{1}{2}\left( {v^{\prime}} \right)^{2}$$

(6)

Bottom slab

$$\varepsilon_{xb} = - h_{b} v^{\prime\prime} + \frac{1}{2}\left( {v^{\prime}} \right)^{2}$$

(7)

Web slab

$$\varepsilon_{xw} = - yv^{\prime\prime} + \frac{1}{2}\left( {v^{\prime}} \right)^{2}$$

(8)

where ε_x is the strain of beam; v is the deflection of beam.

Total Energy Expression

The strain energy under live loads can be written as

$$U = \hat{U} + \bar{U}$$

(9)

where $\hat{U}$ is the strain energy under dead loads ($\hat{p}$); $\bar{U}$ is the strain energy under live loads ($\bar{p}$),

$$\bar{U} = \frac{1}{2}\iiint_{V} {\bar{\sigma }_{x} }\bar{\varepsilon }_{x} {\text{d}}V$$

(10)

$$\hat{U} = \iiint_{V} {\hat{\sigma }_{x} \bar{\varepsilon }_{x} {\text{d}}V}$$

(11)

where the positive stress $\left( {\hat{\sigma }_{x} ,\bar{\sigma }_{x} } \right)$ is the bending normal stress produced by dead loads ($\hat{p}$) and live loads ($\bar{p}$), respectively. It should be noted that the direct stress $\left( {\hat{\sigma }_{x} } \right)$ is a constant stress caused by dead loads, but the direct strain $\left( {\bar{\varepsilon }_{x} } \right)$ is a strain caused by live loads. The linear strain–displacement relationship provided by Eq. (1) is used for the calculation of $\bar{U}$. The nonlinear strain–displacement relationship provided by Eq. (5) is used for the calculation of $\hat{U}$. It should be noted that the dead load’s effect of this part is the deterrent effect caused by both the middle surface tension of beam and the bending state stress of dead loads $\left( {\hat{\sigma }_{x} } \right)$. It is assumed that the stress–strain relation is linear.

$$\bar{\sigma }_{x} = E\bar{\varepsilon }_{x}$$

(12)

$$\hat{\sigma }_{x} = E\hat{\varepsilon }_{x}$$

(13)

All the strain energy caused by live loads ($\bar{p}$) can be expressed as follows:

The strain energy of top slab

$$\bar{U}_{u} = \frac{1}{2}\iiint_{V} {\bar{\sigma }_{xu} }\bar{\varepsilon }_{xu} {\text{d}}V = \frac{1}{2}\iiint_{V} {E\left( { - h_{u} v\prime\prime} \right)^{2} }{\text{d}}V = \frac{1}{2}\int_{0}^{L} {\iint_{A} {Eh_{u}^{2} v^{\prime\prime2} }{\text{d}}A{\text{d}}x} = \frac{1}{2}\int_{0}^{L} {EI_{su} } v^{\prime\prime2} {\text{d}}x$$

(14)

The strain energy of bottom slab

$$\bar{U}_{b} = \frac{1}{2}\int_{0}^{L} {EI_{bu} \bar{v}^{\prime\prime2} {\text{d}}x}$$

(15)

The strain energy of web slab

$$\bar{U}_{w} = \frac{1}{2}\int_{0}^{L} {EI_{w} } \bar{v}^{\prime\prime2} {\text{d}}x$$

(16)

So, the strain energy caused by live loads ($\bar{p}$) can be written as

$$\bar{U} = \bar{U}_{u} + \bar{U}_{b} + \bar{U}_{w} = \frac{1}{2}\int_{0}^{L} {E\left( {I_{su} + I_{bu} + I_{w} } \right)} \bar{v}^{\prime\prime2} {\text{d}}x = \frac{1}{2}\int_{0}^{L} {EI} \bar{v}^{\prime\prime2} {\text{d}}x$$

(17)

All kinds of strain energy caused by dead loads ($\hat{p}$) can be expressed as follows:

The strain energy of top slab

$$\begin{aligned} \hat{U}_{u} &= \iiint_{V} {\hat{\sigma }_{x} \bar{\varepsilon }_{x} {\text{d}}V} \\ &= \iiint_{V} {E\left( {h_{u} \hat{v}^{\prime\prime} + \frac{1}{2}\hat{v}^{\prime2} } \right)\left( {h_{u} \bar{v}^{\prime\prime} + \frac{1}{2}\bar{v}^{\prime2} } \right)}{\text{d}}V \\ &= \int_{0}^{L} {\iint_{A} E\left( {h_{u}^{2} \hat{v}^{\prime\prime} \bar{v}^{\prime\prime} + \frac{1}{2}h_{u} \hat{v}^{\prime\prime} \bar{v}^{\prime2} + h_{u} \hat{v}^{\prime2} \bar{v}^{\prime\prime} + \frac{1}{4}\hat{v}^{\prime2} \bar{v}^{\prime2} } \right){\text{d}}z{\text{d}}y{\text{d}}x} \\ &= \int_{0}^{L} {E\left[ {I_{su} \hat{v}^{\prime\prime} \bar{v}^{\prime\prime} - \frac{1}{2}S_{su} \hat{v}^{\prime\prime} \bar{v}^{\prime2} - \frac{1}{2}S_{su}^{prime} \hat{v}^{\prime2} \bar{v}^{\prime\prime} + \frac{{A_{su} }}{4}\hat{v}^{\prime2} \bar{v}^{\prime2} } \right]} {\text{d}}x \\ \end{aligned}$$

(18)

The strain energy of bottom slab

$$\hat{U}_{b} = \int_{0}^{L} {E\left[ {I_{sb} \hat{v}^{\prime\prime} \bar{v}^{\prime\prime} - \frac{1}{2}S_{sb} \hat{v}^{\prime\prime} \bar{v}^{\prime2} - \frac{1}{2}S_{sb} \hat{v}^{\prime2} \bar{v}^{\prime\prime} + \frac{{A_{sb} }}{4}\hat{v}^{\prime2} \bar{v}^{\prime2} } \right]} {\text{d}}x$$

(19)

The strain energy of web slab

$$\begin{aligned} \hat{U}_{w} &= \iiint_{V} {E\left( { - y\hat{v}^{\prime\prime} + \frac{1}{2}\hat{v}^{\prime2} } \right)\left( { - y\bar{v}^{\prime\prime} + \frac{1}{2}\bar{v}^{\prime2} } \right)}{\text{d}}V \\ &= \iiint_{V} {E\left( {y^{2} \hat{v}^{\prime\prime} \bar{v}^{\prime\prime} - \frac{1}{2}y\hat{v}^{\prime\prime} \bar{v}^{\prime2} - \frac{1}{2}y\hat{v}^{\prime2} \bar{v}^{\prime\prime} + \frac{1}{4}\hat{v}^{\prime2} \bar{v}^{\prime2} } \right){\text{d}}V} \\ &= \int_{0}^{l} {\iint_{A} {\left[ {Ey^{2} \left( {\hat{v}^{\prime\prime} \bar{v}^{\prime\prime} } \right) - Ey\left( {\frac{1}{2}\hat{v}^{\prime\prime} \bar{v}^{\prime2} + \frac{1}{2}\hat{v}^{\prime2} \bar{v}^{\prime\prime} } \right) + \frac{1}{4}\hat{v}^{\prime2} \bar{v}^{\prime2} } \right]{\text{d}}z{\text{d}}y{\text{d}}x}} \\ &= \int_{0}^{L} {E\left[ {I_{w} \hat{v}^{\prime\prime} \bar{v}^{\prime\prime} - \frac{1}{2}S_{w} \left( {\hat{v}^{\prime\prime} \bar{v}^{\prime2} + \hat{v}^{\prime2} \bar{v}^{\prime\prime} } \right) + \frac{{A_{w} }}{4}\hat{v}^{\prime2} \bar{v}^{\prime2} } \right]} {\text{d}}x \\ \end{aligned}$$

(20)

So, the strain energy caused by live loads ($\hat{p}$) can be given as

$$\begin{aligned} \hat{U} = \hat{U}_{u} + \hat{U}_{b} + \hat{U}_{w} \\ = \int_{0}^{L} {E\left[ {\left( {I_{su} + I_{sb} + I_{w} } \right)\hat{v}^{\prime\prime} \bar{v}^{\prime\prime} - \frac{1}{2}\left( {S_{su} + S_{sb} + S_{w} } \right)\hat{v}^{\prime\prime} \bar{v}^{\prime2} } \right.} - \frac{1}{2}\left( {S_{su} + S_{sb} + S_{w} } \right)\hat{v}^{\prime2} \bar{v}^{\prime\prime} \left. { + \frac{1}{4}\left( {A_{su} + A_{sb} + A_{w} } \right)\hat{v}^{\prime2} \bar{v}^{\prime2} } \right]{\text{d}}x \\ = \int_{0}^{L} {\left[ {EI\hat{v}^{\prime\prime} \bar{v}^{\prime\prime} + \frac{{EA_{w} }}{4}\hat{v}^{\prime2} \bar{v}^{\prime2} } \right]} {\text{d}}x \\ \end{aligned}$$

(21)

The total strain energy of the box beam becomes

$$U = \bar{U} + \hat{U} = \int_{0}^{l} {\left[ {\frac{1}{2}EI\left( {\bar{v}^{\prime\prime} } \right)^{2} + \frac{EA}{4}\left( {\hat{v}^{prime} } \right)^{2} \left( {\bar{v}^{\prime}} \right)^{2} + EI\hat{v}^{\prime\prime} \bar{v}^{\prime\prime} } \right]{\text{d}}x}$$

(22)

The potential energy of external loads is

$$V = - \int_{0}^{l} {\left( {\bar{p} + \hat{p}} \right)\bar{v}{\text{d}}x}$$

(23)

With the effect of rotational inertia neglected, the kinetic energy of beam can be expressed as follows:

$$T = - \int_{0}^{l} {\frac{\rho A}{2}\left( {\dot{\bar{w}}} \right)^{2} {\text{d}}x}$$

(24)

Controlling Differential Equation

According to Hamilton’s principle, as an object move from a location at the time (t₁) to another location at the time (t₂), to all the distance the object may experience, the distance follows Newton’s law at every moment is the distance makes the value of Lagrangian function average on time become the extreme value [16, 17] ,

$$\delta I = \delta \int_{{t_{1} }}^{{t_{2} }} {\left( {T - U - V} \right){\text{d}}t} = 0$$

(25)

Substituting Eqs. (22), (23), (24) into Eq. (25) gives

$$\begin{aligned} \delta I & = \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\left\{ {\rho A\ddot{\bar{v}} + EI\bar{v}^{\prime\prime\prime\prime} - \frac{EA}{2}\left[ {\left( {\hat{v}^{\prime} } \right)^{2} \bar{v}^{\prime} } \right]^{\prime} + EI\hat{v}^{\prime\prime\prime\prime} - \left( {\bar{p} + \hat{p}} \right)} \right\}\delta v{\text{d}}x{\text{d}}t} } \\ & \quad + \int_{{t_{1} }}^{{t_{2} }} {\left. {\left( {EI\bar{v}^{\prime\prime} + EI\hat{v}^{\prime\prime} } \right)\delta v^{\prime} } \right|_{0}^{L} {\text{d}}t} + \int_{{t_{1} }}^{{t_{2} }} {\left. {\left[ { - EI\bar{v}^{\prime\prime\prime} - EI\hat{v}^{\prime\prime\prime} + \frac{EA}{2}\left( {\hat{v}^{\prime} } \right)^{2} \bar{v}^{\prime} } \right]\delta \bar{v}} \right|_{0}^{L} {\text{d}}t} \\ & = 0 \\ \end{aligned}$$

(26)

where, as the beam is subjected to dead loads, one can get the following equation,

$$EI\hat{v}^{\prime\prime\prime\prime} - \hat{p} = 0$$

(27)

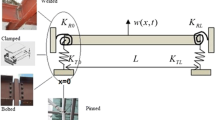
The boundary conditions are that,

$$\begin{aligned} \hat{v} = 0 \, , \, or\;\hat{v}^{\prime} = 0,\quad x = 0,L; \hfill \\ \hat{v}^{\prime\prime} = 0 \, ,or\;\hat{v}^{\prime\prime\prime} = 0,\quad x = 0,L. \hfill \\ \end{aligned}$$

(28)

In Eq. (26), considering the effect of dead loads on bending deformation, the control differential equation of the beam can be written as

$$\rho A\ddot{\bar{v}} + EI\bar{v}^{\prime\prime\prime\prime} - \frac{EA}{2}\left[ {\left( {\hat{v}^{\prime} } \right)^{2} \bar{v}} \right]^{\prime} = \bar{p}$$

(29)

The boundary conditions are that

$$\left\{ {\begin{array}{*{20}l} {\bar{v} = 0, \, or\; \bar{v}^{\prime} = 0,x = 0,L \, ;} \hfill \\ {\bar{v}^{\prime\prime} = 0,or\; EI\bar{v}^{\prime\prime\prime} - \frac{EA}{2}\left( {\hat{v}^{\prime}} \right)^{2} \bar{v}^{\prime} = 0, \, x = 0,L \, .} \hfill \\ \end{array} } \right.$$

(30)

The Solution of Differential Equation

Considering the effect of dead loads, controlling Eq. (29) can be modified as

$$\rho A\ddot{\bar{v}} + EI\bar{v}^{\prime\prime\prime\prime} - \frac{EA}{2}\left[ {\left( {\hat{v}^{\prime}} \right)^{2} \bar{v}} \right]^{\prime } = \bar{p}$$

(31)

The boundary conditions are

$$\left\{ {\begin{array}{*{20}l} {\bar{v} = 0, \, or \; \bar{v}^{\prime} = 0, \, x = 0,L;} \hfill \\ {\bar{v}^{\prime\prime} = 0,or\; EI\bar{v}^{\prime\prime\prime} - \frac{EA}{2}\left( {\hat{v}^{\prime}} \right)^{2} \bar{v}^{\prime} = 0 \, , \, x = 0,L.} \hfill \\ \end{array} } \right.$$

(32)

The displacement ($\bar{v}$) can be expressed as

$$\bar{v}\left( {x,t} \right) = \bar{\varPsi }\left( x \right)\varPhi \left( t \right)$$

(33)

Substituting Eq. (33) into Eq. (31) gives

$$\bar{\varPsi }^{\prime\prime\prime\prime} - \frac{1}{{2r^{2} }}\left[ {2\hat{v}^{\prime}\hat{v}^{\prime\prime} \bar{\varPsi }^{\prime} + \left( {\hat{v}} \right)^{2} \bar{\varPsi }^{\prime\prime} } \right] = k^{4} \bar{\varPsi }$$

(34)

$$\ddot{\varPhi }\left( t \right) + \omega^{2} \varPhi \left( t \right) = 0$$

(35)

Among them,

$$k^{2} = \omega \sqrt {{{\rho A} \mathord{\left/ {\vphantom {{\rho A} {EI}}} \right. \kern-0pt} {EI}}}$$

(36)

Define the parameter $\bar{v}$ as

$$\bar{\varPsi }\left( x \right) = \bar{\varPsi }_{n} f_{n} \left( x \right);\;\left( {n = 1,2,3, \ldots \infty } \right)$$

(37)

Among them, the definition of f_n is defined as follows:

For simply supported box beam,

$$f_{n} = \sin \frac{n\pi x}{L}$$

(38)

For box beam fixed at both ends,

$$f_{n} = \sin \frac{\pi x}{L}\sin \frac{n\pi x}{L}$$

(39)

For cantilevered box beam,

$$f_{n} = 1 - \cos \frac{{\left( {2n - 1} \right)\pi x}}{2L}$$

(40)

For box beam fixed at one end and simply supported at the other end,

$$f_{n} = \left[ {1 - \cos \frac{{\left( {2n - 1} \right)\pi x}}{L}} \right]\sin \frac{\pi x}{L}$$

(41)

By using Galerkin method, the controlling differential equation for the effect of bending deformation on the natural frequencies of beam can be expressed as

$$\int_{0}^{L} {Q\delta \bar{\varPsi }{\text{d}}x = 0}$$

(42)

$$\delta \bar{\varPsi }_{n} : { }\sum\limits_{m = 1} {\bar{\varPsi }_{m} \left( {A_{mn} - k^{4} B_{mn} } \right)} = 0$$

(43)

As the effect of initial bending deformation is considered, the natural frequencies of beam should be

$$\omega_{i} = k_{i}^{2} \sqrt {{{EI} \mathord{\left/ {\vphantom {{EI} {\rho A}}} \right. \kern-0pt} {\rho A}}} ;\;\left( {n = 1,2,3, \ldots \infty } \right)$$

(44)

Without considering the effect of initial bending deformation, the natural frequencies of beam are

$$\omega_{0n} = k_{0n}^{2} \sqrt {{{EI} \mathord{\left/ {\vphantom {{EI} {\rho A}}} \right. \kern-0pt} {\rho A}}} ;\;\left( {n = 1,2,3, \ldots \infty } \right)$$

(45)

Among them, the parameter k_0n is defined as follows:

For simply supported box beam,

$$k_{0n}^{2} = \left( {{{n\pi } \mathord{\left/ {\vphantom {{n\pi } L}} \right. \kern-0pt} L}} \right)^{2}$$

(46)

For box beam fixed at both ends,

$$\cos \left( {k_{0n} L} \right)\cosh \left( {k_{0n} L} \right) = 1$$

(47)

For cantilevered box beam,

$$\cos \left( {k_{0n} L} \right)\cosh \left( {k_{0n} L} \right) = - 1$$

(48)

For box beam fixed at one end and simply supported at the other end,

$$\tan \left( {k_{0n} L} \right) = \, \tanh \left( {k_{0n} L} \right)$$

(49)

Example and Analysis

The following parameters are adopted for the beam: E = 210 GPa; I₀ = 2.5 × 10⁻⁴ m⁴; L₀ = 8 m, A₀ = 0.01 m² (the reference value of gyration radius is that: $r_{0} = \sqrt {I_{0} /A_{0} } = 0.158\;{\text{m}}$). The dead load intensity is assumed to be: $\hat{p}_{0} = 6.8\;{\text{kN}}/{\text{m}}$. The variables ($\hat{p}$, l, I, r) can be expressed as follows: $\hat{p} = \alpha_{{\hat{p}}} \hat{p}_{0}$, $l = \alpha_{l} l_{0}$, I = α_II₀, r = α_rr₀. The numerical results change by the above parameters.

The effect of initial bending deformation on the natural frequencies of simple box beam is analyzed. So, in the following expression, ω_i represents the circular frequencies of the ith vibration mode effected by initial bending deformation. ω_i0 represents the circular frequencies of the ith vibration mode without the effect of initial bending deformation. $\hat{p}_{0}$ represents a reference dead load per unit length of the beams. $\hat{p}$ represents the practical value of initial load per unit length of the beams. Dimensionless form of coordinate, linear coordinate and logarithmic coordinate are adopted, respectively, for the lateral axis ($\bar{p}_{0} /\hat{p}$), while linear coordinate is used for the vertical axis $\left( {\Delta = \left( {\omega_{i} - \omega_{i0} } \right)/\omega_{i0} \times 100\% } \right)$.

The relationship between the natural frequencies of the box beam and the change of initial load is shown in Fig. 3. It’s evident that natural frequencies of simple box beams have improved with increase loads. Further, the improvement is more obvious for the first natural frequency. Here the increase of natural frequencies should be regarded as a real increase of the natural frequencies produced by initial load stress. It is different from the natural frequencies those vary with the normal change of beam quality (m) at unit length [3].

Fig. 3

Relationship between Δ and $\bar{p}_{0} /\hat{p}$ with various constraint conditions

Figures 4, 5 and 6 show the relationship between ∆ (affected by the change of sectional inertia moment α_I, span length α_L and gyration radius α_r, respectively) and $\bar{p}_{0} /\hat{p}$ (affected by different constraint conditions). Among them, the gyration radius changes under the condition that the area changes and the sectional inertia moment keep constant. Figure 7 shows comparison of effects of initial loads when the above parameters (α_I, α_L and α_r) of simply supported beam changes. It is demonstrated that the smaller the sectional inertia moment or the gyration radius (the area changes and the sectional inertia moment keeps constant) is or the larger the span length is, the larger effect of dead loads on the natural frequencies of beam will be. Among them, the change of span length makes the largest effect.

Fig. 4

Relationship between Δ and $\bar{p}_{0} /\hat{p}$ for various α_I and constraint conditions

Fig. 5

Relationship between Δ and $\bar{p}_{0} /\hat{p}$ for various α_L and constraint conditions

Fig. 6

Relationship between Δ and $\bar{p}_{0} /\hat{p}$ for various α_r and constraint conditions

Fig. 7

Relationships between varying deterrent effect and $\bar{p}_{0} /\hat{p}$

Conclusion

This paper analyzes the effect of dead loads on the thin-walled box structures. A nonlinear differential equation considering the effect of dead loads is taken into account for formulating box beam model, based on Hamilton’s principle. By using Galerkin method, the effect of dead load on the natural frequencies of various box beams, with various restraint conditions being simply supported, fixed at both ends, cantilevered and fixed at one end and simply supported at the other end. The effects of key physical parameters, including the magnitude of dead load, sectional inertia moment and inertia radius, span length, and restraint conditions are discussed, and the natural frequencies are presented for these box beams, with the nonlinear effect of dead load is taken into account.

The following conclusions can be drawn:

• 1. The bending deformation generated by dead loads will produce deterrent effect which causes an increase of the natural frequencies of box beam. This trend will get more obvious when the natural frequencies belong to a lower-order range or larger weight.

• 2. The stiffness of box beam has an impact on the deterrent effect which caused by the initial bending deformation. It is concluded that more flexible structures which have a smaller sectional inertia moment, a larger span length or a lower gyration radius, the effect becomes more significant. Among them, the change of span length makes the largest effect.