Introduction

The last decade has witnessed a wonderful development in the field of power electronics and magnetic materials that have led to vast improvements in electromagnetic devices, which in turn, have led to development of smart structures. The smart devices are now being effectively deployed as vibration dampers in the suspension systems to enhance the ride comfort, road handling and safety. Fischer and Isermann [1] have shown how each part in a vehicle suspension plays a role in ride comfort in dynamic model. Lin and Kanellakopoulos [2] have shown that a system can have dual purpose of comfort and safety. Xu [3] has shown how the vibrations can effect the life of various components in a mechanism. Though advantageous in the above aspects, the electromagnetic dampers have lesser reliability because of dependence on external power source and higher weight [4, 5]. It has been reported that hybrid dampers using passive dampers such as hydraulic/eddy current dampers in conjunction with electromagnetic dampers is a better solution in this regard. In this study a combination of hydraulic damper and electromagnetic damper is used in a hybrid damping device which has been modeled. The damping values are optimized and the frequency response and energy balance are studied for its practical usage.

Modeling

Electromagnetic System

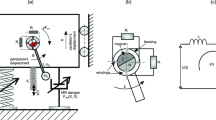
The block diagram of a hybrid electromagnetic single wheel suspension system is shown in Fig. 1. In this hybrid system an electromagnetic linear actuator is used, which has energy harvesting capability. The electromagnetic damper consists of a fixed stator and a movable slider. In the stator the windings are integrated into metal cylinder. The slider component utilizes permanent magnets that are screwed to an aluminum rod via iron spacers. The regenerative magnet converts the vibration of the body mass into useful electrical energy. The electromagnetic damper converts the relative motion between the slider and stator into electromotive force (emf) induced in coils which in turn causes an opposing force which causes a viscous damping effect. This effect depends on the velocity of the mover.

Fig. 1
figure 1

Block diagram of a hybrid electromagnetic suspension system for a quarter car

Full size image

General Formulation

  • In the dynamic mode ED acts as motor which operates the activation of stator coils. The maximum current density distribution along the stator is obtained by

    $$ {\text{K}}_{\text{sp}} = \frac{{{\text{N}}_{\text{c}} \lambda_{\text{c}} {\text{N}}}}{{\tau {\text{p}}}}{\hat{\text{I}}} $$
    (1)

  • The stator winding currents cause a reaction flux density that effects the PMs. The flux density is given by

    $$ \varDelta {\text{B}}_{\text{m}} = \frac{16}{{\pi_{{}}^{3} }}\frac{{{\text{K}}_{\text{sp}} \tau }}{{\left( {\left( {2lm + 2s} \right)_{{}}^{2} - \left( {4s_{{}}^{2} } \right)} \right)\left( {4{\text{Rgap}} + {\text{Rmag}}} \right)}} $$
    (2)

The minimum magnetic flux density in PM must be higher than a minimum value to avoid irreversible demagnetization [6].

  • Another important aspect is the winding temperature which limits the electric loading. The copper losses (PCU) calculated by thermal analysis is given by

    $$ {\text{P}}_{\text{CU}} = \frac{{\pi p^{2} \tau^{2} }}{{\sigma N_{c} }}\frac{{(D + {\text{l}}_{\text{m}} + 2{\text{s}})}}{{\lambda {\text{c}}^{3} S_{\text{CA}} }} $$
    (3)

  • The maximum force developed by the Electro Magnetic damper can be calculated by

    $$ {\text{F}} = 4{\text{p }}\left( {{\text{l}}_{\text{m}} + {\text{s}} + {\text{g}}} \right){\text{ B}}_{\text{g}} {\text{K}}_{\text{sp}} \tau \sin \frac{\pi }{2}\frac{{(\tau - \tau_{\text{m}} )}}{r} $$
    (4)

After optimization for the maximum force per weight for various lm/D and δw/hc values, the EM damper has been designed to produce a maximum damping coefficient equal to 9,000 Ns/m. The maximum power generation is expected to be about 320 W for each damper and maximum force achievable can be about 1,200 N. The passive hydraulic damper which is used in conjunction with the EM damper has damping coefficient of 2,000 Ns/m.

Analytical Model

In this section the electromagnetic suspension system (EMS) is modeled in a quarter car model and its system was discussed. EMS consists of an EMD and a coil spring. The Electromagnetic suspension model was shown in Fig. 2. In order to identify an inertial inertia Iz and heavier weight of EMD due to mechanical damper, a suspension mount is considered. The system is considered to be of 3 DOF system and the equations are as follows.

Fig. 2
figure 2

3 DOF quarter-car model

Full size image
$$ {\text{m}}_{\text{s}} \textit{\"{x}} + {\text{k}}_{ 2} \left( {{\text{x}}_{\text{s}} - {\text{x}}_{\text{u}} } \right) + {\text{k}}_{ 3} \left( {{\text{x}}_{\text{s}} - {\text{x}}_{\text{r}} } \right) \, + {\text{c}}_{ 3} (\dot{x}_{\text{s}} - \dot{x}_{\text{r}} ) = 0 $$
(5)
$$ {\text{m}}_{\text{r}} \textit{\"{x}}_{\text{r}} - {\text{k}}_{ 3} \left( {x_{\text{s}} - x_{\text{r}} } \right) - {\text{c}}_{ 3} (\dot{x}_{\text{s}} - \dot{x}_{\text{r}} ) = {\text{f}}_{\text{d}} $$
(6)
$$ {\text{m}}_{\text{u}} \textit{\"{x}}_{\text{u}} - {\text{k}}_{ 2} \left( {{\text{x}}_{\text{s}} - {\text{x}}_{\text{u}} } \right) + {\text{k}}_{ 1} \left( {{\text{x}}_{\text{u}} - {\text{x}}_{0} } \right) \, + {\text{c}}_{ 3} (\dot{x}_{\text{u}} - \dot{x}_{0} ) = {\text{f}}_{\text{d}} $$
(7)

Several studies propose different controlled suspensions in order to minimize acceleration of the mass [7, 8].The objective of these studies is to reduce the acceleration of the mass to ensure the comfort of the passengers. In our experiment a proportional integral differential (PID) with feed back on measure of acceleration was used. In the present system the current of the motor in the system has to follow the required output force uref by PI controller [9]. The required output force, reference signal for control output force is calculated as follows.

$$ {\text{u}}_{\text{ref}} = - {\text{ C}}_{\text{s}} \dot{x}_{\text{s}} - {\text{ C}}_{\text{g}} \dot{x}_{\text{u}} $$
(8)

Cs and Cs are feed back gains from the sprung and un-sprung mass respectively. The positive feedback gain of spring mass velocity means the skyhook damper for isolation and negative feedback gain of sprung mass means the ground hook damper for the road holding.

Energy Consumption

In order to validate the modeling of EMS, the energy consumption of EMS is introduced and the capability of regenerating energy of EMS is evaluated. Energy consumed by EMD will be normally the external power supply in the system which is a product of current and voltage.

$$ \varepsilon = {\text{i v }} = \frac{{u_{{}}^{2} }}{{C_{eq} }} + {\text{u}}\dot{z} $$
(9)

where,

$$ {\text{C}}_{\text{eq}} = \frac{{\phi_{2} }}{R} $$
(10)

ε can be assumed to be a combination of regeneration and consumption terms after considering the following assumptions.

  1. (a)

    The control input is equal to the reference signal u − uref.

  2. (b)

    The velocity of mass of the rod is equal to that of the sprung mass.

The control input is given as

$$ {\text{U}} = - \left( {{\text{C}}_{\text{s}} + {\text{C}}_{\text{g}} } \right) + {\text{C}}_{\text{z}} \dot{z} $$
(11)

where, stroke speed \( \dot{z} = \dot{x}_{\text{s}} - \dot{x}_{\text{u}} \)

Substituting in Eq. 9 the energy consumption can be given by

$$ \varepsilon = \frac{{\left( {{\text{C}}_{\text{s }} + {\text{C}}_{\text{g}} } \right)^{2} }}{{{\text{C}}_{\text{eq}} }}\dot{x}_{s} ^{2} - \frac{{\left( {{\text{C}}_{\text{s }} + {\text{C}}_{\text{g}} } \right)^{2} }}{{{\text{C}}_{\text{eq}} }}\left( {{\text{C}}_{\text{eq}} + 2 {\text{C}}_{\text{g}} } \right)\dot{x}_{s} \dot{z} + \frac{{{\text{C}}_{\text{g}} }}{{{\text{C}}_{\text{eq}} }}\left( {{\text{C}}_{\text{eq}} + {\text{C}}_{\text{g}} } \right)\dot{z}_{{}}^{2} $$
(12)

First term relates to the consumption of energy for reducing vibrations of spring mass. The second term depends on both gain setting and phase relation between the spring mass velocity and stroke speed. The third term is regenerative energy feedback gain of un-sprung mass velocity and should be defined in the range of −Ceq ≤ Cg < 0 for system stability.

Experimental Setup

Description

The experiments are performed on a drop test bench which consists of a static part and dynamic part. Two columns and a base make up the static part. The mobile part consists of the quarter part of a vehicle (wheel suspension, sprung mass, un-sprung mass and the upper system. A ball bearing runner ensures the guide of the mobile part and impact in vertical direction. The maximum admissible height is set to 0.4 m. Acceleration are set in each mass. Speeds and displacements are determined by numerical integration. A force transducer between the shock absorber and sprung mass measures force transmitted. A linear inductive displacement transducer gives the stroke of the suspension.

Simulation and Analysis

Magnification factor and transmissibility are normally the two important criteria for the ride comfort of the passengers in a vehicle. To improve them and the effectiveness and reliability of the damping system in this experimentation, we are using a hybrid system which is a combination of active damper EMD and a passive damper i.e., a hydraulic system. An experimental and theoretical coupled approach has been developed. A parametric study through simulation has been made. The theoretical approach has been tested on experimental setup. Initially the shock absorber is subjected to small bounce equivalent to a condition of safety for a car riding on bumpy road. After several simulations the damping coefficient is so chosen that the suspension is softer and guarantee to minimize the bounce.

  • ms = 275 kg

  • mu = 24.5 kg

  • mr = 5.2 kg

  • k1 = 1,50,000 N/m

  • k2 = 16,000 N/m

  • k3 = 32,000 N/m

  • c3 = 2,000 Ns/m

The following Fig. 3 is the result of simulation. The simulation is done by considering the body as a linear model and also a multi body system. The phase shift between the two may be due to the frictional force taken into consideration in multi body model. The first peak depends on the characteristics of the suspension and the second peak depends on the stiffness of the tyre. Important oscillations of upper sprung mass generate stress in the frame and lead to deterioration and discomfort. Excitation force is transmitted through the suspension, thus, to control the dynamic behavior of the suspension allows us to minimize the oscillation of the mass.

Fig. 3
figure 3

Excitation force on sprung mass—analytical model

Full size image

In a passive system, the upper system can be made more rigid by adding stiffeners. Normally a suspension is defined by stiffness and damping. In order to simplify the system and to distinguish the influence of each parameter, various physical parameters are dissociated. In this regard, as mentioned earlier, a combination of varying damping co-efficient of hydraulic damper and input parameters of EM were studied. The results obtained for different configurations are shown in the Figs. 4 and 5. Out of these configurations, it can be seen that configuration (4) shows more satisfying results. They led to a variation in approximately 15–20 % of the peak of acceleration. The damping parameters are modified to optimize dissipation of energy. Optimization is based on displacement and damping force. The increase in stroke represents dissipation of damping force.

Fig. 4
figure 4

Optimization—measured stroke

Full size image
Fig. 5
figure 5

Optimization—measured acceleration

Full size image

Analysis of the results

The simulations under passive, active and hybrid systems are shown in Fig. 6. There has been substantial decrease of 15–20 % in the acceleration when a PID controller is used. Hence the primary requirement of maximum stability and the passive hydraulic shock absorber dissipating the energy is achieved. Simultaneously the active EMD is effectively producing the opposing force in the desired direction. The passive device may not absorb a lot of energy but is effective in case of failure of the EMD and the stability of the system is thus ensured. The controller is composed of two steps. The first step consists of determining the target control force from measures on drop test bench via feedback controllers which are previously designed and exposed in this paper. The second step consists of calculating the supply current of proportional servo valve. In order to determine it, an inverse model of proportional servo valve was developed. In fact, the inverse model calculates supply current corresponding to desired target control force. In the following, we present results of experiments of hybrid system for a given input speed. The PID controller with minimization of acceleration of the upper sprung mass (ms) is chosen in order to determine the target control force [10]. Moreover, the controller starts only at the impact of the system on the ground. The impact is detected according to a condition on the amplitude of the stroke of the suspension. As soon as the stroke of the suspension is positive, the system lands.

Fig. 6
figure 6

Acceleration of sprung mass: comparison between different systems

Full size image

Further, the simulation results and experimentation results are compared with frequency response function (FRF) of quarter car model, FRF of active EMD and also frequency characteristics of energy balance between energy consumption and regeneration.

With the impact of the given level, the FRFs of sprung mass acceleration are calculated in terms of isolation of sprung mass, ride comfort and road holding stability respectively and are shown in Fig. 7. The results of passive suspension model is also shown. The simulation results are in good agreement with the experimental results up to the resonance frequency of the sprung mass. In addition it is shown that EMD is capable of fully damping the resonance mode of sprung mass.

Fig. 7
figure 7

Transfer characteristics of the sprung mass acceleration

Full size image

In a similar way, the FRF of EMD force is calculated as shown in Fig. 8. The sprung and unsprung mass velocity feedback gains are represented in the damping ratio expression as ξs = 1.5 and ξg = 0.45. The profiles of the magnitudes of frequency are similar even though there is variation in the amplitudes between both results around the resonance frequency. This may be caused by the difference of frequency characteristics of PI controller.

Fig. 8
figure 8

Transfer characteristics of the output force

Full size image

The spectra of energy balance of the simulation and experiment is shown in Fig. 9. The feedback gains of sprung and unsprung mass are ξs = 1.5 and ξg = 0.45. Energy is consumed to isolate the vibration of sprung mass below 2 Hz. Naturally there is a maximum of consumed energy at the resonance frequency of the sprung mass. Above 2 Hz the energy is regenerated. The experimental results are in good agreement with the simulation values, showing the validation of the EMS in terms of energy balance as well.

Fig. 9
figure 9

Spectrum of energy balance

Full size image

Conclusions

Here an analytical model was designed in order to understand damping phenomenon in hybrid damper. Then cross checking of modeling from measurement on drop test bench has been done, leading to good prediction of dynamic behavior of real system. Following this, an original method of minimization of vibrations using mechanical coupling has been developed and experimentally validated. This method based on experimental and theoretical coupled approach, consists in design a characteristic damping law of shock absorber dealing with optimization of the dissipation of energy. This one gives a reduction of 15 % on first peak of acceleration of upper sprung mass. Finally, different anti vibratory active methods of control have been designed and have been analyzed from numerical simulations. Using mechanical coupling, a sliding mode controller has proved its efficacy in order to minimize the acceleration of an upper sprung mass system located on an equivalent quarter part of vehicle system. In fact, a reduction of 20–30 % on first peak of acceleration has been predicted. This control force must be reachable by a dynamical tuning of the damping coefficient of the hydraulic shock absorber. Thus, a hybrid device has been designed. Hybrid device using PID controller with minimization of acceleration of mass as generator of target control force, is experimented. This device is experimented on drop test bench and results are compared to optimal passive device. A decrease of 20 % on first peak of acceleration of upper sprung mass has been obtained. Further there is an agreement of both the frequency response properties and the energy balance between simulation and experiments. Thus the vibration isolation and regeneration ability of a hybrid damper are demonstrated using the vibration tests.