Scaling Effect on the Behaviour and Design of Prestressed Stayed Steel Columns

Abstract

This study presents the results of a small-scale experimental campaign on prestressed stayed steel columns, subsequent numerical model validation and design guideline development. The majority of previous experimental studies have focused on large-scale systems, which are expensive and can be difficult to perform due to the required specialised experimental set-up, whereas small-scale experiments are less restrictive with both space and experimental set-up requirements. Also, existing design guidelines were developed from a single system scale, so have not been shown to be applicable to changes in geometric scale. Thus, the scaling effect on prestressed stayed steel columns was investigated to promote the use of small-scale experiments in the study of large-scale prestressed stayed steel column systems and update design guidelines for change in geometric scale. A total of 17 prestressed stayed steel columns and a control column with no cross-arms were tested. These tests investigated the symmetric and antisymmetric buckling behaviour as well as the interactive post-buckling phenomenon. These tests were designed to investigate the scaling effect on the behaviour of the system and to determine the optimal prestress level of prestressed stayed steel columns close to the transition point. A numerical model was also validated by the experimental results to perform a full geometric scaling comparison study and update existing design guidelines. It was found that small-scale structures are capable of representing the behaviour of large-scale prestressed stayed steel columns. Furthermore, it was shown that the highest efficiency in terms of the weight of materials is found close to the transition point between symmetric and antisymmetric buckling behaviour. Various scale systems were modelled numerically, and the results compared with existing guidelines, which resulted in low levels of accuracy. Therefore, existing design guidelines were updated using the validated numerical model and shown to yield more accurate results for the L/400 and L/200 imperfection levels.

Introduction

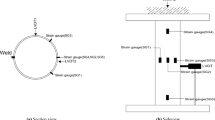
A major issue with the use of slender steel columns is the reduction in load-carrying capacity due to buckling instability. A system to improve the load-carrying capacity of steel columns that inhibits the instability through the addition of cross-arms and prestressed stays is commonly known as a prestressed stayed steel column. These systems, shown in Fig. 1, typically have load-carrying capacities several times that of unstayed columns as the prestressing force provides restraint against lateral instability. Examples of the usage of prestressed stayed columns in the construction industry include at Chiswick Park in London where they are used to support an overhanging shading structure and Algarve stadium in Portugal, where they are used to support the stadium roof with further examples highlighted by [1].

Fig. 1

Prestressed stayed steel column with applied axial load P, length of column and cross-arm L and a respectively

Prestressed stayed steel columns have two distinct buckling modes; symmetric (Fig. 2a) and antisymmetric (Fig. 2b) which take the form of a half sine wave and a full sine wave, respectively, while an interactive post-buckling shape can result from a combination of the distinct modes (Fig. 2c). Interactive post-buckling is an important phenomenon that is primarily triggered close to the transition point of symmetric and antisymmetric modes: i.e. critical loads of symmetric and antisymmetric buckling modes are similar in magnitude.

Fig. 2

Buckling modes of prestressed stayed columns; a symmetric, b antisymmetric and c Interactive

Investigations on prestressed stayed steel columns have been carried out since the 1960s [2]. Several experimental studies have been carried out on full-scale prestressed stayed steel column systems with symmetric critical modes [3–8]. Studies investigating the behaviour of small-scale prestressed stayed steel columns with symmetric critical modes have been carried out by [9] and [10]. However, no investigation has been carried out on the effect of the specimen scale on the observed behaviour of these structures. Furthermore, only one previous experimental study has investigated the antisymmetric/interactive post-buckling behaviour of these systems [11]. Though, the sensitivity of the system to prestress at the transition point was not studied. An analytical study by [12] showed that the greatest efficiency in terms of weight of materials for prestressed stayed steel columns can be obtained close to the transition point, highlighting the importance of understanding how these systems behave in this region. Previous numerical studies [13–16] have highlighted the prestress which yields the highest load-carrying capacity for prestressed stayed steel columns with varying cross-arm lengths, though this has not been done experimentally for systems close to the transition point. Therefore, this study aims to investigate the optimal prestress level for prestressed stayed steel column configurations close to the transition point through the use of small-scale experiments. The ability to use small-scale experiments to accurately capture the behaviour of large-scale prestressed stayed steel columns will also be investigated.

The previous researchers [17] developed design guidelines to determine the load carrying capacity of systems with various prestress levels. However, these design guidelines were developed from results of a full-scale experimental campaign and haven’t been shown to be applicable to stayed columns in other geometric scales. Therefore, this study will also attempt to investigate the suitability of existing guidelines for the design of stayed columns at varying geometric scales.

Material Testing

Stay System Testing

Testing was performed to obtain the material properties of the cable stay system. The cable stay system was made up of a mini rigging screw to apply the prestress, ferrules and thimble eyes to connect the cable, a load cell to measure the cable tension, eye nuts to connect to the load cell and a quick link. In the cable system, the galvanised steel wire made up approximately 50% of the total length. The tested system is shown in Fig. 3, the cable is made up of 3 mm 7 × 7 strand galvanised steel wire rope with the cross section shown in Fig. 4.

Fig. 3

Cable system used in the cable tests and column tests

Fig. 4

Cross-section profile of the 3 mm galvanised steel wire rope

The cable system was tested in a 10kN Hounsfield uniaxial testing machine, in tension. This allowed key material properties such as the Young’s modulus and the breaking load of the cable system to be established. The cable system was tested according to the guidelines in [18]: if Young’s modulus of the material is less than 150GPa then the stress rate of the tensile test should be between 2 MPa/s and 20 MPa/s. The equivalent displacement rate was calculated using the approximate Young’s modulus from the material suppliers and chosen in between the two limits. This allowed the stiffness of the cable system to be determined from the stress–strain curve obtained from the test. Figure 5 depicts the stress–strain behaviour of the cable system from the tensile tests of 34 specimens.

Fig. 5

Stress–strain curves of the stay system tests

From the stress–strain curve of the cable systems, the behaviour is seen to be approximately linear until failure, exhibiting brittle fracture. The average stiffness is calculated from the slope, up to 2% strain, with the average being 40.9 GPa and standard deviation 1.3GPa. As predicted by [19], the Young’s modulus of the cable system is significantly lower than that of conventional mild steel due to the construction of the wire inducing contact forces between individual strands. It should be stated that throughout the main tests the cable system was not stressed past 50% of its failure load.

Column and Cross-Arm Testing

To obtain the material properties for the column and cross-arm material, tensile coupon tests were performed according to [18] and the gauge length was obtained, using Eq. (1).

$${\text{Gauge length}} = 5.65\sqrt {A_{{\text{c}}} }$$

(1)

where A_c is the area of the cross section. The method adopted by [11] was utilised for these tests, where a section of the material was removed from either side of the coupon specimen to ensure failure occurred within this region. The length of the milled section was just longer than the gauge length to allow the extensometer to grip the milled section. Half gauge lengths were lightly scribed on the milled section to ensure fracture occurred within the gauge length. Also, rod adapters were placed in the ends of the specimen to allow connection to the machine jaws, shown in Fig. 6, the adapters were then connected directly to the testing machine and coupon with pins through either end of the adapters.

Fig. 6

Column material test coupon specimen with adapters

An Instron 4483 150kN load frame was used to perform the material tests, with an Instron 2620–601 dynamic clip-on extensometer used to measure the extension of the gauge length. This extensometer is capable of measuring travel up to 5 mm, giving it a maximum strain reading of 40%, thus it was used throughout the tests up to failure. A Squirrel 2010 data logger was used to store the load and extension values throughout the test. Based on the recommendations in [18], the stress rate was kept within the limits of 6–60 MPa/s for materials with Young’s modulus greater than 150GPa. Thus, the rate of separation of the cross-heads was set at 0.125 mm/min throughout the test, meaning that fracture occurred after about 40 min. A total of 30 coupon specimens were tested for the column material to obtain statistical data for a future reliability study, with 3 coupon specimens tested for the cross-arm material to obtain the mean material property values. Mean and standard deviation values of the material properties are presented in Table 1, with the test set-up shown in Fig. 7. Stress–strain curves of the column and cross-arm tests are shown in Fig. 8; these values are similar to those found from a previous study by [11].

Table 1 Material properties of the column and cross-arm obtained through tensile testing. Where E is Young’s modulus, σ_y is the Yield stress taken as the 0.2% proof stress, σ_u is the ultimate stress, ε_u is the percentage strain at the ultimate stress and ε_f is the percentage strain at fracture

Fig. 7

Set-up of the column tensile coupon test

Fig. 8

Typical stress–strain curves for a column and b cross-arm coupon tests

Prestressed Stayed Steel Column Testing

The main prestressed stayed steel column testing consisted of one unstayed control column and 17 prestressed stayed steel columns. Of these, five were designed to demonstrate antisymmetric buckling, six to demonstrate symmetric buckling and six were around the transition point to investigate interactive behaviour. These were scaled down from a previous study [11], with the column length of 1 m chosen due to the maximum capacity of the testing machine. This is consistent with other previous small-scale experiments that have tested systems of similar scale ([9, 10]). Comparison of several system configurations with different buckling modes and prestress levels was done to verify the scaling method.

Preparation of Specimens

The prestressed stayed steel column system included a one-metre section of the column material with the cross-arms welded directly onto the column face at mid-height at 90° intervals. Additionally, 5 mm thick flat endplates were added at either end of the column, parallel to each other. Connecting plates were also added to the endplates and cross-arms to accommodate the stays. The completed assembly is shown in Fig. 9.

Fig. 9

Assembled prestressed stayed steel column specimens

Initial Prestress

The initial prestress used for each test was decided according to the zone of behaviour to be studied. The zonal nature of prestressed stayed steel columns was first derived by [3] and is shown in Fig. 10. This highlights that if the prestress in the stays is less than T_min then there is no increase in critical buckling load from the Euler load. This is known as zone 1. If the stay prestress is between T_min and T_opt there is a linear increase in the critical buckling load (zone 2). T_opt is a theoretical value of prestress which gives the maximum critical buckling load, beyond which the prestress has a negative effect on the critical buckling load (zone 3). The prestressed stayed steel columns in this study have been designed to have prestress values in both zones 2 and 3 to investigate the effect on the post-buckling behaviour.

Fig. 10

Theoretical zonal behaviour of prestressed stayed steel columns, where N^C_max is the maximum critical buckling load of the column, N^C_min is the minimum critical buckling load or Euler load, T_min is the minimum prestress and T_opt is the optimum prestress

Measurement of Specimen Dimensions

Before testing, the key dimensions of the specimens were measured, including the average outer diameter of the main column, cross-arm and stays as well as initial imperfections. The diameter along the supplied lengths of steel tubes was measured to obtain a record of how the diameter changes along its length. Thicknesses were also measured at the ends of the column and cross-arm for three points around the perimeter to obtain an average, this was repeated once the tubes were cut to their final lengths. The column material was supplied in 6 m lengths and had an average outer diameter of 15.9 mm and wall thickness of 1.25 mm. The cross-arms were supplied in 5.8 m length and had an average outer diameter of 9.98 mm and a wall thickness of 1.06 mm. These sections were chosen to be class 1 according to [20] to avoid local buckling of the cross section before yielding.

Measurement of Initial Imperfections

Following assembly of the specimens, the initial out-of-straightness was measured before testing by using an approximate method. The specimens were laid flat on a workbench and the curvature of the main column traced onto the paper underneath and a straight line was then drawn connecting the ends of the curve. Distances between the straight line and the curve of the column were measured for various points along its length. This method yielded the approximate shape of the imperfections in the buckling plane before prestressing was applied. The imperfection shapes of all specimens had a roughly half sine wave shape. Imperfection amplitudes ranged from L/106 to L/426, owing to the relatively large initial curvature from transportation and handling of the main column material. This imperfection amplitude is in line with the specifications in British Standards for hot finished structural hollow sections of L/200 [21]. Key dimensions of the specimens are reported in Table 2, highlighting the imperfection amplitude at mid-height of each specimen and the zone of behaviour to be investigated.

Table 2 Measured dimensions for the experimental test specimens, where a is the cross-arm length, w₀ is the imperfection amplitude at mid-height and T is the initial prestress

Testing Procedure

The main compression tests of the prestressed stayed steel columns were performed using an INSTRON 250kN universal testing machine. Pinned end conditions were achieved using knife edges attached to the column ends, only allowing rotation in the plane of buckling. The knife edges added 80 mm to the total column length, making the buckling length 1080 mm. Four linear displacement sensors were used along the length of the column to measure the displacements at the quarter points and at 35 mm on either side of mid-height. Four strain gauges were used on either side of the column in the buckling plane at quarter height and at 25 mm on either side of the mid-height to check for yielding of the column. Load cells were also used in each of the eight stays to measure the change in prestress during the tests. All data channels were recorded using the SignalExpress computer software. The mid-height rotation was calculated from the linear displacement sensor readings. End shortening results from the tests were displacement values from the Instron controller and thus are not appropriate for validation purposes as they included slack in the system. Therefore, the initial part of the end-shortening curves is not linear. In hindsight, an LVDT should have been used to measure the true displacement of the column endpoint. The general test set-up can be seen in Fig. 11.

Fig. 11

General setup of prestressed stayed column tests

Cross-arm lengths were chosen to investigate a wide range of rotational stiffnesses such that the optimal configuration could be found. Also, the level of initial pretension was varied for each cross-arm length so that the optimal level of prestress of each configuration could be found. The labelling convention of the stays in the buckling plane used in the experimental campaign is shown in Fig. 12.

Fig. 12

Stay labelling convention used during the experiments

Control Column

The control column exhibited symmetric failure mode and the Euler load of the control column was adjusted to account for the initial imperfection according to Eq. (2) [22].

$$N_{{\text{C}}} = \frac{{P_{{{\text{cr}}}} }}{{\frac{{w_{0} }}{w} + 1}}$$

(2)

where N_C is the ultimate load of the column, P_cr is the Euler load, w₀ is the measured imperfection and w is the mid-height deflection at the ultimate load. The calculated ultimate load for the control column using Eq. (2) was 1.769kN which is about 3% higher than that obtained from the experiment (1.723kN) (Fig. 13).

Fig. 13

Force versus mid-height deflection of the control column

Main Tests

A total of 17 prestressed stayed column systems were tested, with varying cross-arm lengths and initial prestress values. These comprised: six specimens with symmetric critical modes, six around the transition point to demonstrate interactive behaviour and five with an antisymmetric critical mode. All stays were prestressed to the levels shown in Table 2, although only the in-plane stays were used to determine the buckling shape. The symmetric buckling mode was defined when the tension in stays 1 and 4 or 2 and 3 were equal, whereas an antisymmetric mode occurred when the stay tension in stays 1 and 3 or 2 and 4 were equal. Interactive behaviour appears when all four stay tensions are notably different. Yield points for each test were measured using the strain gauges to confirm an important assumption in previous numerical modelling that the columns remain in the elastic region until the ultimate load is reached. Therefore, these tests will attempt to verify this assumption by showing the yield point of each column. However, there was a failure of the strain gauges in tests C2 and C6 so the yield point was not measured. Furthermore, test C3 experienced a failure of one of the cable components at around the ultimate load as the thread was not fully tightened so the yield point was not observed. For the remainder of the tests, the yield point was shown to be after the ultimate load point, as seen in previous experimental studies [6, 11]. This verifies the assumption that the columns remain in the elastic region until after the ultimate load point for numerical modelling.

Symmetric Specimens C1-C3

Table 3 presents a summary of obtained results for specimens designed with symmetric buckling modes (C1-C3) while Figs. 14 and 15 show the force versus mid-height deflection and stay tension versus end shortening curves, respectively. It can be seen that the load-carrying capacity is roughly constant across different prestress levels. This is because the increase in load-carrying capacity due to the increase in prestress is being balanced by the effect of the resultant increase in initial imperfection. Also, the level of tension in the stays on the concave side of the column remains roughly the same throughout the test, resulting in symmetric buckling shapes. However, an interactive shape occurred after the ultimate load was achieved. This was caused by the main column reaching the yield point and the stay stresses being redistributed.

Table 3 Summary of results for specimens C1-C3, with ultimate load N_u, the ratio of ultimate load and the control column N_u/N_C, end shortening at ultimate load Δ_u and the first observed buckling mode

Fig. 14

Force versus mid-height deflection for specimens C1-C3

Fig. 15

Stay tension versus end shortening for specimens C1-C3

Symmetric Specimens C4-C6

Results for specimens C4-C6 are summarised in Table 4. Figures 16 and 17 show the force versus mid-height deflection and stay tension versus end shortening curves, respectively. Specimens C4-C6 had longer cross-arms than C1-C3, i.e. closer to the transition point and are used to show how the cross-arm length affects the post-buckling behaviour. For specimen C4, the stress in the stays on the concave side is roughly the same throughout the test, suggesting symmetric buckling mode. However, small differences are seen for specimens C5 and C6, suggesting interactive behaviour in these specimens. It should be noted for specimen C5 that the quick link in the stay on the convex side of the specimen was not tightened during the test, and the results from this test are ignored. The appearance of interactive behaviour leads to a significant reduction in the load-carrying capacity of specimen C6. The load-carrying capacity of the specimens varies with varying prestress levels, with the highest occurring for specimen C4 at 3.65 times higher than the control column. This is due to the imperfection of specimen C6 being double that of specimen C4, i.e. increase in prestress having no benefit on the load-carrying capacity as it is cancelled out by the effect of the initial imperfection. Also, an interactive shape occurred for specimen C6 which contributed to the reduction in ultimate load.

Table 4 Summary of results for specimens C4-C6, with ultimate load N_u, the ratio of ultimate load compared to the control column N_u/N_C, end shortening at ultimate load Δ_u and the first observed buckling mode

Fig. 16

Force versus mid-height deflection for specimens C4-C6

Fig. 17

Stay tension versus end shortening for specimens C4-C6

Symmetric/Interactive Specimens E1-E3

Results for specimens E1-E3 are summarised in Table 5. Figures 18 and 19 show the force versus mid-height rotation and stay tension versus end shortening curves, respectively. These specimens were designed to have a symmetric critical mode just before the transition point to determine whether these systems were the optimal configuration. For specimens E1-E3, the tension in the stays during loading suggests that the buckling shapes start as symmetric but become interactive soon after or just before the ultimate load. However, the stay tension plots suggest that specimen E1 remains in the symmetric mode for longer than E2 and E3. This suggests that an increase in prestress results in the interactive shape occurring sooner. Also, the occurrence of mid-height rotation of the column and all four stay tensions being different highlights the interactive nature of the post-buckling shapes. Load-carrying capacities of these specimens also appear to increase with increase in prestress, with a significant increase for specimen E3, suggesting that higher levels of prestress result in increased load carrying capacity for this configuration. This is consistent with previous studies [6, 11, 13,14,15,16, 23] in that the load-carrying capacity of prestressed stayed steel columns with symmetric critical modes increases with increase in prestress, with specimen E3 being 4.65 times higher than the control column.

Table 5 Summary of results for specimens E1-E3, with ultimate load N_u, the ratio of ultimate load compared to the control column N_u/N_C, end shortening at ultimate load Δ_u and the first observed buckling mode

Fig. 18

Force versus mid-height rotation for specimens E1-E3

Fig. 19

Stay tension versus end shortening for specimens E1-E3

Antisymmetric/Interactive Specimens E4-E6

Results for specimens E4-E6 are summarised in Table 6. Figures 20 and 21 show the force versus mid-height rotation and stay tension versus end shortening curves, respectively. These specimens were designed to observe the load carrying capacity of systems with an antisymmetric critical mode just beyond the transition point. For configurations E5-E6 it can be seen that the post-buckling shape is interactive almost immediately the load is applied, as the stay stresses are all distinctly different. Also, a mid-height rotation was recorded throughout the test. Changes in stay stress during loading for specimen E4 show that the column took the symmetric shape until around the ultimate load point, where an interactive shape occurred. Specimen E4 taking the symmetric shape appears to have increased the ultimate load significantly, as specimens E5-E6 exhibited interactive shape quicker, resulting in a much lower load carrying capacity. The results suggest that the load-carrying capacity is negatively affected by an increase in prestress, as the highest load-carrying capacity is recorded for configuration E4 at 5.15 times higher than the control. This also suggests that an increase in prestress increases the likelihood that these systems will take an interactive shape. The reduction in load-carrying capacity for higher prestress levels for prestressed stayed steel columns with an antisymmetric critical mode is similar to previous work [11, 13, 16], although it occurs for lower prestress levels in this study, with the maximum occurring for a prestress of 0.5T_opt.

Table 6 Summary of results for specimens E4-E6, with ultimate load N_u, the ratio of ultimate load compared to the control column N_u/N_C, end shortening at ultimate load Δ_u and the first observed buckling mode

Fig. 20

Force versus mid-height rotation for specimens E4-E6

Fig. 21

Stay tension versus end shortening for specimens E4-E6

Antisymmetric Specimens B1-B5

Results for specimens B1-B5 are summarised in Table 7. Figures 22 and 23 show force versus mid-height rotation and stay tension versus end shortening curves, respectively. These specimens were scaled down from a previous experimental study by the researchers [11] to demonstrate antisymmetric/interactive behaviour so that the effect of changes in geometric scale could be investigated. Test B2 was stopped prematurely as the Instron’s static break detector was still enabled, so the mid-height rotation results of B2 aren’t as high as the other tests. For the remainder of the tests, the static break detector was not used as the tests did not include any material failure. All tests gave a significant increase in load-carrying capacity over the control column. Specimen B4 gave the highest load-carrying capacity for a prestress around 1.73T_opt, with an increase in load-carrying capacity of 4.59 times the control column. This is also in part due to the initial imperfection of specimen B4 being significantly lower than the other specimens. Examining the stay stresses in Fig. 23 it can be seen that specimens B3-B5 exhibited an interactive post-buckling shape as the stay stresses are all significantly different. Specimens B1-B2 had lower levels of prestress so interactive behaviour occurred later in the tests. Also, the mid-height rotation for all five specimens further highlights the interactive behaviour of these specimens. It is also highlighted that the load-carrying capacity of prestressed stayed steel columns with an antisymmetric critical mode is negatively affected by an increase in prestress beyond a certain level. Obtained load carrying capacities are compared with results of the corresponding large-scale tests from the researches [11] in the scaling comparison section.

Table 7 Summary of results for specimens B1-B5, with ultimate load N_u, the ratio of ultimate load compared to the control column N_u/N_C, end shortening at ultimate load Δ_u and the first observed buckling mode

Fig. 22

Force versus mid-height rotation for specimens B1-B5

Fig. 23

Stay tension versus end shortening for specimens B1-B5

Post-Buckling Shapes

Typical images of failure modes observed during the experiments are presented in Fig. 24. Symmetric buckling shapes were observed for specimens C1-C6, similar to Fig. 24a. Symmetric shape was also observed for specimen E4 even though the critical mode was antisymmetric, this is expected to be caused by the large half sine wave initial imperfections. It has also been observed that the increase in prestress leads to the interactive mode occurring sooner. Antisymmetric buckling shapes were only observed at the very beginning of the tests on specimens B1-B5 as they quickly turned interactive, hence the small deflections seen in Fig. 24b. Interactive post-buckling as shown in Fig. 24c was seen in the majority of the specimens but was particularly pronounced for specimens E4-E6 and B1-B5 which had an antisymmetric critical mode.

Fig. 24

Post-buckling shapes seen during testing; a symmetric, b antisymmetric, c interactive

Analysis of Results

Symmetric Configurations C1-C6

Specimens C1-C6 which had symmetric critical modes maintained symmetric buckling shapes until after the ultimate load, where interactive post-buckling occurs. The interactive post-buckling shape occurred sooner for specimen C6 as the cross-arm length of this system is closer to the transition point, so the symmetric and antisymmetric critical loads are closer together. However, specimen C4 maintained the symmetric shape throughout the test, which was expected to be caused by the low level of initial prestress. Interactive behaviour was seen in some of these specimens after the yield point as the stresses in the column were redistributed.

Interactive Configurations E1-E6

Specimens E1-E3 were all designed to have symmetric critical modes and the symmetric buckling shape occurred initially but with a quick transition to an interactive post-buckling shape. Specimen E1 remained in the symmetric mode longer than the other specimens due to lower initial prestress. It should be noted that this phenomenon also occurred for specimens E4-E6 as an interactive shape occurred sooner for the specimens with higher prestress. The appearance of an interactive shape occurs as all four stay tensions begin to diverge and soon have different values. Specimens E1-E3 were designed to have symmetric critical load just below that of the antisymmetric, thus close to the transition point on the symmetric side. Interactive post-buckling is normally a phenomenon only seen in prestressed stayed steel columns with an antisymmetric critical mode or with symmetric critical mode beyond the ultimate load [11]. However, specimens E1-E3 show that specimens with symmetric critical modes can take an interactive shape before the ultimate load is reached. Although, it is unclear whether this was due to the amplitude of the imperfections, unintentional eccentricities in loading or other factors. Specimens E4-E6 were designed to have an antisymmetric critical load just below that of the symmetric mode. Accordingly, specimens E5-E6 took an interactive post-buckling shape almost immediately and remained interactive throughout the tests. However, specimen E4 appeared to take the symmetric shape until around the ultimate load point, resulting in an increase in load carrying capacity. It was initially thought that the configuration yielding the greatest load-carrying capacity would be one with symmetric critical mode just before the transition point to avoid interactive behaviour and gain maximum benefit from the cross-arms. However, it can be seen that the specimen yielding the greatest increase in load-carrying capacity is E4 which was designed to have an antisymmetric critical mode, although it took the symmetric shape.

Antisymmetric Configurations B1-B5

Specimens B1-B5 were designed to be scaled-down versions of the specimens with an antisymmetric critical mode tested in previous work [11] to investigate the scaling effect. As in the study by the researches [11], specimens B1-B5 all took an interactive post-buckling shape almost immediately, with the highest load-carrying capacity seen for specimen B4. Also, it should be noted that only specimen B5 had all four stays active at the ultimate load point due to the prestress being much larger than T_opt. Specimens B3 and B4 lost the prestress of one stay on the concave side at around the ultimate load due to the initial prestress being closer to T_opt. However, all four stays in specimens B3-B5 had significantly different stress values during loading suggesting an interactive mode. A full comparison of the relative load-carrying capacities of these tests compared to previous work will be carried out subsequently.

Efficiency

To assess the optimal configuration from the various systems tested, the load-carrying capacity of each system is non-dimensionalised by the sum of the weight of the column, cross-arms and stays. This results in an overall efficiency indicator which can be used to determine the most efficient system in terms of the weight of materials, shown in Table 8. It can be seen that the greatest efficiency is achieved for specimens E3 and E4. This highlights that prestressed stayed steel columns designed close to the transition point have optimal efficiency. Specimen E3 was designed with symmetric critical mode just before the transition point and a prestress level of 1.5T_opt. Specimen E4 was designed with an antisymmetric critical mode just lower than the symmetric and an initial prestress level of 0.5T_opt.

Table 8 Efficiency of each prestressed stayed steel column specimen in terms of the weight of materials

Scaling Comparison

As well as investigating the behaviour of prestressed stayed steel columns with various cross-arm lengths, the experiments were also designed to compare the results from this small-scale study to a previous full-scale experimental study. The experiments were based on scaled-down versions of the full-scale experimental study by the researchers [11]. This allowed a comparison of the results from the small-scale tests with corresponding systems from the full-scale study. The previous works  [11] focused on large-scale structures in order to demonstrate interactive behaviour. However, the interactive systems were only investigated with a single prestress level. Therefore, a key difference between this study and the work [11] is that the interactive systems were tested for multiple prestress levels to investigate how the behaviour changes as well as forming the basis of the scaling comparison study. A comparison of the load-carrying capacity of corresponding systems is shown in Table 9. This scaling comparison highlights that small-scale experiments can be used to investigate the behaviour of large-scale structures as the ratio of load-carrying capacities of the small-scale against the corresponding large-scale is fairly constant across all configurations, with an average value of 0.101, although small discrepancies between the various configurations occur due to differences in the initial prestress level and imperfection. Also, similar post-buckling shapes were observed between the small-scale and the corresponding large-scale systems.

Table 9 Scaling comparison of the ultimate load carrying capacities of corresponding configurations from this study and those of researches [11]

Numerical Modelling

Model Development

The numerical model was developed in the ABAQUS commercial software. Validation of the model was performed, based on the small-scale experimental results, before prestressed stayed columns with different geometrical scales were investigated. The same model formulation as that used in previous studies was utilised [13–16, 23–26]. The column and cross-arms were modelled using B32 beam elements, while the stay was modelled with a single T3D2 truss element. A convergence study was carried out to establish the optimum mesh size after which a 2 mm element size was chosen for both the column and cross-arm. As the stays are cables that go slack under compressive loading, the ‘no compression’ option was used to enable the stays to go slack when they lost their prestress. A buckling analysis was used to obtain the eigenmode shapes of the system which were subsequently used as initial imperfections in the Riks analysis [27].

Initial Imperfections

To induce the post-buckling behaviour in the Riks analysis, a combination of the first two buckling modes was used. Generally, a distinct symmetric imperfection is used to model systems with symmetric critical modes. However, in this experimental study, interactive behaviour was observed for all the specimens. The specimens designed with symmetric critical modes had symmetric buckling shapes initially but became interactive before or just after the ultimate load. Therefore, a combination of the first two buckling mode shapes was used in the models to induce an asymmetric post-buckling shape. To calculate the amplitude of each of the first two modes, the equation from the literature [16] was used (Eq. 3).

$$\mu_{1}^{2} + 4\mu_{2}^{2} = 1$$

(3)

where µ₁ is the imperfection coefficient for the symmetric mode and µ₂ is the imperfection coefficient for the antisymmetric mode. The imperfection level of each column was multiplied by µ₁ and µ₂ to obtain the imperfection amplitude of the symmetric and antisymmetric modes, respectively, to be used in the Riks post-buckling analysis.

Numerical Model Validation

A comparison of the load-carrying capacities and mid-height displacement/rotation of the experimental results and finite element (FE) model is shown in Table 10. Mid-height rotation results at ultimate load were compared for systems close to the transition point and systems with an antisymmetric critical mode as interactive behaviour dominated, whereas mid-height displacement results at ultimate load were used for systems with symmetric critical mode as they remained in the symmetric mode until around the ultimate load point. A mean ratio of FE to the experimental ultimate load of 0.98 and a standard deviation of 0.06 highlights the ability of the numerical model to capture the load-carrying capacity of the experiment tests. Furthermore, the mean and standard deviation of the ratios of the mid-height rotation and mid-height displacement results also show the FE model is capable of accurately modelling the load-deformation behaviour of prestressed stayed columns. Force versus mid-height displacement/rotation curves of specimens C4, E1 and B1 are shown in Figs. 25, 26 and 27, respectively. These highlight the effectiveness of the numerical model in capturing the behaviour of the specimens including the yield point. The numerical model was validated across all tests, including systems with symmetric buckling mode, antisymmetric buckling mode and those close to the transition point with interactive modes at various prestress levels. Thus, the numerical modelling has been shown to be suitably accurate in capturing the behaviour of various system configurations, validating the method.

Table 10 Comparison of the ultimate loads and mid-height displacement/rotation between the FE model and experimental values. Where N_u is the ultimate load, θ is the mid-height rotation, δ is the mid-height displacement and the subscripts ‘FE’ and ‘exp’ represent the FE model and experiment results respectively

Fig. 25

Comparison of the force versus mid-height displacement between the FE model and experimental results for specimen C4

Fig. 26

Comparison of force versus mid-height rotation obtained from the FE model and physical experiments for specimen E1

Fig. 27

Comparison of force versus mid-height rotation relationship obtained from the FE model and physical experiments for specimen B1

It can be deduced from Figs. 28, 29 and 30 that the numerical model is capable of capturing the deformed shapes of the experiments. The specimens with symmetric critical modes had symmetric shapes until around the ultimate load where an interactive shape occurred (Fig. 28). Specimens with an antisymmetric critical mode only took an antisymmetric shape at the very start of the tests, before an interactive shape occurred, hence the small displacements seen in Fig. 29. Specimens close to the transition point with symmetric critical modes had symmetric shape until they turned interactive soon after or just before the ultimate load (Fig. 30).

Fig. 28

Comparison of symmetric mode deformed shapes from FE model and experimental investigation

Fig. 29

Comparison of antisymmetric mode deformed shapes from FE model and experimental investigation

Fig. 30

Comparison of interactive mode deformed shapes from FE model and experimental investigation

Thus, the FE model has been shown to be capable of capturing the physical behaviour of the system, including the load-carrying capacity, load-deformation response, yield point and deformed shapes and will therefore be utilised in performing a full geometrical scale comparison of the prestressed stayed steel columns’ behaviour.

Geometric Scale Comparison

Following validation of the numerical model, an investigation into the scaling effect on the behaviour of prestressed stayed columns was carried out. This was done by investigating the behaviour of systems with varying geometric scale up to that in the previous works [11]. All other dimensions were scaled according to the ratio of the new column length and the full-scale column length. In order to focus on the scaling effect, the slenderness of the small-scale system was maintained irrespective of the geometric scale as well as the cross-arm length ratios, relative imperfection and prestress levels. Dimensions of the main columns for various geometric scales investigated are presented in Table 11.

Table 11 Dimensions and geometric scales of studied prestressed stayed columns, where the geometric scale is the length of each column L divided by the full-scale length L_f, d_o and d_i are the outer and inner dimensions of the main column respectively

The initial imperfection amplitude ratio was kept constant and the initial prestress for each system was kept to the same proportion of T_opt. The ratio of cross-arm to column length was also kept constant for each column scale to ensure an accurate comparison. All models used in the validation of the numerical model from Table 10 were scaled according to the ratios in Table 11. The maximum load-carrying capacity of each configuration was then non-dimensionalised by the load-carrying capacity of the corresponding full-scale system as shown in Fig. 31.

Fig. 31

Non-dimensional load-carrying capacity vs length ratio

The trend for the non-dimensional load-carrying capacity against length ratio, L/L_f, highlights that the non-dimensional load-carrying capacity is roughly proportional to the square of the length ratio. This can be compared by looking at the governing equations for the critical buckling load of prestressed stayed columns. Firstly, all dimensions including the inner d_i and outer diameter d_o of the column were scaled according to the length ratio, thus the proportionality relationship between the column length and diameter in Eq. (4) is true.

$$\frac{{d_{{\text{s}}} }}{{d_{{\text{f}}} }} \propto \frac{{L_{{\text{s}}} }}{{L_{{\text{f}}} }}$$

(4)

where the subscripts ‘s’ and ‘f’ represent the small- and full-scale columns, respectively. Dividing the second moment of area of the small-scale I_s by the full-scale I_f in Eq. (5), results in a proportional relationship between the second moment of area and the diameter to the power of four.

$$\frac{{I_{{\text{s}}} }}{{I_{{\text{f}}} }} = {\raise0.7ex\hbox{${\frac{{\pi \left( {d_{{\text{o,s}}}^{4} - d_{{\text{i,s}}}^{4} } \right)}}{64}}$} \!\mathord{\left/ {\vphantom {{\frac{{\pi \left( {d_{{\text{o,s}}}^{4} - d_{{\text{i,s}}}^{4} } \right)}}{64}} {\frac{{\pi \left( {d_{{\text{o,f}}}^{4} - d_{{\text{i,f}}}^{4} } \right)}}{64}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\frac{{\pi \left( {d_{{\text{o,f}}}^{4} - d_{{\text{i,f}}}^{4} } \right)}}{64}}$}} = \frac{{\left( {d_{{\text{o,s}}}^{4} - d_{{\text{i,s}}}^{4} } \right)}}{{\left( {d_{{\text{o,f}}}^{4} - d_{{\text{i,f}}}^{4} } \right)}} \therefore \frac{{I_{{\text{s}}} }}{{I_{{\text{f}}} }} \propto \left( {\frac{{d_{{\text{s}}} }}{{d_{{\text{f}}} }}} \right)^{4}$$

(5)

Lastly, dividing the critical buckling load of the small-scale by the full-scale in Eq. (6) using the relationships from Eqs. (4) and (5) results in the same relationship for the non-dimensional load-carrying capacity as obtained from the numerical modelling in Fig. 31.

$$\begin{gathered} \frac{{N_{{\text{u,s}}} }}{{N_{{\text{u,f}}} }} = {\raise0.7ex\hbox{${\frac{{4D_{{\text{s}}}^{2} E_{{\text{s}}} I_{{\text{s}}} }}{{L_{{\text{s}}}^{2} }}}$} \!\mathord{\left/ {\vphantom {{\frac{{4D_{{\text{s}}}^{2} E_{{\text{s}}} I_{{\text{s}}} }}{{L_{{\text{s}}}^{2} }}} {\frac{{4D_{{\text{f}}}^{2} E_{{\text{f}}} I_{{\text{f}}} }}{{L_{{\text{f}}}^{2} }} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\frac{{4D_{{\text{f}}}^{2} E_{{\text{f}}} I_{{\text{f}}} }}{{L_{{\text{f}}}^{2} }} }$}} \equiv \frac{{I_{{\text{s}}} L_{{\text{f}}}^{2} }}{{I_{{\text{f}}} L_{{\text{s}}}^{2} }} \equiv \left( {\frac{{L_{{\text{s}}} }}{{L_{{\text{f}}} }}} \right)^{4} \frac{{L_{{\text{f}}}^{2} }}{{L_{{\text{s}}}^{2} }} \hfill \\ \therefore \frac{{N_{{\text{u,s}}} }}{{N_{{\text{u,f}}} }} \propto \left( {\frac{{L_{{\text{s}}} }}{{L_{{\text{f}}} }}} \right)^{2} \hfill \\ \end{gathered}$$

(6)

The trends for non-dimensional end shortening, mid-height displacement and mid-height rotation at ultimate load highlight that there is no scaling effect on these parameters as they follow a roughly linear trend. The minor variation from the linear trend in these cases is due to uncertainties in the numerical model rather than any underlying physical behaviour. Following the confirmation that the behaviour of prestressed stayed columns can be scaled, existing design guidelines will be compared with results from the numerical model for varying levels of geometrical scales to ascertain their applicability.

Design Guidelines

Existing design guidance developed by the researchers [17] was used to calculate the maximum load-carrying capacity for the configurations studied in the geometric scale comparison section from Table 11. Results calculated using existing design guidelines were then compared with the load-carrying capacity found through finite element modelling. It has been previously shown by the researches [28] that the accuracy of the design expressions by earlier investigators [17] for the L/400 and L/200 imperfection levels is low. A similar trend was found in this section when comparing the load-carrying capacity from the design expressions and numerical model. Therefore, this section attempts to update the design guidance for varying imperfection levels using the numerical model. It should also be noted that the design guidance by [17] was developed using a two-dimensional numerical model, whereas this study utilises a three-dimensional model. Several cross-arm lengths for each buckling mode were modelled to determine design curve trends across the range of cross-arm lengths. Unlike the numerical model validation, a distinct symmetric imperfection was used for the systems with symmetric critical modes as this has been shown to be the worst-case scenario [16]. Similarly, the worst-case imperfection combination for the systems with an antisymmetric critical mode was used, i.e. a combination of the two modes was used to induce interactive behaviour. Design curves for the symmetric critical mode for the three imperfection amplitudes are shown in Fig. 32, with the updated guidance developed for the different zones of behaviour shown in Table 12.

Fig. 32

Design curves for the symmetric critical mode with three imperfection levels for cross-arm length ratio 2a/L = 0.05

Table 12 Updated design guidance for the normalised maximum load-carrying capacity (N_max/N^C) for symmetric critical mode. Where the subscripts z1, T_opt and 3T_opt refer to zone 1, the optimal prestress boundary between zone 2 and 3 and the upper boundary of zone 3

A similar procedure was repeated for the antisymmetric critical mode, with the design curves shown in Fig. 33, and updated design guidance in Table 13.

Fig. 33

Design curves for the antisymmetric critical mode with three imperfection levels for cross-arm length ratio 2a/L = 0.3

Table 13 Updated design guidance for the normalised maximum load-carrying capacity (N_max/N^C) for antisymmetric critical mode. Where the subscripts z1, T_opt and 3T_opt refer to zone 1, the optimal prestress boundary between zone 2 and 3 and the upper boundary of zone 3

Following the completion of the development of updated design guidance, the expressions were then compared with existing guidance. The validated finite element numerical model was used to determine the relative improvement in the guidance. The experimental configurations from Table 2 were scaled according to Table 11 and results from the numerical model for each imperfection level are compared with existing and updated design guidance. Comparison of existing design guidance and the finite element model for the L/200 imperfection level is shown in Fig. 34, while that of the updated guidance is shown in Fig. 35. A closer fit between the numerical model results and the design guidance is observed for the updated design guidance.

Fig. 34

Comparison of FE and analytical load-carrying capacity results from existing design guidance, where the dashed line represents 100% fit (imperfection level = L/200)

Fig. 35

Comparison of FE and analytical load-carrying capacity results from updated design guidance, where the dashed line represents 100% fit (imperfection level = L/200)

A comparison of the updated guidance with existing guidance for all three imperfection levels is shown in Table 14. Results obtained using the updated guidance for the L/400 and L/200 imperfection levels show an improvement over existing guidance, with the average ratio of ultimate load from numerical modelling to design guidance being lower as well as a lower standard deviation/COV and improved correlation. However, results obtained using the updated guidance for the L/1000 imperfection level show a higher average value of FE to design guidance ultimate load, with improvement in the other measures. Therefore, no significant improvement is observed with the updated guidance for the L/1000 imperfection level. Consequently, the updated guidance for the L/400 and L/200 imperfection levels are recommended for use, whereas existing guidance for the L/1000 imperfection level is still applicable for variation in geometric scale.

Table 14 Comparison of results obtained using numerical modelling with updated guidance and existing guidance [17], where P_u,FE, P_u,Wadee and P_u,updated are the ultimate loads from the numerical model, existing guidance [17] and updated guidance respectively, Std. dev. is the standard deviation, COV is the coefficient of variation and R² is a measure of the correlation of the results

Conclusions

The experimental campaign included tests on 17 small-scale prestressed stayed steel columns with varying cross-arm lengths and initial prestress values as well as a control column with no cross-arms. This investigation aimed at studying systems close to the transition point for varying prestress to establish the optimal configuration and to examine the effect of scale on the behaviour of prestressed stayed steel column systems. The scaling effect was investigated through experimental investigations and numerical modelling. Furthermore, the applicability of existing design guidance to other geometric scales is studied.

This study investigated various prestressed stayed steel column configurations close to the transition point between symmetric and antisymmetric modes. It was previously suggested by the researchers [12] that the greatest efficiency in terms of weight of materials can be found close to the transition point. This study found that configurations E3 and E4, which are either side of the transition point, gave the greatest efficiency in terms of weight of materials, confirming the hypothesis by previous investigators [12]. Furthermore, this highlights that there is no real benefit in designing prestressed stayed steel columns to have an antisymmetric critical mode significantly higher than the symmetric as a lower efficiency is achieved. Also, it has been shown that for systems close to the transition point, with symmetric critical modes, that an increase in load-carrying capacity is obtained with prestress levels higher than T_opt. Additionally, interactive behaviour is also possible before the ultimate load is achieved, although the exact cause is not yet clear. However, for systems close to the transition point with an antisymmetric critical mode, prestress levels lower than T_opt have been shown to yield the highest load-carrying capacity. These findings are applicable to prestressed stayed steel columns with a single cross-arm and further studies are required to verify if the same conclusions can be drawn for more complex configurations.

It has been shown by comparing the load-carrying capacities of corresponding configurations from this study and the full-scale experimental study by the researchers [11] that small-scale systems can effectively model the load-carrying capacity and post-buckling shape of large-scale systems. This comparison includes prestressed stayed steel columns with symmetric and antisymmetric critical modes as well as systems close to the transition point for varying levels of prestress. The numerical model was also validated against results from the experimental study and used to conduct a full geometric scaling comparison study. It was found that small-scale systems are capable of replicating the load-deformation response of large-scale structures.

Following the geometric scaling comparison study, the numerical model was then used to investigate the applicability of existing design guidelines to systems with various geometric scales. Existing design guidelines were compared with results from the validated finite element model. It was shown that existing design guidelines had low accuracy for small-scale systems. Therefore, updated design guidance was developed using the numerical model and shown to yield results closer to the numerical model for a range of system scales compared to existing design guidelines.