Analysis of Mid-Rise Moment Resisting Steel Frames by Nonlinear Time History Analysis using Force Analogy Method

Abstract

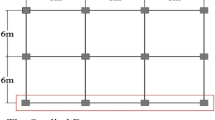
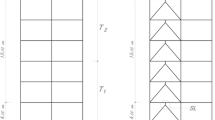
This paper presents a detailed systematic investigation to assess detailed dynamic behaviours of mid-rise moment resisting steel frames by performing nonlinear time history analysis using force analogy method. Both material and geometric nonlinearities have been considered in the analysis. Three building heights with seven earthquake ground accelerations have been examined. The building responses in terms of floor displacement, storey drift ratio and plastic energy dissipation have been investigated. It has been found that maximum seismic responses occur within 18–40% height of the building. Further, the position of maximum response along the building height has been seen to decrease as the height of building decreases. It has also been seen that building responses, when excited by short period ground accelerations, decreases when the building height increase; whereas building responses, when excited by long period ground accelerations, increases when the building height increases. In general, maximum seismic responses have been found to be more consistent with peak ground velocity rather than peak ground acceleration.

Appendices

Appendix A

Formulation of FAM in Nonlinear Dynamic Problems

Dynamic equation of motion resulted from earthquake excitation

$${\rm{M\ddot{x}}}(t) + {\rm{C\dot{x}}}(t) + K(t)x^{\prime}(t) = - {\rm{M\ddot{g}}}(t) - F_{{\rm{a}}} (t)$$

(11)

where F_a(t) is imposed load on the structure resulted from geometric nonlinearity (mainly P-∆ effect). This additional force vector F_a(t) is related to the lateral displacement vector x(t) as:

$$F_{\rm a} (t) = K_{\rm a} x(t)$$

(12)

where K_a is a stiffness formed due to gravity load. Value of K_a depends on column height but is not a function of time.

$$K(t) = K_{{\rm{L}}} + K_{{\rm{G}}} (t)$$

(13)

where K_L is the elastic stiffness that depends on gravity load, whereas K_G(t) is the stiffness that keeps changing due to variation in axial load during earthquake excitation. The elastic stiffness K_L will be computed once initially, and it may be used consistently until the entire nonlinear dynamic problem is solved, which becomes the unique advantage in FAM.

State Space Methods in FAM

After the application of static condensation, the equation of motion becomes

$$M_{{{\rm{dd}}}} \ddot{x}_{d} (t) + C_{{{\rm{dd}}}} \dot{x}_{{\rm{d}}} (t) + \overline{K}(t)x_{{\rm{d}}} ^{\prime}(t) = - M_{{{\rm{dd}}}} \ddot{g}_{{\rm{d}}} (t) - F_{{\rm{a}}} (t)$$

(14)

$$M_{{{\rm{dd}}}} \ddot{x}_{{\rm{d}}} (t) + C_{{{\rm{dd}}}} \dot{x}_{{\rm{d}}} (t) + \overline{K}_{{\rm{L}}} x_{{\rm{d}}} (t) = - M_{{{\rm{dd}}}} \ddot{g}_{{\rm{d}}} (t) - K_{{\rm{a}}} x_{{\rm{d}}} (t) - \overline{K}_{{\rm{G}}} (t)x_{{\rm{d}}} (t) + \overline{K}(t)x_{{\rm{d}}}^{\prime\prime} (t)$$

(15)

Let,

$$\overline{K}_{{\rm{e}}} = \overline{K}_{{\rm{L}}} + K_{{\rm{a}}}$$

where $\overline{K }$ _e represents the elastic stiffness of the whole structure. Substituting the value of $\overline{K}_{{\rm{e}}}$ into equation (15.)

$$M_{{{\rm{dd}}}} \ddot{x}_{{\rm{d}}} (t) + C_{{{\rm{dd}}}} \dot{x}_{{\rm{d}}} (t) + \overline{K}_{{\rm{e}}} x_{{\rm{d}}} (t) = - M_{{{\rm{dd}}}} \ddot{g}_{{\rm{d}}} (t) - \overline{K}_{{\rm{G}}} (t)x_{{\rm{d}}} (t) + \overline{K}(t)x_{{\rm{d}}} (t)$$

(16)

Material nonlinearity term $\overline{K }\left(t\right){x}_{d}"(t)$ and geometric nonlinearity term $-{\overline{K} }_{\mathrm{G}}\left(t\right){x}_{\mathrm{d}}(t)$ on the right hand side of Eq. (16) can be considered as the equivalent forces applied due to nonlinearities on the structures. Dynamic equation of motion (16) can be solved by using state space method. Refer Wong and Speicher [31] for detail formulation.