1 Introduction

The stock market allows an added property of investment chance for investors and, thus, market practitioners are interested in acquiring the nature and behavior of stock market yields [18]. Stock market growth has to be maintained by overall financial and macro economic sector environments. Furthermore, decreased fiscal deficits, completely market based issuance of Government bonds and relaxation of interest rates will assist in the growth of a stronger and a more efficient stock market [21].

In this study, BSE indices BSE SENSEX and BSE BANKEX have been considered in our experiment that play an important role in emerging stock market. We have also considered BSE indices which are market portfolios as benchmarks.

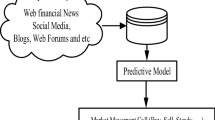
A new stock portfolio management approach, fusing a stepwise regression analysis (SRA), ANFIS and capital asset pricing model (CAPM), has been suggested in this research paper for stock prediction and portfolio optimization in Indian stock market. The system consists mainly of two modules: the SRA-ANFIS module, to predict the future price value of each stock, and CAPM module, to discover the optimal investment allocation to minimize risk and maximize return of a stock portfolio.

The stock market prediction is viewed as a challenging job because of the uncertainties involved in the stock market movement. According to many academic research studies, stock price movements are not random. Instead, they perform in a highly dynamic and non-linear manner [14]. Likewise, the ability to forecast the stock trend and the correct value of the stock prices in the future are the most significant factors in earning money utilizing financial forecasting [3]. All the investor’s needs are to be judged while making a bid at the right time. In addition, research studies have confirmed that forecasting stock movement is compared to value that can produce higher returns.

In recent times, several recent applications are developed by soft computing techniques such as fuzzy systems (FS), neural networks (NN), and genetic algorithms (GA). Soft computing is an emerging approach to computing, which relates the significant capability of the human knowledge to understand and learn in an environment of imprecision and uncertainty [4, 9, 32]. The relationships between process variables in the stock markets are mostly too complicated to get grounded decisions using traditional system theory [27]. Each of these intelligent techniques has specific properties (adaptability, ability of learning, classifying, modeling, solving optimizing tasks, etc.) meeting particular kind of applications [8, 31]. A hybrid intelligent system integrates at least two computational intelligent techniques, i.e. fusion of these intelligent systems produces neuro-fuzzy system, neuro-GA system and fuzzy-GA system [20].

Technical indicators are used to find out the behavior of traders and their impact on the future price movement of the stock from past movements [1]. The prediction module SRA-ANFIS generates the trading signals with the assistance of the technical indicators. Some standard technical indicators have been applied, such as simple moving average (SMA), bollinger bands and commodity channel index (CCI) are used to determine the price trend, arms index is used to measure the volume movement and money flow index is applied to study both price and volume trend [13].

Portfolio optimization is a primary issue in asset management, and it handles with suitable investment allocation to minimize risk and maximize return of a stock portfolio through diversification. Stock portfolio optimization in asset management is a significant activity in predicting stock movements to earn superior returns. Modern portfolio theory is a refined portfolio management approach, and it offers how to choose a portfolio with superior feasible expected returns. Markowitz [17] created the groundwork of this theory. Diversification of the portfolio is made up of non-correlated stocks that can earn the maximum returns along with the smallest amount of standard deviation.

CAPM was developed by Sharpe [24] and Lintner [15]. CAPM is an equilibrium model that motivates all modern financial theories and clarifies why various assets have yielded various expected returns [16]. It creates more yields from the stock portfolio, and hence maximizes the return and minimizes the risk of a stock portfolio through diversification and right investment allocation to the particular stock under uncertainty [2]. CAPM concerns the expected return of a stock based on its level of risk.

The paper is organized in the following manner: Sect. 2 outlines the overview of stock portfolio management system, Sect. 3 examines the results and evaluates the performance of the proposed system with other portfolio strategies and benchmark indices, Sect. 4 briefly presents the discussion. Lastly, Sect. 5 represents the conclusion of this paper and future directions of the research.

2 Stock portfolio management system

In this study, a stock portfolio management system of SRA, ANFIS and CAPM is developed to predict stock prices and yield higher returns. Figure 1 shows the over all block diagram of the stock portfolio management system. In the block diagram, a SRA and ANFIS module is applied to create the trading signals for buying or selling the stocks. The CAPM module is employed to construct and diversify the portfolio with the help of ANFIS module. The efficiency of the proposed model can also be evaluated by analyzing the returns generated by the proposed model compared to other portfolio strategies.

Fig. 1
figure 1

Block diagram of the stock portfolio management system

Full size image

2.1 Mathematical formulation of the stock portfolio optimization problem

Let us, for the present study, consider a stock portfolio optimization problem with long-term perspective changing from months to more than a year. Let n is the portfolio size with weights w i of asset i, E(R p ) is the portfolio’s expected return, E(R i ) be the weighted average of the expected return of the independent assets, σ i is the standard deviation of stock i, \( \rho_{ij} \) is the correlation coefficient of the two assets i and j, and \( \sigma_{ij} \) is the covariance of the two assets i and j. The correlation coefficient \( \rho_{ij} \) is used to measure the effectiveness of portfolio diversification whose value lies between 1 and −1. If the correlation coefficient is −1, the diversification is most effective; else the diversification is least effective.

The correlation coefficient of the two assets is written as

$$ \rho_{ij} = \frac{{\sigma_{ij} }}{{\sigma_{i} \sigma_{j} }} $$
(1)

The expected return of the portfolio is measured from the weighted average of the expected return of the independent assets using the above-mentioned notational terms.

$$ E(R_{p} ) = \sum\limits_{i = 1}^{n} {w_{i} \times E(R_{i} )} $$
(2)

The risk or variance of the three asset portfolios is written as

$$ \sigma_{P}^{2} = w_{1}^{2} \sigma_{1}^{2} + w_{2}^{2} \sigma_{2}^{2} + w_{3}^{2} \sigma_{3}^{2} + 2w_{1} w_{2} \sigma_{12} + 2w_{1} w_{3} \sigma_{xz} + 2w_{2} w_{3} \sigma_{23} $$
(3)
$$ \sigma_{P}^{2} = \sum\limits_{i = 1}^{3} {w_{i}^{2} } \sigma_{i}^{2} + 2\sum\limits_{i = 1}^{2} {\sum\limits_{j = i + 1}^{3} {w_{i} w_{j} \sigma_{ij} } } $$
(4)

The risk or variance of the n assets portfolio is defined as

$$ \sigma_{P}^{2} = \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {w_{i} w_{j} \sigma_{ij} } } = \;\sum\limits_{i = 1}^{n} {w_{i}^{2} \sigma_{i}^{2} } + 2\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {w_{i} w_{j} \sigma_{ij} } } $$
(5)

Let us assume that a portfolio has identical weights of n assets. The proportional weight of each asset \( w_{i} \) is 1/n and the formula of the portfolio’s variance can be modified as

$$ \sigma_{P}^{2} = \sum\limits_{i = 1}^{n} {\left( \frac{1}{n} \right)^{2} \sigma_{i}^{2} } + 2\sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\left( \frac{1}{n} \right)^{2} \sigma_{ij} } } $$
(6)

Diversification permits an investor to minimize the risk level of a stock portfolio beyond the independent risk levels of the stocks it has. Diversification of the portfolio is made up of non-correlated stocks that can earn the maximum returns along with the smallest amount of standard deviation [22].

The mathematical formulation of the stock portfolio optimization problem is given by

$$ Min\left( {\lambda \cdot \sigma_{p} - (1 - \lambda ) \cdot E(R_{p} )} \right) = \;Min\left( {\lambda \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {w_{i} w_{j} \sigma_{ij} } } - (1 - \lambda )\sum\limits_{i = 1}^{n} {w_{i} E(R_{i} )} } \right) $$
(7)

where λ ∈ [0, 1] is the risk aversion factor.

Another formula of the portfolio optimization called the Sharpe Ratio [25] is given as

$$ Max\left( {R_{p} - R_{f} } \right)/\sigma_{p} $$
(8)

where R f is the risk free return.

2.2 Development of a prediction system by SRA and ANFIS

This section attempts to develop a prediction system to predict the future price value of each stock. The system of hybrid prediction model developed from SRA and ANFIS to learn buying and selling signal.

2.2.1 Stepwise regression analysis (SRA)

A set of technical indicators involving the stock price trend have been discussed as follows. There are totally seven main indicators to be taken from and they are

  • X 1 = SMA: determines the average value of a stock’s price over a specified period.

  • X 2 = Exponential moving average (EMA): averages the last n day’s closing price but allocates a larger weight to the more recent prices creating it more responsive to current price.

  • X 3 = Moving average convergence-divergence (MACD): measures the distance between two moving averages and it also measures how two SMAs move together and separately over time.

  • X4 = Money flow index (MFI): calculates the amount of money flowing into and out of a stock. It applies both price and volume to evaluate buying and selling pressure.

  • X5 = Arms index (AI): discovers market strength and breadth by analyzing the relationship between advancing and declining issues and their respective volume.

  • X6 = Relative strength index (RSI): compares the averages of n days a stock closes up against the same days it closes down.

  • X7 = CCI: evaluates the current price level proportional to an average price level over a particular period. High values indicate that stock prices are extraordinarily high compared to average prices while low values show that prices are extraordinarily low.

These main input factors will be further chosen using the SRA model. The SRA is used to decide the set of independent variables that almost nearly affect the dependent variable. This is implemented by iterating the procedure of variable selection. The step-by-step process of the SRA approach is briefly described in the following:

  1. Step 1:

    Estimate the correlation coefficient (r) of each input variable (X1, X2,…,Xn), i.e., technical indicators, and output data (Y), i.e., buying and selling signal. Put all values in a correlation matrix.

  2. Step 2:

    Select the biggest r2 value from the correlation matrix and develop a regression model, i.e., \({\widehat{Y}} \) = f (X i ); then, consider the correlation of Y with different input data. Where X i is the biggest one in the present stage.

  3. Step 3:

    Select the biggest correlation coefficient among these input variables (Let us consider it as Xj). Then, derive new regression model \({\widehat{Y}} \) = f (X i ,X j ). Estimate partial F value from all input data.

    $$ F_{j} = \frac{{SSR/1(X_{j} \left| {X_{i} )} \right.}}{{SSE/(n - 2)(X_{j} ,X_{i} )}} $$
    (9)

    where sum of squares regression \( SSR = \sum\limits_{i = 1}^{n} {(\widehat{{Y_{i} }}} - \overline{Y} )^{2} \) sum of squares errors \( SSE = \sum\limits_{i = 1}^{n} {(Y_{i} - \widehat{{Y_{i} }}} ) \)

  4. Step 4:

    Find the partial F value of input variable Xj. If the value is lesser than a user defined threshold, it is eliminated from the model.

  5. Step 5:

    Normalize the finalized variables from SRA as follows:

    $$ X_{i}^{'} = \frac{{X_{i} - X_{\hbox{min} } }}{{X_{\hbox{max} } - X_{\hbox{min} } }} $$
    (10)
  6. Step 6:

    Normalized variables are inputted to ANFIS for predicting the future price of the stock.

2.2.2 Adaptive neuro-fuzzy inference system (ANFIS)

ANFIS is an integrated system applying the adaptive NN with hybrid learning algorithms and the fuzzy inference system [10]. ANFIS shows the capability of FS to simulate explicitly the linguistic concepts, uncertainty, and the knowledge of human experts, also achieving fuzzy reasoning together with the learning capabilities and noise robustness of NN [5–7]. The framework of ANFIS model is shown in Fig. 2. The ANFIS architecture has five layers: nodes in layers 2, 3 and 5 are fixed nodes, and nodes in remaining layers are adaptive.

Fig. 2
figure 2

Framework of ANFIS

Full size image

The nodes that are described by a square, named adaptive nodes, have parameter sets that can be adjusted, whereas the circle-shaped nodes are named fixed nodes, which have parameter sets that should be fixed.

  • Layer 1: The nodes that are described by a square, named adaptive nodes. a, b and c are premise parameters that specify the membership function of the node. The node function is represented as

    $$ O_{i}^{1} = \mu A_{i} (x),\quad {\text{i}} = 1, 2 $$
    (11)

    In general, membership function is triangular-shaped with the maximum equal to 1 and the minimum to 0, as follows.

    $$ \mu A_{i} (x) = \hbox{max} \left( {\hbox{min} \left( {\frac{x - a}{b - a},\frac{c - x}{c - b}} \right),0} \right) $$
    (12)

    where x is the input node and {a,b.c} are the basis parameter set.

  • Layer 2: All nodes in this layer employ a scaling factor to incoming signals and transmit the product out as pictured by a circle.

    $$ O_{i}^{2} = w_{i} = \mu A_{i} (x) \cdot \mu B_{i} (y),\quad {\text{i}} = 1, 2 $$
    (13)

  • Layer 3: All nodes in this layer estimate the weights corresponding to the proportion of the ith rule’s firing strength to the summation of all rules’ firing strengths:

    $$ O_{i}^{3} = \overline{{w_{i} }} = \frac{{w_{i} }}{{w_{1} + w_{2} }},\quad {\text{ i}} = 1, 2 $$
    (14)

  • Layer 4: All nodes in this layer are adaptive nodes, marked by square that carry out the linear arrangement of inputs x and y by involving consequent parameters a, b, and c, as follows:

    $$ O_{i}^{4} = \overline{{w_{i} }} z_{i} = \overline{{w_{i} }} (a_{i} x + b_{i} y + c_{i} ),\quad {\text{i}} = 1,{ 2} $$
    (15)

    where z1 and z2 are fuzzy if–then rules of Takagi and Sugeno as described in the below equation

    1. 1.

      If x is a 1 and y is b 1, then z 1 = a 1 x + b 1 y + c 1

    2. 2.

      If x is a 2 and y is b 2, then z 2 = a 2 x + b 2 y + c 2

  • Layer 5: The single node in this layer is a fixed node, noticed by square, which estimates the output signal as the adding up of all incoming signals, i.e.

    $$ O_{1}^{5} = \sum\limits_{i} {\overline{{w_{i} }} z_{i} } = \frac{{\sum\limits_{i} {w_{i} z_{i} } }}{{\sum\limits_{i} {w_{i} } }},\quad {\text{ i}} = 1, 2 $$
    (16)

The hybrid algorithm is implemented as ANFIS learning algorithm which combines the backpropagation gradient descent algorithm and the least squares estimation algorithm to adjust the membership arguments [23, 26]. The backpropagation gradient descent algorithm modifies the premise parameters in the backward pass of the learning algorithm. The least squares estimate method depicts the consequent parameters in the forward pass.

2.3 Capital asset pricing model (CAPM)

CAPM is an equilibrium model that motivates all modern financial theories and clarifies why various assets have yielded various expected returns. Four decades later, CAPM is still mostly using in financial applications, such as calculating the cost of capital for business firms and measuring the performance of managed stock portfolios. Portfolio management can be viewed as discovering the combination of stocks that provide an investor the ideal trade-off between the expected return, and the risk associated with it [2].

The CAPM is an optimization model of forecasted expected return and risk of respective stock and portfolio. CAPM concerns the expected return of a stock based on its level of risk. In specific, this asset-pricing model impressively states that assets have various expected returns because they have various betas. The risk and reward of each stock are described by its expected return \( E(R_{i} ) \) and its volatility \( \sigma_{i} \). The expected return can be calculated as follows:

$$ E(R_{i} ) = \beta_{i} (R_{m} - R_{f} ) + R_{f} $$
(17)

where \( R_{m} \) is the average rate of market portfolio return, \( R_{f} \) is risk free return, and \( \beta_{i} \) is the beta value of stock i.

$$ \beta_{i} = \frac{{\text{cov} (R_{i} - R_{m} )}}{{\text{var} (R_{m} )}} $$
(18)

Sharpe–Lintner model forecasts that the intercept is the riskless rate and the coefficient on beta is the expected stock market return in excess of the riskless or risk-free rate, \( E(R_{p} ) - R_{f} \). The volatility of a particular stock is measured by beta (\( \beta_{i} \)) and it is further compared with the stock market. The relation between beta of a stock and expected return can be plotted in the form of security market line (SML) using the Sharpe–Lintner CAPM equation as follows,

$$ E(R_{i} ) - R_{f} = \beta_{i} (R_{m} - R_{f} ) $$
(19)

The SML is illustrated in Fig. 3. It compares the risk (β i ) and the expected return (R i ) of individual stock in the benchmark market portfolio. If β i  = 0, then the expected return is R f . If β i  = 1, then moves in the same market trend R i  = R m . If \( \beta_{i} \) > 1, it travels more than the market movements and the risk and expected return will be better than the market portfolio. If \( \beta_{i} \) < 1, there is contrast between actual movement and market trends and the risk and expected return will be lesser than the market portfolio.

Fig. 3
figure 3

Security market line

Full size image

According to the CAPM portfolio theory, stocks above the SML are called underpriced stocks when the stocks are selling less than the market reasonable value and the expected returns of their stocks are high. Stocks below the SML are called overpriced stocks when the stocks are selling more than the market reasonable value and the expected returns of their stocks are very low.

3 Experimental results and performance comparison

3.1 Data sources

The integrated model has been examined by employing stocks in BSE SENSEX and BSE BANKEX indices to test the performance of the proposed technique. The model is tested applying earlier period stock data from 2007 to 2012. Consequently, the overall quantity of observations for every stock and index is 1,272. Training and testing data of BSE are obtained from www.bseindia.com and they are represented in Table 1.

Table 1 Training and test data
Full size table

The price histories of stock, with time and volume information have been considered as the main data of the forecasting system. Down and up trends of the price on the stock market depend on supply and demand of stocks. Important technical indicators including price and volume have been used for data preprocessing and predicting the stock market. Technical indicators are used to develop the quality of the data, improve the efficiency and ease the stock prediction process [12].

3.2 Experimental setup

In the ANFIS module of the proposed model, a five layer has been chosen, which is completely linked architecture that has been shown in Fig. 2. Inputs X1 to X7 indicate several technical indicators namely SMA, EMA, MACD, MFI, AI, RSI and CCI in Table 2. The value of every variable is described by one of a feasible five fuzzy membership sets (VL L M H VH) which means very low (VL), low (L), medium (M), high (H), and very high (VH). Fuzzy membership functions may be crisp data observations about the membership degree of these fuzzy sets. Figure 4 represents a visualization of the triangular-shaped membership functions for the exponential moving average (EMA) indicator.

Table 2 Example of combination of fuzzy rule base representation
Full size table
Fig. 4
figure 4

Triangular-shaped membership functions for the exponential moving average (EMA)

Full size image

Finally, resultant output has a single floating-point value from the set {0.0, 0.25,…,1.0}. As a result, the total number of probable if–then rules for fuzzy system is 78125 (57). The output of the ANFIS system has five unique fuzzy sets i.e. Strong Buy, Buy, Hold, Sell, Strong Sell that are defined. A Strong Buy signal is created when the output is almost to 1.0 and a Strong Sell signal is created when the output is almost to 0.0 from the above-mentioned case.

The preliminary fuzzy rules are measured by the prediction system with technical indicators generating the following a few fuzzy if–then rules.

  • If SMA is Very High and EMA is Very High and MACD is Very High and MFI is Very Low and AI is Very Low and RSI is Very High and CCI is Very High, then rating = 0.0 (Strong Sell)

  • If SMA is High and EMA is High and MACD is High and MFI is Low and AI is Low and RSI is High and CCI is High, then rating = 0.25 (Sell)

  • If SMA is Medium and EMA is Medium and MACD is Medium and MFI is Medium and AI is Medium and RSI is Medium and CCI is Medium, then rating = 0.5 (Hold)

  • If SMA is Low and EMA is Low and MACD is Low and MFI is High and AI is High and RSI is Low and CCI is Low, then rating = 0.75 (Buy)

  • If SMA is Low and EMA is Very Low and MACD is Very Low and MFI is Very High and AI is Very High and RSI is Very Low and CCI is Very Low, then rating = 1.0 (Strong Buy)

To optimize the stock portfolio applying CAPM, let us take risk free return R f is 9 % (i.e. Money Market Instruments), stock market return R m is 17.9 % (BSE Sensex return measured from index value 100 in year 1979 to 19136 in April 2011), beta value \( \beta_{P} \) is 1.5, and portfolio’s expected return E (R p ) is 22.35 %.

3.3 Performance metric

The efficiency of the proposed system has been measured and compared with benchmark indices and other portfolio strategies. The first portfolio is a benchmark of all other portfolios, BSE SENSEX and BSE BANKEX indices. The second portfolio is buy-and-hold strategy which is made by randomly choosing specific stocks from 30 stocks in which picked out stocks have the equal ratio of investment. Finally, the momentum-investing portfolio is rebalanced to retain the top 25 % of stocks every 30 days. It sells negative return stocks and buys superior return stocks over the last 4 months.

The following principles are implemented in all portfolios.

  1. (i)

    Initial investment amount of all portfolio models is equal to the benchmark indices and last month’s profit can be spent.

  2. (ii)

    The portfolio is measured monthly and cumulative profits are taken at the end of estimation.

  3. (iii)

    Transaction expenses are added 0.5 % of value per transaction.

Both the returns and the risks of all portfolios are measured by following well-known standard statistic measures to compare the performance of various portfolio models [29].

  1. (1)

    Portfolio return: Annualized return and Return on Investment (ROI) are considered to measure the portfolio return.

  2. (2)

    Sharpe ratio: The Sharpe ratio estimates surplus returns of a portfolio [25], \( R_{p} - R_{f} \) as a method of standard deviation \( \sigma_{p} \)

    $$ Sharpe = \frac{{(R_{p} - R_{f} )}}{{\sigma_{p} }} $$
    (20)
  3. (3)

    M 2 ratio: Modigliani and Modigliani [19] developed the M2 ratio to measure the efficiency of the portfolio after fine-tuning for risk. The risk-adjusted return of portfolio is evaluated against risk-adjusted return of stock market index.

    $$ M^{2} = R_{p} + \sigma_{p} SR - \sigma_{m} SR $$
    (21)

    where SR is Sharpe Ratio

  4. (4)

    Treynor Ratio: Treynor and Black [30] developed the Treynor Ratio that calculated returns gained in excess of the risk-free rate divided by the systematic risk \( \beta \).

    $$ TR = \frac{{\left( {R_{p} - R_{f} } \right)}}{\beta } $$
    (22)

    If the TR value is positive, the portfolio has done good performance; otherwise, it has not done well.

  5. (5)

    Sortino Ratio: It measures the performance of downside risk adjusted return, so it adds downside volatility, in the denominator as a replacement for the standard deviation [28].

    $$ Sortino = \frac{{(R_{p} - R_{f} )}}{{\sigma_{d} }} $$
    (23)
  6. (6)

    Jensen’s alpha: It calculates the additional return that the portfolio yields after correcting for its “beta” risk [11].

    $$ \alpha_{J} = R_{p} - \left( {R_{f} + \beta_{p} (R_{m} - R_{f} )} \right) $$
    (24)

3.4 Result

In order to compare the efficiency of the different portfolio models, it is important to estimate them on earlier undetected stock market data. The forecasted results and returns of the proposed portfolio model are compared with actual returns of the benchmark indices for assessing better portfolio model among various portfolio models.

The statistical metrics like the annualized returns and the various ratios are evaluated to measure the returns and the risks for the stock portfolio models. Portfolio returns and risks of the all portfolio strategies have been compared with benchmark portfolio by using these statistical metrics. Table 3 shows financial evaluation results of the system-generated portfolios and the benchmark portfolio, BSE Sensex index. Figure 5 represents the return of all portfolios that with the return of the BSE SENSEX index for the 40 months holding period.

Table 3 Performance comparisons of portfolio models with BSE SENSEX
Full size table
Fig. 5
figure 5

Comparison of portfolios values with BSE sensex

Full size image

Tables 3 and 4 summarize the performance comparisons of portfolio models, the test results achieved for the two stock indices BSE SENSEX and BSE BANKEX respectively. From the result in Tables 3 and 4, we have obviously found that our proposed SRA-ANFIS-CAPM portfolio model obtains the highest total return as compared with other portfolio models.

Table 4 Performance comparisons of portfolio models with BSE BANKEX
Full size table

4 Discussion

In this paper, we integrate the forecasting tool SRA-ANIFS with the portfolio optimization model CAPM to solve the portfolio optimization problem. To validate the use of the proposed portfolio model, the empirical results are presented in Table 3. The proposed method is compared with two existing portfolio models and it is also validated by two well-known BSE indexes BSE SENSEX and BSE BANKEX. The annualized returns of our SRA-ANFIS-CAPM portfolio model were 41.08 and 53.27 % which obtains a superior return than other portfolio models for the BSE SENSEX and BSE BANKEX indices respectively. From the experimental tests, all ratios values of the proposed portfolio model are always higher than other portfolio models for both indexes.

Moreover, systematic risk indicator Beta is an important coefficient of measuring the returns. Our proposed portfolio model (\( \beta \) = 0.89) is less than 1 which implies that the stocks are less volatile than the BSE SENSEX and BSE BANKEX indices. Figures 5 and 6 show the test results for the return of all portfolios with BSE SENSEX index and BSE BANKEX index respectively. It indicates that the return on investments of the integrated portfolio model is always higher than other existing portfolio strategies in all the months.

Fig. 6
figure 6

Comparison of portfolios values with BSE BANKEX

Full size image

From the experimental tests, we clearly observe that SRA-ANFIS-CAPM prediction model significantly outperformed the other portfolio models without prediction. This illustrates that proposed portfolio model is capable of performing better than other portfolio models with respect to the returns and risks. Obviously, experimental results confirm that the new approach significantly improves the forecasted values of the return of our portfolio.

5 Conclusion

In this paper, we have integrated CAPM portfolio model into SRA-ANFIS prediction model to optimize the trade-off between risk and return of the portfolio. Portfolio optimization is one of important decision making methods for all stock investors. The SRA is employed to preprocess the complex dimensionality and inconsistency of stock price data. An example was specified to demonstrate the proposed SRA-ANFIS-CAPM portfolio model using real data from BSE indices in which the results showed the high performance of model. On the basis of the experimental results, we have discovered that integrated computational intelligence models are capable of simulating the dynamic volatile stock markets easily and make better predictive results compared to conventional linear models. Furthermore, it slightly minimized the standard deviation of stocks’ allocation which shows that the forecasting gets less uncertain. The SRA-ANFIS-CAPM has generated highest return values which can completely explain the nonlinear relationship between the stock price and the technical indicators.

In the future, a different combination of new computational intelligence methods can be further employed in a more complex stock market problem. Furthermore, more sophisticated pattern recognition algorithm can be incorporated in the prediction system to discover significant patterns from the historical stock data for comparison with the present stock market data. The performance of SRA-ANFIS-CAPM can be further improved for handling a relative combination of human, economic, and political events.