A Commensal Consumer-Induced Mediation Effects on Resource–Consumer Interactions

Abstract

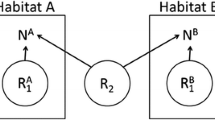
A general view of resource–consumer interactions is that resource intake by the consumers reduces the growth rate of resource population but it leads to an increase of consumer population. This view is proficiently interpreted with the classic Lotka–Volterra model that successfully describes the effects of changes in consumption rates due to changes in resource and consumer population densities. These effects are resulted in perpetual oscillatory dynamics of both the population densities, and the extent of the effects for given initial densities is measured by the oscillating frequency determined by the model parameters. But in many ecosystems, it has often observed a steep decline and delayed recovery in resource population that cannot be explained by the traditional Lotka–Volterra model. Foraging habits and behaviors of a consumer population may facilitate others, those usually do not affect them directly, to feed on the same resource and then to reproduce successfully. Such commensal consumers (facilitated population) can heavily influence the rate of resource exploitation and thereby affect the usual resource–consumer cycles. While involving such commensal consumer-induced effects, called here commensal mediation, into the Lotka–Volterra type models, it shows that the commensal mediation can have stabilizing or destabilizing effects on resource dynamics depending on the strength of interactions and the conditions in which the interactions occur. In the natural ecosystems where the growth rate of resource population depends on its own density even in absence of consumers, the commensal mediation provides a destabilizing effect on resource dynamics; increasing commensal population density increases the amplitude of resource fluctuations and the time laps from one peak to the next. On the other hand, in the managed ecosystems where the growth rate of resource population is expected to be maintained at a constant level in absence of consumers, the commensal mediation provides stabilizing effect at a certain condition; with a given restriction on the consumer population, decreasing mortality of the commensal population can stabilize the resource population dynamics at a stable, steady-state. Moreover, while the resource population experiences saturation effect, resource–consumer interactions with the commensal mediation exhibit a range of dynamical behaviours starting from stable equilibrium, then damped oscillation, to limit cycles as the resource carrying capacity increases from a critical level. In addition, commensal mediations with both controlling facilitator consumer population and resource harvesting are analyzed separately and the results are discussed for some exemplified managed and natural ecosystems.

Appendices

Appendix 1: Stability of the System (2)

In all the calculations, the Routh–Hurwitz criteria has been used for examining the local stability of the interaction system; if the characteristic equation of the Jacobian matrix of a system of differential equations at an equilibrium point, it is of the following form,

$$ a_{0} \lambda^{3} + a_{1} \lambda^{2} + a_{2} \lambda + a_{3} = 0, $$

(8)

where $a_{0} > 0$, and $\Updelta_{1} = a_{1}$, $\Updelta_{2} = { \det }\left( {\begin{array}{*{20}c} {a_{1} } & {a_{0} } \\ {a_{3} } & {a_{2} } \\ \end{array} } \right)$, the equilibrium point is stable iff$\Updelta_{1} > 0$, $\Updelta_{2} > 0$ and $a_{3} > 0$.The system (2) has a feasible equilibrium point $\left( {\frac{c}{d},\frac{dm}{cn},\frac{an}{bm}} \right)$, and the associated Jacobian matrix is,

$$ J(x,y,z) = \left[ {\begin{array}{*{20}c} { - byz} & { - bxz} & { - bxy} \\ {dy} & { - c + dx} & 0 \\ {nyz} & {nxz} & { - m + nxy} \\ \end{array} } \right]. $$

Therefore the Jacobian matrix at the equilibrium point is,

$$ A = J\left( {\frac{c}{d},\frac{dm}{cn},\frac{an}{bm}} \right) = \left[ {\begin{array}{*{20}c} { - \frac{ad}{c}} & { - \frac{acn}{dm}} & { - \frac{bm}{n}} \\ {\frac{{d^{2} m}}{cn}} & 0 & 0 \\ \frac{adn}{bc} & {\frac{{acn^{2} }}{bdm}} & 0 \\ \end{array} } \right] $$

The characteristic equation, ${ \det }(A - \lambda I) = 0$, is

$$ \lambda^{3} + ad/c\lambda^{2} + (ad + adm/c)\lambda + adm = 0 $$

Here, $\Updelta_{1} = a_{1} = ad/c > 0$ and $a_{3} = adm > 0$; therefore if $\Updelta_{2} > 0$, $\left( {\frac{c}{d},\frac{dm}{cn},\frac{an}{bm}} \right)$ is a stable equilibrium point, i.e.

$$ \Updelta_{2} = { \det }\left( {\begin{array}{*{20}c} \frac{ad}{c} & 1 \\ {adm} & {ad + \frac{adm}{c}} \\ \end{array} } \right) = \frac{{a^{2} d^{2} }}{c} + \frac{{a^{2} d^{2} m}}{{c^{2} }} - adm > 0 $$

The above noted condition can be written as ${{a > c^{2} m} \mathord{\left/ {\vphantom {{a > c^{2} m} {(cd + md)}}} \right. \kern-0pt} {(cd + md)}}$. On the contrary, if ${{a < c^{2} m} \mathord{\left/ {\vphantom {{a < c^{2} m} {(cd + md)}}} \right. \kern-0pt} {(cd + md)}}$, the equilibrium point, $\left( {\frac{c}{d},\frac{dm}{cn},\frac{an}{bm}} \right)$ is unstable as $\Updelta_{2} < 0$. While ${{ad = c^{2} m} \mathord{\left/ {\vphantom {{ad = c^{2} m} {(c + m)}}} \right. \kern-0pt} {(c + m)}}$, the Routh–Hurwitz criteria do not provide any clue about stability of the equilibrium point. With this condition, the characteristic equation, ${ \det }(A - \lambda I) = 0$, can be simplified to $(\lambda^{2} + cm)(\lambda + cm/(c + m)) = 0$. Therefore, the linearized system of the Eq. (2), $G'(t) = AG(t)$, has a general solution

$$ G(t) = c_{1} K_{1} { \exp }\{ - \sqrt {cm} it\} + c_{2} K_{2} { \exp }\{ \sqrt {cm} it\} + c_{3} K_{3} { \exp }\{ - cm/(c + m)\} $$

Here $G(t) = (u(t),v(t),w(t))'$; $c_{1} ,c_{2} ,c_{3}$ are arbitrary real numbers; $K_{1} ,K_{2} ,K_{3}$ are the eigenvectors corresponding to the eigenvalues $\lambda_{1} ,\lambda_{2} ,\lambda_{3}$ respectively. Using the eigenfunction in Mathematica 4.0, it obtains

$$ K_{1} = \left( { - \frac{{{\text{b(}}\sqrt {\text{c}} + i\sqrt {\text{m}} )}}{\sqrt c n}, - \frac{{{\text{ibc}}^{ 2} m^{\frac{5}{2}} }}{{a^{2} n^{2} (\sqrt {\text{c}} - i\sqrt {\text{m}} )^{2} (\sqrt {\text{c}} + i\sqrt {\text{m}} )}},1} \right)^{\prime } $$

$$ K_{2} = \left( { - \frac{{{\text{b(}}\sqrt {\text{c}} + i\sqrt {\text{m}} )}}{\sqrt c n},\frac{{{\text{ibc}}^{ 2} m^{\frac{5}{2}} }}{{a^{2} n^{2} (\sqrt {\text{c}} - i\sqrt {\text{m}} )^{2} (\sqrt {\text{c}} + i\sqrt {\text{m}} )}},1} \right)^{\prime } $$

$$ K_{3} = \left( {\frac{bm}{cn}, - \frac{{bcm^{3} }}{{a^{2} n^{2} (c + m)}},1} \right)^{\prime } $$

Although $G(t)$ is known, the stability of the equilibrium point remains undecided analytically at the condition, ${{ad = c^{2} m} \mathord{\left/ {\vphantom {{ad = c^{2} m} {(c + m)}}} \right. \kern-0pt} {(c + m)}}$.

Appendix 2: Stability of the System (3)

There are two equilibrium points of the system described by the set of Eq. (3): the trivial one is (0,0,0) and the other one is the feasible equilibrium point, $\left( {\frac{c}{d},\frac{dm}{cn},\frac{acn}{bdm}} \right)$. The associated Jacobian matrix is,

$$ J(x,y,z) = \left[ {\begin{array}{*{20}c} {a - byz} & { - bxz} & { - bxy} \\ {dy} & { - c + dx} & 0 \\ {nyz} & {nxz} & { - m + nxy} \\ \end{array} } \right]. $$

Therefore, the Jacobian matrix at both the equilibrium points are,

$$ A = J(0,0,0) = \left[ {\begin{array}{*{20}c} a & 0 & 0 \\ 0 & { - c} & 0 \\ 0 & 0 & { - m} \\ \end{array} } \right]\;{\text{and}}\;B = J\left( {\frac{c}{d},\frac{dm}{cn},\frac{acn}{bdm}} \right) = \left[ {\begin{array}{*{20}c} 0 & { - \frac{{ac^{2} n}}{{d^{2} m}}} & { - \frac{bm}{n}} \\ {\frac{{d^{2} m}}{cn}} & 0 & 0 \\ \frac{an}{b} & {\frac{{ac^{2} n^{2} }}{{bd^{2} m}}} & 0 \\ \end{array} } \right]. $$

Obviously, (0,0,0) is unstable for $\lambda_{1} = a > 0$. The characteristic equation, $\det (B - \lambda I) = 0$, is

$$ \lambda^{3} + a(c + m)\lambda + acm = 0 $$

Therefore, the equilibrium,$\left( {\frac{c}{d},\frac{dm}{cn},\frac{acn}{bdm}} \right)$ is unstable as $\Updelta_{2} = - acm < 0$.

Appendix 3: Stability of the System (4)

Since $y' = 0$, Eq. (2) can be simplified to,

$$ \begin{aligned} & x' = a - by_{0} xz, \\ & z' = - mz + ny_{0} xz. \\ \end{aligned} $$

(9)

When $y_{0} = y(0) = 0$, the system becomes,

$$ \begin{aligned} & x' = a, \\ & z' = - mz. \\ \end{aligned} $$

(10)

The solution of the system (10) is $\left( {x_{0} + at,\;z_{0} { \exp }\{ - mt\} } \right)$, where $x_{0} = x(0) \ge 0,\,z_{0} = z(0) \ge 0$. While $y_{0} > 0$, the system (9) has a feasible equilibrium point $\left( {\frac{m}{{ny_{0} }},\frac{an}{bm}} \right)$and the Jacobian matrix is

$$ J(x,z) = \left[ {\begin{array}{*{20}c} { - by_{0} z} & { - by_{0} x} \\ {ny_{0} z} & { - m + ny_{0} x} \\ \end{array} } \right]. $$

Therefore, the Jacobian matrix at the equilibrium point is,

$$ A = J\left( {\frac{m}{{ny_{0} }},\frac{an}{bm}} \right) = \left[ {\begin{array}{*{20}c} { - \frac{{any_{0} }}{m}} & { - \frac{bm}{n}} \\ {\frac{{an^{2} y_{0} }}{bm}} & 0 \\ \end{array} } \right] $$

Then characteristic equation, ${ \det }(A - \lambda I) = 0$, is $\lambda^{2} + any_{0} /m\lambda + any_{0} = 0$. Obviously $\left( {\frac{m}{{ny_{0} }},\frac{an}{bm}} \right)$ is stable, which means that $\left( {\frac{m}{{ny_{0} }},y_{0} ,\frac{an}{bm}} \right)$ is a stable equilibrium point of the system (4). If $y_{0} < \frac{{4m^{2} }}{an}$, $\left( {\frac{m}{{ny_{0} }},y_{0} ,\frac{an}{bm}} \right)$ is a stable spiral point; if $y_{0} > \frac{{4m^{2} }}{an}$, $\left( {\frac{m}{{ny_{0} }},y_{0} ,\frac{an}{bm}} \right)$ is a stable node; if $y_{0} = \frac{{4m^{2} }}{an}$, $\left( {\frac{m}{{ny_{0} }},y_{0} ,\frac{an}{bm}} \right)$ may be either a stable spiral point, a stable node, or a degenerate stable node depending on the parameter values (see Fig. 10.25 in Zill & Cullen’s (2001) book).

Appendix 4: Stability of the System (5)

Since $y' = 0$, Eq. (5) can be simplified to

$$ x' = ax - by_{0} xz, \quad z' = - mz + ny_{0} xz. $$

(11)

When $y_{0} = 0$, Eq. (11) become

$$ x' = ax, \quad z' = - mz. $$

(12)

The solution of the system (12) is $\left( {x_{0} { \exp }\{ at\} ,\;z_{0} { \exp }\{ - mt\} } \right)$.

While $y_{0} > 0$, the system (11) becomes the classic Lotka–Volterra model. There are two equilibrium points of the system (11): the trivial one is (0,0) and the other one is the feasible equilibrium point $\left( {\frac{m}{{ny_{0} }},\frac{a}{{by_{0} }}} \right)$; the Jacobian matrix is

$$ J(x,y,z) = \left[ {\begin{array}{*{20}c} {a - by_{0} z} & { - by_{0} x} \\ {ny_{0} z} & { - m + ny_{0} x} \\ \end{array} } \right]. $$

Therefore, the Jacobian matrix at the equilibrium points are:

$$ A = J(0,0) = \left[ {\begin{array}{*{20}c} a & 0 \\ 0 & { - m} \\ \end{array} } \right]\;{\text{and}}\;B = J\left( {\frac{m}{{ny_{0} }},\frac{a}{{by_{0} }}} \right) = \left[ {\begin{array}{*{20}c} 0 & { - bm/n} \\ {an/b} & 0 \\ \end{array} } \right]. $$

Obviously, the equilibrium point, (0,0) is unstable as $\lambda_{1} = a > 0$. For the matrix B, it has been found that $\lambda_{1} = \lambda_{2} = 0$. Thus, the stability of the equilibrium point $\left( {\frac{m}{{ny_{0} }},\frac{a}{{by_{0} }}} \right)$ remains in doubt. Using the phase-plane method, a first-order differential equation has obtain:

$$ \frac{{{\text{d}}z}}{{{\text{d}}x}} = \frac{{( - m + ny_{0} x)z}}{{(a - by_{0} z)x}}. $$

After separating variables, it becomes,

$$ \int {\frac{{a - by_{0} z}}{z}{\text{d}}z} = \int {\frac{{ - m + ny_{0} x}}{x}{\text{d}}x} , $$

which can be expressed as

$$ \frac{{z^{a} }}{{{ \exp }\{ by_{0} z\} }} = K\frac{{{ \exp }\{ ny_{0} x\} }}{{x^{m} }}. $$

(13)

Here K is a constant. Let $f(z)$ denotes $z^{a} /{ \exp }\{ by_{0} z\}$ and $g(x)$ denotes $x^{m} /{ \exp }\{ ny_{0} x\}$. It is not difficult to find that $f'(a/(by_{0} )) = 0$, $f''(a/(by_{0} )) < 0$, $g'(m/(ny_{0} )) = 0$ and $g''(m/(ny_{0} )) < 0$, which mean that $f(z)$ has a maximum at $z = a/(by_{0} )$ and that g(x) has a maximum at $x = m/(ny_{0} )$. Let $M_{z}$, $M_{x}$ represent the maximum of $f(z)$ and $g(x)$, respectively. Obviously, in the case $K > M_{z} M_{x}$, Eq. (11) has no solutions; in the case of $K = M_{z} M_{x}$, Eq. (11) has a solution $\left( {\frac{m}{{ny_{0} }},\frac{a}{{by_{0} }}} \right)$. Next, it needs to consider the case of $K < M_{z} M_{x}$. In Eq. (13), suppose that $K = sM_{z}$, where $s < M_{x}$ is a positive real number. Here $g(x)$ have two different solutions $x_{m}$ and $x_{M}$ that satisfy $x_{m} < m/(ny_{0} ) < x_{M}$. Then it is easy to prove three cases. In the first case $x < x_{m}$ or $x > x_{M}$, the equation also has no solutions; in the second case $x = x_{m}$ or $x = x_{M}$, the equation has a solution $z = a/(by_{0} )$; in the third case $x_{m} < x < x_{M}$, the equation has two solutions $z_{m}$ and $z_{M}$ that satisfy $z_{m} < a/(by_{0} ) < z_{M}$. As x approaches $x_{m}$ or $x_{M}$, $f(z)$ approaches $M_{z}$, i.e. $z_{m}$ and $z_{M}$ both approach $a/(by_{0} )$. Thus the trajectories of Eq. (11) have periodicity, which implies that the trajectories of Eq. (5) have periodicity.

Appendix 5: Stability of the System (6)

There are two equilibrium points of the system described by the set of equations (6): one is $\left( {\frac{a}{h},0,0} \right)$ and another is the feasible equilibrium point, $\left( {\frac{c}{d},\frac{dm}{cn},\frac{n(ad - ch)}{bdm}} \right)$; the Jacobian matrix is

$$ J(x,y,z) = \left[ {\begin{array}{*{20}c} { - byz - h} & { - bxz} & { - bxy} \\ {dy} & { - c + dx} & 0 \\ {nyz} & {nxz} & { - m + nxy} \\ \end{array} } \right]. $$

Therefore, the Jacobian matrices at both the equilibrium points are:

$$ A = J\left( {\frac{a}{h},0,0} \right) = \left[ {\begin{array}{*{20}c} { - h} & 0 & 0 \\ 0 & { - c + \frac{ad}{h}} & 0 \\ 0 & 0 & { - m} \\ \end{array} } \right] $$

and

$$ B = J\left( {\frac{c}{d},\frac{dm}{cn},\frac{ns}{bdm}} \right) = \left[ {\begin{array}{*{20}c} { - \frac{s}{c} - h} & { - \frac{cns}{{d^{2} m}}} & { - \frac{bm}{n}} \\ {\frac{{d^{2} m}}{cn}} & 0 & 0 \\ \frac{ns}{bc} & {\frac{{cn^{2} s}}{{bd^{2} m}}} & 0 \\ \end{array} } \right], $$

where $s = ad - ch$ for simplicity. For the matrix A, if $h > ad/c$, $\lambda_{2} = - c + ad/h < 0$, which implies that the equilibrium point $\left( {\frac{a}{h},0,0} \right)$ is stable. On the contrary, if $h < ad/c$, $\lambda_{2} > 0$, which implies that the equilibrium $\left( {\frac{a}{h},0,0} \right)$ is unstable. For the matrix B, according to $\det (B - \lambda I) = 0$, the characteristic equation is

$$ \lambda^{3} + ad/c\lambda^{2} + (c + m)s/c\lambda + ms = 0. $$

Now $\Updelta_{1} = \frac{ad}{c} > 0$. If $\Updelta_{2} = \frac{{s[ad(m + c) - mc^{2} ]}}{{c^{2} }} > 0$ and $a_{3} = ms > 0$, $\left( {\frac{c}{d},\frac{dm}{cn},\frac{n(ad - ch)}{bdm}} \right)$ will be a stable critical point. Namely, it requires that $ad > c^{2} m/(c + m)$ and $s > 0$ hold simultaneously. When $s < 0$ or $ad < c^{2} m/(c + m)$, the critical point $\left( {\frac{c}{d},\frac{dm}{cn},\frac{n(ad - ch)}{bdm}} \right)$ is not stable.

Appendix 6: The Stability of Eq. (7)

There are two equilibrium points of the system described by the set of Eq (7): the trivial one is (0,0,0) and the another is the feasible equilibrium point, $\left( {\frac{c}{d},\frac{dm}{cn},\frac{(a - h)cn}{bdm}} \right)$; the Jacobian matrix is

$$ J(x,y,z) = \left[ {\begin{array}{*{20}c} {a - h - byz} & { - bxz} & { - bxy} \\ {dy} & { - c + dx} & 0 \\ {nyz} & {nxz} & { - m + nxy} \\ \end{array} } \right]. $$

Therefore the Jacobian matrices at both the equilibrium points are:

$$ A = J(0,0,0) = \left[ {\begin{array}{*{20}c} {a - h} & 0 & 0 \\ 0 & { - c} & 0 \\ 0 & 0 & { - m} \\ \end{array} } \right] $$

and

$$ B = J\left( {\frac{c}{d},\frac{dm}{cn},\frac{(a - h)cn}{bdm}} \right) = \left[ {\begin{array}{*{20}c} 0 & { - \frac{{(a - h)c^{2} n}}{{d^{2} m}}} & { - \frac{bm}{n}} \\ {\frac{{d^{ 2} m}}{cn}} & 0 & 0 \\ {\frac{(a - h)n}{b}} & {\frac{{(a - h)c^{2} n^{2} }}{{bd^{2} m}}} & 0 \\ \end{array} } \right]. $$

If $a - h < 0$, the characteristic equation, $\det (A - \lambda I) = 0$, has three negative real eigenvalues, which implies that the equilibrium point (0,0,0) is stable. If $a - h > 0$, the characteristic equation $\det (A - \lambda I) = 0$ has a positive real eigenvalue, which implies that the equilibrium point (0,0,0) is unstable. The characteristic equation $\det (B - \lambda I) = 0$ is $\lambda^{3} + (a - h)(c + m)\lambda + (a - h)cm = 0$. $\Updelta_{1} = 0$, $\Updelta_{2} = - (a - h)cm$, $a_{3} = (a - h)cm$. If $a \ne h$, there must be $\Updelta_{2} < 0$ or $a_{3} < 0$. That means that $\left( {\frac{c}{d},\frac{dm}{cn},\frac{(a - h)cn}{bdm}} \right)$ is an unstable equilibrium point.