Skip to main content
SpringerLink
Log in

An Advanced Learned Type-3 Fuzzy Logic-Based Hybrid System to Optimize Inventory Cost for a New Business Policy

  • SCIENTIFIC RESEARCH PAPER
  • Published:
Proceedings of the National Academy of Sciences, India Section A: Physical Sciences Aims and scope Submit manuscript

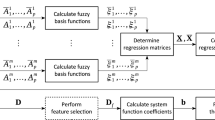
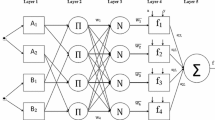
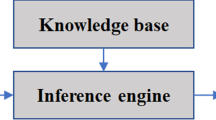
Abstract

In this paper, a type-3 fuzzy logic-based system has been created by accumulating the demand as the input variable to design the ideal inventory level that would minimize the overall inventory cost for the economic order quantity model. The new adaptation law based on the extended Kalman filter, and the unscented Kalman filter is carried out to tune the rule parameters and antecedent parameters of the suggested IT3-FLS. A real-life data set is collected to feed and test the IT3-FLS model. Some statistical measures like root-mean-square error, variance, correlation coefficient (R), and Theil’s coefficient are calculated to examine the prediction accuracy. The lowest RMSE observed is 0.02138, and the highest R is 0.99975 for IT3-FLS. Furthermore, the optimal total variable cost is calculated by collecting the estimated inventory. Additionally, to demonstrate the applicability of the suggested methodology, one real-life issue and its managerial resolution have been highlighted.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Data availability statement

The authors confirm that the data supporting the findings of this study are available within the article and its supplementary materials.

References

  1. Ghare PM, Schrader GF (1963) A model for an exponentially decaying inventory. J Ind Eng 14:238–243

    Google Scholar 

  2. Harris FW (1915) Operations and costs (factory management series). Aw Shaw Co., Chicago

    Google Scholar 

  3. Chang HJ, Dye CY (1999) An EOQ model for deteriorating items with time varying demand and partial backlogging. J Oper Res Soc 50(11):1176–1182

    Article  MATH  Google Scholar 

  4. Sana SS (2020) A two-echelon inventory model for ameliorating/deteriorating items with single vendor and multi-buyers. Proc Nat Acad Sci, India 90A:601–614

    MathSciNet  MATH  Google Scholar 

  5. Ghosh PK, Manna AK, Dey JK, Kar S (2022) A deteriorating food preservation supply chain model with downstream delayed payment and upstream partial prepayment. RAIRO-Oper Res 56(1):331–348

    Article  MathSciNet  MATH  Google Scholar 

  6. Pando V, San-José LA, García-Laguna J, Sicilia J (2018) Optimal lot-size policy for deteriorating items with stock-dependent demand considering profit maximization. Comput Ind Eng 117:81–93

    Article  Google Scholar 

  7. Rout C, Chakraborty D, Goswami A (2021) A production inventory model for deteriorating items with backlog-dependent demand. RAIRO-Oper Res 55:S549–S570

    Article  MathSciNet  MATH  Google Scholar 

  8. Kumar S, Singh AK, Kar S (2019) A deteriorating inventory model with price dependent consumption rate and exponentially declining partial backlogging. Proc Nat Acad Sci India 89A:525–532

    MathSciNet  Google Scholar 

  9. Sharma AK, Tiwari S, Yadavalli VS, Jaggi CK (2020) Optimal trade credit and replenishment policies for non-instantaneous deteriorating items. RAIRO-Oper Res 54(6):1793–1826

    Article  MathSciNet  Google Scholar 

  10. Rahaman M, Mondal SP, Alam S (2021) An estimation of effects of memory and learning experience on the EOQ model with price dependent demand. RAIRO-Oper Res 55(5):2991–3020

    Article  MathSciNet  MATH  Google Scholar 

  11. Mishra VK, Shanker K (2019) Optimal ordering quantity for substitutable products under quantity discount with cost of substitution. Pro Natl Acad Sci, India 89A:497–508

    MathSciNet  Google Scholar 

  12. Guo Z, Wang H (2023) Implications on managing inventory systems for products with stock-dependent demand and nonlinear holding cost via the adaptive EOQ policy. Comput Oper Res 150:106080

    Article  MathSciNet  MATH  Google Scholar 

  13. Sarkar B, Dey BK, Sarkar M, Hur S, Mandal B, Dhaka V (2020) Optimal replenishment decision for retailers with variable demand for deteriorating products under a trade-credit policy. RAIRO-Oper Res 54(6):1685–1701

    Article  MathSciNet  Google Scholar 

  14. Kar C, Roy TK, Maiti M (2022) EOQ model with price, marketing, service and green dependent neutrosophic demand under uncertain resource constraint: a geometric programming approach. Neutrosophic Sets Syst 51:797–823

    Google Scholar 

  15. Cárdenas-Barrón LE, Shaikh AA, Tiwari S, Treviño-Garza G (2020) An EOQ inventory model with nonlinear stock dependent holding cost, nonlinear stock dependent demand and trade credit. Comput Ind Eng 139:105557

    Article  Google Scholar 

  16. Zadeh L (1965) Fuzzy sets. Inform. Control 8:338–353

    Article  MathSciNet  MATH  Google Scholar 

  17. Ashraf Z, Malhotra D, Muhuri PK, Lohani QD (2021) Interval type-2 fuzzy vendor managed inventory system and its solution with particle swarm optimization. Int J Fuzzy Syst 23(7):2080–2105

    Article  Google Scholar 

  18. Shekarian E, Kazemi N, Abdul-Rashid SH, Olugu EU (2017) Fuzzy inventory models: a comprehensive review. Appl Soft Comput 55:588–621

    Article  Google Scholar 

  19. Das A, Bera UK, Maiti M (2019) A solid transportation problem in uncertain environment involving type-2 fuzzy variable. Neural Comput Appl 31:4903–4927

    Article  Google Scholar 

  20. Kumar RS (2018) Modelling a type-2 fuzzy inventory system considering items with imperfect quality and shortage backlogging. Sādhanā 43:1–10

    Article  MathSciNet  Google Scholar 

  21. Debnath BK, Majumder P, Bera UK, Maiti M (2018) Inventory model with demand as type-2 fuzzy number: a fuzzy differential equation approach. Iran J Fuzzy Syst 15(1):1–24

    MathSciNet  MATH  Google Scholar 

  22. Rout C, Kumar RS, Chakraborty D, Goswami A (2019) An EPQ model for deteriorating items with imperfect production, inspection errors, rework and shortages: a type-2 fuzzy approach. Opsearch 56:657–688

    Article  MathSciNet  MATH  Google Scholar 

  23. Panja S, Mondal SK (2019) Analyzing a four-layer green supply chain imperfect production inventory model for green products under type-2 fuzzy credit period. Comput Ind Eng 129:435–453

    Article  Google Scholar 

  24. De A, Khatua D, Kar S (2020) Control the preservation cost of a fuzzy production inventory model of assortment items by using the granular differentiability approach. Comput Appl Math 39:1–22

    Article  MathSciNet  MATH  Google Scholar 

  25. Poswal P, Chauhan A, Boadh R, Rajoria Y K (2022) A review on fuzzy economic order quantity model under shortage. In: AIP Conference Proceedings. AIP Publishing LLC, vol 2481, No 1, p 040023

  26. Raj S A, Henrietta M H, Kalaiarasi K, Sumathi M (2021) Rethinking the limits of optimization economic order quantity (EOQ) using self generating training model by adaptive-neuro fuzzy inference system. In: Soft computing and its engineering applications: second international conference, icSoftComp 2020, Changa, Anand, India, December 11–12, 2020, Proceedings 2. Springer, Singapore, pp 123–133

  27. Mohammadzadeh A, Sabzalian MH, Zhang W (2019) An interval type-3 fuzzy system and a new online fractional-order learning algorithm: Theory and practice. IEEE Trans Fuzzy Syst 28(9):1940–1950

    Article  Google Scholar 

  28. Qasem SN, Ahmadian A, Mohammadzadeh A, Rathinasamy S, Pahlevanzadeh B (2021) A type-3 logic fuzzy system: Optimized by a correntropy based Kalman filter with adaptive fuzzy kernel size. Inf Sci 572:424–443

    Article  MathSciNet  Google Scholar 

  29. Castillo O, Castro JR, Melin P (2023) Interval type-3 fuzzy systems: a natural evolution from type-1 and type-2 fuzzy systems. Fuzzy logic and neural networks for hybrid intelligent system design. Springer, Cham, pp 209–221

    Chapter  Google Scholar 

  30. Castillo O, Castro JR, Melin P (2023) Forecasting the COVID-19 with interval type-3 fuzzy logic and the fractal dimension. Int J Fuzzy Syst 25(1):182–197

    Article  Google Scholar 

  31. Nabipour N, Qasem SN, Jermsittiparsert K (2020) Type-3 fuzzy voltage management in PV/hydrogen fuel cell/battery hybrid systems. Int J Hydrogen Energy 45(56):32478–32492

    Article  Google Scholar 

  32. Liu Z, Mohammadzadeh A, Turabieh H, Mafarja M, Band SS, Mosavi A (2021) A new online learned interval type-3 fuzzy control system for solar energy management systems. IEEE Access 9:10498–10508

    Article  Google Scholar 

  33. Mosavi A, Qasem SN, Shokri M, Band SS, Mohammadzadeh A (2020) Fractional-order fuzzy control approach for photovoltaic/battery systems under unknown dynamics, variable irradiation and temperature. Electronics 9(9):1455

    Article  Google Scholar 

  34. Balootaki MA, Rahmani H, Moeinkhah H, Mohammadzadeh A (2021) Non-singleton fuzzy control for multi-synchronization of chaotic systems. Appl Soft Comput 99:106924

    Article  Google Scholar 

  35. Cao Y, Raise A, Mohammadzadeh A, Rathinasamy S, Band SS, Mosavi A (2021) Deep learned recurrent type-3 fuzzy system: Application for renewable energy modeling/prediction. Energy Rep 7:8115–8127

    Article  Google Scholar 

  36. Vafaie RH, Mohammadzadeh A, Piran MJ (2021) A new type-3 fuzzy predictive controller for MEMS gyroscopes. Nonlinear Dyn 106(1):381–403

    Article  Google Scholar 

  37. Gheisarnejad M, Mohammadzadeh A, Farsizadeh H, Khooban MH (2021) Stabilization of 5G telecom converter-based deep type-3 fuzzy machine learning control for telecom applications. IEEE Trans Circuits Syst II Express Briefs 69(2):544–548

    Google Scholar 

  38. Wang JH, Tavoosi J, Mohammadzadeh A, Mobayen S, Asad JH, Assawinchaichote W, Vu MT, Skruch P (2021) Non-singleton type-3 fuzzy approach for flowmeter fault detection: experimental study in a gas industry. Sensors 21(21):7419

    Article  ADS  Google Scholar 

  39. Tarafdar A, Majumder P, Deb M, Bera U K (2023) Application of a q-rung orthopair hesitant fuzzy aggregated Type-3 fuzzy logic in the characterization of performance-emission profile of a single cylinder CI-engine operating with hydrogen in dual fuel mode. Energy 126751.

  40. Tarafdar A, Majumder P, Deb M, Bera UK (2023) Performance-emission optimization in a single cylinder CI-engine with diesel hydrogen dual fuel: a spherical fuzzy MARCOS MCGDM based Type-3 fuzzy logic approach. Int J Hydrogen Energy. https://doi.org/10.1016/j.ijhydene.2023.04.019

    Article  Google Scholar 

  41. Castillo O, Castro JR, Melin P (2022) Interval type-3 fuzzy systems: theory and design. Springer, Berlin

    Book  MATH  Google Scholar 

  42. Castillo O, Melin P (2022) Towards interval Type-3 intuitionistic fuzzy sets and systems. Mathematics 10(21):4091

    Article  Google Scholar 

  43. Karnik NN, Mendel JM (1999) Applications of type-2 fuzzy logic systems to forecasting of time-series. Inf Sci 120(1–4):89–111

    Article  MATH  Google Scholar 

  44. Castillo O, Amador-Angulo L, Castro JR, Garcia-Valdez M (2016) A comparative study of type-1 fuzzy logic systems, interval type-2 fuzzy logic systems and generalized type-2 fuzzy logic systems in control problems. Inf Sci 354:257–274

    Article  Google Scholar 

  45. Wu D (2012) On the fundamental differences between interval type-2 and type-1 fuzzy logic controllers. IEEE Trans Fuzzy Syst 20(5):832–848

    Article  Google Scholar 

  46. Mendel JM (2021) Non-singleton fuzzification made simpler. Inf Sci 559:286–308

    Article  MathSciNet  MATH  Google Scholar 

  47. Mendel JM, John RI, Liu F (2006) Interval type-2 fuzzy logic systems made simple. IEEE Trans Fuzzy Syst 14(6):808–821

    Article  Google Scholar 

  48. Mendel JM (2013) General type-2 fuzzy logic systems made simple: a tutorial. IEEE Trans Fuzzy Syst 22(5):1162–1182

    Article  Google Scholar 

  49. Khosravi A, Nahavandi S (2013) Load forecasting using interval type-2 fuzzy logic systems: optimal type reduction. IEEE Trans Industr Inf 10(2):1055–1063

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology Agartala, Jirania, West Tripura, 799046, India

    Anirban Tarafdar, Pinki Majumder & Uttam Kumar Bera

Authors
  1. Anirban Tarafdar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pinki Majumder
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Uttam Kumar Bera
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Uttam Kumar Bera.

Ethics declarations

Conflicts of interests

All the authors have no potential conflicts of interest. The research does not involve human participants and/or animals.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tarafdar, A., Majumder, P. & Bera, U.K. An Advanced Learned Type-3 Fuzzy Logic-Based Hybrid System to Optimize Inventory Cost for a New Business Policy. Proc. Natl. Acad. Sci., India, Sect. A Phys. Sci. 93, 711–727 (2023). https://doi.org/10.1007/s40010-023-00849-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40010-023-00849-5

Keywords

Search

Navigation