Introduction

Remote sensing applications are common techniques to map TSS concentrations and their temporal and spatial fluctuations. Nechad et al. (2010) demonstrated that using just one Landsat band can yield a sensitive approach for estimating TSS but only if the right band is selected; the first four Landsat bands are closely correlated with total suspended matter, according to several studies, but the strength of this link varies with wavelength and water depth (Cox et al. 1998; Dekker et al. 2002; Brezonik et al. 2005; Akbar et al. 2010).

Few remote sensing studies have been carried out in which a long-term follow-up is performed for monitoring biophysical variables in lakes, particularly in the case of TSS. In the history of remote sensing, the monitoring of coastal water quality dates back almost to the beginning of the satellite exploration era, and these studies have continued to be developed, mainly based on the correlation between "in situ" observations and the direct correlation with satellite images of the same dates. Nevertheless, these studies focus on river mouths and coastal systems, with important studies including estimates of TSS input to the ocean (Overeem et al. 2017), variability in sediment plume size (Brando et al. 2015), reservoir impacts on the concentration of sediments (Pereira et al. 2017), the impacts of land use change on the entry of sediments (Telmer et al. 2006) and the variability of sediments in the lagoons (Volpe et al. 2011). An important primary continental source of freshwater for industrial, recreational, and irrigating purposes is the lakes (Carvalho et al. 2013).

Due to limitations in time, money, and space, the traditional on-site monitoring system has been found to be ineffective (Philipson et al. 2016). For instance, total suspended solids (TSS), organic properties (TOC and TIC), or microbiological properties (chlorophyll-a (Chl-a)) can all be computed simultaneously using remote sensing, which records synoptic radiation from the water surface (Matsushita et al. 2015; Tyler et al. 2016; Dörnhöfer et al. 2018). Numerous research projects have attempted to determine the concentration of TSS using mainly two satellite remote platforms and sensors: Landsat (Zhou et al. 2007; Kallio et al. 2008; Wu et al. 2008; Zhang et al. 2014; Vanhellemont and Ruddick 2014; Wu et al. 2015), and MODIS (Miller and McKee 2004; Chen et al. 2007, 2015; Raag et al. 2013; Hudson et al. 2014; Petus et al. 2014; Ayana et al. 2015).

Three approaches are generally used to establish the relationship between spectral properties detected by satellite and in situ measurements (Ma and Dai 2005). These are: (i) establishing a relationship through theoretical formulas, (ii) the empirical method in which curve fitting is used, and (iii) the semi-empirical method, which is the combination of theoretical and empirical techniques. Analytical models consider parameters related to water surface reflectance affected by TSS concentration, and regression methods are commonly used in empirical approaches. The regression method is one of the most widely used techniques to study the relationship between reflectance values of multispectral images and in situ measurements. Acquired satellite data are used to establish relationships with water quality parameters using multiple regression techniques. In empirical approaches, remote sensing data are correlated with TSS concentration using interpolation techniques applied to a set of in situ sampling samples. Several AI-based algorithms have been proposed for the empirical approach (Balaguer-Ballester et al. 2002).

The use of a standard linear, or non-linear, regression between band-spectrum data and in situ water quality measurements is the remote sensing research method most frequently used to study inland waters. In these models, a single spectral band or combinations of few of several spectral bands are used (Tyler et al. 2006; Kallio et al. 2008; Kratzer et al. 2008; Wang et al. 2008; Wu et al. 2008; Duan et al. 2009; Cui et al. 2013; Espinoza-Villar et al. 2013; Qiu 2013; Choi et al. 2014; Kaba et al. 2014; Shen et al. 2014; Chen et al. 2015; Shi et al. 2015; Membrillo-Abad et al. 2016). However, there are no techniques that employ all the spectral bands as input variables to correlate with the results of in situ measurements.

Due to their straightforward development, empirical approaches are the most widely employed to estimate TSS concentration; however, because these methods lack physical foundation, their applicability is restricted to the location and time in which they were produced (Chen et al. 2015). Empirical approaches are primarily constrained to the place where they were developed by their inability to generalize over wide spatial and temporal scales, because of the changes in water composition and the significant variability in the spectral signatures. As a result, the range and frame of the input data limit the reliability of empirical model predictions. These models, however, do not incorporate any inverse models of the optical qualities that are inherent to a particular body of water. Semi-empirical models use multiband ratio values based on the physical properties of interest, like land vegetation indices.

The results of previous studies indicate the need for new approaches to replace traditional methods. An inherent limitation of the traditional approaches is the difficulty to generalize their results into large spatial and temporal scales due to variations in atmospheric composition and the specific characteristics of the studied area. In previous investigations, the TSS determination algorithm has been generated using linear regression in a single band or a combination of several bands as predictors (Nezlin and DiGiacomo 2005; Nechad et al. 2010; Caballero et al. 2014). However, the linear regression method has some major drawbacks: (i) training can be expensive; (ii) minimizing training errors can lead to poor algorithm performance in generalization.

In this work, a novel method is presented to determine the concentration of various parameters (TSS, Chl-a, TOC and TIC) in lakes that can be used to evaluate water quality, this method is based on the spectral response related to those parameters and the use of artificial intelligence. The main contribution of this method is that instead of using a specific combination of bands (ratios, indices, etc.), the 7 bands of the Landsat images are used simultaneously and subsequently a multiple correlation is performed using unsupervised artificial intelligence, in order to make this method more robust. The site chosen to develop this method, as well as to test its precision and accuracy, was Lake Chapala, because of the availability of a data time series that represents more than a decade of in situ sampling, and its environmental, economic, and social importance. Lake Chapala is located in the central part of Mexico, and it is currently in imminent risk of collapse mainly due to 3 factors: high levels of pollution caused by industrial discharges, overexploitation of its waters, and lack of wastewater treatment plants. The negative impacts are accentuated by climate change, the introduction of exotic species, the construction of local infrastructure, changes in land use on the shore and increased anthropogenic activities that result in eutrophication processes and pollution. This has caused its size to decrease and affects its water levels and productive capacity.

Study area

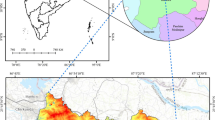
Lake Chapala is located in the western part of central Mexico (20° 06′ 36''–20° 18′ 00'' North, 102° 42′ 00''–103° 25 ′30'' West, 1520 m altitude) in the Lerma-Chapala basin (Fig. 1) and has an area of approximately 1,100 km2. Its major axis has an east–west orientation with a maximum length of 77 km, and its minor axis has a length of 22 km (De Anda et al. 1998). The region's climate is classified as subtropical, according to the modified Köppen scale (García 1988), with strong winds, up to 8–10 m/s that generate strong mixing in the water column (Filonov et al. 1998). Its main tributary is the Lerma River, which is fed mainly by drainage in the Lerma–Chapala basin; the main flow losses are related to evaporation and its use for human consumption, and only in the case of accumulation to its maximum capacity, there is an outflow of water towards the Santiago River towards the north (Sandoval 1994; Aparicio 2001). Due to the shallow depth of the lake, a great inorganic turbidity is produced due to fine clay resuspension (Lind and Dávalos 2001). In addition, the clay particles act as a substrate for plankton growth, which promotes changes in the optical properties of the water column (Sandoval 1994; Aparicio 2001).

Fig. 1
figure 1

Location of Lake Chapala and extension of the Lerma–Santiago–Pacifico basin (de Membrillo-Abad et al. 2016)

Full size image

The cartography reveals two clearly differentiated periods in the lacustrine contours: one prior to the construction of the embankment or dike of the area known as Ciénega de Chapala (in 1905) in the dusty north-eastern end of the old lake. The storage capacity of the lake was a maximum of 5600 Mm3, before the Ciénega construction that reduced its volume to 4,500 Mm3. This work was carried out between 1905 and 1910.

Lake Chapala has tributaries in the Lerma–Chapala–Santiago hydrological system with an estimated area of 130,000 km2 (Fig. 1), and the calculated average annual total volume of solids contributed by the tributaries to Lake Chapala is 69,506 tonnes per year, which for the 400 ha of Lake reservoir area means that the average sediment deposit is 40 cm per year (Zarate et al. 2001).

Materials and methods

Methodology

To develop the TSS prediction model is necessary to determine the relation between remote sensing data and the in situ data. Since field measurements do not always coincide in space and time with satellite images, a selection was made with the closest correspondence between the dates and the corresponding pixels.

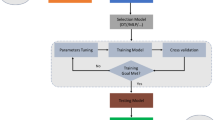
The methodology to correlate Landsat images with in situ measurements consists of four phases (Chang et al., 2014): “(1) radiometric correction; (2) extraction of spectral reflectance values in sample point windows; (3) statistical analysis of in situ data and (4) generation of the most efficient multiple linear regression model by statistical analysis”; in this work, the selected statistical tools selected were the following: EDA statistical analysis, multiple linear regression, MRL generation, and advanced machine learning application.

Remote sensing data

Satellite data acquisition Landsat satellite images

The data used in this study included 32 cloud-free Multispectral Landsat-5 TM and Landsat ETM + scenes from May 2005 to November 2016 (Table 1) that cover the total area (path 28-row 46 and path 29-row 46).

Table 1 Dates of water sampling, acquisition of Landsat images and number of in situ observations
Full size table

Pre-processing

Pre-processing operations involve georeferencing and atmospheric correction as image restoration and rectification, they are aimed to correct for atmospheric radiometric distortions of data, and platform geometric distortions of data. The atmospheric correction was calculated using Jensen’s (1996) dark body reflectance method. After pre-processing Landsat data and pairing with in situ measured TSS, a total of 22 matched data sets were available for development of the turbidity simulation model.

On-site measurements

In Lake Chapala, the Mexican government agency responsible for water resources management carries out continuous monitoring of water quality (IMTA, 2009). They collect field information on turbidity and visibility using Secchi disc and water sampling. Chemical laboratory analyses are performed on the collected water samples to determine TSS concentration. The chemical data of the lake water are available from the database of the National Water Commission (CONAGUA). The data used here are those that coincide with the available cloud-free Landsat images from 2005 to 2015.

Satellite-in situ match-ups

The TSS-RS model requires determination of the relationship between satellite data and in situ experimental data. A match-up is obtained following consecutive steps. First, satellite data are extracted over a pixel that corresponds to the location of the field station. Second, the value of reflectance is obtained. In situ measurements were matched with reflectance values from the processed Landsat Images. Match-up data are obtained by coordinating the in situ observations with the satellite data.

Model construction

The objective of this step was to generate a general model to quantify the concentrations of suspended solids present in the water, using the information obtained through remote sensors regardless of the time. Thus, multiple regressions with all independent variables combined were considered, taking care to avoid dependency between covariables.

Considering that the sample size of this work is not large enough, all observations (Table 1) were used to compute the MLR model, due to the probabilistic assumptions of this set of models: the sample size for the multiple regression analysis requires at least 10 cases per independent variable in the analysis, in our case 90 samples. The determination of this sample size is based on the 95% confidence intervals associated with correlations at the degree of precision (Green, 1991). After adjustment, a cross-validation step could be performed. In this work, two processing steps were considered in the machine learning processing for the prediction of TSS, the first is the model development from a training subgroup, and the second is the test with a data set different from the one used in the first group. In this study, we used 80% of the collected data for machine learning training and 20% for testing.

The model to estimate the TSS of the Chapala Lake is developed using the relation between the Landsat data and the measured TSS data for each date. The model development method, multiple linear regression (MLR) algorithm, was selected for the TSS model, assuming that the dependent variable TSS ground measurement is a linear function of reflectance values from the Landsat image bands. The regression variance ratio can be denoted as R2, which indicates the model prediction ability. Additionally, the magnitude of R2 represents the correlation between the independent and dependent variables for each date as presented in Table 2.

Table 2 Descriptive statistics, including sampling date, minimum (Min), maximum (Max), mean (Mean), standard deviation (Std Dev), R-squared linear regression analysis (R2), and the root mean square error (RMSE). No single analysis indicates that was not possible to calculate the linear regression due to the scarce number of samples
Full size table

Statistical methods

Statistical analysis of in situ data

We selected the value for each point and correlated all bands with TSS ground data, we treat each event as an independent sample. We first performed exploratory data analysis (EDA) and completed an examination of the data to suggest partial descriptions and hidden relationships, regardless of the statistical criteria used in confirmatory settings (Table 2).

Regression analysis can be used to estimate the concentration of TSS, and a model generated through a best-fit equation can describe the relationship between field data and the corresponding in situ data. The correlation coefficient R2 is used to evaluate the precision of these models. The objective of regression analysis is to build a function of predictor variables to express the response variable.

Exploratory data analysis (EDA)

Exploratory data analysis (EDA) is a term coined by John W. Tukey in his book on Statistics (Tukey 1977), it is also known as descriptive statistics. The purpose of EDA is to inspect and explore data, use summary statistics. The EDA is the forerunner of any geostatistical analysis; it is performed to familiarize with the data and detect pattern regularities. Exploratory analysis provides the distribution and experimental or empirical behaviour of the data regardless of their location (Kitanidis 1997). One of the most important purposes of the EDA on geospatial data is to characterize the range of autocorrelation presented by the data, as well as the possible correlation between different variables. The application of geostatistical techniques to environmental variables requires that these data have a normal distribution (Webster and Oliver 2007); therefore, a previous evaluation of the data is necessary.

Regression analysis

The simple linear regression model has been used successfully by many investigators in a wide variety of disciplines to relate the dependent variable to a single predictor variable. However, in many situations, the relationship between the dependent variable and single predictor variables is not strong. Therefore, the MLR has been proposed recently as a better approach to solve this problem. The application of these techniques helps in the interpretation of complex data matrices; in this work, we use multiple linear regression models (MLR). Multiple linear regression models relate dependent variables to several independent variables (explanatory variables) using a predefined equation (Rogerson 2001). Equation 1 shows the general multiple linear regression model:

$${\text{Y }} = {\text{ A }} + {\text{ B1X1 }} + {\text{ B2X2 }} + \, \cdot \, \cdot \, \cdot \, + {\text{ BnXi}}$$
(1)

where Y is the dependent variable, Xi are the independent variables, and B1… Bn are the regression coefficients. If the coefficients and input variables are known, then the regression equation can be used to make predictions. However, the prediction made by the regression model (Eq. 1) frequently does not coincide with the observed values of Y, so it is necessary to calculate the error of the model, that is, the difference between the predicted values and the actual values (Eq. 2):

$${\text{Y }} = {\text{ A }} + {\text{ B1X1 }} + {\text{ B2X2 }} + \, \cdot \, \cdot \, \cdot \, + {\text{ BnXi}}, + \, {{\epsilon}}$$
(2)

where ε is the random error, the value that indicates the amount of dispersion in the estimation of the Y value. The most common method to estimate the regression coefficients is the least squares, which is used in this work. In regression analysis, three criteria are required so that the fitness of the function would be acceptable: (1) the mean and the variance of the random error should be zero and a constant value, respectively; (2) the function fitted to the data should be significant (α = 0.05 is the significant level) so that the analysis of variance could be used; and (3) the value of the coefficient of determination (R2) is as close to 1 as possible. Based on Granian et al. (2015), the criteria to evaluate the regression analysis are: “1. The variance and the mean of the random error should be a constant value and zero, respectively. 2. The coefficient of determination value which is called (R2) should be tested 3. Given the fact that adding independent variables to the model will increase the R2 value, the adjusted determination coefficient which is called (R2adj) 4. In regression analyses, the p value of final coefficients for each specific model could be applied after choosing the best model. Accordingly, the p value of the regression model in the analysis of variance test should be acceptable (less than or equal to 0.05)”.

Best regression subset for the data set

When there are multiple predictor variables, there are many combinations that can be used in a regression model, the optimal combination can be determined through a series of trial-and-error attempts. The need for selecting a subset of the available Landsat spectral bands to reduce the dimensionality of remote sensing data was considered in many works of the TSS relation with remote sensing. Considerable attention has been paid in the literature to the choice of the criterion used to evaluate and determine the best subset. There are automatic variable selection procedures that choose which variables to include in a regression model in a scenario where there are many predictor variables (spectral bands in the Landsat image) and a response variable (TSS), the method to select the best regression model is the best regression subset (BRS).

In the best subset regression method, all possible models based on the specified independent variables are fitted, and then, BRS compares all possible models using a specific set of predictors and shows the most appropriate models that contain one predictor, two predictors, etc. The criterion for selecting the most suitable models for this process is R2, because R2 is used to determine the degree of predictability of the dependent variable based on the set of predictive variables to determine the best model, the best subset would be the one with the R2 nearest to 1.

Machine learning

Machine learning (ML) is an evolution of artificial. ML is great for solving problems where our theoretical knowledge is still incomplete, but we have numerous observations and additional data. Such systems can be massively multivariate, involving even thousands of variables. Through retrieval algorithms, ML has been shown to be useful in numerous applications in many parts of the Earth system (land, ocean, and atmosphere) and beyond. In remote sensing, ML is an effective empirical method for regression and classification.

When analysing remote sensing data, the four most common goals of machine learning are classification, clustering, regression, and dimensionality reduction. Regression methods are suitable when the objective is to estimate or predict the effect of a variable based on a set of covariates. A regression model is developed or trained based on a set of input variables with known answers. In this work, the regression results estimate or predict TSS concentrations from spectral bands extracted from Landsat images.

In supervised machine learning, an artificial intelligence system "learns" to determine the best fit for the predictor variable by analysing the supplied data (examples). The goal of supervised ML is to learn the rules for mapping sets of inputs and outputs; in this case, the input set consists of the Landsat spectral bands, and the output consists of the TSS. The construction of the model from a training subgroup was the first phase that was performed in the ML processing for the prediction of TSS. The second step involved testing the model using data that was distinct from the training subgroup. In this study, we randomly selected 80% of the obtained data for machine learning training and 20% for testing. By explicitly fitting a model to the data, machine learning seeks to identify the optimal relationship between the input (reflectance) and output (TSS). In order to find the ideal settings for the model, the model parameters are modified by minimizing the prediction error in the validation data set.

Results and discussion

Match-up between satellite images and in situ measurements and EDA of in situ TSS data

As a result of the match-up of all images and field observations, a total of 315 observations were obtained (Table 1). We used these data to predict TSS in Lake Chapala. Table 2 shows the descriptive statistics of TSS concentration measured which ranged from 1 (mg/L), on 05/25/2009, to 257 (mg/L); on 04/06/2015. The lowest average value is 10.34, 06/09/2011, (mg/L) to the highest average value 70.46 (mg/L), 02/27/2013.

MRL results of data sets for each date

22 MLR-models were constructed to identify the single relation for each date and explain the highest variance proportion of TSS measurements, inferred from R2 and adjusted R2. The performance of MLR with respect to minimum, maximum, mean, standard deviation, R2, and RMSE for the 22 models is displayed in Table 2.

The objective of this calculation was to identify the feasibility to generate a general the model of TSS present in the water from the Landsat satellite images for every specific date and then use all data to obtain a general relation for the eleven years. To evaluate the general multiple linear regression model, it is necessary to analyse the results for a single date. In Table 2, R2 and RMSE for all the single date analysis are presented. The values of R2 nearest to 1 correspond to the 05/24/2006 data, with 0.96, which is a very good correlation, and the RMSE value is 3.01. Conversely, the lowest value of R2 is 0.44, 25/05/2009 with a RMSE value of 9.61, which is a very poor correlation. Other important aspect to consider is that these particular results yield a correlation that is valid only for each specific date and are not valid for a general model. In the last line of Table 2, the results for all data sets were input in the model, assuming that all the in situ measurements are independent variables; in this general model, the correlation R2 is 0.52 and RMSE is 25.52; however, this exercise is useful to compare the results of a broad model constructed by simply including all data in the MRL without the application of machine learning in the calculation process. It is important to consider that in this specific case using all data, the results are not valid because the data are not independent and do not fulfil the requirements of the method.

Best regression subset

Table 3 shows the results of the best subset regression for all data sets (see Table 1 for data sets). The regression of the best subset method calculates all possible models and shows the best candidates (the spectral bands of the Landsat images) based on R2 (Table 3). Each row represents a different case, showing the best two options for each number of included independent variables. The X denotes the independent variables used in each model.

Table 3 Results of the application of regression of the best subsets for all data sets. X indicates the variables included in each model. R2 represents the maximum value for each subset
Full size table

After calculation of all the possible band combinations, Table 4 presents the result of the best subgroup analysis regression for all sampling dates, including the group "all data". R2 min is the minimum value of R2 in the analysis and corresponds to 1 band and Max is the maximum R2 that represents the best subset of the regression group; the best results always use the 7 Landsat spectral bands. This analysis shows that the best TSS MLR requires the use of all available satellite imagery bands. It is important to note that the “all data” group does not yield the best R2.

Table 4 Minimum (1 spectral band) and maximum (7 spectral bands) R2 of the regression of the best subsets
Full size table

Machine learning

Using the best-fitted model for all cloud-free available Landsat scenes for the study area, we obtained the best-estimated correlation between Landsat images and TSS for the period February 2005 to August 2015.

As mentioned in the Methods section, predictive performance was evaluated using the correlation coefficient (R2) and the root mean square error (RMSE) from predictions of the training model, by using machine learning to create a model to correlate the in situ measurements of the TSS and Landsat satellite data.

The multiple linear regression model presented in Eq. (3) was generated using multiple linear regression, and applying machine learning to correlate the TSS in situ sampling data with the 7 bands of the Landsat satellite:

$${\text{TSS}} = {18}.{246} - {1}.{\text{637B1}} - 0.{\text{826B2}} + {2}.{\text{541B3}} + {2}.{\text{322B4}} - {1}.0{\text{18B5}} + 0.{\text{373B6}} - 0.{\text{824B7}}$$
(3)

where B1, B2, B3, B4, B5, B6, B7 are the Landsat image bands.

This model has R2 value of 0.818, RMSE of 22.89 and p values less than 0.05. These 3 values indicate that the model is valid and reliable. The correlation equation was better than the previously obtained correlations using all data, R2 increased from 0.56 to 0.818 and RMSE decreased from 31.52 to 22.89, a decrease of 37%.

This model shows that the Landsat spectral bands B3 [red], B4 [near infrared] and B6 [thermal infrared] have a positive correlation, conversely B1 [blue], B2 [green], B5 [medium infrared] and B7 [medium infrared] have a negative correlation. Similarly, the obtained coefficients indicate that B1, B3, B4 and B5 had the strongest linear relationship with TSS, on the other way B6 had the weakest linear relationship with TSS. That is consistent with previous works about correlation of TSS spectral characteristics.

Equation (3) represents the relationship between the TSS data measured in situ and the reflectance information contained in the spectral bands of the Landsat images (Fig. 2). Figure 2 shows the scatter plot of the predicted values vs actual values in (mg / L), when all the calculated values are correct this plot must follow a 45 degree line that indicates that values are the same in both axes: predicted and actual values. We can note that most values are concentrated in a region close to that relation. Therefore, model assumptions seemed to be satisfactory.

Fig. 2
figure 2

Comparison of measurements of TSS (predicted value) and predicted values of the multiple linear regression (MLR) model of AI TSS (response)

Full size image

Figure 3 shows the residual patterns of the computed model (Eq. 3). As it can be observed, the model residuals seemed to have a normal distribution with mean value 0, and no marked trend (homoscedasticity) in residuals versus fitted values.

Fig. 3
figure 3

Residual plot of the correlation between the observed TSS and the machine learning multiple linear regression model in mg/L

Full size image

The plot in Fig. 3 can be used to complement and better understand these values; the difference between the predicted values for the model versus the real values in the set of data to generate the model is plotted. A red 45-degree line is included to help to visualize the results presented in this plot. The best-fitted values of the model are the values that are closest to that red line and the worst-fitted values are the values that are far from the line. In this plot, some outliers are evident, in the lowest values and most importantly in the highest values of the TSS. This is an important issue because it indicates that the model is good to predict values lower than 100 mg/L, but at higher values, the model correlation decreases.

MLR with machine learning using the 315 observations was implemented with the best performance to determine the predictive relationships for all spectral bands of Landsat images (independent variables) with TSS in situ measurements and obtained the best regression relationship (p < 0.01) (R2 = 0.818; Table 5).

Table 5 Multiple linear regression with machine learning EDA summary
Full size table

Application to the Landsat image of Lake Chapala

The resulting equation by the MLR method was applied to a multispectral Landsat image of Lake Chapala. This image was selected because there is a previous investigation that determined the content of SST in numerous sampling sites correlated with the date of a satellite image (Membrillo-Abad et al. 2016).

The results of applying the TSS MLR-ML model (Eq. 3) to the January 2013 Landsat TM image are shown in Table 6. The calculated TSS interval is compared with the observations: the lowest measured TSS is 10.00 mg/L, and the highest TSS is 215 mg/L; on the other hand, the lowest calculated TSS is 10.79 mg/L and the highest TSS is 252.83 mg/L, with a mean and a range of 59.29 ± 70.46 standard; 73.71 ± 7.54, respectively (Table 6). Average, maximum, and minimum values are overestimated in the MRL-ML calculation by approximately 15–20%. More importantly, the calculated and measured patterns of TSS variation are similar, allowing the sources and their distribution in the lake to be identified.

Table 6 Descriptive statistics, including observed suspended sediments and calculated suspended sediments, minimum (Min), maximum (Max), mean (Mean), standard deviation (Std Dev)
Full size table

Figure 4 shows the results of applying the MLR-ML model to satellite imagery, which was developed in this research to determine the concentration of TSS using the multiple linear regression model with machine learning in the Landsat image from January 2013. The map generated is the result of the application of Eq. 3 to the 7 bands of the Landsat image of January 2013; the statistical results are shown in Table 6. The map in Fig. 4 shows the calculated TSS concentration distribution, in which it is clear that the highest concentration occurs in the eastern part of the Chapala Lake, where the tributary rivers discharge the major contribution of sediments, (see Fig. 1). Correspondingly, the lowest values are in the western area of Chapala Lake because the major entrance of sediments in the east does not disturb the central and western area of the lake and results in low TSS values. The calculated TSS values have a good correlation with the actual TSS data.

Fig. 4
figure 4

Map of the estimated TSS concentration based on the multiple linear regression model (Eq. 3) applied to a Landsat ETM image taken in January 2013. The black dots indicate the sampling sites for TSS determination

Full size image

Discussion

The results have shown that multiple linear regression analysis can be improved by the addition of machine learning to the modelling. The use of various statistical methods in data analysis is a strategy that should be more widely applied because the statistical methods provide suitable correlations among any amount of data, in a way that any outliers are evident from the results.

This study correlated Lake Chapala in situ TSS measurements paired with spectral images from the Landsat satellite using the MLR model. 22 data and associated image pixels, or 315 TSS data, obtained from Lake Chapala were measured and used for model development. The MLR model was selected to build the TSS machine learning model, and R2 was used to assess the accuracy of the model. MLR was performed to determine the relationships of different variables, for each in situ measurement, as well as a linear regression for the complete data (315 data), in which we obtained a correlation of 0.818, which is one of the highest correlations obtained for this type of applications.

The comparison between the MRL and the MRL-ML results demonstrates that machine learning has the capability to improve the accuracy of predictions, the results of this study support the hypothesis that implementing ML algorithms to predict water quality parameters improves the overall predictive accuracy of spectral relationships and interactions.

The methodology presented in this work is the first attempt to correlate in situ measurements with surface reflectance provided by Landsat images that do not use “a specific combination of bands” method, but a more robust approach that applies multiple linear correlation to both data sets. The results show that the developed MLR algorithm successfully correlated the values of TSS with spectral data from Landsat TM images using a multiple linear regression algorithm applied to measurements in situ with the reflectance of the 7 spectral bands, and that the application of machine learning techniques contributed to make this model more robust. This technique provided a linear equation, which was used to generate a TSS map of Lake Chapala by correlating the reflectance measured by the Landsat TM satellite with the TSS values. The obtained map correlates well with previously published reports; therefore, Landsat TM images can be used to produce high-precision TSS maps, and such a model can be used to monitor the variation in TSS values of Lake Chapala without performing continuing in situ measurements.

Conclusion

This research has accomplished two different aims: first one to improve a methodology to combine remote sensing, multiple linear correlation, and machine learning to correlate Landsat satellite images; and the second is to obtain the multiple linear regression between predictor variables (Landsat spectral bands) and dependent variable (TSS) in Chapala Lake. Multiple R-values show the reliability of the relationship between the Landsat data and TSS field data.

The results of this research contribute to the search for a global empirical model that has become very important in order to develop a continuous monitoring system for inland water masses, as they provide a reliable relationship between the TSS concentrations, and the reflectance pattern of the water surface detected by satellite images (Gordon et al. 1980, 1983; Clark 1981).

Two important improvements in the proposed methodology can be considered. The first is to reduce the errors involved in the correlation algorithms between remote sensing and TSS values, using all available spectral bands instead of band combinations or trial and error to obtain the best match. The second improvement is the use of multiple regression with machine learning as an application of the multiple correlation model.

In addition to proposing this new methodology, it was applied to a case study with the main objective of showing its pertinence and how processing methodology is used to found relationships between Landsat images and TSS samples. As a result, an applicable algorithm for Lake Chapala was developed and demonstrated its suitability. From this study, it is clear that the information obtained from the developed MLR model can be used to map water bodies in a wide range of conditions and sizes, using freely available data, which will make more feasible to keep control on the environmental health of water bodies.

Unsupervised artificial intelligence has been used in this work to find a general multiple correlation model. This is the most important contribution of this work because the use of a robust statistical method, artificial intelligence, implies that a multiple regression can be obtained that applies to the entire data series and this general model can be employed to carry out extrapolations and to monitor TSS in lakes, in our case Lake Chapala, without the requirement of continuing in situ sampling data. The results of this study indicate that the established model has a great potential for reliably mapping different water quality parameters.