Skip to main content

Advertisement

SpringerLink
Log in

Modeling of land surface temperature–multiscale curvatures relationship using XGBoost algorithm (Case study: Southwestern Iran)

  • Original Paper
  • Published:
International Journal of Environmental Science and Technology Aims and scope Submit manuscript

Abstract

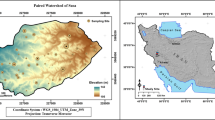
Land surface temperature (LST) is a fundamental variable in determining surface energy and water balances due to its control over the exchange of mass and energy between the soil surface and the atmosphere. This research aimed to investigate the relationship between spatial–temporal variability of LST and multiscale curvatures using the Extreme Gradient Boosting (XGBoost) algorithm in southwestern Iran. For this purpose, six curvatures were derived using the Wood method in three neighborhood scales (5 × 5, 15 × 15, and 25 × 25) from the 30-m Shuttle Radar Topography Mission digital elevation model. The Gaussian method was used for the landform classification. Emissivity was estimated based on the thresholding method of Normalized Difference Vegetation Index, and the average seasonal LST was calculated based on the Landsat 8 images taken during the 2013–2021 period using the inversion of Planck's function. The results depicted that neighborhood is a regulating factor in the amount of the detailed display of land surface features that in case of increasing its size, the rate of topographic surface bending decreases. In landform maps, four units that include the hill, closed depression, convex saddle, and concave saddle were identified, which have the lowest to the highest area within the studied region, respectively. The results of the Kruskal–Wallis test indicated that only the difference of each of the average LSTs of spring, summer, and winter between landform units classified based on 25 × 25 curvatures is significant (p-value < 0.05). The best performance of XGBoost models in explaining the variability in the average seasonal LST was obtained when the predictor variables were 25 × 25 curvatures (R2 values between 0.20 for spring LST and 0.11 for winter LST). XGBoost models predicted the values of average LST of the spring and summer more accurately than those of the autumn and winter. The difference between the R2 values of the XGBoost models based on the curvatures of 5 × 5 and 25 × 25 for the average LST of spring to winter is 0.14, 0.16, 0.15, and 0.11, respectively. The overall results of this research indicated the critical importance of neighborhood scale in capturing the variability of the environmental process studied in the landscape, while in many studies, the multiscale geomorphometric modeling has not been considered.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Source: Florinsky (2016)

Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Dataset and code availability

All datasets and codes used in this research are available on the https://khanifar.github.io/LSTMVs.html.

References

  • Albani M, Klinkenberg B, Andison DW, Kimmins JP (2004) The choice of window size in approximating topographic surfaces from digital elevation models. Int J Geogr Inf Sci 18(6):577–593

    Article  Google Scholar 

  • Bertoldi G, Notarnicola C, Leitinger G, Endrizzi S, Zebisch M, Della Chiesa S, Tappeiner U (2010) Topographical and ecohydrological controls on land surface temperature in an alpine catchment. Ecohydrol Ecosyst Land Water Process Interact Ecohydrogeomorphol 3(2):189–204

    Google Scholar 

  • Carslaw DC, Ropkins K (2012) Openair—an R package for air quality data analysis. Environ Model Softw 27:52–61

    Article  Google Scholar 

  • Chen T, Guestrin C (2016) Xgboost: a scalable tree boosting system. In: Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. ACM, New York, pp 785–794

  • Evans IS (1980) An integrated system of terrain analysis and slope mapping. Zeitschrift Für Geomorphologie Supplementband Stuttgart 36:274–295

    Google Scholar 

  • Fekrat H, Asghari Saraskanrood S, Alavipanah SK (2020) Estimation of Ardabil land surface temperature using Landsat images and accuracy assessment of land surface temperature estimation methods with ground truth data. J RS GIS Nat Resources 11(4):114–136

    Google Scholar 

  • Firozjaei MK, Makki M, Lentschke J, Kiavarz M, Alavipanah SK (2019) Spatioltemporal modeling the impact of surface characteristics variations on land surface temperature variations: a case study of Samalghan Vally. Int Arch Photogrammet Rem Sens Spat Inf Sci 42:401–405

    Article  Google Scholar 

  • Florinsky IV (1998) Accuracy of local topographic variables derived from digital elevation models. Int J Geogr Inf Sci 12(1):47–62

    Article  Google Scholar 

  • Florinsky I (2016) Digital terrain analysis in soil science and geology, 2nd edn. Academic Press, Amsterdam, pp 7–68

    Book  Google Scholar 

  • Florinsky IV (2018) Multiscale geomorphometric modeling of Mercury. Planet Space Sci 151:56–70

    Article  Google Scholar 

  • Franklin SE (2020) Interpretation and use of geomorphometry in remote sensing: a guide and review of integrated applications. Int J Rem. Sens 41(19):7700–7733

    Article  Google Scholar 

  • Gauss KF (1828) Disquisitiones generales circa superficies curvas. Comment Societ Regiae Scie Gottingen 6:99–146

    Google Scholar 

  • Gorelick N, Hancher M, Dixon M, Ilyushchenko S, Thau D, Moore R (2017) Google earth engine: planetary-scale geospatial analysis for everyone. Remote Sens Environ 202:18–27

    Article  Google Scholar 

  • He L, Cheng Y, Li Y, Li F, Fan K, Li Y (2021) An improved method for soil moisture monitoring with ensemble learning methods over the Tibetan plateau. IEEE J Sel Top Appl Earth Observ Remote Sens 14:2833–2844

    Article  Google Scholar 

  • Huggett R, Cheesman J (2002) Topography and the environment. Prentice Hall

    Google Scholar 

  • Khanifar J, Khademalrasoul A (2020) Importance of multi-scale geomorphometric algorithms in soil-landscape analysis. In: 7th National conference of iranian association of geomorphology (geomorphology, a new approach), Tehran, Iran (Persian Literature)

  • Khanifar J, Khademalrasoul A, Amerikhah H (2020) Modelling of soil aggregate stability as an index of soil erodibility using geomorphometric parameters. J Agric Eng Soil Sci Agric Mechanizat (sci J Agric) 43(1):45–60

    Google Scholar 

  • Khanifar J, Khademalrasoul A (2021) Effects of neighborhood analysis window forms and derivative algorithms on the soil aggregate stability–Landscape modeling. CATENA 198:105071

    Article  Google Scholar 

  • Lam NS-N (2019) Resolution. In: Wilson JP (ed) The geographic information science & technology body of knowledge (2nd Quarter 2019 Edition). https://doi.org/10.22224/gistbok/2019.2.11.

  • MacMillan RA, Shary PA (2009) Landforms and landform elements in geomorphometry. In: Hengle T, Reuter HI (eds) Geomorphometry: concepts, software, applications. Elsevier, Amsterdam, pp 227–254

    Chapter  Google Scholar 

  • Minár J, Evans IS, Jenčo M (2020) A comprehensive system of definitions of land surface (topographic) curvatures, with implications for their application in geoscience modelling and prediction. Earth Sci Rev 211:103414

    Article  Google Scholar 

  • Mokarram M, Sathyamoorthy D (2018) A review of landform classification methods. Spat Inf Res 26(6):647–660

    Article  Google Scholar 

  • Mola Mehr Alizadeh F, Jannati M, Shayan S (2005) Efficiency of remote sensing (RS) data in landform mapping and its role in environmental planning. Hum Sci Modares 9(4):111–148

    Google Scholar 

  • Olaya V (2009) Basic land-surface parameters. In: Hengle T, Reuter HI (eds) Geomorphometry: concepts, software, applications. Elsevier, Amsterdam, pp 141–170

    Chapter  Google Scholar 

  • Peng X, Wu W, Zheng Y, Sun J, Hu T, Wang P (2020) Correlation analysis of land surface temperature and topographic elements in Hangzhou. China Sci Rep 10(1):1–16

    Google Scholar 

  • Raschka S (2018) MLxtend: Providing machine learning and data science utilities and extensions to Python’s scientific computing stack. J Open Source Softw 3(24):638

    Article  Google Scholar 

  • Rigol-Sanchez JP, Stuart N, Pulido-Bosch A (2015) ArcGeomorphometry: a toolbox for geomorphometric characterisation of DEMs in the ArcGIS environment. Comput Geosci 85:155–163

    Article  Google Scholar 

  • Roecker SM, Thompson JA (2010) Scale effects on terrain attribute calculation and their use as environmental covariates for digital soil mapping. In: Boettinger JL, Howell DW, Moore AC, Hartemink AE, Kienast-Brown S (eds) Digital soil mapping: bridging research, environmental application, and operation. Springer, Dordrecht, pp 55–66

    Chapter  Google Scholar 

  • Shamsoddini A, Madadi F (2019) Land Surface Temperature Mapping Based on Emissivity Fusion in Urban Areas. J Geomat Sci Technol (JGST) 9(2):77–91

    Google Scholar 

  • Shary PA (1995) Land surface in gravity points classification by a complete system of curvatures. Math Geol 27(3):373–390

    Article  Google Scholar 

  • Soil and Land Suitability Evaluation report of justification studies of Watershed Management in the Remains of Dez Dam watershed (n.d.) Natural Resources organization of Iran (Persian Literature)

  • Taghizadeh-Mehrjardi R, Schmidt K, Toomanian N, Heung B, Behrens T, Mosavi A, Band SS, Amirian-Chakan A, Fathabadi A, Scholten T (2021) Improving the spatial prediction of soil salinity in arid regions using wavelet transformation and support vector regression models. Geoderma 383:114793

    Article  CAS  Google Scholar 

  • Wilson JP (2018) Environmental applications of digital terrain modeling. Wiley

    Book  Google Scholar 

  • Wood J (1996) The geomorphological characterisation of digital elevation models (Doctoral dissertation, University of Leicester)

  • XGBoost Parameters. 27 July 2021. https://xgboost.readthedocs.io/en/latest/parameter.html.

  • Zevenbergen LW, Thorne CR (1987) Quantitative analysis of land surface topography. Earth Surf Proc Land 12(1):47–56

    Article  Google Scholar 

  • Zhao W, Duan SB, Li A, Yin G (2019) A practical method for reducing terrain effect on land surface temperature using random forest regression. Remote Sens Environ 221:635–649

    Article  Google Scholar 

  • Zhang S, Zhang D, Qiao J, Wang X, Zhang Z (2020) Preventive control for power system transient security based on XGBoost and DCOPF with consideration of model interpretability. CSEE J Power Energy Syst 7(2):279–294

    Google Scholar 

  • Zhong R, Johnson R Jr, Chen Z (2020) Generating pseudo density log from drilling and logging-while-drilling data using Extreme Gradient Boosting (XGBoost). Int J Coal Geol 220:103416

    Article  CAS  Google Scholar 

  • Zhu AX (2008) Keynote paper: spatial scale and neighborhood size in spatial data processing for modeling the natural environment. In: Mount N, Harvey G, Aplin P, Priestnall G (eds) Representing, modeling, and visualizing the natural environment. CRC Press, pp 147–165

    Chapter  Google Scholar 

Download references

Acknowledgements

This research is based on the datasets of Landsat 8, SRTM DEM, and meteorology. Remote sensing and machine learning analyses were performed in Google Earth Engine and Google Colaboratory. We thank all those who participated in the preparation and provision of these datasets and services.

Funding

This work was supported by Shahid Chamran University of Ahvaz [SCU.AS98.364].

Author information

Authors and Affiliations

  1. Soil Science Department, Faculty of Agriculture, Shahid Chamran University of Ahvaz, Ahvaz, Iran

    J. Khanifar & A. Khademalrasoul

Authors
  1. J. Khanifar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Khademalrasoul
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Khademalrasoul.

Ethics declarations

Conflict of interest

The author declares no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Editorial responsibility: Agnieszka Galuszka.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khanifar, J., Khademalrasoul, A. Modeling of land surface temperature–multiscale curvatures relationship using XGBoost algorithm (Case study: Southwestern Iran). Int. J. Environ. Sci. Technol. 19, 11763–11774 (2022). https://doi.org/10.1007/s13762-022-04409-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13762-022-04409-z

Keywords

Search

Navigation