Modeling of electrochemical removal of cadmium under galvanostatic mode using an artificial neural network

Abstract

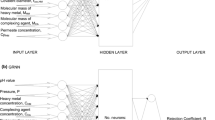
In this research, the final concentration of cadmium in an electrochemical removal process is estimated by an artificial neural network (ANN) model. The ANN model based on experimental data obtained by a removal process of cadmium from dilute aqueous solutions under galvanostatic mode in a flow-through cell. The pH, current density, and electrolysis time were considered as input variables. An analysis of the hyperbolic tangential-sigmoidal (TANSIG) and logarithmic-sigmoidal (LOGSIG) transfer function was developed to obtain the best accuracy model. To validate the accuracy and the adaptability of the model proposed, statistical and linearity tests (slope-intercept) were performed. The best model with architecture 3:3:1 was validated with a R² value of 0.9850 and a MSE value of 0.00166, besides approved linearity tests with 99% confidence.

Appendix A

• Sensitivity analysis is obtained according to the following equation:

  $$ RI_{j} = \frac{{\mathop \sum \nolimits_{h = 1}^{m} \left( {\left| {W_{ih} W_{ho} } \right|/\mathop \sum \nolimits_{i = 1}^{n} \left| {W_{ih} } \right|} \right)}}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\mathop \sum \nolimits_{h = 1}^{m} \left( {\left| {W_{ih} W_{ho} } \right|/\mathop \sum \nolimits_{i = 1}^{n} \left| {W_{ih} } \right|} \right)} \right)}} $$

  (A.1)

where $RI_{j}$ is the relative importance of the input variable on the output variable; $i$, $h$ and $o$ refer to input, hidden, and output layers neurons, respectively. $W_{ih} ,$ and $W_{ho}$ are the connection weights between input-hidden layer; and hidden-output layer, $n$ is the total number of input layer neurons and $m$ correspond to the total number of hidden layer neurons.

To do so, first it’s necessary to build the matrix with absolute weights $W_{ih}$, and $V_{ho}$.

$$ \left| {W_{ih} } \right| = \left[ {\begin{array}{*{20}c} {w_{11} } & {w_{12} } & {w_{13} } \\ {w_{21} } & {w_{22} } & {w_{23} } \\ {w_{31} } & {w_{32} } & {w_{33} } \\ \end{array} } \right]\,\,\,\,\,\,\,\, \left| {V_{ho} } \right| = \left[ {\begin{array}{*{20}c} {v_{11} } \\ {v_{21} } \\ {v_{31} } \\ \end{array} } \right] $$

(B.1)

Second, for each line in the matrix $\left| {W_{ih} } \right|$ the sum is obtained.

$$ W_{1} = w_{11} + w_{12} + w_{13} $$

$$ W_{2} = w_{21} + w_{22} + w_{23} $$

$$ W_{3} = w_{31} + w_{32} + w_{33} $$

The numerator of Eq. (B.1) was represented by the multiplication of $\left| {W_{ih} } \right|\left| {V_{ho} } \right|$ and divided by sum of each column as showed in the next matrix:

$$ \left| N \right| = \left[ {\begin{array}{*{20}c} {\frac{{w_{11} v_{11} }}{{W_{1} }}} & {\frac{{w_{12} v_{11} }}{{W_{1} }}} & {\frac{{w_{13} v_{11} }}{{W_{1} }}} \\ {\frac{{w_{21} v_{21} }}{{W_{2} }}} & {\frac{{w_{22} v_{21} }}{{W_{2} }}} & {\frac{{w_{23} v_{21} }}{{W_{2} }}} \\ {\frac{{w_{31} v_{31} }}{{W_{3} }}} & {\frac{{w_{32} v_{32} }}{{W_{3} }}} & {\frac{{w_{33} v_{33} }}{{W_{3} }}} \\ \end{array} } \right]\begin{array}{*{20}l} {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; N_{1} = \frac{{w_{11} v_{11} }}{{W_{1} }} + \frac{{w_{21} v_{21} }}{{W_{2} }} + \frac{{w_{31} v_{31} }}{{W_{3} }}} \hfill \\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N_{2} = \frac{{w_{21} v_{21} }}{{W_{2} }} + \frac{{w_{22} v_{21} }}{{W_{2} }} + \frac{{w_{23} v_{21} }}{{W_{2} }}} \hfill \\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; N_{3} = \frac{{w_{31} v_{31} }}{{W_{3} }} + \frac{{w_{32} v_{32} }}{{W_{3} }} + \frac{{w_{32} v_{32} }}{{W_{3} }}} \hfill \\ \end{array} $$

The denominator is represented by $N_{T} :$

$$ N_{T} = N_{1} + N_{2} + N_{3} $$

Finally, the relative importance $I_{j}$ for each input variable was calculated as follows:

$$ I_{1} = \left( {N_{1} /N_{T} } \right)\left( {100} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;I_{2} = \left( {N_{2} /N_{T} } \right)\left( {100} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;I_{3} = \left( {N_{3} /N_{T} } \right)\left( {100} \right) $$