Introduction

In Poland, as well as in a lot of industrialized European countries, the energy production sector is widely regarded as the biggest source of atmospheric pollution (Eurostat). This is due, among other things, to the huge amount of fuel combusted on the one hand and the unavoidable emission of toxic substances from the combustion process on the other. Both gaseous and liquid as well as solid fuels are mostly hydrocarbons and, as a result, during combustion processes, carbon dioxide and partly carbon monoxide are formed. All combustion processes are also accompanied by the emission of nitric oxides (nitrogen monoxide and dioxide) and sulfur oxides (dioxide and trioxide) as well (Wielgosinski 2012). On the other hand, non-combustible substances in the fuel (especially in solid fuels) are the source of dust emissions. Without going into details of the mechanism of pollutant formation during combustion processes which has been well described in many works (Annamalai and Puri Ishwar 2006; Glassman and Yetter 2014; Keating 2007; Kuo 2005; McAllister et al. 2011; Nissen 2010; Ragland and Bryden 2011; Turns 2011; Wielgosiński 2012), it can be assumed that the combustion of solid fuels inevitably results in the emission of sulfur dioxide (SO2), nitric oxides (mainly NO and NO2), carbon monoxide and dioxide (CO and CO2), as well as dust whose particle size distribution is dependent on fuel, combustion technology, and emission control devices. This list is supplemented by a considerable number of the so-called products of incomplete combustion (PICs) which include polycyclic aromatic hydrocarbons (PAHs), polychlorinated dibenzo-p-dioxins and furans (PCDDs/Fs), or simple aliphatic (e.g., formaldehyde) and aromatic hydrocarbons, and often also chlorinated hydrocarbons (Fernandez-Martinez et al. 2002; Wielgosiński 2012). Emissions of these pollutants, as well as emission coefficients related to the mass of fuel burned, or the amount of energy produced, have already been investigated. It has also been attempted to analyze the interdependencies between emissions of certain pollutants, for example a positive correlation between the sum of organic compounds contained in the exhaust gas with carbon monoxide, or a negative correlation between carbon monoxide and nitrogen monoxide emissions (de Souza-Santos 2010; Guttikunda and Jawahar 2014; Levy and Spengler 2002; Li et al. 2012; Streets and Waldhoff 2000; Williams 2000; Zhao et al. 2008; Zhu et al. 2013).

Pollutants emitted during combustion processes are dispersed in the atmosphere (Turner 1994, Cichowicz et al. 2017). They are often carried over large distances by winds, especially as the emitters of large fuel combustion sources (e.g., power plants) are high. Principles of modeling of dispersion of pollutants in the atmosphere have been a subject of studies since the 1940s and they are presented in numerous monographs (Caputo et al. 2003; De Visscher 2013; Douw and Rohit 2014; Gifford 1960, 1976; Moreira and Vilhena 2009; Pasquill 1974; Turner 1979, 1994; Venkatram 1996; Zannetti 1990). Pollutants emitted into the atmosphere undergo many changes which are a subject of the field of science called atmospheric chemistry. At the same time, the relationships between pollutants emitted to the atmosphere are changing.

A particular problem is the analysis of the impact which—due to the height of emitters and problems of the atmospheric pollution modeling—large power plants have on the emissions introduced practically above the boundary layer of the Earth’s atmosphere (Czarnowska and Frangopoulos 2012; Deligiorgi et al. 2013; Holmes and Morawska 2006; Martin et al. 2003; Maruntalu et al. 2015; Vairo et al. 2014).

The purpose of this work was to analyze variations in time the pollution immission field observed at a measuring station located in the vicinity of a large-size lignite-fired power station in time and to explore changes in relations between some pollutants emitted by the power plant and meteorological parameters.

Materials and methods

Location of the monitoring station

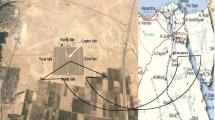
The analysis was based on the results of research recorded in the years between 2009 and 2015 at the Laski monitoring station located in the vicinity of the Adamów power plant. The atmospheric air monitoring station was located in the eastern part of the Wielkopolska Voivodeship, in Laski, Turek district, Przykona commune. The container in monitoring station was located in the pumping station transporting leachate from the nearby disposal site ashes generated during the process of lignite burning at the Adamów power plant. Ashes were stored by the wet method. Both the ash disposal site and the pumping station itself do not cause secondary dusting and therefore do not affect air pollution measured by the station. The location of the power plant is shown in Fig. 1.

Fig. 1
figure 1

Location of the monitoring station in relation to the Adamów power plant (http://mapy.geoportal.gov.pl)

Full size image

The area surrounding the station is mainly in the form of farmland and meadows, covered with forests which occupy 26% of the total area of the Przykona municipality on the northeast. The largest populated centers are the city of Turek (about 28,000 inhabitants) located at the northwest of the station at a distance of about 4.0 km, as well as neighboring villages: Laski (292 inhabitants, distance 0.5 km), Rogów (335 inhabitants, distance 2.7 km), and Chlebów (348 inhabitants, 1.3 km distance). Figure 1 shows the location of the Laski monitoring station (marked as “A”) in relation to the largest atmospheric pollutant emission source, the Adamów power plant (marked as “1”).

The district of Turek occupies an area of 929.3 km2 with a population density of 91 persons/km2 and is part of the Wielkopolska Lowland. The main river is Warta; the eastern border of the district, with tributaries Kiełbaska, Topiec, Teleszyn, and Powa, provide drainage of the Turek district. Forests cover 24.8% of the total area of the district. The Turek district is at an altitude from about 95 to 160 m above sea level in its northwest part. The natural resource of the region is lignite, mined in a nearby mine, about 6.4 km east of the monitoring station. It is used as fuel in the local conventional Adamów power plant (the installed total capacity of 5 power units is 600 MW), 2.5 km away from the air immission monitoring station in the northwest direction (Fig. 2). The Adamów power plant is part of the Pątnów-Adamów-Konin Power Plant Complex S.A. (ZE PAK S.A.). The Adamów power plant belongs to the oldest Polish professional power plants. It was built in the years of 1960–1966 and is scheduled for shutdown by the end of 2017.

Fig. 2
figure 2

Terrain conditions between the Laski monitoring station (blue—the beginning of the profile) and Adamów power plant (yellow—the end of the profile)

Full size image

The atmospheric air pollutants in the following concentration range are measured and analyzed the monitoring station:

  • suspended particulate matter PM10, from 5.0 µg/m3 up to several mg/m3;

  • sulfur dioxide (SO2), from 0 to 500 ppb;

  • carbon monoxide (CO), from 0 to 50 ppm;

  • nitrogen monoxide (NO), from 0 to 500 ppb;

  • nitrogen dioxide (NO2), from 0 to 500 ppb;

  • nitrogen oxides NOx (as the sum of NO and O2), from 0 to 500 ppb;

  • ozone (O3), from 0 to 500 ppb.

Measurements of the above pollutants are made by individual analyzers whose measurement methods are in accordance with the reference methods specified in Annex VI of the Directive of the European Parliament and Board no. 2008/50/WE (Directive 2008/50/EC 2008). All units operate 24 h in whole on all days of the year, with small breaks (approximately 1% of the time) dedicated to service and calibration.

Measurement of some meteorological parameters in the monitoring station is performed to determine the direction of flowing air masses and potential sources of pollution. This is made using two sensors that measure following parameters: air temperature (°C), relative air humidity (%), wind direction (0°–359°), and wind speed (m/s).

Analysis of variations in the measured pollutant emissions

The Laski monitoring station conducts continuous measurements of immission concentrations of the following pollutants: PM10, sulfur dioxide (SO2), carbon monoxide (CO), nitrogen oxides NOx (separately and as the sum of NO and NO2), and ozone (O3) with also recording at the same time the meteorological parameters such as air temperature, relative air humidity, wind speed, and direction. Examples of the results of measurements, recorded at the Laski monitoring station in the years 2009–2015, are presented in Figs. 3, 4, 5, 6, 7 and 8.

Fig. 3
figure 3

Changes in air temperature recorded in 2009–2015

Full size image
Fig. 4
figure 4

Changes in sulfur dioxide concentration recorded in 2009–2015

Full size image
Fig. 5
figure 5

Changes in nitrogen monoxide concentration recorded in 2009–2015

Full size image
Fig. 6
figure 6

Changes in carbon monoxide concentration recorded in 2009–2015

Full size image
Fig. 7
figure 7

Changes in the concentration of suspended particulate matter recorded in 2009–2015

Full size image
Fig. 8
figure 8

Changes in ozone concentration recorded in 2009–2015

Full size image

Analyzing the data presented in Figs. 3, 4, 5, 6, 7 and 8, it is easy to notice a general decrease in SO2, CO, and PM10 concentrations at the intersections of the analyzed years. On the contrary, in the case of ozone, we observe an increase in concentrations, whereas in the case of NO, no significant changes are observed. The drop in concentrations of SO2, CO, and PM10 can be explained by the reduction in emissions of these pollutants from the power plant. The increase in O3 concentration is the result of the increase in vehicle traffic, and the stabilization of NO concentration is the result of both factors presented above—NO concentration decreases due to the reduction in emissions from the power plant and at the same time increases due to increased automobile.

On the basis of the analysis of the temperature and the concentrations of some pollutants measured at the monitoring station in the years of 2009–2015, the mean values of the measured parameters (air temperature and concentrations of SO2, NO, NO2, CO, O3, and PM10) as well as their variability (minimum and maximum values) in the considered period were determined. Results of this analysis are summarized in Table 1.

Table 1 Average and extreme (minimum and maximum) values recorded at the Laski monitoring station in the years 2009–2015
Full size table

With having a pollution dataset which covers monitoring at a defined data collection point in the vicinity of a large emitter, it was decided to check to what extent the predictions based on the modeling of the diffusion of pollutants in the atmosphere correspond to the actual long-term results. Taking advantage of the fact that the Adamów power plant as a large source of emissions is subject to the IPPC regulations of the Industrial Emissions Directive (Directive 2010/75/EC 2010), it was found that the emission source was a 150-m-high single-flue chimney of diameter 10.2 m. It introduces into the atmosphere exhaust gas from five OP-380B boilers with thermal output of 351 MW each. A single boiler consumes a maximum of about 179 Mg/h of brown coal with a calorific value of about 8.2 MJ/kg, sulfur content of about 0.35%, and ash content of about 10.5%. Thus, it is possible to calculate that the maximum emission of the primary pollutants from one boiler as values of:

  • sulfur dioxide—1049.8 kg/h,

  • nitrogen monoxide—403.7 kg/h,

  • dust (approx. 97% is suspended particulate matter PM10)—17.7 kg/h,

  • carbon monoxide—716.7 kg/h,

by satisfying the following emission standards: SO2—1300 mg/m3u, NOx—500 mg/m3u, PM10—100 mg/m3u (where u means that concentration is calculated for temperature 273 K, atmospheric pressure 1013 hPa, dry flue gases, and 6% of oxygen). Efflux velocity is maximum 27.1 m/s (with 5 boilers running) and temperature about 150 °C.

Calculations of predicted air pollution in the area of impact of the power plant emitter, and in particular at the data collection point corresponding to the location of the monitoring station, were based on an atmospheric diffusion model which is the solution of the atmospheric diffusion equation (Zannetti 1990):

$$\begin{aligned} & \frac{\partial S}{\partial \tau } + u_{x} \frac{\partial S}{\partial x} + u_{y} \frac{\partial S}{\partial y} + u_{z} \frac{\partial S}{\partial z} \\ & \quad = \frac{\partial }{\partial x}\left( {\sigma_{x} \frac{\partial S}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\sigma_{y} \frac{\partial S}{\partial y}} \right) + \frac{\partial }{\partial z}\left( {\sigma_{z} \frac{\partial S}{\partial z}} \right) + I(x,y,z,t) \\ \end{aligned}$$

The model was proposed by Pasquill (1961). It is valid in Poland for modeling the diffusion of atmospheric pollutants and predicting air pollution for point sources. The solution is:

$$S_{xyz} = \frac{E}{{\pi \cdot \bar{u} \cdot \sigma_{y} \cdot \sigma_{z} }} \cdot \exp \left( { - \frac{{y^{2} }}{{2 \cdot \sigma_{y}^{2} }}} \right) \cdot \left\{ {\exp \left[ { - \frac{{\left( {z - H} \right)^{2} }}{{2 \cdot \sigma_{z}^{2} }}} \right] + \exp \left[ { - \frac{{\left( {z + H} \right)^{2} }}{{2 \cdot \sigma_{z}^{2} }}} \right]} \right\}$$

where Sxyz—pollutant concentration at the data collection point with coordinates x, y, z (μg/m3); E—pollutant emission (kg/h); σy—atmospheric diffusion coefficient in the direction of the Y-axis (m); σz—atmospheric diffusion coefficient in the direction of the Z-axis (m); \(\bar{u}\)—average wind speed (m/s); H—height of the apparent point of emission (emitter height plus the height of gas emission (m).

Calculated values of average annual concentrations of primary pollutants, i.e., sulfur dioxide, sum of nitric oxides, suspended particulate matter PM10, and carbon monoxide, are shown in Table 2. In addition, the average concentrations of these pollutants recorded in 2009–2015 by the continuous immission monitoring system at the Laski station are included in the same table as well. The permissible concentration values according to Directive 2008/50EC and polish law are added to Table 2 as an extra.

Table 2 Calculated and actual mean concentrations of pollutants at the site of the monitoring station (in μg/m3)
Full size table

The average values recorded by the pollutant concentration monitoring system are significantly higher than the calculated mean annual concentrations. Hence, the question arises why this is so. It may be hypothesized that pollutants such as carbon monoxide and suspended particulate matter PM10 recorded at the Laski monitoring station can be derived from sources other than the Adamów power plant, whereas pollutants such as sulfur dioxide and nitric oxides can undergo changes in the atmosphere, and as a result their concentration at a distance of more than 2.5 km from the emission source may be lower than would result from the transport of pollutants in the air. It was therefore decided to analyze the correlations between some variables (recorded parameters) to verify whether the dependencies observed directly for emissions from the fuel combustion source are confirmed and observed at the monitoring station located about 2.5 km from the source.

Results and discussion

Analysis of monitoring data

The simplest and most obvious relation is the dependence of pollutant concentrations on temperature. There is no doubt that during the winter season, at low temperatures, the power plant operates with much more power, consuming more fuel and emitting more pollutants into the atmosphere than in the summer when the power demand is much lower. To illustrate this phenomenon, the variability of pollutant concentrations and temperature recorded each time are summarized in one diagram. This is shown in Figs. 9, 10, 11, 12, 13 and 14.

Fig. 9
figure 9

Variability of SO2 concentrations and air temperature in the years 2009–2015

Full size image
Fig. 10
figure 10

Variability of NO concentrations and air temperature in the years 2009–2015

Full size image
Fig. 11
figure 11

Variability of NO2 concentrations and air temperature in the years 2009–2015

Full size image
Fig. 12
figure 12

Variability of CO concentrations and air temperature CO in the years 2009–2015

Full size image
Fig. 13
figure 13

Variability of O3 concentrations and air temperature in the years 2009–2015

Full size image
Fig. 14
figure 14

Variability of PM10 concentrations and air temperature in the years 2009–2015

Full size image

They clearly show that there is a dependence of pollutant concentrations recorded at the Laski monitoring station on temperature. For SO2, CO, and PM10, this relationship is inverse, i.e., high concentrations of these pollutants occur at low temperatures. For ozone, this dependence is obviously positive—an increase in temperature causes an increase in O3 concentrations. In the case of nitrogen oxides—for NO2, it can be seen that, in the initial period (in 2009–2012), the dependence of concentrations of this pollutant on the reverse is the opposite (analogically to SO2, CO, and PM) indicating the impact of the power plant. In the second part of the analyzed period (2013–2015), this dependence is chaotic, which may be caused by a significant increase in the emission of nitrogen oxides from road transportation traffic. The barrack of the unambiguous dependence of recorded NO concentrations on temperature occurs throughout the analyzed period—probably NO comes mainly from vehicle traffic. They take into account the distance of the monitoring station from the power plant (about 2.5 km), so is highly probable that the NO emitted from the chimney oxidizes in the air to NO2; hence, the impact of changes in NO emissions from the power plant is not recorded at the monitoring station in the form of NO concentration changes but the form of NO2 concentration changes.

In view of the difficulty in analyzing the dependencies presented in Figs. 9, 10, 11, 12, 13, and 14, we decided to perform a statistical analysis of interrelations that we sought. The variables [temperature (°C), SO2 concentration (µg/m3), NO concentration (µg/m3), NO2 concentration (µg/m3), CO concentration (µg/m3), O3 concentration (µg/m3), and PM10 concentration (µg/m3)] presented in the form of time series of numerical data in which each observation is related to a particular moment were analyzed. Time series of daily data covered the period from January 1, 2009, to December 6, 2015. Calculations for the analyses were performed in STATISTICA 12, GRETL, and Excel 2007. To study the effect of temperature—Temp. (°C) on the variables: SO2 concentration (µg/m3), NO concentration (µg/m3), NO2 concentration (µg/m3), CO concentration (µg/m3), O3 concentration (µg/m3) and PM10 concentration (µg/m3), dynamic econometric modeling was used. For this reason, error correction models (ECM) were applied (Hylleberg and Mizon 1989; Phillips and Loretan 1991). These are models for variable increments, supplemented with the so-called error correction component. They are important because while estimating models for variable increments, we can get information only about the short-term effects of explanatory variables on a response variable. The error correction component expresses the long-term (equilibrium) relationship between non-stationary variables. For this reason, ECM models make it possible to distinguish between long-term and short-term relationships and to reduce the probability of inference on the basis of models characterized by apparent regression.

The ECM model can be written as follows:

$$\Delta Y_{t} = \gamma_{0} + \gamma_{1} \Delta X_{t} + \gamma_{2} {\text{ECM}}_{t - 1} + \eta_{t}$$

or

$$\Delta Y_{t} = \gamma_{0} + \gamma_{1} \Delta X_{t} + \gamma_{2} \left( {Y_{t - 1} - \alpha_{0} + \alpha_{1} X_{t - 1} } \right) + \eta_{t}$$

where ECM is the vector of residuals of long-term equilibrium:

$$Y_{t} = \alpha_{0} + \alpha_{1} X_{t} + \xi$$

ECMt−1 is the measure of an equilibrium error committed in the previous period, hence is referred to as the error correction component; it is the correction factor of the error.

Estimation of the models began with the verification of integration of the tested variables using the augmented Dickey–Fuller test (ADF). Results of the test show that the first increments of the analyzed variables are stationary, which means that the variables are integrated in the first degree (p < 0.05). The cointegration of variables entering the estimated models was then investigated. For this purpose, the Engle–Granger method (Engle and Granger 1987) has been used to show that the rest of the models are stationary (p < 0.05) (zero-integrated) and thus cointegrating. This means that the analyzed variables are aimed at long-term equilibrium and the investigated relationships between the Yt and Xt variables are not apparent regressions. In what follows, the estimated error correction models and the surface graphs of variables entering the models are presented in detail (Figs. 15, 16, 17, 18, 19, 20 and Tables 3, 4, 5, 6, 7, 8).

Fig. 15
figure 15

Model 1: dependence of SO2 concentration in the immission on temperature

Full size image
Fig. 16
figure 16

Model 2: dependence of NO concentration in the immission on temperature

Full size image
Fig. 17
figure 17

Model 3: dependence of NO2 concentration in the immission on temperature

Full size image
Fig. 18
figure 18

Model 4: dependence of CO concentration in the immission on temperature

Full size image
Fig. 19
figure 19

Model 5: dependence of O3 concentration in the immission on temperature

Full size image
Fig. 20
figure 20

Model 6: dependence of PM10 concentration in the immission on temperature

Full size image
Table 3 Model parameters [ΔSO2 concentration (µg/m3)] and R2
Full size table
Table 4 Model parameters [ΔNO concentration (µg/m3)] and R2
Full size table
Table 5 Model parameters [ΔNO2 concentration (µg/m3)] and R2
Full size table
Table 6 Model parameters [ΔCO concentration (µg/m3)] and R2
Full size table
Table 7 Model parameters [ΔO3 concentration (µg/m3)] and R2
Full size table
Table 8 Model parameters [ΔPM10 concentration (µg/m3)] and R2
Full size table

The model 1 (Fig. 15 and Table 3) explains 15% variability of the dependent variable. Only one parameter of the ECMt  − 1 model is statistically significant, the others are statistically insignificant. Interpretation of the model is as follows:

  • the average increase in SO2 pollution increment resulting from the unit increase in temperature increments is 0.046 µg/m3,

  • 27.75% of the imbalance from the long-term trajectory of SO2 pollution is corrected by the short-term adjustment process.

The model 2 (Fig. 16 and Table 4) explains 22.3% variability of the dependent variable. Parameters with the exception of absolute terms are statistically significant. Interpretation of the model is as follows:

  • the average decrease in NO pollution increments resulting from the unit increase in temperature increments is 0.036 µg/m3,

  • 42.7% of the imbalance from the long-term trajectory of NO pollution is corrected by the short-term adjustment process.

The model 3 (Fig. 17 and Table 5) explains 17.0% variability of the dependent variable. Parameters with the exception of the absolute term are statistically significant. Interpretation of the model is as follows:

  • the average decrease in NO2 pollution increments resulting from the unit increase in temperature increments is 0.076 µg/m3,

  • 31.6% of the imbalance from the long-term trajectory of NO2 pollution is corrected by the short-term adjustment process.

The model 4 (Fig. 18 and Table 6) explains 21.5% variability of the dependent variable. Parameters with the exception of the absolute term are statistically significant. Interpretation of the model is as follows:

  • the average decrease in CO pollution increments resulting from the unit increase in temperature increments is 4.074 µg/m3,

  • 38.6% of the imbalance from the long-term trajectory of CO pollution is corrected by the short-term adjustment process.

The model 5 (Fig. 19 and Table 7) explains 18.7% variability of the dependent variable. Parameters with the exception of the absolute term are statistically significant. Interpretation of the model is as follows:

  • the average increase in O3 pollution increments resulting from the unit increase in temperature increments is 1.145 µg/m3,

  • 23.4% of the imbalance from the long-term trajectory of O3 pollution is corrected by the short-term adjustment process.

The model 6 (Fig. 20 and Table 8) explains 23.2% variability of the dependent variable. The parameter of the ECMt − 1 model is statistically significant, and the others are statistically insignificant. Interpretation of the model is as follows:

  • the average increase in PM10 pollution increments resulting from the unit increase in temperature increments is 0.244 µg/m3,

  • 45.0% of the imbalance from the long-term trajectory of PM10 pollution is corrected by the short-term adjustment process.

Conclusion

The energy sector is generally considered to be the most important source of atmospheric pollution, particularly with respect to sulfur dioxide, nitrogen oxides, and particulate matter. Emissions from the combustion processes to the atmosphere through high emitters are dispersed in the air and then entrained by the wind often reaching very long distances, which affects air pollution in the areas far exhausted from the emission source.

The purpose of this work was to analyze the changes in the pollutant immission field recorded in the years 2009–2015 at a monitoring station located near a large-size lignite-fired power plant. The emission of pollutants from the power plant and immission recorded at the nearby monitoring station was analyzed. It has been attempted to analyze changes in the interrelationship between some pollutants emitted from power plants and meteorological parameters.

Mean values of pollutant concentrations recorded by the monitoring system were also compared with the results of modeling the dispersion of these pollutants in the atmosphere using the well-known Pasquill’s atmospheric diffusion model. It was found that the values recorded by the monitoring system were much higher than the calculated mean annual concentrations, however for some pollutants such as SO2 and NO2 were lower than the predicted (calculated) hourly concentrations and for other pollutants such as PM10 and CO were much higher than the calculated hourly concentrations. It was observed that the impact of other sources emitting pollutants on the atmosphere was highly probable (for carbon monoxide and particulate matter PM10), and as a result the values recorded at the monitoring station were much higher than the calculated mean annual or hourly concentrations. This indicates that the mathematical modeling of dispersion of pollutants in the atmosphere, in particular in the vicinity of high (over 100 m) emitters, may give as a results—immission concentration lower than in reality.

The interrelations between some variable air parameters and pollution were also analyzed. The simplest and most obvious dependence was that of pollutant concentrations on temperature. There is no doubt that during the winter season, at low temperatures, the power plant operates with much more power, consuming more fuel and emitting more pollutants into the atmosphere than in the summer when power demand is much lower. It was therefore decided to find out whether these correlations, so obvious in the emission variability analysis, will also be confirmed in the analysis of immission variations recorded at a nearby monitoring station.

In this analysis, the error correction models (ECM) of statistical–econometric analysis of measurement data using were used which made it possible to explain part of the variability of the dependent variable. As a result of the estimation of models illustrating the impact of temperature on the emission of pollutants: SO2, NO, NO2, CO, O3, and PM10, it was found that the models of PM10 and NO emissions were characterized by the highest error correction, while those of SO2 and CO emissions had the lowest one.

The applied statistical modeling method is the first attempt to explain seasonal variations of the pollutant immission field relative to the corresponding emissions of these pollutants. As a result of using this method, it can be stated that having a dataset covering the pollution monitoring in a defined data collection point surrounded by a large emission source, it can be explained to what extent the predicted spread of pollutants in the atmosphere based on the modeling of pollutant concentrations corresponds to the actual results of long-term measurements.