Abstract
Performing experiments with mixed commercial waste, sampling is unavoidable for material analysis. Thus, the procedure of sampling needs to be defined in a way that guarantees sufficient accuracy regarding the estimation of the examined analytes. In this work, a sampling procedure for coarsely shredded mixed commercial waste, based on the Austrian Standard ÖNORM S 2127, the horizontal sampling standard DS 3077 and the theory of sampling, was established, described and examined through a replication experiment determining the relative sampling variability. The analytes are described through a matrix of nine (9) material classes and nine (9) particle size classes. It turns out that the typical threshold value of 20% can be reached for some fractions of the particle size–material matrix (for example, wood 20–40 mm and cardboard 60–80 mm) but gets as bad as 231% (wood 200–400 mm) for others. Furthermore, a decrease in the relative sampling variability with the mass share of a fraction is observed. Part of the observed variability is explainable through the fundamental sampling error, while contributions of other types of sampling errors are also evident. The results can be used for estimating confidence intervals for experimental outcomes as well as assessing required sample sizes for reaching a target precision when working with mixed commercial waste.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Coarse shredding followed by one or more screening stages is often the first step when processing mixed commercial waste (MCW). Besides size reduction and definition, this combination contributes to the concentration of different materials as well as their contained chemical elements in different fractions. Reasons for this are the different particle size distributions of the material classes in the original material, as well as differences in comminution behaviour—e.g. brittle fracturing of glass and passing through or tearing of plastic foils.
Aiming at systematically steering this concentration process, optimal shredder and screen parametrization are intended to be found through empirical regression models for the particle size–material matrix as well as for the distribution of the concentrations of contained elements over particle sizes, based on experimental results. Because of the high inherent inhomogeneity of MCW, performing such experiments demands processing of large amounts of material to homogenize the variability of the input stream regarding composition and particle size between the single runs. These high amounts of material cause the infeasibility of analysing the complete shredding product so that samples need to be taken.
Various standards and recommendations concerning sampling of MCW are available, giving guidelines on sample extraction, increment sizes, sample numbers and sizes, and sample processing for different applications. Regarding masses, they aim at ensuring that the amount of analyte contained in the sample is sufficient to keep the effect of single particles ending up in the sample—or not—at an insignificant level. This is, for example, done through average particle masses and shares of sorting fractions by Felsenstein and Spangl (2017). In contrast, the technical report CEN/TR 15310 (European Committee for Standardization 2006) for uses inhomogeneity descriptors in combination with the cubic diameter of the largest particles, as well as bulk density, as an estimate for maximum particle contributions to the analyte.
In Austria, the Austrian Standard ÖNORM S 2127—Basic characterization of waste heaps or solid waste from containers and transport vehicles (Austrian Standards Institute 2011)—is usually applied, demanding a minimum increment mass \(m_{\text{inc}}\) [kg] according to Eq. (1)—where \(d_{95}\) is the 95th percentile particle size [mm]—and a minimum number of 10 increments per (representative) sample. Furthermore, at least one sample per 200 t of waste investigated is required. Multiplying these requirements leads to a minimum for the total sample mass.
However, the standard does not give information about the statistical significance of the sampling result. Furthermore, the linear consideration of the diameter for the resulting sample mass is very likely to underestimate the masses required to get reliable information about coarse fractions. It is a compromise between reliability and practicability in terms of comprehensibility and economically feasible (sorting) analyses of the resulting sample masses. According to Wavrer (2018), a comparable practically oriented approach called MODECOM™ is used in France.
The technical report CEN/TR 15310—characterization of waste—sampling of waste materials (European Committee for Standardization 2006) is another available reference. It defines the minimum increment mass \(m_{\text{inc}}\) [kg] according to Eq. (2), where \(\rho\) [kg/m3] is the bulk density of the material.
The equation describes the resulting mass, when using a sampling device which is at least three times as long as the maximum particle diameter (practically determined through \(d_{95}\)) in each dimension, as demanded by the report. This shall ensure that all particles can easily enter the sampling device. The resulting increment mass is about 50 times the maximum particle mass, according to the report. It furthermore suggests a minimum sample mass \(m_{\text{sam}}\) [g], calculated according to Eq. (3), where \(p\) [m/m] is the fraction of the particles with a specific characteristic, \(g\) [–] is the correction factor for the particle size distribution of the material to be sampled, and CV [–] is the desired coefficient of variation caused by the fundamental error.
The value of \(g\) depends on the quotient of the 95th and 5th percentile particle sizes (\(d_{95} /d_{05}\)), according to Eq. (4). 0.1 is suggested as a well-accepted value for CV, and \(p\) needs to be determined from knowledge about waste consistency.
While the report also provides formulae for calculating the significance of the analytical results, determining it requires a priori knowledge about the material, as does the determination of minimum increment and sample masses.
Another reference is the Guidelines for statistical evaluation of sorting and particle gravimetric analyses from Vienna University of Technology (TU Wien) and the University of Natural Resources and Life Sciences in Vienna (BOKU) (Felsenstein and Spangl 2017). It provides theory-based instructions on required sample masses for different significance levels, while mainly addressing the sampling of the total mixed municipal waste of Austrian federal provinces and demanding prior particle weight analyses for calculating sample masses.
Gy (2004a), the founder of the theory of sampling (TOS), also provides formulae supporting the determination of required sample masses by calculating the minimum possible sampling error—the fundamental sampling error (FSE). It is calculated according to Eq. (5), where \(\sigma_{\text{FSE}}^{2}\) [–] is the variance caused by the FSE, \(m_{\text{sam}}\) [g] and \(m_{\text{lot}}\) [g] are the masses of the sample and of the lot to be sampled and \({\text{HI}}_{\text{lot}}\) [g] is the heterogeneity invariant of the lot (Gy 2004a). \({\text{HI}}_{\text{lot}}\) can be calculated through Eq. (6), which contains the following parameters:
\(c\) [g/cm3]: constitutional parameter, which can vary from values lower than 1, up to millions
\(\beta\) [–]: liberation parameter with \(0 \le \beta \le 1\)
\(f\) [–]: particle shape parameter with \(0 \le f \le 1\) and common values near \(0.5\)
\(g\) [–]: size range parameter with \(0 \le g \le 1\)
\(d_{95}\) [cm]: 95th percentile particle size
While Gy states that values for these parameters can be found for different materials in literature, no references were found for MCW. Furthermore, according to Gy (2004a), no satisfactory formula is known yet for determining \(f\). Hence, the heterogeneity invariant needs to be evaluated experimentally.
However, according to Wavrer (2018), a simplified formula exists for “simple particles,” meaning cases where the particles are assumed to consist either of 0% or 100% of an analyte—as is typically the case for waste sorting analyses, where each particle is assigned to a sorting fraction. In that case, the FSE can be calculated through Eq. (7), where \(m_{c}\) and \(m_{k}\) are the average particle masses of the constituent of interest \(c\) and the other constituents \(k\), and \(w_{c}\) and \(w_{k}\) are their mass shares, respectively. \(q\) stands for the number of constituents.
Still, a priori knowledge is needed in terms of average particle masses and assumptions about the composition of the constituents, as is the case in Felsenstein and Spangl’s (2017) guideline. Moreover, applying the formulae for the FSE does not provide information about the real sampling error beyond the contribution of the fundamental one.
In conclusion, no satisfactory guidance was found for a priori determination of required increment masses or sample masses for achieving a certain level of significance when sampling MCW. Furthermore, the general estimation error (GEE) for the elements of the particle size–material matrix as well as for the distribution of chemical elements throughout particle sizes is the result of several processing steps and subsampling steps. Thus, to evaluate analytical data quality for modelling purposes, as well as for interpreting experiments, the total error of the data acquisition process, from primary sampling to chemical analysis (which is the GEE), needs to be determined experimentally. This is done through a replication experiment (REx) as described in the Danish standard DS 3077, which is a horizontal sampling standard based on the TOS (Danish Standards Foundation 2013).
Even though the other described references may deliver more profound statements regarding necessary sample masses, the Austrian standard ÖNORM S 2127 was chosen for the REx in this work for multiple reasons: the necessary information about the material (which is only \(d_{95}\)) was available and analysing the resulting masses was expected to be feasible in practice. Furthermore, the REx offered the opportunity to evaluate this standard, which is widely applied in Austria.
The investigation to be presented will be published in two parts. In part I (i.e. the present contribution), a procedure for sampling MCW-shredding experiments is developed, based on TOS, DS 3077 and ÖNORM S 2127. Furthermore, the applied steps of sample processing from the primary sample to the particle size–material matrix are described. Finally, the results of a REx are presented, providing information about data quality when applying the described procedure. The corresponding experimental work was conducted from October to December 2018 in Allerheiligen im Mürztal, Styria, Austria.
Part II, presented by Viczek et al. (2019), deals with the distribution of several chemical elements, especially heavy metals, in different grain size fractions of coarsely shredded MCW. Post-sorting processing of the material for analysing the concentrations of these elements is described. Furthermore, the GEE is evaluated for the concentrations in different particle size classes through the REx. Ultimately, the distribution of the chemical elements throughout particle sizes, as well as correlations to the results of sorting analysis are presented.
Materials and methods
Theory of sampling
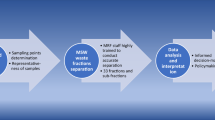
According to Esbensen and Wagner (2014), the theory of sampling is a universal, scale-invariant fundamentum for understanding sampling and the potential errors caused by it. It is based on the fundamental sampling principle, requiring all increments of the lot to have the same likelihood of ending up in the (representative) sample. It describes all errors contributing to the total sampling error (TSE). The GEE consists of this TSE in addition to the, often well-determined, total analytical error (TAE) (Esbensen and Wagner 2014). Its components are shown in Fig. 1.
Gy (2004b) divides the contributions to the TSE into correct sampling errors (CSE) and incorrect sampling errors (ISE). The first are caused by constitutional and distributional heterogeneities of the material to be sampled and are unavoidable, whereas the latter come from avoidable sampling mistakes and should, therefore, be avoided as far as possible.
CSE consists of two kinds of errors, the FSE and the grouping and segregation error (GSE). The FSE is caused by the constitutional heterogeneity, which describes chemical and physical differences between fragments of the lot—in the case of MCW: particles—and can only be altered through physical interventions like comminution. The GSE, on the other hand, is present due to the distributional heterogeneity, meaning the spatial distribution of different particles, e.g. through segregation, or regarding MCW because of compositional differences of different, joined but not homogenized, waste sources (Esbensen and Julius 2009). The distributional heterogeneity is the reason why samples need to consist of a number of increments spaced around the lot to achieve acceptable levels of GSE.
ISEs are the sum of incorrect delimitation errors (IDEs), incorrect extraction errors (IEEs) and incorrect processing errors (IPEs). The IDEs describe errors in defining geometrical domains to be potentially taken as a sample. According to Gy (2004b), they can be avoided when collecting materials of a stream using equal time intervals. The IEEs appear, when the delimited domain (including all particles whose centre of mass is contained) cannot be precisely extracted, meaning particles end up in the sample that should not have and vice versa. Finally, IPEs mean all errors caused by incorrect processing of the sample after extraction and consist of six elements: contamination by foreign material, loss of material (e.g. dust), alteration in chemical and alteration in physical composition, involuntary operator faults and deliberate faults for manipulating results (Gy 2004b).
Replication experiment
The GEE manifested as the variability of repeated sampling can be quantified through a REx as described in DS 3077 (Danish Standards Foundation 2013). It is performed by extracting and analysing replicate samples of the same lot. The variability in analytical results obtained for these repeated samples is then expressed through the relative sampling variability (RSV), giving a measure for sampling quality evaluation. It is calculated according to Eq. (8), where \(s\) [arbitrary concentration unit (conc. u.)] is the standard deviation and \(\bar{x}\) [conc. u.] is the arithmetic mean of the concentrations of a specific analyte in the repeated samples—functioning as an estimate for the true value.
In this investigation, the single samples cover equal time spans in which material falls from the conveyor belt. Hence, for calculating \(\bar{x}\), the contribution of each sample needs to be weighted by sample mass, as time spans with lower throughputs contribute less to the concentrations in the total lot. Therefore, \(\bar{x}\) is calculated according to Eq. (9), where \(m_{{{\text{sam}},k}}\) is the sample mass [kg] of the kth replicate sample and \(x_{k}\) [conc. u.] is the concentration of a specific analyte according to sample \(k\). As each of the samples is equally likely to be taken, \(s\) is calculated without weighting, according to Eq. (10), where \(n\) [–] is the number of samples.
According to DS 3077, the absolute minimum number of replicates for performing a REx is 10 (Danish Standards Foundation 2013). Due to the enormous amount of manual work needed in waste sorting analytics, this minimum number of samples is chosen for this work. Furthermore, the standard gives guidance for RSV interpretation, stating that 20% is a consensus acceptance threshold. This value is to be understood as a rough indication—the threshold applied in practice needs to be defined based on the potential impacts of analytical uncertainties.
Shredding experiment and primary sampling
Experimental set-up
The shredding experiment in this investigation was performed using a mobile single-shaft coarse shredder Terminator 5000 SD with the F-type cutting unit from the Austrian company Komptech (Fig. 2). It was fed using an ordinary wheel loader. The shredding product was discharged using the conveyor belt included in the machine, forming a windrow.
The experiment was performed operating the machine on 60% of the maximum shaft rotation speed (18.6 rpm) and with the cutting gap completely closed. The waste used was MCW from Styria in Austria.
Sample and increment mass
For defining the total sample mass to be taken, in this work the Austrian standard ÖNORM S 2127 was considered as a reference. Multiplying the minimum increment mass from Eq. (1) with the minimum number of increments, which is 10, and considering that the expected amount of waste to be processed in the experiment is less than 200 t, the minimum sample mass \(m_{\text{sam}}\) is calculated according to Eq. (11). With 400 mm being a conservative estimate for \(d_{95}\) from prior experiments, a minimum sample mass of 240 kg is defined.
As a rising number of increments forming a sample of a mass \(m_{\text{sam}}\) leads to better spatial coverage of the lot, it is very likely that dividing this mass into more than 10 increments—resulting in values for \(m_{\text{inc}}\) lower than defined by Eq. (1)—does not negatively influence sampling quality, but rather improve it while keeping the total mass to be analysed constant. For practical reasons consisting of the manageable sample device volume and increment mass when sampling by hand, as well as the maximum practicable sampling frequency and the target of keeping the experimental duration as short as possible because of the high throughput, 20 was chosen as the number of increments, resulting in a minimum increment mass of 12 kg.
Practical implementation of primary sampling
For reasons of practical implementation, sampling during the shredding experiments was performed by hand. This was done by holding a suitable open container into the falling stream at the end of the product conveyor belt, allowing preferable one-dimensional sampling. The container was held by two people standing at each side of the conveyor belt. At certain times, they received a starting signal to introduce the container into the stream. After a defined time (determination described below), the container was removed, containing one increment. To guarantee the accessibility of the belt, it was kept low during sampling intervals, needing the shredder to keep moving in the opposite direction of the output material stream, forming a long windrow.
According to CEN/TR 15310, each dimension of the sampling device should be at least three times as long as \(d_{95}\), to allow the entry of all particles (European Committee for Standardization 2006). For the described sampling method, a container of (1.2 m)3 would have been unmanageable. The inner dimensions of the sampling device used (built from two mortar buckets) are 1.17 × 0.37 × 0.30 (length × width × depth in m), which corresponds to a volume of 0.13 m3. With the width of the conveyor belt being 1 m and holding the device very close to the belt, it was observed that all falling material entered the container.
For determining the duration of each sampling step, the mass flow was estimated at the beginning of the experiment. To do so, the mean volume flow on the conveyor belt was measured for a duration of 3 min using a laser triangulation measurement bar above the end of the belt. The REx was part of an experimental series: prior to the experiment, a calibration experiment was performed, processing a total mass of 3.5 t for linking volume flows to mass flows. It showed a bulk density of 161.8 kg/m3. At the end of the three minutes, the sampling duration for the extraction of an increment, \(t_{\text{inc}}\) was calculated from the average volume flow \(\dot{V}\), the bulk density estimate \(\rho\) and the target increment mass \(m_{\text{inc}}\) of 12 kg, according to Eq. (12), rounding up to time intervals of 0.5 s. This resulted in a \(t_{\text{inc}}\) value of 4 s.
The first sample was taken after an operation time of 5 min, three for averaging mass flow and two for performing the corresponding calculation and for instructing the sampling teams.
Having four sampling teams of two people each and four sampling devices, a sampling interval of 30 s was feasible. The assignment of the increments to the ten samples was alternated, leading to a sampling interval of 5 min for each sample. After a total time of 107 min, the experiment was completed.
Sample processing
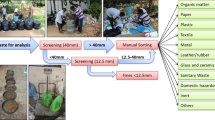
Each sample taken was collected in seven waste disposal bins of 220 l each. From there, the path to the particle size–material matrix is a sequence of mass reduction, screening and sorting, as shown in Fig. 3. The single steps are described in the following subchapters.
Mass check and mass reduction
The lower the sample mass, the lower the efforts for screening and sorting. Thus, the primary samples, as well as fine fractions produced through screening, are subject to a mass check. There, it is evaluated whether mass reduction is applicable. Reasons for masses higher than needed are high momentary throughputs during primary sampling time intervals, as well as low coarse fraction shares, while minimum fine fraction masses are recalculated with the new maximum particle diameter, according to Eq. (11). In this work, it was decided to apply mass reduction, when at least 30% of the material can be discarded while adding a safety buffer of 10% of the minimum mass to be kept. This is the case if the inequality shown in Eq. (13) is true for the mass of the evaluated sample part \(m_{\text{part}}\), the maximum particle diameter \(d_{\hbox{max} }\), as defined by the preceding screening step (400 mm for the primary sample), and a mass reduction factor \(f_{\text{red}}\) [–] of 0.7. Discarding less material was considered as not being feasible due to the needed effort for mass reduction. The mass reduction factor defines the fraction of the sample that is preserved. Three possible values for \(f_{\text{red}}\) were defined, being 0.5, 0.6, and 0.7, respectively. The lowest valid one according to Eq. (13) is chosen. Lower values were not applied, to support spatial coverage of the sample part by taking at least five increments when applying mass reduction, which is a process of subsampling. Being such, it needs to be kept in mind, that all of the described potential sampling errors also apply to subsampling and are added to the primary sampling error. On the other hand, the latter is smaller for these fractions than for coarse ones, due to lower average particle masses, leading to more contained particles per mass.
Various implementations of mass reduction were described and evaluated by Petersen et al. (2004). Most of them, like riffle splitters, revolver splitters or Boerner dividers are not applicable, as they require the material to be pourable. This is not the case with coarse MCW, which has a high agglomeration tendency. Others, like alternate or fractional shovelling (Petersen et al. 2004) or coning and quartering (Wagner and Esbensen 2012), which are often used for waste mass reduction, show high sampling errors according to the references. Therefore, a mass reduction procedure based on the method of bed blending as described by Wagner and Esbensen (2012) was applied—a comparable approach was used by Pedersen and Jensen (2015) while sampling impregnated wood waste in Denmark.
The sample to be reduced was emptied onto a plastic foil to avoid contamination from the floor or possible loss of material. On this foil, it was spread out, forming an evenly distributed windrow of a length of 5 m (Fig. 4). Using random numbers from 1 to 10 a number of 5–7 segments (0.5 m each)—depending on \(f_{\text{red}}\)—was chosen for preservation. The other segments were extracted from the windrow and pushed to the floor beside the plastic foil, using a broom. To support this, lines with a distance of 0.5 m were drawn on the floor next to the foil and on the foil in advance for increment delimitation. The material to be preserved as well as the material to be discarded was shovelled into containers to be weighed. From these masses (i.e. preserved: \(m_{\text{pres}}\), discarded: \(m_{\text{disc}}\)) the real reduction factor \(f_{\text{red}}^{*}\) [–] is calculated according to Eq. (14).
Screening
The samples were screened into nine different particle size classes, using screen plates with circular holes of eight different diameters. Screening was performed using a batch drum screen, which has the shape of an equilateral octagonal prism formed by the screen plates. The dimensions are shown in Fig. 5. Screen plates with the following hole diameters were used (in mm): 200, 100, 80, 60, 40, 20, 10, and 5. The screen was operated using material batches of 75 l for screen cuts of 20–200 mm. The volumetric batch size was reduced by 50% for the smaller ones, as the high mass of the material, caused by the higher bulk density of finer fractions, would have overworked the motor of the screen. Screening times were chosen based on experience, ensuring mass constancy: 180 s for screen cuts of 40–200 mm and 270 s for the smallest three screen cuts. The rotation speed of the screen was set to 5 rpm.
Sorting and mixing
Coarse fractions produced in the screening steps that have particle sizes larger than 20 mm (i.e. in total six fractions), were hand-sorted into nine different material classes. Finer material (i.e. three fractions having particle sizes smaller than 20 mm) was not sorted due to infeasibility, considering the immense amount of work needed to sort such fine materials. Furthermore, finer materials are rarely sorted in practical analyses, as processing them in treatment plants for extracting valuable materials is often disproportionately costly. The material classes were chosen in regard to potential valuables (i.e. from the waste management point of view) contained in the waste, they are: metals (ME), wood (WO), paper (PA), cardboard (CB), plastics 2D (2D), plastics 3D (3D), inert materials including glass (IN), textiles (TX), and a residual fraction (RE). Fractions finer than 20 mm were assigned to the residual fraction. After weighing the sorted fractions, they were joined again, as the subsequent chemical analysis was performed for each particle size class, but not for individual sorting fractions.
Weighing
The weighing was carried out using two different scales. The bigger scale was used for containers with a filled weight higher than 30 kg. With a maximum container weight of about 16 kg, this corresponds to partial samples with a weight of up to 14 kg. The uncertainty of this scale is 100 g. Lighter containers were weighed using a scale with an uncertainty of 0.1 g.
In practice, this means that screening fractions and mass reduction fractions were usually weighed using the big scale. Sorting results were always weighed using the more precise small scale.
Calculations
Particle size–material matrices
The particle size–material matrices regarding masses \(\mathbf{M}\) are \(v \times w\) matrices, where the elements \(m_{ij}\) represent the mass of the ith of \(v\) particle size classes and the jth of \(w\) material classes in an original sample. The assignment of the indices to the classes is shown in Table 1. For calculating the masses in the original sample, mass reduction steps must be considered mathematically. Thus, the mass \(m_{ij}\) is calculated according to Eq. (15), where \(m_{ij}^{*}\) is the mass weighed in the sorting analysis and \(f_{{{\text{red}},r}}^{*}\) is the real mass reduction factor (according to Eq. 14), when reducing the fine fraction produced in the \(\left( {r - 1} \right)\)th screening step. \(r = 1\) stands for the original material (0–400 mm) and \(f_{{{\text{red}},r}}^{*}\) is 1 if no mass reduction was performed.
The elements \(w_{ij}\) of the particle size–material matrices regarding mass fractions \(\mathbf{W}\) represent the shares of masses \(m_{ij}\) of the total sample mass and are calculated according to Eq. (16):
As the definition of material classes as well as the choice of screen cuts is arbitrary, further classes can be defined and evaluated by summing up the masses of specific fractions. This allows calculating standard deviations and RSV values for the mass shares of larger fractions, up to the total material. To calculate all different combinations of materials, a binary matrix \(\mathbf{B}_{w}\) containing all possible combinations of ones and zeros for \(w\) digits is needed. To generate it, the \(j\) column of the matrix contains the \(w\)-digit binary representation of the number \(j\), while each of the \(w\) rows contains one digit. For \(w\) digits, the matrix has \((w^{2} - 1)\) columns. For the actual data, \(w\) is 9. Equation (17) shows the matrix \(\mathbf{B}_{ 4}\) as an example.
Regarding particle size, only adjacent classes are combined, corresponding to an alternating choice of screen cuts. For \(v\) particle size classes a binary matrix \(\mathbf{A}_{v}\) is needed, containing all possible combinations of zeros and 1 to \(v\) adjacent ones in its rows. The matrix has \(v\) columns and \(\left( {v \cdot \left( {v + 1} \right)} /2\right)\) rows. For the present data, \(v\) is 9. Equation (18) shows the matrix \(\mathbf{A}_{4}\) as an example.
The matrices \(\mathbf{W}_{\text{mp}}\), containing the weight fractions of all possible combinations of materials and adjacent particle sizes, are calculated according to Eq. (19) and have 45 rows and 511 columns.
Results and discussion
Process and material analysis and primary sampling mass
The mean throughput—determined at the end of the experiment—was 25.2 t/h or 71.8 m3/h, resulting in a total mass of 45.0 t, a total bulk volume of 128.1 m3 on the product conveyor belt and thus a bulk density of 351.4 kg/m3. This means that the bulk density of the shredded material of the REx is much higher than the expected density of 161.8 kg/m3. Still, the target primary sample masses were approximately achieved, with a mean of 241 kg, a standard deviation of 22 kg, a minimum of 215 kg, and a maximum of 284 kg. The weighted mean values of the particle size–material matrix as well as of the sums of size classes and material classes are shown in Table 2.
Sampling error
The relative sampling variabilities related to the material classes in Table 2 are shown in Table 3. Beyond that, Fig. 6 shows the RSV values as well as the standard deviations \(s\) for all 22,995 classes in the matrices \(\mathbf{W}_{\text{mp}}\), plotted against the correspondent weighted mean values. The grey triangles mark the data corresponding to the original matrices \(\mathbf{W}\).
Incorrect sampling errors
Primary sampling
Increment delimitation is done by defining time intervals during which all material falling from the product conveyor belt of the shredder is collected. Therefore, no IDEs are expected.
Correct increment extraction, on the other hand, turns out to be challenging: some increments could not be taken at the defined time, because the end of the conveyor belt was too high. The reason for this was the wheel loader feeding material into the shredder, not allowing the latter to move forward. Because of this, the belt had to be elevated, producing a higher heap. In these situations, increment extraction started as soon as it was possible again. Furthermore, communication between the samplers and the person responsible for timing was difficult during sampling, due to the loudness of the machine. Because of this, the end of the defined 4 s of sampling was determined by the samplers through counting. Considering the real mass flow of 25.2 t/h, the average sample mass with 20 increments of 4 s each would have been 560 kg, while the observed average was less than half of that, i.e. about 241 kg. Consequently, it can be assumed that the real sampling time was less than 2 s, because of the subjective sense of time, which might also have been influenced by the weight of the increments taken. Nonetheless, this did not negatively affect the target sample mass of 240 kg. Furthermore, all samples fulfil Eq. (11) as the empirical value for \(d_{95}\) is 194 mm (calculated through linear interpolation from Table 2). Still, the deviation from the defined sampling time of 4 s is not very likely to be uniform, leading to scattering of real sampling time and thus to IEE.
Regarding IPE, it cannot be assured that all particles of the taken increments reached the final samples, as handling the bulky sampling device, which is also heavy when filled, might have led to unintentional falling out of some particles.
Mass reduction
Mass reduction is a subsampling process. Consequently, all potential sampling errors might as well occur at this step. Regarding increment delimitation, drawing the equidistant lines on the foil is a quite exact process. So—if IDEs occur at all—the order of magnitude should be negligible compared to IEE:
Extracting the increments correctly turned out to be problematic, especially for coarse fractions. This is because of material wedging, impeding pourability. Because of this, when pushing the segments to be discarded from the foil, it was unavoidable to extract material from the neighbouring segments as well. Therefore, IEE could not be completely avoided with the mass reduction method applied.
Regarding increment preparation, the main expectable error is loss of dust blown away when handling the material.
Screening and sorting
As screening and sorting are not sampling operations, IDE and IEE cannot occur. IPE, on the other hand, are expected due to blowing away of dust, as well as the loss of particles falling from the sorting table unnoticed.
Loss of water
The samples taken were processed during several weeks. Although stored in closed disposal bins, loss of humidity is possible as the bins are not hermetical, leading to IPE.
The total loss of material, calculated comparing the sum of the individual fraction masses according to Eq. (14) to the primary sample masses, shows a mean value of 5.6% and ranges between 4.6 and 7.2%.
Container and equipment contamination
For practical reasons, before reusing containers, and equipment like the screen or shovels, they could only be cleaned using hand brushes. Thus, cross-contamination of different samples and subsamples cannot be completely excluded, leading to further potential IPE. These contaminations are expected to be low, due to small contact areas in relation to sample masses.
Sampling quality
Applying an RSV of 20% as a threshold for good sampling, Table 3 shows that the applied procedure only produces good results for some of the examined fractions. Figure 6 further shows that RSV tends to be better for large fractions, indicating that small fractions require better sampling and analytics for achieving acceptable relative errors. This is the case, although the absolute standard deviation seems to increase with mass share, reaching a maximum for fraction ratios of 50%.
Figure 7 shows the RSV contribution of the FSE over the mass share (according to Eq. 7) of a constituent \(c\) for different average particle masses \(m_{c}\) for the present lot mass and target primary sample mass, assuming a two-component composition. For the average particle mass of the other constituent \(m_{k}\) a value of 0.1 kg was chosen. \(m_{k}\) has little influence on \(\sigma_{\text{FSE}}\), as long as it is significantly smaller than the sample mass \(m_{\text{sam}}\). Comparing Figs. 6 and 7, it is apparent that the general trend of the empirical RSV shows similarities to the trend of the FSE’s contribution to the sampling error. Especially for coarse particles which are either heavy (e.g. metal 100–200), have very low mass shares (e.g. paper 200–400), or both (e.g. metal 200–400), the FSE explains very well why RSVs far beyond 20% were observed.
Relative standard error caused by FSE versus mass share of a constituent \(c\) of a two-component composition, according to Eq. (7), for different average particle masses \(m_{c}\) of constituent \(c\) with a lot mass of 45,000 kg, a sample mass of 240 kg and an average particle mass for the other constituent \(k\) of 0.1 kg
However, keeping in mind that only few particle size-material fractions—if any—have average particle masses as high as 1 kg, the figures show that primary sampling FSE only explains part of the observed sampling errors. For example, for a fraction with a mass share of 0.1 \(\sigma_{\text{FSE}}\) is 3.4% in Fig. 7, while the RSV values in Fig. 6 range somewhere between 5 and 25%. Therefore, other sampling errors obviously also show significant contributions. Wavrer (2018) highlights the high distributional heterogeneity of municipal solid waste. For MCW, it is known to be even higher, therefore the GSE is likely to significantly contribute to the sampling error. Furthermore, the described ISEs, as well as CSEs and ISEs from subsampling also contribute to the observed RSVs. These contributions, along with the different average particle masses and numbers of subsampling stages for the different data points, as well as errors in estimating RSV due to the low number of 10 taken samples, also explain the scattering of the data in Fig. 6 along the ordinate axis.
Knowing the standard deviation, confidence intervals for estimated concentrations can be calculated as a corresponding measure. But doing so, care has to be taken for very large RSVs: the high relative errors indicate a positively skewed distribution of the values (and therefore not a normal distribution), as commonly used confidence intervals like 95% would otherwise include negative percentages. Ultimately, the quality of sampling needs to be rated dependent on the analytical target.
Conclusion
A sampling and sample processing procedure for screening and sorting analysis of shredded mixed (i.e. commercial) solid waste was established and is reported, based on the TOS, the Danish horizontal sampling standard DS 3077 and the Austrian standard ÖNORM S 2127. Assessment of sampling quality, rated through the relative sampling variability, shows that the procedure gives good results for some values of the particle size-material matrix (at a threshold of 20%) but not for all of them—it gets as bad as 231%. It is further shown that the RSV is better for larger fractions. In conclusion, especially when analysing small fractions, a reduction in the occurring sampling errors is necessary. Regarding the CSEs, in a first step, it should be assured that the sample mass suffices to keep the FSE within a reasonable range. For this, building a database of typical particle masses, as suggested by Wavrer (2018), is highly encouraged. Equation (7) then provides a (necessary, but not sufficient) minimum sample mass.
As it was shown that FSE only contributes a part of the observed RSVs, compensating the high distributional heterogeneity of the waste by increasing the number of increments might also significantly improve sampling quality by reducing GSE. To handle the resulting higher sampling frequencies, automated primary sampling, e.g. using a reversible conveyor belt, is encouraged.
Such automated sampling might as well contribute to reducing ISEs, i.e. IEEs, as it allows to extract samples exactly in time, while still preserving the benefits of sampling from a falling stream (one-dimensional sampling and good separation of agglomerated particles). Moreover, IEEs during mass reduction (caused by agglomerations, especially for coarse fractions) could as well be reduced by (automatic) subsampling from a falling stream. Furthermore, the analytical error can be decreased by using a more precise big scale.
Finally, when evaluating very small fractions through screening and sorting, increasing sample masses will be unavoidable for reliable analyses. In addition to the discussed estimation of the FSE, the determined values for the RSV help to estimate them in advance.
Abbreviations
- \(\mathbf{A}_{v}\) :
-
Binary matrix for combining adjacents of \(v\) particle size fractions [–]
- \(\mathbf{B}_{w}\) :
-
Binary matrix for combining 1 to \(w\) material classes [–]
- c :
-
Constitutional parameter [kg/m3]
- CV:
-
Coefficient of variance [–]
- \(d_{05}\) :
-
5th percentile particle size [mm], [cm]
- \(d_{95}\) :
-
95th percentile particle size [cm]
- \(d_{\hbox{max} }\) :
-
Maximum particle diameter [mm]
- \(f\) :
-
Particle shape parameter [–]
- \(f_{\text{red}}\) :
-
Mass reduction factor [–]
- \(f_{\text{red}}^{*}\) :
-
Real mass reduction factor [–]
- \(f_{{{\text{red}},r}}^{*}\) :
-
\(f_{\text{red}}^{*}\) when reducing the fine fraction of the \(\left( {r - 1} \right)\) th screening step [–]
- \(g\) :
-
Particle size parameter [–]
- \({\text{HI}}_{\text{lot}}\) :
-
Heterogeneity invariant of the lot [g]
- \(\mathbf{M}\) :
-
Particle size–material matrix (masses) [kg]
- \(m_{c}\) :
-
Average particle mass of the constituent \(c\) [g]
- \(m_{\text{disc}}\) :
-
Mass discarded during mass reduction [kg]
- \(m_{ij}\) :
-
Mass of the ith particle size fraction and jth material class in the primary sample [kg]
- \(m_{ij}^{*}\) :
-
Weighed mass of the ith particle size fraction and jth material class [kg]
- \(m_{\text{inc}}\) :
-
Minimum increment mass [kg]
- \(m_{k}\) :
-
Average particle masses of the constituents \(k\) [g]
- \(m_{\text{lot}}\) :
-
Mass of the lot to be sampled [g]
- \(m_{\text{part}}\) :
-
Mass of sample part [kg]
- \(m_{\text{pres}}\) :
-
Mass preserved during mass reduction [kg]
- \(m_{\text{sam}}\) :
-
Minimum sample mass [g]
- \(m_{{{\text{sam}},k}}\) :
-
Mass of the kth sample [kg]
- \(n\) :
-
Number of samples [–]
- \(p\) :
-
Fraction of particles with a specific characteristic [–]
- \(q\) :
-
Number of constituents [–]
- \({\text{RSV}}\) :
-
Relative sampling variability [%]
- \(s\) :
-
Standard deviation [conc. u.]
- \(t_{\text{inc}}\) :
-
Increment extraction time [s]
- \(\dot{V}\) :
-
Volume flow [kg/m3]
- \(v\) :
-
Number of particle size fractions [–]
- \(\mathbf{W}\) :
-
Particle size-material matrix (mass shares) [kg/kg]
- \(\mathbf{W}_{\text{mp}}\) :
-
Matrix of all regarded particle size fraction and material class combinations (mass shares) [kg/kg]
- \(w\) :
-
Number of material classes [–]
- \(w_{c}\) :
-
Mass share of the constituent \(c\) [g]
- \(w_{ij}\) :
-
Mass share of the ith particle size fraction and jth material class in the primary sample [kg/kg]
- \(w_{k}\) :
-
Mass shares of the constituents k [g]
- \(\bar{x}\) :
-
Weighted arithmetic mean [conc. u.]
- \(x_{k}\) :
-
Concentration of a specific analyte according to sample k [conc. u.]
- \(\beta\) :
-
Liberation parameter [–]
- \(\rho\) :
-
Bulk density [kg/m3]
- \(\sigma_{\text{FSE}}^{2}\) :
-
Variance caused by the fundamental sampling error [–]
References
Austrian Standards Institute (2011) ÖNORM S 2127 Grundlegende Charakterisierung von Abfallhaufen oder von festen Abfällen aus Behältnissen und Transportfahrzeugen [Basic characterization of waste heaps or solid wastes from containers and transport vehicles]. Austrian Standards Institute, Vienna. ICS: 13.030.01
Danish Standards Foundation (2013) DS 3077 Representative sampling—Horizontal standard. Danish Standards Foundation, Charlottenlund. ICS: 03.120.30, 13.080.05
Esbensen KH, Julius LP (2009) Representative sampling, data quality, validation—a necessary trinity in chemometrics. In: Tauler R, Walczak B, Brown SD (eds) Comprehensive chemometrics: chemical and biochemical data analysis, 1st edn. Elservier, Burlington, pp 1–20
Esbensen KH, Wagner C (2014) Theory of sampling (TOS) versus measurement uncertainty (MU)—a call for integration. TrAC. https://doi.org/10.1016/j.trac.2014.02.007
European Committee for Standardization (2006) CEN/TR 15310-1 characterisation of waste—sampling of waste materials—part 1: guidance on selection and application of criteria for sampling under various conditions. European Committee for Standardization, Brussels. ICS: 13.030.10, 13.030.20
Felsenstein K, Spangl B (2017) Richtlinien für die statistische Auswertung von Sortieranalysen und Stückgewichtsanalysen [Guidelines for statistical evaluation of sorting and particle mass analyses], pp 34–68. http://www.argeabfallverband.at/fileadmin/bilder/PDFs/Anhaenge_RA_OOE_2018.pdf. Accessed 19 Mar 2019
Gy P (2004a) Sampling of discrete materials: II. Quantitative approach—sampling of zero-dimensional objects. Chemom Intell Lab Syst 74(1):25–38. https://doi.org/10.1016/j.chemolab.2004.05.015
Gy P (2004b) Sampling of discrete materials—a new introduction to the theory of sampling: I. Qualitative approach. Chemom Intell Lab Syst 74(1):7–24. https://doi.org/10.1016/j.chemolab.2004.05.012
Pedersen PB, Jensen JH (2015) Representative sampling for a full-scale incineration plant test—how to succeed with TOS facing unavoidable logistical and practical constraints. TOS Forum 3(1):213–217
Petersen L, Dahl KD, Esbensen KH (2004) Representative mass reduction in sampling—a critical survey of techniques and hardware. Chemom Intell Lab Syst 74(1):95–114. https://doi.org/10.1016/j.chemolab.2004.03.020
Viczek SA, Khodier K, Aldrian A, Sarc S (2019) Sampling and analysis of coarsely shredded mixed commercial waste; part II: grain size dependent elemental distribution. In preparation for submission in a peer reviewed process (status Aug 2019)
Wagner C, Esbensen KH (2012) A critical review of sampling standards for solid biofuels—missing contributions from the theory of sampling (TOS). Renew Sustain Energy Rev 16(1):504–517. https://doi.org/10.1016/j.rser.2011.08.016
Wavrer P (2018) Theory of sampling (TOS) applied to characterisation of municipal solid waste (MSW)—a case study from France. TOS Forum 5(1):3–11
Acknowledgements
Open access funding provided by Montanuniversität Leoben. The Competence Center Recycling and Recovery of Waste 4.0—ReWaste4.0—(Grant Number 860 884) is funded by the Austrian Federal Ministry of Transport, Innovation and Technology (BMVIT), Austrian Federal Ministry of Science, Research and Economy (BMWFW) and the Federal Province of Styria, within COMET—Competence Centers for Excellent Technologies. The COMET programme is administered by the Austrian Research Promotion Agency (FFG).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Editorial responsibility: Binbin Huang.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Khodier, K., Viczek, S.A., Curtis, A. et al. Sampling and analysis of coarsely shredded mixed commercial waste. Part I: procedure, particle size and sorting analysis. Int. J. Environ. Sci. Technol. 17, 959–972 (2020). https://doi.org/10.1007/s13762-019-02526-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13762-019-02526-w