Abstract
The majority of tornado fatalities occur during severe thunderstorm occurrences that produce a large number of tornadoes, termed tornado outbreaks. This study used extreme value theory to estimate the impact of tornado outbreaks on fatalities while accounting for climate and demographic factors. The findings indicate that the number of fatalities increases with the increase of tornado outbreaks. Additionally, this study undertook a counterfactual analysis to determine what would have been the probability of a tornado outbreak under various climatic and demographic scenarios. The results of the counterfactual study indicate that the likelihood of increased mortality increases as the population forecast grows. Intensified El Niño events, on the other hand, reduce the likelihood of further fatalities. La Niña events are expected to increase probability of fatalities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the United States, tornadoes threaten human health and property constantly. Nowhere else in the world has more tornadoes than the United States (U.S.), which account for about one-fifth of all natural hazard fatalities and nearly 20% of U.S. billion-dollar disasters between 1973 and early 2007 (Swienton et al. 2021). Most tornado deaths happen when there are a lot of tornadoes at the same time, which is called a tornado outbreak. A tornado outbreak is a series of many tornadoes that happen close together in time (Tippett et al. 2016; Fricker and Allen 2022).
Numerous studies have combined fatalities, injuries, and property damage statistics to give a comprehensive analysis of tornado hazards. For instance, Anderson-Frey and Brooks (2019) studied the impact of tornadoes on fatalities using machine learning domains and discovered that deadly tornadoes are more likely to have high Enhanced Fujita Scale (EF-scale) ratings (which indicate the intensity of the tornado impact) and occur in the winter and spring. Around 87% of tornadoes resulting in deaths were warned of in advance, and nearly 95% of tornado deaths happened during an active warning.
Biddle et al. (2020) examined the regional differences in the risk of mortality from tornadoes in the United States. Their findings revealed that southern states have seen considerable increases in the probability of mortality and injury when compared to northern states. Fricker and Allen (2022) investigated the risk variables for tornado fatalities on a community level by conducting a place-based analysis of tornado fatalities in Louisiana to assess the potential impact of many physical and social systems on the area’s tornado fatality rates. They argued that smoother, lower-lying terrain is more susceptible to tornadoes and tornado fatalities, and that residents of mobile homes are more vulnerable to becoming tornado casualties than residents of permanent residences.
In contrast to the studies treating tornadoes as independent events, there are few that have examined how fatalities are affected by a tornado outbreak (Swienton et al. 2021). Fuhrmann et al. (2014) showed that the great majority of tornado-related fatalities occurred during outbreaks by developing two comparable measures for determining the physical size, or intensity, of tornado outbreaks in the Rocky Mountains. Heather (2019) examined the association between tornado severity (as measured by the Fujita Scale), tornado frequency, and morbidity and mortality trends over time using geographic information system (GIS) technology and statistical analysis of historical data in Texas. They showed that there was a statistically significant relationship between tornado severity and associated morbidity and death during “tornado outbreaks” in a 30-year period. The authors also noted changes in the regional and temporal distributions of outbreak and nonoutbreak tornadoes due to climatological factors.
Most recently, Swienton et al. (2021) explored the associations between tornado severity, number, and geography of occurrence as they relate to direct injuries and fatalities in severe weather events using nonparametric statistical and spatial analyses for a 35-year period in Texas. The findings revealed that tornado severity exacerbates causality, but tornado outbreaks also have an influence on the fatality rate. Although tornadoes are arguably extreme events much of the analysis of the current literature has used standard statistical techniques to analyze these. An exception in this regard is Tippett et al. (2016), who used extreme value methods to analyze tornado outbreaks in the United States during 50 years. They found no significant trend in the annual number of tornadoes but an increase in the number of more extreme outbreaks over time. However, the authors did not relate these extreme outbreaks to the number of induced fatalities.
This study contributes to the current tornado literature on two fronts. First, it utilizes extreme value statistics to estimate the risk of fatalities during tornado outbreaks, defined as sequences of six or more tornadoes that occur with no more than six hours between consecutive tornadoes covering the period of 1950 to 2018. Extreme value theory is an alternative and superior approach to quantifying the stochastic behavior of tornado outbreaks since it provides the statistical framework to make inferences about the probability of these very rare and extreme events. This study is interested in the tails of the tornado distribution (that is, tornado fatalities in outbreaks). The utilized dataset comes from the aforementioned study of Tippett et al. (2016). Importantly, in this regard the approach utilized allows for the distribution of fatalities to have changed over time due to housing density and climate factors.
Second, in addition to Tippett et al. (2016), who discovered that the frequency of U.S. tornado outbreaks has been increasing, this analysis contributes to the tornado-outbreak-fatality complex by examining the impact of fatality risk due to tornado outbreaks under several climate change and demographic counterfactual scenarios. As such it might help in formulating policies and warning systems that could prevent more losses, not just in terms of health (Chiu et al. 2013; Swienton et al. 2021), but also in terms of the many layers that result from the loss of community services and resources (Simmons and Sutter 2007; Carbone and Echols 2017; Danielson et al. 2017).
2 Methods
This section describes the extreme value theory, the key equations and the data sources of key variables, dependency, stationarity, and the counterfactual implementation.
2.1 Extreme Value Theory
Extreme value theory (EVT) is a probabilistic area of statistics that deals with so-called rare or extreme events. Three classical approaches—the block maxima, threshold excess, and point process—are usually considered. This study focused on the latter because the point process (PP) allows us to define events in time or space and can be used to simulate time-dependent threshold excesses, which is particularly to the case of tornado outbreaks. The PP model is originally attributed to Pickands (1971), which considers excess limits as events over time to model the occurrence of these events. Following Gilleland and Katz (2016) and Towler et al. (2020), the non-homogeneous Poisson point process with intensity measure, \(\Lambda\), on the set \(A=\left({t}_{1},{t}_{2}\right)\times (x,\infty )\) is given by:
where \(-\infty <\mu ,\xi <\infty ,\) and \(\sigma >0\) are location, shape, and scale parameters, respectively, and \(I(\cdot )\) is an indicator function that is zero if the argument is not true and one otherwise. Substituting \(\left[{t}_{1},{t}_{2}\right]=\) \([\mathrm{0,1}]\) to represent 1 year, and if the indicator function is equal to 1, the Poisson rate parameter, \(\lambda\), can be calculated to obtain the frequency of exceeding a particular threshold, \(u\):
The threshold value \(u\) is frequently selected as a compromise between having a sufficient number of observations to lower the variance of the estimates and guaranteeing that the remaining data do indeed follow an extreme value distribution. To determine the best threshold, the mean value of the excesses over \(u\) is plotted against \(u\) via a mean residual life (MRL) plot. More precisely, for a given threshold \(\widehat{u}\), the MRL for any threshold \(u > \widehat{u}\) is:
which is linear in \(u\) with gradient \(\frac{\xi }{1-\xi }\) and intercept \(\frac{{\sigma_{{\widehat{u}}} }}{1 - \xi }\). This study used the Northrop et al. (2017) method, which involves Bayesian leave-one-out cross-validation to compare the extreme value predicting performance of a set of thresholds. The approach evaluates the trade-off between model misspecification bias caused by an excessively low threshold and the loss of estimate accuracy caused by an unduly high threshold. The threshold selection is further examined by the mean residual life plot. The mean residual life plot aids the selection of a threshold for the point process models.
To estimate the parameters of the PP model for a given choice of threshold, u, the PP \(\mathrm{log}-\) likelihood, \(\ell\), is estimated via maximum likelihood (MLE) as:
where \({n}_{y}\) indicates the number of years of data and \([\cdot {]}_{{x}_{i}>u}\) is the indicator function as shown in Gilleland and Katz (2016, Eq. 10).Footnote 1 The \(n\)-observation return level \({x}_{n}\) is the level exceeded on average once every n years (Coles et al. 2001; Lipika 2018) in a subset of k-dimensional space, \(k\). It can be written by first defining \({p}_{i}\), when \(1+{\xi }_{i}\left(\frac{{x}_{n}-{\mu }_{i}}{{\sigma }_{i}}\right)>0\)
and when \(\left(\frac{{x}_{n}-{\mu }_{i}}{{\sigma }_{i}}\right)<0\) then \({p}_{i}=1\). It follows that \({x}_{n}\) satisfies,
thus using a log form of equation (6) gives
Diagnostic tools for the PP-approach include graphical techniques such as the Z-plot and the QQ plots (Finkenstadt and Rootzén 2003). The Z-plot is a diagnostic quantile-quantile graphic in which the mean duration between occurrences should follow an exponential distribution (Smith 1989). The QQ plots may be used to evaluate and analyze the model’s fit when the parameters are transformed to those of the generalized Pareto distribution and the quantiles are the data’s threshold excesses.
2.2 Data
The tornado dataset was obtained from the study of Tippett et al. (2016).Footnote 2 The rich dataset consists of information about the number of injured people and fatalities, which are a great factor to capture the impact of tornadoes on society. The data also contain the intensity of tornado impact (Enhanced Fujita Scale and Fujita Scale). The Fujita Scale (F-Scale) was originally developed in 1971, by Theodore Fujita to assess the wind speed of a tornado based on the damage to buildings, structures, and trees. The greatest degree of destruction in a tornado’s path was given an F-scale rating (see Table 1). The EF-Scale was devised to account for various elements impacting wind pressures on structures. The dataset contains information of both indices and information before 1971 has been gathered retroactively utilizing newspaper accounts and images of tornadoes that happened prior to this period following Tippett and Cohen (2016).
Following Caldera et al. (2018) only tornadoes that occurred in the outbreak are included in the analysis, where a tornado outbreak is defined as consisting of 6 or more F1+ tornadoes, which occur within no more than six hours in succession as stated previously. To identify tornadoes that are part of an outbreak, the storms were first sorted in chronological order, and later the rule of definition of tornado outbreak was applied. The definition allows tornado outbreaks to be located across states and possibly longer than 1 day. The period 2015 to 2018 from the NOAA Storm Prediction Center (SPC) (NOAA 2020) was included in the analysis in accordance with the methods of Tippett et al. (2016), as the authors only analyzed until 2014.
Socioeconomic and climatic variables are included in the analysis. Data on the housing unit density from the U.S. Census Bureau (2020) are included since it is expected to influence the number of tornado fatalities. Because the covariate is based on census data, the housing density variable was created via linear interpolation method. In terms of the climatic factor, the covariate was created combining the atmospheric component of the El Niño-Southern Oscillation (ENSO) and the oceanic component Surface Sea Temperature (Niño 3.4 SST) as described in Smith and Sardeshmukh (2000). The seasonality was removed from the combined time series and the values were standardized by month so that each month has a mean of 0 and a standard deviation of 1.0. The combined climatic measures named BestENSO is active during two phases, El Niño/La Niña, and inactive during so-called neutral years, when climatic conditions in the equatorial Pacific tend to be near their long-term average (Power and Delage 2018). El Niño/La Niña events can be taken from the positive/negative values of the BestENSO index. The assumption that ENSO may influence the frequency and location of tornadoes and other severe storm systems is not new. It is already known to have a significant impact on temperature and rainfall in the United States, as well as the location of the jet stream. According to Allen et al. (2015), ENSO influences the large-scale environment, and the large-scale environment influences tornado occurrence. Tippett and Lepore (2021) also acknowledged that ENSO modulates severe thunderstorm activity (tornadoes, big hail, and damaging straight-line winds) in the United States.
2.3 Dependency
By and large, there is evidence that tornado outbreaks depend on one another, and it is highly improbable that these occurrences are independent (Sparrow and Mercer 2016). As such, the data need to be tested for dependence and declustered if necessary. Coles et al. (2001) outlined ways to diagnose the dependence, for instance, using visual inspection, such as the auto-tail dependence function (atdf) plot and the extremal index. The extremal index ranges between 0 and 1, with values closer to 1 indicating less dependence. Coles et al. (2001) also described ways to break up clusters (declustering).Footnote 3
2.4 Nonstationarity
Additionally, Coles et al. (2001) showed that covariates can be used to overcome the existence of trends or cycles by modeling the parameters. In this study, the location parameter was modeled as a linear function of a covariate, \(Int\), which represents the wind speeds considering the nature and extent of the destruction the tornadoes cause. The intensity of the tornado outbreak was included as part of the location parameter since changes in location parameters correspond to shifts in typical or average tornado-related deaths. The location parameter can be expressed as:
It is also possible to add a covariate to the shape parameter, \(\xi\). Addressing nonstationarity, the analysis incorporated climatic and demographic covariates in contrast to Tippett et al. (2016). The climatic covariate was included in the analysis assuming that El Niño/La Niña events will influence linearly the number of fatalities as the BestENSO variable is standardized. Also, the simplest functional form was adopted as a precautionary approach. The housing unit density variable was also linearly included in the shape parameter.Footnote 4 The shape parameter takes the following form:
To test covariate significance, a likelihood-ratio test was used. Citing Coles et al. (2001) and Towler et al. (2020), if a model \({M}_{0}\) is a nested model of \({M}_{1}\), the deviance statistic, \(D\), can be calculated from the maximized log-likelihoods for the models:
If \(D>{c}_{\alpha }\), then \({M}_{0}\) can be rejected for \({M}_{1}\), where \({c}_{\alpha }\) is the \((1-\alpha )\) quantile of the \({\chi }_{k}^{2}\) distribution. The level of significance is \(\alpha\), and the \({\chi }_{k}^{2}\) distribution is the large sample approximation with degrees of freedom, \(k\). The results from the likelihood-ratio test can be provided upon request. Models are compared based on the Akaike Information Criterion (AIC) (Adams and Comrie 1997), which can be calculated as:
where \({l}\) is the likelihood function estimate, and \(K\) is the number of parameters being estimated.
2.5 Counterfactual Simulations
Different counterfactual scenarios were calculated to determine the effect of each covariate on the return levels. A counterfactual analysis compares the probability \({p}_{1}\) of seeing the event (exceeding the threshold in terms of fatalities) in the present day with existing climatic and socioeconomic conditions (the baseline condition) to the probability \({p}_{0}\) of seeing the event in an ever-changing demographic dynamics and changing climate (a counterfactual world) (Otto 2017; Yiou et al. 2020).
Güneralp et al. (2017) showed that the rise in expected floor space for North America is equivalent to that projected for emerging regions. By 2050, Güneralp et al. (2017) calculated that North America would have a 60% increase in floor built area, reflected in habitation construction. In this setting, probabilities can be calculated from the fitted extreme value distributions. Considering different housing scenarios, the following were calculated: (1) the baseline scenario with the average of house unit density of 2018; (2) the scenario in which the housing system increases by 60% on the average terms of 2018, as predicted by Güneralp et al. (2017); and (3) the scenario in which the average housing density is stated in the first year of the studied period (1950). The climatic covariate was held constant on the average value of 2018.
For climatic schemes, according to the findings of Bonfils et al. (2015) and Power and Delage (2018), there will be an increase of at least 15% in La Niña/El Niño occurrences relative to the historical record. This corresponds to an increase in the second (50% of the ordered sample) and third (75% of the ordered sample) BestENSO quantiles. The counterfactual considered the following scenario: (1) the baseline scenario with the average value of the BestENSO index for 2018; and (2) the adjusted probability considering an increase of 15% on the quantiles of the BestENSO index. These are related to the frequency of El Niño/La Niña events. The housing density was held constant expressing the average value for the year 2018. The shape parameters for the counterfactual analyses are modeled identically to those stated in Eq. 9.Footnote 5
3 Results
This section presents the results of the analysis of the estimated impact of tornado outbreaks on fatalities while accounting for climate and demographic factors using extreme value theory and counterfactual simulations.
3.1 Descriptive Statistics
Table 2 shows the summary of the dataset containing only tornadoes belonging to a tornado outbreak event. The death toll from tornadoes varied significantly. The maximum death toll in a tornado event was 158. The intensity of tornado events was on average approximately one. A positive BestENSO index on average indicates that there were more El Niño events in the sample. Also, the average housing density was equal to 38.
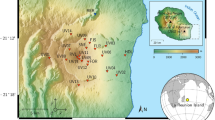
A total of 4662 fatalities was registered throughout the study period. This equates to an average of 554 tornadoes and 68 fatalities every year. Tornado outbreaks and fatalities, on the other hand, fluctuate significantly from year to year. In total, 2508 outbreaks have been found from 1950 to 2018. Figure 1 shows this fluctuation in the number of tornado outbreaks and fatalities in the United States over the study period. The data cover the 51 states of the United States from 1950 to 2018. As can be seen, tornado outbreak incidence is not uniform across states over the period. Some states experienced much more tornadoes than others, such as Illinois, Oklahoma, and Texas, with 1817, 2756, and 5140 events, respectively.

Source Adapted from Tippett et al. (2016). Interactive version of the map is available at https://datawrapper.dwcdn.net/W5JkZ/1/
Tornado outbreak activity by number of fatalities in the United States, 1950−2018. The point locations refer to the beginning path of the tornado outbreak and the size refers to the number of fatalities.
In addition, as seen in Fig. 2, we observed that some years were more extreme than others. For example, in 1965, there were 39 tornado outbreaks and 293 fatalities. This number almost doubled in 2004 with 64 events and 34 human losses.

Source Adapted from Tippett et al. (2016). Interactive version of the map is available at https://datawrapper.dwcdn.net/LVD08/5/
Number of fatalities given the occurrence of tornado outbreaks in the United States, 1950−2018.
3.2 Threshold Selection
The Bayesian leave-one-out cross-validation suggested three fatalities as the appropriate threshold of extremes. This threshold is supported by the mean residual life plot that shows three fatalities to be a reasonable choice.Footnote 6 In addition, AIC and log-likelihood findings reveal that the best model fit is the model with a threshold of three fatalities, as can be seen in Table 3.
3.3 Stationary and Nonstationary Results
Assuming stationarity, Table 3 summarizes the results for the selected threshold. It can be observed that all parameters are significant, and the shape is positive, indicating a Fréchet distribution that decays slowly tending to infinity. Following the analysis, when plotting the auto-tail dependence function plot, some dependence can be seen. The dataset was subsequently declustered to address the dependence issue. In accordance with Coles et al. (2001) and Gilleland and Katz (2016), the dataset was declustered using groups of tornado outbreaks to indicate that the declustering technique was done to each tornado outbreak event.
A preference for the nonstationary model specification using the demographic and climatic covariates was confirmed by comparing the log-likelihood and Akaike’s information criterion (AIC) compared from Tables 3 and 4. For the selected threshold, the shape, location, and scale parameters are significant. As with the stationary model, the location and scale parameters are positive. Similarly, the scale parameter is positive and with a value \(0.407\) and in line with assuming stationarity, and suggests a heavy tailed distribution (Brooks and Doswell III 2001; Dotzek 2002).
The return periods of the nonstationary model were examined. Return level time series for 5, 10, 20, and 50-year return levels were plotted (see Fig. 3). It can be seen that return levels fluctuate and rise with time, with a longer return duration reflecting a larger return level. The number of fatalities was predicted to be about 25 every five years, and close to 38 every 10 years. Every 20 years, 53 people are expected to die, and every 30 years, 63 deaths from tornado outbreaks are expected.
Finally, based on the probability of exceedance, the results suggest that the chance that at least five people will die, which is less than the double of the chosen extreme threshold, for 5, 10, 20, and 30-year return periods, decreases with longer return periods. For a 5-year return period, the chance is 76%, for a 10-year return period 43%, for a 20-year return period 18%, and around 10% for a 30-year return period.
3.4 Counterfactual Calculations
Following the counterfactual scenarios description in Sect. 2.5, Table 5 shows that an increase in housing density increases the probability of exceedance for 5, 10, and 50 fatalities, respectively. The probability of exceedance increases marginally with an increase in the demographic scenario. Comparing 1950s probabilities to the 2018 world state, it appears that the fatality probability has increased over time. When it comes to climate change scenarios, it is possible to see that the probability of fatalities increases during El Niño episodes. When compared to the baseline model, the probability of at least 50 fatalities occurring in a tornado outbreak increases during episodes of La Niña. See Figs. 4 and 5 for a spatial distribution of the counterfactual simulations.
Counterfactual calculations of the probability of at least five fatalities occurring as a result of a tornado outbreak across U.S. states with different demographic scenarios. Panel a shows the expected probability using housing density at the beginning of the study period in 1950; Panel b shows a baseline model in 2018; Panel c shows the predicted probability using housing density of 2050
Counterfactual calculations of the probability of at least 50 fatalities occurring as a result of a tornado outbreak across U.S. states with different climatic scenarios. Panel a shows a baseline model in 2018; Panel b shows the predicted probability of 50 fatalities with an increase in El Niño events; Panel c shows the predicted probability of 50 fatalities with an increase in La Niña events
4 Discussion
Tornadoes have a significant impact on the lives of many individuals in the United States. This study examined the impact of tornado outbreaks on human life, particularly fatalities, using extreme value theory while accounting for climatic and demographic factors. Using the point process technique, all parameter estimations are significant in the stationary and nonstationary models.
The positive shape parameter indicates that the underlying data have a Fréchet distribution. This implies a heavy tailed distribution in which underlies the effect of severe tornado outbreaks and higher number of tornadoes. This type of distribution was observed in studies by Brooks and Doswell III (2001) and Dotzek (2002), which modeled the distribution of tornadoes based on the F-scale. They suggested that the frequency of occurrence of severe tornado events is related to their severity, with the frequency of recurrence essentially following a logarithmic form with increasing intensity. This can also be seen in the way that fatalities are spread out. Also, Anderson-Frey and Brooks (2019) unearthed similar results in Texas but using a different approach. They observed a direct and positive relationship between tornado intensity and deaths, particularly during tornado outbreaks. Schroder and Elsner (2021) recently found that accumulated tornado power (ATP) is increasing in the United States. Convective available potential energy (CAPE), shallow-layer bulk shear (SLBS), and deep-layer bulk shear (DLBS) all have a direct influence on tornado outbreaks (at least 10 tornadoes) and death counts, according to the research.
Counterfactual simulations indicate that the possibility of more fatalities increases with an ever increasing demographic projection. Arguably this is because more densely populated locations would tend to have a more crescent housing structure, which will result in greater tornado damage and, thus, more fatalities (See Fig. 4). This finding can be corroborated by Ashley and Strader (2016) who showed how the catastrophic components of tornadoes vary greatly across locations in the United States, but that the likelihood of catastrophe increases when demographic exposure and risk coincide. Also, Fricker et al. (2017) found a power-law relationship with respect to tornado fatalities and number of tornadoes within the most tornado-prone region of the United States, such as northern Mississippi and Alabama.
Although not detected in this investigation owing to a lack of data for analysis, Brooks and Doswell III (2002) and Ashley (2007) found significant results for the tornado-fatalities relationship in mobile homes in the United States. Despite making up less than 10% of all dwellings, they claimed that around half of all tornado fatalities take place in mobile homes. Mobile home residents have a death rate that is 15−20 times higher than those who live in fixed residences. Therefore, counterfactual simulations for mobile homes, for example, would surpass the observed results for housing density calculations.
Holding housing status at 2018 average levels, the climatic counterfactual findings illustrate how the effect of El Niño/La Niña on climate would have a detrimental impact on the number of deaths caused by tornado outbreaks. Because it is possible to observe the evolution of the El Niño/La Niña, starting during its development phase in boreal summer and continuing into its final mature phase in winter, seasonal climate prediction is possible in the United States, even with respect to weather extremes (McPhaden et al. 2020). The consequences of these occurrences on extreme rains and floods, particularly in the southeast region of the nation, may drive fortification of homes and, in the worst-case scenario, guard against tornado damage. This can be explained by the decreasing effect of the counterfactual calculation of tornado outbreaks on mortality with different climatic scenarios. It is noteworthy to draw attention that for La Niña events the probability increases for a large number of fatalities. Tippett and Lepore (2021) examined meteorological trends, including ENSO, that regularly follow tornadoes in Texas, Oklahoma, Arkansas, and Louisiana using 8,000 years of synthetic data using a computer model. In the computed model, they discovered that there is a strong relationship between ENSO and tornado meteorological conditions. However, the model suggests that more tornadoes than normal are expected during La Niña conditions but that the exact number is highly uncertain. This corroborates to the present findings since more tornadoes during La Niña events will increase the probability in the number of fatalities (see Fig. 5).
From the results, it is possible to infer that climate change will impact the frequency of tornado outbreaks in the country. However, caution is needed for this statement. Recent studies demonstrate limited consensus on climate change and ENSO-related sea surface temperature fluctuations during the next century (Arias et al. 2021).Footnote 7 This evidences the unpredictable nature of El Niño/La Niña occurrences, as well as the need of researching the processes by which they affect society.
5 Conclusion
This study used extreme value theory to estimate the impact of tornado outbreaks on fatalities while accounting for climate and demographic factors. The findings indicate that the number of fatalities increases with the increase of tornado outbreaks. Intensified El Niño events reduce the likelihood of further fatalities, and La Niña events are expected to increase probability of fatalities. The current study is restricted by the fact that many more meteorological and social variables are required in order to strengthen the conclusions but they are not readily available, for example a detailed assessment on mobile homes or Global Climate Models (GCMs) thunderstorm ingredients (Tippett and Lepore 2021). Nonetheless, understanding the impact of tornado outbreaks in relation to fatalities and determining their effects are key to disaster mitigation policy making. The results presented might be used to validate policy design and preparedness, early warning, and public education for those who are at danger. Examining the frequency of tornado outbreaks given the demographic and climatic implications may thus help to reduce the number of tornado-related fatalities across the country.
Notes
For a detailed description and derivation of the point process, see Coles et al. (2001, pp. 124141).
The tornado dataset from Tippet et al. (2016) presents the record of tornado outbreak activities in the United States and includes tornadoes reported in 19502014. The tornado dataset for the remaining years (20152018) was obtained from NOAA Storm Prediction Center (SPC) at https://www.spc.noaa.gov/products/. All code for data cleaning and analysis associated with the current submission is available upon request with the required permissions.
Different variables were tried to see whether they improved model performance and explanatory power such as population density and a nonlinear term of housing density. With these variables, no distinction or improvement was obtained. The results of these model computations may be requested from the corresponding author.
The counterfactual analysis and the extreme value model estimation were conducted with the R programming language (R version 4.0.2, 2020-06-22) using many packages such as the extRemes package developed by Gilleland and Katz (2016).
Results available on request from the corresponding author.
For example, Callahan et al. (2021) indicated that long-term CO2 forcing dampens ENSO. Using a high-resolution climate model, Wengel et al. (2021) predicted that under GHG-induced warming, El Niño activity decreases. On the other hand, Cai et al. (2021) demonstrated that future ENSO sea surface temperature variability and, as a result, ENSO magnitude are predicted to increase as a result of greenhouse warming. If anything, this supports the Arias et al. (2021) conclusion that ENSO will alter over time with minimal predictability.
References
Adams, D.K., and A.C. Comrie. 1997. The North American monsoon. Bulletin of the American Meteorological Society 78(10): 2197–2214.
Allen, J.T., M.K. Tippett, and A.H. Sobel. 2015. Influence of the El Niño/Southern Oscillation on tornado and hail frequency in the United States. Nature Geoscience 8(4): 278–283.
Anderson-Frey, A.K., and H. Brooks. 2019. Tornado fatalities: An environmental perspective. Weather and Forecasting 34(6): 1999–2015.
Arias, P., N. Bellouin, E. Coppola, R. Jones, G. Krinner, J. Marotzke, V. Naik, M.D. Palmer, et al. 2021. Technical summary. In Climate change 2021: The physical science basis. Contribution of Working Group I to the sixth assessment report of the Intergovernmental Panel on Climate Change, ed. V. Masson-Delmotte, P. Zhai, A. Pirani, S.L. Connors, C. Péan, S. Berger, N. Caud, Y. Chen, et al., 33−144. Cambridge, UK: Cambridge University Press.
Ashley, W.S. 2007. Spatial and temporal analysis of tornado fatalities in the United States: 1880–2005. Weather and Forecasting 22(6): 1214–1228.
Ashley, W.S., and S.M. Strader. 2016. Recipe for disaster: How the dynamic ingredients of risk and exposure are changing the tornado disaster landscape. Bulletin of the American Meteorological Society 97(5): 767–786.
Biddle, M.D., R.P. Brown, C.A. Doswell III., and D.R. Legates. 2020. Regional differences in the human toll from tornadoes: A new look at an old idea. Weather, Climate, and Society 12(4): 815–825.
Bonfils, C.J.W., B.D. Santer, T.J. Phillips, K. Marvel, L.R. Leung, C. Doutriaux, and A. Capotondi. 2015. Relative contributions of mean-state shifts and ENSO-driven variability to precipitation changes in a warming climate. Journal of Climate 28(24): 9997–10013.
Brooks, H., and C.A. Doswell III. 2001. Some aspects of the international climatology of tornadoes by damage classification. Atmospheric Research 56(1–4): 191–201.
Brooks, H.E., and C.A. Doswell III. 2002. Deaths in the 3 May 1999 Oklahoma City tornado from a historical perspective. Weather and Forecasting 17(3): 354–361.
Cai, W., A. Santoso, M. Collins, B. Dewitte, C. Karamperidou, J.-S. Kug, M. Lengaigne, and M.J. McPhaden et al. 2021. Changing El Niño-Southern Oscillation in a warming climate. Nature Reviews Earth & Environment 2(9): 628–644.
Caldera, H.J., S.C. Wirasinghe, and L. Zanzotto. 2018. Severity scale for tornadoes. Natural Hazards 90(3): 1051–1086.
Carbone, E.G., and E.T. Echols. 2017. Effects of optimism on recovery and mental health after a tornado outbreak. Psychology & Health 32(5): 530–548.
Chiu, C.H., A.H. Schnall, C.E. Mertzlufft, R.S. Noe, A.F. Wolkin, J. Spears, M. Casey-Lockyer, and S.J. Vagi. 2013. Mortality from a tornado outbreak, Alabama, April 27, 2011. American Journal of Public Health 103(8): e52–e58.
Coles, S., J. Bawa, L. Trenner, and P. Dorazio. 2001. An introduction to statistical modeling of extreme values. London: Springer.
Danielson, C.K., J.A. Sumner, Z.W. Adams, J.L. McCauley, M. Carpenter, A.B. Amstadter, and K.J. Ruggiero. 2017. Adolescent substance use following a deadly US tornado outbreak: A population-based study of 2,000 families. Journal of Clinical Child & Adolescent Psychology 46(5): 732–745.
Dotzek, N. 2002. Severe local storms and the insurance industry. Journal of Meteorology-Trowbridge Then Bradford On Avon 27(265): 3–12.
Finkenstadt, B., and H. Rootzén (eds.). 2003. In Extreme values in finance, telecommunications, and the environment. Boca Raton: CRC Press.
Fricker, T., and D.L. Allen. 2022. A place-based analysis of tornado activity and casualties in Shreveport. Louisiana. Natural Hazards 113(3): 1853–1874.
Fricker, T., J.B. Elsner, V. Mesev, and T.H. Jagger. 2017. A dasymetric method to spatially apportion tornado casualty counts. Geomatics, Natural Hazards and Risk 8(2): 1768–1782.
Fuhrmann, C.M., C.E. Konrad, M.M. Kovach, J.T. McLeod, W.G. Schmitz, and P.G. Dixon. 2014. Ranking of tornado outbreaks across the United States and their climatological characteristics. Weather and Forecasting 29(3): 684–701.
Gilleland, E., and R.W. Katz. 2016. extRemes 2.0: An extreme value analysis package in R. Journal of Statistical Software 72(8): 1–39.
Güneralp, B., Y. Zhou, D. Ürge-Vorsatz, M. Gupta, S. Yu, P.L. Patel, M. Fragkias, X. Li, and K.C. Seto. 2017. Global scenarios of urban density and its impacts on building energy use through 2050. Proceedings of the National Academy of Sciences 114(34): 8945–8950.
Heather, A.S.M. 2019. Effect of tornado outbreaks on morbidity and mortality in Texas. Prehospital and Disaster Medicine 34(s1): s50–s50.
Lipika, B. 2018. Multivariate extreme value theory with an application to climate data in the Western Cape Province. Master’s thesis. Department of Statistical Sciences, University of Cape Town, South Africa.
McPhaden, M.J., A. Santoso, and W. Cai (eds.). 2020. In El Niño Southern Oscillation in a changing climate. Hoboken, NJ: John Wiley & Sons.
Mehta, K.C. 2013. Development of the EF-scale for tornado intensity. Journal of Disaster Research 8(6): 1034–1041.
NOAA (National Oceanic and Atmospheric Administration). 2020. Storm Prediction Center – NOAA/National Weather Service. https://www.spc.noaa.gov/. Accessed 20 Jul 2021.
Northrop, P.J., N. Attalides, and P. Jonathan. 2017. Cross-validatory extreme value threshold selection and uncertainty with application to ocean storm severity. Journal of the Royal Statistical Society: Series C (Applied Statistics) 66(1): 93–120.
Otto, F.E.L. 2017. Attribution of weather and climate events. Annual Review of Environment and Resources 42: 627–646.
Pickands, J. 1971. The two-dimensional Poisson process and extremal processes. Journal of Applied Probability 8(4): 745–756.
Power, S.B., and F.P. Delage. 2018. El Niño-Southern Oscillation and associated climatic conditions around the world during the latter half of the twenty-first century. Journal of Climate 31(15): 6189–6207.
Schroder, Z., and J.B. Elsner. 2021. Estimating “outbreak”-level tornado counts and casualties from environmental variables. Weather, Climate, and Society 13(3): 473–485.
Simmons, K.M., and D. Sutter. 2007. Tornado shelters and the housing market. Construction Management and Economics 25(11): 1119–1126.
Smith, R.L. 1989. Extreme value analysis of environmental time series: An application to trend detection in ground-level ozone. Statistical Science 4(4): 367–377.
Smith, C.A., and P.D. Sardeshmukh. 2000. The effect of ENSO on the intraseasonal variance of surface temperatures in winter. International Journal of Climatology: A Journal of the Royal Meteorological Society 20(13): 1543–1557.
Sparrow, K.H., and A.E. Mercer. 2016. Predictability of US tornado outbreak seasons using ENSO and northern hemisphere geopotential height variability. Geoscience Frontiers 7(1): 21–31.
Swienton, H., C.M. Thompson, M.A. Billman, F.J. Bowlick, D.W. Goldberg, A. Klein, J.A. Horney, and T. Hammond. 2021. Direct injuries and fatalities of Texas tornado outbreaks from 1973 to 2007. The Professional Geographer 73(2): 171–185.
Tippett, M.K., and J.E. Cohen. 2016. Tornado outbreak variability follows Taylor’s power law of fluctuation scaling and increases dramatically with severity. Nature Communications 7(1): Article 10668.
Tippett, M.K., and C. Lepore. 2021. ENSO‐based predictability of a regional severe thunderstorm index. Geophysical Research Letters 48(18): Article e2021GL094907.
Tippett, M.K., C. Lepore, and J.E. Cohen. 2016. More tornadoes in the most extreme US tornado outbreaks. Science 354(6318): 1419–1423.
Towler, E., D. Llewellyn, A. Prein, and E. Gilleland. 2020. Extreme-value analysis for the characterization of extremes in water resources: A generalized workflow and case study on New Mexico monsoon precipitation. Weather and Climate Extremes 29: Article 100260.
U.S. Census Bureau. 2020. Decennial census of population and housing. http://data.census.gov. Accessed 12 Dec 2020.
Wengel, C., S.-S. Lee, M.F. Stuecker, A. Timmermann, J.-E. Chu, and F. Schloesser. 2021. Future high-resolution El Niño/Southern Oscillation dynamics. Nature Climate Change 11(9): 758–765.
Yiou, P., J. Cattiaux, D. Faranda, N. Kadygrov, A. Jézéquel, P. Naveau, A. Ribes, and Y. Robin et al. 2020. Analyses of the Northern European summer heatwave of 2018. Bulletin of the American Meteorological Society 101(1): S35–S40.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sales, V.G., Strobl, E. Using Extreme Value Theory to Assess the Mortality Risk of Tornado Outbreaks. Int J Disaster Risk Sci 14, 14–25 (2023). https://doi.org/10.1007/s13753-023-00474-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13753-023-00474-1