1 Introduction

Wildfires contribute to significant biodiversity and human asset losses as well as to increasing human health problems (Boegelsack et al. 2018; Yu et al. 2019; Xu et al. 2020). Increasing trends have been projected for the entire Mediterranean basin (Lozano et al. 2017; Ruffault et al. 2020), and Turco et al. (2017) have highlighted the paramount impact of predicted severe drought conditions in the Mediterranean, which may trigger higher intensity wildfires. The need of innovative and efficient fire management strategies constitutes a major challenge given the dramatic evolution and impacts of wildfires around the world.

Resilience constitutes an approach that has been extensively integrated in numerous scientific fields (for example, ecology, engineering, operations research), illustrating the resistance/absorption and adaptation/transformation of any natural or anthropogenic system to abrupt changes (Folke 2016; Cumming and Allen 2017; Fraccascia et al. 2018). Resilience plays a critical role in natural hazard research, indicating the resistance to and recovery from disasters of social-ecological systems, a fact that requires the estimation and mapping of these systems’ vulnerability (Fuchs and Thaler 2018; Van Well et al. 2018). A special case of resilience constitutes the resilience to wildfires, which due to climate change has been declining. This raises serious questions about the viability of one of the most important ecosystems, namely, the forest ecosystems (Díaz-Delgado et al. 2002; Stevens‐Rumann et al. 2018). In this article, we demonstrate the spatial resilience to wildfires, focusing on the territorial planning of firefighting resources to tackle the destructive effects of wildfires, especially under a projected warmer environment (Marey-Perez et al. 2021).

Programming techniques—linear, nonlinear, integer, and goal programming—have been integrated in wildfire management and prevention to solve optimization problems (Minas et al. 2015; Rodríguez-Veiga et al. 2018; Zhou and Erdogan 2019). Mixed stochastic linear and nonlinear programming models (Arrubla et al. 2014; Van Der Merwe et al. 2015; Belval et al. 2016) have been used extensively to estimate the optimal locations for the initial firefighting attack against wildfires. Haight and Fried (2007) and Lee et al. (2013) assessed the optimal distribution of firefighting resources to minimize the occurrence of fires that are not addressed by the appropriate mix of firefighting forces at the appropriate time (uncontrolled fires), considering the current financial constraints and the respective fire agencies’ capacities. In the same context, Wei et al. (2015) used a stochastic programming model to determine the optimal deployment and mixture of firefighting forces required, based on fire simulation outputs.

Sakellariou, Samara, et al. (2020) developed a spatial decision support system that considers the strategic (optimal spatial arrangement of firefighting vehicles) and operational planning to deal with forest and urban fires that occur in the wildland urban interface (WUI). Sakellariou, Parisien, et al. (2020) established differentiated location schemes for initial attack under several scenarios based on the combination of optimization techniques and wildfire likelihood. They concluded that based on the estimated burn probability (BP) of the following year, the current structure of fire agency is not optimized, suggesting the relocation of fire headquarters in other places with higher hazard and population concentration. Such recommendations enhance spatial resilience, since they try to adapt the spatial structure of fire resources to minimize future losses due to large wildfires. Rodrigues et al. (2019) estimated the spatial distribution of optimal zones for initial attack based on factors such as the fire detection and arrival time, the fire spread potential, and the availability of fire resources. These zones could facilitate the targeted deployment of fire forces.

To the authors’ knowledge, our article constitutes a first approach that explores the determination of optimal location schemes based on the interplay of BP and the impact of anthropogenic factors, simultaneously considering the effect of topography and road network characteristics on critical time of response. In addition, we proceeded to a comparative analysis of the current and the suggested locations of fire resources, highlighting the importance of simulation and spatial modeling integration to the establishment of optimal location schemes for initial attack.

The primary aim of this study was the determination of minimum and optimal locations of firefighting resources for the initial firefighting attack under differentiated scenarios. Sub-objectives of the analysis were: (1) The calculation and finding of the minimum number of optimal locations so that the fire vehicles can fully cover the study area based on fire vulnerability (enhanced BP), and the current features of the road network (travel time based on the maximum allowed speed); (2) The calculation and finding of optimal locations for all the available fire vehicles (based on fire agencies’ capacities) to maximize the coverage of the most susceptible regions in terms of enhanced BP, adjusting the time of response to more realistic conditions (integrating topography effect with travel time and speed); and (3) The determination of the type of installation (for example, temporary patrol locations; watchtowers; fire hydrants; water tanks; totally random locations) where the optimization process suggests optimal positions for the firefighting vehicles.

2 Materials and Methods

This section presents the primary features of the study area, followed by the description of the main categories of geospatial data as well as the methodological steps adopted in this study.

2.1 The Study Area

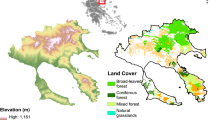
Chalkidiki Prefecture is situated in the northern part of Greece, at about 40°20′N latitude and 23°30′E longitude (Fig. 1d). The total area of Chalkidiki is 2918 km2. The aggregated land cover distribution is depicted in Fig. 1a. The most dominant land cover type is agricultural land, including some regions of natural vegetation (~ 42%), followed by shrubs (including sclerophyllous vegetation) (~ 21%), broad-leaved forests (~ 19%), mixed forests (~ 7%), and coniferous forests (~ 4%), while the discontinuous urban fabric occupies approximately 2% of the entire study area (CLMS 2018). The Natura 2000 networkFootnote 1 territory occupies 35% of the prefecture, highlighting the existence of a high degree of biodiversity in the study area.

Fig. 1
figure 1

The Chalkidiki Prefecture study area in Greece. a Land cover distribution; b Spatial distribution of the road and residential network in conjunction with slope; c Firefighting resources distribution; d Geographical location of the study area (red rectangle). Data sources National Cadastre and Mapping Agency (https://www.ktimatologio.gr); CLMS (2018); Geodata.gov.gr (2018); Geofabrik GmbH and OpenStreetMap Contributors (2018); Fire Agency of Polygyros.

Full size image

The spatial distribution of the road and residential networks are presented in Fig. 1b. The total length of roads amounts to 8000 km, and there are 161 towns/villages with a total population of 96,000. The majority of the residential nodes have very few people and the largest town has about 6000 people.

The spatial distribution of the current fire resources—that is, the exact positions of the fire agency headquarters, the temporary positions of fire trucks in the fire season, and the location of watchtowers, fire hydrants, and water tanks—are depicted in Fig. 1c. The dense network of fire resources is justified by the collectively large number of burned areas. More than 5500 ha of forests have been burned (91% of the total burned areas) in a time frame of 18 years (2000–2017) (HFB 2018). The Mediterranean weather conditions contribute to intense fire regimes, if we consider that the mean temperature in the summer amounts to 27 °C, the mean relative humidity is just 51%, and the mean level of precipitation for the same season is just 21 mm (HNMS 2018).

2.2 Materials

The primary datasets used in the current analysis consist of the number and location of fire resources—that is, the fire agency headquarters and branches, the number of fire vehicles, temporary patrol locations, watchtowers, fire hydrants, water tanks; the BP map (100 × 100 m) that depicts the spatial distribution of the fire hazard magnitude; elevation (5 × 5 m) and road network data, useful for travel time simulation; built-up areas (50 × 50 m) (ESM 2017); and random points to be used as candidate positions for alertness.

2.3 Methodology

Before applying the spatial optimization for finding the most suitable locations for initial attack, three distinct analytical procedures should take place. The first procedure is related to the analysis of Demand Points. Demand points consist of each geographic location (that is, pixel) that concentrates the degree of fire hazard. To this end, we integrated the BP modeling outcomes with the fuzzy logic modeling. The first produces a map with a scalable degree of BP based on certain conditions (for example, fuel features, topography, weather, and fire history), whereas the second process applies a series of fuzzy logic modeling for the proximity (and the respective hazard) of road and human settlement networks to forested territory. So, we created the BP and Anthropogenic Influence (AI) Weighted Units. In the second procedure, we enriched the current locations of fire resources with more candidate locations satisfying the geographical coverage of the study area. Consequently, we applied a spatial systematic sampling creating new positions “moved” to the nearest road network segment, far away from the existing fire resources. So, we created the Enriched Supply Units. In the third procedure, we edited the road network features so that they can be a representative input for realistic travel time analysis and simulation. The manipulation process primarily incorporated the integration of slope coefficients with travel time. This adjustment approaches a more realistic situation for the initial attack of fire vehicles. Figure 2 depicts the interaction of all the above processes.

Fig. 2
figure 2

Flowchart of the proposed methodology for spatial resilience to wildfires

Full size image

2.3.1 Simulation and Spatial Modeling—Integration of Anthropogenic Effect on Burn Probability

Burn probability has been estimated through simulation modeling using a spatial fire simulation model that explicitly simulates the ignition and spread of a significant number of fires. This model is composed of three distinct submodules: (1) the fire ignitions module; (2) the burning conditions module; and (3) the fire growth module (Parisien et al. 2005). For the first module, we used the number of historical large fire ignitions (> 3ha) from 2000 to 2017, the seasonal number, and the historical locations of fire ignitions from 2013 to 2017, as provided by the European Forest Fire Information System (EFFIS) to reliably simulate the fire ignitions pattern of the study area. For the second module, we estimated the fire weather index (FWI) for the entire time frame and kept the most fire-conducive days (FWI > 19). For the same module, we simulated the interaction of wind and topography with respect to fire behavior. The third module includes all these settings that represent the fire environment in the study area (estimation of burning hours under maximum conditions, grass moisture) (Sakellariou et al. 2022b). The Prometheus fire growth engine is integrated into the Burn P3 model that produces deterministic outputs of fire propagation (Tymstra et al. 2010), based on the interaction of all the above modules.

The composite or enhanced BP map, which includes the enrichment of the initial BP map with the effect of anthropogenic factors, constitutes the primary input for the spatial optimization of the firefighting units. Each geographical unit (1 ha) of the study area is characterized by a specific BP value that falls into one of five categories. These categories indicate the degree of fire vulnerability. Each geographical unit functions as a demand point in the optimization process. The higher the BP, the greater the weight for any given location. The weight indicates the degree of “attractiveness” for any fire vehicle for initial attack within a specified threshold in terms of travel time. Table 1 summarizes the specified weights for each category of BP based on natural breaks classification.

Table 1 Burn probability (BP) and degree of fire vehicle location attractiveness (weight) for each geographical unit in the Chalkidiki study area
Full size table

The original BP outputs (Sakellariou et al. 2022b) are primarily based on natural factors—estimated fire behavior of forest fuels, long-term weather conditions, partial effect of anthropogenic factors through fire history, if it existed (Parisien et al. 2005). To this end, we developed a composite BP map that integrates the influence of anthropogenic factors through the spatial arrangement of the residential and road networks. Both networks usually constitute the most appropriate ground for the ignition of human-caused fires (either accidental or intentional) (Ricotta et al. 2018; Pinto et al. 2020).

The construction of the composite BP map included several analytical processes: (1) Selection of road network segments and built-up regions that are located within or in immediate proximity (within 300 m) to forested areas (including shrubs). These geographical regions are susceptible to deliberate fires or to deforestation due to unregulated urban growth (Sakellariou et al. 2021); (2) Removal of any type of urban road network, since the proximity to this type of roads makes it impossible for any forest fire event to break out; (3) Calculation of the Euclidean distance from built-up regions with a radius of 500 m (that is, wildland urban interface, WUI); (4) Calculation of the Euclidean distance from the road network with a radius of 60 m (on both sides of the road network, with a total bandwidth of 120 m); and (5) Spatial modeling through fuzzy logic modeling for the quantification of the anthropogenic impact through the proximity of anthropogenic entities to forests (Table 2). The fuzzy logic modeling has been used due to the high degree of uncertainty in the predefined distance of human structures to forests and the respective wildfire hazard (Sakellariou, Cabral, et al. 2020).

Table 2 Fuzzy logic modeling weighting scheme for the proximity of residential and road network entities to forested areas in the Chalkidiki study area
Full size table

After the weighting process of key anthropogenic factors to fire ignitability, we proceeded to the development of the composite BP map. That is, the initial BP map (Sakellariou et al. 2022b) was transformed to an enhanced map version of fire susceptibility, including the impact of anthropogenic structures. Four additional analytical procedures took place for the creation of the integrated BP map, such as the development of a new coefficient for each pixel:

  1. (1)

    When there is no value (that is, weight) derived from the road network or built-up proximity (for example, forested regions far away from roads or inhabited regions), the coefficient receives the value of 0;

  2. (2)

    When there is a value for the proximity to the road network and built-up region simultaneously (overlapping), the coefficient receives the average of these two values to mitigate extreme values from one or the other variable;

  3. (3)

    Conversely, when there is no value for proximity to built-up regions, but there is a value for proximity to the road network, the coefficient takes the value for proximity to the road network and vice versa; and

  4. (4)

    The value of 1 was added to the coefficient. The coefficient now is a weighted coefficient for the final BP for each pixel. This occurs since the fuzzy logic modeling yields values from 0 to 1. Hence, the corrected coefficient is multiplied by the value of the initial BP. A coefficient with a value of 1 (complete absence of anthropogenic factors close to forests) does not affect the initial BP. A factor of more than 1 adds corresponding weight resulting from the fuzzy logic modeling of one or both of the factors involved in the analysis. The intervals of Table 1 remain the same highlighting the anthropogenic effect on any pixel. There might be pixels that fall into higher categories now, due to the combined impact of road network and built-up area proximity. Therefore, the higher the final BP (higher susceptibility), the higher the location attractiveness for fire vehicles for initial attack.

2.3.2 Unbiasedness and Representativeness of Supply Points—Satisfaction of Geographical Coverage

Spatial optimization requires two categories of data. The weighted demand points, as described in the simulation and spatial modeling, and the supply points. The supply points constitute the existing fire agencies, the water tanks, the fire hydrants, and the temporary patrol positions for immediate detection and prevention of fire hotspots. However, in order to ensure the unbiasedness of location options and examine the existing effectiveness of these locations, independent location options should be added that cover the entire reference area. To this end, a spatial systematic sampling took place that selected one position every 2 km2 in the entire study area. Inevitably, many of the locations defined by the sampling process are located off-road, which makes their choice impossible (every truck needs absolute accessibility). Thus, a separate analytical process took place, so that the positions of the grid far away from the road network can be transferred to the nearest segment of road network (the Near tool of the Spatial Analyst Toolbox in ArcGIS). Thus, unbiasedness and feasibility of location options are achieved.

The next step included the exclusion of all grid points that fall within a radius of influence (2 km) of the preexisting supply points (that is, water tanks, fire hydrants, patrol positions) to avoid redundancy. Therefore, a satisfactory geographical distribution of all candidate location options is achieved, covering the entire prefecture of Chalkidiki.

Finally, each supply point receives a weight depending on the type of fire service. The fire agency headquarters are considered required and fixed positions and will always be included in any suggested spatial scheme. Water tanks receive more weight than all the other candidate supply locations, since they are considered the second-best options for initial attack (due to the possibility of immediate water refueling of vehicles). All the other points (fire hydrants, existing patrol locations, random locations) have the same weight for the final selection.

2.3.3 Road Network Feature Manipulation—Integration of Topography (Terrain) Effect on Travel Time Simulation

The first stage of the existing road network manipulation incorporated the removal of all road segments that are not accessible to fire trucks, such as sidewalks, paths, or roads leading to private parking lots. Next, in order to adjust the speed and the respective travel time of fire trucks to real conditions, we calculated the absolute slope difference of the ground at the starting and arrival point of each road segment. However, the distance of each road segment should not be long—otherwise, the slope effect could be quite variable, heavily affecting the actual travel time. To this end, the entire road network considered in the optimization process was fragmented to a maximum length of 1.5 km, a distance that can be considered adequate for calculating the difference in ground slope. Consequently, we calculated the slope at the beginning and at the end of each section of the road network with the contribution of the digital elevation model (DEM) and created an extra geo-database column depicting the absolute slope difference that will determine the corresponding weight adjustment of speed and travel time.

Next, the maximum speed limits were determined based on the type of road network (that is, functional classification, geometrical properties) and the capabilities of the fire trucks. Specifically, the maximum speed limit ranges are set at: from 90 to 100 km/h on highways; from 70 to 90 km/h on primary and secondary roads; 60 km/h on the tertiary road network; from 40 to 50 km/h on urban roads; and 30 km/h on service roads. There are a few sections with a maximum speed limit of 10 to 20 km/h (especially in urban areas). The direction of the road network (one-way and so on) was included in the modeling. The travel time was calculated considering the length of each section and the corresponding maximum speed. Therefore, the travel time (in minutes) of each road segment was calculated based on the formula:

$$t_{r} = \frac{{\left( {d_{i} \times 60} \right)}}{{v_{i} }},$$
(1)

where tr = actual travel time without any adjustments (in minutes); di = length of each segment of road network (in km); and vi = maximum permitted speed per section of road network.

Next, the travel time and speed should be calculated considering the effect of the topography that constitutes a crucial factor in differentiating the final travel time and speed for each route. Therefore, in order to adjust the travel time based on the geomorphology of the study area, the following adjustment weight was determined (Price 2008):

$$Slope_{adj} = 1 + \left( {\frac{Slope}{{10}}} \right)^{2} ,$$
(2)

where Slopeadj = adjustment weight of travel time and speed due to slope effect; and Slope = slope of each section of road resulting from the absolute difference of slope at the beginning and at the end point of each road segment (maximum length: 1.5 km). Table 3 shows the percentage change of slope, the adjustment weight as calculated by Eq. 2, and the possible travel time delay of vehicles.

Table 3 Slope effect on travel time of fire trucks in the Chalkidiki study area
Full size table

Thus, the estimation of the travel time and speed due to the slope effect is determined by the two formulas (Price 2008):

$$t_{adj} = t_{r} \times Slope_{adj} ,$$
(3)
$$v_{adj} = \left( {\frac{{d_{i} }}{{t_{adj} }}} \right) \times 60,$$
(4)

where tadj and vadj are the adjusted travel time and speed due to the topography effect.

Finally, additional parameters were integrated into the road network geo-database, such as the expected time delay due to road turns (Price 2008, p. 54, adapted):

  • 40 seconds delay in turns ranging from 150 to 210 degrees;

  • 20 seconds delay in turns ranging from 210 to 330 degrees;

  • 15 seconds delay in turns ranging from 30 to 150 degrees;

  • 4 seconds delay in turns ranging from 330 to 30 degrees in the direction of the vehicle.

2.3.4 Spatial Optimization

The spatial optimization process explores the determination of the minimum number of supply points by maximizing the coverage of the most susceptible regions based on the synergy of BP, anthropogenic effect, and the impact of road network features. To this end, two scenarios were developed. The first scenario examines the spatial distribution of firefighting vehicles without the topography effect, while the second scenario integrates the slope effect on travel time and speed. Hence, when we do not consider the topography effect, we estimate the minimum number of best locations for initial attack based on fire vulnerability. When we adjust the time of response to more realistic conditions (integrating the inevitable time delays due to slope effect), we need to employ all the available forces to maximize the coverage of the most susceptible territory. However, all the available forces are determined as half of all the forces from all fire agencies to be allocated across the study area. This occurs because half of the fire agencies’ forces should be located at the fire headquarters for other purposes (for example, urban fires). Hence, based on the fire agencies’ capabilities, we can calculate the most appropriate location schemes for 24 (of 48) potential locations including the five positions of the current fire agencies. Another critical parameter constitutes the defined time of response. The average time of response for the prefecture of Chalkidiki has been estimated at 27 min (Tsagari et al. 2011).

All the above parameters should be integrated in a geo-algorithm. The algorithm is implemented through the Network Analysis module of ArcGIS, an algorithm that is based on Church and ReVelle’s (1974) project on maximizing the coverage of a given geographical space, which is structured by demand and supply points (Church and ReVelle 1974; Sakellariou, Parisien, et al. 2020):

\(Maximize\,Coverage = \sum\limits_{{i \in I}} {w_{i} } y_{i} ,\)

$$\begin{array}{*{20}l} {{\text{Subject}}\,{\text{to}}:\,\sum\nolimits_{j \in Ni} {x_{j} > y_{i} } ,{\text{for}}\,{\mkern 1mu} {\text{all}}{\mkern 1mu} \,i \in I} \hfill \\ {\quad \quad \quad \quad \quad \sum\nolimits_{j \in J} {x_{j} = V} } \hfill \\ {\quad \quad \quad \quad \quad x_{i} = \left( {0,1} \right){\mkern 1mu} {\text{for}}\,{\mkern 1mu} {\text{all}}{\mkern 1mu} j \in J} \hfill \\ {\quad \quad \quad \quad \quad y_{i} = \left( {0,1} \right){\mkern 1mu} {\text{for}}{\mkern 1mu} \,{\text{all}}{\mkern 1mu} i \in I} \hfill \\ \end{array}$$

where, I = the demand points; J = the candidate supply points’ locations; Th = the threshold (travel distance or time) within which coverage is expected; dij = the least value of travel time from demand point i to facility at point j; xj = a binary variable that equals one when a facility is allocated at the jth point and zero otherwise; yi = a binary variable that equals one if point i is covered by at least one facility stationed within the Th and zero otherwise; Ni = {j ∈ J | dij ≤ Th} = the points j that are within a distance of the Th to point i; wi = population to be served at demand point i (degree of fire vulnerability); V = the number of fire-fighting vehicles to be located.

3 Results

This section presents the results of the study, such as the enhanced burn probability map, the spatial distribution of candidate (preexisting and random) locations for initial attack, the current service areas of fire agency headquarters, and the optimized spatial schemes of fire resources with and without topography effect on travel time simulation.

3.1 Simulation and Spatial Modeling

The original BP map (Sakellariou et al. 2022b) indicated the increased BP in the second extension of the Chalkidiki peninsula as well as in the northwestern part of the study area (Fig. 3a). Figure 3b shows the integration of spatial modeling (anthropogenic effect due to the close proximity of the road network and residential regions to forests) with wildfire simulation modeling. The simulation modeling yielded an area with a scalable degree of BP, where the maximum BP reaches the value of 0.036. The enhanced BP depicts a differentiated mosaic of BP. The effect of linear and polygonal entities is apparent where there is a high presence of road networks and human settlements in immediate contact with forested regions. This effect may delimit regions that present three times higher BP compared to the initial BP. The most susceptible regions are located in the second extension of the peninsula where there is a high density of forests and road networks. This region is considered one of the most popular with tourists, so the possibility of fire ignition by accident may be increased exponentially.

Fig. 3
figure 3

a Original burn probability (BP) map from Sakellariou et al. (2022b), adjusted; b Integration of anthropogenic effect on BP—Enhanced BP map for the Chalkidiki study area

Full size image

Additional vulnerable regions are located throughout the study area. These areas are representative parts of the WUI (a few residential clusters in contact with forests). This is the reason that many road network branches (highlighted in yellow—moderate BP) converge to these clusters (little red clusters with high BP). Such regions are located (beyond the second extension of the peninsula) in the western part of the prefecture, in the middle of the first extension of the peninsula, as well as in many scattered parts of the eastern part of the study area. Each geographical unit (that is, a pixel) of the study area functions as a demand point with a weight (that is, degree of attractiveness for a fire vehicle) based on the estimated enhanced BP, while the maximum BP now is 0.07.

3.2 Unbiasedness and Representativeness of Supply Points—Satisfaction of Geographical Coverage

All the supply points included in the optimization process are depicted in Fig. 4. These locations consist of the required facilities (fire agency headquarters), the preexisting fire infrastructure (fire hydrants, water tanks, temporary patrol positions), and the manipulated random locations as derived from the spatial systematic sampling (1 location every 2 km2). Figure 4 presents a complete uniform grid of supply points, so that the best location options can be selected for initial attack.

Fig. 4
figure 4

Candidate firefighting supply points (existing and random locations for initial attack) in the Chalkidiki study area

Full size image

3.3 Current Service Areas

Before proceeding to the analysis of the optimal location options, the current service areas of the fire agency headquarters for both scenarios (with and without topography effect on travel time) must be estimated. Service areas were calculated for every 10 min. Figure 5a shows the zones of proximity every 10 min with a maximum threshold of 60 min. Figure 5a does not consider the slope effect to travel time. There are relatively small zones, within which the fire services can immediately react (0–20 min). The first zone that triggers immediate reaction within 10 min covers only 8% of the total area. The zone of reaction within 20 min covers 33% of the total, while the zone of reaction within up to 30 min covers 61% of the study area. Of the entire prefecture, 30% remain accessible in a time frame greater than 30 min, while 9% of the entire study area are not accessible for more than 60 min.

Fig. 5
figure 5

Service area of fire agencies a without slope effect, and b with slope effect in the Chalkidiki study area

Full size image

When we adjusted the response time due to topography effect, we observed fundamental changes in the mapping of service areas. Figure 5b depicts the limited accessibility zones of fire trucks from the current locations of the fire agency headquarters. It becomes clear how topography can play a key role in the initial attack and the consequent fire management effectiveness. Now, the spatial coverage of fire trucks has dramatically changed within the same intervals. Specifically, the immediate reaction zone within 10 min covers only 3% of the total area. The zone of reaction within 20 min covers 10% of the total, while the zone of reaction within 30 min covers 20% of the study area. Of the entire prefecture, 35% remain accessible in a time frame greater than 30 min, while 44% of the entire study area is not accessible for more than 60 min.

3.4 Determination of Minimum Number of Optimal Supply Points by Maximizing Demand Coverage Based on Burn Probability and Anthropogenic Effect

The first scenario explores the optimal spatial distribution of supply points without considering the adjustment of travel time due to slope effect. The spatial layout of optimal locations for initial attack is presented in Fig. 6a. The determination of the minimum number of supply points that maximize the coverage (99.2% of the study area) of demand (in terms of fire vulnerability) yielded 18 optimal locations, which highlights the necessity for fewer forces compared to the maximum number of fire trucks that all fire agencies may provide.

Fig. 6
figure 6

Estimation of the minimum number of locations for initial attack (without topography effect) maximizing the coverage of the most susceptible regions. a Spatial determination of recommended locations; b Service area of the selected locations in the Chalkidiki study area

Full size image

Ten positions of 18 consist of locations identified by the modified spatial systematic sampling; five positions are locations near fire hydrants, whereas the remaining three positions are locations identified by the fire agencies as temporary patrol locations. The longest distance between a candidate point of demand and a selected point of supply is 18 km, which is covered in 26.9 min.

Figure 6b presents the service area of the proposed spatial scheme. Almost the entire area can be reached within 30 min. In particular, 29% of the prefecture is covered within 10 min; 80% within 20 min, and 89% within 30 min. The remainder of the prefecture can be reached within one hour (91%), whereas 9% of the study area is almost inaccessible from the road network.

Next, we estimated the optimal locations for initial attack for all the available firefighting forces (24 vehicles + 5 fire agency headquarters) based on the adjustment of travel time due to topography effect. Now, the time required for the firefighting vehicles to reach any given territory is significantly increased. The current capacity of the fire agencies can be considered inadequate, so additional forces might be required. The suggested 29 locations can cover 80% of the study area within 27 min. The proposed spatial scheme that should be considered especially in case of predicted high hazard (for example, forecast of extreme meteorological weather) is depicted in Fig. 7a.

Fig. 7
figure 7

Estimation of locations of the available forces for initial attack (considering the topography effect on travel time and speed) maximizing the coverage of the most susceptible regions. a Spatial determination of recommended locations; b Service area of the selected locations in the Chalkidiki study area

Full size image

Twelve positions of the 29 are locations identified by the modified spatial systematic sampling; seven positions are locations near fire hydrants; two positions are locations next to water tanks, whereas the remaining three positions are locations identified by the fire agencies as temporary patrol locations. The longest distance between a candidate point of demand and a selected point of supply is 5.7 km, which is covered in 26.9 min.

Figure 7b presents the service area of the second proposed spatial scheme. There are significant differences compared to the previous map. Specifically, 15% of the entire prefecture is covered within 10 min, 56% within 20 min, and 81% within 30 min. The remainder of the study area is reached within one hour (85%), without ignoring the fact that there are sections of Chalkidiki that are almost inaccessible from the road network.

4 Discussion

The optimal allocation and deployment of firefighting resources for effective initial attack constitutes a challenging issue, since many interrelated factors should be integrated into this type of analysis (Costafreda-Aumedes et al. 2015; Rodrigues et al. 2019; Wei et al. 2015). In this study, we developed a composite BP map that simultaneously considers the simulation modeling of a high number of potential fires, compounded by the effect of human activity through the proximity of inhabited regions and road networks to forested regions. The concept is in line with other significant projects that have combined simulation modeling and spatial optimization processes for initial attack (Lee and Lee 2018; Rashidi et al. 2018; Sakellariou, Parisien, et al. 2020; Wei et al. 2015). However, we enhanced this combination for more realistic outcomes. Beyond the integration of human factors (through spatial modeling) into BP, we incorporated a significant number of feasible locations to be included in the optimization (beyond the existing fire resources). Finally, we integrated the slope effect into travel time simulation to assess the initial attack effectiveness along with the best possible allocation of firefighting resources based on wildfire susceptibility.

The spatial allocation of fire agency resources varies for each scenario. The spatial scheme as well as the number of required forces is totally differentiated due to slope effect. When we ignore the topography effect, a limited number of fire vehicles is required to achieve the maximization of coverage (99.2% of the entire study area) giving priority to the most susceptible regions (that is, employing 18 of 24 available fire vehicles). When we adopt more realistic conditions that integrate the slope effect, all 24 available fire vehicles are required to maximize the coverage of the most vulnerable regions within 27 min. This process yields 80% of total coverage. This occurs due to the adjustment of travel time and speed when considering the topography effect. The suggested spatial scheme of fire forces, without adjusting the travel time and speed, can cover approximately 80% of the entire prefecture within 20 min and about 90% within 30 min. When integrating the slope effect, the modified suggested spatial scheme of fire forces can cover just 55% of the entire prefecture within 20 min and about 80% within 30 min. However, the number of fire forces employed is different for each scenario.

The integration of anthropogenic influence into BP is considered of utmost importance, since human-caused ignitions constitute the usual fire cause in many Mediterranean countries (Ruffault and Mouillot 2017; Vilar et al. 2016). Most of these events take place due to a high density of road networks and inhabited regions close to forested territories (Pinto et al. 2020; Ricotta et al. 2018).

Another important aspect of the analysis constitutes the increase of candidate supply points with random locations (based on the application of spatial systematic sampling and the consequent topological rules) in order to sufficiently cover the entire prefecture. The primary aim of this type of analysis was the comparative assessment of the current patrol positions with the newly selected locations that resulted from the optimization process. The results revealed new optimized (random) locations that can be considered more efficient for initial attack given the current level of enhanced BP for each geographical unit of the study area. Hence, the fire agencies could exploit the results either for constructing new firefighting facilities (for example, fire hydrants and water tanks) or relocating the fire vehicles from previous patrol positions to the new recommended ones. The latter would ensure better locations, reducing the time of response to cover the most vulnerable regions.

The maximal coverage optimization model has been adopted by many authors in wildfire management, since it can be used to achieve certain targets, such as the coverage of the largest area of the most susceptible territory in terms of fire risk or values at risk (Minas et al. 2015; Sakellariou, Samara, et al. 2020; Sakellariou, Parisien, et al. 2020), or to estimate the ignition location that may have the largest fire perimeter as the most destructive event (Rashidi et al. 2018). Other authors have determined the optimal locations of fire resources using stochastic integer programming models including financial details of fire suppression operations as distinct management objectives (Arrubla et al. 2014; Zhou and Erdogan 2019).

However, there are some perspectives and limitations that are primarily related to the different types of modeling and the reliability of some specific data types. There are some potential errors with respect to the road network, primarily in the northern part of the study area. We observed the existence of a few unconnected roads that could possibly affect the spatial optimization process. Hence, the optimization modeling may designate a few additional supply points to cover these small regions. If we managed to fix these problems, these few regions might be adequately covered by the adjacent fire vehicles (traveling just a few kilometers more). Finally, the perspective of spatial optimization with the help of aviation firefighting resources should be considered, given the existence of the respective infrastructure (that is, helipads) and the high added value that they offer in wildfire mitigation (Calkin et al. 2014; Davey et al. 2021). The aviation forces could cover the entire study area, including areas not adequately covered by the terrestrial forces in certain geographical areas (for example, due to the combined effect of the shortage of firefighting forces, the impact of topography on travel time and speed, and the level of BP in any given area). In this context, it is important to further explore the interrelation of response delay, fire spread, and the structure (number and location) of firefighting resources under several scenarios (Rashidi et al. 2018), so that fire managers can make the most rational decisions for the minimization of destructive effects of wildfires. In addition, the optimal location of a certain number of watchtowers (Sakellariou et al. 2017; Sakellariou, et al. 2022a) would drastically enhance the immediate fire detection, reducing the response time.

5 Conclusion

This study proposed specific measures to enhance the spatial resilience to wildfires in a fire-prone region in Greece. These measures focus on the resistance and adaptation of strategies to wildfire management based on the mapping of fire vulnerability, including the effect of anthropogenic factors on fire ignition. The proposed location schemes consider both the fire susceptibility and topography effect on travel time, highlighting the impact of road slope on initial attack effectiveness. Consequently, the integration of the topography effect to initial attack effectiveness leads to the demand of the total available firefighting vehicles in order to cover 80% of the entire area (primarily covering the most vulnerable territories) within the specified threshold (average response time). When the topography effect is ignored, far fewer vehicles are needed to cover the entire region (~ 99%). In addition, based on the interaction of fire susceptibility and travel time, the analysis revealed that the current locations of fire resources should be supplemented by additional positions to minimize the response time to reach the most vulnerable areas. The proposed methodology is characterized by a high degree of flexibility adapted to local conditions, providing optimized solutions to decision makers that consider key factors that greatly affect the effectiveness of initial attack.