Abstract
Equitable and efficient allocation of emergency resources is critical to ensure the success of relief efforts. The challenge comes largely from two aspects: the resources available for allocation are usually limited in quantity, especially in the early period of emergency response; and a large amount of uncertain information in the relief process affects the decision making of resource allocation. A multiperiod allocation model of emergency resources that takes into account both efficiency and equity based on uncertain disaster information is proposed. Interval number and triangular fuzzy number are introduced to describe the different sources of uncertainty (for example, demand, transportation time, and maximum transport amount), and the loss caused by unmet demand is used to quantify equity. Then, the deterministic transformation method of uncertain parameters is designed and the linear weighted sum method is applied to solve the proposed model. Finally, a computational case based on the 2017 Jiuzhaigou earthquake in Sichuan Province, China was conducted to validate the proposed model. The results show that the proposed model is feasible in the multiperiod allocation of emergency resources among multi-disaster sites, and the findings can help emergency managers to allocate emergency resources more scientifically, equitably, and effectively under uncertainty.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, large-scale disasters such as earthquakes, tsunamis, volcanic eruptions, and floods have occurred frequently in many regions of the world (Eshghi and Larson 2008; Adeagbo et al. 2016; Ogie and Pradhan 2019; Wang 2021), causing huge loss of life, property, and the economy (Barbarosoğlu and Arda 2004; Ahmadi et al. 2022). Especially in China, large-scale earthquake disasters such as the 1976 Tangshan earthquake and the 2008 Wenchuan earthquake caused catastrophic damage and impacts. According to the statistics from the China Earthquake Administration (2022), from 2001 to 2021, 9353 earthquakes occurred in China, including 138 earthquakes with a magnitude of 6.0 or above (Fig. 1). In situations such as these, governments and researchers devote increasing attention to disaster relief to mitigate losses and impacts (Rising and Lurie 2013; Su et al. 2016).
In post-disaster emergency rescue work, material relief is the key to meet the survival needs of victims and the recovery of disaster-affected locations (Hu, Wang, et al. 2016; Wang et al. 2019). In addition to the efficient allocation of resources, equitable allocation of available resources is also crucial in emergency relief (Erbeyoglu and Bilge 2020). Ignoring equity in emergency resource allocation leads to discontentment of victims and social unrest, increasing the burden of additional relief work and negative social impact (Ahmadi et al. 2022). After disasters, the key to effectively reducing the casualties and losses in the disaster area lies in the equitable and efficient allocation of emergency resources (Kovacs and Spens 2009; Wang et al. 2019).
However, there are some challenging problems in the process of emergency resource allocation. First, the initial supply of emergency resources is limited, and there may be conflicts between different rescue objectives; and second, information about resource demand, transportation time, and the maximum total amount of resources that can be transported from supply sites to affected locations is uncertain and inaccurate. Therefore, how to ensure the multiperiod equitable and efficient allocation of emergency resources among multiple disaster-affected locations under uncertain information conditions is an important practical problem to be solved urgently in the field of emergency relief operations.
This study proposes a multiperiod emergency resource allocation model that balances equity and efficiency under uncertainty. The objective of the proposed model is to minimize the total time of allocating emergency resources and the total losses caused by unmet demand. The purpose is to obtain an optimal multiperiod emergency resource allocation scheme by balancing the two objectives of equity and efficiency, so as to provide support for emergency rescue decision making under uncertainty. The main contributions of this work are threefold: (1) the development of a multiperiod emergency resource allocation model under uncertainty that can maximize equity as well as efficiency, and explore trade-offs between these two decision criteria; (2) the introduction of the interval number and triangular fuzzy number to describe different sources of uncertainty, and the design of a deterministic transformation method to deal with the uncertainty; and (3) the illustration of the advantages of the proposed model in achieving equitable and efficient resource allocation under uncertainty with a multi-angle case analysis.
Section 2 reviews the literature relevant to our work, Sect. 3 describes the research problem and proposes the notations and model formulation, Sect. 4 presents the solution method to solve the proposed model. A case study of the 2017 Jiuzhaigou earthquake in Sichuan Province, China is used to illustrate the applicability and potential advantages of the proposed model in Sect. 5. Finally, the conclusion is stated in Sect. 6.
2 Literature Review
Emergency resource allocation in humanitarian logistics has attracted increasingly more attention in recent research due to the increased frequency and destructive effects of disasters (Sheu and Pan 2014; Kamran et al. 2016; Moreno et al. 2016; Farahani et al. 2020). Constructing and solving models to provide decision support for emergency resource allocation has become the focus of existing research (Tzeng et al. 2007; Mete and Zabinsky 2010; Anaya-Arenas et al. 2014; Özdamar and Ertem 2015; Wang 2021).
As the primary mission of humanitarian relief operations is saving lives, alleviating suffering, and reducing property losses, the majority of the studies focus on efficiency or effectiveness objectives/criteria (Hoyos et al. 2015; Wang 2021), that is, the shortest total allocation time (Wex et al. 2014; Luan et al. 2020; Tang and Ye 2021), the lowest total transportation cost (Barbarosoğlu and Arda 2004; Minas et al. 2015; Zhou and Erdogan 2019; Zahedi et al. 2020; Han et al. 2021), the minimum total casualties (Fiedrich et al. 2000), and the shortest total distribution path (Sigal and Pritsker 1980; Yuan and Wang 2009; Hu et al. 2020). Tang and Ye (2021), for example, developed an emergency medical resource allocation model for multiple distribution centers and multiple demand points with the objective of minimizing the total allocation time of loading, unloading, and transportation. Han et al. (2021) constructed an optimization model of emergency supplies allocation for post-disaster relief operations with time window constraints to minimize total transportation costs. Fiedrich et al. (2000) proposed an optimization model for allocating emergency resources to minimize the total number of casualties during the search and rescue period. Hu et al. (2020) established a dynamic allocation model of emergency medical supplies considering the urgency of demand points with the goal of minimizing vehicle distribution paths.
Another criterion, equity, has been gradually paid attention to in recent years due to the need of realistic emergency relief decision making (Rennemo et al. 2014; Wang and Sun 2020). Equity and efficiency are two important but conflicting goals in disaster relief operations (Feng et al. 2017). Fast distribution may lead to inaccurate allocation of resources, while the allocation scheme with the lowest transportation cost will lead to unfair allocation of resources among multiple disaster sites (Wang et al. 2019). In disaster relief operations, the most efficient allocation scheme may not be the most equitable, and inequities in the allocation of emergency resources may lead to increased social costs and negative impacts (Hu, Liu, et al. 2016). Especially in the case of resource shortage, equitable allocation is of great significance for improving the overall effects of emergency relief operations (Wang 2021). In the equity models, equity criteria are usually measured by factors such as demand satisfaction, deprivation cost, or deprivation time (Huang and Rafiei 2019). Holguín-Veras et al. (2013) introduced deprivation cost into an emergency resource allocation model for post-disaster relief, which mainly quantifies equity through a series of negative impacts caused by a lack of resources. Huang and Rafiei (2019) used deprivation time—which reflects the time of delay between sequential deliveries—as an equity criterion for allocation of emergency supplies. Chen and Fu (2018) developed a model for allocation of the first batch of emergency resources at the initial stage of large-scale disasters, taking the minimum total weighted envy value as the equity target and proportional equity as the constraint. He et al. (2021) took minimizing the comprehensive jealousy value as the equity objective, and then proposed an emergency resource allocation model with multiple rescue centers and multiple epidemic affected areas.
The allocation of emergency resources is usually a multi-objective optimization problem, and some researchers have gradually begun to consider both equity and efficiency in recent research (Fu and Chen 2018; Wang et al. 2019; Wang 2021). Fu and Chen (2018) developed a bi-objective model for the allocation of the first batch of post-disaster emergency resources, in which efficiency is measured by the latest delivery time and equity is measured by the demand satisfaction rate of the affected point. Wang (2021) designed an optimal allocation model of emergency resources for cross-regional collaborative relief with the goal of minimizing total delivery time and total distribution costs (efficiency) while maximizing coverage of resources (equity). However, these studies all centered on deterministic emergency rescue information conditions, ignoring the impact of the uncertainty of the information on emergency material distribution in disaster relief situations.
Uncertainty exists widely in post-disaster emergency rescue operations, which has an important impact on the equitable and efficient allocation of emergency resources (Hu, Liu, et al. 2016). Existing studies mainly focus on the uncertainty of emergency demand (Beraldi et al. 2004; Zhang et al. 2010; Wang et al. 2014; Qin et al. 2017), and some studies also focus on the uncertainty of transportation time caused by road network damage (Lai et al. 2020; Wang and Sun 2020). Zhang et al. (2010) introduced interval numbers to represent the material demand of disaster affected locations and proposed an emergency resource allocation optimization model with the goal of minimizing the total costs. Wang et al. (2014) analyzed the problem of relief resource allocation under fuzzy demand conditions by constructing an optimization model with the goal of minimizing the total costs and transportation time. Qin et al. (2017) aimed at minimizing the total costs and proposed an optimization model of vehicle routing for emergency relief resource allocation, considering insufficient supplies and uncertain demand. Lai et al. (2020) applied the discrete scenario set to describe the uncertainty of transport time and established an optimization model of emergency resource allocation with efficiency goal priority.
These studies have provided a sound theoretical basis for our work. The brief review of related research work indicates that it is crucial to consider efficiency, equity, and uncertainty in emergency resource allocation. However, since the ultimate goal of disaster relief is to minimize casualties, the efficiency criterion is often given the first attention by previous studies. Although some studies began to consider both efficiency and equity, most of them lack detailed quantification and analysis of the sources of uncertainty in disaster information. In addition, previous emergency resource allocation problems in uncertain situations usually focused on the uncertainty of demand or time, which makes it easy to ignore other factors related to emergency rescue operations. Thus, we attempted in this study to develop a multiperiod and multi-objective optimization model for emergency resource allocation that simultaneously captures equity and efficiency under uncertainty. In contrast to most existing works, three different sources of uncertainty in emergency situations—demand, transportation time, and maximum transport amount—are simultaneously considered and quantified in this article. We also explored methods of managing uncertainty in an emergency context to help obtain high-quality or optimal resource allocation schemes. We verified the validity and feasibility of the proposed model through a case study of the Jiuzhaigou earthquake, aiming to provide decision support for the multiperiod equitable and efficient allocation of emergency resources in large-scale disaster relief operations.
3 Mathematical Model
This section describes the research problem, explains the notations for model formulation, and proposes the multiperiod equitable and efficient allocation model of emergency resources.
3.1 Problem Description
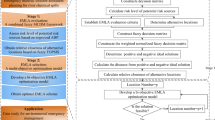
Large-scale sudden disasters usually have the characteristics of large impact scope, strong destructiveness, and high rescue urgency. Emergency decision makers are unable to accurately obtain the required relief information because the relevant information—such as material demand, delivery time, and transportation volume—can only be determined in a certain range through limited information. To meet the reality of disaster relief, interval number is introduced to describe the uncertainty of emergency resource demand and transportation time, and triangular fuzzy number is used to represent the maximum total transport amount of resources per period under the condition of limited road network capacity. The equity objective is quantified by the loss caused by unmet demand and the efficiency objective is measured by the allocation time. Therefore, the research problem of this study is the multiperiod equitable and efficient optimal allocation of large-scale disaster emergency relief resources under uncertainty (Fig. 2). Decision makers should consider both equity and efficiency of resource allocation at each period to minimize the total losses caused by unmet demand for all disaster-affected locations as soon as possible within the shortest time.
3.2 Notations
The sets, parameters, and variables used in the model formulation are as follows.
3.2.1 Sets
- \(D\) :
-
Set of affected locations indexed by \(d \in D\).
- \(S\) :
-
Set of supply sites indexed by \(s \in S\)
- \(M\) :
-
Set of types of emergency relief resources indexed by \(m \in M\)
- \(N\) :
-
Set of time periods of emergency resource allocation indexed by \(n \in N\)
.
3.2.2 Parameters
- \(C^{\prime}_{smn}\) :
-
New supply of resource \(m \in M\) at supply site \(s \in S\) at the beginning of time period \(n \in N\).
- \(\mathop C\nolimits_{{{\text{s}}mn}}\) :
-
Actual supply of resource \(m \in M\) at supply site \(s \in S\) during time period \(n \in N\).
- \(\mathop {\tilde{B}}\nolimits_{dmn}\) :
-
New demand for resource \(m \in M\) at affected location \(d \in D\) at the beginning of time period \(n \in N\) represented by interval number. \(\mathop {\tilde{B}}\nolimits_{dmn} = \left[ {\mathop B\nolimits_{dmn}^{ - } ,\mathop B\nolimits_{dmn}^{ + } } \right]\), \(\mathop B\nolimits_{dmn}^{ - }\) and ̃ \(\mathop B\nolimits_{dmn}^{ + }\) are the lower limit and upper limit of the interval number, respectively.
- \(\mathop B\nolimits_{dmn}\) :
-
Actual demand for resource \(m \in M\) at affected location \(d \in D\) during time period \(n \in N\).
- \(\mathop O\nolimits_{{{\text{s}}mn}}\) :
-
Inventory of resource \(m \in M\) at supply site \(s \in S\) at the end of time period \(n \in N\).
- \(\mathop {\tilde{R}}\nolimits_{sdn}\) :
-
Maximum total amount of resource \(m \in M\) that can be transported from supply site \(s \in S\) to affected location \(d \in D\) during time period \(n \in N\). It is expressed by triangular fuzzy number, \(\mathop {\tilde{R}}\nolimits_{sdn} = \left( {\mathop {R^{\prime}}\nolimits_{sdn}^{ \, L} , \, \mathop {R^{\prime}}\nolimits_{sdn}^{ \, M} , \, \mathop {R^{\prime}}\nolimits_{sdn}^{ \, U} } \right)\), where \(\mathop {R^{\prime}}\nolimits_{sdn}^{ \, L}\), \(\mathop {R^{\prime}}\nolimits_{sdn}^{ \, M}\) and \(\mathop {R^{\prime}}\nolimits_{sdn}^{ \, U}\), respectively, represent the pessimistic, normal, and optimistic estimates of the maximum amount of transportation.
- \(\mathop {\tilde{T}}\nolimits_{sdn}\) :
-
Transportation time for allocating resources from supply site \(s \in S\) to affected location \(d \in D\) during time period \(n \in N\) represented by interval number, \(\mathop {\tilde{T}}\nolimits_{sdn} = \left[ {\mathop T\nolimits_{sdn}^{ - } ,\mathop T\nolimits_{sdn}^{ + } } \right]\), \(\mathop T\nolimits_{sdn}^{ - }\) and \(\mathop T\nolimits_{sdn}^{ + }\) are the shortest and longest transportation time, respectively.
- \(\mathop T\nolimits_{dmn}\) :
-
Unloading time per unit of resource \(m \in M\) at location \(d \in D\) during time period \(n \in N\).
- \(\mathop T\nolimits_{smn}\) :
-
Loading time per unit of emergency resource \(m \in M\) at supply site \(s \in S\) during time period \(n \in N\).
- \(\mathop \lambda \nolimits_{dn}\) :
-
Disaster coefficient of the affected location \(d \in D\) during time period \(n \in N\) reflects the impact and damage degree of the location caused by the disaster, which can be measured by factors such as disaster intensity, road conditions, and vulnerability of victims.
- \(\mathop H\nolimits_{dmn}\) :
-
Unmet amount (shortage) of required resource \(m \in M\) at affected location \(d \in D\) at the end of time period \(n \in N\).
- \(Loss\left( {\mathop H\nolimits_{dmn} } \right)\) :
-
Loss caused by the unmet demand of resource \(m \in M\) at affected location \(d \in D\) at the end of time period \(n \in N\).
3.2.3 Variables
- \(\mathop q\nolimits_{sdmn}\) :
-
Amount of resource \(m \in M\) allocated to affected location \(d \in D\) from supply site \(s \in S\) during time period \(n \in N\).
- \(\mathop \rho \nolimits_{dmn}\) :
-
Preset maximum unmet rate of resource \(m \in M\) at affected location \(d \in D\) during time period \(n \in N\).
- \(\mathop U\nolimits_{sdn}\) :
-
Binary variable indicating whether resources are allocated to affected location \(d \in D\) from supply site \(s \in S\) during time period \(n \in N\). If so, the value is 1; otherwise, it is 0.
3.3 Model Formulation
The objective functions and constraints of the proposed model are as follows.
3.3.1 Objective Function
The objective function (1) minimizes the total losses caused by unmet demand at each affected location in all emergency periods to pursue the equity criterion. The objective function (2) minimizes the total time of resource allocation in all emergency periods to pursue the efficiency criterion.
3.3.2 Constraints
Constraint (3) guarantees that the amount of allocated resource to the affected location in a given period cannot exceed the sum of the new demand and the shortage remaining from previous periods. Constraint (4) ensures that the amount of allocated resource from the supply site in a given period cannot exceed the sum of the new supply and the inventory remaining from previous periods. Constraint (5) ensures that the resource allocation at each affected location is not higher than the preset maximum unmet rate. Constraint (6) gives an expression for measuring the loss caused by unmet demand at the affected point. Constraint (7) shows the transportation capacity limit under the condition of road network damage. Constraint (8) indicates the demand for each affected location should be met as much as possible in a given period. Constraint (9) defines the logical relationship between the decision variables, indicating whether to allocate resources. Constraints (10) and (11), respectively, denote the dynamic changes in the supply and demand of emergency resources. Constraint (12) gives an expression for measuring the unmet demand. Constraint (13) requires that the binary variable must be equal to either 0 or 1. Constraint (14) gives the nonnegative constraints of the decision variables.
4 Model Solution Method
We first transform the uncertain parameters in the objective function and constraints of the proposed model into deterministic parameters, and then use the linear weighted sum method to solve the model.
4.1 Deterministic Transformation Processing of the Uncertain Parameters
In this study, interval number and triangular fuzzy number in the corresponding objective functions and constraints are deterministically transformed according to the following definitions.
4.1.1 Deterministic Transformation of Interval Number
Definition 1.
Interval linear programming \(f\left( X \right) = f\left( {\mathop x\nolimits_{1} ,\mathop x\nolimits_{2} , \cdots ,\mathop x\nolimits_{n} } \right) = \left[ {\mathop Z\nolimits_{1} + \alpha \cdot \left( {\mathop Z\nolimits_{2} - \mathop Z\nolimits_{1} } \right)} \right] \cdot \sum\limits_{i = 1}^{n} {\mathop x\nolimits_{i} }\), \(s.t. \, AX \le \,B\). In the formula, the solution of the objective function is called the α-level solution of the original interval programming and \(\alpha \in \left[ {0,1} \right]\) is the optimization level of the objective function, and \(\mathop Z\nolimits_{1}\) and \(\mathop Z\nolimits_{2}\) are the lower and upper bounds of the interval value, respectively (Molai and Khorram 2007).
According to Definition 1, given a optimization level \(\alpha\), the objective function (2) of the proposed model can be transformed into the following deterministic form:
where \(\mathop T\nolimits_{sdn}^{ - }\) and \(\mathop T\nolimits_{sdn}^{ \, + }\) are the lower and upper bounds of the transport time value, respectively.
For the objective function (1), in order to minimize the loss caused by unmet demand for emergency resources under the worst conservative condition, the demand \(\mathop {\tilde{B}}\nolimits_{dmn} = \left[ {\mathop B\nolimits_{dmn}^{ - } ,\mathop B\nolimits_{dmn}^{ + } } \right]\) at the disaster-affected location is set as the maximum demand \(\mathop B\nolimits_{dmn}^{ \, + }\) for emergency resources. The form after deterministic transformation is as follows:
Definition 2.
For any solution \(x \in X\) of the general interval linear programming model, \(\beta = P\left( {\sum\nolimits_{i = 1}^{n} {\mathop a\nolimits_{ij} \mathop x\nolimits_{i} \le \mathop B\nolimits_{j} } } \right)\) is called the optimization level of \(x \in X\) for the constraint \(\sum\nolimits_{i = 1}^{n} {\mathop a\nolimits_{ij} \mathop x\nolimits_{i} \le \mathop B\nolimits_{j} }\) (Molai and Khorram 2007; Guo et al. 2010).
According to Definition 2, given a optimization level \(\beta\), constraint (3) of the proposed model can be transformed into the deterministic form:
4.1.2 Deterministic Transformation of Triangular Fuzzy Number
Constraint (7) of the proposed model contains triangle fuzzy number. It is deterministically transformed according to the research of Guo and Qi (2011).
Theorem 1.
A fuzzy equality constraint \(\sum\nolimits_{j} {\mathop {\tilde{a}}\nolimits_{j} \mathop x\nolimits_{j} = \tilde{b}}\) is equivalent to two non-fuzzy inequality constraints:
where \(\mathop {\left( {\mathop {\tilde{a}}\nolimits_{j} } \right)}\nolimits_{a}^{L}\) and \(\mathop {\left( {\mathop {\tilde{a}}\nolimits_{j} } \right)}\nolimits_{a}^{R}\) are the left and right boundaries of the a-cut set of the fuzzy number \(\mathop {\tilde{a}}\nolimits_{j}\), respectively, \(\mathop {(\tilde{b})}\nolimits_{a}^{R}\) and \(\mathop {(\tilde{b})}\nolimits_{a}^{L}\) are the right and left boundaries of the a-cut set of the fuzzy number \(\tilde{b}\), respectively.
The maximum transportation amount in the constraints is \(\mathop {\tilde{R}}\nolimits_{sdn} = \left( {\mathop {R^{\prime}}\nolimits_{sdn}^{ \, L} , \, \mathop {R^{\prime}}\nolimits_{sdn}^{ \, M} , \, \mathop {R^{\prime}}\nolimits_{sdn}^{ \, U} } \right)\), where \(\mathop {R^{\prime}}\nolimits_{sdn}^{ \, L}\), \(\mathop {R^{\prime}}\nolimits_{sdn}^{ \, M}\) and \(\mathop {R^{\prime}}\nolimits_{sdn}^{ \, U}\) are real numbers, \(\mathop {R^{\prime}}\nolimits_{sdn}^{ \, L} \mathop {R^{\prime}}\nolimits_{sdn}^{ \, M} \mathop {R^{\prime}}\nolimits_{sdn}^{ \, U}\), then the fuzzy membership degree is:
Given a optimization level \(\gamma \left[ {0,1} \right]\), the maximum transport amount \(\mathop {\tilde{R}}\nolimits_{sdn}\) can be deterministically transformed by the following equations:
Thus, the triangular fuzzy number in constraint (7) can be transformed into the following deterministic form:
4.2 Solution Step Design
The proposed model is a multi-objective model, which needs to be solved by using multi-objective optimization theory. The commonly used methods are: linear weighted sum method, ideal point method, minimax method, and hierarchical sorting method (Yang and Zhang 2008). In this study, the linear weighted sum method is used to solve the proposed model. The specific solution steps are as follows.
Step 1. Solve the extreme value of each objective function.
Calculate the maximum and minimum values of sub-objective functions \(\mathop F\nolimits_{1} (q_{sdmn} )\) and \(\mathop F\nolimits_{{2}} (q_{sdmn} )\) within the given constraints, which are denoted as \(\mathop F\nolimits_{1} (q_{sdmn} )_{\max }\) and \(\mathop F\nolimits_{1} {(}q_{sdmn} {)}_{\min }\), \(\mathop F\nolimits_{{2}} (q_{sdmn} )_{\max }\) and \(\mathop F\nolimits_{{2}} {(}q_{sdmn} {)}_{\min }\), respectively.
Step 2. Standardization processing.
The (0–1) interval transformation method is used to solve the problem that the dimensional units of the proposed two objective functions are not unified.
For cost indicators:
For benefit indicators:
Step 3. Determine the ideal weight.
The ideal weight (that is, decision preference coefficient) of objective functions \(\mathop F\nolimits_{1} (q_{sdmn} )\) and \(\mathop F\nolimits_{{2}} (q_{sdmn} )\) are recorded as \(\mathop \omega \nolimits_{1}\) and \(\mathop \omega \nolimits_{{2}}\) respectively, satisfying \(\mathop \omega \nolimits_{2} + \mathop \omega \nolimits_{2} = 1\). In this study, the fuzzy weighting method in unstructured decision making is used to quantify the weight of each objective function to reduce the subjectivity of directly assigning weights. The specific process is as follows:
(1) Qualitative ranking of importance. Considering the importance of each objective function, the consistency scale matrix of importance binary comparison is constructed, the importance of each indicator is obtained by calculating the matrix, and the importance of each indicator is ranked in order from large to small.
Assuming there is a factor set \(V = (\mathop v\nolimits_{{\mathop F\nolimits_{1} (q_{sdmn} )}} ,\mathop v\nolimits_{{\mathop F\nolimits_{2} (q_{sdmn} )}} , \cdots ,\mathop v\nolimits_{{\mathop F\nolimits_{e} (q_{sdmn} )}} )\), we compare the importance between \(\mathop v\nolimits_{{\mathop F\nolimits_{j} (q_{sdmn} )}}\) and \(\mathop v\nolimits_{{\mathop F\nolimits_{g} {(}q_{sdmn} {)}}}\), and use \(\mathop Z\nolimits_{{\mathop F\nolimits_{jg} (q_{sdmn} )}}\) to represent the scale of the importance ranking index. The importance binary contrast consistency scale matrix composed of the factor set is:
Then, the sum of each row in the consistency scale matrix is arranged in order from large to small, and the importance order of the factor set under the condition of ranking consistency is given.
(2) Quantitative determination of the weight of factor set. According to the consistency scale matrix \(Z\) of importance ranking, mark the sequence numbers \(i = 1,2, \cdots ,r\) in the order of importance from large to small, make a binary comparison on the importance of the qualitative ranking factor set, combined with the relationship between tone operator and quantitative scale, and then obtain the ordered binary comparison matrix.
Meet the conditions:
where \(\mathop p\nolimits_{{\mathop F\nolimits_{gj} (q_{sdmn} )}}\) is the quantitative scale of the importance of factor \(\mathop v\nolimits_{{\mathop F\nolimits_{g} (q_{sdmn} )}}\) to factor \(\mathop v\nolimits_{{\mathop F\nolimits_{j} (q_{sdmn} )}}\) in binary comparison; and \(\mathop p\nolimits_{jg}\) is the quantitative scale of the importance of factor \(\mathop v\nolimits_{{\mathop F\nolimits_{j} (q_{sdmn} )}}\) to factor \(\mathop v\nolimits_{{\mathop F\nolimits_{g} (q_{sdmn} )}}\) in binary comparison. \(i\) and \(j\) are sorting subscripts, \(i = 1,2, \cdots ,r\), and the ordinals are arranged in descending order according to the sum of the rows of the matrix \(Z\).
Then we can get:
where
Step 4. Build a single objective model.
The single objective programming model can be converted as follows:
Step 5. Solve the single objective programming model.
The converted single objective model can be solved by using the Matlab software.
5 Computational Case
In this section, a case study of the 2017 Jiuzhaigou earthquake is used to test the effectiveness and feasibility of the proposed model.
5.1 The Case of the 2017 Jiuzhaigou Earthquake in Sichuan Province, China
A magnitude 7.0 earthquake occurred at 21:19:46 p.m., China Standard Time, on 8 August 2017 in Jiuzhaigou County, Aba Prefecture, Sichuan Province, China (\({33}{\text{.20}}^{^\circ } N,{ 103}{\text{.82}}^{^\circ } E\)). According to Chinese state officials, as of 20:00 on 13 August 2017, the earthquake caused 25 verified deaths, 525 people were injured, 6 people were missing, 176,492 people were affected (including tourists), and 73,671 houses were damaged to varying degrees (among which 76 collapsed). The basic infrastructure systems such as transportation, telecommunication, and power and water supply had also been damaged. In such emergency situations, decision makers face two main challenges: (1) the immediate need for a large number of various emergency resources at each disaster-affected location; and (2) some relief information from the affected locations is uncertain in terms of transportation time, demand for different resources, and maximum total transport amount due to the damaged infrastructure systems. Thus, in this context, equitable and efficient allocation of emergency resources is crucial to reduce the destructive impact and improve the relief effect after the disaster.
In this case, we considered allocating two types of emergency resources—tents (\(\mathop m\nolimits_{{1}}\)) and drinking water (\(\mathop m\nolimits_{{2}}\))—from two supply sites, Chengdu (CD) and Ziyang (ZY), to five severely affected locations—Jiuzhaigou County (JZG), Ruoergai County (REG), Hongyuan County (HY), Songpan County (SP), and Pingwu County (PW). We took seven days as the time period to analyze the resource allocation in the 28 days (a total of 4 emergency periods, nearly a month) after the disaster. The reason is that the four periods can usually reflect the entire process of earthquake disaster relief, including the initial stage of emergency response (supply is less than demand), the middle stage (supply continues to increase), and the later stage (supply exceeds demand). The relevant data for the computational case were chosen using a combination of real and hypothetical data, since some disaster data were not published or could not be obtained through official reports. For example, the new supply of emergency resources at the supply sites at the beginning of each period (Table 1) was estimated according to the resource storage before the disaster and the mobilization ability during the disaster. The new demand for emergency resources at the affected locations at the beginning of each period (Table 2) was estimated based on the number of victims and the severity of the disaster. Based on interviews conducted in September 2017 with five staff members of the volunteer service center who participated in the entire process of emergency resource allocation, the maximum total amount of emergency resources transported from the supply sites to the affected locations in each time period (Table 3) was estimated. The disaster coefficient of affected locations in each time period (Table 4) was measured by disaster intensity and vulnerability of victims. The transportation time of allocating resources from the supply sites to the affected locations in each period (Table 5) was obtained via Baidu Maps. The loading and unloading times per unit of emergency resources (Table 6) were estimated based on the same five interviews. All types of emergency resources are in units of thousands. The weights of the two objective functions are calculated according to the fuzzy weighting method (see Sect. 4.2). In the qualitative ranking of importance, we set the two objective functions to have the same degree of importance. Then through calculation, we derived the weights of these two objective functions, which are \(\mathop \omega \nolimits_{{1}} { = }\mathop \omega \nolimits_{{2}} { = }0.{5}\)(this also represents the consideration of both the efficiency criterion and the equity criterion). The optimization levels of the deterministic transformation of uncertain parameters are set as \(\alpha = 0.9\),\(\beta = 0.9\), and \(\gamma { = }0.9{5}\), respectively, and the maximum unmet rate of resource allocation is set here as \(\mathop \rho \nolimits_{dmn} = 40 \% \). We solved the computational case in Matlab R2016a on a computer with an Intel(R) Core(TM) 1.90 GHz processor with 16.0 GB of RAM.
5.2 Computational Results
This section analyzes the following three computational results to illustrate the effectiveness and potential advantages of the proposed model.
5.2.1 Overall Emergency Resource Allocation Scheme
Table 7 shows the overall allocation scheme of emergency resources from supply sites to affected locations, and Fig. 3 shows the allocation network structure for emergency resources, which is an optimal strategy for balancing efficiency and equity. It comprehensively considers multiple factors, including the disaster coefficient of affected locations, the maximum total amount of resources that can be transported under the condition of limited road network capacity, the transportation time, and the loading time and unloading time for allocating resources. Among them, we found that the loss from unmet demand of resources in Pingwu County (PW) is zero, which is mainly due to the fact that the resource needs of this affected location were fully met throughout the emergency rescue operations. In addition, Fig. 4 shows that, on the whole, the higher the disaster coefficient of the affected location, the greater the total loss caused by unmet demand, and the longer the required resource allocation time.
Network structure diagram of overall emergency resource allocation. CD Chengdu; ZY Ziyang; JZG Jiuzhaigou County; REG Ruoergai County; HY Hongyuan County; SP Songpan County; PW Pingwu County. The data format in this figure is (\(\mathop m\nolimits_{{1}}\), \(\mathop m\nolimits_{{2}}\)), which respectively represents the overall allocation results of resource \(\mathop m\nolimits_{{1}}\) and resource \(\mathop m\nolimits_{{2}}\) from supply sites to affected locations in the entire emergency period. The value unit of the numbers is one thousand tents and one thousand boxes of drinking water.
5.2.2 Emergency Resource Allocation Scheme in Each Period and Corresponding Loss and Time
The allocation results, losses caused by unmet demand, and time associated with the allocation of all types of emergency resources in each time period are shown in Table 8. Figure 5 presents the emergency resource allocation network structure for each period. The trends of the losses and allocation time in each time period are shown in Fig. 6. Figure 7 shows the shortfalls and satisfaction rates of required resources at the end of each time period.
Network structure diagram of emergency resource allocation in each time period (7 days). CD Chengdu; ZY Ziyang; JZG Jiuzhaigou County; REG Ruoergai County; HY Hongyuan County; SP Songpan County; PW Pingwu County. The data format in this figure is (\(\mathop m\nolimits_{{1}}\), \(\mathop m\nolimits_{{2}}\)), which respectively represents the allocation results of resource \(\mathop m\nolimits_{{1}}\) and resource \(\mathop m\nolimits_{{2}}\) from supply sites to affected locations in each time period (7 days). The value unit of the numbers is one thousand tents and one thousand boxes of drinking water.
Figure 5 shows that the model allocates emergency resources to all disaster-affected locations in every emergency period as long as the locations have resource needs, so as to ensure that their needs are met to the greatest extent, thus preventing each disaster-affected location from having large losses due to unmet demand.
Table 8 and Fig. 6 show that in the entire emergency period (28 days from period 1 to period 4), the loss caused by unmet demand shows a trend of gradual decline, and the allocation time presents a trend that first increases and then decreases. This is consistent with the actual resource allocation in emergency situations. The required resources are often insufficient in the initial period of emergency relief operations, resulting in greater loss caused by unmet demand, and the allocation time is relatively short due to the small amount of resources that can be allocated initially. With the development of rescue activities, the supply of resources gradually increases. In order to make up for the shortage of resources in the early time period, the allocation of resources in the middle time period of the emergency response will be greatly increased, so that the loss is gradually reduced and the allocation time is gradually increased. In the later period of the emergency response operations, as the demands of the affected locations are gradually met, the loss is gradually reduced to zero, and the allocation time is also reduced due to the reduction of the amount of resources that need to be allocated.
Figure 7 shows a large degree of resource shortfall at the disaster-affected locations in the first period, but through the resource allocation operations, the shortfall in the subsequent periods gradually decreases and the satisfaction rate gradually increases. When there is no shortfall of resources, the satisfaction rate reaches 100% (that is, the satisfaction rate of resources \(\mathop m\nolimits_{{2}}\) and \(\mathop m\nolimits_{{1}}\) reaches 100% in period 3 and period 4, respectively). This shows that the proposed model is effective for multiperiod scientific allocation of emergency resources under the condition of uncertain disaster information.
5.2.3 Loss, Time, and Satisfaction Rate of Resource Allocation at Each Affected Location
The specific quantity of emergency resources allocated at each disaster-affected location in each time period and the corresponding loss and time are shown in Table 9. The resource satisfaction rate at each affected location in each time period is shown in Fig. 8. Figures 9 and 10 show the trends of the loss caused by unmet demand and the time for allocating resources to each affected location in each time period, respectively.
Figure 8 shows that the emergency resource satisfaction rate of all affected locations in each time period shows a gradual upward trend. Even in the initial period of emergency rescue (period 1), the resource satisfaction rate of all affected locations remains at 60% or above, and eventually the satisfaction rate of all affected locations reaches 100%. This shows that the proposed model is effective in improving the resource satisfaction rate of disaster-affected locations.
From Figs. 9 and 10, we can see that through continuous resource allocation, the loss caused by unmet demand at each affected location in each time period is gradually reduced, reaching zero at the end of the fourth period, which indicates that the resource shortfall of each disaster-affected location is gradually reduced, and the resource demand of all disaster-affected locations is finally fully satisfied. At the same time, the general trend in the time required for allocating resources is gradually increased. The reason is that in order to reduce the loss caused by unmet demand as far as possible, supply sites often need to allocate resources to disaster-affected locations that are far away, which means that, to a certain extent, the reduction in loss caused by unmet demand comes at the cost of increased allocation time.
Among the disaster-affected locations, the site with the least loss and the shortest allocation time is Pingwu County (PW). In each period of emergency relief operation, the resource demand of PW is minimal among the five affected locations, the transportation time between PW and the supply sites is the least, and the unloading time is also the shortest. So the supply sites—on the premise of guaranteeing equity in allocation in the shortest time—give priority to allocating all the required resources to PW. This is crucial for reducing the total loss and allocation time, and also indicates that the model can take into account both the efficiency and equity of resource allocation in each time period, and minimize the loss caused by unmet demand of all affected locations in the shortest time.
6 Conclusion
From the computational results and analysis, four major conclusions and insights can be drawn:
-
(1)
The reduction of loss usually comes at the expense of the increase of allocation time, and the optimal resource allocation strategy requires a scientific trade-off between these two criteria.
-
(2)
The disaster coefficient affects the allocation effect of emergency resources. The higher the disaster coefficient of the affected location, the greater the total loss caused by unmet demand, and the longer the required allocation time.
-
(3)
On the premise of balancing efficiency and equity, the proposed model can maximize the satisfaction rate of resource allocation at each disaster-affected location, even at the initial period of emergency rescue.
-
(4)
The model considers uncertain disaster information such as demand, transportation time, and maximum transport amount in resource allocation, which is more in line with the actual emergency rescue operation situation.
One recommendation for further research is to extend the proposed model to consider more realistic uncertain factors (for example, damage degree of road network and the impact of secondary disasters). With the increasing complexity of research problems, more efficient model solving methods should be designed. Future research of these issues will be beneficial for optimal multiperiod allocation of large-scale emergency resources in real world situations.
References
Adeagbo, A., A. Daramola, A. Carim-Sanni, C. Akujobi, and C. Ukpong. 2016. Effects of natural disasters on social and economic well-being: A study in Nigeria. International Journal of Disaster Risk Reduction 17: 1–12.
Ahmadi, G., R. Tavakkoli-Moghaddam, A. Baboli, and M. Najaf. 2022. A decision support model for robust allocation and routing of search and rescue resources after earthquake: A case study. Operational Research 22(2): 1039–1081.
Anaya-Arenas, A., J. Renaud, and A. Ruiz. 2014. Relief distribution networks: A systematic review. Annals of Operations Research 223(1): 53–79.
Barbarosoğlu, G., and Y. Arda. 2004. A two-stage stochastic programming framework for transportation planning in disaster response. Journal of Operational Research Society 55(1): 43–53.
Beraldi, P., M.E. Bruni, and D. Conforti. 2004. Designing robust emergency medical service via stochastic programming. European Journal of Operational Research 158(1): 183–193.
Chen, G., and J. Fu. 2018. Multi-objective emergency resources allocation with fairness and efficiency considerations. Chinese Journal of Management 15(3): 459–466 (in Chinese).
China Earthquake Administration. 2022. Earthquake query system - earthquake channel of China earthquake administration. https://www.cea.gov.cn/cea/dzpd/index.html. Accessed 6 Jan 2022 (in Chinese).
Erbeyoglu, G., and U. Bilge. 2020. A robust disaster preparedness model for effective and fair disaster response. European Journal of Operational Research 280(2): 479–494.
Eshghi, K., and R.C. Larson. 2008. Disasters: Lessons from the past 105 years. Disaster Prevention and Management: An International Journal 17(1): 62–82.
Farahani, R.Z., M.M. Lotf, A. Baghaian, R. Ruiz, and S. Rezapour. 2020. Mass casualty management in disaster scene: A systematic review of OR&MS research in humanitarian operations. European Journal of Operational Research 287(3): 787–819.
Feng, C., Y. Xiang, K. Xue, and R. Feng. 2017. Multi-objective optimization model of the emergency logistics distribution with multicycle and multi-item. Chinese Journal of Management Science 25(4): 124–132 (in Chinese).
Fiedrich, F., F. Gehbauer, and U. Rickers. 2000. Optimized resource allocation for emergency response after earthquake disasters. Safety Science 35(1): 41–57.
Fu, J., and G. Chen. 2018. A bi-objective emergency resources allocation model considering the trade-off between fairness and efficiency. Systems Engineering 36(6): 149–153 (in Chinese).
Guo, Z., and M. Qi. 2011. Emergency material collection decision model with fuzzy parameters. Computer Engineering and Applications 47(23): 217–219 (in Chinese).
Guo, Z., M. Qi, and Q. Zhang. 2010. Minimum cost selection model of emergency material reserve based on interval number. Operations Research and Management Science 19(1): 15–20 (in Chinese).
Han, M., J. Ding, M. Chen, and K. Huo. 2021. Optimization of emergency material distribution path based on hybrid genetic algorithm. Science Technology and Engineering 21(22): 9432–9439 (in Chinese).
He, Y., P. Jiang, L. Wen, H. Zhao, and M. Fan. 2021. Distribution strategy of multiple epidemic prevention materials weighing fairness, economy and efficiency. Industrial Engineering and Management 26(6): 146–153 (in Chinese).
Holguín-Veras, J., N. Pérez, M. Jaller, L.N. Van Wassenhove, and F. Aros-Vera. 2013. On the appropriate objective function for postdisaster humanitarian logistics models. Journal of Operations Management 31(5): 262–280.
Hoyos, M.C., R.S. Morales, and R. Akhavan-Tabatabaei. 2015. OR models with stochastic components in disaster operations management: A literature survey. Computers & Industrial Engineering 82(1): 183–197.
Hu, C.L., X. Liu, and Y.K. Hua. 2016. A bi-objective robust model for emergency resource allocation under uncertainty. International Journal of Production Research 54(24): 7421–7438.
Hu, X.W., L. Song, B. Yang, and J. Wang. 2020. Optimal matching of urban emergency medical supplies under major public health events. China Journal of Highway and Transport 33(11): 55–64 (in Chinese).
Hu, X.B., M. Wang, T. Ye, and P. Shi. 2016. A new method for resource allocation optimization in disaster reduction and risk governance. International Journal of Disaster Risk Science 7(2): 138–150.
Huang, K., and R. Rafiei. 2019. Equitable last mile distribution in emergency response. Computers & Industrial Engineering 127(1): 887–900.
Kamran, M.A., B. Karimi, H. Bakhtiari, and S. Masoumzadeh. 2016. A resource allocation model in a healthcare emergency center using goal programming. Journal of Engineering Research 4(4): 81–97.
Kovacs, G., and K. Spens. 2009. Identifying challenges in humanitarian logistics. International Journal of Physical Distribution & Logistics Management 39(6): 506–528.
Lai, Z., Z. Wang, D. Ge, and Y. Chen. 2020. A multi-objective robust optimization model for emergency logistics center location. Operations Research and Management Science 29(5): 74–83 (in Chinese).
Luan, S., Q. Yang, Z. Jiang, W. Wang, and C. Chen. 2020. A multi-stage emergency supplies preallocation approach for freeway black spots: A Chinese case study. PLOS ONE 15(10): 1–20.
Mete, H., and Z. Zabinsky. 2010. Stochastic optimization of medical supply location and distribution in disaster management. International Journal of Production Economics 126(1): 76–84.
Minas, J., J. Hearne, and D. Martell. 2015. An integrated optimization model for fuel management and fire suppression preparedness planning. Annals of Operations Research 232(1): 201–215.
Molai, A.A., and E. Khorram. 2007. Linear programming problem with interval coefficients and an interpretation for its constraints. Iranian Journal of Science & Technology, Transaction A 31(A4): 369–390.
Moreno, A., D. Alem, and D. Ferreira. 2016. Heuristic approaches for the multiperiod location-transportation problem with reuse of vehicles in emergency logistics. Computers & Operations Research 69(1): 79–96.
Ogie, R.I., and B. Pradhan. 2019. Natural hazards and social vulnerability of place: The strength-based approach applied to Wollongong, Australia. International Journal of Disaster Risk Science 10(3): 404–420.
Özdamar, L., and M. Ertem. 2015. Models, solutions and enabling technologies in humanitarian logistics. European Journal of Operational Research 224(1): 55–65.
Qin, J., Y. Ye, B. Cheng, X. Zhao, and L. Ni. 2017. The emergency vehicle routing problem with uncertain demand under sustainability environments. Sustainability 9(2): 1–24.
Rennemo, S.J., K.F. Ro, L.M. Hvattum, and G. Tirado. 2014. A three-stage stochastic facility routing model for disaster response planning. Transportation Research Part E: Logistics and Transportation Review 62(1): 116–135.
Rising, K.L., and N. Lurie. 2013. Working together to prepare for disasters. Science 342(6155): 191–192.
Sheu, J.B., and C. Pan. 2014. A method for designing centralized emergency supply network to respond to large-scale natural disasters. Transportation Research Part B: Methodological 67: 284–305.
Sigal, C., and A. Pritsker. 1980. The stochastic shortest route problem. Operational Research 28(5): 1122–1129.
Su, Z., G. Zhang, Y. Liu, F. Yue, and J. Jiang. 2016. Multiple emergency resource allocation for concurrent incidents in natural disasters. International Journal of Disaster Risk Reduction 17: 199–212.
Tang, D., and C. Ye. 2021. Study on fair distribution of emergency medical supplies in the early stage of epidemic. Science Technology and Industry 21(10): 212–218 (in Chinese).
Tzeng, G.-H., H.-J. Cheng, and T.D. Huang. 2007. Multi-objective optimal planning for designing relief delivery systems. Transportation Research Part E: Logistics and Transportation Review 43(6): 673–686.
Wang, H., L. Du, D. Hu, and J. Wang. 2014. Location-routing problem for relief distribution in emergency logistics under certainties. Chinese Journal of Management Science 22(1): 55–64 (in Chinese).
Wang, Y. 2021. Multiperiod optimal allocation of emergency resources in support of cross-regional disaster sustainable rescue. International Journal of Disaster Risk Science 12(3): 394–409.
Wang, Y., and B. Sun. 2020. Multi-period optimization model of multi-type emergency materials allocation based on fuzzy information. Chinese Journal of Management Science 28(3): 40–51 (in Chinese).
Wang, Y., V.M. Bier, and B. Sun. 2019. Measuring and achieving equity in multiperiod emergency material allocation. Risk Analysis 39(11): 2408–2426.
Wex, F., G. Schryen, S. Feuerriegel, and D. Neumann. 2014. Emergency response in natural disaster management: Allocation and scheduling of rescue units. European Journal of Operational Research 235(3): 697–708.
Yang, B., and K. Zhang. 2008. Research on theory, method and application of multi-objective decision analysis. Shanghai: Donghua University Press (in Chinese).
Yuan, Y., and D. Wang. 2009. Path selection model and algorithm for emergency logistics management. Computers & Industrial Engineering 56(3): 1081–1094.
Zahedi, A., M. Kargari, and A.H. Kashan. 2020. Multi-objective decision-making model for distribution planning of goods and routing of vehicles in emergency. International Journal of Disaster Risk Reduction 48: 1–13.
Zhang, L., J. Wang, and J. Huang. 2010. Robust optimal resource allocation model for uncertain demands. Journal of Systems Science and Mathematical Sciences 30(10): 1283–1292 (in Chinese).
Zhou, S., and A. Erdogan. 2019. A spatial optimization model for resource allocation for wildfire suppression and resident evacuation. Computers & Industrial Engineering 138(1): 1–16.
Acknowledgments
This work was supported by the National Social Science Foundation of China (Grant No. 21CGL044).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Y., Sun, B. Multiperiod Equitable and Efficient Allocation Strategy of Emergency Resources Under Uncertainty. Int J Disaster Risk Sci 13, 778–792 (2022). https://doi.org/10.1007/s13753-022-00437-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13753-022-00437-y