1 Introduction

Urban pluvial flooding is attracting growing public concern and research focus worldwide. In the context of global environmental change, the urban hydrological environment has evolved under the combined effect of natural and anthropogenic factors (Du et al. 2012; Yin et al. 2016a; Gu et al. 2019). There is a growing consensus that climate change will result in more extreme precipitation events (IPCC 2012, 2013; Zhang, Gu et al. 2018). Moreover, rapid urban expansion significantly increases impervious surface areas, causing sharp increases in urban discharge and runoff (Du et al. 2012; Zhang, Villarini et al. 2018). In addition, the existing drainage network systems in most cities are outdated and rapid urbanization has significantly outpaced the construction of urban infrastructure, thus making cities more vulnerable to pluvial flooding. These combined factors result in an increase in the frequency and severity of urban pluvial flooding.

As a critical infrastructure component in urban environments, the storm sewer system is responsible for draining excess surface runoff in cities. According to the Code for the Design of Outdoor Wastewater Engineering (GB 50014-2006),Footnote 1 the capacity of urban drainage systems in China is generally designed to cope only with 1- to 3-year return period rainfall, which is significantly lower than the design standards (5- to 10-year) of urban drainage systems in countries such as the United States, the United Kingdom, and Japan. Given insufficient drainage capacity, torrential rains can overwhelm the storm sewer system, leading to extensive surface water flooding throughout cities, particularly in developing countries. In recent years, the “ocean views in the city” have become a new landscape in more than half of China’s cities in the flood season (Xia et al. 2017). In September 2013, for example, an extreme rainfall event occurred in Shanghai, with precipitation of 124 mm/h in the Pudong New Area, resulting in flood inundation of more than 80 roads with water depths of 200–500 mm and associated widespread disruption of urban traffic. In order to protect against the increasingly severe storms and urban floods, the concept and framework of the “sponge city” have been proposed, based on the ecological drainage and pipe network drainage system. The Chinese government is also actively promoting the pilot construction of sponge cities (Wang et al. 2018).

The simulation of urban surface water flooding is more complex than that of traditional hydrologic modeling in river basins, and it is necessary to comprehensively consider the hydrodynamic processes in urban areas, both at the surface and underground. Since the 1960s, the development of urban pluvial flood modeling has gone through several stages, including the development of hydrological methods, 1D hydrodynamic methods, 1D/2D coupled hydrodynamic methods, and, more recently, Geographic Information System (GIS)-based simplified hydrodynamic methods. Traditional urban stormwater models—such as the storm water management model (SWMM), the storage treatment overflow runoff model (STORM), and the Wallingford models—generally simulate the urban rainfall–runoff process using hydrological methods or 1D hydraulic modeling of urban drainage networks. The main shortcoming of these models is that 2D surface water flooding cannot be simulated, and thus the location and extent of inundated areas cannot be determined for urban flood management.

During the past decades, the SWMM has been linked with 2D models (first by Hsu et al. 2002), which was unidirectional from sewer to surface. Some commercial software has also coupled 2D hydrodynamic modules and developed a new generation of 1D/2D coupled urban stormwater models such as PC-SWMM (the updated version of the SWMM), InfoWorks (the updated version of Wallingford), Sobek Urban, MIKE-Urban, and TUFLOW. In these new models, the output of the 1D module is used as the input boundary condition of the 2D module to simulate the overflow process on the surface (Phillips et al. 2005; Bolle et al. 2006; Leandro et al. 2009; Seyoum et al. 2012). However, this type of model usually requires an unstructured mesh to represent the urban topography. The modeling is very complex and most models are not freely available (Yin et al. 2015). In recent years, GIS-based urban flood inundation models have become popular in the academic field and research applications of flood modeling. Yu and Coulthard (2015) established an urban pluvial flood model (FloodMap-HydroInundation2D), which uses a high-resolution digital elevation model (DEM) for the 2D numerical modeling of urban rainfall–runoffprocesses, but the model uses a generalized scheme for the urban drainage capacity and does not consider the hydrodynamic processes of the storm sewer system. In order to overcome the shortcomings of the above-mentioned two types of models, some researchers have combined the open-access 1D urban stormwater model with the GIS-based 2D flood model to simulate the flood inundation processes. For example, the SWMM was linked bi-directionally with P-DWAVE, a 2D overland flow model (Leandro et al. 2014; Leandro and Martins 2016). Wu et al. (2017) combined the SWMM and LISFLOOD-FP models to simulate future urban pluvial flooding in the city of Dongguan, Guangdong Province, but such case studies and the associated technical methods are still very limited.

In this study, we coupled the underground 1D stormwater model (SWMM) with a newly developed 2D urban flood inundation model (ECNU-Flood Urban) to conduct a scenario analysis of stormwater flooding in downtown Shanghai under different precipitation return periods. We compared the simulation results with the modeling outputs of FloodMap-HydroInundation2D, which is well established and has a similar 2D model structure but with a different treatment of urban drainage, to determine the feasibility and robustness of the 1D/2D coupled model. The proposed method extends the existing methods and provides a numerical simulation of urban storm flooding. The results may serve as a technical reference for Chinese cities in terms of flood control, disaster risk reduction, and sponge city construction and have important scientific and practical significance. An up-to-date framework of surface flood modeling for cities is established. This provides a strong scientific basis for urban flood risk management for various stakeholders and the construction of sponge cities in an uncertain future.

Section 2 introduces the geography of the study area. Section 3 provides the materials and methods, including the available data and the description of coupled modeling. Section 4 presents the results and discussion, and Sect. 5 summarizes the key conclusions.

2 Study Area

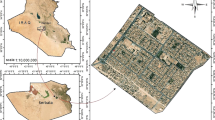
The central business district (CBD) of East Nanjing Road, which is the downtown area of Shanghai, was chosen as the study site because it has a high risk of urban pluvial flooding. The study area is located in the North Huangpu District and borders the Huangpu River to the east and Suzhou Creek to the north (Fig. 1). It covers approximately 3.2 km2 and has low elevation (on average about 3 m above the Wusong DatumFootnote 2). The region is located in a northern subtropical monsoon climate zone characterized by cyclonic storms and intense precipitation that frequently occur in the flood season from July to September. According to the historical records, severe pluvial flooding events have occurred in Shanghai 272 times from AD 251 to 2000, accounting for over half of the total flood disasters (Quan 2014).

Fig. 1
figure 1

Location of the study area in Shanghai

Full size image

In order to cope with the adverse impacts of surface water flooding in the downtown area of Shanghai, an urban drainage system was established and has been continuously expanded and upgraded since 1990s. However, problems such as lagging construction of the drainage pipe network system, small diameter of some pipelines, and low drainage capacity result in an inability of the storm sewer system in the central urban area to meet the increasing drainage demand; these are the major reasons for urban rainstorm waterlogging. The influence of human activities on the structure of the urban river network, such as garbage dumping and land reclamation, also greatly reduce the retention, storage, and drainage capacity of stormwater in the urban area when waterlogging occurs. In addition, rapid urban expansion significantly increases the impervious surface area, which sharply reduces the infiltration capacity of the rainstorm runoff and makes it difficult to discharge the water naturally.

3 Materials and Methods

Urban pluvial flooding processes can be categorized as surface and underground flooding. When extreme precipitation events occur and urban surface runoff exceeds the drainage capacity, the stormwater flow spills out of the ground from the underground pipe network through manholes or pump stations, resulting in urban surface water flooding. In this study, the SWMM was used to simulate the 1D water flow movement in the drainage pipelines and the process of water overflow on the ground was simulated using the ECNU-Flood Urban model. The output of the 1D hydrodynamic model was used as the input to drive the 2D surface flood modeling.

3.1 Rainfall Scenarios

Rainfall is the most important input variable of urban pluvial flooding and the parameters of rainfall intensity and rainfall duration were considered. The Shanghai Municipal Engineering Design Institute (2003) developed the following rainstorm intensity equation that is based on the precipitation of a specified return period (5, 10, 20, 50, 100 years):

$$q = 1995.84(p^{0.30} - 0.42)/(t + 10 + 7\lg P)^{0.82 + 7\lg P}$$
(1)

where q is the rainfall intensity; P is the return period of rainfall; and t is the duration of rainfall.

The Chicago design storm method, developed for a study of stormwater flooding in Chicago by Keifer and Chu (1957), describes the temporal variations of rainfall based on the rainfall intensity before and after the peak. The Chicago design storm data represent a time series of the storm intensity and the rain peak coefficient r (0 < r < 1) and are used to describe when the rainfall peak occurs. The rainfall duration is divided into the pre-peak time tx and the post-peak time ty. Considering the local conditions in Shanghai, the rain peak coefficient is empirically set at 0.4 (Yin et al. 2016b). Combined with the Shanghai rainstorm intensity equation, the design storm with 2-h duration is generated for specified return periods. The Chicago design storm is defined as follows:

$$i_{\text{a}} = \frac{{a \times \left[ {\frac{{\left( {1 - c} \right) \times t_{y} }}{1 - r} + b} \right]}}{{\left( {\frac{{t_{y} }}{1 - r} + b} \right)^{c + 1} }}$$
(2)
$$i_{\text{b}} = \frac{{a \times \left[ {\frac{{\left( {1 - c} \right) \times t_{x} }}{r} + b} \right]}}{{\left( {\frac{{t_{x} }}{r} + b} \right)^{c + 1} }}$$
(3)

where ia, ib are the rainfall intensity before and after the rain peak (mm/min); tx, ty are the time intervals before and after the rain peak (min); r is the rain peak coefficient (0 < r < 1); and a, b, and c are the local parameters in the storm intensity formula.

3.2 Storm Water Management Model (SWMM) Modeling

In this study, the SWMM developed by the U.S. Environmental Protection Agency (EPA) was used to simulate the flow in the underground drainage system. The storm water management model is a 1D dynamic rainfall–runoffmodel that can simulate runoff quantity and quality from primarily urban areas. Since its development, the SWMM has been used in thousands of storm sewer and stormwater studies throughout the world, including the evaluation of the impact of inflow and infiltration on storm sewer overflows. The flow calculation in the drainage system usually describes the flow movement in the pipeline in a 1D form, allowing the water flows from one node to the next through the pipe.

In general, channel and pipe flow routings are governed by the Saint–Venant equations. In the transport component, the SWMM solves the Saint–Venant equation using the implicit finite difference method and successive approximation. The flow equation is defined as follows:

$$\frac{\partial A}{\partial t} + \frac{\partial Q}{\partial x} = 0$$
(4)
$$\frac{Q}{gA} \cdot \frac{\partial }{\partial x}\left( {\frac{Q}{A}} \right) + \frac{1}{gA} \cdot \frac{\partial Q}{\partial t} + \frac{\partial h}{\partial x} + S_{f} - S_{0} = 0$$
(5)

where Q is the outflow (m3/s); A is the cross-sectional area of the water (m2); h is the water depth (m) in the pipeline; t is time (s); x is the length of the pipe along the water flow direction (m); Sf is the resistance slope; and S0 is the bottom slope of the pipeline.

The drainage network data used in this study were obtained from the Shanghai Municipal Sewerage Company, including the geographic and geometric information of pipes, nodes, and manholes; the attributes include the network length, pipe diameter (or length and width), elevation at the beginning of the pipeline, depth of the manholes, and ground elevation. The diameters of the pipes ranged from 300 to 400 mm, and the depths of the manholes ranged from 1.2 to 1.4 m. There were 620 drainage pipe sections in the modeling area and 500 inspection well nodes (including 5 pump stations), with a total length of about 45 km. To reduce the modeling complexity and computational cost, the urban drainage system was simplified in the SWMM. Using the Thiessen polygon method in ArcGIS, the study area was automatically divided into 495 subcatchments corresponding to the inspection well nodes. The subcatchments were further modified according to the distribution of the roads and pipe networks in the study area (Fig. 2).

Fig. 2
figure 2

Simplification of the urban drainage network in the Shanghai study area

Full size image

3.3 Model Coupling

The SWMM model was used to calculate the hydrodynamics in the pipe network, and the time series (for example, 1, 5, or 15 min intervals) of the surcharges of the storm sewer system (manholes) was then used as the flow boundary condition of the 2D surface water flooding model to achieve the coupling of the 1D and 2D models (Fig. 3). We developed a SWMM link to define the location of manhole inflow in the ECNU Flood-Urban model. It should be noted that this is only a loosely coupled scheme of urban pluvial flood modeling. The SWMM and ECNU Flood-Urban models were run, respectively, and thus the dynamic flow exchanges between the 1D and 2D models were ignored.

Fig. 3
figure 3

Coupled modeling of urban pluvial flooding in the Shanghai study area. DSM: digital surface model

Full size image

3.4 Surface Flood Inundation Modeling

To determine the surface flood inundation in the urban area, we developed a new raster-based 2D hydrodynamic model (ECNU-Flood Urban). The urban inundation model has the same structure as the diffusion-wave treatment of Bradbrook et al. (2004) and Yu and Lane (2006a, 2006b, 2011). The ECNU-Flood Urban model is coded in JAVA and is based on the discretization of the Manning equation; it ignores the inertial and advection forces of water flow. The general form of the Manning equation is as follows:

$$Q = \frac{{AR^{2/3} S^{0.5} }}{n}$$
(6)

where Q is the flow; A is the cross-sectional area; R is the hydraulic radius; n is Manning’s roughness coefficient; and S is the energy slope. In a regular grid, the flow area is calculated as follows:

$$A = w \times d$$
(7)

where w is the width of the grid; and d is the flow depth. The hydraulic radius R is equal to the depth of the grid (d), and thus the Manning equation can be expressed as follows:

$$Q = \frac{{wd^{5/3} S^{0.5} }}{n}$$
(8)

Considering a regular grid and the adjacent four cells, the orthogonal directions of the grids are defined as i and j. The energy slope S in each orthogonal direction is represented by the difference in water levels between the grid centers. If the slope of the source grid toward the other adjacent grids is positive, water is allowed to flow out of the grid.

$$S_{i} = \frac{{h_{i,j} - h_{i \pm 1,j} }}{w}$$
(9)
$$S_{j} = \frac{{h_{i,j} - h_{i,j \pm 1} }}{w}$$
(10)

The flow direction is determined by the vector sum of the energy slope Si and Sj. Therefore, the energy slope S can be calculated as:

$$S = \sqrt {S_{i}^{2} + S_{j}^{2} }$$
(11)

In each of the four directions, the effective depth is represented by the water surface elevation in the source grid that is higher than the two ground elevations in the i or j direction:

$$d_{i} = h_{i,j} - { \hbox{max} }\left| {g_{i,j} ,g_{i \pm 1,j} } \right|$$
(12)
$$d_{j} = h_{i,j} - { \hbox{max} }\left| {g_{i,j} ,g_{i,j \pm 1} } \right|$$
(13)

where d is the effective depth; h is the water surface level; and g is the ground level. The effective depth in the outflow direction is expressed as the arithmetic mean of the effective depths of both flows in the direction of the steepest slope:

$$d = \frac{{d_{i} S_{i}^{2} + d_{j} S_{j}^{2} }}{{S^{2} }}$$
(14)

Manning’s equation is then solved in the i and j directions of the grids, and the flows into and out of each grid at each time step are calculated as follows:

$$Q_{i} = Q\frac{{S_{i} }}{S} = \frac{{wd^{5/3} S_{i} }}{{nS^{0.5} }} = \frac{{wd^{5/3} \left( {\frac{{h_{i,j} - h_{i \pm 1,j} }}{w}} \right)}}{{n\left[ {\left( {\frac{{h_{i,j} - h_{i \pm 1,j} }}{w}} \right)^{2} + \left( {\frac{{h_{i,j} - h_{i,j \pm 1} }}{w}} \right)^{2} } \right]^{1/4} }}$$
(15)
$$Q_{j} = Q\frac{{S_{j} }}{S} = \frac{{wd^{5/3} S_{j} }}{{nS^{0.5} }} = \frac{{wd^{5/3} \left( {\frac{{h_{i,j} - h_{i,j \pm 1} }}{w}} \right)}}{{n\left[ {\left( {\frac{{h_{i,j} - h_{i \pm 1,j} }}{w}} \right)^{2} + \left( {\frac{{h_{i,j} - h_{i,j \pm 1} }}{w}} \right)^{2} } \right]^{1/4} }}$$
(16)

The flow depth change in each of the grids is determined at the start of each time step:

$$\Delta d = \frac{{\left( {\mathop \sum \nolimits_{d = 1}^{4} Q_{{{\text{in}}i,j}}^{d} - \mathop \sum \nolimits_{d = 1}^{4} Q_{{{\text{out}}i,j}}^{d} + Q_{\text{inflow}} } \right)\Delta t}}{w}$$
(17)

where ∆t is the time step.

The input into the ECNU-Flood Urban model includes model parameters, topographic data, and the boundary condition. The main model parameter used in this study is Manning’s roughness coefficient n. An empirical Manning’s n value of 0.04, which has provided good predictions in previous studies, was used in the simulation of the design flood scenarios; the value reflects the effect of urban features on flood routing (Yin et al. 2016b). A high-resolution airborne LiDAR digital surface model (DSM) provided by the Shanghai Survey Bureau was used for the topographic data of the study site. The original LiDAR point cloud data had a horizontal resolution of about 0.6 m and a vertical resolution of 0.1–0.2 m. The TerraSolid software was used for quality control and hierarchical processing to remove specific urban surface features such as trees. Finally, the remaining data in the point cloud were converted into a standard grid resolution of 2 m. The drivers of the coupled model are the rainfall scenarios, but the infiltration/evapotranspiration in urbanized areas can be neglected during short-term heavy rainfall. The model was set up to run four hours until a steady state of urban flooding was reached by the end of the simulation.

4 Results and Discussion

The hydrodynamic characteristics of rainfall–runoffprocesses in urban environments are investigated successively in the sewer system (Sect. 4.1) and on the ground surface (Sect. 4.2). The coupled modeling outputs of urban pluvial flooding are further compared with crowd-sourced data and the simulated results derived from FloodMap-HydroInundation2D (Sect. 4.3), and the key findings are discussed.

4.1 Storm Water Management Model (SWMM) Modeling

The rainfalls of different return periods are input into the SWMM model as the driving condition to simulate the water flows in the storm sewer system of the study area. The overflow nodes and overloaded pipelines were determined to evaluate the drainage capacity of the pipe network. The simulation results are shown in Table 1.

Table 1 Storm water management model (SWMM) simulation results in different rainstorm return periods for the Shanghai study area
Full size table

The surface runoff, as expected, increases as the rainfall increases. This is largely due to the significant impervious surface areas and the insufficient drainage capacity in the study area. Specifically, there are 253, 276, 282, 301, and 313 overflow nodes under the rainfall events with return periods of 5, 10, 20, 50, and 100 years. The total overflow of the sewer system is predicted to increase from 94,928 m3 at the 5-year return period to 222,764 m3 at the 100-year return period. These results indicate that there is a proportionate and linear relationship between the rainfall magnitudes and the total overflow and surface runoff of the pipe network in the study area. More than 30% of the pipeline network is overloaded when the rainstorm return period is five years or longer, because the rainfall intensity exceeds the designed drainage capacity of the pipes. However, an important finding is that the differences of overloaded pipelines among various return period events are small. This suggests that overflow mainly occurs through a limited number of terminal nodes for each simulation, albeit with a different rainfall magnitude corresponding to a different return period.

The spatial distribution of the surcharges of the drainage pipe network at the first hour of simulations under different rainfall return periods is shown in Fig. 4. The varying degrees of node overflow in the drainage network are highly correlated to the intensity of the rainfall. For a 5-year return period, there is a large number of overflow nodes, mainly along the East Beijing Road, West Nanjing Road, and Fuzhou Road. As the return period increases, overflow nodes gradually spread across the study area, with a significant rise in the amount of surcharges. Under a 100-year return period event, over 50 nodes, accounting for 16% of the total, are predicted to overflow more than 0.8 m3/s. However, similar patterns of the overflow nodes of the sewer system can be observed among the five scenarios, further confirming the simulation results of drainage capacity in Table 1. The predicted surcharges of the drainage network are relatively small in the southwest part (that is, the People’s Park) of the region under all rainfall return periods, as the overflow peaks in the large open green spaces occur at around ~ 45 min of simulations and then rapidly decrease.

Fig. 4
figure 4

Node overflows of the drainage network at different rainstorm return periods in the Shanghai study area

Full size image

4.2 Surface Water Flood Modeling

The 1D and 2D models are coupled and the surface water flooding under different rainfall scenarios is simulated. The result of maximum inundation (extent and depth) for each simulation is shown in Fig. 5. The general pattern of surface water flooding is characterized by a high degree of consistency among the five scenarios. In each simulation, the inundation with shallow water depth (generally less than 0.3 m) can be observed mostly in the low-lying road network of the study area. The maximum inundation area is expected to slightly increase from 60,500 m2 for a 5-year rainfall event to 106,536 m2 for a 100-year rainfall event, because of the minor differences among the predicted surcharges of the sewer system under each rainfall scenario. Although the surface water flooding is associated with significant overflow from the drainage network, roads around the People’s Park are found to be subject to obvious flood inundation. This can be explained by the mild relief, flat topography, and the relatively high drainage capacity (36–49.6 mm/h), suggesting that pluvial flood inundation is greatly dependent on the interplay among rainfall intensity, topographic features, and drainage capacity.

Fig. 5
figure 5

Maximum water depth and inundation area at different rainfall return periods in the Shanghai study area

Full size image

Figure 6 shows the time series of the predicted wet area for all flood scenarios. The time-area curves are in line with each other, suggesting similar inundation dynamics throughout the simulations. Furthermore, node overflow leads to a proportionate and linear effect on the time evolution of the flood inundation. Generally, surface water flooding occurs at the first hour of simulations, and then rapidly extends along the road network at the second hour when a large amount of water overwhelms the drainage network. A steady state is reached afterwards, but the flood extent continues to slightly increase till the end of each simulation, even without any surcharges from the sewer system.

Fig. 6
figure 6

Time series of inundation area throughout the simulation for each scenario in the Shanghai study area

Full size image

4.3 Model Validation and Comparison

A complete picture of observed flood extent and height (for example, remote sensing images, reliable field surveys, and high-water marks) is not available for the study area. Instead, the SWMM-ECNU Flood-Urban coupled modeling scheme is validated by comparing the model prediction of a severe pluvial flood event that occurred in August 2011 with flood incidents reported by the public. Distributed precipitation data are used as input to drive the 1D/2D coupled modeling. Predicted maximum inundation and the crowd-sourced flood points are presented in Fig. 7. The result shows that all of the 17 reported flood locations fall within the simulated inundation areas with a water depth higher than 40 cm. In addition, social media also reported that some main roads such as East Nanjing Road were heavily inundated during the event. These findings suggest a good match between the model estimates and observed flood records.

Fig. 7
figure 7

Predicted maximum inundation overlain with reported flood locations during the August 2011 pluvial flood event in the Shanghai study area

Full size image

The coupled modeling of the SWMM and ECNU Flood-Urban models is comparable to the 2D hydrodynamic modeling such as the FloodMap-HydroInundation2D simulation (Fig. 5 in Yin et al. 2016a). The major difference between these two methods is the drainage setting. The SWMM model in the coupled modeling is used to simulate the dynamic process of the water flowing in the urban storm sewer system, while the amount of runoff loss is simply calculated in the FloodMap-HydroInundation2D model by scaling the drainage capacity for each time step with an assumption that the sewer system drains water away at the maximum design capacity. In practice, urban sewer system is always difficult to achieve the maximum design drainage capacity. Therefore, the maximum inundation areas during the August 2011 pluvial flood event obtained from the 1D/2D coupled modeling are larger than those directly predicted by the FloodMap-HydroInundation2D.

5 Conclusion

In this study, a new methodology for urban pluvial flood modeling was developed by loosely coupling the 1D SWMM model and the 2D surface water flood model (ECNU Flood-Urban). Using a recent pluvial flood event that occurred in the city center of Shanghai, we validated the coupled modeling through the comparison between model prediction and crowd-sourced data. The approach was further used to simulate urban pluvial flooding for the study area under rainfall scenarios with different return periods. A number of conclusions can be drawn. First, the inundation predicted by the coupled modeling of the SWMM and ECNU Flood-Urban models agrees well with the observed flood locations, and is larger than those directly simulated by the 2D hydrodynamic modeling (FloodMap-HydroInundation2D). Second, the risk of overloading the sewer system and associated surface water flooding is determined by the interaction among rainfall intensity, topographic features, and drainage capacity. Third, surface water flooding occurs extensively in the low-lying road network with relatively shallow water depth.

The simplified modeling method presented here could be easily applied in other flood-prone cities, compared to other 1D/2D coupled modeling schemes. It may contribute to better understanding of insufficient drainage capacity of urban sewer systems, and thus help to inform adaptation measures for sustainable flood risk management. However, to arrive at more reliable results, future studies could be conducted in the following aspects: (1) tightly 1D/2D coupled modeling should be developed to explore the dynamic flow exchanges between the 1D and 2D models; (2) full 2D solutions for the treatment of flood routing would be a significant advance, particularly for including the inertial effect of water flow; and (3) the use of massive online social networks on platforms like Weibo and WeChat would enable big data collection for model validation.