1 Introduction

The Dominican Republic remains among the top economic performers in Latin America and the Caribbean. The country experienced economic expansion at a rate of 6.6% in 2016, compared to an average contraction of 1.4% of gross domestic product (GDP) in the region. Poverty declined by nearly 12%, from 43.6% in 2007 to 32.4% in 2015. Despite this economic growth and steady decline in poverty, the government of the Dominican Republic continues to face structural rigidities, and inadequate revenue collection sharply limits its capacity to respond to imminent natural hazard-induced disasters. Coupled with the likelihood of future disasters and weather-related shocks, the Dominican Republic is thus at risk of economic and social losses without the adoption of adequate risk reduction strategies and an enhanced management of the contingent fiscal liabilities associated with disasters. Based on historical data for 1961–2014, losses associated with all types of natural hazard-induced disasters in the Dominican Republic averaged USD 420 million annually, or 0.69% of 2015 GDP (MEPyD and World Bank 2015). As climate change is expected to increase the likelihood, intensity, and frequency of extreme weather events in the Caribbean, strengthening disaster and climate risk reduction will be critical (Villarini and Vecchi 2012, 2013; Taylo et al. 2018).

According to the World Bank’s Country Disaster Risk Profile,Footnote 1 the projected average annual loss over the long term from hurricanes alone will be USD 337 million in the Dominican Republic, or 0.49% of 2015 GDP. A large portion of the country’s population and key productive activities—related to agriculture, energy, and tourism—are situated in areas highly exposed to natural hazards. Between 2005 and 2014 the vulnerable population in the Dominican Republic increased at a faster rate (5.5%) than in Latin America and the Caribbean as a whole (2%) (Ferreira et al. 2013). Moreover, because of incomplete or inadequate risk management strategies, vulnerable households in the country may be a disaster away from falling below the poverty line or sliding further back into poverty. Shocks created by disasters have regressive distributional effects as vulnerability to climate shocks is higher for the poorest households (Báez et al. 2017).

The Dominican Republic is one of the more hurricane-prone countries within the Atlantic Basin, averaging a damaging storm about every 3 years (Bertinelli et al. 2016). A recent telling example of how damaging these storms can be is Hurricane Georges (1998), a category 4 storm that is estimated to have induced damages in the Dominican Republic of up to USD 1.9 billion (2019 USD).Footnote 2 Despite such potentially large losses, it is not clear by how much these losses translate into actual reductions in economic activity and for how long such an effect might persist. Although there are now a number of studies that have empirically examined this issue, these studies have tended to pool data across countries, thus estimating only an average country effect. Generally the impact of tropical cyclones has been found to have been on average a significant one, particularly for large events, but with a relatively short-lived impact on country level economic wealth.Footnote 3 Realistically, however, due to heterogeneities in ex ante and ex post resilience, country-specific effects may be widely dispersed around this “mean” impact, and thus the mean may not provide a clear indication of what is to be expected for individual countries. In this article, we explicitly focus on examining what the economic wealth consequences of tropical storms are for the Dominican Republic.

In considering how to estimate to what extent tropical storms might impact economic activity, it is important to recognize that damages arising from such a storm are inherently local in nature and often display considerable spatial heterogeneity. Not taking account of this local heterogeneity can induce considerable measurement error in trying to estimate the aggregate economic impact of tropical storm damage (Strobl 2012). One of the main obstacles in incorporating such local differences in damages due to these storms into economic assessments has traditionally been the lack of comprehensive economic data over space and time. However, the recent availability of satellite-derived nightlight intensity measures at a highly spatially disaggregated level has provided researchers with a potential proxy of local economic wealth and activity (Chen and Nordhaus 2011). These data have now also found use in the context of tropical storm impacts. Bertinelli and Strobl (2013) and Elliott et al. (2015) examined the impact of these weather events on nightlight intensity for the Caribbean and China, respectively. Both studies showed that “localizing” the nature of the investigation can provide important insights into the question as to what economic impact tropical cyclones may have.

One drawback of these studies using nightlights to assess the economic impact of tropical cyclones is that they have largely been restricted to using annual data, in part because the publicly available nightlight data is at annual frequency. In reality, most of the damages, direct and indirect, are likely to take place at a much higher temporal frequency. A recent study by Ishizawa et al. (2017) of six Central American countries using monthly versions of the publicly available annual nightlight images showed that there is considerable heterogeneity of impact even within the year of a hurricane strike and that this is masked in annual data. This result is echoed by Mohan and Strobl (2017) using a different monthly nightlight satellite data source to investigate the impact of 2015 Typhoon Pam in the South Pacific.

In this study, we used monthly nightlight composites to examine the short-term local impact of hurricanes on the Dominican Republic since 1992. To this end, we constructed local maximum wind speeds for damaging storms for every pixel in the nightlight data using a wind field model and best track data. These were then inserted into a stylized damage function and used to econometrically estimate the impact of the storms on local monthly nightlight intensity. Our estimated luminosity impact was then translated into monetary values by relating quarterly nightlight values to quarterly national GDP.

Our analysis found that there was a negative impact of tropical storms on local nightlight intensity and that this lasted up to 15 months after a strike, with the largest effect observed 9 months after the storm strikes. The estimates suggest that the 19 damaging storms that occurred over the 22-year sample period induced on average a 2.1% fall in nighttime brightness. Overall, translating nightlight units into monetary values using quarterly GDP suggests that on average the storms reduced GDP by about USD 1.1 billion.

In the next section, we describe the data sets, and Sect. 3 outlines the damage function and wind field model employed. Section 4 states our econometric specification and provides econometric results. Section 5 uses the estimates from Sect. 4 to derive the monetary values of the economic impact.

2 Data

In this section we describe the data used and how we construct the variables for our empirical analysis.

2.1 Nightlight Data

Nightlight data consist of the monthly composites of the United States Air Force Defense Meteorological Satellite Program—Operational Linescan System (DMSP-OLS). The source satellites have a 101-minute sun-synchronous, near-polar orbit at approximately 830 km above the Earth’s surface and provide coverage across the globe twice a day, at 20 h 30 and 22 h local time. The raw data are processed to remove cloud obscured pixels and other sources of transient light, and are normalized to range between 0 and 63. We used the monthly composites purchased from NASA for satellites F10, F12, F14, F15, F16, and F18. These provide information on the average stable monthly nightlight intensity, as well as the number of cloud-free days from which these averages are calculated. A summary of the coverage and the missing monthly composites are provided in Table 1. In order to derive unique monthly values for overlapping satellite observations we calculate simple averages across satellites for each pixel. Ishizawa et al. (2017), in a similar analysis of six Central American countries found that alternatively using cloud weighted averages or the newest images produced qualitatively similar results.

Table 1 Missing months in the nightlights sample for the Dominican Republic
Full size table

We also depict the kernel density distribution of average monthly nightlight cells in the Dominican Republic for 2013 in Fig. 1. Essentially a third of the pixels are unlit over the year. Of those that experienced a non-zero value, the average value is around 9.5, with a standard deviation of 11.5. A small proportion of cells is characterized by values much larger than the average. For the sample used in the regression analysis we assumed that any pixel that over our sample period had only zero values had no economic activity, and these pixels were dropped from the analysis. This left us with a total of 38,535 of 59,392 cells covering the Dominican Republic.

Fig. 1
figure 1

Kernel density estimate of average monthly nightlight intensity in the Dominican Republic in 2013

Full size image

A discussion is warranted as to the legitimacy of DMSP nightlight imagery as a proxy for economic activity. There are two aspects to consider: (1) weaknesses of the data in capturing what they are explicitly supposed to capture, that is brightness due to artificial lighting at night; and (2) weaknesses in nightlight data per se to capture economic activity. With regard to the second aspect, a number of studies have examined how nightlights are related to measures of GDP (see, for example, Chen and Nordhaus 2011; Henderson et al. 2012). In general, these studies suggest that at the national level nightlights can act as reasonable proxies of GDP. At a more localized level, Doll (2008), Ghosh et al. (2013), and Mellander et al. (2015) found, for countries in the European Union, for China, India, and Mexico, and for Sweden, respectively, moderate correlation between nightlight intensity and localized economic activity measures.

In terms of the first aspect there are a number of features of the data that are relevant. While the processed data provide intensity measures at roughly the 1 km level (near the equator), the actual swaths of the data are around 3 km, and thus processed cells are locally not independent of each other (Yi et al. 2014). Perhaps more importantly, given the normalization of the data, there is likely to be considerable top-coding, so that very bright cells are capped well below their true value and thus underestimated. Worryingly this may start as early as at a value of 55 (Bluhm and Krause 2016).

More generally, one has to be very clear about which nightlights are possibly a reasonable proxy for what sort of economic activity. Artificial light at night is likely to come from three sources: (1) commercial residences; (2) private residences; and (3) infrastructure. Nightlights are thus likely to capture and/or are correlated with income/wealth, use of electricity for manufacturing and service industries, and household wealth, but it is less likely to be a good proxy for agricultural production. This may mean that nightlights will be relatively poorer in capturing the impact of tropical cyclones in rural areas. Unfortunately, there is no available high frequency spatial data for the Dominican Republic in this regard.

2.2 Best Track Data

The source for hurricane tracks is the HURDAT Best Track Data, which provides six-hourly data on all tropical cyclones in the North Atlantic Basin, including the position of the eye of the storm and the maximum wind speed. We linearly interpolated these to hourly positions. We also restricted the set of storms to those that came within 500 km of the Dominican Republic and achieved hurricane strength (at least 119 km/h) at some stage in their lifetime, since those were likely to have caused damage due to wind exposure.Footnote 4

3 Damage Function and Wind Field Model

We now describe the hurricane damage function we employ, and how we use a wind field in order to construct local maximum wind speeds during a hurricane.

3.1 Damage Function

The damage due to tropical storms takes three main forms: wind destruction, flooding/excess rainfall, and storm surge. These are all correlated with wind speed and hence wind speeds experienced can be used as a general proxy for potential damages due to tropical storms. To translate wind speed into potential damage, one should note that property damage due to tropical storms should vary with the cubic power of the wind speed experienced on physical grounds, and it is for this reason that previous studies have simply used the cubic power of wind speed as a destruction proxy (Strobl 2012). However, there is likely to be a threshold below which there is unlikely to be any substantial physical damage (Emanuel 2011). Moreover, the fraction of property damaged should approach unity at very high wind speeds. To capture these features the index proposed by Emanuel (2011) that approximates the fraction of property damaged is employed:

$${\text{FINDEX}}_{ijt} = \frac{{v_{ijt}^{3} }}{{1 + v_{ijt}^{3} }}$$
(1)

where

$$v_{ijt} = \frac{{{\text{MAX}}[(V_{ijt} - V_{\text{thresh}} ),0]}}{{V_\text{half} - V_{\text{thresh}} }}$$
(2)

where Vijt is the wind experienced at point i at time t due to storm j, Vthresh is the threshold below which no damage occurs, and Vhalf is the threshold at which half of the property is damaged. Following Emanuel (2011) we use a value of 93 km (50 kts) for Vthresh and a value of 278 km (150kts) for Vhalf. We depict the damage profiles of FINDEX in Fig. 2 as well as three consecutive bars reflecting the wind associated with the Saffir-Simpson Scales (SSS) 1, 3, and 5. Wind speeds classified as SSS level 1 (119 km/h), 3 (178 km/h), and 5 (252 km/h) correspond to f values of about 0.003, 0.090, and 0.39, respectively.

Fig. 2
figure 2

Hurricane damage function

Full size image

3.2 Wind Field Model

The damage function in Eq. 1 requires measures of local wind speed during a storm. What level of wind a location will experience during a passing hurricane depends crucially on that location’s position relative to the storm and the storm’s movement and features, and thus requires explicit wind field modeling. In order to calculate the wind speed experienced due to a hurricane we use Boose et al.’s (2004) version of the well-known Holland (1980) wind field model. The wind experienced at time t due to hurricane j at any point i = 1,….N, that is, Vi,j,t is given by:

$$V_{i,j,t} = GF\left[ {V_{m,j,t} - S\left( {1 - \sin \left( {T_{i,j,t} } \right)} \right)\frac{{V_{h,j,t} }}{2}} \right]\left[ {\left( {\frac{{R_{m,j,t} }}{{R_{i,j,t} }}} \right)^{{B_{jt} }} \exp \left( {1 - \left[ {\frac{{R_{m,j,t} }}{{R_{i,j,t} }}} \right]^{{B_{jt} }} } \right)} \right]^{{\frac{1}{2}}}$$
(3)

where Vm is the maximum sustained wind velocity anywhere in the hurricane, T is the clockwise angle between the forward path of the hurricane and a radial line from the hurricane center to the pixel of interest i, Vh is the forward velocity of the hurricane, Rm is the radius of maximum winds, and R is the radial distance from the center of the hurricane to point i. The remaining parameters in Eq. 3 consist of the gust factor G and the scaling parameters F, S, and B, for surface friction, asymmetry due to the forward motion of the storm, and the shape of the wind profile curve, respectively.

In terms of implementing Eq. 3 one should note that Vm is given by the storm track data described below, Vh can be directly calculated by following the storm’s movements between locations along its track, and R and T are calculated relative to the point of interest i. All other parameters have to be estimated or assumed. For instance, we have no information on the gust wind factor G, but a number of studies (Paulsen and Schroeder 2005) have measured G to be around 1.5, and we also use this value. For S we follow Boose et al. (2004) and assume it to be 1. While we also do not know the surface friction to directly determine F, Vickery et al. (2009) note that in open water the reduction factor is about 0.7 and reduces by 14% on the coast and by 28% 50 km further inland. We thus adopt a reduction factor that linearly decreases within this range as we consider points i further inland from the coast. Finally, to determine B we employ Holland’s (2008) approximation method, whereas we use the parametric model estimated by Xiao et al. (2009) to estimate Rm.

We used the local wind speeds to calculate the damage index of Eq. 1 and list in Table 2 those storms that produced a non-zero value in the Dominican Republic over the sample period 1992–2013 (see Table 1). A total of 19 damaging storms occurred according to this damage index. Of these 1998 Hurricane Georges was the most destructive, causing an average damage of 29%, followed by Floyd (1999), Irene (2011), and Ike (2008). The remaining 15 storms, while sometimes damaging in some areas of the island, overall produced relatively little destruction.

Table 2 Damage index by storm in the Dominican Republic
Full size table

4 Econometric Specification and Results

To measure the impact of tropical cyclones on local (logged) nightlight intensity the following specification is estimated:

$$\log ({\text{NIGHTLIGHT}}_{it} ) = \alpha + \sum\limits_{s = 0}^{S} {\beta_{s} {\text{FINDEX}}_{it - s} } + m_{t} + y_{t} + \mu_{i} + e_{it}$$
(4)

where subscripts i and t denote pixel i and time t, m and y constitute a set of monthly and yearly indicator variables, µ are pixel fixed effects, and e is the error term. In order to purge µ from Eq. 4 we employ a standard linear fixed effects estimator. To allow for serial and cross-sectional correlation we calculate Driscoll and Kraay (1998) standard errors. We allow for lagged impacts of the storms by including up to s = 0,…, S lags of its value in Eq. 4. In order to avoid dropping the large number of zero nightlight observations we added 0.1 to all cells.

In estimating Eq. 4 we set S to 24 months.Footnote 5 The resultant coefficients on these lags, as well as the associated 95% confidence intervals, are depicted in Fig. 3, and the estimates are given in the first column of Table 3. While there is a negative significant effect for the first 3 months, this is relatively small. For example, the coefficients indicate that even a storm like Hurricane Georges would have reduced logged monthly pixel level nightlight intensity in the Dominican Republic by only between 9.1% and 10.5% in the first 3 months relative to its mean value.Footnote 6 If we compare this to the average destruction of damaging hurricanes observed over our sample period, 1992 to 2013, then the fall in logged brightness would have varied between 0.6% and 0.7%.

Fig. 3
figure 3

Marginal impact implied by pixel level regression

Full size image
Table 3 Pixel level regression results
Full size table

While there is no significant effect 3 months after a strike, the negative consequences of tropical cyclones increase substantially thereafter, reaching a climax 9 months after the strike. At this point, the average monthly activity for a storm like Hurricane Georges would have fallen by 108% relative to the mean logged nightlight value, whereas for the average storm the reduction would be about 7.5%. While there still remains a large effect 10 months after the storm, this is very imprecisely measured. More importantly, however, the overall net impact begins to subside until about 15 months, at which point the average storm would reduce logged nightlight intensity by 1.5%, whereas 15 months after Hurricane Georges the logged nightlight intensity was still reduced by 21.0%. Sixteen months after the event there is no longer any discernable impact. More generally, one should note that the observed pattern—a relatively small negative effect, followed by a larger negative effect until the impact subsides—would be consistent with the idea that the first few months are driven by the effect of direct damages, but then the indirect effects dominate, until there is finally a slow recovery and the local economy returns to its equilibrium path by the middle of the second year. Our results provide no evidence of a short-term boost after a hurricane.

We also depict the cumulative effect of a hurricane strike from our estimates in Fig. 4. In congruence with the marginal effect, the overall impact stabilizes 15 months after a hurricane damages the local economy. For Hurricane Georges this suggests an overall reduction in the affected (16) months of about 31% in economic activity, as measured by the brightness at night observed from above, whereas the average storm during the 1992–2013 sample period would have reduced economic production by 2.1%.

Fig. 4
figure 4

Cumulative impact of hurricanes on pixel level nightlight intensity in the Dominican Republic

Full size image

While earlier the argument was made that since the damages due to tropical storms are local and thus require local modeling, ultimately the purpose here is to use the local grid cell level regressions to gain insight into the economic costs of tropical cyclones in the Dominican Republic. In this regard one possibly needs to worry about aggregation bias, in that local heterogeneity and non-linearity may not aggregate themselves as a simple sum to a higher level (Blundell and Stoker 2005). In their study of the impact of tropical cyclones in the Caribbean using annual nightlights, Bertinelli and Strobl (2013) show that national level regressions substantially underestimate the local impact. This issue is investigated here by dividing the Dominican Republic into its 155 municipalities and redoing the analysis. More specifically, the dependent variable is defined as the log of the average nightlight intensity within municipalities, whereas the tropical cyclone destruction index is defined as the average of the nightlight weighted index. The weights for the latter are taken as the share of nightlight intensity of that cell within the municipality for the prior month, so as to avoid that weights are dependent of the tropical cyclone event in question. The resultant coefficients and their standard errors of this exercise are provided in the second column of Table 3. The results are qualitatively similar to the cell level regression, except that the 16th rather than 15th month is significant and, somewhat peculiarly, the 22nd month is now also significant in the aggregate specification. Importantly, and as was found by Bertinelli and Strobl (2013), the coefficients are generally substantially smaller in the aggregate results, suggesting that there may be aggregation bias.

5 Translating the Hurricane Impact into Monetary Values

It is informative to translate our quantitative impact into monetary values and we do so below.

5.1 Conversion from Nightlight to Monetary Values

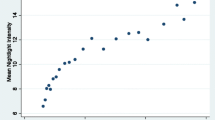
A basic assumption behind our analysis is that nightlight intensity at the pixel level is a reasonable proxy for local economic activity. To then put monetary values on the estimated impact of tropical cyclones we need to obtain a conversion factor. An obvious approach is to relate country level nightlight values to measures of national GDP. To this end quarterly series of national GDP are available for the Dominican Republic. We averaged the logged cell intensity values to aggregate quarterly country specific values, as well as normalized quarterly GDP by km2 area. A scatter plot of the area normalized quarterly GDP in millions of 2013 USD and average quarterly logged nightlights are depicted in Fig. 5. There is clearly a positive, albeit imperfect, correlation between the two variables. To quantify this relationship, we estimated the following:

$$\frac{{\text{GDP}}}{{\text{Area}}}_{r} = \beta \left( {\frac{1}{N}\sum\limits_{i = 1}^{N} {\log \left( {{\text{NIGHTLIGHT}}_{ir} } \right)} } \right) + e_{r}$$
(5)

where subscript r denotes a quarter-year time unit, subscript i denotes nightlight pixel i of all pixels i = 1,… N within the Dominican Republic, and e is an error term. We estimated Eq. 5 using the ordinary least squares (OLS) method with robust standard errors. The coefficient β was estimated to be 0.107 with a standard error of 0.003, and suggests a positive and highly significant relationship between quarterly logged aggregate nightlights and GDP (Table 4). To further demonstrate the link between quarterly GDP and nightlights we depict the actual and predicted quarterly series (Fig. 6), where the latter is generated using the product of logged nightlights and the estimated coefficient for each quarter. While there are some obvious outliers, overall the fitted series seems to capture the actual series reasonably well.

Fig. 5
figure 5

Quarterly GDP per km2 versus average log(Nightlights) in the Dominican Republic

Full size image
Table 4 Linear regression of national quarterly GDP on nightlight intensity in the Dominican Republic
Full size table
Fig. 6
figure 6

Predicted versus actual quarterly GDP per km2 in the Dominican Republic

Full size image

5.2 Monetary Impact of Hurricanes

We depict the implied losses in GDP for each storm in Table 5. Overall, the storms over our sample period produced on average a USD 1.1 billion fall in economic activity. Relative to the annual GDP at the time of each storm this translated into losses of around 3.62%. Losses were largest from Hurricane Georges, standing at over USD 14 billion, and at least 10 times as large as any other storm over our sample period. This storm also had the largest impact on the GDP at the time, estimated to have reduced it by around 50%. The rather high figure may suggest that our approach is less suitable for really damaging storms.

Table 5 Implied losses of hurricanes in the Dominican Republic
Full size table

6 Conclusion

This study used monthly nightlight composites in conjunction with a wind field model to estimate the impact of tropical cyclones on local economic activity in the Dominican Republic. The econometric results show that the negative impact lasts up to 15 months after a cyclone strike, with the largest effect observed 9 months after the storm strikes. The 19 damaging storms that occurred over the 22-year sample period resulted on average in a reduction in nightlight intensity of about 2.1%, whereas the most damaging storm, 1998 Hurricane Georges, caused brightness to reduce by 31%. Translating the reduction in nightlight intensity into monetary losses by relating it to quarterly GDP suggests that on average the storms reduced GDP by about USD 1.1 billion (4.5% of GDP 2000 and 1.5% of GDP 2016). Hurricane Georges caused a reduction in activity by about USD 14.7 billion (69.4% of GDP 1998 and 20% of GDP 2016) and more than five times the direct and indirect losses reported by CEPAL(1998). One of the weaknesses of our analysis is that by using nightlights we were not able to capture the direct impact on agriculture and the costs that impact would add.