Systemic Risks: A Homomorphic Approach on the Basis of Complexity Science

Abstract

Although the notion of systemic risk gained prominence with respect to financial systems, it is a generic term that refers to risks of increasing importance in many domains—risks that cannot be tackled by conventional techniques of risk management and governance. We build on a domain-overarching definition of systemic risks by highlighting crucial properties that distinguish them from conventional risks and plain disasters. References to typical examples from various domains are included. Common features of systemic risks in different domains—such as the role of agents and emergence phenomena, tipping and cascading, parameters indicating instability, and historicity—turn out to be more than noncommittal empirical observations. Rather these features can be related to fundamental theory for relatively simple and well-understood systems in physics and chemistry. A crucial mechanism is the breakdown of macroscopic patterns of whole systems due to feedback reinforcing actions of agents on the microlevel, where the reinforcement is triggered by boundary conditions moving beyond critical tipping points. Throughout the whole article, emphasis is placed on the role of complexity science as a basis for unifying the phenomena of systemic risks in widely different domains.

Introduction

The history of the last four decades has been a success story in terms of conventional risk management, which is well documented. Taking the example of Germany, the number of fatal accidents at work decreased from almost 5000 in 1960 to less than 400 in 2014, the number of traffic accidents from 22,000 in 1972 to 3700 in 2014, and the number of fatal heart attacks and strokes from 109 cases per 100,000 to 62 in the time period between 1992 and 2002 (Renn 2014). In addition, the number of chronic illnesses as well as fatal diseases from environmental pollution or accidents has steadily declined over the past three decades.

Conventional risks in terms of accidents and most illnesses have been successfully tamed, at least in core segments of fully industrialized societies (Rosa et al. 2014). In such situations, a fire, for example, may break out in a school, which could lead to the direct loss of lives and of the facility and to the interruption of the affected children’s education. In an age when fires are prevented from consuming entire cities, however, the impact of almost any blaze is likely to be limited. When fire breaks out at a school, safety equipment, sprinklers, and routine fire drills (some of the basic tools of conventional risk management) are likely to be effective. With appropriate safeguards in place, the odds are minimal that lives will be lost, or even that anyone will suffer serious physical harm. What is more, the economic cost is almost certain to be limited by insurance claims and contingency budgets, while disaster planning means that the lives of teachers and students are disrupted for probably no more than a few days. The main task with regards to conventional risks is to enable humankind as a whole to share the capacities for their management and governance that are in principle available.

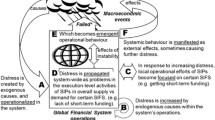
The picture becomes less favorable if we look at globally interconnected, nonlinear risks such as those posed, for example, by climate change or the present global financial system, and the closely related growing inequalities between rich and poor. Indeed, current societies are challenged by a number of pressing systemic risks. Some arise from global environmental change (Shi et al. 2010), in particular climate change (Bendito and Barrios 2016), others from social inequality (Milanovic 2016), from breakdown of infrastructures (Gheorghe et al. 2007; Fekete 2011), including financial systems (Reinhart and Rogoff 2009), or from threat to biological diversity (Polidoro et al. 2010). Related developments include new political transitions towards post-democratic regimes (Crouch 2004) and the emergence of post-factual tendencies that underestimate the value of plurality (Keyes 2004). In order to take account of this situation, especially with regard to natural hazard-induced as well as human-made disasters, the Organization for Economic Co-operation and Development (OECD) introduced the new category of “systemic risk” (OECD 2003). It is this category that has led Shi et al. (2017) to argue for global systemic risk management in view of future transboundary disasters.

A widely-used definition of a systemic risk was provided by Kaufman und Scott (2003). Although they defined systemic risks in the context of financial systems, their definition can be expanded to accommodate much broader systems, like the coupled climate-humankind system. “Systemic risk refers to the risk or probability of breakdowns in an entire system, as opposed to breakdowns in individual parts or components, and is evidenced by co-movements (correlation) among most or all parts” (Kaufman and Scott 2003, p. 372).

The Kaufman–Scott definition captures the starting point for the largest body of literature on systemic risks available so far: the one that deals with systemic risks in financial markets (Anand 2016). In this literature, two different threads can be distinguished: one dealing with the quantification of risks, and one with the causalities behind them.

The quantification of risk lies at the origins of both modern risk management and the scientific understanding of risk. Insurance would be impossible without it. It became possible with the development of probability theory and the discovery that often human preferences can be represented by utility indices (in standard practices of cost-benefit analysis, these indices are usually taken to correspond to amounts of money). On this basis, risk can be quantified as the expected value of utility given a probability distribution over possible outcomes.

Conventional risks are risks that at least in principle can be so quantified. The risk of fatal heart attacks and strokes in Germany in 1992, for example, can be quantified as an expected value of roughly 80,000 events, and progress in risk management can be quantified through an expected value of roughly 50,000 events 10 years later (Renn 2014). This way of quantifying risk presupposes two things. First, a well-defined event space with associated probabilities. In the case of those fatal events, the event space can be taken to be the set of natural numbers from 0 to the total population, where only numbers closed to the expected values will be assigned a nonzero probability. The second presupposition is the existence of sufficiently well-defined utility indices. In the present case, one can simply take the number of events as the relevant index.

Systemic risks in finance made both presuppositions questionable, while increasing the need for regulators and bank managers to quantify risks. Data are insufficient to produce reasonably sound probability estimates, and even a relevant event space is hard to define. As for utility indices, preferences differ between the different actors, including organizations and individuals. Moreover, the relevant preferences are neither stable nor complete, and perhaps not even always consistent.

Building on the seminal work by Artzner et al. (1999), considerable advances have been made with regard to the quantification of financial risks, although many open questions remain (Föllmer and Schied 2002; Alon and Schmeidler 2014; Zhang et al. 2014; Biagini et al. 2018). A good introductory overview is given by Gilboa et al. (2008). Although this aspect of the systemic risks challenge calls for much additional work, we will not address it in the present article.

We want to address the second topic found in the literature on systemic risks in finance: the quest for causal structures. Here, too, major advances have been made, mainly by using network approaches to contagion processes (Feinstein and El-Masri 2017; Amini and Minca 2016). Interestingly, this work has led to synergies with studies of systemic risks in critical infrastructures (Kröger 2008; Cassidy et al. 2016; Mureddu et al. 2016). Cross-fertilization across disciplines has also resulted from work on biodiversity in ecology (Haldane and May 2011), and more generally with the study of complex systems (Markose et al. 2012; Battiston et al. 2016).

Building on this line of research, we focus on the causal mechanisms involved in complex systems where networks of agents—be they molecules, organisms, people, or organizations—display a double dynamic: a large number of microinteractions and a small number of macroprocesses. The latter can result in periods of macroconfiguration stabilized by suitable external conditions. When these conditions change beyond a certain range, the macroconfiguration breaks down, and the overall dynamics can be shaped by the amplification of microevents until a new macroconfiguration has been reached. The main idea of the present article is that this kind of critical transition plays a key role in many, perhaps all, systemic risks. In other word, we suggest a homomorphism between important aspects of systemic risks in different domains.

Against this background, the Kaufman–Scott definition can be further improved. Thinking of a car as a system of parts, the total breakdown of a car would certainly not qualify as a systemic risk. On the other hand, the partial breakdown of the world’s finance system experienced in 2007 and the following years is a paradigmatic example of a systemic risk, although the system as a whole clearly did not break down.

Renn et al. (2017) have therefore suggested use of a more Wittgensteinian approach by specifying the properties that are associated with systemic risks without claiming to have a complete or mutually exhaustive list. The main thrust of systemic risks, however, is clear: systemic risk refers to the possibility of a catastrophic regime shift or even breakdown of a global system that involves many interacting elements that are poorly understood. This dimension of a large potential threat within a complex web of interacting elements is a key difference between systemic and conventional risks.

Renn et al. (2017) emphasize four major properties of systemic risks: they are (1) global in nature; (2) highly interconnected and intertwined leading to complex causal structures and dynamic evolutions; (3) nonlinear in the cause-effect relationships and often show unknown tipping points or tipping areas, and (4) stochastic in their effect structure. Systemic risks tend to be underestimated and do not attract the same amount of attention as catastrophic events. The main reason for this is that complex structures defy human intuition based on the assumption that causality is linked to proximity in time and space. But complexity implies that far-fetched and distant changes can have major impacts on the system under scrutiny. Another reason is that humans tend to learn by trial and error. Faced with nonlinear systems with tipping points/areas, people are encouraged to repeat their errors because the feedback is uncritical for a long time. If one trespasses the tipping point, however, the effect of error may be so dramatic that learning from crisis is either impossible or extremely costly. Furthermore, systemic risks touch upon the well-known common pool problem: each actor contributes only marginally to the systemic risk so there is no incentive to change one’s behavior (Renn 2011). Finally, every actor may win if he or she takes the free rider position and lets all the others invest in reducing the risk, since all will in the end share the benefits. So there are many reasons for systemic risks to be underestimated or, at least, undermanaged compared to conventional risks.

Another key characteristic that sets systemic risks apart from conventional risks is that their negative impacts (sometimes immediate and obvious, but often subtle and latent) have the potential to trigger severe ripple effects outside of the domain where the risk is located (OECD 2003). When a systemic risk becomes a calamity, the resulting ripple effects can cause a dramatic sequence of secondary and tertiary spin-off impacts (Kasperson et al. 2003). They may be felt in a wide range of systems seemingly well buffered from each other, like real estate and the health system, inflicting harm and damage in domains far beyond their own. Industrial sectors, for example, may suffer significant losses as a result of a systemic risk as we witnessed in the financial crisis in the aftermath of the Lehman Brothers collapse. Even fairly healthy financial institutions were negatively affected and, in the end, taxpayers had to pay the bill for poor institutional design and the reckless behavior of a few.

Another example is the BSE (Bovine Spongiform Encephalopathy) debacle in the United Kingdom, which not only affected the farming industry but also the animal feed industry, the national economy, public health procedures, and politics (Wynne and Dressel 2001). People refused to eat British beef, regardless of the tangible evidence showing little danger to their health or safety.

Systemic risks represent wicked problems as they are difficult to anticipate and identify, have no clear solutions, and are seemingly intractable, often plagued by chronic policy failures and intense disagreement (Nursimulu 2015). They can trigger unexpected large-scale changes of a system or imply uncontrollable large-scale threats to it (Helbing 2010) and may cause ripple effects beyond the domain in which the risks originally appear (Renn 2016). The consequences of failing to appreciate and manage the characteristics of complex global systems and problems can be immense (Helbing 2012).

The following paragraphs present an attempt to take advantage of insights from the natural sciences, notably physics and chemistry, about complex systems and their dynamics for studying the domain of large systemic risks that include complex interactions between human and natural systems that bridge ecological, social, natural, and cultural domains. The objective is to develop a conceptual, deductive approach to understand the generic fabrics of systemic risks. Such an understanding stems from the analysis of physical and chemical systems. These insights cannot be applied to societal processes one by one, but they reveal generic patterns and clusters that serve as homomorphic prototypes valid for many complex domains. The claim is not that the properties of physical systems can be literally transferred to social systems, but that complex structures and dynamics are characterized by typical patterns that manifest themselves in a multitude of contexts in the physical and social world. Similar to mathematical equations, they may be considered a priori true in the Kantian sense, yet it needs to be empirically proven whether they can be applied to different domains of reality.

Nonequilibrium Complexity

Systemic risks pertaining to systems of nature, technology, and society often manifest themselves as dynamic macroscopic phenomena that result from actions of agents, among each other and with their environment, on the microlevel in a complex system. In this context, we use the notion of agents in a most general perspective, ranging from atoms and molecules in physical and chemical systems up to humans in socioeconomic systems. Clearly, the possible interactions between such different agents vary widely, from simple and well-understood physicochemical interaction laws between molecules up to nonlocal, adaptive decisions and interactions including memory effects within and among human individuals. It goes without saying that such widely different interaction patterns preclude any general predictive theory for the system’s dynamic behavior and the associated systemic risks. Inherent properties of complexity limit their predictability and make them often counter-intuitive. Yet, and this is the primary message of this communication, some very fundamental patterns of dynamic behavior do not depend crucially on details of the agent’s interactions with the remarkable effect that systems, with very different types of agents, can show in terms of rather similar patterns of dynamic behavior. We refer to this phenomenon as homomorphism. This insight, together with using the instruments of complexity science, will be shown to support significantly the understanding and governance of systemic risks.

Complexity has many aspects and this is reflected by the many different branches and instruments of complexity science. In the context of systemic risks, we make use in particular of those typically associated with dynamic structure generation in open systems under strong external and/or internal perturbations. We refer to such situations as nonequilibrium with reference to the notion of equilibrium typically used in physical chemistry: that is, a state without any change of its macroscopic behavior over time in spite of rapid and active dynamic processes on the microlevel. They are characterized by tipping and cascading phenomena along with dynamic pattern formation. We use the term nonequilibrium complexity. Such processes have been studied in detail and depth in the natural sciences, notably physics and chemistry. Interestingly and most importantly, as already mentioned above, it can be shown that the principal patterns of behavior revealed there can be found across all domains, from biology to ecology up to socioeconomics. Thus, for the benefit of analyzing systemic risks in any domain, advantage can be taken of the detailed knowledge accumulated by studies of relatively simple systems in physics and chemistry, studies that would not be possible in more complex systems such as those of biology, ecology, or society. In the following paragraphs, we summarize some of these insights of nonequilibrium complexity relevant to systemic risks with the emphasis on generating awareness of their provenience and the benefit derived from recognizing this.

Some Common Features of Systemic Risks

A collection of empirical evidence associated with systemic risks in the framework of nonequilibrium complexity science reveals a fundamental homomorphism with respect to their basic structures across all domains, based essentially on universal strategies of information processing between the agents and the global system. This opens up a large body of empirical knowledge that forms the basis for their understanding and analysis.

Agents and Emergence

Dynamic structures, associated with systemic risks, are phenomena of emergence, typically appearing out of system instability. They are collective effects resulting from the elementary actions of the agents on the microlevel. So, they are only observable on the macroscopic level, not on the microlevel of the agents. In physicochemical systems, single molecules do not display the coherent patterns observable in flow or chemical reaction systems with a large number of molecules; in social systems single individuals do not show the patterns of mass phenomena and political mass radicalism frequently observed in situations with many human individuals. Identifying the microlevel of the agents for analysis of dynamic structure generation is a matter of intelligent choice. Any system will display a more or less complicated stratification over various levels of interactions, and so it turns out that the adequate choice of the microlevel is a matter of the theoretical or empirical information that is available. To illustrate, it is instructive to look at one of the most elementary and least stratified model system of dynamic structure generation in physics—the laser. The agents to consider are the atoms of the laser material and the photons of the light wave (Haken 1977). It is the nonlinear and originally localized feedback interaction between the atoms of the laser material and the photons of the light field that is responsible for the emergence processes stabilizing the macroscopic light wave. Information processing of the agents is affected by local statistical sampling from patterns that are able to spread over the whole system. The interactions between these agents are known from quantum-electrodynamics and so the analysis can be based on this theory, and thus a full understanding of the structure generation mechanisms can be obtained. The importance of this analysis goes much beyond this particular physical device. It constitutes a metaphorical interpretation of these effects as a learning and adapting behavior of the agents in principle. The laser represents a model system that is rather informative and instructive for dynamic structure generation in general and for associated systemic risks in a wide variety of domains.

For autocatalytic chemical systems, a typical model system for dynamic structure generation in chemistry, such elementary information is not available in the general case. The analysis of structure generation is thus rather based on the mesolevel of empirical gross reactions for selected molecular species and on their time evolution in terms of associated rate equations. Strong nonlinear effects as provided by the autocatalytic reactions with the associated feedback effects are a necessary condition for structure generation in these systems (Prigogine and Lefever 1968). By mechanisms in principle analogous to those in a laser, initial and localized patterns such as stripes and rings of alternating color spread over the whole system by information processing, and lead to a global pattern in the system.

It is rewarding to apply these fundamental insights about the role of agents and their particular types of interactions in dynamic structure generation, which are gained by analyzing relatively simple physical and chemical systems, to the much more complicated socioeconomic systems. Here, agents may be organizations, human individuals, social groups, and at whatever level for which proper information is available or sensible modeling can be applied. Besides structure generation by external control, such as in the systems of physics and chemistry addressed above, there are many examples of self-organized emergence in social systems even without external impact. Markets can be seen as emerging from the individual actions of traders, business organizations as emerging from the activities of their owners and employees, in addition to the actions of groups such as legislators, lawyers, advertisers, and suppliers. The choice of the agents is not separable from the definition of the interactions between them and their environment. Although the agent’s interactions are clearly entirely different from those physicochemical systems mentioned above, basic mechanisms of dynamic structure generation and pattern formation are pretty much analogous. In socioeconomic systems, similar to the physicochemical model systems, strong and reinforcing interactions generate feedback loops and circular causality between the macroscopic structures and the actions of the agents. To paraphrase Clifford Geertz (1973, p. 5), we are animals suspended in webs of meaning that we ourselves have spun. Agents learn from and adapt to the environment created by themselves. It is frequently the interaction of human individuals as agents with a field of information derived from the media, public opinion, or other sources that stabilizes the structures in socioeconomic systems. In this way, local patterns are again able to spread over the whole system by appropriate information distribution.

Tipping and Cascading

The object of study in systemic risks is invariably a system along with its boundaries. Boundary conditions may keep the system in a stable macroscopic state with continuous microdynamic change. But when the boundary conditions exceed threshold values they can drive the system into a regime of instability out of which new dynamic structures may suddenly emerge when appropriate internal conditions prevail. This phenomenon is referred to as tipping or as a bifurcation.

In nonequilibrium thermodynamics as the appropriate theory of molecular systems, it is shown that in such situations, unlike situations in equilibrium or close to it, driving forces and resulting effects have a nonlinear relationship to each other. A potential function then no longer exists (Prigogine 1980). As a consequence, small and random fluctuations that are normally inconsequential may trigger a dramatic change in behavior, referred to as a phase transition. Molecular interactions like information processing in a network spread the new state in a cascading process over the whole system. A well-known example from chemistry is the local emergence and subsequent spatial cascading of a dynamical chemical structure, which creates a regular chemical space-time pattern (Gray and Scott 1990). Similar patterns are found in the study of pandemics and the spread of disease (Chen et al. 2017). Further examples are failures of infrastructure, such as the electrical grid (Koonce et al. 2008), the breakdown of a financial system (Hurd et al. 2016), or such phenomena as public opinion formation or economic innovations (Weidlich 2000).

Phenomenologically, an approach to such a tipping point becomes noticeable by an amplification of fluctuations. These fluctuations are of a random nature, which makes the future of the system unpredictable in detail, although the system normally can choose only out of a few macroscopic patterns. As a consequence of nonlinearity, the average dynamical behavior of the system in such situations no longer corresponds to the average of the individual activities of its agents. Rather, a new structure may originate from the amplification of one particular microscopic fluctuation at the right moment and under the right conditions. A momentary individual activity can thus determine the dynamic future of the macroscopic system. These effects make intuitive predictions of system behavior rather questionable. Tipping and cascading phenomena can be and have been studied in detail in some prototype systems of physics and chemistry based on rigorous theory. In more complex domains, for example, socioeconomics, we observe essentially the same phenomena, a homomorphism, although a detailed theoretical analysis is still missing. But recognizing the analogies paves the way for an adequate ordering of the empirical observations during dynamic pattern formation across domains.

Parameters Indicating Instability

An immediate, practically relevant consequence of transferring established knowledge from physics and chemistry to more complex domains is the recognition that parameters exist that indicate instability even in those domains where there is no theory to directly provide them. As theoretically established in physics and chemistry, the dynamic structure generation in such unstable regimes is initiated by selection processes on the microlevel. In the course of elementary fluctuations, the system tests its various modes of dynamic behavior, which may be considered as a population of macroscopic patterns. Hierarchies of time scales and strengths of interaction during the elementary dynamics are responsible for a selection process that stabilizes the new dynamic structures. The same principles identified by rigorous theory in a laser, as well as in flow or chemical pattern formation, are effective in other domains.

In socioeconomic systems, such effects lead to the formation of a stratification and topology of the system with widely autonomous and interacting substructures such as families, organizations, ethnic subgroups, and the like. As a result of these selection processes only few modes of behavior win the competition and become visible macroscopically. They can be described in terms of so-called order parameters, that is, the relevant macroscopic variables for representing the dynamics of a system. This results in a drastic reduction of complexity of the dynamics close to tipping points as compared to the chaos on the microlevel. In this sense, we witness the emergence of order out of chaos (Prigogine and Stengers 1984).

It is therefore promising to look for simple macroscopic parameters that describe the approach to instabilities. Generally, such parameters are nondimensional in nature, and balance enhancing and hindering effects by a suitable combination of external and internal quantities. Examples from physics and chemistry are the Reynolds-number or Rayleigh-number in flow systems and the ratio of pumping energy to light loss in a laser, where these parameters are easily derived from theory. Similar parameters have been identified empirically in socioeconomic systems, such as the ratio of local uprisings to police interventions in the forefront of revolutions (Schröter et al. 2014), the size of the economy to the amount of private debt in the onset of a financial crisis (Minsky 2008), or the index of conflict-related news before the outbreak of war (Chadefaux 2014). In cascading processes, the relation of time scales for propagation and adaption are the crucial parameters that announce instability such as that of chemical reaction to diffusion rates in chemical pattern formation. The elementary selection processes on the microlevel are ultimately responsible for a hierarchy in macroscopic time scales. For example, the universally observable phenomenon of a slow approach to an instability regime is followed by a sudden phase transition with systemic risks in widely differing domains. Typical examples are the sudden tipping phenomena of ecosystems or social upheavals after a long time of enduring stress.

Historicity

The dynamics of the system has a past and a future about which some general statements can be made. The approach to instability is frequently followed by a phase transition in the form of a bifurcation, that is, a sudden change of system behavior without external design. Even in the particularly simple flow system of the Bénard convection, two different structures, for example left and right turning convection cells, become available at a phase transition from the unstructured state close to equilibrium (Bénard 1900). The system then chooses at random one possible stable branch of the dynamics and thereafter proceeds in a deterministic evolution until a new regime of instability is reached. Here again a phase transition with the system making a choice may take place. The overall dynamics is thus determined by the fact that, depending on increasing temperature difference as impact over the boundaries in the Bénard convection, the system chooses stable states by sudden phenomena of self-organization, with deterministic and smooth periods of development in between, and thereby follows a particular path. The behavior of the system thus exhibits an individual history, consisting of an interplay between chance and determinism, and the final flow structure may be quite complicated.

Analogous patterns are visible during structure generation in socioeconomic systems, be it traffic congestion, political revolution, technological innovation, or urban settlements. For example, the adoption of one of a pair of alternative technologies within a society or the market success of a particular company can be greatly influenced by minor contingencies about who chooses which technology or which company at an early stage. This pattern clearly is reminiscent of the butterfly effect usually observed in chaotic systems. This early choice can determine the further fate of the system and explains the remarkable success of one technology or one company over others when the winner takes all. Such a path dependence excludes any purely local and momentary origins of systemic risks, for instance of a stock market crash (Sornette 2003) or the recent refugee crisis (Lucas 2016). It is indispensable to study the history of the system if one aims at an adequate understanding of the dynamics of the system. Rather advanced mathematical methods of time series data analysis are available to discover early warning signals.

Eventually, the system will be drawn to a particular attractor as its ultimate dynamic domain. This end result may be simply a fixed state, but it may also be of a more complicated nature, such as periodic oscillation between fixed states or even chaos, depending on the system’s parameters and history. If more than one attractor is present each one will be approached by the dynamics of the system from its individual basin of attraction as the initial condition, such as a water divide establishes two basins of attraction deciding to which side the rainwater will flow. It is crucial to analyze attractors, since they are the basis for suitable mitigation measures of systemic risks.

Quantitative Modeling

As shown above, there is strong empirical evidence of homomorphism with respect to fundamental dynamic patterns associated with systemic risks. Yet, more support and instruments for practical exploitation on the basis of complexity science can be provided by turning to quantitative modeling.

This homomorphism is mirrored in the mathematical theory of dynamic systems. It is shown there that a class of rather different mathematical models tailored to rather different systems essentially reproduces the same patterns of dynamic behavior, notably universal types of attractors. Contrary to many standard problems of physics and chemistry, an individual mathematical model in complexity theory is just the beginning of an understanding; its evaluation over time, be it in the form of an iterated function or a differential equation, produces unforeseen dynamical structures. Well- defined rules, often surprisingly simple, when applied in active repetition without any intentionality over and over again, lead to an evolution in time showing a remarkable creativity and richness of structures. This result is not to be expected from the simple underlying model specifying the rules. These structures in terms of the associated attractors can be visualized in so-called bifurcation diagrams that are specific in detail but universal in the basic patterns associated with the dynamical behavior of complex systems, up to amazing universalities even in the range of chaos.

The time behavior of a complex system, as described by such deterministic equations, is not entirely unpredictable. As different as the models may be for one system or another, the attractors can be predicted quite well. Although in a case where there is more than one attractor, the particular choice the system takes will be stochastic and thus unpredictable. Even in the case of chaos, the attractor of the system, referred to as a strange attractor and representing the general framework of long-term system behavior, is predictable from a model, even though the particular choice of the dynamics along this attractor over time is sensibly dependent on the initial conditions and thus clearly unpredictable over sufficiently long times. A prediction of short run evolution is possible even in a chaotic system, contrary to any long-time development, as is well known from domains such as weather forecasting.

More frequently than not a mathematical model is not available. But if data over time can be acquired, these can be analyzed by appropriate mathematical methods to extract patterns of dynamic behavior that, in favorable cases, will allow some prediction to be made about the future behavior of the system. This predictive ability includes the occurrence of systemic risks. Examples are known from challenges as different as stock market analyses, weather forecasts, heart attacks warnings, and many other cases.

More specific information about the rules governing the emergence of dynamic structures and systemic risks can be introduced in quantitative models through methods of computer simulation. In such simulations the rules on the microlevel can be tailored to the information available about a system. In particular, the stochastic nature of such data, often responsible for the empirically observed unpredictability, notably in socioeconomic systems, may be taken into consideration.

In physical chemistry, the emerging system state—the relationship between the microlevel, the molecules, and the macrolevel—is quantitatively accessible through a particular type of computer simulations within the framework of statistical mechanics (Lucas 2007). In molecular dynamics the dynamics of molecules is studied on the basis of Newton’s equations of motion and appropriate interaction models. The equilibrium attractors of dynamical properties are found in the limit of long runs by time averaging. In a pioneering paper, Alder and Wainwright (1957) demonstrated that a simulation of the dynamics of a relatively small number of molecules, modeled crudely as hard spheres, explained the emergence of solid order in a fluid system of randomly distributed molecules under suitable external and internal conditions. Although no condensation phenomena could be found in a hard sphere system, it was shown later that such a phase transition appeared as soon as attractive forces were added to the model of intermolecular interactions. When a realistic model of the interactions, as accessible today from quantum mechanics, was introduced, predictions in good agreement with experiments could be achieved for the equilibrium behavior of fluid systems (Luckas and Lucas 1989). These early results in physical chemistry indicate the power of such simulation approaches. They draw attention to the phenomenon common to complex systems that basic properties of the system’s dynamics can be studied by rather crude models of the interaction rules of the agents.

In more general systems, notably those of socioeconomics, analogous types of quantitative modeling have been established. The phenomena associated with systemic risks invariably emerge from agent actions that can be studied and modeled on various levels of depth and empirical trustworthiness, depending on the system under study. As a consequence, there is, beyond qualitative pattern recognition and understanding, a quantitative access to their analysis by introducing these models into computer simulations or mathematical equations within the framework of complexity science. Various approaches in this category have been developed. Most prominent are agent-based computer simulation (Railsback and Grimm 2011) and mathematical formulations in terms of master equations (Weidlich 2000). These are similar in spirit, although differing in detail, to computer simulation of molecular systems, and much has been learnt from these roots.

In multiagent simulation formalisms, based on the direct pair and higher order interactions between agents and their environment, it can be demonstrated (as found in the physicochemical systems) that rather simple elementary rules for the agents may result in the emergence of a rather complex dynamic behavior of the system as a whole. But the agents in such systems differ fundamentally from molecules. They have many more internal properties, that is modes of potential behavior, and the excitation of these degrees of freedom depends on the situation of all the subsystems. Care must be taken to account properly for the modes of possible actions in a given system and to model the actions properly, based on empirical analysis. In particular, the actions are not only direct and instantaneous as in molecular systems but they also may be intermediate, antisymmetric, and associated with subjective wishes and memories. In physicochemical systems, wholeness patterns simply emerge from the undirected and short-range interactions of atoms and molecules; in socioeconomic systems, however, patterns emerge by intentional activities of human individuals in an environment that humans themselves create. By bottom-up effects the agents’ actions in the form of cultural and economic activities generate a collective field. This is a sociocultural field that acts back top-down upon the agents in an ordering manner by influencing their actions. Stochastic effects that reflect the uncertainties of the actual agent behavior may, among other strategies, be included by adding random noise to their action rules.

Clearly, any tight analogy to physics and chemistry systems is here restricted to the method of analysis and the emergence of the typical phenomena associated with dynamic systems discussed earlier. In detail, of course, there is a richness of behavior in socioeconomic systems far beyond what can be found in the relatively simple systems in physics and chemistry. The analogies revealed through insights form the physical world can, first, act as a heuristic tool to look for similar phenomena in the social world, and, second, to provide the basis for exploring functional or even causal properties that may lead to further implications that are eligible for statistical analysis of data sets.

An illustration of agent-based computer simulation studies that is still close to molecular dynamics in physical chemistry is the analysis of crowd disasters during mass events (Moussaid et al. 2011). The goal of such studies is to clarify the cause of such disasters and then to look for governance strategies to improve crowd safety. The dynamics of crowd behavior is complex and often counterintuitive. A systemic failure is usually not the result of one single event on the microlevel of the individuals. Instead, it is the interaction between many events that cause a situation to get out of control. Computer simulations are able to shed light on the crucial and generalizable phenomena and behavioral patterns of human agents responsible for the emergence of disasters in mass events. Crowded situations, where instinctive physical interactions dominate over intentional movements, give rise to global breakdowns of coordination, and cause strongly fluctuating and uncontrollable patterns of motion to occur (Helbing et al. 2015). Whereas simple proportionalities exist between crowd density and crowd flow in uncritical situations, this assumption fails at crowd densities passing a critical threshold. In such cases, fatalities may result from a phenomenon called crowd turbulence, notably close to geometrically sensitive situations (Hoogendoorn and Daamen 2005). The occurrence of crowd turbulence can be understood and reproduced in computer simulations by means of force-based models in combination with Newton’s equations of motion to describe the microlevel dynamics. The most important lesson learned with respect to governance is to stay away from the threshold of local density. The problem is that local densities are hard to measure without a proper monitoring system, which is not available at many mass events. Existing technologies, based on video, WiFi, GPS, and mobile tracking, do offer useful monitoring systems that allow for real-time measurements of density levels and predictions of future crowd movements. By a combination of computer simulations, real time monitoring systems, and complexity science, important progress in the governance of systemic risks during mass events has been achieved (Wirz et al. 2013; Ferscha 2016).

In the master equation formalism, the microlevel dynamics being defined by considerations, decisions, and actions of individuals is modeled by probabilistic elementary steps in which the individuals perform specific actions, thereby changing their properties and thus the macroconfiguration as a whole, referred to as the socio-configuration. Particular transitions may or may not happen, guided by decision and action generating motivations, which are quantified by a priori undetermined parameters. While this is analogous to the procedure in agent-based simulation, different use is made of the elementary steps. Balancing in- and outgoing probabilities leads to the master equation, a differential equation for the probability function of the social configuration. Long time attractors are found by suitable mean value operations.

As an illustrative example of the master equation formalism, we consider dynamic structure generation in the migration of interacting populations (Weidlich and Haag 1980). Modeling this dynamic sheds light on and supports understanding of the emergence and evolution of parallel societies as a major systemic risk in modern societies. The agents in the migration phenomenon are the n individuals of the system. This may be a country or a city with C different and distinguishable areas i, such as regions of a country or quarters of a city. The analytical goal is to scrutinize the conditions under which an original social configuration, for example, a relatively homogeneous distribution of individuals over all areas in the system, may become unstable and perform a transition to a nonhomogeneous distribution, such as the stable formation of ghettos or the rhythmic oscillation of otherwise inhomogeneous distributions. Migration of interacting populations and its effect on the population distribution in a system is the result of economic, social, and in particular multicultural interactions between the individuals. External impacts may be political regulations, which set forth rules for the living together of individuals in the society, or also the informational flow into the system from other societies, where migration phenomena have been demonstrated to be either advantageous or harmful to those individuals who have decided to migrate. Internal effects may be the advent of strong cultural or ethnic feelings leading to agglomeration or segregation movements. A critical combination of external and internal random fluctuations in a selection process may drive the system out of one societal configuration into another one. An elementary action is the transition of one individual from region i to region j, which changes the social configuration in a particular way. The associated transition probability is formulated in terms of the attractiveness of such a transition as felt by the considered individual. In the absence of any deterministic theory for the dynamics on the elementary level, the transition probability has to be formulated empirically, but so doing must make use of the insights that nonequilibrium complexity provides. Solving the master equation shows that starting from a homogeneous distribution and turning on external and internal impacts in terms of the appropriate nondimensional parameters, the system approaches a particular regime of instability from where a sudden phase transition to a particular new distribution may occur on exceeding a threshold. Out of this distribution further thresholds that induce additional phase transitions to changing distributions will appear. Over long periods, the process of dynamic structure generation will yield to an attractor, calculable from the master equation, which may be a homogeneous distribution of the individuals over the areas, a stable ghetto structure, or also an oscillation between these states.

Many studies of computer simulations in the social sciences are available in the literature. Some key references with extensive further citations include Weidlich (2000), Gilbert (2007), and Helbing (2015). These works are rooted in the established methods of such studies in physics and chemistry, and reveal analogous or even homomorphic fundamental patterns of behavior by appropriate applications of statistical methods. But, in detail, they address a much more comprehensive and complex richness of patterns, which makes those patterns much more difficult to interpret. Since fundamental interaction laws, contrary to the systems of physics and chemistry, are not available from independent theories, they must be parametrized. As a consequence, the final outcome of such studies is, again contrary to the systems of physics and chemistry, not a prediction of the future behavior of the system but rather a study of scenarios that describe what may happen under particular conditions. These scenarios are not only thought experiments of what one could imagine, but rather constitute consistent and coherent simulations of further developments of complex and dynamic systems. These possible visions occur within a range of potential “futures” that depend on collective human actions as well as unforeseen changes in context conditions.

What Can Be Learned from Nonequilibrium Complexity?

Due to the much more complicated interactions that take place during systemic risk events, as compared to those in physics and chemistry, any benefit obtained from a knowledge transfer from these sciences to more general systems has occasionally been questioned. Clearly, the architecture of the systems relevant to systemic risk analysis, in particular socioeconomic systems, is much more complex than in the molecular systems of physics and chemistry. The elementary constituents, that is the human individuals of a society, form a vertical, hierarchical stratification in terms of families, groups, social organizations, firms, nations, and so on. These subpopulations overlap and generate a multitude of horizontal and diagonal interactions. An analogous vertical hierarchy is also present in molecular systems in principle, such as elementary particles that form nuclei, which combine with electrons to produce atoms, these different atoms then forming molecules, crystals, fluids, planets, and so on. Clearly the horizontal interactions in socioeconomic systems are much more complex. A further feature of human societies that makes them unique is that the agents, human individuals, can recognize emergent phenomena and therefore respond to them. The individual human units from which societies are formed vary greatly in their capabilities, desires, needs, and knowledge, in contrast to typical systems of physics and chemistry that are composed of similar or identical units, for example, molecules. For these reasons among others, while models of complexity developed for the understanding of natural systems can illuminate and guide the analysis of social systems, it is still impossible to apply them directly to social phenomena.

Is there anything that can be learned for analyzing systemic risks in such complex socioeconomic systems in the framework of nonequilibrium complexity as developed in the natural sciences? The physicochemical systems from which this detailed knowledge about nonequilibrium complexity has been generated by rigorous physical-mathematical methods are special cases. A wealth of empirical evidence, however, reveals strong analogies between the dynamic structures in these relatively simple systems and those much more complex systems in nature, technology, and society that are relevant in systemic risk analysis. These analogies are deeply rooted in the widely universal laws for collective dynamics, in spite of the rather differing rules between the agents, in systems that otherwise do not show any similarity. The appearance of these analogies has been traced back in physicochemical systems to ordering processes on time scales in which the elementary dynamics takes place. They are also reproduced in the mathematical theory of dynamic systems. Taking them into consideration significantly supports the understanding and analysis of systemic risks in any domain.

The detailed study of physicochemical systems made it clear that, although the global situation and evolution of a system is the result of very many microactions on the part of the elementary constituents, these are not fully free in their actions but are guided and coordinated by the global field generated by them, of whatever nature this may be. This cyclical relation creates and sustains such macroscopic dynamic phenomena as collective intelligence, ad hoc network formation, adaptiveness, natural and assisted self-organization, flexibility, resilience, and robustness with respect to local requirements and temporary failures. The overall behavior of the system is the result of a huge number of somehow coordinated decisions made every moment by many individual entities. Further, nonequilibrium complexity indicates the nature of phenomena that are to be expected in dynamic evolution. An observer must be alert to different macroscopic time scales: while the system may evolve slowly and hardly noticeably under the continuous influence of some exogenous impact, there may at one moment appear a sudden tipping, a harmful disaster, of unpredictable consequences. This provides further motivation to look for characteristic parameters that indicate instability regions, which will announce themselves empirically by irregularities, as discovered, for example, by a time series analysis. Finally, historical insight into a system should be valued, since the path the system takes cannot be understood without an historical perspective. In this way, nonequilibrium complexity provides a mental framework for ordering the analysis and helps to systematize the empirical considerations of systemic risks in socioeconomic systems. It appears that more can be done on this basis qualitatively than just to identify spots of instability and stay away from them, muddle through, and keep one’s eyes wide open (Münchau 2017).

In addition to this qualitative structuring of empirical evidence, more quantitative and useful insight may be obtained. Although significant alterations have to be applied to the computer simulation methods of molecular physics, the basic insights to be gained are essentially the same in both worlds. In the applications to physics and chemistry, computer simulations in their early stages have often been criticized, notably by experimentalists and practitioners, as artificial and essentially useless because they were unable to generate practically applicable results for real systems. This was true in the sense that no reliable information about the intermolecular interactions was available. While this deficiency has improved, it is still true that predictions from computer simulations do not normally reach the accuracy required for practical application in real systems, although they have often been able to fathom fundamental effects in areas difficult or even dangerous to probe experimentally. From the very beginning of these methods, it was clear that their essential, unquestionable, and unbeatable contribution was to a different field—the test and development of theories. By applying the same model for intermolecular interactions in a statistical theory and in simulations, it was possible to gain insight into, verify, or falsify a theory that linked the level of molecules with macroscopic behavior. The results of the theory were tested against those of computer simulations, which were then considered as essentially correct pseudo-experimental data. Alternatively, when experimental data of real systems were available, contrasting them with results of computer simulations allowed the testing of models for the interaction laws between the molecules and thus helped fathom the microscopic world. By such means, computer simulations in physics and chemistry made major contributions to the development of adequate theories (Hoheisel and Lucas 1984).

This experience has been transferred fruitfully to socioeconomic studies. The value of computer simulations in this domain is to generate a virtual laboratory in which knowledge about fundamental social mechanisms can be collected. It is thus possible to carry out experiments on artificial social systems that would be quite impossible or unethical to perform on human population. Assumptions about the behavior of social systems may be tested for plausibility and processes of emergence as well as historicity may be studied. A model can be run on a computer that allows researchers to study the behavior of a system under controlled conditions. The results that are gained may be, among other insights, a source of inspiration to evaluate possibly successful or unsuccessful governance strategies to deal with systemic risks.

Because systemic risks are phenomena of emergence out of unstable situations, a crucial question related to governance is how the associated approach to instability can be avoided or how the resulting dynamics can be nudged to move in a desired direction. This requires an intervention into system conditions. Quantitative simulations are able to shed light on outcomes of such measures. The behavior of complex systems is frequently determined by an interplay of internal properties with external impacts, although cases in which only one type of impact dominates are also known. The external impacts may be supervised by creating new boundary conditions in the form of regulatory top-down measures. But when the interactions between the agents are strong and reinforcing, as practically is often the case, the internal self-organization of the system will dominate external effects. Then an intervention into the interactions between the agents in the system locally and specifically, that is by bottom-up and decentralized measures, may be more adequate, while an unqualified top-down regulation may even be counter effective. In practical cases a combination of both approaches will frequently recommend itself. Then top-down governance may be one of the many inputs to actors in such situations. Such governance may intervene in the process of self-organization from the bottom up. If data are available, these inputs may be used to parametrize a model and thus generate an instrument of prediction.

Last but by no means least, computer simulations require the researcher to think through basic assumptions very clearly in order to create a useful simulation model. Every relationship to be modeled has to be specified exactly. Every parameter has to be given a reasonable value, for otherwise it will be impossible to run a meaningful simulation. This mental discipline may be a significant contribution to designing well-understood models of social dynamics far beyond the usual perspectives of purely empirical approaches.

Conclusion

Until this day, we lack an adequate understanding of the structure and dynamics of systemic risks. The lack of a well-defined event space and sufficiently defined preferences impedes the application of conventional risk assessment methods, based on the combination of probability distributions and utility functions. This raises significant empirical, mathematical, and logical issues (Jaeger 2016), but as mentioned in the introduction, with this article we did not want to address the important and thorny issue of preference formation in the face of systemic risks. The relevant preferences will need to transcend national interests without negating them. How this can be achieved is one of the great open questions of our times. What our inquiry into causal mechanisms involved in systemic risks does show, however, is that a framework where a single idealized agent optimizes the expected value of actions with uncertain outcomes will be insufficient to tackle systemic risks.

The focus should rather be on multiagent models that link the microlevel to the macrolevel and include emerging properties, since each agent is linked to other agents by multiple feedback loops. Experiences from the physical and chemical sciences can be used as heuristic tools for building such models and filling them with substantive empirical data. The challenge will be to improve our modeling capability to include intentional behavior in these models, considering large degrees of freedom and variability. In addition, systemic risk evolves dynamically and produces behavioral changes over time in a historic time dependency. It is still unclear how much of these dynamics is idiosyncratic and how much generalizable. The concepts that were laid out in this article may provide guidelines for collecting empirical data and constructing complex multiagent models in an effort to develop a more profound analysis and to test governance strategies by different agents in different domains.

Responding adequately to global systemic risks is a challenge for a world society where national interests, different cultures, and lack of adequate concepts conflict with the need to find common answers to global challenges. Governance of systemic risks requires strategies that address the complexity, scientific uncertainty, and sociopolitical ambiguity of the relationships underlying them. However, national as well as international attempts to address systemic risks have not used much of what has been accomplished in complexity science over the last two decades (Bloesch et al. 2015). In the end, risk management and communication need to address key properties of systemic risks that we have outlined, and develop appropriate instruments and institutions to deal with global, interconnected, stochastic, and nonlinear risks.

It would be naïve to assume that such instruments and institutions could simply be defined and then implemented in the present historical situation, where globalization raises unprecedented challenges (Lederer and Müller 2005). Rather our analysis of systemic risks leads to the following hard question: how is the risk paradox (Renn 2014)—the increasing difficulty of societies to reach a reasonable assessment of the risks they face—connected to the globalization paradox (Rodrik 2011)—the increasing difficulty of humankind to shape economic globalization in a sustainable way? Answering this question is likely to require decades of inquiry, involving researchers and practitioners of many disciplines and professions. By moving beyond the study of conventional risks and investigating with a creative mind the systemic risks of disasters in the environmental, financial, and other domains, the risk research community can play a vital role in this effort.