1 Introduction

Resource allocation is a common practice in disaster prevention, mitigation, and relief, and it often plays an extremely important role in determining the performance of these activities (IPCC 2012; World Bank 2014; UNISDR 2015). Given limited resources, what is the best allocation scheme in order to achieve the best performance of disaster reduction and risk governance (DRRG)? This is often a difficult task because DRRG usually involves multiple stakeholders who may have conflicting interests. Each stakeholder mainly focuses on maximizing their own benefits and minimizing their losses. For example, in the case of agriculture risk governance, local governments may want use funds to reinforce relevant infrastructures for disaster prevention, farmers may prefer direct financial support for disaster relief, and insurance companies would like subsidies to share risks. Therefore a reasonable trade-off has to be made when determining a resource allocation scheme. Because there are often many reasonable trade-off allocation schemes, the question is: how can decision-makers efficiently decide on a certain allocation scheme? How to optimize resource allocation in DRRG has long been studied. Most existing studies mainly focus on those aspects that are directly related to disaster risks, and choosing a proper optimization methodology is largely treated as a minor issue. For example, cost-benefit analysis has long dominated studies of resource allocation in DRRG (Jonkman et al. 2004; Mechler 2005; Rose et al. 2007; Li 2012; Kull et al. 2013; Liel and Deierlein 2013), and many recent advances in optimization theory are rarely introduced or attempted. Nowadays it is widely acknowledged that DRRG is a multidisciplinary challenge and demands a comprehensive integration of advances not only in disaster risk science but also in many other research domains, such as complex systems science and optimization theory (OECD 2011; Ball 2012; Helbing 2013). Involving multiple stakeholders in DRRG implies that resource allocation in DRRG is a multiobjective optimization problem (MOOP). This article introduces a newly developed MOOP methodology into resource allocation optimization in DRRG.

In the community of optimization research, the most important concept in MOOP is the Pareto front, which originates from the concept of “Pareto efficiency” proposed by Vilfredo Pareto, an Italian engineer and economist in the late nineteenth and early twentieth centuries, to study economic efficiency and income distribution (Barr 2004). In economics, given an initial allocation of goods among a set of individuals, a change to a different allocation that makes at least one individual better off without making any other individual worse off is called a Pareto improvement. An allocation is defined as “Pareto efficient” or “Pareto optimal” when no further Pareto improvements can be made. In general MOOPs, a solution is defined as a Pareto-optimal solution if there exists no other solution that is better in at least one objective and is not worse in all other objectives (Sawaragi et al. 1985; Steuer 1986). The projection of a Pareto-optimal solution in the objective space is called a Pareto point. All Pareto points, that is, the projections of all Pareto-optimal solutions, compose the complete Pareto front of an MOOP. Resolving a MOOP usually requires calculation of the Pareto front.

A long history of research supports the development of methods used to resolve various MOOPs. Basically, most methods can be classified into three categories: aggregate objective function-based (AOF) methods (Das and Dennis 1998; Figueira et al. 2005; Messac et al. 2003), constrained objective function-based (COF) methods (Stadler and Dauer 1992; Marler and Arora 2004; Figueira et al. 2005), and Pareto-compliant ranking-based (PCR) methods (Srinivas and Deb 1994; Knowles and Corne 2000; Van Veldhuizen and Lamont 2000; Deb 2002; Jones et al. 2002; Lei and Shi 2004; Konak et al. 2006). Most AOF methods originate from those methods that are proposed for single-objective optimization problems (SOOPs)—an intuitive approach usually is used to extend such single-objective methods to MOOPs by simply constructing a single aggregate objective function (AOF) that combines all of the objectives. The COF methods are also based on SOOPs because, in a COF method, only one single objective is optimized while all other objectives are treated as extra constraints. The PCR methods, by favoring nondominated solutions and employing population-based evolutionary approaches (such as a genetic algorithm, particle swarm optimization, and ant colony optimization), generate and operate on a pool of candidate solutions, and therefore are capable of identifying multiple Pareto optimal candidate solutions. Because of these features, PCR methods are currently very popular in the study of MOOPs (Srinivas and Deb 1994; Knowles and Corne 2000; Van Veldhuizen and Lamont 2000; Deb 2002; Jones et al. 2002; Lei and Shi 2004; Konak et al. 2006).

Most existing methods only focus on finding an approximation of the Pareto front (Das and Dennis 1998; Messac et al. 2003; Figueira et al. 2005; Craft et al. 2006; Erfani and Utyuzhnikov 2011), and it has rarely been discussed how to guarantee, theoretically and practicably, the finding of complete Pareto front. In particular, as pointed out in Figueira et al. (2005), very few results are available on the quality of the approximation of the Pareto front for discrete MOOPs. Figure 1 gives a simple illustration of a complete Pareto front and its approximation. In Fig. 1, two conflicting objectives, representing the interests of two stakeholders, need to be maximized simultaneously. Squares and solid lines compose the complete Pareto front, circles and dash-and-dot lines give an approximation, and triangles and dash lines another approximation. As illustrated in Fig. 1, there is often a difference between the complete Pareto front and an approximation. The difference is usually uncertain to decision-makers. In other words, if an approximation of the Pareto front is provided, decision-makers will have no idea whether there exists any other Pareto-optimal solution (for example, in Fig. 1, Approximation 2 misses out by one Pareto point, which is probably the best tradeoff between two objectives), or even whether a provided solution associated with a point on the approximated Pareto front is really Pareto optimal (for instance, in Fig. 1, Approximation 1 actually has 4 false Pareto points). Therefore, using an approximation of a Pareto front implies: (1) some solutions most preferable by decision-makers might be actually missed out; and (2) argument might occur in the decision-making process, because different stakeholders as decision-makers could choose different approximation methods. Obviously, if we can calculate the complete Pareto front rather than approximating it, then decision-makers will be free of the above issues and can get the most comprehensive support in their decision-making process.

Fig. 1
figure 1

Complete Pareto front and approximations

Full size image

Is it possible to calculate the complete Pareto front for MOOPs? Theoretically, some nonlinear AOF based methods can prove that, for any Pareto point on the Pareto front, there definitely exist a set of AOF parameters that enables the associated AOF to identify that Pareto point. However, the difficulty is that there is a lack of practicable methods to find those sets of AOF parameters that will lead to the complete Pareto front (Marler and Arora 2004). Similar situations in which there are some theoretical analyses but no practicable methods exist for COF methods (Stadler and Dauer 1992). For PCR methods, guaranteeing a complete Pareto front is theoretically a mission impossible, largely because of the stochastic nature of the population-based algorithms employed (Konak et al. 2006).

We have recently proposed a deterministic method that can, theoretically and practically, guarantee the finding of complete Pareto front for discrete MOOPs (Hu et al. 2013). Some theoretical conditions and a general methodology were reported in Hu et al. (2013), and they were successfully applied to a multiobjective route planning problem (Hu et al. 2013) and a new products development problem (Hu et al. 2014). In this article, by optimizing the investment scheme in agriculture risk governance (ARG), we will illustrate how to introduce the MOOP methodology of Hu et al. (2013) into resource allocation optimization in DRRG. Since the resource allocation problem in ARG is different from those case studies in Hu et al. (2013) and Hu et al. (2014), we first make some necessary modifications in Sect. 2 to the methodology of Hu et al. (2013). Then, we apply the modified method to the resource allocation problem in agriculture risk governance (ARG) in Sect. 3. The article ends with some conclusions and a brief discussion on future work in Sect. 4.

2 Theoretical Preparation to Find a Complete Pareto Front for Discrete MOOP

First, we need a general mathematical formulation of discrete MOOPs as follows:

$$ \mathop {\hbox{min} }\limits_{x} \left[ {g_{1} (x),g_{2} (x), \ldots ,g_{{N_{Obj} }} (x)} \right]^{T} , $$
(1)

subject to

$$ h_{I} (x) \le 0, $$
(2)
$$ h_{E} (x) = 0, $$
(3)
$$ x \in \varOmega_{X} , $$
(4)

where g i is the ith objective function of the total N Obj objective functions, h I and h E are the inequality and equality constraints, respectively, x is the vector of optimization or decision variables belonging to the set of ΩX, and x is of discrete value. A Pareto-optimal solution x* to the above problem is such that there exists no x that makes

$$ g_{i} (x) \le g_{i} (x^{*} ),\;{\text{ for all}}\;i = 1,\; \ldots ,\;N_{\text{Obj}} , $$
(5)
$$ g_{j} (x) < g_{j} (x^{*} ),\;{\text{ for at least one}}\;j \in [ 1,\; \ldots ,\;N_{\text{Obj}} ]. $$
(6)

The projection of such an x* in the objective space is called a Pareto point. The above problem usually has a set of Pareto-optimal solutions, whose projections compose the complete Pareto front.

2.1 Conditions

According to the theoretical results in Hu et al. (2013), we have the following statements for discrete MOOPs.

Lemma 1

Suppose we sort all discrete \( x \in \varOmega_{X} \) according to a certain objective function g j (x), and x j,i has the ith smallest g j . For a given constant c, if there exists an index k that satisfies

$$ g_{j} (x_{j,k} ) \le c < g_{j} (x_{j,k + 1} ), $$
(7)

then the number of Pareto points whose g j  ≤ c is no more than k, and all the associated x values are included in the set [x j,1,…,x j,k ].

Lemma 2

Suppose we have a constant vector \( [c_{1} , \ldots ,c_{{N_{Obj} }} ] \) , the element c j is for objective function g j , and after sorting all discrete \( x \in \varOmega_{X} \) according to each objective function g j , we have k j satisfying Condition 7. If for any j = 1,…,N Obj ,

$$ g_{i} (x_{{j,k_{j} }} ) \le g_{i} (x_{{i,k_{i} }} ),{\text{ for all}}\;i \ne j, $$
(8)

then the total number of Pareto points is no more than

$$ N_{PP} \le \sum\limits_{j = 1}^{{N_{Obj} }} {k_{j} } , $$
(9)

and all associated x values are included in the union set

$$ \varOmega_{U1} = \bigcup\limits_{j = 1}^{{N_{Obj} }} {[x_{j,1} ,\; \ldots ,\;x_{{j,k_{j} }} ]} ,\quad j = 1,\; \ldots ,\;N_{\text{Obj}} . $$
(10)

For more details about Lemma 1 and Lemma 2, one may refer to Hu et al. (2013). Based on Lemma 1 and Lemma 2, Hu et al. (2013) reported a methodology which employs an iteration process to calculate the k j best solutions in terms of objective function g j , for all j = 1, …, N Obj. In the iteration process, k j is increased step by step for all j = 1, …, N Obj, until a set of \( [k_{1} ,\; \ldots ,\;k_{{N_{Obj} }} ] \) is found to make Condition 8 hold.

In this article, we give an upper bound for k j (or upper bound for c j ), j = 1, …, N Obj, in order to improve the computational efficiency of the methodology in Hu et al. (2013). To this end, we need the following new theorems.

Theorem 1

Suppose there exist \( x_{1} ,\; \ldots ,\;x_{{N_{Obj} }} \) such that for any \( j \in [1,\; \ldots ,\;N_{Obj} ] \),

$$ g_{i} (x_{j} ) \le g_{i} (x_{i} ), \quad {{ for\,all}}\;i = 1, \ldots ,\;N_{\text{Obj}} . $$
(11)

Then all Pareto-optimal solutions are included in the union set

$$ \varOmega_{U2} = \mathop \cup \limits_{i = 1}^{{N_{Obj} }} \{ x:g_{i} (x) \le g_{i} (x_{i} )\} $$
(12)

Proof

Assume Theorem 1 is false. Therefore, there exists at least one Pareto-optimal solution, say x*, that does not belong to the union set ΩU2, which means, according to the definition of ΩU2 in Eq. 12, we have \( g_{i} (x_{i} ) < g_{i} (x*) \) for all i = 1, ···, N Obj. Then for any \( j \in [1,\; \ldots ,\;N_{Obj} ] \), we have

$$ g_{i} (x_{j} ) \le g_{i} (x_{i} ) < g_{i} (x^{*} )\;,{\text{ for all}}\;i = 1,\; \ldots ,\;N_{\text{Obj}} . $$
(13)

This means \( x_{1} ,\; \ldots ,\;x_{{N_{Obj} }} \) are all more Pareto efficient than x*. In other words, x* is not a Pareto-optimal solution at all. Therefore, the assumption must be false, and Theorem 1 must be true.

Corollary 1

Obviously, the set of the first best single-objective solutions \( [x_{1,1} ,\; \ldots ,\;x_{{N_{Obj} ,1}} ] \) satisfies Condition 11 in Theorem 1. Therefore, all Pareto-optimal solutions are included in the union set

$$ \varOmega_{U3} = \mathop \cup \limits_{i = 1}^{{N_{Obj} }} \left\{ {x:g_{i} (x) \le g_{i} (x_{i,1} )} \right\} . $$
(14)

With the union set defined by Eq. 14 , we have

Theorem 2

The constant vector \( [c_{1} ,\; \ldots ,\;c_{{N_{Obj} }} ] \) in Lemma 2 has an upper bound defined by

$$ \overline{c}_{j} = \mathop {\hbox{max} }\limits_{{i = 1, \ldots ,N_{Obj} }} g_{j} (x_{i,1} ) ,\quad j = 1, \ldots ,N_{\text{Obj}} $$
(15)

Suppose the \( \overline{c}_{j} \) in Eq. 15 is the (\( \overline{k}_{j} \))th best solution in terms of g j , then \( \overline{k}_{j} \) can be used as an upper bound for k j in Lemma 2, j = 1, …, N Obj .

Proof

Assume Theorem 2 is false, that is, for at least a \( j \in [1,\; \ldots ,\;N_{Obj} ] \), there exists no \( c_{j} \le \overline{c}_{j} \) that can make Condition 8 hold. This means that the complete Pareto front is not covered by the union set ΩU1—in other words, there exists at least one Pareto-optimal solution x* that has \( \bar{c}_{j} < g_{j} (x^{*} ) \). Then according to Eqs. 14 and 15, a condition exists in which this x* is not included in the union set ΩU3, which is obviously against Corollary 1. Therefore, Theorem 2 must be true.

2.2 General Methodology

In this subsection, based on Theorem 1 and Theorem 2, we will modify the methodology reported in Hu et al. (2013), in order to improve the computational efficiency. The modified general methodology to calculate complete Pareto front for discrete MOOP is described as follows:

  • Step 1 Design a problem-dependent deterministic algorithm that is capable of calculating any global kth best solution in terms of a single objective function g j , for any j = 1, …, N Obj.

  • Step 2 Calculate the set of the first best single-objective solutions \( [x_{1,1} ,\; \ldots ,\;x_{{N_{Obj} ,1}} ] \), and then determine the upper bound set \( [\bar{c}_{1} ,\; \ldots ,\;\bar{c}_{{N_{Obj} }} ] \) according to Eq. 15.

  • Step 3 Initialize k j  = 1, for every j = 1,…, N Obj. Initialize the Pareto front associated x value set as \( \varOmega_{PFX} = \varnothing \). Calculate the (k j  + 1)th global best solutions in terms of the single objective function g j , that is, calculate \( x_{{j,k_{j} + 1}} \), for every j = 1,…,N Obj.

  • Step 4 If for every j = 1,…,N Obj,

    $$ g_{j} (x_{{j,k_{j} }} ) < g_{j} (x_{{j,k_{j} + 1}} ) $$
    (16)
    $$ g_{i} (x_{{j,k_{j} }} ) \le g_{i} (x_{{i,k_{i} }} ),\;{\text{ for all}}\;i \ne j, $$
    (17)

    then go to Step 6. Otherwise, fix k j for any j that has Conditions 16 and 17 both satisfied or has \( g_{j} (x_{{j,k_{j} }} ) \ge \bar{c}_{j} \), and increase k j by one, that is, k j  = k j  + 1, for the j that has Condition 16 satisfied for the most i values.

  • Step 5 For the newly increased k j , calculate the (k j  + 1)th global best solutions in terms of g j , that is, update \( x_{{j,k_{j} + 1}} \). Go to Step 4.

  • Step 6 Calculate the union set of \( [x_{j,1} ,\; \ldots ,\;x_{{j,k_{j} }} ] \), j = 1,…,N Obj, denoting as \( \varOmega_{UX} \).

  • Step 7 For any \( x \in \varOmega_{UX} \), if there exists no \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} \in \varOmega_{UX} \) such that \( g_{i} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} ) \le g_{i} (x) \), for all i = 1,..,N Obj, and \( g_{j} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x} ) < g_{j} (x) \), for at least one j ∈[1,..,N Obj], then we know the point \( [g_{1}(x) ,\; \ldots ,\;g_{{N_{Obj}}}(x) ] \) is a Pareto point. Therefore, add x into \( \varOmega_{PFX} \), i.e., \( \varOmega_{PFX} = \varOmega_{PFX} + \{ x\} \).

The basic methodology in Hu et al. (2013) needs to keep calculating the k best solutions in terms of each single-objective function in the iteration process, while the modified methodology only calculates the kth best single-objective solution in Step 2, Step 3, and Step 5. Another improvement in the modified methodology is the introduction of upper bound \( \bar{c}_{j} \) in Step 4, which avoids the unnecessary operation of increasing any k j with \( g_{j} (x_{{j,k_{j} }} ) \ge \bar{c}_{j} \). These modifications may improve the computational efficiency to find the complete Pareto front for a discrete MOOP.

3 A Case Study of Agriculture Risk Governance

The case study in Hu et al. (2013) demonstrates that it is practicable to calculate the complete Pareto front for a route planning problem. In this article, we will show that the methodology of calculating the complete Pareto front can also be applied to the resource allocation problem in agriculture risk governance (ARG). The route planning problem is a minimization problem based on static networks, while the resource allocation problem in ARG is a maximization problem based on dynamical networks. Therefore, some necessary modifications are required before the proposed methodology can be applied to the ARG.

3.1 Agriculture Risk Governance

Agricultural Risk Governance (ARG) is an important topic in disaster and risk science, and effective tools for decision making are demanded by policymakers to improve food security and safeguard the livelihoods of farmers (Ray 1980; OECD 2011; Ye et al. 2012; Helbing 2013). In this case study, we consider a real-world ARG problem, where a regional government needs to invest a given amount of money in some agriculture disaster and risk reduction activities, in order to provide the best protection to the regional agriculture against droughts and floods. Basically, there are three activities to invest in: reinforcing relevant infrastructures (RRI); subsidizing insurance (SI); and improving disaster relief (DR). These investments have two objectives: maximize the amount of crop yields saved from disasters and increase insurance levels. Each of the three activities will have an impact on both objectives. A mathematical description of this ARG program is as follows.

Let x denote the investment vector, and x(1), x(2), and x(3) are the money invested in RRI, SI, and DR, respectively. The total investment budget is \( \bar{x} \), the investment unit is \( \Delta x \), and it is assumed that \( \bar{x} = N_{TNIU} \Delta x \), where N TNIU > 0 is an integer. Therefore, for each activity, the possible amount of investment money is

$$ x(i) \in \left\{ {0,\Delta x,2\Delta x,\; \ldots ,\;N_{TNIU} \Delta x} \right\},i = 1,\; 2,\; 3, $$
(18)

and x(1), x(2), and x(3) are subject to

$$ \sum\limits_{i = 1}^{3} {x(i)} = \bar{x}. $$
(19)

Let g 1 and g 2 be the objective functions associated with saved crop yields (SCY) and increased insurance level (IIL), respectively, and they take the following form

$$ g_{j} = \sum\limits_{i = 1}^{3} {g_{j,i} (x(i))}, \quad j = 1, 2, $$
(20)

where \( g_{j,i} (x(i)) \) defines the contribution of investment x(i) to objective g j . In this study, \( g_{j,i} (x(i)) \) is given as a contribution curve by analyzing and fitting the relevant historical data in Changde City, Hunan Province, China (Ye et al. 2012). Figures 2, 3 and 4 plot the effects of investment in RRI, SI and DR on SCY and IIL in order to calculate g 1 and g 2. Basically, the greater the investment in an activity, the more effect can be expected. Figure 2 shows that the investment in reinforcing relevant infrastructures must be above a certain threshold (for example, RMB 15 million Yuan or roughly USD 2.31 million, in this case) before any effect is achieved. This is understandable because reinforcing relevant infrastructure is often related to construction projects, which usually demand a certain minimal investment.

Fig. 2
figure 2

Contribution curves of x(1) to the two objectives

Full size image
Fig. 3
figure 3

Contribution curves of x(2) to the two objectives

Full size image
Fig. 4
figure 4

Contribution curves of x(3) to the two objectives

Full size image

The ARG can be formulated as the following biobjective maximization problem

$$ \mathop {\hbox{max} }\limits_{x} g_{j}, \quad j = 1, 2, $$
(21)

subject to conditions 18, 19, and 20. The goal of ARG is to find the best way to allocate the budget among the three activities, so that the two objective functions will be maximized. One may argue that the ARG may also be addressed as a single-objective maximization problem, because: (1) crop yields and insurance level can both be measured in monetary value; and (2) all contribution curves in Figs. 2, 3 and 4 have the same trend as x(i) increases. However, the experimental results will later explain why the biobjective maximization problem (Eq. 21) is more suitable to resolve the ARG.

The ARG can be viewed as an investment portfolio optimization problem. Since the 1950s, many methods have been developed to resolve various portfolios optimization problems (Markowitz 1952; Black and Litterman 1992; Castro et al. 2011), but little work has been reported to calculate the complete Pareto front of such problems. In this case study, we targeted the complete Pareto front of ARG, and this will provide some advantageous capabilities to help decision-makers with their portfolio-optimization problems.

3.2 A Ripple-Spreading Algorithm for ARG

The most difficult part of the methodology in Sect. 2.2 is Step 1, which demands an algorithm capable of calculating the kth best single-objective solutions. There are many algorithms to calculate the first best single-objective solution for various problems. However, there are very few algorithms ever reported to calculate the general kth best single-objective solution, and most of such algorithms only focus on the k shortest paths problem (Yen 1971; Aljazzar and Leue 2011). Therefore, the application potential of the methodology in Sect. 2 largely relies on whether we can develop effective algorithms to calculate the kth best single-objective solution for a particular MOOP. In this subsection, we will describe a ripple-spreading algorithm that finds the kth best single-objective solution for ARG.

The natural ripple-spreading phenomenon reflects an optimization principle: a ripple spreads out at the same speed in all directions, and therefore, given there are some points of interest distributed in the space, the ripple always reaches the closest spatial point first (Hu et al. 2016). Ripple-spreading algorithms take advantage of this optimization principle to resolve route optimization problems by mimicking the natural ripple-spreading phenomenon (Hu et al. 2016). In the algorithm, an initial ripple starts from the source node. When the initial ripple reaches a node, a new ripple will be triggered at that node. The new ripple can trigger other new ripples. When the destination node is reached for the first time by a ripple, the first shortest route from the source node to the destination node is then found; when the destination node is reached for the kth time, then the kth shortest route is found (Hu et al. 2016). This is likened to a ripple relay race from the source to the destination, and the optimization principle reflected in the natural ripple-spreading phenomenon guarantees the optimality of the algorithms (Hu et al. 2016).

To develop a ripple-spreading algorithm for the ARG in this study, (1) the ARG needs to be transformed into a special route optimization problem, and (2) a new ripple needs to select out feasible links from established links.

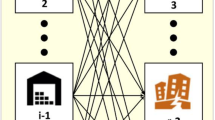
To transform the ARG into a route optimization problem, we need to construct two directed route networks for the ARG, one for g 1 and the other for g 2. In the route network for g j , we first set up a dummy source node. Then we add N TNIU + 1 new nodes representing different investment in RRI, and establish directed links from the source to each of these N TNIU + 1 nodes. The length of the link that connects to the node of \( n\Delta x \) investment in RRI is set as

$$ l_{n,1} = g_{j,1} (\bar{x}) - g_{j,1} (n\Delta x),\;n = 0,\; \ldots ,\;N_{{{\text{TNIU}}.}} $$
(22)

Then we add other N TNIU + 1 new nodes representing different investments in SI. We establish directed links from RRI nodes to SI nodes subjected to constraint 19. The length of the link that connects to the node of \( n\Delta x \) investment in SI is set as

$$ l_{n,2} = g_{j,2} (\bar{x}) - g_{j,2} (n\Delta x),\;n = 0,\; \ldots ,\;N_{{{\text{TNIU}}.}} $$
(23)

We next add a dummy destination node, and establish a directed link from every SI node to the destination. As explained fully later, the length of a link connected to the destination, denoted as l n,3, will be dynamically set up during the following ripple relay race. Figure 5 illustrates how to construct a route network for the ARG, where N TNIU = 3.

Fig. 5
figure 5

The construction of a route network for g j in ARG

Full size image

With the constructed route network for g j , we can develop a ripple relay race to calculate the k best solutions in terms of objective g j for the ARG. Basically, the new race process is similar to that in Hu et al. (2016), which aims to resolve the k shortest path problem, and the major modifications are: (1) a new ripple at a node needs to select out feasible links from established links; and (2) the length l n,3 needs to be dynamically reset according to the investment in RRI and SI. Because a ripple-spreading algorithm is actually a bottom-up, agent-based simulation model, we can easily define problem-specific node behavior to achieve the above two modifications. Because of these two modifications, the route network for g j in the ARG can be viewed as a dynamic network rather than the static ones encountered in Hu et al. (2016). In this case study, since there are only three activities to invest in, the modification for selecting out feasible links is not necessary.

The following are the details of the new ripple relay race to calculate the k best solutions in terms of objective g j for the ARG.

  • Step 1 Set the ripple spreading speed as s. Set time t = 0. Let n DNR = 0 denote how many times the dummy destination node has been reached by ripples. Start an initial ripple at the dummy source node. In the relay race, every ripple needs to record which existing ripple triggers it and from which node it originates. The initial ripple at the dummy source node, however, is triggered by no other existing ripple.

  • Step 2 If n DNR < k, update t = t + 1, and repeat the following process. For each existing ripple, increase its radius by s. Compare its radius with the length of every feasible link. Since there are only three activities in this case study, all links that starts from the origin node of the ripple are feasible. The length of a link from an RRI node to the dummy destination node depends on the RRI node at which the stimulating ripple of the current SI ripple originates. Suppose the stimulating ripple originates from the RRI node of \( n_{RRI} \Delta x \), and the current SI ripple originates from the SI node of \( n\Delta x \), then the link length from the SI node of \( n\Delta x \) to the dummy destination node is

    $$ l_{n,3} = g_{j,3} (\bar{x}) - g_{j,3} (\bar{x} - n_{RRI} \Delta x - n\Delta x),\quad n = 0,\; \ldots ,N_{{{\text{TNIU}}.}} $$
    (24)

    If the radius is larger than a feasible link,

    • Step 2.1 If the end node of the feasible link is not the dummy destination node, then a new ripple will be triggered at the end node of the feasible link, and the initial radius of the new ripple is the radius of the stimulating ripple minus the length of the feasible link.

    • Step 2.2 If the end node of the feasible link is the dummy destination node, then update n DNR = n DNR + 1. Track back the current ripple to reveal the (n DNR)th best solution in terms of objective g j . If n DNR = k, go to Step 3.

  • Step 3 Stop the ripple relay race, and output the k best solutions in terms of objective g j .

It is easy to derive that the kth shortest path in the constructed route network for g j is associated with the kth best solution in terms of maximizing the value of g j . With use of our ripple-spreading algorithm, the methodology in Sect. 2.2 becomes practicable for the ARG. One may argue that, for the sake of computational efficiency, the methodology in Sect. 2.2 demands an algorithm to calculate the kth best single-objective solution rather than the k best single-objective solutions. This is not a problem at all. When integrating the above ripple-spreading algorithm into the methodology in Sect. 2.2, the ripple relay race will be initialized once and only once. Every time the dummy destination node is reached by a ripple, the race process will be paused or frozen. Then the newly found best solution will be checked with all previously found best solutions, to see if the complete Pareto front is covered. If not, then the race process is resumed to find the next best solution.

Those link lengths defined by Eqs. 22, 23, and 24 are especially used to transform the ARG from a maximization problem to a minimization problem, because the ripple-spreading algorithms in Hu et al. (2016) are basically designed to find the shortest routes.

3.3 Simulation Results

In this subsection, we give some simulation results to demonstrate the practicability and effectiveness of the proposed methodology to calculate the complete Pareto front for the ARG. There are three parts to the simulation results: (1) comparative results with a brute-force search method to prove the finding of the complete Pareto front; (2) comparative results with an AOF method and a PCR method to show the advantage of the new method; and (3) analyses based on the complete Pareto front to illustrate the usefulness of the new method. In the simulation, the total budget \( \bar{x} \) has 9 options: [15 20 25 30 35 40 45 50 55] (million Yuan), which represent the 9 scenarios. The investment unit \( \Delta x \) is set as 0.1 million Yuan.

We apply our method to calculate complete Pareto fronts in the different scenarios of ARG. Figure 6 plots the Pareto fronts calculated by our method. To verify the completeness of the calculated Pareto fronts, a brute-force search method is used for every scenario of ARG. The results of the brute-force search method are exactly the same as those of the new method. For the sake of illustration, Fig. 7 plots the solution spaces as well as the Pareto fronts calculated by the new method in scenarios with \( \bar{x} \) = 25 million, \( \bar{x} \) = 30 million, \( \bar{x} \) = 35 million, and \( \bar{x} \) = 50 million, respectively. The comparative results prove that the reported method can guarantee the finding of the complete Pareto front for the ARG.

Fig. 6
figure 6

Calculated Pareto fronts in different scenarios of ARG

Full size image
Fig. 7
figure 7

Completeness of the calculated Pareto fronts in the ARG

Full size image

We compare our new method with two of the most popular MOOP methods: one is an AOF method; and the other is a well-known PCR method, that is, the NSGA-II in Deb (2002). In the AOF method, the two objective functions g 1 and g 2 are integrated as follows:

$$ g_{AOF} = wg_{1} + (1 - w)g_{2} $$
(25)

where \( 0 \le w \le 1 \) is a weight. In the simulation, for each scenario of ARG, we change the value of w from 0 to 1 with a step of 0.01. For each w value, we run the AOF method, and get a Pareto point. Then we use all Pareto points generated by the AOF method to approximate the true Pareto front. In the simulation, the NSGA-II has a population size of 50, a crossover probability of 0.4, a mutation probability of 0.1, and evolves for 200 generations. For each scenario of ARG, the NSGA-II is run 100 times. Table 1 gives the results of different methods, where N FPP shows how many real Pareto points a method has found, N TPP is the total number of real Pareto points in a certain scenario, and P FCPF is the probability for a method to find the complete Pareto front. From Table 1, one can see clearly that: (1) the new method is the best, because it can always guarantee finding the complete Pareto fronts for the ARG; (2) except in the scenario of \( \bar{x} \) = 15 million, the AOF method cannot find any complete Pareto front, because those fronts are not convex (Fig. 6); and (3) NSGA-II is better than the AOF method, but, due to its stochastic nature, NSGA-II can sometimes fail in some complex scenarios such as \( \bar{x} \) = 50 million and \( \bar{x} \) = 55 million.

Table 1 Comparative results between AOF, NSGA-II, and the new method
Full size table

We conclude by suggesting how a complete Pareto front may be useful for decision-makers. One reason for why AOF methods are widely accepted in the practice of MOOP is because decision-makers have to make only one single choice. Once decision-makers can agree on and provide a set of weights, AOF methods will output a unique Pareto-optimal solution as the final choice. Given a set of weights, a complete Pareto front can also help decision-makers with making the same single choice. In the case of ARG, decision-makers just need to provide a coefficient α to indicate how much IIL (increased insurance level) money (×104 Yuan) equals one ton of SCY (saved crop yields). Then in the objective space, we move a straight-line with α as the gradient, from the right top towards the left bottom, until it touches the Pareto front, and the point of tangency gives the ideal choice to decision-makers. Although AOF methods can also find such an ideal choice given the α value, the new method offers much more details to decision-makers. In particular, a complete Pareto front provides the most comprehensive support to backup solutions. Figure 8 gives some examples in the ARG scenario of \( \bar{x} \) = 50 million. For instance, assuming decision-makers provide α = 0.15, we plot an initial straight line with α = 0.15 as the gradient at the right top of Fig. 8, and then we move the straight line towards the left bottom of Fig. 8 (the gradient of the straight line is always kept as α = 0.15), until the straight line touches the Pareto front at the deep blue point, which means that the ideal solution under α = 0.15 is to invest 24 million in RRI, 10 million in SI, and 16 million in DR.

Fig. 8
figure 8

Using complete Pareto front to help with single-choice making: For a given α value, an ideal solution can then be identified by the complete Pareto front

Full size image

The AOF methods are often criticized for their subjectiveness as they demand weights from decision-makers. For the new method, the coefficient α largely relies on decision-makers’ experience or their understanding of the current and future economic environment. There are usually many uncertainties in making ARG decisions and no decision-maker can be 100 % sure about the α value they provide. A complete Pareto front can minimize the influence of such uncertainties. With a complete Pareto front at hand, we can easily and accurately work out for what range of α value each individual Pareto point may serve as the ideal choice for decision-makers. Figure 9 gives an illustration in the ARG scenario of \( \bar{x} \) = 30 million. If we invest 20 million in RRI, 10 million in SI, and none in DR (the associated Pareto point is plotted as solid deep-blue circle), then the complete Pareto front tells that even when the economic environment is turbulent with 0.25 ≤ α ≤ 1.8, the solution is still the ideal choice. The capability of accurately assessing to what extent a solution may serve as the ideal choice is no doubt highly useful to decision-makers.

Fig. 9
figure 9

To what extent a Pareto-optimal solution may serve as the ideal choice: The solution associated with the solid deep-blue point is always the ideal choice to decision-makers when the economic environment is turbulent with 0.25 ≤ α ≤ 1.8

Full size image

4 Conclusions and Future Work

This study is concerned with how to find the complete Pareto front for resource allocation optimization in disaster reduction and risk governance (DRRG). To this end, the article first improves both the theoretical results and basic methodology reported in Hu et al. (2013). Then, it chooses the resource allocation problem in agriculture risk governance (ARG) as case study to test the proposed method. In the case study, a problem-specific ripple-spreading algorithm is developed to guarantee the practicability of calculating the complete Pareto front for the ARG problem. The simulation results show that finding the complete Pareto front can provide a better support to decision-makers in ARG because it enables decision-makers to conduct many new useful analyses that are basically impossible when based on an approximation of Pareto front. In future work, efforts will be made to apply the proposed method to various resource allocation optimization problems in DRRG reality (for example, in many DRRG projects, three objectives—project cost, time, and performance—need to be optimized subject to limited resources) and conduct deep analyses (for example, a comprehensive analysis on the sensitivity of solutions is important as decision-makers want to know under what circumstances a Pareto-optimal solution should be chosen).