Multiple networks modules identification by a multi-dimensional Markov chain method

Abstract

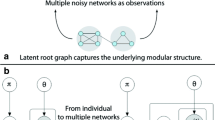
As a general approach to study interactions among small biological molecules such as genes and proteins, network analysis has aroused great interest of people from various research disciplines. However, the construction of network is usually quite sensitive to noise which is unavoidable in real data. Besides, the parameter selections for network construction can also affect the result significantly. These two factors largely decrease the consistency of results generated in network analysis. In particular, we consider detecting closely connected subgraphs named module structure. As an important common property of biological networks, this module structure is often destroyed corrupted by both noise and poor parameter selections in network construction. To conquer these two disadvantages to improve the consistency of module structure identified, we propose to process multiple networks for same set of biological molecules simultaneously for common module structure. More specifically, we combine multiple networks together by building an order 3 tensor data with each layer as one of the multiple networks. Then given any molecule(s) as prior information, a novel tensor-based Markov chain algorithm is proposed to iteratively detect the module that includes the prior node. Moreover, the proposed algorithm is capable of evaluating the contribution scores of each network to the detected module structure. The contribution scores from multiple networks can be not only useful criteria to measure the consistency of module structure, but also valid indicator of corruption in networks. To demonstrate the effectiveness and efficiency of the proposed tensor-based Markov chain algorithm, experimental results on synthetic data set as well as two real gene co-expression data sets of human beings are reported. We also validate that the identified common modules are biologically meaningful.

Appendix

Let us first consider the following lemma:

Lemma 1

$$\begin{aligned} \sum ^{n_1}_{i=1}[\mathbf {M_1}]_{i,k} = 1 \nonumber , \quad \ \sum ^{n_2}_{i=1}[\mathbf {M_2}]_{i,k} = 1 \nonumber \end{aligned}$$

Proof

$$\begin{aligned} \sum ^{n_1}_{i=1}[\mathbf {M_1}]_{i,k}=\sum ^{n_1}_{i=1}[\mathcal {A}^{(1)}\times _2 \mathbf {x}]_{i,k}=\sum ^{n_{1}}_{j=1}a_{i,j,k}x_{j} \end{aligned}$$

$$\begin{aligned} \sum ^{n_{1}}_{i=1}[\mathbf {M_1}]_{i,k}= & {} \sum ^{n_{1}}_{i=1}\sum ^{n_{1}}_{j=1}a_{i,j,k}x_{j} = \sum ^{n_{1}}_{j=1} \left( \sum ^{n_{1}}_{i=1}a_{i,j,k}x_{j} \right) =\sum ^{n_{1}}_{j=1}x_{j}=1 \end{aligned}$$

we also easy get $\sum ^{n_2}_{i=1}[\mathbf {M_2}]_{i, k}=1$ via the similar way. $\square$

This Lemma 1 guarantees that both $\mathbf {M}_1$ and $\mathbf {M}_2$ are transition probability matrices. Then we may show that both $\mathbf {x}$ and $\mathbf {y}$ satisfying (3) and (4) are unique:

Lemma 2

For $\alpha \in (0,1)$ , there exist unique $\mathbf {x}$ and $\mathbf {y}$ satisfying (3) and (4).

Proof

From Lemma 1, we get that

$$\begin{aligned} \Vert \mathbf {M}_{1}\Vert _1=\Vert \mathbf {M}_{2}\Vert _1 \end{aligned}$$

therefore

$$\begin{aligned} \Vert \mathbf {M_1}\mathbf {M_2}\Vert _1\le \Vert \mathbf {M_1}\Vert _1\Vert \mathbf {M_2}\Vert _1 \end{aligned}$$

denote the radius of $\mathbf {M_1}\mathbf {M_2}$ as $\rho (\mathbf {M_1}\mathbf {M_2})$ and it is not larger than its norm, we get $\rho (\mathbf {M_1}\mathbf {M_2})\le 1$.

From (3) and (4),

$$\begin{aligned} \mathbf {x}= \; & {} (1-\alpha )\mathbf {M_1}\mathbf {M_{2}}\mathbf {x}+\alpha \mathbf {p}\\ \mathbf {y}= \; & {} (1-\alpha )\mathbf {M_2}\mathbf {M_{1}}\mathbf {y}+\alpha \mathbf {p} \end{aligned}$$

then

$$\begin{aligned} (\mathbf {I}-(1-\alpha )\mathbf {M_1}\mathbf {M_2})\mathbf {x}= \; & {} \alpha \mathbf {p} \\ (\mathbf {I}-(1-\alpha )\mathbf {M_2}\mathbf {M_1})\mathbf {y}= \; & {} \alpha \mathbf {p} \end{aligned}$$

where $\mathbf {I}$ is identity matrix because $\rho ((1-\alpha )\mathbf {M_1}\mathbf {M_2})=(1-\alpha )\rho (\mathbf {M_1}\mathbf {M_2})\le (1-\alpha )<1$ and $\rho ((1-\alpha )\mathbf {M_2}\mathbf {M_1})\le 1-\alpha <1$. Therefore, $\mathbf {I}-(1-\alpha )\mathbf {M_1}\mathbf {M_2}$ and $\mathbf {I}-(1-\alpha )\mathbf {M_2}\mathbf {M_1}$ are nonsingular,

$$\begin{aligned} \mathbf {x}= \; & {} \alpha [\mathbf {I}-(1-\alpha )\mathbf {M_1}\mathbf {M_2}]^{-1}\mathbf {p} \\ \mathbf {y}= \; & {} \alpha [\mathbf {I}-(1-\alpha )\mathbf {M_2}\mathbf {M_1}]^{-1}\mathbf {p} \end{aligned}$$

$\square$

Now consider the iteration in (5) and (6), we may give the following Lemma:

Lemma 3

The iteration guarantees the sequences $\{\mathbf {x_k}\}$ and $\{\mathbf {y_k}\}$ satisfying $\Vert \mathbf {x}_k\Vert _1=1$ and $\Vert \mathbf {y}_k\Vert _1=1$.

Proof

The iteration can be written as the following

$$\begin{aligned} \mathbf {x_{k+1}}= & {} (1-\alpha )\mathbf {M_1}\mathbf {M_2}\mathbf {x_k}+\alpha \mathbf {p} \\ \mathbf {y_{k+1}}= & {} (1-\alpha )\mathbf {M_2}\mathbf {M_1}\mathbf {y_k}+\alpha \mathbf {p} \end{aligned}$$

let $e=[1,1,\ldots ,1]^{\rm T}$, then

$$\begin{aligned} e^{\rm T}\mathbf {x_{k+1}}= & {} (1-\alpha )e^{\rm T}\mathbf {M_1}\mathbf {M_2}\mathbf {x_k}+e^{\rm T}\alpha \mathbf {p} \\= & {} (1-\alpha )e^{\rm T}\mathbf {M_2}\mathbf {x_k}+\alpha =(1-\alpha )e^{\rm T}\mathbf {x_{k}}+\alpha \end{aligned}$$

If $\Vert \mathbf {x_k}\Vert _1=1$, then $\Vert \mathbf {x_{k+1}}\Vert _1=1$. The same consequence can be obtained for sequence $\{\mathbf {y_k}\}$. $\square$

Based on previous two lemmas, we may give the following remarks.

Remark 1

• 1. If we set $\Vert \mathbf {x_0}\Vert _1=\Vert \mathbf {y_0}\Vert _1=1$, then the $\Vert \cdot \Vert _1=1$ can keep during the iteration.

• 2. $\Vert \mathbf {M_1}\Vert _1=\Vert \mathbf {M_2}\Vert _1=1$ is established under the condition $\Vert \mathbf {x}\Vert _1=1$ which the iteration promised.

Then we are ready to present the following Theorem:

Theorem 1

The iterations (5) and (6) are convergent when $\alpha \in (2/3,1)$.

Theorem 1 can be proved easily via the similar proof of Lemma 2. This theorem demonstrates the convergence of the iterative scheme in the second stage of Algorithm 1. Then according to Algorithm 1, it is easy to get:

$$\begin{aligned} \mathbf {x}(t)= & {} (1-\alpha )\mathbf {M_1}(t-1)\mathbf {M_2}(t-1)\mathbf {x}(t)+\alpha \mathbf {p} \\ \mathbf {y}(t)= & {} (1-\alpha )\mathbf {M_2}(t-1)\mathbf {M_1}(t-1)\mathbf {y}(t)+\alpha \mathbf {p} \end{aligned}$$

then

$$\begin{aligned} \mathbf {x}(t)= & {} [\mathbf {I}-(1-\alpha )\mathbf {M_1}(t-1)\mathbf {M_2}(t-1)]^{-1}\alpha \mathbf {p} \\ \mathbf {y}(t)= & {} [\mathbf {I}-(1-\alpha )\mathbf {M_2}(t-1)\mathbf {M_1}(t-1)]^{-1}\alpha \mathbf {p} \end{aligned}$$

It is not difficult to see that the convergence of $\{\mathbf {y}(t)\}$ is guaranteed if $\{\mathbf {x}(t)\}$ converges. Therefore, it is enough that we only consider the convergence of $\{\mathbf {x}(t)\}$ here. For simplicity, let

$$\begin{aligned} \mathbf {x}(t+1)=F(\mathbf {x}(t)) \end{aligned}$$

(7)

where $F(\mathbf {x}(t))=(\mathbf {I}-(1-\alpha )\mathbf {M_1}(t)\mathbf {M_2}(t))^{-1}\alpha \mathbf {p}$.

Let us consider the mapping

$$\begin{aligned} F: \mathbf {x}\rightarrow \mathbf {F}(\mathbf {x}) \end{aligned}$$

where $\mathbf {F}(\mathbf {x})=(\mathbf {I}-(1-\alpha )\mathbf {M_1}(\mathbf {x})\mathbf {M_2}(\mathbf {x}))^{-1}\alpha \mathbf {p}$. $\mathbf {M}_1(\mathbf {x})= \mathcal {A}^{(1)}\times _{2}\mathbf {x}$ and $\mathbf {M}_2(\mathbf {x})=(\mathcal {A}^{(2)}\times _{2}\mathbf {x})^{\rm T}$.

Denote $\mathbf {Q}(\mathbf {x})=(\mathbf {I}-(1-\alpha )\mathbf {M_1}(\mathbf {x})\mathbf {M_2}(\mathbf {x}))^{-1}$, $\mathbf {G}(\mathbf {x})=(\mathbf {Q}(\mathbf {\mathbf {x}}))^{-1}=\mathbf {I}-(1-\alpha )\mathbf {M_1}(\mathbf {x})\mathbf {M_2}(\mathbf {x})$ and let $\mathbf {L}(\mathbf {x})=\mathbf {M}_1(\mathbf {x})\mathbf {M}_2(\mathbf {x})$, we have:

$$\begin{aligned} \frac{{\rm d}\mathbf {F}(\mathbf {x})}{{\rm d}\mathbf {x}}=\frac{{\rm d}(\alpha \mathbf {Q}(\mathbf {x})\mathbf {p})}{{\rm d}\mathbf {x}}=\alpha \frac{{\rm d}\mathbf {Q}(\mathbf {x})}{{\rm d}\mathbf {x}}\mathbf {p} \end{aligned}$$

$$\begin{aligned} \frac{{\rm d}\mathbf {Q}(\mathbf {x})}{{\rm d}\mathbf {x}}=-\mathbf {Q}(\mathbf {x})\frac{{\rm d}\mathbf {G}(\mathbf {x})}{{\rm d}\mathbf {x}}\mathbf {Q}(\mathbf {x}) \end{aligned}$$

$$\begin{aligned} \frac{{\rm d}\mathbf {G}(\mathbf {x})}{{\rm d}\mathbf {x}}=\frac{{\rm d}(\mathbf {I}-(1-\alpha )\mathbf {M}_1\mathbf {M}_2)}{{\rm d}\mathbf {x}}=-(1-\alpha )\frac{{\rm d}L(\mathbf {x})}{{\rm d}\mathbf {x}} \end{aligned}$$

$$\begin{aligned} \frac{{\rm d}\mathbf {L}(\mathbf {x})}{{\rm d}\mathbf {x}}=\frac{{\rm d}\mathbf {M}_1(\mathbf {x})\mathbf {M}_2(\mathbf {x})}{{\rm d}\mathbf {x}}=\frac{{\rm d}\mathbf {M}_1(\mathbf {x})}{{\rm d}\mathbf {x}}\mathbf {M}_2(\mathbf {x})+\mathbf {M}_1(\mathbf {x})\frac{{\rm d}\mathbf {M}_2(\mathbf {x})}{{\rm d}\mathbf {x}} \end{aligned}$$

In addition, if rewrite

$$\begin{aligned} \mathbf {M}_1(\mathbf {x})= & {} \mathcal {A}^{(1)}\times _{2}\mathbf {x}\\= & {} \left( \begin{array}{ccc} \sum ^{n_{1}}_{j}a^{(1)}_{1,j,1}x_{j} &{} \cdots &{}\sum ^{n_{1}}_{j}a^{(1)}_{1,j,n_{2}}x_{j} \\ \vdots &{} \ddots &{} \vdots \\ \sum ^{n_{1}}_{j}a^{(1)}_{n_{1},j,1}x_{j} &{} \cdots &{} \sum ^{n_{1}}_{j}a^{(1)}_{n_{1},j,n_{2}}x_{j} \end{array}\right) \\= & {} \left( \begin{array}{ccccccc} a^{(1)}_{1,1,1} &{} \cdots &{} a^{(1)}_{1,n_{1},1} &{} \cdots &{} a^{(1)}_{1,1,n_{2}} &{} \cdots &{} a^{(1)}_{1,n_{1},n_{2}} \\ \vdots &{} \ddots &{} \vdots &{} \cdots &{} \vdots &{} \ddots &{} \vdots \\ a^{(1)}_{n_{1},1,1} &{} \cdots &{} a^{(1)}_{n_{1},n_{1},1} &{} \cdots &{} a^{(1)}_{n_{1},1,n_{2}} &{} \cdots &{} a^{(1)}_{n_{1},n_{1},n_{2}} \end{array}\right) \; (\mathbf {x}\otimes \mathbf {I}_{n_{2}})\\= & {} \mathcal {A}^{(1)}(1) \; (\mathbf {x}\otimes \mathbf {I}) \end{aligned}$$

and

$$\begin{aligned} \mathbf {M}_2(\mathbf {x})= & {} (\mathcal {A}^{(2)}\times _{2}\mathbf {x})^{\rm T}\\= & {} \left( \begin{array}{ccccccc} a^{(2)}_{1,1,1} &{} \cdots &{} a^{(2)}_{1,n_{1},1} &{} \cdots &{} a^{(2)}_{n_{1},1,1} &{} \cdots &{} a^{(2)}_{n_{1},n_{1},1} \\ \vdots &{} \ddots &{} \vdots &{} \cdots &{} \vdots &{} \ddots &{} \vdots \\ a^{(2)}_{1,1,n_{2}} &{} \cdots &{} a^{(1)}_{1,n_{1},n_{2}} &{} \cdots &{} a^{(2)}_{n_{1},1,n_{2}} &{} \cdots &{} a^{(2)}_{n_{1},n_{1},n_{2}} \end{array}\right) (\mathbf {x}\otimes \mathbf {I}_{n_{1}})\\= \; & {} \mathcal {A}^{(2)}(3) \; (\mathbf {x}\otimes \mathbf {I}) \end{aligned}$$

where $\mathcal {A}^{(1)}(1)$ is unfolding of tensor $\mathcal {A}^{(1)}$ from 1st direction, $\mathcal {A}^{(2)}(3)$ is the unfolding of tensor $\mathcal {A}^{(2)}$ from 3rd direction, we may get

$$\begin{aligned} \frac{{\rm d}\mathbf {M}_{1}(\mathbf {x})}{{\rm d}\mathbf {x}}= & {} \; \mathcal {A}^{(1)}(1)\mathbf {I} \\ \frac{{\rm d}\mathbf {M}_{2}(\mathbf {x})}{{\rm d}\mathbf {x}}= & {} \; \mathcal {A}^{(2)}(3)\mathbf {I} \end{aligned}$$

Then

$$\begin{aligned} \Vert \frac{{\rm d}\mathbf {L}(\mathbf {x})}{{\rm d}\mathbf {x}}\Vert _{1}\le & {} \; \Vert \frac{{\rm d}\mathbf {M}_{1}(\mathbf {x})}{\mathbf {x}}\Vert _{1}\Vert \mathbf {M}_{2}(\mathbf {x})\Vert +\Vert \mathbf {M}_{1}(\mathbf {x})\Vert \Vert \frac{{\rm d}\mathbf {M}_{2}(\mathbf {x})}{{\rm d}\mathbf {x}}\Vert _{1}\\= & {} \; \Vert \frac{{\rm d}\mathbf {M}_{1}(\mathbf {x})}{{\rm d}\mathbf {x}}\Vert _{1}+\Vert \frac{{\rm d}\mathbf {M}_{2}(\mathbf {x})}{{\rm d}\mathbf {x}}\Vert _{1}=2 \end{aligned}$$

In addition, we may also get

$$\begin{aligned} \Vert \mathbf {Q}(\mathbf {x})\Vert _1= & {} \; \Vert (\mathbf {I}-(1-\alpha )\mathbf {M_1}(\mathbf {x})\mathbf {M_2}(\mathbf {x}))^{-1}\Vert _1 \\\le & {} \frac{1}{1-\Vert (1-\alpha )\mathbf {M_1}(\mathbf {x})\mathbf {M_2}(\mathbf {x})\Vert _1}\\= & {} \frac{1}{1-(1-\alpha )} \end{aligned}$$

Therefore, we have

$$\begin{aligned} \Vert \frac{{\rm d}\mathbf {F}(\mathbf {x})}{{\rm d}\mathbf {x}}\Vert _1= & {} \; \Vert (1-\alpha )\mathbf {Q}(\mathbf {x})\frac{{\rm d}\mathbf {L}(\mathbf {x})}{{\rm d}x}\mathbf {Q}(\mathbf {x})\alpha \mathbf {p}\Vert _{1}\\= & {} \; (1-\alpha ) \alpha \Vert \mathbf {Q}(\mathbf {x})\frac{{\rm d}\mathbf {L}(\mathbf {x})}{{\rm d}\mathbf {x}}\mathbf {Q}(\mathbf {x})\mathbf {p}\Vert _1\\\le & {} \; 2(1-\alpha ) \alpha \frac{1}{[1-(1-\alpha )]^{2}}=\frac{2-2\alpha }{\alpha } \end{aligned}$$

In conclusion, when $\alpha >\frac{2}{3}$, $\Vert \frac{{\rm d}F(\mathbf {x})}{{\rm d}\mathbf {x}}\Vert _1<1$, it is easy to see that the mapping F is a contract mapping. From the Banach fixed point theorem, the Eq. (7) converges to a unique fixed point $\mathbf {x}_*$ which means the algorithm 1 converges.