Two-row and two-column mixed-integer presolve using hashing-based pairing methods

Abstract

In state-of-the-art mixed-integer programming solvers, a large array of reduction techniques are applied to simplify the problem and strengthen the model formulation before starting the actual branch-and-cut phase. Despite their mathematical simplicity, these methods can have significant impact on the solvability of a given problem. However, a crucial property for employing presolve techniques successfully is their speed. Hence, most methods inspect constraints or variables individually in order to guarantee linear complexity. In this paper, we present new hashing-based pairing mechanisms that help to overcome known performance limitations of more powerful presolve techniques that consider pairs of rows or columns. Additionally, we develop an enhancement to one of these presolve techniques by exploiting the presence of set-packing structures on binary variables in order to strengthen the resulting reductions without increasing runtime. We analyze the impact of these methods on the MIPLIB 2017 benchmark set based on an implementation in the MIP solver SCIP.

1 Introduction

Presolve for mixed-integer programming (MIP) is a set of routines that remove redundant information and strengthen the model formulation with the aim of accelerating a subsequent main solution process, which is usually a branch-and-cut approach. Further, presolve is an excellent complement to branch-and-cut, because it focuses on model reductions and reformulations that are commonly not in the working space of branch-and-cut, e.g., greatest common divisor reductions or redundancy detection. Presolve can be very effective, and it frequently makes the difference between a problem being intractable and solvable (Achterberg and Wunderling 2013).

Considering that presolve is undisputedly an important building block in solving MIP problems, there exist comparatively few articles in the MIP literature. Only in the last few years there has been a moderate increase in the number of publications on this subject. One of the earliest contributions was by Brearley et al. (1975). Later Johnson and Suhl (1980), Guignard and Spielberg (1981), Crowder et al. (1983), and Hoffman and Padberg (1991) investigated presolve techniques for zero-one inequalities. Savelsbergh (1994) published preprocessing and probing techniques for MIP problems. Many of the methods published in it are now standard in almost every MIP solver. Presolve also plays an important role in linear programming (Andersen and Andersen 1995) and especially for interior point algorithms (Gondzio 1997). In recent years, presolve as a research topic has become increasingly important (Gamrath et al. 2015; Achterberg et al. 2014). Finally, the very recent publication by Achterberg et al. (2019) deserves special attention. Not only does it present many new presolve methods, but also highlights theoretically interesting details of presolve reductions and relations to number theory.

How the presolve algorithms are implemented frequently makes the difference between a beneficial and a harmful method. Often it is reasonable to weight the strength of the reductions against the runtime behavior in order to rank the presolve methods appropriately. Details on implementation of various presolve reductions are discussed in Suhl and Szymanski (1994), Martin (2001), Atamtürk and Savelsbergh (2005), and Achterberg (2007). Investigations concerning the performance impact of different features of a MIP solver were published in Bixby et al. (2004), Bixby and Rothberg (2007), and Achterberg and Wunderling (2013). These publications confirmed that presolve and cutting plane techniques are by far the most important components of modern MIP solvers.

In the most simple and usually fastest case, individual rows or columns are considered for presolve reductions. Some interactions between reductions may take place through, e.g., tightened variables bounds, but strictly speaking this approach is limited to local information and thus often yields weak reductions. On the other hand one could try to find stronger reductions by building global data structures such as for example the clique table, which collects mutual incompatibilities between binary variables, or by considering larger parts of the problem or even the whole problem, which generally leads to higher runtimes.

It is therefore important to strike a good balance between effectiveness and computational overhead. One way to achieve this would be to examine two rows or two columns simultaneously. Bixby and Wagner (1987) published an efficient algorithm to find parallel rows or columns of the constraint matrix. Multi-row presolve reductions were also the subject of research in Achterberg et al. (2014), where they derive improvements to the model formulation by simultaneously examining multiple problem constraints. Finally, considering more than one row or column at a time allows more techniques to be used. For instance, matrix sparsification techniques as described in Chang and McCormick (1993), Gondzio (1997) and, more recently, Achterberg et al. (2019), cannot be applied when considering only one row or one column at a time.

In many of the publications mentioned above, amazing results have been achieved with presolve reductions for solving MIPs. However, these results often are closely related to the exact details of the underlying implementation. In particular, two-row or two-column techniques immediately raise the question of how to find promising pairs of rows or columns as simple enumeration of all combinations is usually too computationally expensive in a presolve context. In most publications there is no answer to this question. Therefore, in this article we develop two efficient methods for determining suitable pairs for presolve reductions via hashing methods (Knuth 1998). In addition, we describe new presolve approaches or extensions of existing techniques that, to the best of our knowledge, have not been published yet.

The paper is organized as follows. Section 2 introduces the notation and some basic concepts used in the remainder of the paper. Sections 3–5 constitute the main part of the paper. Five new presolve approaches or extensions of already published methods are described in Sect. 3. The first two methods deal with sparsification of the constraint matrix, two more methods focus on bound tightening, and the method presented last is a dual approach resulting in variable and constraint fixings. Next, in Sect. 4, we describe the hashing methods we use to address the question of finding promising pairs of two rows or columns of the problem for the previously presented presolve methods. Subsequently, Sect. 5 provides computational results to assess their performance impact. Finally, we summarize our conclusions in Sect. 6.

2 Notation and background

This document builds on the following notation. Let $\mathcal {N}= \{1,\ldots ,n\}$ and $\mathcal {M}= \{1,\ldots ,m\}$ be index sets. Given a matrix $A \in \mathbb {R}^{m \times n}$, vectors $c\in \mathbb {R}^n$, $b\in \mathbb {R}^m$, $\ell \in (\mathbb {R}\cup \{-\infty \})^n$, $u\in (\mathbb {R}\cup \{\infty \})^n$, variables $x \in \mathbb {R}^{n}$ with $x_j \in \mathbb {Z}$ for $j \in \mathcal {I}\subseteq \mathcal {N}$, and relations $\circ _i\in \{=,\le ,\ge \}$ for all $i \in \mathcal {M}$ of A, a mixed-integer program (MIP) can be formulated in the following form:

$$\begin{aligned} \begin{aligned} \min \quad&c^\top x \\ \text {s.t.} \quad&Ax \circ b, \\&\ell _{j} \le x_{j} \le u_{j}&\text { for all }j \in \mathcal {N}, \\&x_{j} \in \mathbb {Z}&\text { for all }j \in \mathcal {I}. \end{aligned} \end{aligned}$$

(1)

The set of feasible solutions of (1) is defined by

$$\begin{aligned} P_{\text {MIP}} :=\{x \in \mathbb {R}^n \mid x_{j} \in \mathbb {Z}\ \forall j \in \mathcal {I}\wedge Ax \circ b\wedge \ell _{j} \le x_{j} \le u_{j} \ \forall j \in \mathcal {N}\}. \end{aligned}$$

In addition, we define the set of feasible solutions of the linear programming relaxation of (1) by

$$\begin{aligned} P_{\text {LP}} :=\{x \in \mathbb {R}^n \mid Ax \circ b\wedge \ell _{j} \le x_{j} \le u_{j} \ \forall j \in \mathcal {N}\}. \end{aligned}$$

The single coefficients of A are denoted by $a_{ij}$ with $i \in \mathcal {M}$ and $j \in \mathcal {N}$. We use the notation $A_{i\cdot }$ to identify the row vector given by the i-th row of A. Similarly, $A_{\cdot j}$ is the column vector given by the j-th column of A. Let $R \subseteq \mathcal {M}$ and $V \subseteq \mathcal {N}$, then $A_{RV}$ denotes a matrix consisting of the coefficients of A restricted to the row indices $i \in R$ and column indices $j \in V$. Similarly, $x_V$ denotes the vector x limited to the index set V.

In some cases, we consult the support function which determines the indices of the nonzero entries of a vector. With ${{\,\mathrm{supp}\,}}(A_{i\cdot })=\{j \in \mathcal {N}\mid a_{ij} \not =0 \}$ we denote the support of row $A_{i\cdot }$. Correspondingly, ${{\,\mathrm{supp}\,}}(A_{\cdot j})=\{i \in \mathcal {M}\mid a_{ij} \not =0 \}$ designates the support of column $A_{\cdot j}$.

Depending on the coefficients of the matrix A and the bounds of the variables x, the minimal activity and maximal activity for each row $i\in \mathcal {M}$ in (1) are given by

$$\begin{aligned} \inf \{ A_{i\cdot } x \mid \ell _{j} \le x_{j} \le u_{j}\,\forall j\in \mathcal {N}\} = \sum _{\begin{array}{c} j \in \mathcal {N}\\ a_{ij}>0 \end{array}} a_{ij} \ell _{j} + \sum _{\begin{array}{c} j \in \mathcal {N}\\ a_{ij}<0 \end{array}} a_{ij} u_j \end{aligned}$$

(2)

and

$$\begin{aligned} \sup \{ A_{i\cdot } x \mid \ell _{j} \le x_{j} \le u_{j}\,\forall j\in \mathcal {N}\} = \sum _{\begin{array}{c} j \in \mathcal {N}\\ a_{ij}>0 \end{array}} a_{ij} u_{j} + \sum _{\begin{array}{c} j \in \mathcal {N}\\ a_{ij}<0 \end{array}} a_{ij} \ell _j, \end{aligned}$$

(3)

respectively. As infinite lower or upper bounds on the variables x are allowed, infinite minimal or maximal activities may occur. To simplify notation we write

$$\begin{aligned} \inf (A_{iV} x_V)&:=\inf \{ A_{iV} x_V \mid \ell _{j} \le x_{j} \le u_{j}\,\forall j\in V\}\\ \sup (A_{iV} x_V)&:=\sup \{ A_{iV} x_V \mid \ell _{j} \le x_{j} \le u_{j}\,\forall j \in V\} \end{aligned}$$

for row i and a subset $V \subseteq \mathcal {N}$ of variable indices, in order to refer to partial minimal and maximal activities. This coincides with (2) and (3) for $V = \mathcal {N}$.

Consider an inequality constraint

$$\begin{aligned} A_{iV}x_V + a_{ij} x_j \ge b_i \end{aligned}$$

where $i\in \mathcal {M}$, $j \in \mathcal {N}$, $V={{\,\mathrm{supp}\,}}(A_{i\cdot }) \setminus \{j\}$, and $a_{ij}\not =0$. Before deriving bounds for $x_j$, an important question is how to determine bounds $\ell _{i}^V$, $u_{i}^V \in {\mathbb {R}} \cup \{-\infty ,\infty \}$ with reasonable computational effort such that

$$\begin{aligned} \ell _{i}^V \le A_{iV} x_V \le u_{i}^V \end{aligned}$$

holds for all $x \in P_{\text {MIP}}$. There are various possibilities in order to achieve this and the most simple approach for single-row presolve is to optimize in linear time over the bounding box, i.e.

$$\begin{aligned} \begin{array}{l} \ell _{i}^V :=\inf (A_{iV}x_V), \quad u_{i}^V :=\sup (A_{iV}x_V). \end{array} \end{aligned}$$

(4)

If $u_{i}^V$ is finite, we can determine bounds on variable $x_j$. Depending on the sign of $a_{ij}$ we distinguish two cases. For $a_{ij}>0$ a valid lower bound on $x_j$ is given by

$$\begin{aligned} x_j \ge (b_i - u_{i}^V)/a_{ij} \end{aligned}$$

(5)

and hence, we can replace $\ell _j$ by

$$\begin{aligned} \max \{\ell _j,(b_i - u_{i}^V)/a_{ij}\}. \end{aligned}$$

(6)

Analogously, for $a_{ij}<0$, a valid upper bound on $x_j$ is given by

$$\begin{aligned} x_j \le (b_i - u_{i}^V)/a_{ij} \end{aligned}$$

(7)

and hence, we can replace $u_j$ by

$$\begin{aligned} \min \{u_j,(b_i - u_{i}^V)/a_{ij}\}. \end{aligned}$$

(8)

If $x_j$ is an integer variable, we replace (6) by

$$\begin{aligned} \lceil \max \{\ell _j,(b_i - u_{i}^V)/a_{ij}\}\rceil \end{aligned}$$

(9)

and analogously (8) by

$$\begin{aligned} \lfloor \min \{u_j,(b_i - u_{i}^V)/a_{ij}\}\rfloor . \end{aligned}$$

(10)

The observations above together with (4) can be used to realize an approach called feasibility-based bound tightening (FBBT), which is an iterative range-reduction technique (Davis 1987). It involves tightening the variable ranges using all of the constraint restrictions. This procedure is iterated as long as the variable ranges keep changing. FBBT might fail to converge finitely (see Achterberg et al. (2019)). Therefore, in practice one stops iterating when the improvement after one or several iterations is too small, an alternate approach to deal with this special case is described in Belotti et al. (2010).

Instead of trivially optimizing over the bounding box one could calculate

$$\begin{aligned} \begin{array}{lcl} \ell _{i}^V &{}=&{} \min \{A_{iV}x_V \mid x \in P_{\text {MIP}}\},\\ u_{i}^V &{}=&{} \max \{A_{iV}x_V \mid x \in P_{\text {MIP}}\}. \end{array} \end{aligned}$$

However, this approach would usually be very time consuming as it amounts to solving problem (1) with a different objective function. A lightweight alternative to solving the complete MIPs is to only consider the linear programming relaxation

$$\begin{aligned} \begin{array}{lcl} \ell _{i}^V &{}=&{} \min \{A_{iV}x_V \mid x \in P_{\text {LP}}\},\\ u_{i}^V &{}=&{} \max \{A_{iV}x_V \mid x \in P_{\text {LP}}\}. \end{array} \end{aligned}$$

Still, this procedure is often too time-consuming.

A more reasonable compromise between computational complexity and tightness of the bounds is to use only a small number of constraints of the system instead of all constraints over which we maximize or minimize. This can again be done via solving a MIP or an LP. If we just use a single constraint, then solving the corresponding LP is of particular interest, since such problems can be solved in linear time in the number of variables, see Dantzig (1957) and Balas and Zemel (1980).

A closely related procedure is the so-called optimization based bound tightening (OBBT), which first has been applied in the context of global optimization by Shectman and Sahinidis (1998) and Quesada and Grossmann (1995). Here, the block we want to minimize and maximize consists of just one variable:

$$\begin{aligned} \min \{x_j \mid x \in P_{\text {MIP}}\} \le x_j \le \max \{x_j \mid x \in P_{\text {MIP}}\}. \end{aligned}$$

Again, instead of solving the full MIP one can solve any relaxation of the problem to obtain valid bounds for $x_j$.

Presolve methods can be classified into two groups: primal and dual presolve methods. Primal presolve methods derive reductions based on the feasibility argument and thus are valid independently of the objective function. In contrast, dual presolve methods derive reductions by utilizing the information from the objective function while ensuring at least one optimal solution is retained, as long as the problem was feasible.

3 Two-row and two-column presolve methods

In this section we will outline five presolve methods for which we developed the pairing mechanisms following in Sect. 4. First, Sect. 3.1 presents a primal presolve method to increase sparsity of the constraint matrix by cancelling nonzero coefficients using pairs of rows and the method in Sect. 3.2 extends this idea onto using columns for nonzero cancellation. The next two primal presolve methods, outlined in Sects. 3.3 and 3.4, improve variable bounds via FBBT on pairs of rows. Although these two methods work in a similar way, they have different advantages. In short, the method in Sect. 3.3 is easier to implement and can be applied to single variables but cannot tighten bounds on all variables present in the involved constraints. Finally, Sect. 3.5 presents a way to reuse the method presented in Sect. 3.4 in order to improve a dual presolve method.

3.1 Two-row nonzero cancellation

This presolve method tries to find pairs consisting of an equality and a second constraint such that adding the appropriately scaled equality to the other constraint sparsifies the latter by cancelling nonzero coefficients. This approach to reduce the number of nonzeros in the constraint matrix A has already been used by Chang and McCormick (1993), Gondzio (1997) and, more recently, Achterberg et al. (2019). More precisely, assume two constraints

$$\begin{aligned} \begin{array}{rcrcrcrcl} A_{iU} x_U &{}+&{} A_{iV}x_V &{}+&{} A_{iW}x_W &{}&{}=&{} b_i, \\ A_{rU} x_U &{}+&{} A_{rV}x_V &{}+&{} &{} A_{rY} x_Y &{} \circ _r &{} b_r, \end{array} \end{aligned}$$

with $i,r \in \mathcal {M}$ and disjoint subsets of the column indices U, V, W, $Y \subseteq \mathcal {N}$. Further, assume there exists a scalar $\lambda \in \mathbb {R}$ such that $A_{rU}-\lambda A_{iU}=0$ and $A_{rk}-\lambda A_{ik}\not =0$ for all $k\in V$. Subtracting $\lambda$ times the equality i from constraint r yields

$$\begin{aligned} \begin{array}{rcrcrcrcl} A_{iU} x_U &{}+&{} A_{iV} x_V &{}+&{} A_{iW} x_W &{} &{} &{}=&{} b_i, \\ &{} &{} (A_{rV} -\lambda A_{iV})x_V &{}-&{} \lambda A_{iW} x_W &{}+&{} A_{rY} x_Y &{}\circ _r&{} b_r - \lambda b_i. \end{array} \end{aligned}$$

(11)

The difference in the number of nonzeros of A is $\vert U \vert -\vert W \vert$. Since the case $\vert U \vert - \vert W \vert \le 0$ does not seem to offer any advantage, the reduction is applied only if the number of nonzeros actually decreases. In all cases, this procedure takes at most $O(|{\mathcal {N}}|)$ time.

For mixed-integer programming, reducing the number of nonzeros of A has two main advantages. First, many subroutines in a MIP solver depend on this number. In particular, the LP solver benefits from sparse basis matrices. Secondly, nonzero cancellation may open up possibilities for other presolve techniques to perform useful reductions or improvements on the formulation. One special case occurs if $W = \emptyset$, that is, the support of the equality constraint is a subset of the support of the other constraint. This case is of particular interest because decompositions may take place.

3.2 Two-column nonzero cancellation

This presolve method extends the idea of the previous presolve method onto columns, i.e. we now aim for nonzero cancellations based on two columns of the constraint matrix A. To be more precise, consider the sum of two columns of problem (1)

$$\begin{aligned} \begin{aligned} \left[ \begin{matrix} A_{Uj} \\ A_{Vj} \\ A_{Wj} \\ \\ \end{matrix} \right] x_j&\ \ +&\left[ \begin{matrix} A_{Uk} \\ A_{Vk} \\ \\ A_{Yk} \\ \end{matrix}\right] x_k, \end{aligned} \end{aligned}$$

(12)

where $j, k\in \mathcal {N}$ and U, V, W, $Y \subseteq \mathcal {M}$ are disjoint subsets of the row indices. We first discuss the case where $x_j$ is a continuous variable. Suppose there exists a scalar $\lambda \in \mathbb {R}$ such that $\lambda A_{Uj} - A_{Uk} = 0$, $\lambda A_{Vj} - A_{Vk} \ne 0$. By rewriting (12) as

$$\begin{aligned} \begin{aligned} \left[ \begin{matrix} A_{Uj} \\ A_{Vj} \\ A_{Wj} \\ \\ \end{matrix} \right] (x_j + \lambda x_k)&\ \ +&\left[ \begin{array}{lll} &{} &{} \\ A_{Vk} &{} -&{} \lambda A_{Vj} \\ &{} -&{} \lambda A_{Wj} \\ A_{Yk} &{} &{} \\ \end{array}\right] x_k, \end{aligned} \end{aligned}$$

and introducing a new variable $z := x_j + \lambda x_k$, we obtain

$$\begin{aligned} \begin{aligned} \left[ \begin{matrix} A_{Uj} \\ A_{Vj} \\ A_{Wj} \\ \\ \end{matrix} \right] z&\ \ +&\left[ \begin{array}{lll} &{} &{} \\ A_{Vk} &{} -&{} \lambda A_{Vj} \\ &{} -&{} \lambda A_{Wj} \\ A_{Yk} &{} &{} \\ \end{array}\right] x_k. \end{aligned} \end{aligned}$$

(13)

From the definition of z, it follows that the lower and upper bounds of z are

$$\begin{aligned} \ell _z =\left\{ \begin{array}{ll} \ \ell _j + \lambda \ell _k, &{}\ \text {for} \ \lambda> 0, \\ \ \ell _j + \lambda u_k , &{}\ \text {for} \ \lambda< 0, \end{array}\right. \ \text {and} \ \ u_z =\left\{ \begin{array}{ll} u_j +\lambda u_k, &{}\ \text {for} \ \lambda > 0, \\ u_j + \lambda \ell _k, &{}\ \text {for} \ \lambda < 0, \end{array}\right. \end{aligned}$$

respectively. However, in order to keep the bounds of $\ell _j \le x_j \le u_j$, the constraint

$$\begin{aligned} \ell _j \le z - \lambda x_k \le u_j \end{aligned}$$

(14)

needs to explicitly be added to problem (1). As is the case for the sparsification method from Sect. 3.1, the new representation consisting of (13) is of interest when $|U| - |W| > 0$ holds. One difference to the row-based version is that the reformulation contains the additional overhead of adding the constraint (14) to the problem (1). However, if $x_j$ is a free variable, i.e. $\ell _j=-\infty$ and $u_j = \infty$ hold, the constraint (14) is redundant and does not need to be added to the problem (1). When the bounds of $x_j$ are implied by the constraints and the bounds of other variables, $x_j$ can also be treated as a free variable. In this case one speaks of an implicit free variable.

We now consider the case where $x_j$ is an integer variable. To maintain integrality, we require that $x_k$ is also an integer variable and $\lambda$ is an integral scalar. This guarantees that, when reversing the transformation during post-processing, we can obtain an integral value of $x_k$ from the values of $x_j$ and the new integer variable z.

Note that applying this presolve method to the problem (1) can be seen as applying the row-based version to the associated dual problem. Therefore it takes time linear in the number of constraints, i.e. its time complexity is $O(|{\mathcal {M}}|)$. Due to the additional overhead resulting from constraint (14), the difference in the number of nonzeros $|U| - |W|$ is generally required to be larger than in the row-based method.

3.3 LP-based bound tightening on two constraints

The idea of using two rows of the constraint matrix A to determine tighter variable bounds or redundant constraints has already been described in Achterberg et al. (2019). We will first present the presolve method and then discuss an important observation to omit unnecessary calculations.

Consider two arbitrary constraints of (1)

$$\begin{aligned} \begin{array}{rcrcrccl} A_{rU} x_U &{}+&{} A_{rV}x_V &{} &{} &{} &{} \ge &{} b_r, \\ A_{sU} x_U &{}+&{} &{} &{} &{} A_{sW} x_W &{} \ge &{} b_s, \end{array} \end{aligned}$$

where $r,s \in \mathcal {M}$ and $U,V,W \subseteq \mathcal {N}$. Note that for any $i \in \mathcal {M}$ with $\circ _i \in \{\le , =\}$ the corresponding constraint can be normalized to be of the form above. Together with the variable bounds $\ell \le x \le u$ we exploit the special form of the two constraints to set up the following two LPs

$$\begin{aligned} \begin{array}{lcclcl} y_{\max } &{}=&{} \max &{} A_{rU}x_U &{} &{} \\ &{}&{}\text {s.t. } &{} A_{sU} x_U + A_{sW} x_W \ge b_s\\ &{}&{} &{} \ell \le x \le u,\\ y_{\min } &{}=&{} \min &{} A_{rU}x_U &{} &{} \\ &{}&{}\text {s.t. } &{} A_{sU} x_U + A_{sW} x_W \ge b_s\\ &{}&{} &{} \ell \le x \le u. \end{array} \end{aligned}$$

(15)

As shown in Dantzig (1957) and Balas and Zemel (1980), each of these problems can be solved within linear time. Provided we have finite values for $y_{\max }$ and $y_{\min }$, i.e. the above problems have been feasible and bounded, the results can be used to, again in linear time, derive potentially stronger variable bounds and detect redundancy of constraint r. Bounds on variables $x_j, j \in V$, can be calculated via (16) where $V' = V \setminus \{j\}$ and constraint r is redundant if condition (17) holds. Note the similarity of (16) to (5) and (7), where $\sup (A_{rU}x_U)$ is replaced by $y_{\max }$ as well as the fact that $y_{\max }$ is at least as strong, and potentially stronger, as $\sup (A_{rU}x_U)$.

$$\begin{aligned} \begin{array}{c} x_j \ge \frac{b_r - \sup (A_{rV'} x_{V'}) - y_{\max }}{a_{rj}}, \text { for } a_{rj} > 0\\ x_j \le \frac{b_r - \sup (A_{rV'} x_{V'}) - y_{\max }}{a_{rj}}, \text { for } a_{rj} < 0 \end{array} \end{aligned}$$

(16)

$$\begin{aligned} \inf (A_{rV} x_V) \ge b_r - y_{\min } \end{aligned}$$

(17)

Note that the roles of the rows r and s are interchangeable. As the following lemma shows, bound tightening on the constraints r and s may only improve the bounds on variables $x_j, j \in V$ if there exists at least one variable $x_i, i \in U$ with $a_{ri}< 0 < a_{si}$ or $a_{si}< 0 < a_{ri}$.

Lemma 3.1

If for all variables $x_i, i \in U$, the corresponding coefficients $a_{ri}$ and $a_{si}$ are either both non-negative or both non-positive, then inequality (16) cannot improve the bounds on the variables $x_j, j \in V$, over regular FBBT on constraint r.

Proof

Let $x_i, i \in U$ be a variable such that its coefficients $a_{ri}$ and $a_{si}$ are both non-negative. In this case, setting the variable $x_i$ to its upper bound maximizes the value of $y_{\max }$ and also contributes most to satisfying the constraint $A_{sU} x_U + A_{sW} x_W \ge b_s$. Analogously, a variable with non-positive coefficients $a_{ri}$ and $a_{si}$ should be set to its lower bound. Hence, the value $y_{\max }$ of the optimal solution coincides with $\sup (A_{rU} x_U)$ such that (16) yields the same bounds as (5) and (7) on constraint r. $\square$

The lemma above shows that in order to improve the bounds over what can be achieved using FBBT on a single constraint, it is of crucial importance to find pairs of inequalities that contain variables such that their respective coefficients have opposite sign.

Remark 3.2

By rewriting the objective function for $y_{\min }$ as $\max -A_{rU}x_U$ we can, by the same arguments as in Lemma 3.1, reason that equal signs are advantageous for detecting redundant constraints. Since we focus on bound tightening, we did not continue this line of thought in this work, but it certainly is an interesting experiment for future research.

Next we give an example to further illustrate the basic idea as well as the statements made in Lemma 3.1 and Remark 3.2.

Example 3.3

Consider the following two constraints

$$\begin{aligned} \begin{array}{rcrcrcrcr} x_1 &{}+&{} 2 x_2 &{}+&{} 3 x_3 &{}+&{} 2 x_4 &{} \ge &{} 4, \\ &{}&{}x_2 &{}+&{} x_3 &{}+&{} x_4 &{}\ge &{} 2, \end{array} \end{aligned}$$

with $x_1,\ldots ,x_4 \in [0,1]$, $U=\{2,3,4\}$, $V=\{1\}$, and $W = \emptyset$. Then we get $y_{\max } = 7$ and $y_{\min } = 4$ and applying (16) and (17) yields

$$\begin{aligned} x_1 \ge 4 - 7&= -3\\ 0 \ge 4 - 4&= 0. \end{aligned}$$

Therefore, the lower bound of $x_1$ could not be tightened over simple FBBT on the first constraint, but we have detected that the first constraint can be removed from the problem as it is redundant with the second constraint.

If we keep the variable bounds and change the problem to

$$\begin{aligned} \begin{array}{rcrcrcrcr} x_1 &{}+&{} 2 x_2 &{}+&{} 3 x_3 &{}+&{} 2 x_4 &{} \ge &{} 4, \\ &{}&{}-x_2 &{} -&{} x_3 &{} - &{} x_4 &{} \ge &{} -1, \end{array} \end{aligned}$$

we obtain $y_{\max } = 3$ and $y_{\min } = 0$. Again, we apply (16) as well as (17) and get

$$\begin{aligned} x_1 \ge 4 - 3&= 1\\ 0 \ge 4 - 0&= 4. \end{aligned}$$

In this case, due to opposite signs for coefficients appearing in both constraints, we were able to tighten the lower bound on $x_1$, but the first constraint is no longer redundant with the second one. Note that FBBT on the first constraint would still yield $-3$ as lower bound on $x_1$.

In certain cases, presolve methods interact with each other. This is one reason why different presolve methods are often grouped by their runtime behavior and executed in repeated rounds (Gamrath et al. 2016). Of particular interest are cases where one method generates a structure that helps another method to perform further useful reductions. As an example, we will look at an interaction between the method of Sect. 3.1 and the method described here.

Example 3.4

Consider the following problem:

With $U=\{1,2\}, V=\{3,4,5\}$ and $W=\{6,7\}$ we perform LP-based bound tightening for the first and second constraints as follows:

to obtain $y_{\max }=4$. Now we would like to determine a tighter lower bound on $x_3$, but this is not possible as $\sup (x_3+x_4)=\infty$. However, if we first use the presolve method of Sect. 3.1 and add the equality to the first constraint, then the variables $x_4$ and $x_5$ disappear. As a results, we obtain $x_3 \ge (6-y_{\max })/1 = 2$.

3.4 Bound tightening on convex combinations of two constraints

Belotti (2013) presented an algorithm to efficiently derive bounds for all variables from the LP relaxation of the problem

$$\begin{aligned} \begin{array}{c} A_{r\cdot } x \ge b_r \\ A_{s\cdot } x \ge b_s \\ \ell \le x \le u \\ x_j \in \mathbb {Z}\;\forall j \in \mathcal {I}\subseteq \mathcal {N}, \end{array} \end{aligned}$$

(18)

where $r,s\in \mathcal {M}$. Note again that for any constraint i with $\circ _i \in \{\le , =\}$ the corresponding constraint can be normalized to be of the same form as constraints r and s above. We will first summarize the original method and then discuss an extension onto two rows together with disjoint set packing constraints.

3.4.1 Basic bound tightening on convex combinations of two constraints

The basic idea is to reformulate the problem using convex combinations of the two constraints in (18). Let $\lambda \in [0,1]$, for the convex combination of the coefficient vectors we write ${\bar{a}}^{rs}(\lambda ) :=\lambda A_{r\cdot } + (1 - \lambda ) A_{s\cdot }$ and ${\bar{b}}^{rs}(\lambda ) :=\lambda b_r + (1-\lambda ) b_s$ for the convex combination of the right-hand side. For single indices $j \in \mathcal {N}$ or index subsets $V \subseteq \mathcal {N}$ we write ${\bar{a}}^{rs}_j(\lambda )$ and ${\bar{a}}^{rs}_V(\lambda )$, respectively, to address the corresponding entries of ${\bar{a}}^{rs}(\lambda )$. One may now perform FBBT on the combined constraint ${\bar{a}}^{rs}(\lambda ) x \ge {\bar{b}}^{rs}(\lambda )$. Note that for $\lambda \in \{0,1\}$ this cannot improve the bounds over FBBT on the original constraints, and we therefore restrict ourselves to $\lambda \in (0,1)$. In short, possibly stronger variable bounds $[{\bar{\ell }}_j, {\bar{u}}_j]$ on a variable $x_j$ can be derived by solving the following one-dimensional optimization problems:

$$\begin{aligned} {\bar{\ell }}_j&= \max \bigg \{ \frac{L_j(\lambda )}{{\bar{a}}^{rs}_j(\lambda )} \mid \lambda \in (0,1) \wedge {\bar{a}}^{rs}_j(\lambda ) > 0 \bigg \} \end{aligned}$$

(19)

$$\begin{aligned} {\bar{u}}_j&= \min \bigg \{ \frac{L_j(\lambda )}{{\bar{a}}^{rs}_j(\lambda )} \mid \lambda \in (0,1) \wedge {\bar{a}}^{rs}_j(\lambda ) < 0 \bigg \} , \end{aligned}$$

(20)

where

$$\begin{aligned} L_j(\lambda ) :=&\ {\bar{b}}^{rs}(\lambda ) - \sup ({\bar{a}}^{rs}(\lambda )_{\mathcal {N}\setminus \{j\}}x_{\mathcal {N}\setminus \{j\}}). \end{aligned}$$

Belotti (2013) has then shown that these problems can be solved by evaluating the piecewise linear $L_j(\lambda )$ for a small finite set of values for $\lambda$, namely the set of all breakpoints of $L_j(\lambda )$. The next proposition summarizes the result.

Proposition 3.5

The set

$$\begin{aligned} \Lambda :=\{ \lambda \in (0,1) \mid (\exists j \in \mathcal {N}:{\bar{a}}^{rs}_j(\lambda ) = 0 \wedge {\bar{a}}^{rs}_j(\lambda ^*) \ne 0 \;\forall \lambda ^* \ne \lambda , \lambda ^* \in (0,1)\} \end{aligned}$$

contains all optimal solutions to the problems (19) and (20).

Note that problems (19) and (20) may not have optimal solutions or are unbounded. However, these edge cases, which are discussed in more detail in the original paper (Belotti 2013), do not affect the overall viability of this approach.

Computing $L_j(\lambda )$ for all variables and each $\lambda \in \Lambda$ individually would result in an algorithm with running time in $O(|{\mathcal {N}}|^3)$. However, it is possible to simultaneously solve the optimization problems for all variables in time in $O(|{\mathcal {N}}|^2)$ by using constant-time update operations for each $\lambda \in \Lambda$ instead of recomputing each $L_j(\lambda )$ individually. We will outline the basic idea as well as the core operations; for full details of the algorithm, see Belotti (2013).

Denote $\Lambda = \{\lambda _1, \ldots \lambda _{|{\Lambda }|}\}$ such that $0< \lambda _1< \cdots< \lambda _{|{\Lambda }|} < 1$ and let ${\tilde{\lambda }} \in (0,\lambda _1)$. We define

$$\begin{aligned} L^r&:=\ b_r - \sum _{{\bar{a}}^{rs}_j({\tilde{\lambda }})> 0} a_{rj} u_j - \sum _{{\bar{a}}^{rs}_j({\tilde{\lambda }})< 0} a_{rj} \ell _j\\ L^s&:=\ b_s - \sum _{{\bar{a}}^{rs}_j({\tilde{\lambda }}) > 0} a_{sj} u_j - \sum _{{\bar{a}}^{rs}_j({\tilde{\lambda }}) < 0} a_{sj} \ell _j, \end{aligned}$$

which, not using ${\tilde{\lambda }}$, can be rewritten as

$$\begin{aligned} L^r&= \ b_r - \sum _{\begin{array}{c} a_{sj}> 0 \vee (a_{sj} = 0 \wedge a_{rj} > 0)\\ j \in {{\,\mathrm{supp}\,}}(A_{r\cdot }) \end{array}} a_{rj} u_j - \sum _{\begin{array}{c} a_{sj}< 0 \vee (a_{sj} = 0 \wedge a_{rj} < 0)\\ j \in {{\,\mathrm{supp}\,}}(A_{r\cdot }) \end{array}} a_{rj} \ell _j \end{aligned}$$

(21)

$$\begin{aligned} L^s&= \ b_s - \sum _{\begin{array}{c} a_{sj} > 0\\ j \in {{\,\mathrm{supp}\,}}(A_{s\cdot }) \end{array}} a_{sj} u_j - \sum _{\begin{array}{c} a_{sj} < 0\\ j \in {{\,\mathrm{supp}\,}}(A_{s\cdot }) \end{array}} a_{sj} \ell _j. \end{aligned}$$

(22)

Since the signs of ${\bar{a}}^{rs}_j(\lambda ), j \in \mathcal {N}$ do not change between 0 and $\lambda _1$, we can compute $L_j(\lambda )$ for all $j \in \mathcal {N}, \lambda \in [0, \lambda _1]$ via

$$\begin{aligned} L_j(\lambda )&= \lambda L^r + (1 - \lambda ) L^s + {\bar{a}}_j^{rs}(\lambda ) d_j\\ d_j&= {\left\{ \begin{array}{ll} u_j, &{}\text { if } {\bar{a}}^{rs}_j(\lambda ) > 0\\ \ell _j, &{}\text { if } {\bar{a}}^{rs}_j(\lambda ) < 0.\\ \end{array}\right. } \end{aligned}$$

In other words, if $L^r$ and $L^s$ are given and $\lambda \in [0, \lambda _1]$, we can compute bounds for a variable $x_j$ in constant time using (23) if ${\bar{a}}^{rs}_j(\lambda ) > 0$ and (24) if ${\bar{a}}^{rs}_j(\lambda ) < 0$.

$$\begin{aligned} x_j&\ge \frac{\lambda L^r + (1 - \lambda ) L^s + {\bar{a}}_j^{rs}(\lambda ) u_j}{{\bar{a}}_j^{rs}(\lambda )} \end{aligned}$$

(23)

$$\begin{aligned} x_j&\le \frac{\lambda L^r + (1 - \lambda ) L^s + {\bar{a}}_j^{rs}(\lambda ) \ell _j}{{\bar{a}}_j^{rs}(\lambda )}. \end{aligned}$$

(24)

In order to derive bounds for $\lambda \in [\lambda _1, \lambda _2]$ we need to first update $L^r$ and $L^s$. More precisely, for each variable $x_j, j \in \mathcal {N}$ with ${\bar{a}}^{rs}_j(\lambda _1) = 0$, i.e. each variable whose combined coefficient switches sign in $\lambda _1$, we need update $L^r$ and $L^s$ via (25) and (26) respectively. If a combined coefficient changes sign from positive to negative, we need to set the corresponding variable from its upper bound to its lower bound. Analogously, a variable needs to be set from its lower bound to its upper bound if its combined coefficient changes sign from negative to positive.

$$\begin{aligned} L^r \leftarrow&L^r + a_{rj}\delta \end{aligned}$$

(25)

$$\begin{aligned} L^s \leftarrow&L^s + a_{sj}\delta \end{aligned}$$

(26)

$$\begin{aligned} \delta =&{\left\{ \begin{array}{ll} u_j - \ell _j, &{}\text { if } a_{rj}< 0< a_{sj},\\ \ell _j - u_j, &{}\text { if } a_{sj}< 0 < a_{rj} \end{array}\right. } \end{aligned}$$

Iteratively repeating the bound calculations and updates for all $\lambda \in \Lambda$ solves the problems (19) and (20). To summarize, we state the resulting procedure in Algorithm 1. For more details, especially on implementation, see Algorithm 1 in Belotti (2013).

3.4.2 Further improvement via disjoint set packing constraints

In this section, we show that Belotti’s approach can be extended to derive bounds from Problem (18) together with an arbitrary number of disjoint set packing constraints of the form

$$\begin{aligned} \begin{aligned} \sum _{j \in S_p} x_j&\le 1 \qquad \quad \forall S_p \in \mathcal {S}\\ x_j&\in \{0,1\} \quad \ \forall S_p \in \mathcal {S}\ \forall j \in S_p, \end{aligned} \end{aligned}$$

(27)

where $\mathcal {S} = \{S_1,\ldots ,S_{|{\mathcal {S}}|}\}$ is a partitioning of a subset of the integer variable index set $\mathcal {I}$. More precisely, for $\lambda \in (0,1)$ we want to derive bounds from the problem

$$\begin{aligned} \begin{aligned} {\bar{a}}^{rs}(\lambda )&x \ge {\bar{b}}^{rs}(\lambda ) \\ \ell \le&x \le u \\&(27) \\ x_j&\in \mathbb {Z}\; \forall j \in \mathcal {I}\subseteq \mathcal {N}. \\ \end{aligned} \end{aligned}$$

(28)

To further simplify notation, we write $S :=\bigcup _{S_p \in \mathcal {S}} S_p$ and $T :=\mathcal {N}\setminus S$.

In the following two examples, we illustrate the effect of the addition of set packing constraints and then proceed to analyze how Belotti’s algorithm needs to be adjusted in order to achieve these results with minimal additional computational effort.

Example 3.6

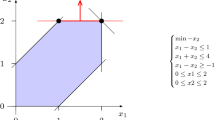
Consider the following mixed-integer problem

with one set packing constraint. Figure 1a shows a comparison between

$$\begin{aligned} \frac{L_3(\lambda )}{{\bar{a}}_3(\lambda )} = L_3(\lambda ) = {\left\{ \begin{array}{ll} -1 + 3\lambda , &{}\quad \text {if } \lambda \in (0, \frac{1}{3}]\\ 0,&{}\quad \text {if } \lambda \in (\frac{1}{3},\frac{2}{3}]\\ 2 - 3\lambda , &{}\quad \text {if } \lambda \in (\frac{2}{3}, 1), \end{array}\right. } \end{aligned}$$

(29)

which results from applying the original method presented in 3.4.1, and solving the following optimization problem for $\lambda \in (0,1)$.

(30)

Whereas the original method cannot tighten the bound at all, when considering the set packing constraint we get a positive lower bound on $x_3$ for $\lambda \in (\frac{1}{3}, \frac{2}{3})$. First, this illustrates one case for which adding a set packing constraint indeed yields a better bound on $x_3$. Second, the example shows that the set $\Lambda$ needs to be extended as it no longer contains all optimal solutions to (30). In this example, there is the new breakpoint $\lambda = \frac{1}{2}$ where we have ${\bar{a}}_1(\frac{1}{2}) = \frac{1}{2} = {\bar{a}}_2(\frac{1}{2})$. This new breakpoint is clearly visible in Fig. 1a. We will see later, that at all new breakpoints $\lambda ^*$ the index $\hbox {argmax}_{j \in S_p}\{{\bar{a}}_j(\lambda )\}$ changes between $\lambda < \lambda ^*$ and $\lambda > \lambda ^*$.

Fig. 1

Bounds on variables $x_3$ in Example 3.6 (left) and $x_4$ in Example 3.7 (right)

Example 3.7

Consider the following mixed-integer program

Again, Fig. 1b shows for $\lambda \in (0,1)$ the comparison between the results obtained by the method presented in 3.4.1, i.e. ,

$$\begin{aligned} \frac{L_4(\lambda )}{{\bar{a}}_4(\lambda )} = {\left\{ \begin{array}{ll} \frac{6\lambda - 2}{3 - \lambda }, &{} \quad \text {if } \lambda \in (0, \frac{2}{5}]\\ \frac{\lambda }{3 - \lambda }, &{} \quad \text {if } \lambda \in (\frac{2}{5}, \frac{3}{4}]\\ \frac{3 - 3\lambda }{3 - \lambda }, &{} \quad \text {if } \lambda \in (\frac{3}{4}, 1], \end{array}\right. } \end{aligned}$$

(31)

and solving

(32)

Similar to the previous example, the set packing constraint allows us to derive stronger bounds. Whereas the original method yields a lower bound of $\frac{1}{3}$ for $\lambda = \frac{3}{4}$, the set packing constraint allows us to tighten that bound to 1 for $\lambda = \frac{2}{3}$ and we get new breakpoints again, namely $\lambda _1 = \frac{1}{3}$ and $\lambda _2 = \frac{2}{3}$. Note that for these breakpoints we also have ${\bar{a}}_1(\frac{1}{3}) = \frac{5}{3} = {\bar{a}}_3(\frac{1}{3})$ and ${\bar{a}}_1(\frac{2}{3}) = \frac{4}{3} = {\bar{a}}_2(\frac{2}{3})$ respectively. As a final note, while $L_j(\lambda )$ and ${\bar{a}}^{rs}_j(\lambda )$ are always (piecewise) linear, this does not necessarily hold for the quotient $\frac{L_j(\lambda )}{{\bar{a}}^{rs}_j(\lambda )}$.

Note that in both examples we have strengthened the bounds of a variable that did not appear in any set packing constraint. In the following, we assume $j \in T$, i.e. the variable $x_j$ is not present in any set packing constraint. For a variable $x_j, j \in S_p, S_p \in \mathcal {S}$, we can still derive bounds by simply relaxing the corresponding set packing constraint to $\sum _{k \in S_p \setminus \{j\}} x_k \le 1$. At the end of the section we present derivations that are stronger than what is achievable by relaxing the set packing constraint.

Let $j \in T$. Since for each subset $S_p \in \mathcal {S}$ we can choose at most one variable $x_k \in S_p$ to be set to one, we obtain, for any given $\lambda \in (0,1)$ with ${\bar{a}}^{rs}_j(\lambda ) > 0$, valid bounds by

$$\begin{aligned} x_j \ge \frac{1}{{\bar{a}}^{rs}_j(\lambda )}\big ({\bar{b}}^{rs}(\lambda ) - \sup ({\bar{a}}^{rs}_{T\setminus \{j\}}(\lambda )x_{T\setminus \{j\}}) - \sum _{S_p \in \mathcal {S}} \max \big \{0, \max _{k \in S_p}\{{\bar{a}}^{rs}_k(\lambda )\}\big \}\big ), \end{aligned}$$

(33)

and analogously for $\lambda \in (0,1)$ with ${\bar{a}}^{rs}_j(\lambda ) < 0$ we have

$$\begin{aligned} x_j \le \frac{1}{{\bar{a}}^{rs}_j(\lambda )}\big ({\bar{b}}^{rs}(\lambda ) - \sup ({\bar{a}}^{rs}_{T\setminus \{j\}}(\lambda )x_{T\setminus \{j\}}) - \sum _{S_p \in \mathcal {S}} \max \big \{0, \max _{k \in S_p}\{{\bar{a}}^{rs}_k(\lambda )\}\big \}\big ). \end{aligned}$$

(34)

Note that (33) and (34) solve, in their respective cases, the problems $\min x_j$, s.t. (28), as well as $\max x_j$, s.t. (28) to optimality. This also shows that for any given $\lambda \in (0,1)$ the set packing constraint corresponding to a subset $S_p \in \mathcal {S}$ is redundant if and only if ${\bar{a}}^{rs}_{j}(\lambda ) > 0$ holds for at most one index $j \in S_p$. To simplify notation, define

$$\begin{aligned}&\Phi _p(\lambda ) :=\max \big \{0, \max _{k \in S_p}\{{\bar{a}}^{rs}_k(\lambda )\}\big \}, \forall S_p \in \mathcal {S},\\&\Gamma _j(\lambda ) :={\bar{b}}^{rs}(\lambda ) - \sup ({\bar{a}}^{rs}_{T\setminus \{j\}}(\lambda )x_{T\setminus \{j\}}) - \sum _{S_p \in \mathcal {S}} \Phi _p(\lambda ). \end{aligned}$$

Transferring bounds (33) and (34) to the problems (19) and (20) then yields

$$\begin{aligned} {\bar{\ell }}_j&= \max \left\{ \frac{\Gamma _j(\lambda )}{{\bar{a}}^{rs}_j(\lambda )} \mid \lambda \in (0,1) \wedge {\bar{a}}^{rs}_j(\lambda ) > 0 \right\} , \end{aligned}$$

(35)

$$\begin{aligned} {\bar{u}}_j&= \min \left\{ \frac{\Gamma _j(\lambda )}{{\bar{a}}^{rs}_j(\lambda )} \mid \lambda \in (0,1) \wedge {\bar{a}}^{rs}_j(\lambda ) < 0 \right\} . \end{aligned}$$

(36)

Similar to problems (19) and (20), the problems (35) and (36) may not have optimal solutions or are unbounded and again, these edge cases do not affect the overall viability of this approach, and hence we restrict ourself to cases where these problems are bounded and have an optimal solution.

In order to show Belotti’s algorithm can be extended to the problems above we prove that for solving these problems a linear number of evaluations of $\Gamma _j(\lambda )$ suffices. As a first step to prove the analogue of Proposition 3.5 for the problems (35) and (36), we show that $\Gamma _j(\lambda )$ is, just like $L_j(\lambda )$ in the original case, a piecewise linear function and determine all its breakpoints.

Lemma 3.8

For any $j \in T$, the function $\Gamma _j(\lambda )$ is piecewise linear on its domain (0, 1) and the set

$$\begin{aligned}&{\tilde{\Lambda }} :=\Lambda \cup \{\lambda \in (0,1) \mid \exists S_p \in \mathcal {S}: \exists k, l \in S_p,k \ne l : ({\bar{a}}^{rs}_{k}(\lambda ) = {\bar{a}}^{rs}_{l}(\lambda ) = \Phi _p(\lambda )\\&\wedge {\bar{a}}^{rs}_k(\lambda ') \ne {\bar{a}}^{rs}_l(\lambda ')\;\forall \lambda ' \ne \lambda , \lambda ' \in (0,1))\} \end{aligned}$$

contains all its breakpoints.

Proof

Each $\Phi _p(\lambda ), S_p \in \mathcal {S}$, is defined as the maximum over the constant zero function and the set of the linear terms ${\bar{a}}^{rs}_k(\lambda ), k \in S_p$, and is hence piecewise linear. Consequently, we have that $\Gamma _j(\lambda )$ is piecewise linear as the sum of linear and piecewise linear functions.

By the same arguments as in the original case the set $\Lambda$ contains all breakpoints of ${\bar{b}}^{rs}(\lambda ) - \sup ({\bar{a}}^{rs}_{T\setminus \{j\}}(\lambda )x_{T\setminus \{j\}})$. Let $\lambda ^* \in (0,1)$ be a breakpoint of $\Phi _p(\lambda )$. We distinguish two cases:

• (i) $\Phi _p(\lambda ^*) = 0$: In this case some ${\bar{a}}^{rs}_k(\lambda )$ intersects the constant zero function in $\lambda ^*$. More precisely, there exists some $k \in S_p$ with ${\bar{a}}^{rs}_k(\lambda ^*) = 0 \wedge {\bar{a}}^{rs}_k(\lambda ) \ne 0 \;\forall \lambda \ne \lambda ^*, \lambda \in (0,1)$, and hence, $\lambda ^*$ is, by definition of $\Lambda$ already contained in ${\tilde{\Lambda }}$.

• (ii) $\Phi _p(\lambda ^*) > 0$: Here we have an intersection between two ${\bar{a}}^{rs}_k(\lambda )$, i.e. there exist distinct indices $k,l \in S_p$ with ${\bar{a}}^{rs}_k(\lambda ^*) = {\bar{a}}^{rs}_l(\lambda ^*) = \Phi _p(\lambda ^*)$ and ${\bar{a}}^{rs}_k(\lambda ) \ne {\bar{a}}^{rs}_l(\lambda ) \;\forall \lambda \ne \lambda ^*, \lambda \in (0,1)$. Therefore the breakpoint $\lambda ^*$ is also contained in ${\tilde{\Lambda }}$ which completes the proof.

$\square$

Note that $|{{\tilde{\Lambda }}}|$ is linear in the number of variables since the set packing constraints are disjoint. Further, the set ${\tilde{\Lambda }}$ can be computed in time in $O(|{\mathcal {N}}| \log {|{\mathcal {N}}|})$. A simple well known algorithm for this would be the following. For each $S_p \in \mathcal {S}$ we first sort the linear functions ${\bar{a}}^{rs}_k(\lambda ), k \in S_p$ by their gradients $a_{rk} - a_{sk}$. For the ${\bar{a}}^{rs}_k(\lambda )$ with the smallest gradient we then have ${\bar{a}}^{rs}_k(\lambda ) = \Phi _p(\lambda )$ for small enough values of $\lambda$. From there, go through the remaining ${\bar{a}}^{rs}_k(\lambda )$ in ascending order of their gradients and iteratively compute the next breakpoint. Since each ${\bar{a}}^{rs}_k(\lambda )$ needs to be considered at most once, the total running time is in $O(|{\mathcal {N}}| \log |{\mathcal {N}}|)$.

Theorem 3.9

If an optimal solution to Problem (35) exists, then at least one optimal solution is also contained in ${\tilde{\Lambda }}$. The same statement holds for Problem (36).

Proof

By Lemma 3.8 the set ${\tilde{\Lambda }}$ contains all breakpoints of the piecewise linear $\Gamma _j(\lambda )$. Together with ${\bar{a}}^{rs}(\lambda )$ being linear, we established the same conditions as in the proof of Proposition 3.5. The remaining proof of this theorem is then identical and can be found in full detail as proof of Proposition 1 in Belotti (2013). $\square$

To extend the original algorithm for computing bounds one now proceeds as follows. First, the extended algorithm must compute $L^r$ and $L^s$ in a slightly different way. For easier notation, let $\kappa _p \in S_p$ be the index of a variable $x_{\kappa _p}$ with $a_{s\kappa _p} = \max _{j \in S_p}\{a_{sj}\}$ and $a_{r\kappa _p} - a_{s\kappa _p} \ge \max \{(a_{rj} - a_{sj}) \mid j \in S_p, a_{sj} = a_{s\kappa _p}\}$. In other words, of the variables $x_j, j \in S_p$, with maximum coefficient ${\bar{a}}^{rs}_{j}(\lambda )$ we choose the one with maximal gradient of ${\bar{a}}^{rs}_{j}(\lambda )$.

$$\begin{aligned}&\tilde{L}^r = \ b_r - \sum _{\begin{array}{c} a_{sj}> 0 \vee (a_{sj} = 0 \wedge a_{rj}> 0)\\ j \in T \end{array}} a_{rj} u_j - \sum _{\begin{array}{c} a_{sj}< 0 \vee (a_{sj} = 0 \wedge a_{rj}< 0)\\ j \in T \end{array}} a_{rj} \ell _j - \sum _{S_p \in \mathcal {S}} \Phi ^r_p\\&\tilde{L}^s = \ b_s - \sum _{\begin{array}{c} a_{sj} > 0\\ j \in T \end{array}} a_{sj} u_j - \sum _{\begin{array}{c} a_{sj} < 0\\ j \in T \end{array}} a_{sj} \ell _j - \sum _{S_p \in \mathcal {S}} \Phi ^s_p \end{aligned}$$

where

$$\begin{aligned} \Phi ^r_p = \left. {\left\{ \begin{array}{ll} 0, &{} \text {if } a_{s\kappa _p}< 0 \vee (a_{s\kappa _p} = 0 \wedge a_{r\kappa _p} \le 0)\\ a_{r\kappa _p}, &{} \text {else } \end{array}\right. }\right. ,\\ \Phi ^s_p = \left. {\left\{ \begin{array}{ll} 0, &{} \text {if } a_{s\kappa _p} < 0 \vee (a_{s\kappa _p} = 0 \wedge a_{r\kappa _p} \le 0)\\ a_{s\kappa _p}, &{} \text {else } \end{array}\right. }\right. \\ \end{aligned}$$

Second, the extended algorithm must compute the new set of breakpoints ${\tilde{\Lambda }}$ which, as mentioned above, can be done in time in $O(|{\mathcal {N}}| \log |{\mathcal {N}}|)$ and therefore does not increase the total time complexity. Note that in the extension it is required to track which variable coefficient currently determines the value of $\Phi _p(\lambda )$ for each $S_p \in \mathcal {S}$. However, this only leads to linear computational overhead if the breakpoints and variables are labeled accordingly while computing ${\tilde{\Lambda }}$. The bound calculations corresponding to (23) and (24) as well as the updates corresponding to (25) and (26) essentially work the same but consist of larger case distinctions due to the set packing constraints.

Before closing this section we will discuss what can be done for variables appearing in the set packing constraints. Let $j \in S_p$ for some fixed $S_p \in \mathcal {S}$ and $\lambda \in {\tilde{\Lambda }}$. We distinguish four cases.

• (i) ${\bar{a}}^{rs}_j(\lambda ) > 0 \wedge {\bar{a}}^{rs}_j(\lambda ) < \Phi _p(\lambda )$: In this case we directly apply (33) since the right-hand side does not involve $x_j$. Due to checking for a lower bound and $x_j \in \{0,1\}$ we assume $x_j = 0$ and with ${\bar{a}}^{rs}_j(\lambda ) > 0$ the expression reduces to

  $$\begin{aligned} 0 \ge \Gamma _j(\lambda ). \end{aligned}$$

  (37)

  Together with the set packing constraint corresponding to $S_p$ the original problem is infeasible if above condition does not hold.

• (ii) ${\bar{a}}^{rs}_j(\lambda ) > 0 \wedge {\bar{a}}^{rs}_j(\lambda ) = \Phi _p(\lambda )$: Here we use a relaxation of (33) to detect infeasibility. More precisely, we assume there exists some $k \in S_p, k \ne j$ with ${\bar{a}}^{rs}_j(\lambda ) = {\bar{a}}^{rs}_k(\lambda )$. Then, as in the previous case, we check for infeasibility via (37).

  A proper lower bound for the given $\lambda$ could be derived by strengthening the summand $\Phi _p(\lambda )$ of $\Gamma _j(\lambda )$ to $\max _{k \in S_p \setminus \{j\}}\{0, \max \{{\bar{a}}^{rs}_k(\lambda )\}\}$ and considering the additional breakpoints of this strengthening that may not already be contained in ${\tilde{\Lambda }}$. However, we are aware of no efficient way to incorporate these calculations without creating additional computational overhead.

• (iii) ${\bar{a}}^{rs}_j(\lambda ) < 0 \wedge \Phi _p(\lambda ) = 0$: Now the set packing constraint corresponding to $S_p$ has no effect and we get an upper bound on $x_j$ via (34).

• (iv) ${\bar{a}}^{rs}_j(\lambda ) < 0 \wedge \Phi _p(\lambda ) > 0$: Any solution with $x_j = 1$ immediately forces $x_k = 0, k \in S_p,k \ne j$. We can therefore adjust (34) to this case and set $x_j = 0$ if

  $$\begin{aligned} \frac{\Gamma _j(\lambda ) + \Phi _p(\lambda )}{{\bar{a}}^{rs}_j(\lambda )} < 1 \end{aligned}$$

  holds. Note that a negative left-hand side does not necessarily imply infeasibility.

Example 3.10

This example illustrates the second case of above distinction. Consider the following mixed-integer problem.

$$\begin{aligned} 3 x_1 + x_2 + 4 x_3&\ge 3\\ 3 x_1 + 4 x_2 + x_3&\ge 3\\ x_1 + \ x_2 + x_3&\le 1\\ x_1, x_2, x_3&\in \{0,1\} \end{aligned}$$

By Lemma 3.8 we have ${\tilde{\Lambda }} = \{\frac{1}{3}, \frac{2}{3}\}$, and for $\lambda = \frac{1}{3}$ we get

$$\begin{aligned} 3 x_1 + 3 x_2 + 2 x_3&\ge 3\\ x_1 + x_2 + x_3&\le 1\\ x_1, x_2, x_3&\in \{0,1\}. \end{aligned}$$

Due to ${\bar{a}}_1(\frac{1}{3}) = 3 = \Phi (\frac{1}{3})$ we can, by the second case of above distinction, check for feasibility via

$$\begin{aligned} 0 \ge \Gamma _1\left( \frac{1}{3}\right) = 0. \end{aligned}$$

(38)

Because of ${\bar{a}}_1(\frac{1}{3}) = {\bar{a}}_2(\frac{1}{3}) = 3$ it is not even possible to strengthen $\Phi _1(\frac{1}{3})$ and similar considerations hold for $\lambda = \frac{2}{3}$. However, $\max \{0, \max _{k \in \{2,3\}}{\bar{a}}_k(\lambda )\}\}$ has an additional breakpoint at $\lambda = \frac{1}{2}$ for which it would be possible to tighten the lower bound of $x_1$ to

$$\begin{aligned} \ell _1 \ge \left( 3 - \frac{5}{2}\right) /3 = \frac{1}{6}. \end{aligned}$$

(39)

Remark 3.11

This presolve method is very similar to the one presented in the previous section, so we want to highlight some of the differences between them. Most importantly, the method in Sect. 3.3 can be implemented in a straightforward manner and it is possible to punctually apply the method to single variables. However, there are two major points that speak in favor of the method of this section.

First, the previous method is restricted to tightening bounds of variables that do not have nonzero coefficients in both constraints, whereas this section’s method is able to tighten bounds of all variables involved. Second, it does not seem the case that the set packing extension translates to the presolve method from Sect. 3.3 in a canonical way. Consider the case that all variables are binary and present in one of the disjoint set packing constraints. Adding all the set packing constraints to the optimization problems shown in (16) results in solving so-called Multiple-Choice Knapsack Problems, see Sinha and Zoltners (1979), which would exceed the scope of this paper.

3.5 Exploiting complementary slackness on two columns of continuous variables

By propagating the dual problem of the linear programming relaxation of problem (1) appropriately, we are able to derive bounds on the dual variables. These bounds can be used to detect implied equalities and to fix variables in (1). This presolve method was first published by Achterberg et al. (2019). We will first describe the basic idea behind this method. Then we will discuss the extension to two columns. Finally, we will go into some details of the implementation.

3.5.1 Description of the basic method

Here we want to outline the basic idea of this presolve method as it was published in Achterberg et al. (2019). Consider the primal LP

$$\begin{aligned} \min \{c^\top x \mid Ax \ge b, x \ge 0, x \in \mathbb {R}^{\vert \mathcal {N}\vert }\} \end{aligned}$$

(40)

and its dual LP

$$\begin{aligned} \max \{b^\top y \mid A^\top y \le c, y \ge 0, y \in \mathbb {R}^{\vert \mathcal {M}\vert }\}. \end{aligned}$$

(41)

Suppose $x^*$ is feasible for (40) and $y^*$ is feasible for (41). A sufficient condition for $x^*$ and $y^*$ to be optimal for (40) and (41), respectively, is complementary slackness (see Schrijver (1986)).

It is possible to exploit certain cases of complementary slackness for mixed-integer programs as well. Let problem (1) with $\circ _i=''\ge ''$ for all $i \in \mathcal {M}$ and lower bounds $\ell =0$ for the x variables be given. While considering only the continuous variable indices $S :=\mathcal {N}\setminus \mathcal {I}$ and applying bound propagation on the polyhedron

$$\begin{aligned} P(S) :=\{y \in \mathbb {R}^{\vert \mathcal {M}\vert } \mid (A_{\cdot S})^\top y \le c_S, y \ge 0\} \end{aligned}$$

to get valid bounds ${\bar{\ell }} \le y \le {\bar{u}}$, we can make the following statements:

$$\begin{aligned} \begin{array}{ll} \text {(i)} &{}{\bar{\ell }}_i> 0,\ i \in \mathcal {M}\text { implies } A_{i\cdot }x^* - b_i = 0\text {, and}\\ \text {(ii)} &{}c_j - \sup ((A_{\cdot j})^\top y \mid {\bar{\ell }} \le y \le {\bar{u}}) > 0, j \in \mathcal {N}\text { implies }x_j=0. \end{array} \end{aligned}$$

The problem $\max \{b^\top y \mid y \in P(S)\}$ is a relaxation of the dual LP (41), since only the constraints that belong to continuous variables in the primal problem are considered.

Note that even if $x_j$ is an integer variable in case (ii) we can fix it to its lower bound. The statements (i) and (ii) are thus a bit of a generalization for complementary slackness in the context of mixed-integer programming.

3.5.2 Extension to two columns of continuous variables

In order to obtain tight bounds for the dual variables we can solve for each variable $y_i$, $i \in \mathcal {M}$ two LPs $\min \{y_i \mid y \in P(S)\}$ and $\max \{y_i \mid y \in P(S)\}$. However, in most cases this is too costly for presolve. On the other side only considering single rows, as shown in Sect. 2, sometimes delivers only weak bounds. A reasonable compromise is to consider two rows of P(S) simultaneously. For this case we apply a hashing-based approach for finding promising pairs of columns as described in Sect. 4 and reuse the method of Sect. 3.4 for determining bounds on the dual variables $y_i$. We illustrate the approach by an example.

Example 3.12

Consider the following mixed-integer program:

(42)

With $S=\{3,4\}$ we obtain from (42) the following polyhedron P(S):

(43)

The sign pattern of the first two columns in (43) prevents us from getting tighter bounds while considering only single rows. Such sign patterns or jammed substructures can only be resolved by a more global view or specifically in this case by a two-row approach. Now using a two-row approach as in Sect. 3.4 gives us improved bounds of $y_1 \in [0,\infty ]$, $y_2 \in [1.25,\infty ]$, $y_3 \in [0,1.1]$, and $y_4 \in [0,5.5]$. The lower bound ${\bar{\ell }}_2=1.25 >0$ implies that constraint $x_2+2x_3-x_4\ge 1$ becomes an equality. Finally, $c_1 - \sup ((A_{\cdot 1})^\top y)=2-1.1>0$ implies $x_1=0$.

It should be noted that it would also be possible to use the presolve method described in Sect. 3.3 to determine tighter bounds for the dual variables. However, this was not done, because the presolve method shown in Sect. 3.4 always delivers bounds that are at least as strong as the bounds determined by LP-based bound tightening on two constraints.

3.5.3 Implementation details

In order to further improve runtime behavior for this method it is advantageous to consider only a subset of the continuous variables to tighten the bounds of the dual variables y. Consider a continuous variable $x_j, j\in \mathcal {N}\setminus \mathcal {I}$, with an explicit upper bound. We can imagine this as an additional constraint, i.e., $-x_j \ge -u_j > -\infty$. The corresponding dual variable, say $y_i$, is a singleton column in the dual formulation or in other words $\vert {{\,\mathrm{supp}\,}}((A^\top )_{\cdot i}) \vert =1$. That is the bounds of $y_i$ can only be improved in the dual constraint $(A_{\cdot j})^\top y \le c_j$. Unfortunately, $y_i$ has an upper bound of $\infty$ and thus the minimal activity (2) needed for propagating bounds for the dual variables $y_k$, $k\in {{\,\mathrm{supp}\,}}(A_{\cdot j})\setminus \{i\}$ is always $-\infty$ as $y_i$ has a coefficient of $-1$. Consequently, no new bounds can be identified from this row for the dual variables $y_k$, $k\in {{\,\mathrm{supp}\,}}(A_{\cdot j})\setminus \{i\}$. In addition, the coefficient of $-1$ only allows the determination of a new lower bound for $y_i$.

At the beginning of our implementation, it is verified which continuous variable has bounds that are implied by constraints and other variable bounds. Careful attention must be paid to interdependencies between bounds. That is, if the redundancy of two bounds depends on each other, only one bound is redundant. Redundant variable bounds are subsequently removed, which usually gives us more implied free variables or variables with only one bound. As free variables are assigned to dual equalities and variables with only a lower bound to dual inequalities, this results mostly in a stronger dual formulation and therefore to tighter bounds on the dual variables. As described above, variables with a finite upper bound are excluded from further consideration.

Let ${\bar{S}}$ be the set of continuous variables without unimplied upper bounds. Our current implementation always performs FBBT (see Sect. 2) on $P({\bar{S}})$, for determining bounds on the dual variables y, which is essentially the approach published in Achterberg et al. (2019). In addition, the current implementation in SCIP uses the previously described two-row approach directly before FBBT. In order to exclude unfavorable situations as shown in (43) the pairing mechanism explicitly searches for jammed substructures to find matching pairs of rows. This makes it possible that the bounds calculated in the two-row approach can be exploited and further tightened in a subsequent FBBT realization.

4 Pairing methods

A straightforward exhaustive search for suitable pairs of rows or columns to which the presolve methods presented in the previous section can be applied may be expected to be impractical due to the quadratic complexity in the number of constraints or variables. Preliminary tests during development of the methods have confirmed that running the presolvers on all possible pairs is prohibitively expensive in terms of runtime and memory requirement. As a result, many problems would run into time or memory limits during presolving. Therefore it is important to avoid excessive usage of computational resources by setting working limits and to restrict the search to pairs of rows or columns that are worthwhile to consider, see also Sect. 5.6. In this section, we want to outline the hashing-based pairing mechanisms that we have developed in order to filter out pairs that are likely or even guaranteed to not lead to reductions for the respective presolvers.

A detailed introduction to hashing can be found in Knuth (1998). The basic idea of our pairing mechanisms is to scan through the problem and punctually remember promising constraints or variables in a hashlist or hashtable. We then go through the problem for a second time and check whether the hashlist or hashtable contains a fitting counterpart for the constraint or variable we are currently looking at.

4.1 Pair-search based on a hashtable

The presolve methods presented in Sects. 3.1 and 3.2 require a high number of matching coefficients. To achieve a favorable trade-off between search time and effectiveness, we use a pairing mechanism on variable pairs and constraint pairs, respectively. In the following we explain the mechanism as used for the presolve method from Sect. 3.1 and highlight the differences to the pairing mechanism required for the other presolve method at the end of this section.

For each pair of variable indices j, k in each equality i, the triple $(j, k, \frac{a_{ij}}{a_{ik}})$, consisting of the variable indices and their coefficients’ ratio, is used as a key to store the quintuple $(i, a_{ij}, j, a_{ik}, k)$. Efficiently storing and querying these tuples is very important for the overall runtime behavior of the algorithm. Therefore, we use the hashtable and collision resolution scheme described in Maher et al. (2017, Sec. 2.1.8), which allows for constant time access under practical assumptions. If the key $(j, k, \frac{a_{ij}}{a_{ik}})$ is already contained in the hashtable, then the entry corresponding to the sparser row is kept. Afterwards, for each pair of variable indices j, k in each inequality r, the hashtable is queried for $(j, k, \frac{a_{rj}}{a_{rk}})$. If the conditions $a_{ij} = a_{rj}, a_{ik} = a_{rk}$, $W = \emptyset$ hold for the corresponding entry $(i, a_{ij}, j, a_{ik}, k)$, then reformulation (11) is applied. To further decrease search time, we use the following set of limits to heuristically prevent unrewarding investigations.

First, we consider at most 4900 variable pairs per row to be hashed and added to the hashtable. The same limit is used when searching through the inequality rows after the hashtable is built. Further, we keep track of the number of failed hashtable queries of the current row. If no reduction is found on the current row, we add the number of failed hashtable queries to a global counter. If a reduction is successfully applied to the current row, we instead decrease the global counter by the number of failed hashtable queries of this row. The presolve method stops when the global counter exceeds 100 $\cdot |\mathcal {M}|$. The rationale is that we want to keep going if, after many useless calls that almost exceeded the budget, we finally reach a useful section of rows. However, for the case that the useful section is all at the beginning and we quickly want to quit afterwards, we do not allow a negative build-up, i.e. the global counter remains at zero if it were to become negative.

In addition, note that a target matrix with as few nonzeros as possible does not necessarily give the best results. In fact, it seems important to preserve special structures by not applying cancellation if it would destroy one of the following properties in the row r above: integrality of the coefficients; more specifically coefficients $+1$ and $-1$; set packing, set covering, set partitioning, or logicor constraint types; variables with no or only one up-/downlock (Achterberg 2007).

Also, it should be mentioned that adding scaled equations to other constraints needs to be done with care. In particular, too large or too small scaling factors $\lambda$ can lead to numerical problems. Currently, as in Achterberg et al. (2019), a limit of $\vert \lambda \vert \le 1000$ is used.

For the presolve method from Sect. 3.2, we consider pairs of constraint indices and their coefficients. The pairing mechanism itself is then identical with the role of rows and columns being reversed. However, we only apply the reduction if we have $|U| - |W| \ge 100$ as the reduction induces a larger computational overhead.

Finally, it is important to note that this hashing mechanism can miss possible reductions in two cases. First, a pair might not be evaluated as one of the imposed limits is hit before it was processed. Second, the hashing mechanism disregards pairs with an overlap of size one. This follows the intuition that the methods presented in Sect. 3.1 and becomes more powerful with increasing overlap.

4.2 Pair-search based on multiple hashlists

The following pairing mechanism is used for the presolve methods presented in Sects. 3.3 and 3.4. It is also used indirectly by the presolve method from Sect. 3.5 as it uses the method from Sect. 3.4 without its extension in order to derive stronger bounds from the dual problem than could be achieved by using regular FBBT. In all three cases, as highlighted by Lemma 3.1, it is important to find pairs of constraints such that variables shared by the constraints have coefficients with opposite sign. In order to do this, we devised a pairing mechanism that uses an open surjective hash function H(j, k) for variable indices $j,k \in \mathcal {N}$ and works as follows.

• Step 1: Create the four sets

  $$\begin{aligned}&L_{++}:=\{ (H(j,k), i) \mid (i,j,k) \in \mathcal {M}\times \mathcal {N}\times \mathcal {N}: a_{ij}> 0 \wedge a_{ik}> 0\} \\&L_{--}:=\{ (H(j,k), i) \mid (i,j,k) \in \mathcal {M}\times \mathcal {N}\times \mathcal {N}: a_{ij}< 0 \wedge a_{ik}< 0\} \\&L_{+-}:=\{ (H(j,k), i) \mid (i,j,k) \in \mathcal {M}\times \mathcal {N}\times \mathcal {N}: a_{ij}> 0 \wedge a_{ik}< 0\} \\&L_{-+}:=\{ (H(j,k), i) \mid (i,j,k) \in \mathcal {M}\times \mathcal {N}\times \mathcal {N}: a_{ij} < 0 \wedge a_{ik} > 0\}. \end{aligned}$$

• Step 2: Separate $L_{++}$, and analogously the other three sets $L_{--}, L_{+-}, L_{-+}$, into subsets

  $$\begin{aligned} L_{++}^h :=\{ i \mid (h, i) \in L_{++}\} \end{aligned}$$

  for each key value h appearing in $L_{++}$. In other words, $L_{++}^h$ contains all indices i of rows such that some variables $x_j, x_k$ had positive coefficients in row i and $h = H(j, k)$.

• Step 3: For each key value h for which $L_{++}^h$ and $L_{--}^h$ have both been created, perform the two-row bound tightening on all row pairs $(r,s) \in L_{++}^h \times L_{--}^h, r \ne s$, as this guarantees that for this row pair there exist at least two variables $x_j,x_k$ whose coefficients $a_{rj},a_{sj}$ and $a_{rk}, a_{sk}$ have opposite sign in the constraints r and s. This is done analogously for key values h for which $L_{+-}^h$ and $L_{-+}^h$ have both been created. While doing so, add each processed pair’s hash to a hashtable. To prevent unnecessarily processing the same pairs multiple times we query the hashtable before applying the two-row bound tightening.

In order to make this approach more efficient, several working limits are used in our implementation. First, creating the four sets $L_{++}, L_{--}, L_{+-}, L_{-+}$ for all rows and variable pairs is too computationally expensive. Therefore, for each row we consider at most 10000 variable pairs and also limit the total number of variable pairs to be considered over all rows by $10 \cdot |{\mathcal {M}}|$. Second, for each processed pair we check whether new bounds have been found and stop searching if 1000 consecutively processed pairs have not yielded tighter bounds. Third, before applying two-row bound tightening on a row pair we check if its hash is already contained in the hashtable tracking the already processed pairs. If 1000 consecutive pairs have been found to already be contained in the hashtable, the method also stops. Finally, the method stops after successfully processing at most $|{\mathcal {M}}|$ row pairs. Even if the method finds many reductions, it is important to prevent the method from taking up too much time. To do this, we chose a limit which is linear in the problem size because the number of constraints in real-world problems as well as our testset can easily range from a few hundred to multiple millions and future instance sizes will increase even further.

Like the hashing mechanism presented in Sect. 4.1, this hashing mechanism can miss possible reductions if one of the limits is hit or a pair has overlap of size one.

5 Computational results

In this section we will present our computational results. First, we discuss a comparison of each individual presolve method with a baseline run where all five methods are disabled (see Sects. 5.1–5.5). Second, we provide an evaluation of the combined impact of all five presolve methods and confirm the importance of working limits (see Sect. 5.6).

The methods have been implemented in SCIP 6.0.2 with SoPlex 4.0.2 as LP solver and the computations were performed on machines running on a Xeon E3-1240 v5 CPU (“Skylake”, 4 cores, HT disabled, 3.5 GHz base frequency) and 32 GB RAM. Aside from en- or disabling the five presolve methods and setting a time limit of 7200 s we ran SCIP on its default settings. The run with all five presolve methods being disabled is referred to as Baseline. (Out of the five methods described in this paper, Two-Row Nonzero Cancellation is the only one that was already included in SCIP 6.0.2.)

Our testset is the second version of the MIPLIB2017 benchmark set (Gleixner et al. 2019; miplib2017 2018) released in June 2019. It consists of 240 instances from varying optimization backgrounds. To further increase the accuracy of our results we run each instance and each setting on four different random seed initializations as well as seed zero, which is used in the release version of SCIP. SCIP uses the random seed initializations to affect numerical perturbations in the LP solver, for tie breakings as well as heuristic decision rules that necessarily occur in many parts of the solving process. Each combination of instance and seed is considered its own data point to tackle the problem of performance variability (Danna 2008; Lodi and Tramontani 2013) where small changes which are neutral from a purely mathematical point of view have a large impact on the performance of a MIP solver. Finally, we discard all combinations of instance and seed where computations ran into numerical difficulties or, as happened in rare cases, the new code revealed bugs in the existing framework.

The result tables in this section each present the comparison between two different runs and are structured as follows. Each row presents the aggregate results on a set of problem instances. The row all contains the entire testset. The subsets corresponding to the brackets [t, T] contain instances that were solved by at least one run and for which the maximum solving time (among both runs) lies between t and T seconds. If a configuration did not solve the problem within the time limit, it is recorded as T seconds. In this work, we set T to the time limit of 7200 s and with increasing t, this provides a hierarchy of subsets by difficulty. In particular, the bracket [0, 7200] contains all instances that have been solved within the time limit and deserves special attention as it is the largest subset where computation times can be compared in a meaningful way. We then compare the number of instances that had been solved, as well as the shifted geometric mean of solving times and branch-and-bound nodes in the columns solved, time and nodes respectively. The shifted geometric mean of values $x_1,\ldots ,x_n$ is

$$\begin{aligned} \left( \prod _{i=1}^n (x_i + s)\right) ^{\frac{1}{n}}-s, \end{aligned}$$

where the shift s is set to 1 s and 100 nodes respectively.

5.1 Two-row nonzero cancellation

For a detailed description of this method we refer to Sect. 3.1. The method found reductions on 390 instances. Despite the method being applied to a large number of instances its performance impact, as presented in Table 1, is slightly negative in terms of runtime and also causes three fewer instances to be solved within the time limit. Although the impact is still only neutral on the subset [100,7200], the results show a tendency toward a positive impact on difficult instances.

Table 1 Performance comparison for two-row nonzero cancellation

If a presolve method does not perform well, this is usually due to one or both of the following two reasons. First, the method itself takes too much time and therefore causes a degradation on models where it does not find enough reductions. Second, the reductions create a new substructure that is unfavorable for subsequent solves. In our case both reasons appear to play a role. From all of the presented presolve techniques, this method creates the largest runtime overhead. However, this does not suffice to fully explain the degradation observed in Table 1.

5.2 Two-column nonzero cancellation

This presolve method was described in detail in Sect. 3.2. Since the rules for applying a reduction in this method are more restrictive than in the row version, we observe reductions on only 115 instances. The performance results for this presolve method are presented in Table 2. In total, its impact can be considered neutral with two more instances being solved at the cost of a slightly prolonged runtime for instances in the subset [1000,7200].

Table 2 Performance comparison for two-column nonzero cancellation

In contrast to the neutral performance impact on the MIPLIB 2017 benchmark set, it has a tremendous impact on the testset studied in Liu et al. (2019). These instances are constructed by Liu et al. (2019) based on a deterministic equivalent mixed-integer programming formulation of the two-sided chance constrained program (TSCCP). In total, 30 instances are publicly available at Küçükyavuz (2019). Additional tests were performed on these instances using the same settings as above. Similar to other tests, each instance was solved five times with different random seed initializations, resulting in a testset consisting of 150 MIPs.

The computational results presented in Table 3 show that the proposed method found reductions on all instances. Overall, the proposed method improves performance by 74% on the TSCCP testset. In addition, with this method, the solver was able to solve 147 instances within the time limit of 7200 s. In comparison, without this method the solver was able to solve only 98 instances within the same time limit.

Table 3 Performance comparison for two-column nonzero cancellation on the TSCCP testset

5.3 LP-based bound tightening on two constraints

For a detailed description of this presolve method we refer to Sect. 3.3. The method applied reductions to 119 instances and the performance results are presented in Table 4. On the entire testset, the method has neutral impact. However, with increasing difficulty we can see a positive impact of up to 4% for the instances in the subset [1000,7200].

Table 4 Performance comparison for LP-based bound tightening on two constraints

5.4 Bound tightening on convex combinations of two constraints

The extension of this presolve method presented in Sect. 3.4 is incorporated using SCIPs so-called clique table which represents the solvers current knowledge of binary variables that may not be set to one at the same time. The clique table is generated from set packing constraints explicitly stated in the model as well as information extracted during earlier presolve and is also used for cutting plane separation, linear constraint propagation, and primal heuristics (see Gleixner et al. 2017). From this clique table we generate the set packing constraints used in the extension. It is important to keep in mind that, although this allows the method to find better bounds than the method presented in Sect. 3.3, it also increases the cost in terms of running time. In our implementations, this amounts to an average of 0.11 s being spent per instance for the method from Sect. 3.3, which increases to an average of 0.31 s being spent per instance for this method. Note, however, that this is in part due to this method running longer as it finds more reductions.

As mentioned in Remark 3.11 this method works on a superset of the variables for which LP-based bound tightening on two constraints from Sect. 3.3 can tighten bounds on. As a result this method applies reductions in 142 instances, i.e. 23 more instances than for LP-based bound tightening. The results presented in Table 5 show that the additional bound tightenings found by this method indeed yield a positive impact on solving times. As for LP-based bound tightening the impact of this presolve method scales with instance difficulty. As a result its impact changes from neutral on the overall testset toward a considerable 6% improvement on the subset [1000,7200].

Table 5 Performance comparison for ConvComb

The results presented in Table 6 illustrate the benefit of the clique extension over the standard procedure developed by Belotti (2013). It can be seen that it has an overall positive impact in terms of runtime. However, we have observed that the overall number of nodes increases slightly when using the extension. In particular, there are ten instances where the node count increases by more than half and six instances where the node count more than doubles. On those ten instances we also observed that significantly more time is spent on branching and the branching tree depth increases as well. Finally, we want to note that when deactivating the clique extension the number of instances where reductions are found drops from 142 to 119.

Table 6 Performance comparison for ConvComb without clique extension

5.5 Exploiting complementary slackness on two columns of continuous variables

For a detailed description of this presolve method we refer to Sect. 3.5. As can be seen in Table 7, the impact of the method is almost neutral on the overall testset as well as all subsets. The method performs reductions on only 11 instances. However, the neutral impact is not necessarily due to the inefficiency of the reductions themselves, but rather a consequence of the very low number of instances where this method can be applied because of missing continuous variables.

Table 7 Performance comparison for CompSlack

On a more specialized testset of real-world supply chain instances, however, we have observed this presolve method to consistently produce more reductions. In Schewe et al. (2020), a testset of 40 real-world supply chain instances was studied. The instances contain 330108 variables and 145450 constraints in arithmetic mean. The proportion of discrete variables is about 3.9%. We performed additional tests on these instances with the same settings as above. These instances are extremely challenging and cannot be solved to optimality with or without this presolve method, but the applicability of the method and the computational efficiency of the hashing-based pairing mechanism becomes clear.

The method found reductions on 35 of the 40 instances, i.e., on 87.5% of the testset. On 6 instances more than 1% of the variables were fixed, and in one instance we were able to fix 14% of all variables. Additionally, on 3 instances more than 2% percent of the inequality constraints were changed to equalities. The runtime of this presolve method was below 1 s for 29 instances, between 1 and 6 s on nine instances and close to 12 s on two instances. As already mentioned, these supply chain instances contain a very high percentage of continuous variables, which is one of the reasons why this presolve method is able to find a reasonable amount of reductions.

5.6 All presolve methods

In order to evaluate whether and how the methods interact, we ran all presolvers presented in this work in the following order: LPBound, CompSlack, ConvComb, TwoRowNonzeroCancel, TwoColNonzeroCancel. As previously illustrated in Example 3.4, different presolve methods can positively interact with each other, even if each method itself is neutral or even slightly negative. However, the results presented in Table 8 show that enabling all five presolve methods presented in this work has a slightly negative impact on solving times.

Table 8 Performance comparison using all presolve methods

Table 9 shows the number of instances each of the presolvers applied reductions to when run individually (left) and with all five methods enabled (right). We can make two noteworthy observations. First, we have an additional confirmation that the presolve methods presented in this work do not enable each other to find additional reductions, i.e. each presolve method finds more reductions when run with the other four being disabled. Second, bound tightening based on convex combinations applies reductions on 99 instances even when run after LP-based bound tightening. This shows that it is indeed the more powerful method.

Table 9 Number of instances with reductions of each presolve method

Finally, we would like to demonstrate empirically how important working limits are for controlling the computational effort. While a comparison with exhaustive search on all pairs of variables and constraints is computationally out-of-scope, we conducted a small experiment where we removed only the working limits described in Sect. 4. Due to limited computational resources we only ran this test on the original 240 instances of the MIPLIB 2017 benchmark set. However, these results already demonstrate the performance deterioration quite clearly.

The removal of working limits changed the number of variables or constraints after presolve only on 36 out of 240 instances; most changes were negligible, only on 14 instances the presolved models became at least 1% smaller when disabling working limits. By contrast, the average presolving time increased by a factor of five, where on 41 instances, the presolving time increased by a factor of ten and on the worst instances we observed a factor of more than 100. Further, without working limits an additional 31 instances ran into memory issues.

Before closing our presentation of computational results, we want to add that for practical development of a fast and stable MIP solver, there are three reasons to include presolve methods that show only neutral or even slightly negative impact on the MIPLIB 2017 benchmark set. First, there may be positive interactions between new and existing presolve methods. However, this was not the case for among the five methods presented in this work. Second, presolve methods with neutral or slightly negative performance impact in the benchmark set may have significant impact on other instances, as we have seen on the two-sided chance-constrained program instances for the technique described in Sect. 3.2 and for real-world supply chain instances for the technique described in Sect. 3.5. Finally, it is also important to actively involve new presolve methods in the development process of a solver to avoid overtuning of established methods. It could be, for example, that a new presolve method, which is not performing well at the moment, will reveal its potential in combination with a newly developed heuristic in the future. If this method had not been included in the development process, this would not have been apparent.

6 Conclusions

In this paper, we considered five two-row and two-column methods for mixed-integer presolve that are generally effective, but suffer from the limitation that simply testing all methods on all pairs of rows or columns is computationally not appropriate. We resolved this bottleneck by introducing two hashing-based pairing mechanisms that identify promising pairs of rows and columns quickly. During discussion of the five two-row and two-column presolve methods we focused on the required properties of promising pairs of rows or columns. Additionally we discussed an extension based on set packing constraints to further strengthen the results of the bound tightening method applied to convex combinations of two rows. We then introduced two hashing-based pairing mechanisms, implemented the ideas in the mixed-integer programming solver SCIP and conducted a performance evaluation on the MIPLIB 2017 benchmark set (miplib2017 2018).

The first pairing mechanism, based on a hashtable, aimed at pairs of rows (or columns) such that there exist at least two coefficients that can be cancelled simultaneously by linearly combining the rows (or columns). This is required by the two nonzero cancellation methods, which turned out to have neutral or slightly negative effect on the performance.

The second pairing mechanism uses four hashlists to find pairs of rows such that there exist at least two variables with opposite sign. This increases the chance of finding stronger variable bounds when applying the two-row bound strengthening methods presented in Sects. 3.3 and 3.4 . Using bound tightening based on convex combinations, we were able to improve solving times by 1% on the entire testset and by up to a considerable 6% for instances with longer solving times.

Finally, we experimented with applying the method presented in Sect. 3.4 to improve the bound strengthening required during the dual presolve method presented in Sect. 3.5, but observed that this leads to only few reductions and no performance impact. This is largely due to the fact that many of the MIPLIB 2017 instances do not contain any continuous variables at all.

To conclude, the results of this paper demonstrate that two-row and two-column presolve methods hold potential for practically solving challenging mixed-integer programming problems when they are combined with a sophisticated selection mechanism. For the methods discussed in this paper, more extensive parameter tuning or extensions of the methods themselves may even lead to larger performance gains.

Other compelling directions for further investigation are finding new combinations of pairing mechanisms and two-row or two-column presolve methods as well as moving on to reductions based on three or even more rows or columns.