Abstract
In the face of a changing climate, yield stability is becoming increasingly important for farmers and breeders. Long-term field experiments (LTEs) generate data sets that allow the quantification of stability for different agronomic treatments. However, there are no commonly accepted guidelines for assessing yield stability in LTEs. The large diversity of options impedes comparability of results and reduces confidence in conclusions. Here, we review and provide guidance for the most commonly encountered methodological issues when analysing yield stability in LTEs. The major points we recommend and discuss in individual sections are the following: researchers should (1) make data quality and methodological approaches in the analysis of yield stability from LTEs as transparent as possible; (2) test for and deal with outliers; (3) investigate and include, if present, potentially confounding factors in the statistical model; (4) explore the need for detrending of yield data; (5) account for temporal autocorrelation if necessary; (6) make explicit choice for the stability measures and consider the correlation between some of the measures; (7) consider and account for dependence of stability measures on the mean yield; (8) explore temporal trends of stability; and (9) report standard errors and statistical inference of stability measures where possible. For these issues, we discuss the pros and cons of the various methodological approaches and provide solutions and examples for illustration. We conclude to make ample use of linking up data sets, and to publish data, so that different approaches can be compared by other authors and, finally, consider the impacts of the choice of methods on the results when interpreting results of yield stability analyses. Consistent use of the suggested guidelines and recommendations may provide a basis for robust analyses of yield stability in LTEs and to subsequently design stable cropping systems that are better adapted to a changing climate.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Contents
-
3. Methodological guidelines for assessing yield stability in LTEs
-
-
3.3.1 Problem description
-
3.3.2 Possible solutions
-
-
3.8.1 Problem description
-
3.8.2 Possible solutions
-
3.9.1 Problem description
-
3.9.2 Possible solutions
-
3.9.3 Example: different options to quantify standard errors
-
4. Conclusion
-
Acknowledgements
-
References
1 Introduction
Stability can be conceptualized in various ways, with specific meanings including invariability, resistance, and resilience (Lehmann et al. 2013). In the context of agriculture, the concept of stability is mostly used as a criterion to measure the temporal or spatial invariability of specific features. Here, stability can thus be understood as constancy of agricultural outputs, especially of yield, over long periods of time or across various spatial environments (Urruty et al. 2016). The stability of agricultural systems is key in adapting to climate change (Olesen et al. 2011) and is an important goal when diversifying agricultural systems (Hufnagel et al. 2020). Analyses of yield stability have become more important in recent years since the increased variability of climate is also associated with a decreased stability of crop yields (Müller et al. 2018; Najafi et al. 2018; Ray et al. 2015; Tigchelaar et al. 2018). For farmers, temporal yield stability is relevant because it determines economic predictability and reduces risk. Yield stability is especially important related to grain legume cultivation, as these crops are perceived to be less stable than others (Watson et al. 2017; Reckling et al. 2020) and in the context of cropping system diversification that is often assumed to increase yield stability (Reckling et al. 2019; St-Martin et al. 2017; Marini et al. 2020). Stability is also highly relevant for plant breeders developing genotypes adapted to a wide range of environmental conditions (Mühleisen et al. 2014). Finally, yield stability has a national and global dimension in the context of food security (Kalkuhl et al. 2016). Large variations of yield from year to year or from location to location are problematic as times of dearth and hunger cannot always and fully be compensated by higher yields in other (previous) years, or other locations (Abbo et al. 2010), thereby leading to potential conflicts over resources.
Because of the increasing importance of yield stability, it is essential to quantify it in an objective and meaningful way. Only then is it possible to answer fundamental questions, e.g.: How does the agronomic system (fertilizer, rotation, tillage, etc.) affect stability? Has yield stability changed over time for specific species or genotypes? What environmental factors (e.g. climate and soil properties) affect temporal stability at a given location?
Yield stability cannot directly be measured in a single field experiment in a single year—it must be assessed based on measurements of yield over years and locations; yield stability is therefore estimated using various statistical approaches that model variability across environments.
For the analysis of long-term field experiments (LTEs), defined as “large-scale field experiments more than 20 years old that study crop production, nutrient cycling, and environmental impacts of agriculture” (Rasmussen et al. 1998), however, there is currently little knowledge on the robustness and validity of the various yield stability indices that have been developed. The selection of particular stability measures is often based on personal or disciplinary preferences rather than systematic knowledge about the properties and suitability of particular indices. Knowing and using information on the advantages and disadvantages of the different measures of stability are essential for identifying differential effects of agronomic systems or other factors on stability. Ultimately, such improved knowledge is also a prerequisite to manipulate stability and design cropping systems that are better adapted to a changing climate.
A huge potential to contribute to a better understanding of yield stability lies in LTEs (Reckling et al. 2018b; St-Martin et al. 2017; Macholdt et al. 2020b). Typically, treatments within LTEs are kept constant depending on the research questions, i.e. the decision rules or technical operations on a given plot over long time periods (Cochran 1939), so that cumulative effects and processes taking several years to become evident can be studied and separated from weather effects and climate trends. The importance of LTEs for studying the sustainability of crop management and the effects of climate change on agriculture have long been recognized, and LTEs are therefore used in agronomy and ecology world-wide (Debreczeni and Körschens 2003; Johnston and Poulton 2018; Richter et al. 2017).
LTEs offer yield data under relatively comparable conditions where crops are grown on the same soil, over long periods of time (Ahrends et al. 2018; Figure 1). While these properties of LTEs make them ideal for quantifying temporal variation, LTEs are only now beginning to be used more extensively to assess yield stability. However, there are several hundreds of experiments available; 620 are listed in a global assessment by Debreczeni and Körschens (2003) alone. In Germany, a total of 205 LTEs were identified by Grosse et al. (2020) with a minimum duration of 20 years, and 140 of these are still ongoing in 2020. Therefore, this tremendous resource could be exploited more effectively in the future. In addition, methods for analysis of long-term data series from field experiments can also be applied to sets of variety trials, which are not measuring cumulative effects on the same field but ensure long-term comparability of measurements through other rigorous rules (Hadasch et al. 2020; Laidig et al. 2017).
a The Rengen grassland LTE was established in 1941 in the Eifel Mountains of Germany on soils of low fertility and compares different fertilization treatments (Picture: Thomas F. Döring/University of Bonn). b The Broadbalk Wheat Experiment was established in 1843 at Rothamsted Research in the UK to compare various combinations of inorganic fertilizers and organic manures on the yield of winter wheat (Picture: Janna Macholdt/JLU Gießen)
For quantifying stability, different disciplines (especially plant breeding but also agronomy and ecology) have developed a wide range of yield stability measures. There are two main contrasting concepts of stability as commonly used in a plant breeding context: (1) the static and (2) the dynamic concepts (Becker and Léon 1988). In the static concept, the most stable genotype maintains a constant yield across environments, while the dynamic concept for a stable genotype implies a yield response having a constant difference to the mean response of all tested genotypes in each environment (Annicchiarico 2002). While stability analysis was originally used to assess the stability of crop genotypes across environments (Becker and Léon 1988), the analysis of yield stability has been widened to various systems, comparing (i) crop production systems, e.g. organic and conventional (Knapp and van der Heijden 2018); (ii) cropping systems (Macholdt et al. 2020b; St-Martin et al. 2017; Marini et al. 2020); and (iii) crop species (Reckling et al. 2018b) and mixtures (Raseduzzaman and Jensen 2017) and (iv) to assess changes of yield stability over time (Reckling et al. 2018a; Döring and Reckling 2018; Singh and Byerlee 1990; Schauberger et al. 2018; Macholdt et al. 2021). Yield stability has especially gained importance in research on impacts of climate change (Tigchelaar et al. 2018; Lobell et al. 2011; Webber et al. 2020).
Over the past decades, many different regression- and variance-based measures of yield stability have been proposed (Becker 1981; Becker and Léon 1988; Dehghani et al. 2008; Eberhart and Russell 1966; Eghball and Power 1995; Huehn 1990; Hussein et al. 2000; Lin et al. 1986; Piepho 1998; Francis and Kannenberg 1978; Lin and Binns 1988; Plaisted and Peterson 1959; Sneller et al. 1997; Tai 1971; Plaisted 1960; Jensen 1976; Wanjari et al. 2004; Kang 1988; Kataoka 1963; Eskridge 1990; Fox and Rosielle 1982; Abou-El-Fittouh et al. 1969; Cotes et al. 2006; Perkins and Jinks 1968; Freeman and Perkins 1971; Hernandez et al. 1993; Sadras and Bongiovanni 2004; Heath 2006; Fernández-Martínez et al. 2018; Bacsi and Hollósy 2019). There is also the GGE (genotype plus genotype-by-environment) biplot analysis available, e.g. Farshadfar et al. (2012), or the AMMI (additive main effects and multiplicative interactions) analysis–based stability indexes, e.g. Farshadfar (2008), Fikere et al. (2014), Fikere et al. (2008), and Purchase et al. (2000). Further, an extensive literature deals with the comparison of various stability indices (Becker and Léon 1988; Crossa 1988; Ferreira et al. 2006; Mohammadi et al. 2012; Mut et al. 2010; Temesgen et al. 2015). As a result, it is known that some indices, though independently developed, are in fact mathematically equivalent, such as Shukla’s stability variance and Grubbs’ measurement error for calibration studies (Lin et al. 1986), while other pairs of indices seem to correlate strongly, such as the variance and the coefficient of regression (Becker 1981). Still, interpretation of the results of stability analyses is often difficult because different stability indices may lead to contrasting conclusions, partly because they reflect different concepts of stability (Dehghani et al. 2008; Piepho 1998).
While there already exists deep knowledge on correlations among individual stability measures especially in plant breeding research, relevant disciplines (i.e. plant breeding, agronomy, and ecology) have remained fragmented so far with little interaction bridging the different research cultures and traditions. Because data sets are often relatively small and different data sources have not been linked up, the current diversity in methodological approaches hinders synthesis to gain more general insights. Moreover, many approaches for stability analysis developed in plant breeding have so far not been applied to agronomy and related disciplines. An extreme example is (agro-)ecological research, where experimenters have often just applied one index, e.g. the inverse of the coefficient of variation, to quantify stability (Isbell et al. 2009; Roscher et al. 2011; Tilman et al. 2006).
The fact that over the past decades, numerous measures of yield stability have been suggested indicates that there is no single, unambiguous, and “intuitive” meaning of stability. The question which indices are appropriate for LTEs, however, is only one of many. In fact, LTEs are characterized by a number of typical issues that affect stability analyses in specific ways, which distinguish them from shorter-term data sets. For example, as already observed by Cochran (1939), with the length of the experiment, the potential for errors and unintended changes increases as well; resulting data gaps need to be dealt with appropriately in the statistical analyses. Further examples of typical issues affecting stability analyses in LTEs include changes in management or genotype during the course of the experiment, temporal autocorrelation, or strong temporal trends of the response variable (especially yield).
We therefore conclude that for assessing yield stability in LTEs, it is currently not primarily a question of lack of data (although data sets are often relatively small and difficult to access) but a question of conceptual gaps. There is currently no broad consensus on how to proceed when analysing stability in LTEs, so that synthesis and comparability are hampered. Little consideration of methodology jeopardizes trust and wider use of yield stability assessments in agriculture. Thus, increased reliability and robustness of results are needed. While we focus on agronomic settings, the methods presented here are also applicable in long-term experiments studying primary production, e.g. in grasslands (Isbell et al. 2009; Roscher et al. 2011; Tilman et al. 2006) or forests (del Río et al. 2017; Morin et al. 2014).
To facilitate interpretation and understanding, this paper presents a methodological guide and consistent terminology that aims to help with the assessment of yield stability in agricultural LTEs. The objectives are to provide guidance on the following topics: (1) quality of data and meta-data, (2) outliers, (3) confounding factors, (4) detrending, (5) temporal autocorrelation, (6) choice of stability measure, (7) dependence of stability measures on the mean, (8) temporal trends of stability, and (9) standard errors and statistical inference of stability measures.
2 Materials and methods
In a workshop on “Methods for analyzing yield stability in long-term field experiments” at the University of Bonn in 2019, nine topics were identified that are of particular relevance for analysing yield stability in LTEs and other long-term data sets. These topics are the basis for the methodological guidelines (Sect. 3). Examples are used to illustrate each topic.
The examples pertain to data sets from LTEs and other long-term variety trial data sets (Table 1), representing different biophysical conditions and cropping systems in a temperate climate. The analyses were performed with the statistical packages R and SAS. Details about the statistical methods employed are explained for each example separately.
3 Methodological guidelines for assessing yield stability in LTEs
In the following sections, we will systematically discuss several issues associated with stability analyses in LTEs. For each of the specific topics (except Sect. 3.1) we first define and explain the problem; describe some potential solutions, each with its pros and cons; and provide examples illustrating the application with data from available LTEs. To reduce complexity, and for didactical reasons, we present the individual data examples with solutions to one problem at a time, rather than discussing solutions to all potential problems that might be pertinent to that example; e.g., we deal with autocorrelation in one example, but we ignore this issue in another one, where we discuss the problem of the dependence of the variance from the mean, even if autocorrelation might be relevant there, too. While this necessarily implies some degree of simplification, we hope that this approach helps to concentrate on the main issues at hand. The notation used differs slightly between sections which is unavoidable because of the different approaches and sources.
3.1 General considerations on quality of data from LTEs
The quality of LTE data sets can vary widely depending on data gaps, restrictions in the experimental design, and/or lack of meta-data. An in-depth check of data quality and availability is thus an important step before the actual analysis can begin. Data gaps might arise in certain years due to harvest failures, for example, caused by hail, storm, and pests. In other cases, data are unavailable because of technical problems or staff changes; or plot-specific yield records are not available, because only means over replicates were kept. Some of the very early experiments are characterized by a restricted experimental design such as the lack of replications or missing or insufficient randomization. Stability analyses need to take this into account as shown, e.g. by Macholdt et al. (2020a).
In unreplicated experiments, i.e. when each plot has a different treatment, plot errors and treatment × year interactions (residuals) cannot be separated. A serial correlation can still be fitted for such data, when the interaction is modeled as random. So the repeated measures nature of data can still be accounted for (see Sect. 3.4). This does not, however, solve the problem of lacking replication. The treatment and plot effects are still confounded (see Sect. 3.3), and there is no way this confounding can be resolved, even if serial correlation is modeled. Consequently, the robustness of the results from such LTEs is limited when comparing the treatments or when analysing if cropping systems achieve a set of objectives. This needs to be kept in mind while interpreting and discussing the results. For the analysis of temporal stability over time, the lack of replications is less problematic (see Sect. 3.8).
All these restrictions are typical for LTEs and might not be remedied. Instead, they should be made transparent and considered during the statistical analysis. Further, the collection of additional information about the experiment is essential. For example, sometimes notes on harvesting problems or bird damage are available. Here, we suggest adding these notes to the data sheet for the analysis in order to check if observed outliers in the analysis were due to such problems or if they were the result of extreme but “natural” conditions such as drought, crop diseases, etc. These notes can be useful when deciding whether or not outliers should be removed (see Sect. 3.2).
Most stability parameters are based on treatment × environment values. In a typical LTE, environments are equivalent to years as there is only one constant location. In unreplicated LTEs, observed plot yields correspond to treatment × year values. In replicated trials, simple means over replicates for each year can be used to calculate treatment × year values. However, simple means can lead to biased estimates if observations are missing and will not correct for LTE-specific properties like autocorrelated residuals due the repeated measure design (Richter and Kroschewski 2006; Piepho et al. 2004). In these cases, the use of mixed models and restricted maximum likelihood estimation (REML) is recommended for LTE stability analysis because they can accommodate LTE-specific properties, including the autocorrelation of residuals over time, non-orthogonal designs, and appropriate variance-covariance structures (Onofri et al. 2016; see Section 3.5). In most LTEs, the variance is not constant over years, and correlation structures and/or variance heterogeneity between years must be considered in models to ensure statistical accuracy (Littell et al. 2006; Onofri et al. 2016).
Such mixed models can be fitted either in a one-stage approach by taking account of the repeated measure design and calculating the desired stability parameter directly or in a two-stage approach by first calculating treatment × year means with their standard errors and then using these means and their standard errors to calculate the stability parameters in a second stage (Macholdt et al. 2019; Piepho 1999). However, the employment of such mixed model approaches is limited to certain stability parameters (Piepho 1999), and models can get very complex resulting in long computation time or non-convergence. In such cases and for a greater set of stability parameters, calculating stability parameters on simple treatment × year means might be necessary.
In the case of LTEs where crop rotations of different length are to be compared and different plots might have been measured in different sets of years, mixed models provide a valid analytical approach. Models can be fitted that take account of the sampling structure and allow heterogeneous error variances between the environments (Payne 2015; Machado et al. 2008; Littell et al. 2006; Singh and Jones 2002).
3.2 How to deal with outliers?
3.2.1 Problem description
An outlier can be defined as “an observation (or subset of observations) which appears to be inconsistent with the remainder of that set of data” (Barnett and Lewis 1994). If outliers are dealt with in the wrong way, this can be a serious reason of distrust in the robustness of a study and affect the analysis of yield stability. It is clearly not appropriate to accept outliers if they comply with the hypothesis, but to argue for exclusion of outliers if they do not comply with the hypothesis. In LTE data, outliers can range from extreme large values to extremely low and even no yield at all due to crop failure.
There are two potentially valid explanations at hand for the interpretation of outliers: (1) it is really an outlier due to some errors in the workflow from the experimental design in LTEs, e.g. technological errors, wrong labeling, confusion with digits in yield data until data arrive on one’s computer (non-natural outlier), and thus the outlier should be removed from the data set; (2) the outlier is real, e.g. bird damage leading to poor crop establishment or winterkill due to heavy frost (natural outlier). The latter can indicate that the period covered by measurements is too short to have a statistically robust basis for critically checking the validity of the outlier’s value. This is well known in hydrology: if a 100-year flood event is observed within a 20-year measurement period, it looks like an outlier, but since its effect is so obvious (flooded areas), it is clear that it should not be removed from the data set. Outlier detection is therefore one of the biggest challenges with short time series and small data sets. Hence, using concepts from extreme value distribution and statistics could also benefit yield stability assessments. In that case, it is however not the large positive outliers that are of interest, but the strongly negative ones, since crop yield failures pose a serious problem to farmers, whereas above-average yields tend to be less dramatic (except, maybe, for logistical issues to bring in the yield).
3.2.2 Possible solutions
We suggest options how to deal with outliers and to explore the impact of including or not including outliers in yield stability analysis in LTEs. The first option to deal with outliers is to keep them in the data set because they are meaningful, in particular in the context of stability analysis (natural outlier, e.g. due to biotic or abiotic stress). The second option is to exclude outliers, e.g. due to methodological and technical issues, which might be desirable because it can dramatically reduce the CV (see example in Sect. 3.2.3). To identify outliers in LTEs with replicates, an analysis within each year using a model with the factors block and treatment can be used to assess the residual variation of treatment effects. If observations from one or several treatments within a given year are missing, appropriate statistical methods such as mixed models can handle this case. However, if a method requires an orthogonal structure of the data set, then all the data of the given year must be removed, to test each treatment with the same set of years. There are other outlier detection methods that can be used also for LTE data, which were described in detail by Hodge and Austin (2004) and Bernal-Vasquez et al. (2016).
Irrespective of the particular case, best practice is to show the data and carry out the analysis with all data and then openly show the result when outliers are removed. We recommend to calculate yield stability measures with and without including the outliers. In the end, the key will be that researchers publish their data along with their papers, to foster fruitful scientific discussions.
3.2.3 Example: impact of including or excluding outliers in yield stability analysis
An example shows the impact of including or excluding outliers in the calculation of the coefficient of variation (CV in %) as a stability measure (Fig. 2). Because the position of the outlier is of no importance for the CV—the time series is treated like a random sample—the effect can be estimated via a simple modeling exercise. The effect of removing a single positive outlier (e.g. a very large observation in the data set) from a 50-year time series, notably if it is still within the realistic range of normally distributed variations (“as is” and thin black line in Fig. 2), is rather marginal; for a CV up to 1.5 (or 150%), the CV changes by ± 5% (or up to 7.5% difference to 150% CV) or less if such an outlier is removed from the calculation. However, if the smallest value is removed from the same time series, then the CV decreases by more than 5% and up to –15% for a CV of 2.0. If CV is expressed as 200%, then the decreased CV ends up being in the 170 to 190% range. As expected, this effect becomes more severe if an outlier is 2× or 5× further away from the mean than what is expected in a normally distributed data set. Removing the largest or smallest observation has the same effect if the CV is close to zero. For realistic values, removing the lowest value by considering it an outlier further reduces the recalculated CV in comparison to the original CV. Removing the largest observation brings back the recalculated CV towards the original CV for larger values and can even lead to an increase in CV if the original CV was already high (solid lines extending above the green area in Fig. 2).
Illustration of the effect that the elimination of a single outlier has on the calculation of the CV in a study with 10, 25, or 50 years of observation, showing the data a with outliers > mean (largest outlier removed) and b with outliers < mean (smallest outlier removed). The relative change in CV (in %) is shown as a function of the following assumptions: (1) the largest negative or positive deviation from the group mean is considered an outlier, although it is well within the expectation of normally distributed variation (“as is”, black colour); (2) the observation with the largest positive or negative deviation is 2× larger than what would be expected if observations were normally distributed (blue colour); and (3) the same with a 5× larger deviation from the mean (extreme outlier; red colour). Green circles indicate the first cut of yield data from the Rengen LTE (data set 3), and orange circles the yield data from the second cut. Lines quantify the effect of one single outlier that is greater or smaller than the group mean. The hashed band shows the ± 5% range around the original CV
In summary, removing an outlier may reduce the CV quite dramatically, except for some special constellations with high original CV and short time series (10 years) and when the outlier represents an exceptionally high yield in the data set. While the effect that a single outlier has on the calculation of the CV is rather simple and obvious, outliers are more challenging in trend analyses because the position of the outlier in the time series is of relevance.
3.3 Confounding factors
3.3.1 Problem description
Confounding factors, which typically appear in LTE data sets, are mostly experimental modifications over time like changes of genotypes, treatments, agronomic management, or plot size. The adaptation of treatment factors (such as increased fertilizer levels or introduction of new cultivars) after some time is seen as inevitable by many researchers managing LTEs. These changes, although they violate the principle of constancy of the LTE, are implemented to maintain relevance and transferability of results to contemporary agronomic practices. Furthermore, the technical implementation may have changed during the experimental period, with, for example, mechanical weeding or larger plot sizes due to technical reasons in former years (1950s, 1960s) switching to possible chemical weed control as well as smaller plot sizes (usage of plot combines) during the last decades. Typically, such changes, whether referring to selected treatments or to the whole trial management, are rare and abrupt because researchers running LTEs will try to maintain integrity of the trial over time. With increasing age of the LTE, however, changes will accumulate—and anyone who has thoroughly looked at an LTE will confirm that they make data analysis difficult.
In this context, the biggest problems in LTE analyses are (i) that potentially confounding factors are often not well or imprecisely recorded in the original documents, (ii) that these factors are not made completely transparent in publications, and (iii) that they are not sufficiently considered in the statistical model, despite having a possible impact on the results of stability parameter estimations. For that reason, it is crucial to search for and document all potentially confounding factors conscientiously before starting the data analysis. Below, we deal with the third problem, showing how confounding factors may be included in the statistical modeling, once all the information about these factors is incorporated into the data set.
3.3.2 Possible solutions
The effect of cultivar is often ignored or considered to be relatively minor in LTEs. If possible, changes of cultivars should be considered in the statistical model, e.g. Macholdt et al. (2020b) fitted their model across years so that the serial correlation of the observations of the same main plot and the different cultivars used could be accounted for. If several cultivars were grown simultaneously in the experiment, a separate factor “cultivar” should be added to the model. If cultivars changed frequently and not constantly, considering the cultivar in the model is difficult.
To account for abrupt experimental changes from one year to another in the statistical model, like the usage of different N-fertilizer levels (or cultivars), a categorical variable P with effects (fixed or random) for the respective time period of a certain N-fertilizer level can be fitted. Constantly changing experimental effects (e.g. related to soil conditions), which are not considered as factors in the model, can be taken into account as a covariate term.
3.3.3 Example: change in fertilizer level
An official long-term variety trial data set (data set 4), which comprises yield of several winter wheat genotypes and fertilization levels in a period from 1983 to 2016, was used to demonstrate confounding factors and how to handle them statistically. The variety trial data allows generating subsets for several locations, to investigate interactions of treatments (N-fertilizer level) with the location, which also may cause confounding effects in LTEs.
To illustrate the data structure of an LTE with a confounding factor, subsets of the variety trial data are considered for two cases of confounding factors, namely (i) a change in fertilizer amount and (ii) confounding due to ageing of the genotype. For each example, a statistical analysis accounting for the confounding factors is presented and compared to an analysis that ignores confounding factors. The analysis is based on linear mixed models, which allow estimating treatment means as well as yield stability parameters in terms of treatment specific error variances according to the concept of Shukla’s stability variances (Shukla 1972). The mixed model analyses were done using ASReml-R, Version 4 (Butler et al. 2017).
For winter rye, the variety trial data (data set 4) comprise two levels (low/high) of N-fertilization until 2005. From 2006 and further, the data only contains the high level of N-fertilization. This structure allows generating a data set comprising the low N-fertilization until 2005 and the high N-fertilization from 2006 on for a given location and reference varieties. Such a data set is very similar to an LTE with a change in the management factor. Figure 3 shows the yield of several reference varieties for low and high N-fertilizations in two locations.
If the change in management is not taken into account, the model for analysis of a single location is written as
where yikl is the yield of the i-th N-fertilizer level in the k-th year and the l-th replicate, μ is the overall mean, Yk is a random effect of the k-th year, and eikl is a random error. Random effects are treated as normally distributed with zero mean and variances \( {\sigma}_Y^2 \) and σ2. To account for the change in the N-fertilizer level, a fixed effect for the N-fertilizer level is added to (1). Further, to allow for different yield stabilities of the N-fertilizer level, the error variances are genotype specific. In this case, the model is
where Pi is the effect of the i-th N-fertilizer level and eikl is the random error with N-fertilizer level specific variances \( {\sigma}_{\mathrm{i}}^2 \).
To illustrate the effect of a management change on yield and yield stability, the data were analysed according to the models (1) and (2) where in (2), the fixed term Pi represents the fertilizer effect. The inference for fertilizer means is only valid if there is no genotype-fertilizer interaction. Estimated mean yield (dt/ha) and yield stability ignoring the change in N-fertilization (model 1) and taking it into account (model 2) for different locations are shown in Table 2. In this table, the values of \( \hat{\mu} \) and \( \hat{\mu}+{\hat{P}}_{\mathrm{i}} \) represent estimates of mean yield, while \( {\hat{\sigma}}^2 \)and \( {\hat{\sigma}}_{\mathrm{i}}^2 \) represent estimates for yield stability (small values indicate high stability). Indices “1” and “2” represent the N-fertilization level (1, before 2006; 2, from 2006 onward).
3.3.4 Example: ageing of genotype(s)
The effect of variety ageing represents another confounding factor that is illustrated in the variety trial data (data set 4). Such ageing effects can be caused by an increased susceptibility of the varieties towards diseases or by a decreasing efficacy of plant protection products. Therefore, either in the presence or absence of plant protection, the yield development of a variety with time indicates if ageing effects exist. In Fig. 4, the yield development over time is shown for two varieties in three locations treated with plant protection in each year.
The scatter plot indicates that the mean performance as well as the variability changes with time or, in other words, with the age (obtained as difference between testing year and first year of testing) of a genotype. The change in mean performance can be modeled by a regression on age, while changes in variability can be taken into account by modeling random regression coefficients for the two genotypes. Ignoring ageing affects the data of a single location which can be analysed according to the model
where yikl is the yield in the l-th replicate of the i-th genotype and the k-th year. The effects μ and Gi are fixed effects for the overall mean and genotypes. Year effects Yk, interactions of genotypes and years (GY)ik, and the errors eikl are random effects with variances \( {\sigma}_{\mathrm{Y}}^2, \) \( {\sigma}_{\mathrm{YG}}^2 \), and σ2, respectively. A model that takes ageing effects into account is
where aik is the age of the i-th variety in the k-th year and bi is a genotype-specific regression slope. The coefficient uikl is a random effect with genotype-specific variances \( {\sigma}_{u_{\mathrm{i}}}^2 \). The variances of eikl are also genotype specific and denoted by \( {\sigma}_{\mathrm{i}}^2 \). In this model, the error variance of a genotype, i.e. the stability of a genotype, is a linear function of age. Therefore, this model describes trends in the stability variance.
Here we estimated the mean yield and yield stability ignoring ageing of genotypes (model 3) and taking it into account (model 4) for different locations of the variety trial data (data set 4). For model (3), \( \hat{\mu}+{\hat{G}}_{\mathrm{i}} \) represents estimates of mean yield, while \( {\hat{\sigma}}^2 \)represents an estimate for yield stability (small values indicate high stability). For model (4), \( \hat{\mu}+{\hat{G}}_{\mathrm{i}} \) represents the mean yield without ageing effect, \( {\hat{b}}_{\mathrm{i}} \) is a slope causing the decrease or increase of mean yield, and \( {\hat{\sigma}}_{u_{\mathrm{i}}}^2 \) indicates the magnitude and direction of the change in yield stability (Table 3).
For model (3), \( \hat{\mu}+{\hat{G}}_{\mathrm{i}} \) represents estimates of mean yield (dt/ha), while \( {\hat{\sigma}}^2 \)represents an estimate for yield stability (dt2/ha2). For model (4), it represents the mean yield without ageing effect, bi is a slope (dt/ha/year) causing decrease/increase of mean yield, and \( {\hat{\sigma}}_{u_{\mathrm{i}}}^2 \) indicates the magnitude and direction of the change in yield stability (dt2/ha2). Negative values of \( {\hat{\sigma}}_{u_{\mathrm{i}}} \)represent an increase in stability with age, while positive values represent a decrease in stability. The indices “black and “red” relate to the colour code of two genotypes in Fig. 4
3.4 Accounting for long-term trend of yield data
3.4.1 Problem description
LTEs often exhibit marked trends of yield over time. This is mostly because effects on crops and soils accumulate and become stronger over time. In very long LTEs, temporal trends of yield can also reflect management changes over time that are not part of the treatments (e.g. changes in cultivars, pesticides, equipment), irrespective of the main treatment effects, e.g. with and without tillage or organic vs. mineral fertilization. Yield trends in LTEs can be positive (e.g. as soil fertility increases) or negative (e.g. in unfertilized controls). Ignoring such trends is likely to compromise yield stability measures. A simple example is the yield variance across years; not taking into account a positive trend in the yield across years would unjustly penalize a treatment by a seemingly high variance, i.e. low stability, simply because variance would be inflated by the general increase of yield over time. Dealing with trends becomes a more complex issue of yield stability analyses for comparisons across sites and crops and when analysing the development of temporal stability over time.
From a theoretical point of view, with the ordering of the data through time being important for stability analyses in LTEs, time series methods are appropriate. Most methods of time series analysis require so-called stationarity of the data (no changes of statistical properties over time), but crop yield time series are often non-linear and not stationary. A typical violation of stationarity is the presence of a deterministic or stochastic trend in the mean (Fig. 5a). This trend does not need to be linear; it can also be a non-linear trend as shown in the example in Fig. 5a. Generally, the presence of trends in the data sets would lead to a strong over- or underestimation of stability when using measures based on the mean and the standard deviation of the data. Contrasting to trend analyses, in stability analyses, yield fluctuations (short-term variability) around the trend (long-term change) are the critical characteristics of interest.
a Yield data of sugar beet observed at the LTE Dikopshof, Germany (data set 1), and trends estimated using the LOESS smoothing (red line) and linear regression (LM, black dotted line) for the treatment omission of potassium fertilizer. b Absolute yield anomalies after additive detrending and c relative yield anomalies after multiplicative detrending.
3.4.2 Possible solutions
One solution is the stratification of the data, i.e. splitting the time series in several subsets, and the subsequent restriction of data analysis to these subsets (see, e.g. Reckling et al. 2018a). If this is not an option, suitable data detrending techniques can be applied (Singh and Byerlee 1990). The type of trend model to which the data are fitted will, in turn, affect the stability measures (Massell 1970; Valle 1979) and, consequently, the quantification of changes in stability over time (see Sect. 3.8). So far, these effects have rarely been quantified (Lu et al. 2017).
The simplest approaches to remove trends in crop yield data include data transformations (see also Sect. 3.4), e.g. the computation of relative yields based on the range of yields for a given year, site, experimental block, and treatment or the use of mathematical operators, such as differencing. Differencing is conducted by subtracting the previous observation from the current observation. Techniques such as differencing (or lagged differencing if data show autocorrelation), however, are based on the assumption that these transformations can convert nonstationary to stationary data.
Classical detrending techniques that have been applied to crop yield data can be grouped into two main categories: (1) approaches that use time and (2) approaches that use time and one or more additional variables to separate trends from variability in the time series. An example for the latter approach is the study by Bönecke et al. (2020) who separated climatic from genetic and agronomic yield effects using linear mixed effect models and estimated the climatic influence based on a coefficient of determination. Mathematically related to both approaches, though often a rather technical consideration, is the transformation of the data (e.g. log transformation).
Approach (1) encompasses a variety of methods that can be broadly differentiated into (1.1) global regression methods, e.g. linear, polynomial, and weighted regression; (1.2) local (adaptive) smoothing or regression methods that are time-dependent, e.g. moving averages, kernel smoothing, and other filtering functions, piecewise or local (polynomial) regression; and (1.3) more complex signal analyses that decompose time series into different components and operate either in the time or in the time-frequency domain, e.g. empirical mode decomposition (Wu et al. 2007), singular spectrum analyses (Broomhead and King 1986), and wavelet analysis (Adamowski et al. 2009). Since the methods mentioned for (1.3) are rather suitable for time series of high-frequency data and/or time series characterized by oscillations and cycles, such as climatological or hydrological data, they are not discussed here. Global regression methods assume that a single trend model, e.g. linear, quadratic, and cubic, can be applied globally to describe the trend, whereas trends derived by local smoothing and regression methods strongly depend on the definition of the time window used for filtering/smoothing.
After separating the trend from the variability, detrending can be basically either additive (trend is subtracted from the data points; yield)
or multiplicative (using the ratio between data value and corresponding trend value)
This processing step directly translates into the use of either absolute values (YAabs, absolute deviations from the trends) or relative values (YArel, percentage deviations from the trend value in each year) and influences statistical properties on the resulting data set and corresponding stability analyses (Fig. 5b and c). Alternatively, a post hoc analysis can be applied to test whether there is any correlation of the stability parameters with a linear trend.
Approach (2) can be used to improve trend models if factors that are relevant for the change in crop yield over time do not only have a time component but strongly interact among each other. Corresponding statistical approaches, such as mixed effect models, allow for explicitly assessing the contribution of factors, such as crop genotype, fertilizer amount and type, and site characteristics (environment) to the overall variability (see, e.g. Bönecke et al. 2020).
3.4.3 Example: impacts of different detrending methods
To illustrate three different methods for detrending, the (i) local polynomial regression smoothing (LOESS) and (ii) linear regression (LM) were applied to the sugar beet yield data and one fertilization treatment (omission of potassium) at the LTE Dikopshof for the period 1955–2008 (data set 1). The overall variance of the detrended yield data (“residuals”) is only slightly affected (Fig. 5). However, the probability distribution is modulated by the detrending technique. Fitting a global trend model with lower flexibility (LM) leads to a larger range of residuals. In general, detrending might lead to a deviation of resulting data from the Gaussian distribution and, thus, compromise subsequent statistical analyses. For the application of stability measures which are based on the probability distribution, e.g. risk-based approaches, careful detrending is required. This is especially true for rather short time series, for the comparison of temporal data subsets (see Sect. 3.8), and for comparing the temporal stability between sites and crops.
3.5 Temporal autocorrelation
3.5.1 Problem description
Carry-over effects of management activities performed in one year can have an effect also on yields in the following year and possibly even up to a few years later (Gulden et al. 2015; Jernigan et al. 2020; Rui et al. 2020). Although this is the best scientific representation of a farmer’s perspective focusing on a specific plot with the goal to improve or maximize the yield from that plot in the long term, it poses some challenging statistical problems to be aware of. In an LTE, repeated measurements are made on the same plots year after year (Onofri et al. 2016). Serial correlation means that a measurement, e.g. of yield, in year t+1 is not statistically independent from the measurement in the previous year t.
This temporal autocorrelation needs to be accounted for when estimating the plot error term. In simple words, if a statistical test (e.g. for differences in yields) is carried out in the standard way that assumes that the data are random samples without serial correlation, then inference about parameter estimates is biased, and significance tests may be invalid as they do not appropriately control type I error rates. This is because the data generating mechanism involves a process causing the correlation which is not accounted for in the model. In other words, due to (constant) plot effects on measured yields, residuals can be correlated between years, and thus the assumption of independence of residuals is violated if this correlation is not incorporated in the model.
As there may be many causes of autocorrelation in LTE, it is crucial to incorporate this prior knowledge into the model. An advantageous feature of mixed models for the analysis of LTE lies in the fact that they allow to include random effects for factors which are not the major scope of the LTE, e.g. years, implying that inference of parameter estimates takes into account the variation caused by years such that inference of estimates holds not only for the observed years but also for other years. Taking such effects as random may cause standard errors to increase compared to analysis with fixed year effects and/or ignoring correlation but will provide inferences that are more realistic and practically relevant. Furthermore, treatment effects in LTE like different fertilizer regimes may be correlated as well, which can be taken into account in a mixed model analysis.
3.5.2 Possible solutions
Temporal autocorrelation could be accounted for by allowing for serial correlation among year main effects and among plot and block effects in linear mixed effect models. In simple statistical comparisons, e.g. using the t-test for testing significance in difference of yields among treatments, repetitions in time are easiest to treat when measurements are made at fixed intervals (time series, e.g. yield measured every year without gaps). This allows to compute the lag 1 autocorrelation coefficient ρ1, which is Pearson’s product-moment correlation coefficient of pairs of observations one step apart in the same time series (the lag 0 autocorrelation coefficient is ρ0 = 1.0 by definition). If ρ1 is significantly different from zero (ρ1 ≠ 0), then a correction for serial correlation is required in any statistical test. If, however, ρ1 is not significantly different from zero, then the time series can be treated in the standard way as if it were a random sample without serial correlation and does not need special attention. This is assuming that higher lags are uncorrelated. However, higher lags may be relevant as well; in particular, in the case of LTEs, higher lags may be justified in an agronomic view as they are able to take legacy effects into account.
If ρ1 > 0, then all statistical tests made with time series data that assume randomness of the variables under consideration lead to an overestimation of significance (too low p values) because of oversampling. Oversampling describes the same statistical artefact as autocorrelation in the time series. A simple approach to treat this problem in statistical tests was presented by Wilks (2006). The key is to reduce the number of samples n in a statistical test to the number of independent samples n′ in the time series and then determine the test statistic with n′ instead of n to define the degrees of freedom of that test, with (Wilks 2006).
Here, the serial correlation is assumed to be positive. For example, a LTE time series with n = 20 years of data in which ρ1 was found to be 0.6 has a statistical information content that corresponds with n’ = 5 random samples. We first present an example where taking into account temporal autocorrelation changes the significance of differences between mean yields in an LTE; the second example deals with a more complex case where we test the effect of taking into account autocorrelation on yield stability estimates.
3.5.3 Example: time series of yields with its autocorrelation
We show an example of the comparison of two treatments from a LTE in Dikopshof (Fig. 6), Germany, with data from 1955 to 2005 (data set 1). During this time period, the yield difference is significantly different from zero (t = 2.0623, df = 50, p = 0.044) if no correction is made for serial autocorrelation in the time series. The correction reduces the degrees of freedom from 50 to 23.8 (using Eq. (5) with ρ1 = 0.3456 as shown in Fig. 6b), and thus the t-test yields p = 0.050 with this correction. Although minor, such effects can be important when trying to extract the maximum of information from available data. Alternatively, this analysis could be done using a mixed model package, fitting a model for autocorrelation and approximating the degrees of freedom using the Kenward-Roger method.
Example of two time series of potato yields a measured in a long-term trial at Dikopshof, Germany, from 1955 to 2005 (data set 1) and the difference in yields in a pairwise comparison with b its autocorrelation at different lags. Lag 1 (ρ1) is used to correct statistical tests for the presence of serial correlation. Horizontal dashed lines in b indicate the band of non-significant autocorrelation coefficients. With random samples, ρ1 is found between these thresholds with 95% confidence, whereas in time series, ρ1 is often (but not always) significantly different from zero
3.5.4 Example: effect of correction for autocorrelation on stability
In order to check if any autocorrelation of plot residuals is present and to assess any effect on estimates of environmental variance, we fit models without any correlation structure (NC), with compound symmetry (CS), and with a power correlation structure (POW). If sampling intervals are constant, the latter will be equivalent to an autoregressive structure (AR1, where 1 indicates that only a time lag of 1 is considered in the analysis), but it also allows for non-constant sampling intervals. We furthermore compare a one-step approach, where the environmental variances and the correlation structure are estimated in one single model, to a two-step approach, where in a first model treatment × year means and their covariance matrix are estimated taking into account different correlations structures, and then in a second model, environmental variances are estimated using the previously estimated T×Y means (Piepho 1999; Piepho et al. 2004). The model for the one-step approach, stated in symbolic notation akin to that used in linear model packages, was:
where Ti is the i-th fixed treatment effect, (TY)ik is the random effect of the k-th year within the i-th treatment, Bj is the j-th random block effect, (BY)ik is the random effect of the k-th year within the j-th block, and eijk is the residual plot error. The correlation structure is modeled with the respective covariance structure for eijk, and environmental variances are modeled through an unstructured covariance matrix on (TY)ik (UN in SAS) with the diagonal representing the environmental variance estimates. In the two-step approach, the model to estimate the treatment × year means is the same as (6), but with (TY)ik as fixed to get LS-means, and correlation structures are similarly implemented for eijk. Using the estimated LS-means \( {\overline{y}}_{\mathrm{ik}} \)for the i-th treatment in the k-th year as response, the model to estimate environmental variances is:
with residual variance-covariance matrix for \( {\overline{e}}_{\mathrm{ik}} \)being fixed at the variance-covariance matrix of the LS-means from the first stage. Environmental variances are again estimated from an unstructured matrix on the (TY)ik effect as in the one-step approach. Additionally, an analysis using simple treatment × year means is compared, where the variance of each treatment is calculated, and SEs are calculated by multiplying this variance by √(2/(t-1)), where t is the number of years (Piepho 1998).
As an example, we illustrate the method by computing the environmental variance estimates and their standard errors (SE) for spring wheat in the Borgeby trial (data set 2).
Three different models to deal with a possible autocorrelation are compared using plot values in a one-step and two-step approach. A lower Akaike information criterion (AIC) indicates better model fit. Additionally, an analysis using simple treatment × year means is compared, where the variance of each treatment is calculated, and SEs are calculated. P(LL) is the significance of a likelihood-ratio test of the given model against the respective NC model, testing if the given model shows a significantly better fit. ρ is the estimated correlation coefficient, and r is correlation coefficient of the estimated environmental variances with the given correlation structure against the calculated variances from simple treatment × year means (Table 4).
In spring wheat in the Borgeby trial (data set 2), AIC and the p value from a likelihood-ratio test suggest that no correlation structure seems to be indicated and that the NC model is to be preferred (Table 4). For other experimental data, e.g. data set 3, there is no convergence with this method, and this method suggests that taking into account possible autocorrelation due to repeated measurement might have only minor effects on estimated stability measures and their standard errors. This could be the case because yield variances react strongly on the weather conditions (Richter and Kroschewski 2006). E.g. for soil organic carbon, Richter and Kroschewski (2006) found that correlations were relatively high and should be included into scientific interpretations of long-term experiments.
3.6 Choice of stability measure
3.6.1 Problem description
With the large number of stability indices that have been proposed over the years (Hussein et al. 2000), it is important to make an informed decision on which indices should be chosen to evaluate stability in a given LTE, for a given research question. This is because (a) not all stability measures are equally suited for LTEs; (b) some indices may be mathematically equivalent to others; and (c) indices represent different concepts of stability. Here we show what criteria can be used to make an initial selection of measures and also how to deal with the potential multiplicity of selected measures in the subsequent data analysis. We note that the values of the regression parameter depend on the units of measurement of the response, but otherwise our inference would be unaffected by a change of units of measurement.
3.6.2 Possible solutions
In the path leading to a choice of indices, it first needs to be recognized that there is no “right” or “true” index. So the question which one of the indices is the best one to represent “true” stability cannot be answered. Different indices simply express and describe different properties of the same data set.
Second, it is necessary to define the research question as precisely as possible. Does the research question focus on fluctuations around a given treatment’s mean across years or on the deviation from the mean of all treatments in each year? A static index should be chosen in the former, and a dynamic one in the latter case. Should negative deviations from the mean be assessed in a different way from positive deviations? In that case, risk-based approaches should be preferred (Macholdt et al. 2020b); otherwise, i.e. if positive and negative deviations are equivalent, variance-based stability measures are fine to be selected.
Third, it needs to be recognized that some stability indices may not be suited to LTEs. Many stability indices have been developed in plant breeding and cultivar evaluation, where a large number of genotypes are tested in many environments. The treatments of LTEs, however, which correspond to the genotypes, may not be as numerous. In fact, some LTEs contain only four different treatments. This becomes an issue with those indices for which the stability of one treatment is dependent on the yields of the other treatments—this is the case with Finlay-Wilkinson’s regression parameter b, for example, but also for the other dynamic stability measures and for some variance-based ones, e.g. Shukla’s stability. When many treatments are included in the LTE, this dependence is diluted, but it becomes problematic when fewer treatments enter into the stability analysis. In the extreme case, with only two treatments, there is no information in the b-value of one treatment that is not already contained in the other. Here we provide a list of 42 yield stability indices and categorize them by their concept and whether they depend on other treatments (Table S1, DOI 10.4228/ZALF.DK.148). A possible approach to help with the decision whether or not to use stability measures that are dependent on other treatments is to (randomly) drop individual treatments from the data set and test in which way the stability of the remaining treatments is affected.
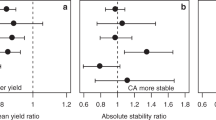
Fourth, understanding the mathematical properties of the different indices (e.g. the dimension and unit of the indices) might help researchers to decide which index to be used. This also includes the unit of an index, which is often not mentioned, but which may be useful for data interpretation. For example, the units of genotypic superiority measure (Lin and Binns 1988) and ecovalence (Wricke 1962) are the square of units for the target trait (e.g. kg2/ha2 for yield). This means that the square roots of these two indices are on the same scale as the mean, and using this information may facilitate data interpretation.
Fifth, an important generally desired property of a stability index is a low correlation with the mean. This is because the aim is a combination of high yield and high stability, but if correlation of a stability measure with mean yield is generally high, i.e. principally and more or less irrespective of the treatment, then this stability measure does not contain any useful information that goes beyond the mean (also see Sect. 3.7). Comparisons between 11 stability indices and mean yield of six crop species in combination with three treatments using the data set from Borgeby (data set 2) show that in this data set, mean yield of a crop correlates highly with the coefficient of regression (Finlay and Wilkinson 1963) and the genotypic superiority measure (Lin and Binns 1988); see example below). However, in our experience, the correlation of a stability measure with mean yield varies largely between sampled populations. A simulation data set shows that the number of levels (e.g. number of crop species or agronomic systems to be compared) and the range of the mean value between levels in the sample population can determine the strength of the correlation of a stability measure with the mean. If the means between levels in the sample population are less different, the coefficient of regression becomes less correlated with the mean of the level. In most cases, the square root of genotypic superiority measure has the highest correlation with the mean yield. While there are several studies on the correlations between mean yields with yield stability measures from variety trial data, e.g. Dehghani et al. (2008) and Cheshkova et al. (2020), little is known about correlations with long-term yield data from LTEs. Further research is therefore needed to elucidate any consistent relationships.
Sixth, whenever possible, more than one stability measure should be calculated, and differences need to be made transparent and be discussed. If multiple indices are derived from the data, good practice is to run a correlation analysis among them (Cheshkova et al. 2020) or a multivariate analysis, e.g. using principal component analysis (PCA; Dehghani et al. 2008). This will help to quantify which indices are similar to each other; but it only makes sense if the general properties of the indices are understood beforehand (e.g. dependence on the mean; see Sect. 3.7).
Finally, a possible (and radical) solution to the task of choosing among the many available stability indicators is to calculate none at all, but instead to consider the entire distribution of the response across varying environments (Fig. 7), rather than to try to summarize stability in one single number representing a certain property of the distribution. The advantage of this (risk-based) approach is that it considers both variability and mean in a very direct and meaningful way at the same time. In addition, other properties of the distribution such as skewness can also be seen. However, with this option, it becomes more difficult to rank different treatments. Dealing with two or three treatments, the decision may be easy which distribution is superior in terms of stability. When dealing with as many as 24 different treatments (Ahrends et al. 2018), the ranking can be based on the probability of a treatment to outperform all other treatments in a given environment (Piepho and van Eeuwijk 2002).
Correlation matrix showing comparisons between mean dry yield and 11 stability measures of six crop species in combination with three treatments (n = 18) using the R package toolStability (Wang et al. 2019) and the data set from Borgeby (data set 2). Correlations are scaled by the colour gradient of the corresponding cell, from highly positive correlation (dark blue) and no correlation (white) to negative correlation (red). Stability measures are represented in the same order on the x- and y-axes
3.6.3 Example: comparison and correlation between stability measures
In this example, we illustrate differences and similarities between 11 different stability measures and the mean yield of the six crop species in combination with three treatments from the LTE Borgeby (data set 2).
We used the R package toolStability (Wang et al. 2019) to compute the stability measures: (1) safety-first index (Eskridge 1990), (2) coefficient of determination (Pinthus 1973), (3) coefficient of regression (Finlay and Wilkinson 1963), (4) deviation mean squares (Eberhart and Russell 1966), (5) environmental variance (Roemer 1917), (6) genotypic stability (Hanson 1970), (7) genotypic superiority measure (Lin and Binns 1988), (8) variance of rank (Nassar and Huehn 1987), (9) stability variance (Shukla 1972), (10) adjusted coefficient of variation (Döring and Reckling 2018), and (11) ecovalence (Wricke 1962).
The average yield stability value is computed from all the six crop species showing positive and negative relationships between stability measures and between the mean yield and these measures (Fig. 7). Here we emphasize that the absolute coefficients of correlation between stability measures depend strongly on the characteristics of the data set, so the coefficient matrix shown in Fig. 7 is rather an example than a generalization. A multivariate analysis using a PCA plot is another option to illustrate the correlation of different stability measures. These relationships should be considered when selecting and interpreting results from yield stability measures.
3.6.4 Example: interpreting stability from the entire yield distribution
Here, we illustrate the option to look at the entire (non-transformed) yield distribution to compare different cropping systems. The example in Fig. 8 shows the cumulative yield distribution for different treatments with winter wheat in two different LTEs, i.e. with different fertilization levels (Broadbalk, data set 5) and with more diverse and less diverse cropping systems (Borgeby, data set 2). While there is only a minor difference in the winter wheat yield distribution between the cropping systems in Borgeby, these differ strongly in the Broadbalk LTE where the systems with fertilization have a lower distribution than the systems with higher fertilization (Fig. 8). The distribution as such gives however only limited information about stability and more about the probability of achieving certain yields.
Empirical cumulative distribution function of the different treatments (in colour) for the different experiment combinations for winter wheat in the LTEs Broadbalk (a, data set 5) and Borgeby (b, data set 2). Treatments are not identified as the figure shall simply represent the different distributions
Further, as another way to consider the entire distribution of yield values in relation to stability, we explore an approach often used in hydrology to assess probabilities and return periods of extreme values (Loaiciga and Leipnik 1999) using the Rengen grassland LTE (data set 3). This approach is based on the Gumbel distribution (Eugster et al. 2010; Gumbel 1958). For each time series of yield values, this simply determines the frequency f with which the yield is lower than or equal to a given reference yield value Yr. For example, for a given plot i (i.e. combination of treatment and replication), the year with the maximum yield Ymax generates the highest frequency of f = 1, because all other years have lower yields than Ymax; conversely, the minimum yield in that time series of plot i would generate the lowest value of f = 1/n where n is the number of years in the time series. With the frequency f(Y ≤ Yr), we can also determine the return interval of a given reference yield value as T=1/f years. With a double-logarithmic transformation z = −log(−log(f)) of the frequency, the data is then displayed against the threshold yield Yr (Fig. 9). To allow calculating the double logarithm, f is determined for each plot as f = (n-m+1)/(n+1), where n is again the number of years in the time series and m is the rank of yield within the time series.
Gumbel plot of the Rengen grassland LTE (data set 3) yield data to investigate low yield extremes. Blue symbols, first cut; red symbols, second cut. Only three out of five treatments are shown, Ca (squares), CaN (triangles), and CaNP (circles). The frequencies are calculated from the mean of 10 field replications. In the case of a perfect Gumbel distribution, the individual lines would be linear. The most frequent occurrence would be every year; the rarest occurrence would be once every 24 years
As smaller threshold yields are chosen, the occurrence of yields lower than that threshold yield becomes rarer, but for a given threshold yield, the frequency of lower yields strongly depends on the treatment. Interestingly, none of the curves intersects with each other. This means that the risks are consistent across the entire distribution. In this data set, whatever the chosen threshold yield, the order of treatments remains the same with regard to the (transformed) frequency of being lower than that threshold.
3.7 Dependence of stability measures on the mean
3.7.1 Problem description
In a data set generating variances σ2 and means μ, such as an LTE, variances may depend on the means in a systematic way. The British ecologist Lionel Roy Taylor found that numerous insect populations could well be described by the equation log(σ2) = log(a) + b log(μ), or expressed differently, σ2 = aμb (Taylor, 1961). Later research demonstrated that this power relationship between variance and mean, termed Taylor’s power law (TPL), or Taylor’s law, is extremely widespread (Ramsayer et al. 2012; Taylor et al. 1998; Xiao et al. 2015), and Döring et al. (2015) showed that this dependence can also be found to hold in crop yield data (also see Fig. 10).
Example for the relationship between log (σ2) and log (μ) of dry matter yield from the Rengen grassland experiment (data set 3; Hejcman et al. 2007). Each point represents a single plot and encompasses means and variances from data over 24 years from 1991 to 2014; each of the 50 plots (from 5 treatments in 10 replications) was cut twice, with the first cut in summer (blue circles and blue dotted line, log(σ2) = – 0.758 + 1.311 log(μ), Adj. R2 = 0.620, df = 48) and the second cut in autumn (red diamonds, red solid line, log(σ2) = – 0.503 + 1.090 log(μ), Adj. R2 = 0.803, df = 48). Original units are t ha−1
However, if such dependence is so widespread, i.e. if it is generally observed, no matter what data set, this may be seen to be problematic for yield stability analysis. For example, it can be shown that if TPL holds and b<2, the coefficient of variation (CV) generally decreases in a non-linear way with increasing mean μ (Döring and Reckling 2018). If this is principally the case, it is not convincing to interpret a low CV value of a particular treatment as high stability when in fact the main reason is a high mean value of this treatment. In other words, if TPL holds, and regularly so, there may not be any genuine information on stability in the data that is not already contained in the mean. As has been shown previously (Döring and Reckling 2018), the problem of significant TPL dependence occurs when the range over which μ varies is large. This is often the case in LTEs, e.g. when full fertilization and an unfertilized control are included in the set of treatments or when different crop species are compared (Reckling et al. 2018b). However, while it is relatively straightforward to test whether or not TPL holds in the data set to be analysed, it is less easy to decide how to deal with the result of that test. Currently, there is no generally accepted or generally applicable tool to deal with TPL in stability analysis.
3.7.2 Possible solutions
Here, we look at three different options to deal with TPL in LTE data analysis. The first option is simply the a posteriori analysis of the data for the presence of TPL. It can be done after conducting the main stability analysis, by plotting log(σ2) against log(μ) and statistically testing the (linear) dependence between these two variables (see Fig. 10 as an example). The stability results can then be discussed in the light of the potential TPL dependence and the slope b of the relationship between log(σ2) against log (μ). This option is relatively easy to implement and has the advantage over previous research tradition that it makes the dependency visible. However, this a posteriori approach does not solve the problem but merely describes it, which may not suffice when the task is to rank treatments by stability and especially if the TPL relationship is strong.
The second option is an attempt to correct the data, basically removing the dependence of the variance from the mean. This idea is the basis for the POLAR stability index (Döring et al. 2015) and for the adjusted coefficient of variation (aCV; Döring and Reckling 2018). Both measures can be used as stability indices, with the advantage of the aCV being expressed unitless when computed as ratios and % when computed as percentages equivalent to the standard coefficient of variation (CV; also called relative standard deviation, RSD). The aCV can therefore be easily used in agronomic studies that aim to provide guidance for farmers and advisors (an example calculation and R code for computing the aCV can be obtained from the corresponding author).
For POLAR and aCV, the slope b is determined before the correction is applied according to Döring and Reckling (2018). If the data is not sufficient to generate a robust value of b, it may be possible to estimate it from other data sets. However, currently, there is no sufficient knowledge about typical values of b generated by yields from LTEs. A meta-analysis is therefore required, to come up with reliable (and maybe more generally applicable) values for b. So far, there are several studies that can be used to estimate b values under various conditions for annual crops (Döring et al. 2015; Döring and Reckling 2018; Knapp and van der Heijden 2018; Reckling et al. 2018b) and from Fig. 10 for grassland. While this option is relatively easy to implement, it needs to be put into the broader context of modeling approaches for variance-mean dependence, of which there are many (Carroll and Ruppert 1988). These approaches also allow accounting for variance-mean dependence in a mixed modeling framework (Damesa et al. 2018).
The third option is to look at the whole distribution of data points, rather than extracting only variance and mean (see Fig. 8).
3.7.3 Example: adjusting the coefficient of variation (aCV) for assessing yield stability
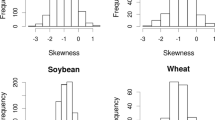
The Rengen grassland LTE (data set 3) was established in 1941 in the Eifel Mountains of Germany on low productive grassland and compares five different fertilization treatments, (1) only Ca (as lime); (2) Ca and N; (3) Ca, N, and P; (4) Ca, N, P, and KCl; and (5) Ca, N, P, and K2SO4 (Hejcman et al. 2007). We tested for TPL by subjecting the dry matter yield data to regression analysis based on log(σ2) = log(a) + b log(μ). In the yield data from the Rengen grassland LTE, there is a (near-)linear relationship between log(σ2) and log(μ) as shown in Fig. 10, with a slope of 1 < b < 2 for both the summer cut and the autumn cut. This means we would expect those treatments with a low mean yield also to have a high coefficient of variation. As Table 5 shows, this is indeed the case, with the treatment receiving Ca only showing the highest CV. However, once TPL is taken into account, i.e. when applying the aCV, the significant differences between the treatments disappear. True stability effects of the fertilizer treatments may therefore be doubtful, and differences among the unadjusted CVs may need to be interpreted with caution.
Data is shown over 24 years, n=10 replications, the first (cut 1) and second cut (cut 2) in the growing season. Treatments with no letter in common are significantly different following Tukey’s HSD test
3.8 Development of stability over time
3.8.1 Problem description
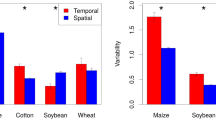
Yield observations from each year over several decades allow for studying changes in yield stability over time. While an assessment of these changes is critical for studies on food security (especially in relation to climate change), differences in the methods applied challenge attempts to perform meta-analyses across crops, locations, and treatments. Exemplarily, for major food crops, some studies suggest a decrease in yield stability over time (e.g. Macholdt et al. 2021; Döring and Reckling 2018; Reckling et al. 2018a), while others suggest no change or an increase in stability over time (Calderini and Slafer 1998; Schauberger et al. 2018; Xu et al. 2020). Assessing changes over time further requires considering that the farmers’ (economic) vulnerability and perception of yield losses or gains change with crop- and location-specific yield levels and yield potentials.
3.8.2 Possible solutions
Most often time series are split into subsets of equal length based on either numeric, e.g. decades (Renard and Tilman 2019; Döring and Reckling 2018), or scientific, e.g. major changes in environmental or management conditions such as rotations (Reckling et al. 2018b). This approach can lead to an indirect detrending (of data subsets; see Sect. 3.4); otherwise data have to be detrended to compute absolute or relative anomalies for each time period. Differences between statistical properties of these subsets can be tested for their significance (e.g. t-test, Wilcoxon tests) or assessed by comparing corresponding changes in stability metrics. An advantage of this method is its high flexibility, especially with respect to the observation periods covered by data subsets. On the other hand, due to the decreasing sample size, results can be modulated by outliers, and the use of statistical tests is often restricted. A generalization of findings is restricted to the selected time windows. If mean yield levels changed over time, the use of relative (e.g. deviations from the trend) vs. absolute yield anomalies will greatly affect findings. With changing yield levels or yield potentials, the significance of absolute yield losses for the farmers’ income and, thus, farmers’ understanding of (absolute) yield stability will change accordingly. Optimal would be the analysis of both absolute and relative yield anomalies with results from the latter further facilitating the comparison across crops and treatments.
A rather data-driven but less flexible approach is testing for breakpoints or “change point” (see, e.g. Killick et al. (2012)) and for linear or non-linear trends in relative or absolute yield anomalies over time and quantifying their position and direction and magnitude, respectively. For the breakpoint analyses according to Piepho and Ogutu (2003), the effect of outliers and differences between algorithms applied has to be tested and documented. Stability metrics based on both the complete observation data and outlier-corrected data should be reported.
The development of yield stability over time can be described by linear mixed models which allow to model trends in mean yield and yield variance as a function of time. Yield variance of such models can be interpreted in terms of yield stability (Shukla 1972), and therefore, the development of yield stability with time can be described by mixed models (Macholdt et al. 2021). Based on the mixed model, a coefficient of variation can be computed for each year which can be seen as a measure for relative yield stability. Furthermore, these models allow to compute the probability of exceeding a threshold value which represents another measure for yield stability.
3.8.3 Example: development of yield stability over time
To illustrate time-dependent trends in stability, the yield of two winter wheat genotypes tested over a period of time is shown in Fig. 11 for two different locations (data set 4).
A model taking time-dependent trends in the mean yield and in yield variance into account is
where Yk is a random effect for the k-th year with variance \( {\sigma}_{\mathrm{Y}}^2 \), Gi is a fixed effect for the i-th genotype, tk is the calendar year, bi is a genotype-specific regression slope, and (YG)ik is a random effect for year-genotype interaction with variance \( {\sigma}_{\mathrm{YG}}^2 \). The coefficient uikl is a random effect with genotype-specific variances \( {\sigma}_{{\mathrm{u}}_{\mathrm{i}}}^2 \). The variances of eikl are also genotype specific and denoted by \( {\sigma}_{\mathrm{i}}^2 \). In this model, the error variance of a genotype, i.e. the stability of a genotype, is a linear function of time. Therefore, this model describes time-dependent trends in the stability variance. The estimated parameters of this model are shown in Table 6.
Estimated mean yield of the genotypes is given by \( \hat{\mu}+{\hat{G}}_{\mathrm{i}} \) (dt/ha), and bi represents the regression slopes (dt/ha/year) associated with time. The values of \( {\hat{\sigma}}_{{\mathrm{u}}_{\mathrm{i}}}^2 \) indicate the magnitude and direction of the time-dependent change in error variance (dt2/ha2) which can be seen as the development in yield stability with time. The indices “black and “red” relate to the colour code of genotypes in Fig. 11
The mixed model allows calculating a coefficient of variation (CV) for each year which can be considered as the development of relative yield stability with time. As the variances in the model above are genotype specific, the development of the CV can be investigated for each genotype. For the i-th genotype in the k-th year, the coefficient of variation based on the mixed model is
The development of the CV for the two genotypes is shown in Fig. 12.
In Fig. 12, the increase in the CV for the site “Rethmar” can be attributed to the negative trends in the mean (negative values of\( {\hat{b}}_{\mathrm{black}} \) and \( {\hat{b}}_{\mathrm{red}} \)), while the trends in the stability variance is positive, causing the CV to increase. For the site “Bad Salzung”, the situation is opposite, i.e. stability variances decrease (negative values of \( {\hat{\sigma}}_{{\mathrm{u}}_{\mathrm{black}}}^2 \) and \( {\hat{\sigma}}_{{\mathrm{u}}_{\mathrm{red}}}^2 \) in Table 6), while the trends in the mean are positive which causes a decrease in the CV. While an increase in yield variability has been observed frequently (Döring and Reckling 2018), there are also studies showing the opposite (Calderini and Slafer 1998). Changes in yield stability can be explained by the interaction of genotype × environment × management at a given site including general changes in climate (Ray et al. 2015). For the given examples, the reasons for the contrasting responses could only be identified when taking the environmental conditions into account which is beyond the scope of this paper.
For a risk analysis based in the mixed model, the probability of a genotype’s yield to fall below a threshold value x in a given year is given by
where F is the distribution function of the standard normal distribution.
Evaluating \( P\left( yield<x\right)=F\left(\frac{x-{\hat{\mu}}_{\mathrm{ik}}}{{\hat{\sigma}}_{\mathrm{ik}}}\right) \)for a range of threshold values results in Fig. 13.
Probabilities of not exceeding a yield threshold value x [dt/ha] for the two genotypes in each location (data set 4), a genotype 1 at the site “Rethmar”, b genotype 1 at the site “Magdeburg Boerde”, c genotype 2 at the site “Rethmar”, and d genotype 2 at the site “Magdeburg Boerde”. The different colours within one plot represent the probabilities for different years. The colours get darker with the year, i.e. for genotype 1, the grey lines represent an early year while the black lines represent a more recent year. For genotype 2, the colours range from red (early year) to dark red (late year)
3.9 Standard errors and statistical inference of stability measures
3.9.1 Problem description
Stability measures can often be defined as functions of variance parameters of a linear mixed model, which can be estimated by REML. As such, asymptotic variance-covariance matrices are readily available based on the maximized residual likelihood, and from this, the standard error of stability measures can be obtained using the delta method (Johnson et al. 2005; Piepho and Edmondson 2018).
In order to be able to compare treatments regarding their stability, it is necessary to have some measure of precision of the estimated values and some measure to test if the estimates differ significantly between treatments. However, while the calculation and reporting of such measures are mostly straight forward and common practice for means, this is still not the case for many stability parameters. In most stability analyses, simply the estimated values are reported without any measure of precision and not testing if estimates differ significantly. E.g., some analyses have tested if estimated stability or environmental variances differ significantly from zero and categorize genotypes or treatments which variance is significantly indifferent from zero as stable, e.g. Fernandez (1991). While such tests of estimated variances may serve model selection, we believe they are not legitimate to identify stable and unstable treatments, as stability is rather a relative measure. Furthermore, if all variances are, e.g., different from zero, it would be not informative to classify all treatments as “unstable”. Thus, statistical tests need to be explored for inferences on the differences between treatments. Such tests need to consider the complexity of some stability parameters, like standard errors or tests for pairwise differences.
3.9.2 Possible solutions
We discuss different approaches on how to calculate standard errors and tests for comparing treatments regarding their stability and recommend some procedures.
-
1)
If the experiment has complete replicate blocks, stability parameters are sometimes calculated for each plot, yielding one value for each plot. Subsequently, an analysis using these values as response values as they would be, e.g. observed plot yields, can be conducted taking into account the experimental design (Cochran 1939). However, estimates of environmental variance in two LTEs using this approach differ substantially from an analysis using treatment × year means (Table 7). We recommend calculating stability measures from treatment means in different environments as the “standard procedure”.
-
2)
When performing an analysis on treatment × year means over replicates or in an unreplicated design, SEs can be calculated based on the number of years of observations, if such equations are available for the respective stability parameter, e.g. for the variance and CV (Ahn and Fessler 2003). For the slope in Finlay-Wilkinson regression, standard errors are produced in most statistical packages. We therefore recommend to display SE and p values to show significant pairwise differences (Table 7). The p values can be represented graphically as suggested by Piepho et al. (2004).
-
3)
Mixed model approaches can be used effectively to calculate stability estimates by residual maximum likelihood (REML). Some mixed model packages provide SE of the estimates (e.g. SAS, SPSS, ASREML, sommer), but not all (e.g. lme4, nlme). However, only few stability parameters, e.g. Shukla’s stability variance, can be calculated based on mixed model approaches (Piepho 1999) which limits the application. Pairwise comparisons between variance estimates can be conducted through linear contrasts in proc glimmix in SAS and turned into a letter display. If the calculation of the stability measure allows it, we recommend to use mixed model approaches.
-
4)
Conducting bootstrap or jackknife approaches to get SEs. Bootstrap assumes that the n observations are independent and identically distributed samples from a parent distribution. For an application in a slightly different context, see Slaets et al. (2017). That assumption must be put into question for LTE data with serial correlation and therefore limits application of the bootstrap method. While bootstrapping is based on randomly sampling n observations (with replacement) from all n observations, for jackknife observations are removed randomly before calculating stability measures. After the random drawing has been repeated r times, distribution of estimates can be investigated, and SEs (if normally distributed) or confidence intervals can be derived. However, we found that SEs for environmental variance based on bootstrapping differ substantially from calculated SEs (Table 7). Such application violates the assumption of independent and identically distribution and cannot be recommended under these conditions.
3.9.3 Example: different options to quantify standard errors
In this example, two LTEs are used to illustrate comparisons between different approaches to calculate standard errors of environmental variances (Table 7): (1) variances per plot, calculating the variance for each plot and then analyse plot values with a linear model taking into account the design; (2) variances on treatment × year means, calculating the variance on treatment × year means and SE by multiplying the variance by sqrt(2/(n-1)), where n is the number of years (Ahn and Fessler 2003); and (3) bootstrap, bootstrapping per treatment with r = 50 000 and taking the standard deviation of the distribution from bootstrapping, referring to variances calculated on T×Y means (Table 7). In the LTE Borgeby (data set 2), three cropping systems with spring wheat were compared, cropping system A simulates an animal-based production system with manure and 2-year ley, B simulates an arable system without ley, and C simulates a more sustainable arable system with a 1-year ley (Bergkvist and Öborn 2011). In the LTE Rengen (data set 3), five fertilization levels for grassland were compared (Hejcman et al. 2007).
4 Conclusion
We conclude that several methodological problems exist when analysing yield stability in LTE and that there are no silver bullet approaches to solve these. We therefore recommend (1) to make data quality and methodological approaches in the analysis of yield stability from LTEs as transparent as possible; (2) to test and deal with yield outliers; (3) to investigate and include confounding factors in the statistical model; (4) to explore the need for detrending of yield data; (5) to account for temporal autocorrelation if necessary; (6) to make explicit choice for the stability measure and consider the correlation between some of the measures; (7) to consider and resolve dependence of stability measures on the mean yield; (8) to explore, if possible, temporal trends of stability; and (9) to report standard errors and statistical inference of stability measures. We suggest to make ample use of linking up data sets, and to publish data, so that different approaches can be tried by other authors and, finally, to be cautious when interpreting results of yield stability analyses from LTEs without strong explanation of the methods and the possible impacts on the results.
As in any research, results need to be robust against slight variations in methods. If differences in yield stability are only revealed by the most elaborate of statistical approaches, but remain hidden when using cruder methods, such subtle differences are unlikely to convince farmers to change their crop management. At the same time, there are some fundamental differences in yield stability concepts (static vs. dynamic, relative vs. absolute) that cannot be ignored when analysing yield data from LTEs. As climate change and the increasing weather fluctuations force us with mounting urgency to identify more stable cropping systems, data sets from long-term field experiments provide an invaluable resource. Analysing yield stability in these data sets with an open mind to multiple approaches, and with the necessary transparency, will help to make better use of this resource in the quest to stabilize yields across the planet.
Data availability
The data sets used in this study were sourced from the Swedish University of Agricultural Sciences, the University of Bonn, Rothamsted Research, and the German Federal Office of Plant Varieties. The data sets are not publicly available but may be obtained from the authors upon reasonable request and with the permission of the mentioned institutions.
References
Abbo S, Lev-Yadun S, Gopher A (2010) Yield stability: an agronomic perspective on the origin of near Eastern agriculture. Veg Hist Archaeobotany 19(2):143–150. https://doi.org/10.1007/s00334-009-0233-7
Abou-El-Fittouh HA, Rawlings JO, Miller PA (1969) Classification of environments to control genotype by environment interactions with an application to cotton. Crop Sci 9:135–140. https://doi.org/10.2135/cropsci1969.0011183X000900020006x
Adamowski K, Prokoph A, Adamowski J (2009) Development of a new method of wavelet aided trend detection and estimation. Hydrol Process 23(18):2686–2696. https://doi.org/10.1002/hyp.7260
Ahn S, Fessler JA (2003) Standard errors of mean, variance, and standard deviation estimators. EECS Department, The University of Michigan, Ann Arbor
Ahrends HE, Eugster W, Gaiser T, Rueda-Ayala V, Hüging H, Ewert F, Siebert S (2018) Genetic yield gains of winter wheat in Germany over more than 100 years (1895–2007) under contrasting fertilizer applications. Environ Res Lett 13(10):104003. https://doi.org/10.1088/1748-9326/aade12
Annicchiarico P (2002) Genotype X environment interactions - challenges and opportunities for plant breeding and cultivar recommendations. Food and Agriculture Organization of the United Nations (FAO), Rome
Bacsi Z, Hollósy Z (2019) A yield stability index and its application for crop production. Anal Tech Szeged 13(1). https://doi.org/10.14232/analecta.2019.1.11-20
Barnett V, Lewis T (1994) Outliers in statistical data, vol XVII, 3rd edn. Wiley, Hoboken. https://doi.org/10.1002/bimj.4710370219
Becker HC (1981) Correlations among some statistical measures of phenotypic stability. Euphytica 30(3):835–840. https://doi.org/10.1007/BF00038812
Becker HC, Léon J (1988) Stability analysis in plant breeding. Plant Breed 101:1–23
Bergkvist G, Öborn I (2011) Long-term field experiments in Sweden – what are they designed to study and what could they be used for? Asp Appl Biol 113:75–85
Bernal-Vasquez A-M, Utz HF, Piepho H-P (2016) Outlier detection methods for generalized lattices: a case study on the transition from Anova to Reml. Theor Appl Genet 129(4):787–804. https://doi.org/10.1007/s00122-016-2666-6
Bönecke E, Breitsameter L, Brüggemann N et al (2020) Decoupling of impact factors reveals the response of German winter wheat yields to climatic changes. Glob Change Biol 26:3601–3626. https://doi.org/10.1111/gcb.15073
Broomhead DS, King GP (1986) Extracting qualitative dynamics from experimental data. Physica D 20(2):217–236. https://doi.org/10.1016/0167-2789(86)90031-X
Butler DG, Cullis BR, Gilmour AR, Gogel BJ, Thompson R (2017) Asreml-R reference manual version 4 - Asreml estimates variance components under a general linear mixed model by residual maximum likelihood (Reml). VSN International Ltd., Hemel Hempstead, HP1 1ES, UK.
Calderini DF, Slafer GA (1998) Changes in yield and yield stability in wheat during the 20th century. Field Crop Res 57(3):335–347. https://doi.org/10.1016/S0378-4290(98)00080-X
Carroll RJ, Ruppert D (1988) Transformation and weighting in regression. Chapman & Hall, New York. https://doi.org/10.1201/9780203735268
Cheshkova A, Stepochkin P, Aleynikov A, Grebennikova I, Ponomarenko V (2020) A comparison of statistical methods for assessing winter wheat grain yield stability. Vavilov. J Genet Breed 24:267–275. https://doi.org/10.18699/VJ20.619
Cochran WG (1939) Long-term agricultural experiments. Suppl J R Stat Soc 6(2):104–140. https://doi.org/10.2307/2983686
Cotes JM, Crossa J, Sanches A, Cornelius PL (2006) A Bayesian approach for assessing the stability of genotypes. Crop Sci 46:2654–2665. https://doi.org/10.2135/cropsci2006.04.0227
Crossa J (1988) A comparison of results obtained with two methods for assessing yield stability. Theor Appl Genet 75(3):460–467. https://doi.org/10.1007/BF00276750
Damesa TM, Möhring J, Forkman J, Piepho H-P (2018) Modeling spatially correlated and heteroscedastic errors in Ethiopian maize trials. Crop Sci 58(4):1575–1586. https://doi.org/10.2135/cropsci2017.11.0693
Debreczeni K, Körschens M (2003) Long-term field experiments of the world. Arch Agron Soil Sci 49(5):465–483. https://doi.org/10.1080/03650340310001594754
Dehghani H, Sabaghpour SH, Sabaghnia N (2008) Genotype × environment interaction for grain yield of some lentil genotypes and relationship among univariate stability statistics. Span J Agric Res 6(3):10. https://doi.org/10.5424/sjar/2008063-5292
del Río M, Pretzsch H, Ruíz-Peinado R, Ampoorter E, Annighöfer P, Barbeito I, Bielak K, Brazaitis G, Coll L, Drössler L, Fabrika M, Forrester DI, Heym M, Hurt V, Kurylyak V, Löf M, Lombardi F, Madrickiene E, Matović B, Mohren F, Motta R, den Ouden J, Pach M, Ponette Q, Schütze G, Skrzyszewski J, Sramek V, Sterba H, Stojanović D, Svoboda M, Zlatanov TM, Bravo-Oviedo A (2017) Species interactions increase the temporal stability of community productivity in Pinus sylvestris–Fagus sylvatica mixtures across Europe. J Ecol 105(4):1032–1043. https://doi.org/10.1111/1365-2745.12727
Döring TF, Reckling M (2018) Detecting global trends of cereal yield stability by adjusting the coefficient of variation. Eur J Agron 99:30–36. https://doi.org/10.1016/j.eja.2018.06.007
Döring TF, Knapp S, Cohen JE (2015) Taylor’s power law and the stability of crop yields. Field Crop Res 183:294–302. https://doi.org/10.1016/j.fcr.2015.08.005
Eberhart SA, Russell WA (1966) Stability parameters for comparing varieties. Crop Sci 6(1):36–40. https://doi.org/10.2135/cropsci1966.0011183X000600010011x
Eghball B, Power JF (1995) Fractal description of temporal yield variability of 10 crops in the United States. Agron J 87(2):152–156. https://doi.org/10.2134/agronj1995.00021962008700020003x
Eskridge KM (1990) Selection of stable cultivars using a safety-first rule. Crop Sci 30(2):369–374. https://doi.org/10.2135/cropsci1990.0011183X003000020025x
Eugster W, Moffat AM, Ceschia E, Aubinet M, Ammann C, Osborne B, Davis PA, Smith P, Jacobs C, Moors E, Le Dantec V, Béziat P, Saunders M, Jans W, Grünwald T, Rebmann C, Kutsch WL, Czerný R, Janouš D, Moureaux C, Dufranne D, Carrara A, Magliulo V, Di Tommasi P, Olesen JE, Schelde K, Olioso A, Bernhofer C, Cellier P, Larmanou E, Loubet B, Wattenbach M, Marloie O, Sanz M-J, Søgaard H, Buchmann N (2010) Management effects on European cropland respiration. Agric Ecosyst Environ 139(3):346–362. https://doi.org/10.1016/j.agee.2010.09.001
Farshadfar E (2008) Incorporation of AMMI stability value and grain yield in a single non-parametric index (Gsi) in bread wheat. Pak J Biol Sci 11(14):1791–1796. https://doi.org/10.3923/pjbs.2008.1791.1796
Farshadfar E, Mohammadi R, Aghaee M, Vaisi Z (2012) GGE biplot analysis of genotype × environment interaction in wheat-barley disomic addition lines. Aust J Crop Sci 6:1074–1079
Fernandez GCJ (1991) Analysis of genotype X environment interaction by stability estimates. Hort Sci 26:947–950
Fernández-Martínez M, Vicca S, Janssens IA, Carnicer J, Martín-Vide J, Peñuelas J (2018) The consecutive disparity index, D: a measure of temporal variability in ecological studies. Ecosphere 9(12):e02527. https://doi.org/10.1002/ecs2.2527
Ferreira DF, Demétrio CGB, Manly BFJ, Machado AA, Vencovsky R (2006) Statistical models in agriculture: biometrical methods for evaluating phenotypic stability in plant breeding. Cerne 12(4):373–388
Fikere M, Tadesse T, Dugo TL (2008) Genotype-environment interactions and stability parameters. Int J Agric Sustain 3:80–87
Fikere M, Bing DJ, Tadesse T, Ayana A (2014) Comparison of biometrical methods to describe yield stability in field pea (Pisum sativum L.) under south eastern Ethiopian conditions. Afr J Agric Res 9(33):2574–2583. https://doi.org/10.5897/AJAR09.602
Finlay KW, Wilkinson GN (1963) The analysis of adaptation in a plant-breeding programme. Aust J Agric Res 14(6):742–754. https://doi.org/10.1071/AR9630742
Fox PN, Rosielle AA (1982) Reducing the influence of environmental main-effects on pattern analysis of plant breeding environments. Euphytica 31(3):645–656. https://doi.org/10.1007/BF00039203
Francis TR, Kannenberg LW (1978) Yield stability studies in short-season maize. A descriptive method for grouping genotypes. Can J Plant Sci 58(4):1029–1034. https://doi.org/10.4141/cjps78-157
Freeman GH, Perkins JM (1971) Environmental and genotype-environmental components of variability Viii. Relations between genotypes grown in different environments and measures of these environments. Heredity 27(1):15–23. https://doi.org/10.1038/hdy.1971.67
Grosse M, Hierold W, Ahlborn MC, Piepho HP, Helming K (2020) Long-term field experiments in Germany: classification and spatial representation. SOIL 6(2):579–596. https://doi.org/10.5194/soil-6-579-2020
Gulden RH, Tenuta M, Mitchell S, Langarica Fuentes A, Daniell TJ (2015) Preceding crop and weed management history affect denitrification and denitrifier community structure throughout the development of durum wheat. Agric Ecosyst Environ 212:49–63. https://doi.org/10.1016/j.agee.2015.06.016
Gumbel EJ (1958) Statistics of extremes. Columbia University Press, New York
Hadasch S, Laidig F, Macholdt J, Bönecke E, Piepho HP (2020) Trends in mean performance and stability of winter wheat and winter rye yields in a long-term series of variety Trials. Field Crop Res 252:107792. https://doi.org/10.1016/j.fcr.2020.107792
Hanson WD (1970) Genotypic stability. Theor Appl Genet 40(5):226–231. https://doi.org/10.1007/BF00285245
Heath J (2006) Quantifying temporal variability in population abundances. Oikos 115:573–581. https://doi.org/10.1111/j.2006.0030-1299.15067.x
Hejcman M, Klaudisová M, Schellberg J, Honsová D (2007) The Rengen grassland experiment: plant species composition after 64 years of fertilizer application. Agric Ecosyst Environ 122(2):259–266. https://doi.org/10.1016/j.agee.2006.12.036
Hernandez CM, Crossa J, Castillo A (1993) The area under the function: an index for selecting desirable genotypes. Theor Appl Genet 87(4):409–415. https://doi.org/10.1007/BF00215085
Hodge VJ, Austin J (2004) A survey of outlier detection methodologies. Artif Intell Rev 22(2):85–126. https://doi.org/10.1007/s10462-004-4304-y
Huehn M (1990) Nonparametric measures of phenotypic stability. Part 1: theory. Euphytica 47(3):189–194. https://doi.org/10.1007/BF00024241
Hufnagel J, Reckling M, Ewert F (2020) Diverse approaches to crop diversification in agricultural research. A review. Agron Sustain Dev 40(2):14. https://doi.org/10.1007/s13593-020-00617-4
Hussein MA, As B, Aastveit AH (2000) SASG × ESTAB: a SAS program for computing genotype × environment stability statistics. Agron J 92(3):454–459. https://doi.org/10.2134/agronj2000.923454x
Isbell FI, Polley HW, Wilsey BJ (2009) Biodiversity, productivity and the temporal stability of productivity: patterns and processes. Ecol Lett 12(5):443–451. https://doi.org/10.1111/j.1461-0248.2009.01299.x
Jensen NF (1976) Floating checks for plant breeding nurseries. Cereal Res Commun 4(3):285–295 http://www.jstor.org/stable/23777590
Jernigan AB, Wickings K, Mohler CL, Caldwell BA, Pelzer CJ, Wayman S, Ryan MR (2020) Legacy effects of contrasting organic grain cropping systems on soil health indicators, soil invertebrates, weeds, and crop yield. Agric Syst 177:102719. https://doi.org/10.1016/j.agsy.2019.102719
Johnson NL, Kemp AW, Kotz S (2005) Univariate discrete distributions, 3rd edn. Wiley, New York. https://doi.org/10.1002/0471715816
Johnston AE, Poulton PR (2018) The importance of long-term experiments in agriculture: their management to ensure continued crop production and soil fertility; the Rothamsted experience. Eur J Soil Sci 69(1):113–125. https://doi.org/10.1111/ejss.12521
Kalkuhl M, von Braun J, Torero M (2016) Volatile and extreme food prices, food security, and policy: an overview. Food price volatility and its implications for food security and policy. In: Kalkuhl M, von Braun J, Torero M (eds) Food Price Volatility and Its Implications for Food Security and Policy. Springer Open, New York City, pp 3–31
Kang MS (1988) A rank-sum method for selecting high-yielding, stable corn genotypes. Cereal Res Commun 16(1/2):113–115 http://www.jstor.org/stable/23782771
Kataoka S (1963) A stochastic programming model. Econometrica 31(1/2):181–196. https://doi.org/10.2307/1910956
Killick R, Fearnhead P, Eckley IA (2012) Optimal detection of changepoints with a linear computational cost. J Am Stat Assoc 107(500):1590–1598. https://doi.org/10.1080/01621459.2012.737745
Knapp S, van der Heijden MGA (2018) A global meta-Analysis of yield stability in organic and conservation agriculture. Nat Commun 9(1):3632. https://doi.org/10.1038/s41467-018-05956-1
Laidig F, Piepho H-P, Rentel D, Drobek T, Meyer U (2017) Breeding progress, genotypic and environmental variation and correlation of quality traits in malting barley in German official variety trials between 1983 and 2015. Theor Appl Genet 130(11):2411–2429. https://doi.org/10.1007/s00122-017-2967-4
Lehmann N, Finger R, Klein T, Calanca P, Walter A (2013) Adapting crop management practices to climate change: modeling optimal solutions at the field scale. Agric Syst 117:55–65
Lin CS, Binns MR (1988) A superiority measure of cultivar performance for cultivar × location data. Can J Plant Sci 68(1):193–198. https://doi.org/10.4141/cjps88-018
Lin CS, Binns MR, Lefkovitch LP (1986) Stability analysis: where do we stand? Crop Sci 26(5):894–900. https://doi.org/10.2135/cropsci1986.0011183X002600050012x
Littell RC, Milliken GA, Stroup WW, Wolfinger RD, Schabenberger O (2006) SAS for mixed models, 2nd edn. SAS Institute Inc., Cary
Loaiciga HA, Leipnik RB (1999) Analysis of extreme hydrologic events with Gumbel distributions: marginal and additive cases. Stoch Env Res Risk A 13(4):251–259. https://doi.org/10.1007/s004770050042
Lobell DB, Schlenker W, Costa-Roberts J (2011) Climate trends and global crop production since 1980. Science 333(6042):616–620. https://doi.org/10.1126/science.1204531
Lu J, Carbone GJ, Gao P (2017) Detrending crop yield data for spatial visualization of drought impacts in the United States, 1895–2014. Agric For Meteorol 237-238:196–208. https://doi.org/10.1016/j.agrformet.2017.02.001
Machado S, Petrie S, Rhinhart K, Ramig RE (2008) Tillage effects on water use and grain yield of winter wheat and green pea in rotation. Agron J 100(1):154–162. https://doi.org/10.2134/agronj2006.0218
Macholdt J, Piepho H-P, Honermeier B (2019) Mineral NPK and manure fertilisation affecting the yield stability of winter wheat: results from a long-term field experiment. Eur J Agron 102:14–22. https://doi.org/10.1016/j.eja.2018.10.007
Macholdt J, Piepho H-P, Honermeier B, Perryman S, MacDonald A, Poulton P (2020a) The effects of cropping sequence, fertilization, and straw management on the yield stability of winter wheat (1986-2017) in the Broadbalk wheat experiment, Rothamsted, UK. J Agric Sci 158:1–15. https://doi.org/10.1017/S0021859620000301
Macholdt J, Styczen ME, Macdonald A, Piepho H-P, Honermeier B (2020b) Long-term analysis from a cropping system perspective: yield stability, environmental adaptability, and production risk of winter barley. Eur J Agron 117:126056. https://doi.org/10.1016/j.eja.2020.126056
Macholdt J, Hadasch S, Piepho HP, Reckling M, Taghizadeh-Toosi A, Christensen BT (2021) Yield variability trends of winter wheat and spring barley grown during 1932–2019 in the Askov long-term experiment. Field Crop Res 264:108083. https://doi.org/10.1016/j.fcr.2021.108083
Marini L, St-Martin A, Vico G, Baldoni G, Berti A, Blecharczyk A, Małecka-Jankowiak I, Morari F, Sawinska Z, Bommarco R (2020) Crop rotations sustain cereal yields under a changing climate. Environ Res Lett 15. https://doi.org/10.1088/1748-9326/abc651
Massell BF (1970) Export instability and economic structure. Am Econ Rev 60(4):618–630
Mohammadi M, Karimizadeh R, Sabaghnia N, Shefazadeh MK (2012) Genotypes X environment interaction and yield stability analysis of new improved bread wheat genotypes. Turkish J Field Crop 17:67–73. https://doi.org/10.33687/pbg.007.02.2847
Morin X, Fahse L, de Mazancourt C, Scherer-Lorenzen M, Bugmann H (2014) Temporal stability in forest productivity increases with tree diversity due to asynchrony in species dynamics. Ecol Lett 17(12):1526–1535. https://doi.org/10.1111/ele.12357
Mühleisen J, Piepho H-P, Maurer HP, Longin CFH, Reif JC (2014) Yield stability of hybrids versus lines in wheat, barley, and triticale. Theor Appl Genet 127(2):309–316. https://doi.org/10.1007/s00122-013-2219-1
Müller C, Elliott J, Pugh TAM, Ruane AC, Ciais P, Balkovic J, Deryng D, Folberth C, Cesar Izaurralde R, Jones CD, Khabarov N, Lawrence P, Liu W, Reddy AD, Schmid E, Wang X (2018) Global patterns of crop yield stability under additional nutrient and water inputs. PLoS One 13(6):e0198748. https://doi.org/10.1371/journal.pone.0198748
Mut Z, Aydin N, Bayramoglu HO, Ozcan H (2010) Stability of some quality traits in bread wheat (Triticum aestivum) Genotypes. J Environ Biol 31(4):489–495 https://pubmed.ncbi.nlm.nih.gov/21186725/
Najafi E, Devineni N, Khanbilvardi RM, Kogan F (2018) Understanding the changes in global crop yields through changes in climate and technology. Earth’s Future 6(3):410–427. https://doi.org/10.1002/2017EF000690
Nassar RH, Huehn M (1987) Studies on estimation of phenotypic stability: tests of significance for nonparametric measures of phenotypic stability. Biometrics 43:45–53. https://doi.org/10.2307/2531947
Olesen JE, Trnka M, Kersebaum KC, Skjelvåg AO, Seguin B, Peltonen-Sainio P, Rossi F, Kozyra J, Micale F (2011) Impacts and adaptation of European crop production systems to climate change. Eur J Agron 34(2):96–112. https://doi.org/10.1016/j.eja.2010.11.003
Onofri A, Seddaiu G, Piepho H-P (2016) Long-term experiments with cropping systems: case studies on data analysis. Eur J Agron 77:223–235. https://doi.org/10.1016/j.eja.2016.02.005
Payne RW (2015) The design and analysis of long-term rotation experiments. Agron J 107(2):772–785. https://doi.org/10.2134/agronj2012.0411
Perkins JM, Jinks JL (1968) Environmental and genotype-environmental components of variability Iii. Multiple lines and crosses. Heredity 23(3):339–356. https://doi.org/10.1038/hdy.1968.48
Piepho HP (1998) Methods for comparing the yield stability of cropping systems. J Agron Crop Sci 180(4):193–213. https://doi.org/10.1111/j.1439-037X.1998.tb00526.x
Piepho H-P (1999) Stability analysis using the SAS system. Agron J 91(1):154–160. https://doi.org/10.2134/agronj1999.00021962009100010024x
Piepho HP, Edmondson RN (2018) A tutorial on the statistical analysis of factorial experiments with qualitative and quantitative treatment factor levels. J Agron Crop Sci 204(5):429–455. https://doi.org/10.1111/jac.12267
Piepho HP, Ogutu JO (2003) Inference for the break point in segmented regression with application to longitudinal data. Biom J 45(5):591–601. https://doi.org/10.1002/bimj.200390035
Piepho HP, van Eeuwijk FA (2002) Stability analysis in crop performance evaluation. In: Kang M (ed) Crop Improvement: Challenges in the Twenty-First Century. Haworth Press, New York, pp 315–351
Piepho HP, Büchse A, Richter C (2004) A mixed modelling approach for randomized experiments with repeated measures. J Agron Crop Sci 190(4):230–247. https://doi.org/10.1111/j.1439-037X.2004.00097.x
Pinthus MJ (1973) Estimate of genotypic value: a proposed method. Euphytica 22(1):121–123. https://doi.org/10.1007/BF00021563
Plaisted RL (1960) A shorter method for evaluating the ability of selections to yield consistently over locations. Am Potato J 37(5):166–172. https://doi.org/10.1007/BF02855271
Plaisted RL, Peterson LC (1959) A technique for evaluating the ability of selections to yield consistently in different locations or seasons. Am Potato J 36(11):381–385. https://doi.org/10.1007/BF02852735
Purchase JL, Hatting H, van Deventer CS (2000) Genotype × environment interaction of winter wheat (Triticum aestivum L.) in South Africa: Ii. Stability analysis of yield performance. S Afr J Plant Soil 17(3):101–107. https://doi.org/10.1080/02571862.2000.10634878
Ramsayer J, Fellous S, Cohen JE, Hochberg ME (2012) Taylor's law holds in experimental bacterial populations but competition does not influence the slope. Biol Lett 8(2):316–319. https://doi.org/10.1098/rsbl.2011.0895
Raseduzzaman M, Jensen ES (2017) Does intercropping enhance yield stability in arable crop production? A meta-Analysis. Eur J Agron 91:25–33. https://doi.org/10.1016/j.eja.2017.09.009
Rasmussen PE, Goulding KWT, Brown JR, Grace PR, Janzen HH, Korschens M (1998) Long-term agroecosystem experiments: assessing agricultural sustainability and global change. Science 282(5390):893–896. https://doi.org/10.1126/science.282.5390.893
Ray DK, Gerber JS, MacDonald GK, West PC (2015) Climate variation explains a third of global crop yield variability. Nat Commun 6:5989. https://doi.org/10.1038/ncomms6989
Reckling M, Döring TF, Bergkvist G, Chmielewski F-M, Stoddard FL, Watson CA, Seddig S, Bachinger J (2018a) Grain legume yield instability has increased over 60 years in long-term field experiments as measured by a scale-adjusted coefficient of variation. Asp Appl Biol 138:15–20
Reckling M, Döring TF, Bergkvist G, Stoddard FL, Watson CA, Seddig S, Chmielewski F-M, Bachinger J (2018b) Grain legume yields are as stable as other spring crops in long-term experiments across Northern Europe. Agron Sustain Dev 38(6):63. https://doi.org/10.1007/s13593-018-0541-3
Reckling M, Albertsson J, Topp CFE, Vermue A, Carlsson G, Watson C, Justes E, Bergkvist G, Jensen ES (2019) Does cropping system diversification with legumes lead to higher yield stability? Diverging evidence from long-term experiments across Europe. European Conference on Crop Diversification September 18-21 September 2019, Budapest, Hungary
Reckling M, Bergkvist G, Watson CA, Stoddard FL, Bachinger J (2020) Re-designing organic grain legume cropping systems using systems agronomy. Eur J Agron 112:125951. https://doi.org/10.1016/j.eja.2019.125951
Renard D, Tilman D (2019) National food production stabilized by crop diversity. Nature. 571:257–260. https://doi.org/10.1038/s41586-019-1316-y
Richter C, Kroschewski B (2006) Analysis of a long-term experiment with repeated-measurement models. J Agron Crop Sci 192(1):55–71. https://doi.org/10.1111/j.1439-037X.2006.00167.x
Richter D, Hofmockel M, Callaham M, Powlson D, Smith P (2017) Global inventory of long-term soil-ecosystem experiments. Access Https://Nicholas.Duke.Edu/Ltse [15.09.2017].
Roemer (1917) Sind Die Ertragreichen Sorten Erstargssicherer? Mitt DLG 32:87–89
Roscher C, Weigelt A, Proulx R, Marquard E, Schumacher J, Weisser WW, Schmid B (2011) Identifying population- and community-level mechanisms of diversity–stability relationships in experimental grasslands. J Ecol 99(6):1460–1469. https://doi.org/10.1111/j.1365-2745.2011.01875.x
Rui Y, Sanford GR, Hedtcke JL, Ruark MD (2020) Legacy effects of liquid dairy manure in grain production systems. Agric Syst 181:102825. https://doi.org/10.1016/j.agsy.2020.102825
Sadras V, Bongiovanni R (2004) Use of Lorenz curves and Gini coefficients to assess yield inequality within paddocks. Field Crop Res 90(2):303–310. https://doi.org/10.1016/j.fcr.2004.04.003
Schauberger B, Ben-Ari T, Makowski D, Kato T, Kato H, Ciais P (2018) Yield trends, variability and stagnation analysis of major crops in France over more than a century. Sci Rep 8(1):16865. https://doi.org/10.1038/s41598-018-35351-1
Shukla GK (1972) Some statistical aspects of partitioning genotype-environmental components of variability. Heredity 29:237–245. https://doi.org/10.1038/hdy.1972.87
Singh AJ, Byerlee D (1990) Relative variability in wheat yields across countries and over time. J Agric Econ 41(1):21–32
Singh M, Jones MJ (2002) Modeling yield sustainability for different rotations in long-term barley trials. J Agric Biol Environ Stat 7(4):525–535. https://doi.org/10.1198/108571102744
Slaets JIF, Piepho HP, Schmitter P, Hilger T, Cadisch G (2017) Quantifying uncertainty on sediment loads using bootstrap confidence intervals. Hydrol Earth Syst Sci 21(1):571–588. https://doi.org/10.5194/hess-21-571-2017
Sneller CH, Kilgore-Norquest L, Dombek D (1997) Repeatability of yield stability statistics in soybean. Crop Sci 37(2):383. https://doi.org/10.2135/cropsci1997.0011183X003700020013x
St-Martin A, Vico G, Bergkvist G, Bommarco R (2017) Diverse cropping systems enhanced yield but did not improve yield stability in a 52-year long experiment. Agric Ecosyst Environ 247:337–342. https://doi.org/10.1016/j.agee.2017.07.013
Tai GCC (1971) Genotypic stability analysis and its application to potato regional trials. Crop Sci 11(2):184. https://doi.org/10.2135/cropsci1971.0011183X001100020006x
Taylor RAJ, Lindquist RK, Shipp JL (1998) Variation and consistency in spatial distribution as measured by Taylor's power law. Environ Entomol 27(2):191–201. https://doi.org/10.1093/ee/27.2.191
Temesgen T, Keneni G, Sefera T, Jarso M (2015) Yield stability and relationships among stability parameters in faba bean (Vicia faba L.) genotypes. Crop J 3(3):258–268. https://doi.org/10.1016/j.cj.2015.03.004
Tigchelaar M, Battisti DS, Naylor RL, Ray DK (2018) Future warming increases probability of globally synchronized maize production shocks. Proc Natl Acad Sci U S A 115(26):6644–6649. https://doi.org/10.1073/pnas.1718031115
Tilman D, Reich PB, Knops JMH (2006) Biodiversity and ecosystem stability in a decade-long grassland experiment. Nature 441(7093):629–632. https://doi.org/10.1038/nature04742
Urruty N, Tailliez-Lefebvre D, Huyghe C (2016) Stability, robustness, vulnerability and resilience of agricultural systems. A review. Agron Sustain Dev 36(1):15. https://doi.org/10.1007/s13593-015-0347-5
Valle PAD (1979) On the instability index of time series data: a generalization. Oxf Bull Econ Stat 41(3):247–248. https://doi.org/10.1111/j.1468-0084.1979.mp41003007.x
Wang T-C, Casadebaig P, Stützel H, Chen T-W (2019) TSI: tool for stability indices. Mitt Ges Pflanzenbauwiss 31:173
Wanjari RH, Singh MV, Ghosh PK (2004) Sustainable yield index: an approach to evaluate the sustainability of long-term intensive cropping systems in India. J Sustain Agric 24(4):39–56. https://doi.org/10.1300/J064v24n04_05
Watson C, Reckling M, Preissel S, Bachinger J, Bergkvist G, Kuhlman T, Lindström K, Nemecek T, Topp C, Vanhatalo A, Zander Z, Murphy-Bokern D, Stoddard F (2017) Grain legume production and use in European agricultural systems. Adv Agron 144(1):235–303. https://doi.org/10.1016/bs.agron.2017.03.003
Webber H, Lischeid G, Sommer M, Finger R, Nendel C, Gaiser T, Ewert F (2020) No perfect storm for crop yield failure in Germany. Environ Res Lett 15(10):104012. https://doi.org/10.1088/1748-9326/aba2a4
Wilks D (2006) Statistical methods in the atmospheric sciences, vol 91. International Geophysics, vol 2. Academic Press, San Diego
Wricke G (1962) Über Eine Methode Zur Erfassung Der Ökologischen Streubreite in Feldversuchen. Zeitschrift für Pflanzenzüchtung 47:92–96
Wu Z, Huang NE, Long SR, Peng C-K (2007) On the trend, detrending, and variability of nonlinear and nonstationary time series. Proc Natl Acad Sci U S A 104(38):14889–14894. https://doi.org/10.1073/pnas.0701020104
Xiao X, Locey KJ, White EP (2015) A process-independent explanation for the general form of Taylor's law. Am Nat 186(2):E51–E60. https://doi.org/10.1086/682050
Xu L, Yuan S, Man J (2020) Changes in rice yield and yield stability in China during the past six decades. J Sci Food Agric 100:3560–3569. https://doi.org/10.1002/jsfa.10385
Acknowledgements
This article is a result of a workshop on “Methods for analyzing yield stability in long-term field experiments” on November 19–20, 2019, at the University of Bonn, Institute of Crop Science and Resource Conservation, Department of Agroecology and Organic Farming. We thank the Swedish University of Agricultural Sciences, the University of Bonn, Rothamsted Research, and the German Federal Office of Plant Varieties for providing the data from their long-term field experiments and variety trials.
Code availability
The code for analysing the data can be obtained from the authors of the individual sections.
Funding
Open Access funding enabled and organized by Projekt DEAL. The research leading to these results received funding from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Grant Agreement numbers 420661662, 420210236, 419973621, and 324840916, provided to MR, JM, TWC, and HPP, respectively. We also thank the DFG for funding the young scientist academy on Agroecosystem Research and Plant Production 2018–2019 that supported MR, JM, and TWC and initiated the collaboration between projects. Additional financial support was received from the Ekhaga Foundation, Stockholm (project RESTOR, 2015-65), and the SusCrop/FACCE-JPI project LegumeGap (Grant 031B0807B).
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. MR and TD coordinated the writing process and wrote the general parts of the manuscript (Abstract, Introduction, Materials and methods, Conclusion). The following chapters were written by the following authors: JM, KS and SK wrote 3.1 General considerations on data quality from LTEs; WE wrote 3.2 How to deal with outliers?; SH, JM, FL, and HPP wrote 3.3 Confounding factors; HA wrote 3.4 Detrending of yield data; WE, SK, and HPP wrote 3.5 Temporal autocorrelation; TD, TWC, SK, and MR wrote 3.6 Choice of stability measure; TD and MR wrote 3.7 Dependence of stability measures on the mean; SH, HA, and HPP wrote 3.8 Development of stability over time; and SK and HPP wrote 3.9 Standard errors and statistical inference of stability measures. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval
Not applicable
Consent to participate
Not applicable
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
ESM 1
(DOCX 24 kb)
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Reckling, M., Ahrends, H., Chen, TW. et al. Methods of yield stability analysis in long-term field experiments. A review. Agron. Sustain. Dev. 41, 27 (2021). https://doi.org/10.1007/s13593-021-00681-4
Accepted:
Published:
DOI: https://doi.org/10.1007/s13593-021-00681-4