The Sibling Distribution for Multivariate Life Time Data

Abstract

A flexible class of multivariate distributions for continuous lifetimes is proposed. The distribution is defined in terms of the age-at-death of m siblings. The expression for the joint density is derived using classical results from mathematical demography. The parameters of the distribution are the age-specific birth and death rates, in addition to a vector of relative death times for the m siblings. For the case of constant birth and death rates we are able to derive an explicit expression for the bivariate sibling density, which is proven to be MTP₂, and hence has positive dependence. Further, we show that a special case of the sibling distribution belongs to the Block-Basu class of multivariate distribution. In the general case, with age-dependent birth and death rates, evaluation of the density involves numerical integration, but is still feasible.

1 Introduction

Classes of multivariate densities for multivariate life time and survival data are well studied in the statistical and demographic literature (Hougaard, 2001; Barreto-Souza and Mayrink, 2019). A common approach for making survival times positively dependent goes via “shared frailties” (Hougaard, 2001, Chpt. 7). A frailty is a latent random variable that proportionally scales the hazard rate in a group of individuals, hence inducing dependence between otherwise independent lifetimes. In the present paper we introduce a new class of latent variable models, named the “sibling distribution”, which is defined in terms of the age-at-death for each of m half siblings. There is no information available about their common mother, except that she had m offspring in total, and was alive at a specified point in time, taken to be t = 0 for convenience. The two latent variables of the model are the mother’s birth and death times. The building blocks of the sibling distribution are the individual birth rates β(a) and death rates ϕ(a), where a is the age of an individual. We define the distribution for general functions, β(a) and ϕ(a), but for most part we shall assume that β(a) and ϕ(a) are constants as functions of a.

The positive dependence between the sibling’s life times comes from conditioning on their (absolute) times of death, in combination with a shared dependence on the mother’s life span. The times-of-death become parameters of the distribution. This somewhat implicit construction will be seen to be a mixture distribution, and can be studied using general theory for multivariate dependence (Shaked and Spizzichino, 1998; Khaledi and Kochar, 2001). We prove that the bivariate constant-rate sibling distribution is multivariate totally positive of order 2 (Karlin and Rinott, 1980), which for instance imply that the correlation is positive.

The constant-rate sibling distribution turns out to have marginal distributions that are perturbated exponential distributions. The exponential distribution plays a special role for univariate life times and several multivariate extensions can be found in the literature (Marshall and Olkin, 1967; Freund, 1961; Block and Basu, 1974; Arnold and Strauss, 1988; Gumbel, 1960; Hougaard, 1986; Sarkar, 1987). One of these extensions was introduced by Block and Basu (Block and Basu, 1974). The Block-Basu bivariate lifetime distribution can be derived by omitting the singular part of a bivariate exponential distribution as outlined by Marshall and Olkin (Marshall and Olkin, 1967), but can also be viewed as a reparametrization of Freund’s distribution (Freund, 1961). We will see that the constant-rate (birth and death) sibling distribution reduces to a Block-Basu distribution, which will be used to shed light on the sibling distribution.

An alternative route to construction of multivariate life time distributions goes via copulae (Andersen, 2005). The implication also goes in the other direction; our sibling distribution induces a novel symmetric two-parameter copula.

The remaining part of the paper is organized as follows. In Section 2 we introduce the general sibling distribution. Explicit expressions in the bivariate case, along with positive dependence property, are derived in Section 3. In Section 4 we discuss the relationship to the Block-Basu distribution and in Section 5 we address simulation and parameter estimation. Finally, we provide a discussion in Section 6.

2 The Sibling Age Distribution

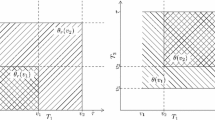
Consider a female who over her lifespan is known to have had m offspring. Denote by t_j and x_j the time of death and age-at-death, respectively, of the j’th offspring. The offspring are arbitrarily ordered, not according to the time of birth. We shall view t and x as random variables taking values on the real line. For notational simplicity we let j = 0 refer to the mother, and we condition on the fact that the mother was alive at time t = 0, i.e. on the event that t₀ − x₀ ≤ 0 ≤ t₀. This assumption should be kept in mind at all times when reading this paper. We define a₀ = x₀ − t₀ as the age of the mother at t = 0, and we denote the joint density of (a₀, t₀) by g(a₀, t₀). Let y_j = t_j − x_j, be the birth time of the j’th offspring. Please refer to Fig. 1 for an illustration of key quantities.

Figure 1

Birth (y₀) and death (t₀) times of mother, and corresponding times (y_j and t_j) for the j’th offspring. Further, a₀ is the age of the mother at the reference point t = 0

We denote random variables by capital letters. Conditionally on (A₀, T₀) = (a₀, t₀), and hence on X₀ = x₀ = a₀ + t₀, the density of Y_j is

$$ f_{Y}(y_{j}|a_{0},t_{0})=\frac{\beta(y_{j}-y_{0})}{{\int}_{0}^{x_{0}}\beta(a)da},\qquad y_{j}\in(y_{0},t_{0}), $$

(2.1)

where β(a) is the age-specific rate at which the mother produces offspring. We shorten our notation for conditional densities, e.g. we write f_Y rather than the full $f_{Y|A_{0},T_{0}}$. The joint conditional density of (X_j, T_j) is

$$ f_{X,T}(x_{j},t_{j}|a_{0},t_{0}) = f_{Y}(y_{j}|a_{0},t_{0})f_{X}(x_{j}) = f_{Y}(t_{j}-x_{j}|a_{0},t_{0})f_{X}(x_{j}), $$

(2.2)

on the support

$$ \left\{(x_{j},t_{j}): (t_{j}-t_{0})_{+}\leq x_{j}\leq t_{j}-y_{0} \right\}, $$

(2.3)

where $z_{+}=\max \limits (z,0)$. The constraints on x_j express the fact that x_j ≥ 0 and y₀ ≤ y_j ≤ t₀, i.e. the offspring must be born in the time window when the mother is alive (see Fig. 1). The latter is related to Eq. 2.3 via the algebraic equivalence y₀ ≤ y_j ≤ t₀ ⇔ t_j − t₀ ≤ t_j − y_j ≤ t_j − y₀. Further, the marginal density f_X(x_j) in Eq. 2.2 is defined in terms of the survival function $l(x_{j})=\Pr (X>x_{j})$ via $f_{X}(x_{j})=-l^{\prime }(x_{j})$. Finally, the marginal density of T_j is obtained from Eq. 2.2 and Eq. 2.3,

$$ f_{T}(t_{j}|a_{0},t_{0})={\int}_{(t_{j}-t_{0})_{+}}^{t_{j}-y_{0}}f_{Y}(t_{j}-x|a_{0},t_{0})f_{X}(x)dx,\qquad t_{j}\geq y_{0}. $$

(2.4)

The births and deaths of the m siblings are assumed to be conditionally independent, given (A₀, T₀) = (a₀, t₀), so the joint density of X_1:m = (X₁,…,X_m) and T_1:m = (T₁,…,T_m) is ${\prod }_{j=1}^{m}f_{X,T}(x_{j},t_{j}|a_{0},t_{0})$, where the density f_{X, T}(x_j, t_j|a₀, t₀) is given by Eq. 2.2. We are now in position to define the sibling distribution as the conditional distribution of X_1:m, given T_1:m = t_1:m.

Remark 1.

The sibling distribution of X_1:m has density

$$ f(x_{1:m}|t_{1:m})=\frac{{\int}_{0}^{\infty}{\int}_{0}^{\infty}{\prod}_{j=1}^{m}f_{X,T}(x_{j},t_{j}|a_{0},t_{0})g(a_{0},t_{0})da_{0}dt_{0}}{{\int}_{0}^{\infty}{\int}_{0}^{\infty}{\prod}_{j=1}^{m}f_{T}(t_{j}|a_{0},t_{0})g(a_{0},t_{0})da_{0}dt_{0}},~ x_{1:m} \in R_{+}^{m}, $$

(2.5)

where f_{X, T} and f_T are given by Eqs. 2.2 and 2.4, respectively, and g is the joint density of (A₀, T₀) for which we will derive the density (2.7) below.

The parameters of the sibling distribution are t_1:m ∈ R^m, in addition to whatever parameters are hidden in the functional forms of the functions β(a) and l(a). Note that the t_j are not restricted to be positive, i.e. the offspring may have died before t = 0. Mostly, we shall parameterize l(a) in terms of the age-specific death rate ϕ(a), which is related to the survival function through the well known relationship $l(x)=\exp \left (-{{\int \limits }_{0}^{x}}\phi (a)da\right )$.

In order to derive an expression for the density g(a₀, t₀), occurring in Eq. 2.5, we use the theory for stable age distributions from mathematical demography (Caswell and Keyfitz, 2005), which we now briefly review. A population in which the age-specific rates ϕ(a) and β(a) do not change with time will settle into a stable age distribution. Further, the population will grow at a rate r given as the solution to the “characteristic equation”

$$ {\int}_{0}^{\infty}\beta(a)l(a)e^{-ra}da=1. $$

The stable age distribution has density $f_{A}(a)= l(a)e^{-ra}/{{\int \limits }_{0}^{a}}l(u)e^{-ru}du$, for a ≥ 0. Our point of view is that the mother is randomly selected among all females alive at t = 0, so that the density of A₀ is given by f_A. This is yet not taking into account the fact that she has m offspring over her life time. The joint density of A₀ and T₀ is

$$ f_{A_{0},T_{0}}(a_{0},t_{0})=f_{T_{0}|A_{0}}(t_{0}|a_{0})f_{A_{0}}(a_{0}),\quad a_{0} \geq0,t_{0}\geq0, $$

(2.6)

where $f_{T_{0}|A_{0}}(t_{0}|a_{0})=-l^{\prime }(a_{0}+t_{0})/l(a_{0})$. Conditionally on A₀ and T₀, and hence on the length of the time period X₀ = A₀ + T₀ that she is alive, her total number of offspring M is Poisson distributed with mean $B(x_{0})={\int \limits }_{0}^{x_{0}}\beta (u)du$. Knowing that the mother had m offspring over her lifetime perturbs the distribution (2.6) as follows

$$ g(a_{0},t_{0})\propto {f_{A_{0},T_{0}}(a_{0},t_{0})B(a_{0}+t_{0})^{m}e^{-B(a_{0}+t_{0})}}. $$

(2.7)

We have now completely specified the sibling distribution via its density (2.5). Instead of providing results about its properties in the general case, we turn to a special case in which explicit results can be found. In Section 6 we briefly return with some discussion of the general case.

3 Constant Birth and Death Rates

We shall refer to the situation

$$ \beta(a) = \beta \quad\text{and}\quad \phi(a)=\phi \quad\text{for all \textit{a}}, $$

(3.1)

as the constant-rate sibling distribution. Under this assumption it follows that the conditional densities (2.1) and (2.2) reduce respectively to

$$ f_{Y}(y_{j}|a_{0},t_{0})= \frac{1}{a_{0}+t_{0}}, \qquad y_{j} \in (-a_{0},t_{0}), $$

(3.2)

and

$$ f_{X,T}(x_{j},t_{j}|a_{0},t_{0})= \frac{1}{a_{0}+t_{0}}\phi e^{-\phi x_{j}}, \qquad (t_{j}-t_{0})_{+}\leq x_{j}\leq t_{j}+ a_{0}. $$

(3.3)

Further, the marginal density (2.4) becomes

$$ f_{T}(t_{j}|a_{0},t_{0})= \frac{e^{-\phi t_{j}}}{a_{0}+t_{0}} \begin{cases} e^{\phi t_{j}}-e^{-\phi a_{0}}, \qquad -a_{0}\leq t_{j}\leq t_{0}, \\ e^{\phi t_{0}} - e^{-\phi a_{0}}, \qquad t_{j} > t_{0}, \end{cases} $$

(3.4)

and the joint density (2.7) becomes

$$ g(a_{0},t_{0}) \propto (a_{0}+t_{0})^{m} e^{-(\phi+\beta)t_{0}} e^{-2\beta a_{0}} , \qquad a_{0},t_{0}\geq 0. $$

(3.5)

Using these expressions we are able to find an explicit expression for the sibling distribution (2.5) of order m = 2. We shall first assume that t₁ = t₂ which simplifies expressions somewhat. Derivations for the case t₁ ≠ t₂ are very similar.

Consider the distribution of the life times X₁ and X₂, given that T₁ = T₂ = t, where t is the common time of death of the two siblings. We have the following expression for the sibling density, which due to symmetry is presented only for x₁ ≤ x₂.

Theorem 1.

With constant-rates (3.1), the sibling density (2.5) with m = 2 becomes (for t > 0):

$$ f(x_{1},x_{2}) = C_{1}^{-1} \begin{cases} e^{-(\beta + \phi) (t-x_{1}) - \phi (x_{1} + x_{2}) }, & 0 \leq x_{1} \leq x_{2} \leq t, \\ e^{2\beta(t -x_{2})-(\beta + \phi)(t -x_{1})- \phi (x_{1} + x_{2}) }, & 0\leq x_{1} \leq t \leq x_{2}, \\ e^{2\beta (t - x_{2}) - \phi(x_{1} +x_{2} )}, & 0\leq t \leq x_{1} \leq x_{2} , \\ \end{cases} $$

(3.6)

and for t < 0:

$$ f(x_{1},x_{2}) = C_{2}^{-1} e^{-(2\beta + \phi)x_{2} - \phi x_{1}}, \quad t<0 \leq x_{1} \leq x_{2}, $$

(3.7)

where C₁ and C₂ are normalizing constants.

Proof.

See Appendix A. □

By integrating over three branches in Eq. 3.6 we obtain the following expression for the normalizing constant:

$$ C_{1}= \begin{cases} \frac{e^{-2 \phi t}(7\beta + 5\phi )}{(2\beta + \phi)(\beta^{2} - \phi^{2})} + \frac{4 e^{-(\beta + 2\phi) t}}{ \phi (2 \beta + \phi) } - \frac{2 e^{-(\beta + \phi) t} }{\phi (\beta - \phi)}, &\beta\neq\phi,\\ \frac{12 \phi e^{\phi t}t -7e^{\phi t} + 8}{6\phi^{2} e^{3\phi t}}, &\beta = \phi, \end{cases} $$

(3.8)

and similarly integration of Eq. 3.7 yields

$$ C_{2} = \left[ (2\beta + \phi)(\beta + \phi) \right]^{-1}. $$

(3.9)

Note that f(x₁, x₂) does not depend on t when t < 0. When we in addition set β = 0 (interpreted as a limit), X₁ and X₂ become independent, exponentially distributed. Further interpretation of the case that t < 0 is given in Section 4 below.

Like the exponential distribution, the constant-rate sibling distribution is closed under change of scale. If we define $X_{j}^{\prime }=c X_{j}$ for c > 0, the parameters of the resulting sibling distribution are $\phi ^{\prime }=c^{-1}\phi$, $\beta ^{\prime }=c^{-1}\beta$ and $t^{\prime }=c t$. Hence, we may set ϕ = 1 and reparameterize the distribution in terms of (c, β, t), which for some purposes is useful.

As seen from Eq. 3.6, the density has a piecewise definition. When using symmetry to include also the case x₁ > x₂, the definition of the sibling density splits the first quadrant, x₁, x₂ ≥ 0, into six regions (Fig. 2 with t₁ = t₂). We see that $\log \{f(x_{1},x_{2})\}$ is piecewise linear over these regions, and is continuous (but not differentiable) across the boundaries of the regions. The density is unimodal, with the mode at (x₁, x₂) = (0,0) when β < ϕ, and while β > ϕ the mode is at (x₁, x₂) = (t, t). Figure 3 shows f(x₁, x₂) for three different parameter.

Figure 2

The six different regions of the sibling density when t₁ = 9 and t₂ = 5. The dashed line indicates ages where the siblings are born at the same time (y₁ = y₂)

Figure 3

Bivariate sibling density f(x₁, x₂) with parameters ϕ = 1, β = 0.8,1.0,1.2 (left to right) and (t₁, t₂) = (4,4). The red dots show expected value (μ, μ). The dashed white curve is the contour c = 1 of c(x₁, x₂) given by Eq. 3.15

In order to present the sibling distribution for the case t₁ ≠ t₂, it is advantageous to introduce a general piecewise log-linear density f over the regions R₁,…,R₆ in Fig. 2:

$$ f(x_{1},x_{2}) = C^{-1} e^{b_{k} + c_{k}x_{1} + d_{k}x_{2}},\qquad (x_{1},x_{2})\in R_{k},\quad k=1,\ldots,6. $$

(3.10)

Here, b_1:6 = (b₁,…,b₆), c_1:6 = (c₁,…,c₆) and d_1:6 = (d₁,…,d₆) are constants satisfying the constraints c₂, c₃, c₄, d₃, d₄, d₅ < 0, which are needed for f to be a proper density. Straightforward, but tedious, integration yields the normalization constant:

$$ \begin{array}{@{}rcl@{}} C\!\!\!&=&\!\!\!- \frac{ \mathrm{e}^{b_{1}} \left( \mathrm{e}^{d_{1} t_{2}} c_{1} \left( \mathrm{e}^{- d_{1} t_{1}} - \mathrm{e}^{c_{1} t_{1}} \right) + \mathrm{e}^{c_{1} t_{1}} \left( c_{1} + d_{1} \right) - c_{1} - d_{1} \right) }{ c_{1} d_{1} \left( c_{1}+ d_{1} \right) } \\ &&\!\!\!+ \frac {\mathrm{e}^{c_{2} t_{1} + b_{2}} \left( 1- \mathrm{e}^{d_{2} t_{2}} \right) }{ c_{2} d_{2}} + \frac{\mathrm{e}^{c_{3} t_{1} + d_{3} t_{2} + b_{3} }}{ c_{3} \left( c_{3} + d_{3} \right) } + \frac {\mathrm{e}^{c_{4} t_{1} + d_{4} t_{2} + b_{4}}}{ d_{4} \left( c_{4} + d_{4} \right) } \\ &&\!\!\!- \frac{\mathrm{e}^{d_{5} t_{2} + b_{5}} \left( \mathrm{e}^{c_{5} t_{1}}-1 \right) }{ c_{5} d_{5}} + \frac{\mathrm{e}^{d_{6} t_{2} + b_{6}} \left( c_{6} \left( \mathrm{e}^{- d_{6} t_{1}} -1 \right) + d_{6} \left( \mathrm{e}^{c_{6} t_{1}} -1 \right) \right) }{ c_{6} d_{6} \left( c_{6} + d_{6} \right) },\\ \end{array} $$

(3.11)

where c₁ + d₁≠ 0 and c₆ + d₆≠ 0 in addition to the constraint c₂, c₃, c₄, d₃, d₄, d₅ < 0. The constants C₁ and C₂ in Theorem 1 are special cases of this.

It is easy to derive the moment generating function of Eq. 3.10:

$$ M(s_{1},s_{2})=E\left( e^{s_{1}X_{1}+s_{2},X_{2}}\right) = \frac{C(b_{1:6},c_{1:6}+s_{1},d_{1:6}+s_{2},t_{1},t_{2})}{C(b_{1:6},c_{1:6},d_{1:6},t_{1},t_{2})}, $$

(3.12)

where c_1:6 + s₁ = (c₁ + s₁,…,c₆ + s₁) and d_1:6 + s₂ = (d₁ + s₂,…,d₆ + s₂). Moments of X₁ and X₂ of various orders can be obtained by repeated differentiation of M(s₁, s₂) at s₁ = s₂ = 0. The resulting expressions are complex, and not well suited for interpretation, but are nevertheless useful for numerical evaluation.

Theorem 2.

With constant rates (3.1), the sibling density (2.5) with m = 2 and t₁ ≠ t₂ has density given by Eq. 3.10 with coefficients as specified in Table 1.

Table 1 Choice of coefficients in Eq. 3.10 yielding the order 2 sibling density when t₁ ≠ t₂

Proof.

The proof is very similar to that of Theorem 1 and is omitted. □

3.1 Positive Association

Intuitively, X₁ and X₂ are positively associated under the sibling distribution, due to their dependence of the lifespan (−A₀, T₀) of their shared mother. Further, for each marginal (j = 1,2) we must have that X_j is stochastically increasing in the parameter t_j. The informal argument for the latter is that since the mother is known to have been alive at t = 0, the larger the death time t_j the older (x_j) the individual is likely to be. We now set out to prove these claims rigorously.

We start out by proving the positive association between X₁ and X₂. An appropriate notion of positive association is the so-called Multivariate Total Positivity of order 2 (MTP₂). A bivariate density f(x), x ∈ R², is is said to be MTP₂ if

$$ f(x\vee z)f(x\wedge z)\geq f(x)f(z), $$

(3.13)

for any x, z ∈ R², where $x\vee z=(\max \limits (x_{1},z_{1}),\max \limits (x_{2},z_{2}))$ and $x\wedge z=(\min \limits (x_{1},z_{1}),\min \limits (x_{2},z_{2}))$. See Karlin and Rinott (1980) for a comprehensive overview of properties of MTP₂ distributions.

Theorem 3.

The sibling densities (3.6) and (3.7) are MTP₂.

This is proved in Appendix C using the definition Eq. 3.13 of MTP₂ directly. We believe that an alternative proof may be based on the fact that mixture distributions, of which the numerator of Eq. 2.5 is an example, under certain conditions are MTP₂ (Khaledi and Kochar, 2001; Shaked and Spizzichino, 1998). Using this approach it may be possible to prove that more general sibling distributions than (3.6) are MTP₂.

MTP₂ is a strong positive dependence property, which among other things imply that cov(X₁, X₂) ≥ 0. Although covariance is (arguably) not the most relevant dependence measure for life times, it nevertheless the most common dependence measure in general, and it is therefore useful to have establish this result.

3.2 Marginal Distribution and Copula

The marginal densities in Eq. 3.6 are both given as

$$ f(x)= \frac{e^{-\phi(t +x)}}{C_{1}} \begin{cases} e^{-\beta(t -x) } \Big[ \frac{\beta + \phi}{\beta \phi} - \frac{e^{-\beta x}}{\beta} - \frac{2\beta e^{\phi(x-t)}}{\phi (2\beta + \phi)} \Big], & x \in (0,t], \\ e^{2\beta(t-x)} \ \Big[ \frac{\beta + \phi}{\beta \phi} - \frac{e^{-\beta t}}{\beta} - \frac{2\beta e^{\phi(t- x)}}{\phi (2\beta + \phi)}\Big] , & x \in (t,\infty), \end{cases} \\ $$

(3.14)

where C₁ is given by Eq. 3.8. As a local measure of dependency between X₁ and X₂ we introduce

$$ c(x_{1},x_{2}) = \frac{f(x_{1},x_{2})}{f(x_{1})f(x_{2})}. $$

(3.15)

The c = 1 contour of c(x₁, x₂) is displayed in Fig. 3. The region in which c(x₁, x₂) > 1 is located around the diagonal x₁ = x₂. This reflects the positive dependence in the sibling distribution.

We can obtain an analytical expression for the cumulative joint distribution F(x₁, x₂) by integrating Eq. 3.6. Similarly, we get an expression for the cumulative marginal distribution function G(x) by integrating Eq. 3.14. Then we can define a copula (Nelsen, 2007), $F\left (G^{-1}(x_{1}),G^{-1}(x_{2})\right )$, based on the sibling distribution, where G^− 1 denotes the inverse of G. Because the sibling distribution is closed under change of scale, we set ϕ = 1, and the copula thus has β and t as free parameters. We do not explore this copula further in this paper.

We next prove that X (X₁ or X₂) is stochastically increasing in t, in the sense of the following theorem.

Theorem 4.

For any $t^{\prime }>t>0$ we have

$$ P(X>x|T=t)\leq P(X>x|T=t^{\prime}). $$

(3.16)

It turns out to be easier to prove the more general statement that (X₁, X₂) is multivariate stochastically increasing (Shaked and Shanthikumar, 2007, p. 265), which imply Eq. 3.16. The reason this is simpler is that the key quantity, the ratio $f(x;t^{\prime })/f(x;t)$, which is involved in Theorem 6.B.8. of Shaked and Shanthikumar (2007, p. 265), takes on a simpler form for the bivariate density (3.6) than for the univariate density (3.14). The details of the proof are given in Appendix D.

Stochastic monotonicity of a random variable X implies that E(X) is an increasing function of t (Shaked and Shanthikumar, 2007, p. 4). This means that, for given ϕ and β, there is a one-to-one correspondence between t and μ = E(X). This fact will play a crucial role when we later devise an estimator for the parameters ϕ, β and t.

3.3 The Role of β and t

Because the family of constant-rate sibling distributions is closed under change of scale we set ϕ = 1. In this section we will study the effect of varying β and t on two characteristics: the correlation (COR) between X₁ and X₂ and $\text {CV}(X_{j})=\sqrt {\text {Var}(X_{j})}/\mathrm E(X_{j})$. Without conditioning on T_j = t, we have that X_j is exponentially distributed with rate ϕ = 1. The process of conditioning on T_j can be expected to deduce CV(X_j). Rather than trying to prove this formally, we provide numerical evidence.

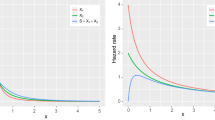
Figure 4 shows correlation and CV as functions of β (top) and t (bottom), and indeed we see that CV ≤ 1 for all β and t. When β and t are both close to zero we have CV ≈ 1 and COR ≈ 0, which reflects the fact that X₁ and X₂ are then approximately independent and exponentially distributed. For increasing β the correlation increases, but not necessarily monotonically, and approaches an asymptotic level (top-left). From the corresponding plot of the CV (top-right) we notice that the overall trend is that the CV decreases as the value of β increases. The decrease is steepest for the highest values of t.

Figure 4

Correlation (left) and CV (right) of the sibling distribution (ϕ = 1) as a function of its parameters. The parameter ϕ is set to 1 and the plots on the top row are plotted as a function of β for five different values of t. The plots on the bottom are plotted as a function of t for five different values of β

Further, we see from the bottom row of Fig. 4 that the correlation increases as a function of t, except for very small t. It can be shown that when β = ϕ the correlation approaches 1 as $t\rightarrow \infty$. When β≠ϕ, the correlation does not approach 1 as $t\rightarrow \infty$, but flattens out at a lower value which depends on the value of β. The CV decrease quickly as a function of t, especially for the higher values of β. When β < ϕ we see that the CV first decrease, then starts to increase for higher values of t.

4 Relationship to the Block-Basu Distribution

In this section we clarify the relationship between the constant-rate sibling distribution and the Block-Basu distribution (Block and Basu, 1974), and we shall use this relationship to interpret the sibling distribution. One way of deriving the Block-Basu distribution goes via (Freund, 1961), and we will refer to this as the “Freund interpretation”. Let now X₁ and X₂ be the lifetimes of two components assumed to be independently exponentially distributed with rate parameters α₁ and α₂, respectively. When one of the component fails, the rate for the remaining component changes from α₁ to $\alpha _{1}^{*}$ or from α₂ to $\alpha _{2}^{*}$, depending on which component fails first. The resulting density (see Freund (1961)) is

$$ f(x_{1},x_{2}) = \begin{cases} \alpha_{1} e^{-x_{1}(\alpha_{1} + \alpha_{2})} \alpha_{2}^{*} e^{-\alpha_{2}^{*}(x_{2}-x_{1})}, \qquad 0 \leq x_{1} \leq x_{2}, \\ \alpha_{2} e^{-x_{2}(\alpha_{1} + \alpha_{2})} \alpha_{1}^{*} e^{-\alpha_{1}^{*}(x_{1}-x_{2})}. \qquad 0 \leq x_{2} \leq x_{1}. \end{cases} $$

(4.1)

When setting

$$ \begin{array}{@{}rcl@{}} \alpha_{j} = \beta + \phi, \qquad \alpha_{j}^{*} = 2\beta + \phi, \qquad j=1,2, \end{array} $$

(4.2)

we see that Eq. 4.1 reduces to the symmetric sibling density (3.7) with t ≤ 0. Since t = 0 is the time point at which the mother is known to have been alive, we are effectively considering a sibling distribution where both offspring are dying before their mother.

The Freund interpretation yields that $X^{(1)}=\min \limits (X_{1},X_{2})$, i.e. the age of the youngest sibling, has an exponential distribution with rate parameter α₁ + α₂ = 2(β + ϕ). Further, the age difference between the oldest and the youngest, X⁽²⁾ = $\max \limits (X_{1},X_{2})-\min \limits (X_{1},X_{2})$, has an exponential distribution with rate parameter α^∗ = 2β + ϕ. In the following paragraphs we interpret the rates (4.2) in the context of the sibling distribution.

If we consider the case with t = 0, we know that the mother and her two offspring were all alive at (or just prior to) t = 0. The Freund interpretation requires us to look backwards in time, starting from t = 0. The “failure” of a component corresponds to an offspring being born. We first look at the event X⁽¹⁾ > x, which can be broken into three sub events:

• (i) The mother was born prior to t = −x, i.e. a₀ > x. Because the stable age distribution of A₀ is exponential with rate β, we have $P(A_{0}>x)=\exp (-\beta x)$.

• (ii) Both offspring were born prior to − x, and because we are conditioning on there being m = 2 siblings in total, this implies that there were no additional births in (−x,0). The latter has probability exp(−βx).

• (iii) Both offspring survived the interval (−x,0), which has probability $\exp (-2\phi x)$.

When combining the independent events i)–iii) we get the Freund interpretation $P\left (X^{(1)}>x\right )=\exp \left [-2(\beta +\phi )x\right ]$.

The event X⁽²⁾ > x can be interpreted similarly, but we must shift our point of view backwards in time to t = −x⁽¹⁾ when the youngest sibling was born. The mother would have to be born prior to t = −(x + x⁽¹⁾). Using the stable age distribution of A₀, this has conditional probability

$$ P\left( A_{0}>x+x^{(1)}|A_{0}>x^{(1)}\right) = \exp\left( -\beta x\right). $$

Secondly, there couldn’t have been any births between $t=-\left (x+x^{(1)}\right )$ and t = −x⁽¹⁾, which has probability $\exp \left (-\beta x\right )$. Finally, the offspring that was born at t = −x⁽²⁾ survived from $t=-\left (x+x^{(1)}\right )$ until t = −x⁽¹⁾, which has probability $\exp \left (-\phi x\right )$. In total we get $P\left (X^{(2)} > x\right ) = \exp \left [-(2\beta +\phi )x\right ]$, which is the Freund interpretation of the sibling distribution. Similar arguments applies to the situation t < 0.

Finally, we discuss a few additional insights gained from the Freund interpretation (4.2). First, the age difference between the siblings, X₁ − X₂ follows a Laplace distribution with rate 2β + ϕ. Further, note that $\alpha _{j}^{*}\rightarrow \alpha _{j}=\phi$ as $\beta \rightarrow 0$. Hence, X₁ and X₂ are independent in the limit $\beta \rightarrow 0$, each having an exponential distribution with rate ϕ.

5 Simulation, Estimation and Application to Real Data

We first devise an algorithm for sampling (x₁, x₂) from the density (3.6). Rather than sampling directly from Eq. 3.6, which would be feasible albeit a bit technical, we choose to go back to the definition of the sibling distribution. This involves explicitly sampling (a₀, t₀) for the mother. As a byproduct, our algorithm sheds light on the sibling distribution, through an expression for the conditional density of (A₀, T₀), given (T₁, T₂).

We also construct a hybrid moment/maximum likelihood estimator for the parameter vector 𝜃 = (β, ϕ, t). The statistical properties of this estimator are investigated on simulated data.

5.1 Simulation

The joint density of (A₀, T₀), (X₁, T₁) and (X₂, T₂) is given by

$$ g(a_{0},t_{0})\prod\limits_{j=1}^{2}f(x_{j},t_{j}|a_{0},t_{0}) =f(t_{1},t_{2})f(a_{0},t_{0}|t_{1},t_{2})\prod\limits_{j=1}^{2}f(x_{j}|t_{j},a_{0},t_{0}), $$

(5.1)

where for notational simplicity we suppress subscripts on densities and range of variables in this section. The quantities on the left-hand side are given by Eqs. 3.3 and 3.5, while the right-hand side is a generic refactoring of the joint density in terms of conditional densities. Dividing through by f(t₁, t₂) in Eq. 5.1 we obtain the target distribution, and the right-hand side (5.1) suggests the following algorithm for sampling (X₁, X₂) conditionally on (T₁, T₂):

• (i) Sample (A₀, T₀) from f(a₀, t₀|t₁, t₂),

• (ii) Using (a₀, t₀) from (i), draw X_j from f(x_j|t_j, a₀, t₀), independently for j = 1,2.

Step (ii) is straight forward, and is seen from Eq. 3.3 to amount to sampling from an exponential distribution with x_j constrained to a certain interval. Step (i) requires more careful consideration. We have

$$ f(a_{0},t_{0}|t_{1},t_{2})\propto g(a_{0},t_{0})\prod\limits_{j=1}^{2} f(t_{j}|a_{0},t_{0}), $$

where f(t_j|a₀, t₀) is given by Eq. 3.4 and g(a₀, t₀) by Eq. 3.5. We have found experimentally for t₁ = t₂ that the following two-step procedure works well. We start by independently drawing A₀ and T₀ from exponential distributions with rates 2β and $\min \limits (\phi +\beta ,t_{1}^{-1},t_{2}^{-1})$, respectively. This is repeated K times to get a pre-sample {(A_0k, T_0k),k = 1…,K}, from which a single pair (A₀, T₀) is drawn with probabilities

$$ p_{k}\propto f(a_{0k},t_{0k}|t_{1},t_{2}) \exp\left[2\beta a_{0k}+\min(\phi+\beta,t_{1}^{-1},t_{2}^{-1})t_{0k}\right]. $$

5.2 Estimation

Consider n observation pairs {(x_1i, x_2i);i = 1,…,n} from Eq. 3.6. While f(x₁, x₂) is continuous as a function of 𝜃 = (β, ϕ, t), it is not differentiable in t at t = x₁ and t = x₂. This implies that the log-likelihood

$$ l(\beta,\phi,t) = n^{-1}\sum\limits_{i=1}^{n}\log\left( f(x_{1i},x_{2i};\beta,\phi,t) \right) $$

has 2n points where the derivative is not differentiable. Standard numerical optimization algorithms typically either do not use derivative information at all, or requires the objective function to be continuously differentiable in all variables. The former types of algorithms are slow and unstable, and the latter type are not directly applicable to our setting. We thus devise a special two-stage estimation algorithm.

Because X₁ and X₂ have the same marginal distribution we define the overall sample mean $\bar x=(2n)^{-1}{\sum }_{i=1}^{n}(x_{1i}+x_{2i})$. We denote by μ(β, ϕ, t) the expectation of X₁ and X₂, and impose the constraint $\mu (\beta ,\phi ,t)=\bar x$ on the parameter estimation problem. An analytical expression for μ(β, ϕ, t) is given in Appendix 7.4. The expression is complicated, but nevertheless well suited for numerical evaluation. Recall that we have proven earlier that μ(β, ϕ, t) is increasing as a function of t.

Our estimation algorithm iterates between the following two steps:

• 1. For given $\hat t$, let $\hat \beta$ and $\hat \phi$ be the maximizer of $l(\beta ,\phi ,\hat t)$.

• 2. For given $\hat \beta$ and $\hat \phi$, let $\hat t$ be the solution of the equation $\mu (\hat \beta ,\hat \phi ,t)=\bar x$.

Both 1) and 2) are solved numerically using the software TMB (Kristensen et al. 2016).

5.3 Simulation Experiment

Using the algorithm of Section 5.1, we sampled n = 1000 observation pairs (x₁, x₂) to which the estimator of Section 5.2 was applied. This process was repeated 1000 times to assess the statistical properties of the estimator. Table 2 shows the results for 20 different parameter combinations (one row per combination). Moments characterizing the distribution of (X₁, X₂), obtained from the moment generating function (3.12), are also given in the table.

Table 2 Performance of the estimator $(\hat \beta ,\hat \phi ,\hat {t})$ with n = 1000 observations drawn using the algorithm in Section 5.2

From Table 2 we see that the estimator for the parameter vector 𝜃 = (β, ϕ, t) is overall stable with respect to the different combinations of the input parameters. More specifically, for the parameter t in the first column, we see that the mean values of the estimates are all very close to the true value of t, but they are slightly worse in the case when β > ϕ. The same trend can be seen in the standard deviations, which are higher in these situations. For the parameter β we see that the mean of the estimates are more accurate for higher values of t, but we also see the trend with better predictions when β > ϕ. The standard deviations are however quite stable for all combinations of the input parameters. The mean values of the estimates for the parameter ϕ are all very similar and they do not seem to be affected by the different combinations of the input parameters. The standard deviations are higher when t = 2, but otherwise quite similar. Figure 5 shows the marginal density (3.14) for some of the parameter combinations used in Table 2.

Figure 5

Marginal density (3.14) when β < ϕ (left) and when β > ϕ (right). The legend refers to the leftmost column of Table 2, which gives the parameter setting used for the different density curves

5.4 Application to Real Data

We have presented the sibling distribution as a distribution for life times, but it may in fact be applied to any set of non-negative quantities with positive dependence. The constant-rate case is applicable only when the CV is less than one, and when t₁ = t₂ the marginals must be the same. We use the “twinData” dataset found in the R-package “OpenMx” (Neale et al. 2016) as an example. These are BMI measurements on twins (around age 18), but nevertheless satisfy the above mentioned restrictions (Table 3).

Table 3 Fitted sibling distribution to BMI data

The dataset consists of BMI measurements for 3569 (male/female, monozygotic/dizygotic) twin pairs. The fitted sibling distribution is unable to accomodate the light left-hand tail of data (Fig. 6). The fitted density is huge perturbation of the unconditional (on T) distribution of X, which for the constant-rate case is an exponential distribution. This illustrates the flexibility of the distribution. Table 3 shows the parameters of the fitted distribution. The lack of fit is reflected in estimated moments not fitting the empirical moments very well. If we look at the estimated parameter values in Fig. 6 we see that these are “outside in the normal range”, in the following sense. The expected life length of an individual is $1/\hat \phi =1/0.94=1.12$, but the mother-offspring duo spanned (mother’s birth to offspring’s death) at least $\hat {t} =21.77$ time units.

Figure 6

Marginal distribution of BMI data, with fitted sibling distribution. The dashed red curve shows the sibling density (3.6)

6 Discussion

The idea of a sibling distribution was conceived during our work with the recently invented Close-Kin Mark-Recapture method (Bravington et al. 2016), in which the joint age distribution of half-siblings plays a crucial role. Its usefulness as a distribution for multivariate life time data in general remains to be explored. The fact that it is a mixture (over A₀ and T₀) of independent life times makes it amenable to analysis in the framework of Shaked and Spizzichino (1998). However, due to the conditioning on T_j its structure, and in particular the moments, is complicated. Moreover, the non-differentiability of the likelihood with respect to the parameter t prevents straight forward application of maximum likelihood estimation.

Our numerical experiments indicate that the constant-rate (3.1) distribution has CV ≤ 1. This is clearly limiting for a general purpose life time distribution, but this restriction can be removed by choosing a non-constant ϕ(a). We have not been able to obtain explicit expressions for the sibling density under more general conditions. In general, the sibling density (2.5) can be evaluated numerically. Both the numerator and denominator involves two-dimensional integrals (with respect to a₀ and t₀). The integrand of the denominator is a product of m functions on form (2.4), which each involves a one dimensional integral. This is by no means computationally prohibitive, but specially tailored numerical integration schemes would have to be devised in order for the general distribution to be practically useful.

We have shown that the constant-rate sibling distribution with t₁ = t₂ = 0 coincides with the exchangeable Block-Basu distribution (α₁ = α₂ and $\alpha _{1}^{*}=\alpha _{2}^{*}$). The non-exchangeable case is not a sibling distribution, as the sibling framework requires that ϕ and β are the same for both siblings. Conversely, the sibling distribution with t₁ ≠ t₂, or t₁ = t₂ > 0, is not a Block-Basu distribution. Also, when allowing age-specific rates, ϕ(a) and β(a), the sibling distribution is no longer a Block-Basu distribution. Kundu and Gupta (2010) extended the Block-Basu distribution by deriving it from components that were Weibull distributed instead of exponential. The additional shape parameter makes the extended Block-Basu distribution more flexible at the cost of being less computational tractable.

Finally, we have proven that the constant-rate sibling distribution is MTP₂ and stochastically increasing in t. We conjecture, based on literature for mixture distributions (Shaked and Spizzichino, 1998, p. 273; Shaked and Shanthikumar, 2007) that these properties hold for a wider class of sibling distributions, but possibly not for all.

Appendices

Appendix A. Proof of Theorem 1

The quantities involved in the expression (2.5) for the sibling density are given by Eqs. 3.3, 3.4 and 3.5. The evaluation of the integrals over (a₀, t₀) in the numerator and denominator of Eq. 2.5 is made difficult by the constraints (2.3). Below we show how these constraints split the first quadrant of the (x₁, x₂) plane into six disjoint regions R₁,…,R₆ (see Fig. 2). In each of these the integrand is just a simple exponential function. Because the density is exchangeable when t₁ = t₂ it is sufficient to specify the expression only over the regions R₁, R₂ and R₃.

Recall that y_j = t_j − x_j denotes the birth time (j = 0,1,2). The integrand of the numerator in Eq. 2.5 is

$$ \begin{array}{@{}rcl@{}} &&f_{X,T}(x_{1},t|a_{0},t_{0})f_{X,T}(x_{2},t|a_{0},t_{0})g(a_{0},t_{0})\\&& \propto e^{-2\beta a_{0}} e^{-(\beta+\phi)t_{0}} \times \exp\left\{-\phi (x_{1}+x_{2})\right\}, \end{array} $$

(A.1)

for values of a₀ and t₀ such that the constraints (2.3) are satisfied for j = 1,2, and zero otherwise. The term after × does not depend on a₀ and t₀, but is included for later reference. Because we assume x₁, x₂ ≥ 0, we can replace the inequality (t_j − t₀)₊ ≤ x_j in Eq. 2.3 by t − t₀ ≤ x_j, which again is equivalent to t₀ ≥ y_j. Similarly, the last inequality x_j ≤ t_j − y₀ in Eq. 2.3 can be re-expressed as a₀ ≥−y_j. Together with the basic constraints a₀, t₀ ≥ 0 we get $a_{0} \geq \max \limits (0,-y_{1},-y_{2}) \ \text {and} \ t_{0} \geq \max \limits (0,y_{1},y_{2}).$ Depending on the relative values of y₁ and y₂, the lower bounds of the integrals over a₀ and t₀ will be qualitatively different. There are 6 different cases, corresponding to the partition R₁,…,R₆ of the (x₁, x₂) plane shown in Fig. 2. When integrating (A.1) with respect to a₀ and t₀, and replacing y_j by t − x_j (j = 1,2), we get

$$ f_{X,T}(x_{1},t) f_{X,T}(x_{2},t) \propto e^{-\phi (x_{1}+x_{2})}\times \begin{cases} e^{-(\beta+\phi)(t-x_{1})}, & (x_{1},x_{2})\in R_{1}, \\ e^{2\beta (t-x_{2})} e^{-(\beta+\phi)(t-x_{1})}, & (x_{1},x_{2})\in R_{2}, \\ e^{2\beta (t-x_{2})}, & (x_{1},x_{2})\in R_{3}, \end{cases} $$

which is Eq. 3.6.

The proof when t < 0 follows in the same vein, where we start out with the integrand of the numerator in Eq. 2.5 given by Eq. A.1. We must find values of a₀ and t₀ such that the constraints (2.3) still hold. The inequality (t_j − t₀)₊ ≤ x_j in Eq. 2.3 which is equivalent to t₀ ≥ y_j can be replaced with t₀ ≥ 0 since we have y₁, y₂ < 0 in combination with the constraint t₀ ≥ 0. For the last inequality in Eq. 2.3, the above arguments still apply such that this term is replace, with by a₀ ≥−y_j. In total we get $a_{0} \geq \max \limits (0,-y_{1},-y_{2})$ and t₀ ≥ 0.

Appendix B. Analytical expressions

The expectation under the density (3.14) is

$$ \begin{array}{@{}rcl@{}} \mu(\beta,\phi,t)&=&\mathrm{E}(X)\\ &=&6 \beta \left( \phi-\beta/3 \right) \left( \beta+\phi \right)^{2} \left( 2 \beta+\phi \right)^{2} \mathrm{e}^{\left( - \beta+\phi \right) t} \\ &&+4 \left( \phi^{2} \left( t\beta-1 \right) + 2\beta^{2}\phi t+2 \beta^{2} \right) \left( -\beta+\phi \right)^{2} \left( \beta+\phi \right)^{2} \mathrm{e}^{-t\beta}\\ &&+ \left( 4 -10 t\beta \right) \phi^{6}- \left( 34 \beta^{2}t+4 \beta \right) \phi^{5} - \left( 18 \beta^{3}t+51 \beta^{2} \right) \phi^{4} + \left( 34 \beta^{4}t-7 \beta^{3} \right) \phi^{3}\\ &&+ \left( 28 \beta^{5}t-23 \beta^{4} \right) \phi^{2} / 8\beta \left( 2 \beta+\phi \right) \left( -\beta+\phi \right) \phi \left( \beta+\phi \right) \\ && \left( 1/2 \left( 2 \beta+\phi \right) \left( \beta+\phi \right) \mathrm{e}^{\left( -\beta+\phi \right) t}+ \left( -\beta^{2}+\phi^{2} \right) \mathrm{e}^{-t\beta}-5/4 \phi \left( \phi+7/5 \beta \right) \right). \end{array} $$

This expression is obtained using computer algebra system Maple.

Appendix C. Proof of Theorem 3

We shall work with $g(x)=\log f(x)$, x ∈ R², which for the sibling density that Eq. 3.6 is a piecewise linear function. The MTP₂ property of f is equivalent supermodularity of g, i.e.

$$ g(x\vee z)+g(x\wedge z)\geq g(x)+g(z). $$

(C.1)

It is trivial to check that a linear function g is supermodular, so it follows directly that Eq. 3.7 is MTP₂.

The density (3.6) requires more careful attention due to its piecewise definition. It suffices to consider x and z such that the four points x, z, (x ∨ z) and (x ∧ z) form a non-degenerate rectangle with sides parallel to the axes. This happens when either x₁ < z₁ and x₂ > z₂ or when x₁ > z₁ and x₂ < z₂. We will consider only the former, where x is the upper-left corner (and z the lower-right corner) of the rectangle. The other case is handled in the same way. When the rectangle is degenerate (a line or a point) it can be checked that Eq. C.1 holds for any function g. Under these constraints, if x and z lie in the same region ($R_{1},\dots ,R_{6}$) of Fig. 7 all four corners of the rectangle lies lies in same region, and by linearity of g within each region we have that Eq. C.1 is satisfied.

Figure 7

Part of the proof of Theorem C. The green dashed line is an example of a level curve (C.2). The red rectangles are used to prove supermodularity

The sum of two supermodular functions is again supermodular, so we may add ϕ(x₁ + x₂) to all three branches of the logarithm of Eq. 3.6, so that we may work with

$$ g(x_{1},x_{2}) = \begin{cases} -(\beta + \phi) (t-x_{1}) , & 0 \leq x_{1} \leq x_{2} \leq t, \\ 2\beta(t -x_{2})-(\beta + \phi)(t -x_{1}), & 0\leq x_{1} \leq t \leq x_{2}, \\ 2\beta (t - x_{2}), & 0\leq t \leq x_{1} \leq x_{2} . \end{cases} $$

(C.2)

The extension of g to all six regions of Fig. 7 (with t₁ = t₂ = t) is g(x₁, x₂) = g(x₂, x₂) when x₁ > x₂. The fact that g(x₁, x₂) does not depend on x₂ in regions R₁ and R₄, and not on x₂ in R₃ and R₆ are visualized via the a level curve (green dashed line) of g in Fig. 7. It is seen that g is unimodal, with the mode at (x₁, x₂) = (t, t).

We start out by restricting ourselves to the case x₂ < t. Under the facts established above, and the assumed restrictions on x and z, there are only three qualitatively different cases that must be considered. Using the red part of Fig. 7 as a reference, these are: i) x = A and $z=C^{\prime }$, ii) x = A and $z=D^{\prime }$ and iii) x = C and $z=D^{\prime }$. With our geometric approach, supermodularity is something that is checked for rectangles. It has the property that we can split a rectangle $(A,C,C^{\prime },A^{\prime })$ in two, $(A,B,B^{\prime },A^{\prime })$ and $(B,C,C^{\prime },B^{\prime })$, and it is sufficient to check Eq. C.1 for the two parts. Hence, to check all of i)–iii) it suffices to check all the red sub-rectangles in Fig. 7, which we will now do. First, $(A,B,B^{\prime },A^{\prime })$ lies in a single region (R₆) so Eq. C.1 holds. For $(B,C,C^{\prime },B^{\prime })$ we find by looking at the level curves of g that g(C) > g(B) and $g(C^{\prime })=g(B^{\prime })$, which imply that Eq. C.1 holds. Finally, the (solid black) vertical line x₁ = t splits $(C,D,D^{\prime },C^{\prime })$ in two parts which each line entirely in R₁ and R₂, respectively. This completes the proof for x₂ < t.

The situation that z₂ > t, i.e. the red part of the figure is moved above the (solid black) horizontal line x₂ = t, follows by symmetry. The remaining case, x₂ > t > z₁, can be handled by splitting in two the rectangle horizontally at the x-axis, for each of which we know Eq. C.1 holds. Since supermodularity is also additive when splitting a rectangle horizontally, we have completed the proof.

Appendix D. Proof of Theorem 4

We prove that f(x₁, x₂;t) is multivariate stochastically increasing (Shaked and Shanthikumar, 2007, Definition (6.B.1)) in the parameter t, where f(x₁, x₂;t) is given by Eq. 3.6. This implies Eq. 3.16, i.e. the marginals are also stochastically increasing (Shaked and Shanthikumar, 2007, Theorem 6.B.16 (c)).

We prove that the conditions in Theorem 6.B.8 in (Shaked and Shanthikumar, 2007) are satisfied. First, it follows from the MTP₂ property that (X₁, X₂) is “associated” in the sense of the theorem (Karlin and Rinott, 1980, Eq. (1.7)). Define the function $h(x_{1},x_{2})=\log \left [f(x_{1},x_{2};t^{\prime })/f(x_{1},x_{2};t)\right ]$. The main condition of Theorem 6.B.8 is that h(x₁, x₂) is increasing in (x₁, x₂) for $t^{\prime }>t$. To verify this we will check that

$$ \frac{\partial h}{\partial x_{1}}\geq 0 \quad \text{and} \quad \frac{\partial h}{\partial x_{2}}\geq 0, $$

(D.1)

which together with the continuity of h is sufficient.

We build on the proof of Theorem 3, and denote the six regions of Fig. 7 associated with $t^{\prime }$ by $R_{1}^{\prime },\ldots ,R_{6}^{\prime }$. We need to verify Eq. D.1 when $(x_{1},x_{2})\in R_{j}\cap R_{k}^{\prime }$ for different values of j and k. When j = k it follows that h(x₁, x₂) = 0 which implies Eq. D.1. Next, due to the fact that $t\leq t^{\prime }$ many combinations of j and k cannot occur, and we are left with the following list to check:

(x1, x2)	h(x1, x2)
$R_{4}\cap R_{5}^{\prime }$	(ϕ + β)x1
$R_{4}\cap R_{6}^{\prime }$	(ϕ + β)x1 + 2βx2
$R_{5}\cap R_{6}^{\prime }$	2βx2
$R_{3}\cap R_{2}^{\prime }$	(ϕ + β)x2
$R_{3}\cap R_{1}^{\prime }$	(ϕ + β)x2 + 2βx1
$R_{2}\cap R_{1}^{\prime }$	2βx1

For all of these combinations (D.1) holds. Note that we have skipped additive terms in h that does not depend on x₁ or x₂. This completes the proof.