Probability distributions of number of children and maternal age at various order births using age-specific fertility rates by birth order

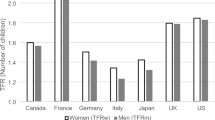
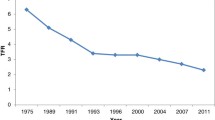
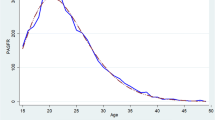
Abstract

In this study, a simple analytical framework to find the probability distributions of number of children and maternal age at various order births by making use of data on age-specific fertility rates by birth order was proposed. The proposed framework is applicable to both the period and cohort fertility schedules. The most appealing point of the proposed framework is that it does not require stringent assumptions. The proposed framework has been applied to the cohort birth order-specific fertility schedules of India and its different regions and period birth order-specific fertility schedules, including the United States of America, Russia, and the Netherlands, to demonstrate its usefulness.

Appendices

Appendix A

Figure 4

Different regions of India and their constituent states.

Figure 5

Fit of various birth order-specific fertility curves for the considered countries.

Figure 6

Fit of various birth order-specific fertility curves for the considered countries.

Table 9 Parameter estimates of various birth order-specific fertility curves fitted to the cohort birth order specific fertility schedules of India and its different regions (variance of conditional probability distributions is also provided).

Table 10 Standard errors of the parameter estimates* of various birth order-specific fertility curves fitted to the cohort birth order-specific fertility schedules of India and its different regions.

Table 11 Parameter estimates of various birth order-specific fertility curves fitted to the period birth order-specific fertility schedules of the considered countries (mean (for Wald’s model is mean) and variance* of conditional probability distributions are also given).

Table 12 Standard errors of the parameter estimates* of various birth order-specific fertility curves fitted to the period birth order-specific fertility schedules of the considered countries.

Appendix B

Proof of Lemma.

Moment Generating Function (MGF)

$$\begin{array}{lll} MGF &=& E(e^{tx} )\\ &=& \int _{-\infty }^{\infty }e^{tx} f(x) dx\\ &=& \int _{-\infty }^{m}e^{tx} \left(\frac{1}{\sigma _{1} \sqrt{2\Pi } } \right)\exp \left(-\frac{1}{2} \left(\frac{x-m}{\sigma _{1} } \right)^{2} \right)dx+\\ && \int _{m}^{\infty }e^{tx} \left(\frac{1}{\sigma _{2} \sqrt{2\Pi } } \right)\exp \left(-\frac{1}{2} \left(\frac{x-m}{\sigma _{2} } \right)^{2} \right)dx . \end{array} $$

Taking x − m/σ ₁  = z ₁ and x − m/σ ₂  = z ₂ , the above expression can be rewritten as

$$\begin{array}{lll} MGF &=& \int _{-\infty }^{0}e^{t\left(\sigma _{1} z_{1} +m\right)} \left(\frac{1}{\sqrt{2\Pi } } \right)\exp \left(-\frac{1}{2} z_{1}^{2} \right)dz_{1} \\ &&+ \int _{0}^{\infty }e^{t\left(\sigma _{2} z_{2} +m\right)} \left(\frac{1}{\sqrt{2\Pi } } \right)\exp \left(-\frac{1}{2} z_{2}^{2} \right)dz_{2}\\ &=& e^{tm} \left(\frac{1}{\sqrt{2\Pi } } \right)\int _{-\infty }^{0}e^{t\sigma _{1} z_{1} -\frac{1}{2} z_{1}^{2} +\frac{1}{2} t^{2} \sigma _{1}^{2} -\frac{1}{2} t^{2} \sigma _{1}^{2} } dz_{1} \\ &&+e^{tm} \left(\frac{1}{\sqrt{2\Pi } } \right)\int _{0}^{\infty }e^{t\sigma _{2} z_{2} -\frac{1}{2} z_{2}^{2} +\frac{1}{2} t^{2} \sigma _{2}^{2} -\frac{1}{2} t^{2} \sigma _{2}^{2} } dz_{2}\\ &=& e^{tm+\frac{1}{2} t^{2} \sigma _{1}^{2} } \left(\frac{1}{\sqrt{2\Pi } } \right)\int _{-\infty }^{0}e^{-\frac{1}{2} (z_{1} -t\sigma _{1} )^{2} } dz_{1} \\ &&+e^{tm+\frac{1}{2} t^{2} \sigma _{2}^{2} } \left(\frac{1}{\sqrt{2\Pi } } \right)\int _{0}^{\infty }e^{-\frac{1}{2} (z_{2} -t\sigma _{2} )^{2} } dz_{2}. \end{array}$$

By taking z ₁ − tσ ₁ = y ₁ and z ₂ − tσ ₂ = y ₂ it can be shown that the above expression is equal to

$$ MGF=e^{tm+\frac{1}{2} t^{2} \sigma _{1}^{2} } \left(\frac{1}{\sqrt{2\Pi } } \right) \int _{-\infty }^{-\sigma _{1} t}e^{-\frac{1}{2} y_{1}^{2} } dy_{1} +e^{tm+\frac{1}{2} t^{2} \sigma _{2}^{2} } \left(\frac{1}{\sqrt{2\Pi } } \right)\int _{-t\sigma _{2} }^{\infty }e^{-\frac{1}{2} y_{2}^{2} } dy_{2} . $$

$$ \therefore M_{X} (t) = e^{mt+(1/2)t^{2} \sigma _{1}^{2} } \; \Phi \left(-t\sigma _{1} \right) + e^{mt+(1/2)t^{2} \sigma _{2}^{2}}(1-\Phi \left(-t\sigma _{2} \right)), $$

where Φ(x) is the cumulative probability distribution function of standard normal distribution.

Mean

$$ Mean = \frac{d}{dt} M_{X} (t)|_{t=0}. $$

Using the result

$$ \frac{d}{dt} \left(\int _{\xi (t)}^{\psi (t)}f(x)dx \right) = f(\psi (t))\, \frac{d}{dt} \left(\psi (t)\right)\, \, -\; f(\xi (t))\, \frac{d}{dt} \left(\xi (t)\right), $$

it is possible to show that

$$\begin{array}{lll} \frac{d}{dt} M_{X}(t)|_{t=0} &=& \left[e^{mt+(1/2)t^{2} \sigma _{1}^{2} } \Phi '\left(-t\sigma _{1} \right) + \Phi (-t\sigma _{1} )e^{mt+(1/2)t^{2} \sigma _{1}^{2} } (m+t\sigma _{1}^{2} )\right]+\\ &&\left[e^{mt+(1/2)t^{2} \sigma _{2}^{2} } (-\Phi '\left(-t\sigma _{2} \right)) + (1-\Phi (-t\sigma _{2} ))e^{mt+(1/2)t^{2} \sigma _{2}^{2} } (m+t\sigma _{2}^{2} )\right]\\ &=&\left[\frac{-\sigma _{1}}{\sqrt{2\Pi}} +\frac{m}{2}\right]+\left[\frac{\sigma _{2} }{\sqrt{2\Pi } } +\frac{m}{2}\right]\\ &=&m+\frac{1}{\sqrt{2\Pi } } \left(\sigma _{2} -\sigma _{1} \right). \end{array}$$

$$ \therefore Mean=m+\left(\frac{\sigma _{2} -\sigma _{1} }{\sqrt{2\Pi } } \right) $$

Variance

$$ E(X^{2} )=\frac{d}{dt^{2} } M_{X} (t)|_{t=0} $$

Proceeding in the same way as was done previously, it can be shown that

$$ E(X^{2} )=\left(\frac{\sigma _{1}^{2} +\sigma _{2}^{2} }{2} \right)+m^{2} +\frac{2m}{\sqrt{2\pi } } \left(\sigma _{2} -\sigma _{1} \right), $$

and

$$ \begin{array}{rll} variance(\textit{X}) &=&E(X^{2} )-[E(X)]^{2} \\ &=&\left(\frac{\sigma _{1}^{2} +\sigma _{2}^{2} }{2} \right)-\frac{1}{2\pi } \left(\sigma _{2} -\sigma _{1} \right)^{2}. \end{array} $$

$$ \therefore Variance=\left(\frac{\sigma _{1}^{2} +\sigma _{2}^{2} }{2} \right)-\frac{1}{2\pi } \left(\sigma _{2} -\sigma _{1} \right)^{2}. $$

It can also be shown that

$$ Median = m, $$

$$ 1^{st} quartile = m+\sigma _{1} {\rm (-0.67449),} $$

and

$$ 3^{rd}quartile = m+\sigma _{2} {\rm (0.67449).} $$