Introduction

A typical mine planner forecasts profits based on extensive assumptions regarding price and reserves. However, these profit determining factors exhibit a high-level risk and uncertainty and can result in substantial miscalculation of future value of a project. Risk refers to the possibility of an adverse occurrence, whereas uncertainty relates to the future outlook regarding the unpredictability of the project. These doubts can be identified and resolved using time, events, and action (Mun, 2006).

The standard discounted cash flow (DCF) technique employed by conventional mining companies does not consider the associated risks and uncertainties. This technique calculates the cash flow model whose profit or loss is determined before the project begins by considering the time value of money (Stermole & Stermole, 2000). Decision-makers frequently change the discount rate to mitigate risk and to integrate the technical risk premium in the DCF method. In addition, they perform a sensitivity analysis to anticipate the impact of changing cash flow parameters. However, depending on the situation, this strategy may impose a significant constraint in terms of adoption and can therefore be inferred to be an inadequate uncertainty valuation technique (Nicholas, 2014).

An option is a financial derivative whose value depends on the price of a stock. Option holders have rights but no obligation to execute their option in the maturity date. These alternatives are quantified by option calculation to justify option value. The adaptation of option calculation in the actual project is called real options (RO). Several academics have developed the RO approach that considers managerial flexibility to modify a future choice if uncertainties are identified. The RO method quantifies value and uncertainty based on historical volatility and projects the probability. However, standard RO approaches, such as the Black–Scholes method (Black & Scholes, 1973) and the lattice valuation technique (Cox et al., 1979), are unable to measure a project with multiple uncertainties.

To date, risk and uncertainty can also be quantified by building a simulation technique based on the Monte Carlo simulation (MCS) methodology (Barraquand & Martineau, 1995). By optimizing the executing and waiting value of the project, lattice and simulation techniques consider management flexibility. Brennan and Schwartz presented a temporal stochastic model with theoretical computations for evaluating natural resource projects (Brennan & Schwartz, 1985). However, the usefulness of RO is constrained by its mathematical difficulty (Haque et al., 2014) and application (Ajak & Topal, 2015).

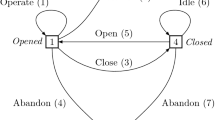
There are many type of options including delay, expansion, contract, and abandon options (Mun, 2006). Related to the case study, this research employed wait to operate option assessment which is important at expansion time. The study involved a tin mining project located at PT Timah Tbk in Indonesia, which focuses on monthly mine planning for underwater mining and uses a dredge as the primary equipment. The project was an expansion of existing production and management had the option to execute the mining location. Economic and geological factors, represented by price and grade, presented significant risks and uncertainties. Therefore, the application of RO in the mining industry can be improved by incorporating these uncertainties.

Our established valuation approach addresses these limitations in RO applications, particularly for assessing several uncertainty sources in a multi-stage short-term mining project. The originality of proposed SSA methodology is exhibited by practical simplicity and enhancement in previous studies (Adachi et al., 2008) by employing the adaptation of spatial uncertainty through conditional simulation (CS) and construction of path generation algorithm to incorporate price and grade uncertainties. Closely related studies demonstrated using empirical models (Brennan & Schwartz, 1985; Cortazar et al., 2001). In contrast, we utilized the simulation method (Barraquand & Martineau, 1995) to assess the uncertainty drivers, which are uncomplicated and flexible.

Materials and methods

Economical (price) uncertainty model

The value of a mining project is determined entirely by the income generated from the sale of materials. We proposed SSA methodology to quantify a project considering selling price and grade uncertainties. To simulate SSA through Java programming, we utilized the developed geometric Brownian motion (GBM) model (Eq. 1) (Cortazar et al., 2001). Brownian motion is a continuous-time stochastic process with three key characteristics: Markov process, Wiener process (probability distribution is independent of other time intervals), and normal distribution with growing variance over time (Dixit and Pindyck 1993). Nevertheless, Augmented Dickey-Fuller (ADF) test has proven that the tin price data followed random walk with trend assumption and therefore GBM model can be applied.

Historical prices (S&P database) from January 2015 to January 2021 were used to assess future price uncertainty. Based on the historical data, a logarithmic natural growth study (Eq. 2) was conducted to reveal the selling price monthly volatility, where \({\mu }_{i}\) represented monthly price logarithmic growth. Moreover, we assumed that the price change would follow a stochastic differential equation model for risk-neutral pricing: the one-factor constant convenience yield model (Cortazar et al., 2001). Equation 1 explains the increment of the spot unit price (P) is calculated based on the risk-free rate of interest (r), convenience yield on holding a one-ton unit of Tin (\(\delta\)), along with price volatility (\({\sigma }_{P}\)), and increments to the standard Gauss-Wiener process. Risk-free rate is the growth rate of the value of money, which typically refers to the treasury bond (Crundwell, 2008). Additionally, benefits of a commodity owner for the future delivery of a commodity are known as convenience yield (Brennan & Schwartz, 1985).

$$\frac{dP}{P}=\text{(r-}\delta \text{)}dt+{\sigma }_{P}{dz}_{P}$$
(1)
$${\sigma }_{P}=\sqrt{\frac{1}{n-1}{\sum }_{i=1}^{n}{({u}_{i}-\overline{u })}^{2}}$$
(2)

Geological (grade) uncertainty model

The company’s reserves were classified based on various levels of geoscientific confidence and modifying factors (JORC, 2012). To gain confidence in grade uncertainty, a mining company needs to do exploration and consequently expend substantial capital. Grade uncertainty is a spatial uncertainty in which the real value emerges after the reserve is exploited. Although the entire quantity of reserves is estimated using Kriging methods, it cannot portray the uncertainty. Therefore, grade uncertainty was measured using the CS technique, calculated based on Kriging data (Dowd, 1994). The CS of the ore body is a spatial MCS-based approach that measures spatial uncertainty. CS reproduces the characteristics of an orebody and quantifies the variability. MCS is used for the net present value distribution function and the anticipated cash flow variability (Jurdziak & Wiktorowicz, 2008).

The exploration data was obtained from a tin company (licence holder). Then, we generated the mine design through GEOVIA Surpac and GEOVIA Whittle; GEOVIA Surpac was used to process exploration data such as “collar” and “assay.” In addition, we created a block model and used a CS technique known as the Sequential Gaussian Simulation (SGSIM) to input the grade into the model. Deutsch and Journel have detailed the explanation of the algorithm, which is publicly accessible via the geostatistic software library (GSLIB) ecosystem (Deutsch & Journel, 1997).

Exploration data consisted of 55 underwater coring drill hole data classified as north, mid, and south resources based on the location. However, based on the reserves calculation through the GEOVIA Whittle mining software, north reserves were not profitable. Therefore, we calculated the project value on both mid and south reserves as a multistage of mining.

We modeled the mine design after obtaining the reserve model through the GEOVIA Whittle mining software. Table 1 resumes the assumptions to do it. The mining, processing, and selling cost were collected and averaged from historical data of company production with similar method.

Table 1 Mine planning parameters
Full size table

Stratified state aggregation

RO analysis is derived from the decision tree and financial option approaches (Crundwell, 2008). The analysis of options was introduced by Black–Scholes Formula (Black & Scholes, 1973) and had been popularly applied in the lattice method developed by Cox et al. (Cox et al., 1979). Myers stated an RO for the first time in the study of corporate debt policies, which account for the flexibility of the company management (Myers, 1977). Another RO approach, stratified state aggression (SSA), was a numerical method developed by Barraquand and Martineau for calculating the value of an American option (Barraquand & Martineau, 1995). The cost of complicated American instruments can be calculated on a workstation in seconds. This algorithm was developed to tackle high-dimensional valuation of an option. The approach used MCS and performed a backward computation to arrive at the current value for modeling uncertainty.

Our SSA is an RO simulation approach written in Javascript which was employed by Adachi et al. (2008) for calculating an oil project value. The original work was in Japanese, which examined oil development projects in their early stages, such as exploration, development, and production, considering price uncertainty. Every level included a monetary outlay and the likelihood of success increased as the outlay increased. However, management has the option of making decisions before each growth stage; therefore, completing the investment in a single disbursement is not necessary.

This study uses an identical Java algorithm in the mining sector; however, mining differs from the oil industry in terms of reserve characteristics. We performed underwater tin mine planning on an established mining location. Every mining area was regarded as a stage extraction owing to the limited number of available dredges as equipment. The novelty of our algorithm was path simulation generation which considered price and reserve uncertainties. As a result, SSA was used as an alternative approach to determine the project’s actual value.

Typically, multiple locations in mining are exploited successively. Therefore, they can be evaluated separately. As an assumption, the mid reserve, which is more valuable, is treated as the first stage, followed by the south reserve. They are evaluated simultaneously in 100,000 simulations of the project value while accounting for the two uncertainties. More number of simulation theoretically would increase the consistency. However, the result did not change significantly even if the number of simulation is increase from 100,000. In our case study, the simulation number is enough to get consistency in the result. Wait to operate and abandon option was used in the option type computation of the case study. Considering the two uncertainties, the firm had the options of execution, waiting for execution, or abandoning the project when the condition is unfavourable.

The SSA technique began by constructing cells of 400 rows and 60 columns as the state space of the project value and the limitation scope of simulation (Fig. 1a). The cells of 400 rows represented the future project value diversion in 60 months of production with equal probability. The next step is path generation to simulate unknown parameters (Fig. 1b). In the case study, there are two simulated parameters of project value accounted for using MCS, which are price and grade uncertainties. Equation 1 is applied in this stage while combining with grade uncertainty to apply the simulation. Simultaneously, the average of grade in CS was assumed as the expected initial reserve amount, while the variance of CS was assumed to simulate the grade uncertainty. Then, the simulation was conducted 100,000 times to capture the future project value probability that has many permutations of selling price and total reserve (Fig. 1c). The number of simulations is chosen to optimize the time of calculation and the consistency of the result. After that, the transition probability and forward exercise value were calculated using Eq. 3 (Fig. 1d). Lastly, we conducted backward calculation (Fig. 1e) and maximized the benefit of exercise and the value of waiting (Eq. 4). This approach is demonstrated using java algorithm and is illustrated in Fig. 1.

$${\prod }_{\mathrm{h},\mathrm{j}}\left(k.k+1\right)= \frac{\mathrm{Number\;of\;paths\;from\;}{\mathrm{C}}_{\mathrm{h},\mathrm{j}}^{\mathrm{k}}\mathrm{\;to\;}{\mathrm{C}}_{\mathrm{h},\mathrm{j}+1}^{\mathrm{k}+1}}{\mathrm{Number\;of\;paths\;through\;}{\mathrm{C}}_{\mathrm{h},\mathrm{j}}^{\mathrm{k}}}$$
(3)
$${\mathrm{P}}_{\mathrm{h},\mathrm{j}}\left(k\right)=\mathrm{max}[{E}_{\mathrm{h},\mathrm{j}}\left(k\right),{V}_{\mathrm{h},\mathrm{j}}\left(k\right)]$$
(4)

where \({\prod }_{\mathrm{h},\mathrm{j},\mathrm{k}}\) is transition probability at time j, stage h, and path k; C is cell value; P is project value; E is exercise value; and V is the waiting value.

Fig. 1
figure 1

Stratified state aggregation (SSA) methodology

Full size image

A firm should wait to operate as long as the value of waiting exceeds the value of operating in the present time. However, an operation should be executed when the values of waiting and executing are identical (Mun, 2006). We based our mine planning and cash flow model on the data and made several assumptions regarding the risk-free rate, convenience yield, discount rate, and density summarized in Table 2.

Table 2 Multi-stage stratified stage aggregation parameters
Full size table

Results

Price uncertainty model

Based on the historical data, a logarithmic natural growth study revealed that the selling price had a monthly growth rate (α) of 0.3% with a volatility of 5.47%. However, because overconfidence in price growth may lead to a blunder, we used Eq. 1 as the starting point. We assumed a risk-free rate (r) and convenience yield (δ) of 0.25% and 0.17%, respectively (Fig. 2). We obtained these assumptions from our expected Treasury US bond (3%/year) and below the average price of tin growth rate. Over time, the expected future price would grow, and the probability distribution would increase.

Fig. 2
figure 2

Price uncertainty model: GBM

Full size image

Reserves uncertainty model

The variogram model obtained from the exploration drilling data formed the basis of our anticipated outcome of CS (Fig. 3). In our case study, the variogram model indicated variance (sill) of 1.2, nugget effect of 0.3, and lag distance of 30 m. The reserve model (Fig. 3(c)) was the average model and generated after 1000 simulations through CS. Our first and last CS model is illustrated in Fig. 3(a) and (b), respectively. The obtained average value provided the expectation of the reserve grade.

Fig. 3
figure 3

Conditional simulation (CS) outcome for modeling reserves. a CS 1; b CS 1000; c expected CS; d color attribution for the model

Full size image

The division of the expected grade with the standard deviation represents volatility of the reserve. Grade tonnage graph (Fig. 4) was obtained from reporting simulation using Surpac software with SGS library from GSLIB. The simulation results show the grade and tonnage of expected and each simulation model. In our 1000th simulation, we obtained a reserves amount of 7.2 MT, a grade of 0.2 kg/ton, and volatility of 9% (Fig. 4(a) and (b)) and a reserves amount of 1.1 MT, a grade of 0.19 kg/ton, and volatility of 15.8% (Fig. 4(c) and (d)) for the mid and south reserves, respectively.

Fig. 4
figure 4

Reserve Grade-Tonnage: a Mid Deposit Standard Deviation; b Mid Deposit Grade Tonnage; c South Deposit Standard Deviation; d South Deposit Grade-Tonnage

Full size image

Stratified stage aggregation

Our multi-stage SSA simulation yielded an RO value of 7.8 million US dollars (MUSD), compared to the corresponding value of 7.5 MUSD obtained from the standard DCF method. In addition, we modeled the changes of important parameters: initial price and initial reserves (Figs. 5 and 6, respectively). Nonetheless, the critical value was specified when the option value approached the present value and was close to zero.

Fig. 5
figure 5

Project value with price changing

Full size image
Fig. 6
figure 6

Project value with reserve changing

Full size image

When the initial price or reserves dropped by more than 10% from our assumption, the option premium was more than our assumed threshold 5% risk (Figs. 5 and 6). Therefore, the decision was shifted from execution to delay decision. Additionally, when the initial price or reserves dropped by 45% and the RO value was almost zero, the decision recommendation was changed to “abandon the project.” The changing reserves parameter (Fig. 6) had a similar result to the price alteration (Fig. 5).

Scenario analysis

Scenario analysis was performed to map the decision recommendation at specific conditions of price and total reserve when the decision is taken. The analysis spread from the original assumption (initial price of 23,199 USD/ton and initial total reserve of 8,327 Kton) to a 90% price and 50% ore grade shift. For instance, Tables 3 and 4 represent the project’s present and option values, respectively. Recommending a decision through RO was performed by comparing the present value and option value, whereas the traditional DCF method only produced the present value as the decision parameter (Tables 3 and 4).

Table 3 Present value of reserve and price relative simulation
Full size table

The colored blocks in Table 3 represent the decision recommendation through the traditional DCF method. A positive present value would be reached if the price exceeded 11,600 dollars per ton ore. With option premium as a consequence of the waiting value resulting from determining uncertainty parameters (Table 2), the SSA approach improved the decision to neither execute (green color) nor reject (red color) the mine project. Instead, it provided waiting recommendations for specific cases, as shown by the yellow color in Table 4.

Table 4 Option value of reserve and price relative simulation
Full size table

Theoretically, option value is shifted as the cash flow parameter or the uncertainty is changed. As a result, we further investigated the change in uncertainties to define their effect on the option value. Uncertainties were not accounted for in the traditional method; therefore, they did not affect the present value and remained constant at 7.5 MUSD. Figure 7 displays the option value alteration where the price and grade uncertainties were changed up to 25% and increments of 5%. The value of waiting at Fig. 7 implied that the project had to be delayed when the option value was far from the calculated present value. A shift in the price uncertainty had an almost symmetrical effect with the reserves uncertainty to the option value. For instance, the methodology recommends delaying the project when the option value exceeded 7.9 MUSD as our assumed threshold.

Fig. 7
figure 7

Real option (RO) value with price and reserve uncertainties alteration

Full size image

Discussion

Incorporating the price and reserve analyses is vital to the profitability of mining project. In addition, understanding the risk and uncertainty related to the economic and geological aspects may aid in anticipation of their future conditions (Mun, 2006). Typically, most mining companies assess risk and uncertainty for price and reserves separately. This standalone analyses in corporate division can potentially cause project failure. Combining the economic and geological analyses would increase the success rate. Therefore, this research study proposed novelty on combination method of both risks to evaluate the mining project comprehensively.

The Geometric Brownian model analyzes historical fluctuations using price expectation and its standard deviation as the base assumptions of the method. The assumption can be made considering statistical analysis through Dickey-Fuller test, which showed the price follows a trend and is not a stationary data. Uncertainty of a cash flow, including price, increases over time despite of a constant risk value (Mun, 2006); Fig. 2 proves that this possibility increases over time. Although the price growth expectation was relatively low (0.3%), we employed the non-overconfident assumption by utilizing the risk-neutral growth formula (Eq. 2), which was applied previously (Adachi et al., 2008; Cortazar et al., 2001; Costa Lima & Suslick, 2006). The historical price volatility was assumed to be price uncertainty and was later analyzed using the SSA methodology.

Reserve is a spatial base parameter depleted over different stages of productions. The company has to increase exploration drilling to guarantee the reserves. The spacing between the drill holes determined the volatility and was therefore added to the data to confirm the reserves amount and the decrease in the grade uncertainty. However, grade uncertainty could not be eliminated owing to the nugget effect. The term “nugget” is borrowed from geostatistics and refers to the unexpected mineral nugget found in a mining process (Yin et al., 2011). Cressie concluded that the nugget effect in geostatistics is caused by micro-scale variation and measurement error (Cressie, 1993). The block model (Fig. 3) was built based on the underwater exploration drill hole data and assumed to be mined as the average grade. Then, we conducted 1000 conditional simulations to quantify grade uncertainty.

Compared to the ordinary Kriging method, CS produced reserves uncertainty and was represented by the standard deviation (Fig. 4(a) and (c)). The CS results can analyze the maximum and minimum reserve grades. Our grade tonnage results (Fig. 4(b) and (d)) were consistent with the theory that ordinary Kriging overestimates high grades. In contrast, CS estimates a higher amount at the low-grade reserves (Jurdziak & Wiktorowicz, 2008). Our 1000 simulations show the adequacy of SGS as it has been stable (Fig. 4). The standard deviation is very high at the beginning of the simulation as SGS is based on MCS with similar data to the Kriging methodology. However, as additional simulation data were obtained, the standard deviation approaches a specific value which indicates ore grade uncertainty. In our two reserve simulations of SGS, every reserve exhibited a particular probability distribution and an adequate amount of simulation to obtain a stable standard deviation. The stability of the result was reached after more than around 400 simulations. Therefore, we concluded that the standard deviation results (15.8% for south reserves and 9% for mid reserves) provided a reliable base for economic evaluation using the RO valuation methodology.

The DCF methodology only considers projected income to determine the decision. Moreover, the assumed project cash flow was sensitive to income parameters. The present value of the projects with our assumption was 7.5 MUSD. Using RO methodology, the critical value was created in Figs. 5 and 6. When the parameter is altered below the critical value, the decision recommendation is changed from execution to waiting or from waiting to abandoning the project as the real option value reached zero. The price and reserve parameters presented the income aspect of the project; therefore, both parameters were incorporated when the company decided to exercise the project. The two uncertainties had similar properties (Figs. 5 and 6) implying future decisions based on future conditions. However, the analysis was independent and could be considered rare instead of a combination of parameter alteration (Tables 3 and 4, Fig. 7).

The superiority of the RO methodology compared to the traditional method was that it enabled the manager to plan a specific action when the uncertainty was revealed. The option value was obtained from the possibility of an improved economic parameter (Crundwell, 2008). Our method improves adaptability by using CS for accounting for grade uncertainty and simplification via java programming. The simplicity is represented by the ability of changing simulation parameter in the algorithm. Furthermore, we made a decision map when the price and reserves changed in the future (Tables 3 and 4). The red, yellow, and green colors represented the decision recommendations to abandon the project, wait to execute, and execute the project, respectively. The critical value was calculated to secure the project profitability. Dixit and Pindyck (1993) emphasized that this critical value is reached when the waiting value is identical to or less than the executing value. However, the uncertainties created a distance between the two values. Mun (2006) stated that the company’s behaviour determined the risk of a project. Therefore, the critical value may vary among decision-makers.

Although both methods recommended immediate execution of the project, SSA improved the results of the traditional method. This improvement caused the RO methodology to recommend the delay decision under several other conditions (Table 4). Project uncertainties have been observed to account for project values in RO values. In Fig. 7, the simulation of the changing volatility parameter changed the option value. For instance, the decision recommendation was shifted to delay when the price and reserve volatilities were increased to 20% and 5%, and vice versa. Nevertheless, the uncertainty alteration did not change the decision using the traditional methodology that is represented by the present value.

This study further demonstrates the application of RO in the mining industry. It successfully combines the advancement of geostatistics in terms of CS and RO valuation through the SSA approach. The current limitation for RO, including mathematical complexity and applicability (Haque et al., 2014), is solved using our methodology. SSA simulation solves the mathematical problem while incorporating grade uncertainty in the simulation to determine the project value and risk. However, the SSA methodology needs optimization on number of simulation and modeling methods. Balancing calculation time and consistency of result is the key of method limitation. Furthermore, comparing to Black–Scholes and binomial lattice methods, only SSA can be performed on the case study. Adding capital assumption and eliminating grade uncertainty, they have similar result with diference less then 1%. Nonetheless, capturing additional uncertainty increases the future applicability of the RO. Each modifying factor in the conversion resource to be reserved and from geological confidence (JORC, 2012) is supposed to be modeled further to obtain proper project value and ultimately guarantee a successful project with calculated risk.

Conclusions

In summary, we constructed a valuation method using the developed SSA methodology to estimate the value of a mining project and provide decision recommendations such as execute, wait to execute, or abandon the project. Uncertainty in mining can be modeled using RO; therefore, the SSA approach was employed to evaluate uncertainties and multi-stage mining (rainbow option).

This research utilized CS for modeling reserves in the RO valuation while incorporating advanced geostatistical applications and economic valuation methodologies which represent the novelty. The simulation revealed that price and grade uncertainties were the dominant determinants of the project value. Therefore, the company should apply the economic and reserve model before executing the project to make it beneficial. In addition, uncertainties would be overcome by management’s flexibility to change their decision in the future when current uncertainties become identified. The proposed methodology is applicable in our case study and other mineral resources based on their properties.

This study presented a pilot project that combined uncertainties and multi projects in mining ventures. We considered pricing and geological factors in two mining locations, whereas other modifying factors were assumed to be stable. Owing to its ability to capture real-world parameters, the utilization of the proposed RO methodology in the mining industry is expected to increase in future. In terms of future development, the valuation method could be further enhanced to combine additional uncertainties, project valuation, and stages of investment. The outcome parameter in cash flow in terms of mining expenditure may present an additional application of the proposed methodology.