Infrared Spectroscopy and Excess Conductivity Analysis for (Y₃Fe₅O₁₂)_x/Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ Composites

Abstract

In this study, the influence of adding Yttrium iron garnet (Y₃Fe₅O₁₂) nanoparticles (NPs) on the microstructure and fluctuation-induced conductivity (FIC) of Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ (CuTl-1223) superconductor was studied. Y₃Fe₅O₁₂ NPs were produced by the co-precipitation technique. By solid state route, (Y₃Fe₅O₁₂)_x/Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ composites, with x = 0.00, 0.02, 0.04, 0.06, 0.08, and 0.10 wt. % were prepared. The tetragonal unit cell parameters of (Y₃Fe₅O₁₂)_x/Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ composites were found to be invariable with Y₃Fe₅O₁₂ content. The volume fraction of the host phase was increased with Y₃Fe₅O₁₂ addition till x = 0.04 wt. %. The different vibrational modes of the samples were identified through Fourier transform infrared spectroscopy (FTIR). The transition from normal to the superconducting state, for the prepared composites, was done through d.c resistivity measurements from room temperature down to zero critical temperature (T₀). The Aslamazov–Larkin (AL) model was used to examine fluctuation regions in resistivity-temperature curves. At high temperatures, short wave fluctuation was observed. A cross-over between short wave fluctuation and the mean-field region was spotted at lower temperatures. The mean field region for the examined composites was composed of two-dimensional fluctuations along with one-dimensional fluctuation. The coherence length along the c-axis ζ_c(0), interlayer coupling (J), and anisotropy parameter (γ) were estimated from the Lawrence–Doniach (LD) model as a function of Y₃Fe₅O₁₂ content.

1 Introduction

From an application point of view, intergrain connections and vortex pinning play a major role in enhancing the superconducting critical parameters (i.e., superconducting transition temperature T_c, critical current density J_c, critical magnetic field, H_c) of high-temperature superconductors (HTSCs). As a consequence, it is vital to enhance intergrain connectivity and develop additional efficient pinning centers in the synthesized HTSCs.

Numerous approaches have been explored to solve this matter, but one of the most straightforward and effective is the insertion of appropriate nanosized structures in bulk HTSCs. This technique, known as chemical pinning, has certain advantages including a less complicated preparation procedure, high thermal stability, and cheap costs. The superconductor may include these nanoscale materials as required, and the pinning effect is much greater as a result. However, finding chemically inert materials that don't react with the superconducting phases is in fact a difficult task.

It was found that the addition of ZnFe₂O₄ nanoparticles increased the onset critical temperature T_c(0) and critical current density (J_c) of GdBa₂Cu₃O₇ superconductor [1]. Sauzlina et al. [2] reported that the addition of Y₂O₃ nanoparticles up to 0.7 wt. % improved the superconducting properties of the Bi_1.6Pb_0.4Sr₂CaCu₂O_y phase. Improvements in microstructure and superconducting parameters were reported for the CuTl-1223 phase added with Fe₂O₃ nanoparticles [3]. The inclusion of BaSnO₃ nanoparticles in the CuTl-1223 matrix was found to enhance its superconductor properties such as relative volume fraction, T_c(0), and J_c [4]. Tiny contents of Zn_0.91Mn_0.03Co_0.06O (x = 0.02 wt. %) in the CuTl-1223 phase [5] have enhanced the intergrain connectivity by healing microcracks, improved the phase percentage, increased the critical temperature and ac conductivity (σ_ac). Mumtaz et al. [6] found that the addition of Zn nanoparticles led to enhance the infield superconducting properties, improved carrier’s density to the optimal level, increased coherence length along the c-axis (ξ_c), and suppressed the anisotropy parameter (γ) of CuTl-1223 phase. Imran et al. [7] reported that the crystal structure of the bulk CuTl-1223 superconducting phase did not change with the inclusion of Co₃O₄ nanoparticles.

Following the review above, the most plausible candidates for use as artificial pinning centers in Cuprate CuTl-1223 superconductor are chemically inert nano-materials with low concentrations. The main aspect of choosing the CuTl-1223 superconductor is its low-cost ambient fabrication conditions, particularly pressure, as well as excellent critical parameter values. The Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ phase is among the most favourable phases in Cu_0.5Tl_0.5Ba₂Ca_n-1Cu_nO_2n+4-δ (n = 2, 3, etc.) superconducting group, with a comparatively high J_c (> 10⁵ A/cm²), high superconducting transition temperature T_c (T_c ~ 106–132 K), long coherence length along the c-axis (ζ_c), and low superconducting anisotropy (γ = ζ_ab/ζ_c) [8]. All the superior characteristics mentioned for the CuTl-1223 phase make it promising for many practical applications, especially for cables, coils, and tape usage.

High-temperature superconductors are used in a variety of highly precise and dependable high-technology applications, including in vivo live body measurements in medicine, terahertz equipment for security systems, quantum bit applications in quantum computers, and bolometers for some types of space research. In addition, high-temperature superconductors have been consistently used in magnetic resonance imaging (MRI), magnetic resonance spectroscopy (MRS), magneto encephalography (MEG), and magnetocardiography (MCG) for analyzing the magnetic activity of various human body regions, such as the brain and heart wave activities, as well as for the early diagnosis of a number of diseases [6, 8].

Y₃Fe₅O₁₂ is a versatile garnet ferrite with unique electromagnetic properties [9]. Y₃Fe₅O₁₂ is a ferrimagnetic material with a cubic structure. Each unit cell consists of eight chemical formula units. Chemically Yttrium Iron garnet can be represented as Y₃Fe₂Fe₃O₁₂ where Y³⁺ ‏ions occupy 24 sites, Fe³⁺‏ ions occupy 40 sites, and O²⁻ ions occupy 96 sites [10]. There are three crystallographic lattice sites labelled a, c, and d that are surrounded by O octahedron, dodecahedron, and tetrahedron, respectively. The c sites are occupied by Y³⁺ ions, and the magnetic Fe³⁺ ions occupy both the a and d sites, while oxygen ions are distributed at the interstitial sites [11]. The ferrimagnetic behaviour of Y₃Fe₅O₁₂ is primarily due to the opposite spin orientation of Fe³⁺ ions at the a and d sites [12].

In this study, further investigations on the Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ superconducting phase were done by adding proper contents of Y₃Fe₅O₁₂ NPs to it. Moreover, the main drawback of the ambient pressure synthesis of the CuTl-1223 phase is the existence of voids and holes in increased density, which affects total superconducting critical parameters. Furthermore, a significant improvement in CuTl-1223 superconducting characteristics can be attained when crucial factors including the size, shape, and orientation of the added Y₃Fe₅O₁₂ NPs are carefully adjusted. As a consequence, this study is targeting the ability of Y₃Fe₅O₁₂ NPs to act as intergrain connectivity/pinning center enhancers in the CuTl-1223 matrix. The effect of adding Y₃Fe₅O₁₂ NPs on the microstructure and fluctuation-induced conductivity (FIC) of Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ phase was studied in detail. Numerous important superconducting parameters, such as fluctuation dimensionality, coherence length along c-axis ζ_c(0), interlayer coupling (J), and anisotropy parameter (γ) were deduced from the excess conductivity data as a function of Y₃Fe₅O₁₂ NP addition.

2 Materials and Method

2.1 Y₃Fe₅O₁₂ Preparation

The co-precipitation method was used to synthesize Y₃Fe₅O₁₂ from YCl₃.6H₂O and FeCl₃.6H₂O as starting materials. The powder was of high purity and purchased from Sigma-Aldrich. In 100 ml of pure water, the powders in the stoichiometric ratio of Y: Fe → 3:5 were dissolved. NaOH of molarity 5 M was added to the solution dropwise with magnetic stirring until the pH reached 12. The solution is then heated at 80 °C for 4 h while being continuously stirred. The samples were then washed until the pH reached 7, as measured by a digital pH meter. The samples were then dried for 18 h at 100 °C. Finally, these samples were calcined at 1050 °C for 2 h.

2.2 Y₃Fe₅O₁₂/CuTl-1223 Preparation

Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ superconducting samples were prepared at ambient pressure using a solid-state reaction method. In their nominal compositions, high-grade starting materials of Tl₂O₃, BaO₂, CaO, and CuO were crushed and sifted through a 65 μm sieve. To obtain (Y₃Fe₅O₁₂)_x/Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ composites, Y₃Fe₅O₁₂ nanoparticles (particle size 50–80 nm) with weight percent 0.00, 0.02, 0.04, 0.06, 0.08 and 0.10 wt. % were added to the sifted powder then mixed and crushed to ensure homogeneity. To reduce Tl loss during the heating procedure, the powder was compressed into a disc and then wrapped in a silver sheet. The samples were sintered in a sealed quartz tube at a rate of 2 °C/min to 760 °C, then at a rate of 1 °C/min to 850 °C, and finally held at this temperature for 6 h. At the end of this step, the samples were slowly cooled to room temperature.

2.3 Characterization and Measurements

For Y₃Fe₅O₁₂ nanoparticles; structural characterization was achieved using x-ray powder diffraction (XRD) technique with XRD-D2 phaser Bruker CuKα radiation (λ = 1.5406 Å) in the range of 10° ≤ 2θ ≤ 80°. Transmission electron microscope (TEM) model JEOL JEM 1400 Plus was used to observe particle size and sample morphology.

(Y₃Fe₅O₁₂)_x/CuTl-1223 (x = 0.02, 0.04, 0.06, 0.08 and 0.10 wt.%) composites were identified using Shimadzu-7000 XRD with CuKα radiation (λ = 1.5418 Å) in 2θ range of 10°–70°. JEOL scanning electron microscope model JSM-IT200 was utilized to study the sample morphology. The device operated at a high voltage of 20 kV, at which low pressure was attained using a rotary pump. The electron source was at a distance of 15 mm from the surface of the sample. The value of magnification at which the pictures were taken is 5000. The different modes of vibration were investigated using Fourier transform infrared spectrometer model SHIMADZU-8400S. The electrical resistivity of the prepared composites was measured using the traditional four-point probe procedure from room temperature down to T₀ using a closed cryogenic cooling system (Displex).

3 Results and Discussion

3.1 XRD and TEM of Y₃Fe₅O₁₂

Figure 1a and b display the XRD pattern and TEM micrograph for Y₃Fe₅O₁₂ nanoparticles, respectively. XRD pattern has affirmed that all peaks are properly indexed with the cubic structure of Y₃Fe₅O₁₂ with space group la-3d (standard sheet number ICDD: 43–0507) [13]. The relevant peaks for garnet structure (400), (420), and (422) are sharply reflected. Spherical grains were observed from the TEM micrograph with an average particle size of ~ 50–80 nm, as shown in Fig. 1b.

Fig. 1

a XRD pattern of Y3Fe5O12 NPs and b TEM micrograph AQof Y3Fe5O12 NPs

Fig. 2

a XRD patterns for (Y3Fe5O12)x/ Cu0.5Tl0.5Ba2Ca2Cu3O10-δ with x = 0.00, 0.02, 0.04, 0.06, 0.08, and 0.10 wt. %. b SEM micrographs of (Y3Fe5O12)x/Cu0.5Tl0.5Ba2Ca2Cu3O10-δ with x = 0.00 and x = 0.04

3.2 XRD and SEM of (Y₃Fe₅O₁₂)_x/CuTl-1223

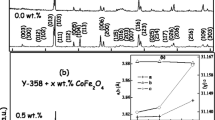
Figure 2a displays XRD patterns for (Y₃Fe₅O₁₂)_x/Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ with x = 0.00, 0.02, 0.04, 0.06, 0.08, and 0.10 wt.%. The (hkl) indices of most diffraction peaks clarify that the prepared samples possess a tetragonal structure with P4/mmm symmetry [14]. The small diffraction peaks marked by asterisk and number sign assign the presence of CuTl-1212 and BaCuO₂ phases. No peaks were reflected for Yttrium or iron-based compounds. Thus, the tetragonal structure of the CuTl-1223 phase is not influenced by Y₃Fe₅O₁₂ addition as these NPs will prefer to enter interstitial places and will not enter the structure of the host phase. The relative volume fraction percentages for CuTl-1223, CuTl-1212, and BaCuO₂ phases are determined as follows:

$$\begin{array}{c}\mathbf{C}\mathbf{u}\mathbf{T}\mathbf{l}-1223\mathbf{\%}=\frac{{\varvec{\Sigma}}\mathbf{I}\left(\mathbf{C}\mathbf{u}\mathbf{T}\mathbf{l}-1223\right)}{{\varvec{\Sigma}}\mathbf{I}\left(\mathbf{C}\mathbf{u}\mathbf{T}\mathbf{l}-1223\right)+{\varvec{\Sigma}}\mathbf{I}\left(\mathbf{C}\mathbf{u}\mathbf{T}\mathbf{l}-1212\right)+{\varvec{\Sigma}}\mathbf{I}\left(\mathbf{B}\mathbf{a}\mathbf{C}\mathbf{u}\mathbf{O}2\right)}\times 100\\ \mathbf{C}\mathbf{u}\mathbf{T}\mathbf{l}-1212\mathbf{\%}=\frac{{\varvec{\Sigma}}\mathbf{I}\left(\mathbf{C}\mathbf{u}\mathbf{T}\mathbf{l}-1212\right)}{{\varvec{\Sigma}}\mathbf{I}\left(\mathbf{C}\mathbf{u}\mathbf{T}\mathbf{l}-1223\right)+{\varvec{\Sigma}}\mathbf{I}\left(\mathbf{C}\mathbf{u}\mathbf{T}\mathbf{l}-1212\right)+{\varvec{\Sigma}}\mathbf{I}\left(\mathbf{B}\mathbf{a}\mathbf{C}\mathbf{u}{\mathbf{O}}_{2}\right)}\times 100\\ \mathbf{B}\mathbf{a}\mathbf{C}\mathbf{u}{\mathbf{O}}_{2}\mathbf{\%}=\frac{{\varvec{\Sigma}}\mathbf{I}(\mathbf{B}\mathbf{a}\mathbf{C}\mathbf{u}{\mathbf{O}}_{2})}{{\varvec{\Sigma}}\mathbf{I}\left(\mathbf{C}\mathbf{u}\mathbf{T}\mathbf{l}-1223\right)+{\varvec{\Sigma}}\mathbf{I}\left(\mathbf{C}\mathbf{u}\mathbf{T}\mathbf{l}-1212\right)+{\varvec{\Sigma}}\mathbf{I}\left(\mathbf{B}\mathbf{a}\mathbf{C}\mathbf{u}{\mathbf{O}}_{2}\right)}\times 100,\end{array}$$

(1)

where ƩI is the summation of the diffraction peaks intensities [15]. Table 1 shows the relative volume fraction percentages for (Y₃Fe₅O₁₂)_x/Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ with x = 0.00, 0.02, 0.04, 0.06, 0.08 and 0.10 wt.%. The volume fraction percentage of the CuTl-1223 phase increases from 87.9 to 91.4% when the Y₃Fe₅O₁₂ NPs is adjusted from 0.00 to 0.04 wt. %. Higher Y₃Fe₅O₁₂ addition contents, x > 0.04 wt. %, cause a delay in the main CuTl-1223 phase percentage and enhance CuTl-1212 and BaCuO₂ phases percentages. Similar results were reported for the addition of Al₂O₃ and MgO NPs to the Bi-2223 phase [16, 17]. The decrease in volume fraction for higher Y₃Fe₅O₁₂ NP additions can be attributed to many reasons such as the ability of these NPs to delay the phase growth to a certain limit and to the ferrimagnetic nature of Y₃Fe₅O₁₂ NPs, which will cause Cooper pairs damage. The tetragonal unit cell parameters (a) and (c) were estimated, and their values are shown in Table 1. Nearly invariable tetragonal unit cell parameters were seen after the addition of Y₃Fe₅O₁₂ NPs to the host CuTl-1223 phase. This suggests that the low concentration of the added NPs is insufficient to cause any change in the unit cell of the host phase. Furthermore, this demonstrates that Y₃Fe₅O₁₂ NPs will prefer to occupy interstitial spaces between the grains. Similar results were observed for the Bi-2223 phase [18, 19] added with NiFe₂O₄ and NiO NPs, respectively.

Table 1 Variation of volume fraction and unit cell parameters of (Y₃Fe₅O₁₂)_x/Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ with x = 0.00, 0.02, 0.04, 0.06, 0.08 and 0.10 wt.%

SEM micrographs of (Y₃Fe₅O₁₂)_x/Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ composites with x = 0.00 and 0.04 wt.% were used to examine the morphology, as shown in Fig. 2b. Solid-state diffusional phase transformation, which includes nucleation, growth, and impingement, is directly responsible for the arrangements of constituent composites, which include a specific volume fraction of spatially distributed phases with various compositions, grain size, and morphology with random orientation, and their spatial distribution. The CuTl-1223 phase formation was confirmed from the observed plate-like grains. Some irregular-shaped grains were assigned for impurity phases such as CuTl-1212 and BaCuO₂. Furthermore, even after high-temperature sintering, there are fine spherical grains that may indicate the presence of Y₃Fe₅O₁₂ nanoparticles in the CuTl-1223 matrix. Also, the micrograph for x = 0.04 wt.% showed apparent suppression in the intergrain voids and improvement in the intergrain weak links that can be visualized in comparison with the pure sample.

3.3 FTIR of (Y₃Fe₅O₁₂)_x/CuTl-1223

FTIR is used to indicate the molecular bonding process in the sample. Moreover, the various oxygen vibrational phonon modes, which play an important role in superconductivity, may be seen via FTIR spectroscopy. Figure 3 depicts room temperature FTIR spectra for the Pure sample and the inset shows the grouped spectra for (Y₃Fe₅O₁₂)_x/Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ with x = 0.00, 0.04, 0.06, 0.08, and 0.10 wt. % in the 400 to 4000 cm⁻¹ range. Apical oxygen atoms and CuO₂ planar oxygen atoms of the prepared samples appeared in wavenumber ranges from 400 to 540 cm⁻¹ and from 541 to 600 cm⁻¹, respectively. Peaks in the 670 to 700 cm⁻¹ range are caused by O_δ atoms in the charge reservoir layer. It is clear that the inclusion of Y₃Fe₅O₁₂ NPs causes a minor shift in the apical modes of CuTl-1223 superconductors, which may be related to the impact of stresses and strains induced in the superconductor matrix on the bond lengths [20]. The existence of a peak at 3778.94 cm⁻¹ and a particular peak at 3485.85 cm⁻¹ corresponds to the stretching vibration of the intermolecular hydrogen bond (O–H), showing that the OH groups are basically stretched [21, 22]. The emergence of a peak at 1617.76 cm⁻¹ confirms the complicated creation of the CuTl-1223 phase, as previously reported [23]. The existence of two consecutive peaks at 1055.26 cm⁻¹ and 1421.38 cm⁻¹ verifies the bond stretching of other metal oxides and carbonates such as CaCo₃, and CuO [23]. The findings of FTIR and XRD confirm that no changes in the structure of the host CuTl-1223 superconductor occur following the addition of Y₃Fe₅O₁₂ NPs. These investigations demonstrate that Y₃Fe₅O₁₂ nanoparticles do not break down or substitute any lattice site in the unit cell of CuTl-1223, but instead reside at grain boundaries.

Fig. 3

FTIR spectra for pure sample. The inset shows FTIR data for (Y₃Fe₅O₁₂)_x/Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ with x = 0.00, 0.04, 0.06, 0.08 and 0.10 wt.%

3.4 Electrical Resistivity of (Y₃Fe₅O₁₂)_x/CuTl-1223

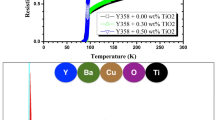
Figure 4 shows the variation of d.c resistivity (ρ) with temperature (T) for (Y₃Fe₅O₁₂)_x/ Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ with x = 0.00,0.02, 0.04, 0.06, 0.08 and 0.10 wt.%. All the samples show a linear ρ-T relationship in the normal state region that starts from room temperature down to the onset critical temperature T_c(0), where T_c(0) was determined as the peak point in dρ/dT versus T curves. At T_c(0) there is a transition from normal to superconducting state and the samples completely lose their resistivity (ρ = 0) at a temperature equal to the zero critical temperature (T₀). The change in T_c(0) with Y₃Fe₅O₁₂ NPs for (Y₃Fe₅O₁₂)_x/ Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ samples is shown in the inset of Fig. 4. T_c(0) rises initially up to x = 0.04 wt. % then falls for additions greater than 0.04 wt. %. The rise in T_c(0) might be attributed to the higher volume fraction of the host CuTl-1223 phase at low Y₃Fe₅O₁₂ contents ( x ≤ 0.04 wt. %). Typically, T_c(0) of cuprates is controlled by the density of the carriers in their CuO₂ planes [24]. The carriers supplied to CuO₂ planes by the charge reservoir layer are determined by the oxygen content of the charge reservoir layer [25]. With the inclusion of these nanoparticles, T_c(0) rises, perhaps owing to optimizing carrier concentration in the CuO₂ planes provided by the charge reservoir layer. The decreasing trend in T_c(0) after a certain optimum limit of these NPs addition (x > 0.04 wt. %) may be due to their aggregation and segregation at the grain boundaries in the CuTl-1223 matrix, which can cause the samples’ quality to degrade and the superconducting volume fraction to decrease [26, 27]. Table 2 lists the values of room temperature resistivity ρ_room with x. The increase of ρ_room with Y₃Fe₅O₁₂ addition may strongly depend on impurities and crystal defects scattering by the charge carriers in the CuO₂ plane.

Fig. 4

Variation of d.c resistivity (ρ) with temperature (T) for (Y₃Fe₅O₁₂)_x/ Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ with x = 0.00,0.02, 0.04, 0.06, 0.08 and 0.10 wt.%. The inset shows the variation of T_c(0) with x

Table 2 Resistivity at room temperature, residual resistivity and resistivity temperature coefficient of (Y₃Fe₅O₁₂)_x/Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ with x = 0.00, 0.02, 0.04, 0.06, 0.08, and 0.10 wt.%

3.5 Excess Conductivity of (Y₃Fe₅O₁₂)_x/CuTl-1223

The fluctuation-induced conductivity (FIC) behaviour can have a significant impact on the superconducting characteristics [28]. At high temperatures (above T_c(0)), the fluctuation comprises the divergence of the electrical resistivity from the linear metallic normal state behaviour. Superconducting fluctuation, which is formed as a result of Cooper pair production, is thought to initiate the excess conductivity area [29]. FIC may be used to calculate the dimensionality of the superconducting fluctuation and the coherence length [30]. Because of the short ζ_c(0), a strong fluctuation may be seen in the cuprates. Because of the rapid rise in conductivity caused by superconducting oscillations, the resistivity curve might deviate slightly above the critical temperature [31]. The superconducting fluctuations may be analyzed using Aslamazov–Larkin (AL) [32, 33] model, Lawrence–Doniach (LD) model, and Maki–Thomson [34,35,36] model. Excess conductivity ($\Delta\upsigma )$ is determined as follows;

$$\Delta {\varvec{\upsigma}}={{\varvec{\upsigma}}}_{\mathbf{m}}(\mathbf{T})-{{\varvec{\upsigma}}}_{\mathbf{n}}(\mathbf{T})=\frac{{{\varvec{\uprho}}}_{\mathbf{n}}\left(\mathbf{T}\right)-{{\varvec{\uprho}}}_{\mathbf{m}}(\mathbf{T})}{{{\varvec{\uprho}}}_{\mathbf{m}}(\mathbf{T}){{\varvec{\uprho}}}_{\mathbf{n}}(\mathbf{T})}$$

(2)

where σ_m (T) and ${\upsigma }_{\mathrm{n}}\left(\mathrm{T}\right)$ are the measured and normal state conductivities, respectively.

The normal state resistivity ρ_n (T) is calculated in a temperature range of 170 K ≤ T ≤ 300 K using the following relation [37]

$${\uprho }_{\mathrm{n}}\left(\mathrm{T}\right)={\uprho }_{0}+\mathrm{\beta T},$$

(3)

where ρ₀ and β are the residual resistivity due to impurity scattering and the temperature resistivity coefficient, respectively. The values of ρ₀ and β are listed in Table 2 with x. The residual resistivity ρ₀ was found to increase with x which is attributed to the increase in impurity scattering in the CuO₂ plane and localization of carriers across these magnetic nanoparticles.

Excess conductivity may be represented using the AL model [32] as follows:

$$\frac{\Delta {\varvec{\upsigma}}}{{{\varvec{\upsigma}}}_{\mathbf{r}\mathbf{o}\mathbf{o}\mathbf{m}}}=\mathbf{A}{\mathbf{t}}^{{\varvec{\upalpha}}}\boldsymbol{ },$$

(4)

where σ_room is the conductivity at 300 K (1/ρ_room) and t is the reduced temperature $\mathbf{t}=\frac{\mathbf{T}-{\mathbf{T}}_{\mathbf{c}}}{{\mathbf{T}}_{\mathbf{c}}}$.

The conductivity exponent α in Eq. (4) is related to the conduction dimensionality D by the following relations:

$${\varvec{\upalpha}}=\left\{\begin{array}{c}-0.3, cr \\ -0.5, 3D \\ -1.0, 2D \\ -1.5, 1D \\ -3.0, SW\end{array}\right.$$

(5)

where cr, 3D, 2D, 1D, and SW denoted the dynamic critical, three-dimensional, two-dimensional, one-dimensional, and short wave fluctuations, respectively. The temperature independent amplitude A in Eq. (4) is given by [38]:

$$\mathrm{A}=\left\{\begin{array}{c}\frac{{\mathrm{e}}^{2}}{32\mathrm{ \hslash }{\xi }_{\mathrm{c}}\left(0\right)}, 3D region\\ \frac{{\mathrm{e}}^{2}}{16\mathrm{ \hslash d}}, 2D region\\ \frac{{e}^{2}{\xi }_{\mathrm{c}}\left(0\right)}{32 \hslash s}, 1D region\end{array},\right.$$

(6)

where ξ_c(0) is the coherence length along the c-axis at T = 0 K, d is the effective layer thickness of 2D systems usually equal to the c-axis length of the unit cell and s is the cross-sectional area of 1D system. The LD model introduces the idea of interlayer coupling, J, which is based on Josephson coupling as a result of ${\xi }_{\mathrm{c}}\left(0\right)$ contact with the superconducting layers. The relation between ${\xi }_{\mathrm{c}}\left(0\right)$ and interlayer coupling, J is given by [39]:

$$J={\left[\frac{{2\xi }_{\mathrm{c}}\left(0\right)}{d}\right]}^{2}.$$

(7)

The anisotropy, γ of layered superconducting systems is estimated from [40]

$$\gamma = \frac{{\xi }_{\mathrm{ab}}\left(0\right)}{{\xi }_{\mathrm{c}}\left(0\right)} ,$$

(8)

where ${\xi }_{\mathrm{ab}}\left(0\right)$ is the ab coherence length which is generally between 10 Å and 20 Å for HTSC [41].

Plots of ln Δσ/σ_room against ln t for (Y₃Fe₅O₁₂)_x/ Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ with x = 0.00,0.02, 0.04, and 0.10 wt.% are shown in Fig. 5a–d. The plots show different fluctuation regions. The conductivity exponent values were estimated by fitting the data according to Eq. (4) at each region. Three primary fluctuating regions are observed for 2D, 1D, and SW fluctuations. Table 3 lists the conductivity exponent values (α_2D, α_1D, and α_SW) and crossover temperatures (T_2D-1D and T_1D-SW) for the observed regions. The region that occurs at high temperatures denotes the termination of the Ginzburg–Landau (GL) approach and the dominance of SW fluctuations [42]. In this temperature range, ln Δσ/σ_room decreases rapidly, with an exponent α_SW ranging between 2.63 and 3.74, which corresponded extremely well with theoretical expectations. Because there are changes in ρ_n, T_c and therefore in the oxygen content of the current samples, structural band fluctuations in the Fermi surface may be accountable for SW behaviour [43]. When the temperature is reduced, a shift from SW fluctuations to the mean-field regime (MFR) occurs at T_{1D- SW}. The MFR for various produced composites consists of two separate linear components. The conductivity exponent α_1D values range from 1.99 to 1.67 in the first portion at temperatures ranging between T_1D-SW and T_{2D- 1D}, indicating the presence of 1D fluctuations and hence the existence of 1D conduction channels. The existence of 1D fluctuation region arises in CuTl-1223 due to the presence of conducting charge stripes [44].

Fig. 5

Plots of lnΔσ/σ_room against ln t of (Y₃Fe₅O₁₂)_x/ Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ with a x = 0.00, b 0.02, c 0.04, and d 0.10 wt.%

Table 3 Conductivity exponent, crossover temperatures, coherence length, interlayer coupling and anisotropy parameter of (Y₃Fe₅O₁₂)_x/Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ with x = 0.00, 0.02, 0.04 and 0.10 wt. %

Just below T_{2D -1D}, the values of the conductivity exponent are varying from 0.92 to 0.99, implying the presence of 2D fluctuations. The mobility of the carriers in the conducting CuO₂ planes indicates the conductivity in the 2D fluctuating area, due to the layered structure of HTSCs materials [45].

Coherence length along the c-axis at T = 0 K $\left({\xi }_{\mathrm{c}}\left(0\right)\right)$, interlayer coupling (J) and anisotropy parameter (γ) values are estimated according to Eqs. (6)–(7) and are listed in Table 3 with x. It can be seen that ${\xi }_{\mathrm{c}}\left(0\right)$ decreases as x increases from 0.00 to 0.10 wt. % for (Y₃Fe₅O₁₂)_x/ Cu_0.5Tl_0.5Ba₂Ca₂Cu₃O_10-δ samples. Khurram et al. [46] reported a lower value of ${\xi }_{\mathrm{c}}\left(0\right)$ for pure sample $({\xi }_{\mathrm{c}}\left(0\right)$= 10 Å) than our reported value ${\xi }_{c}\left(0\right)=6$Å. All the values of interlayer coupling J are less than one, indicating a weak coupling between the CuO₂-planes. Also, J decreases as the Y₃Fe₅O₁₂ content increases. At x = 0.10 wt. %, the shortest ${\xi }_{\mathrm{c}}\left(0\right)$ was estimated as 2.45 Å. This sample also has the lowest J value (0.082) as well as the greatest anisotropy (4.07). As a result, Y₃Fe₅O₁₂ inclusions reduced ${\xi }_{\mathrm{c}}\left(0\right)$, increased the anisotropy of the samples and decreased the interlayer coupling strength.

4 Conclusions

In this study, the advantages and disadvantages of adding Y₃Fe₅O₁₂ NPs to the microstructure and superconducting properties of the CuTl-1223 superconductor were presented and interpreted. Selected amounts of Y₃Fe₅O₁₂ NPs were implemented into the CuTl-1223 matrix through solid-state reaction method. From XRD and FTIR results, it was concluded that Y₃Fe₅O₁₂ was a chemically inert material that did not react with the CuTl-1223 superconducting phase. The optimum content of Y₃Fe₅O₁₂ (x = 0.04 wt. %) has a significant effect on improving the microstructure and the superconductivity of the CuTl-1223 phase. The microstructure was enhanced by filling gaps created by the inclusion of Y₃Fe₅O₁₂ nanoparticles at the grain boundaries of the CuTl-1223 matrix. The onset critical temperature T_c(0) increased from 106 K to 119.5 K by raising the concentration of Y₃Fe₅O₁₂ NPs from 0.00 to 0.04 wt. %. This increase in T_c(0) was attributed to the ability of Y₃Fe₅O₁₂ NPs to act as an effective chemical pinning center. On the other hand, the retardation in superconductivity and microscopic parameters were drawbacks of adding large concentrations of Y₃Fe₅O₁₂ NPs (x > 0.04 wt. %) to the CuTl-1223 matrix. The superconducting microscopic parameters determined by FIC analysis showed a reduced ${\xi }_{\mathrm{c}}\left(0\right)$, increased anisotropy and decreased interlayer coupling strength. These disadvantages happened due to the agglomeration and segregation of Y₃Fe₅O₁₂ NPs at the grain boundaries of the CuTl-1223 matrix.