Propagation and Collision Phenomena of Ion Acoustic ZK Solitons in Quantum Plasmas: Effects of External Force and Exchange–Correlation Potential of Degenerate Electrons

Abstract

Propagation of ion acoustic waves (IAWs) and collision of double-, triple-, and quadruple IAWs have been studied in a magnetized plasma system consisting of cold ions and degenerate electrons. It is considered that the ions are inertial and non-degenerate while the electrons are degenerate and non-inertial. The reductive perturbation method is used to derive the Zakharov-Kuznetsov (ZK) equation. The multi-soliton solutions of the ZK equation are derived using the Hirota bilinear method. The consequences of external periodic force and exchange–correlation potential on the propagation and overtaking collision of ion acoustic (IA) ZK solitons are investigated taking into account the plasma parameters as observed in astrophysical objects. The considered quantum fluid model is valid for astrophysical conditions in non-relativistic degenerate plasmas where the plasma density and magnetic field strength are ${10}^{26}\le {{\varvec{n}}}_{0}\le {10}^{29}{\mathbf{c}\mathbf{m}}^{-3}$ and ${10}^{6}\le {{\varvec{B}}}_{0}\le {10}^{9}$ G, respectively. It is found that the amplitude and width of the IAZK solitons are modified due to the periodic force and exchange–correlation potential. It is also found that the large-amplitude solitons always overtake the smaller one.

Appendices

Appendix A

In absence of external periodic force, the standard solution of ZK equation (Eq. (37)) is

$${\varvec{\uppsi}}={{\varvec{\uppsi}}}_{{\varvec{m}}}{\mathbf{s}\mathbf{e}\mathbf{c}\mathbf{h}}^{2}\left(\frac{{\varvec{\chi}}}{{{\varvec{W}}}_{{\varvec{m}}}}\right),$$

(42)

where ${\varvec{\chi}}={\varvec{\xi}}{\varvec{l}}+{\varvec{\eta}}{\varvec{m}}-{\varvec{V}}{\varvec{\tau}}$, V is the constant velocity of IA wave, normalized by thermal ion acoustic speed, ${{\varvec{c}}}_{{\varvec{s}}{\varvec{i}}}$; ${\varvec{l}}$ and ${\varvec{m}}$ are the direction cosines along the x- and y-axis, respectively, and ${{\varvec{l}}}^{2}+{{\varvec{m}}}^{2}=1$. ${{\varvec{W}}}_{{\varvec{m}}}$ is the width of IA soliton and ${{\varvec{\Psi}}}_{{\varvec{m}}}$ is the amplitude of IA soliton which are defined as

$${{\varvec{\uppsi}}}_{{\varvec{m}}}=\frac{3{\varvec{V}}}{{\varvec{L}}{\varvec{l}}}\,{\mathrm{and}}\,{{\varvec{W}}}_{{\varvec{m}}}=\sqrt{\frac{4\left({\varvec{M}}{\varvec{m}}+{\varvec{N}}\right)}{{\varvec{V}}}}$$

(43)

It is evident that ${{\varvec{\Psi}}}_{{\varvec{m}}}$ and ${{\varvec{W}}}_{{\varvec{m}}}$ depend on the force potential applied in the concerned system. Therefore, for approximate solution, they can be related as follows

$${\varvec{\uppsi}}={{\varvec{\uppsi}}}_{{\varvec{m}}}\left({\varvec{\tau}}\right){\mathbf{s}\mathbf{e}\mathbf{c}\mathbf{h}}^{2}\left(\frac{\stackrel{\sim }{{\varvec{\chi}}}}{{{\varvec{W}}}_{{\varvec{m}}}\left({\varvec{\tau}}\right)}\right),$$

(44)

where $\stackrel{\sim }{{\varvec{\chi}}}={\varvec{\xi}}{\varvec{l}}+{\varvec{\eta}}{\varvec{m}}-{\varvec{V}}\left({\varvec{\tau}}\right){\varvec{\tau}}$. In absence of external periodic force in the plasma system, ${\varvec{I}}={\int }_{-\boldsymbol{\infty }}^{+\boldsymbol{\infty }}{{\varvec{\uppsi}}}^{2}{\varvec{d}}{\varvec{\xi}}$ is a conserved quantity for the ZK equation. To investigate, the considerable influence of the external periodic force ${{\varvec{F}}}_{0}{\varvec{c}}{\varvec{o}}{\varvec{s}}\left(\boldsymbol{\varpi }{\varvec{\tau}}\right)$ on the propagation of IA wave is introduced. In the present state, due to the influence of periodic force, one can evaluate

$${\varvec{I}}={\int }_{-\boldsymbol{\infty }}^{+\boldsymbol{\infty }}{{\varvec{\uppsi}}}^{2}{\varvec{d}}{\varvec{\xi}},$$

(45)

and obtain, ${\varvec{I}}=\frac{4}{3}{{\varvec{\uppsi}}}_{{\varvec{m}}}^{2}\left({\varvec{\tau}}\right){{\varvec{W}}}_{{\varvec{m}}}\left({\varvec{\tau}}\right)$. Hence,

$${\varvec{I}}=24\frac{\sqrt{\left({\varvec{M}}{\varvec{m}}+{\varvec{N}}\right)}}{{{\varvec{L}}}^{2}}{{\varvec{V}}\left({\varvec{\tau}}\right)}^{3/2}.$$

(46)

Differentiating (45) w. r. to ${\varvec{\tau}}$, one can find

$$\frac{{\varvec{d}}{\varvec{I}}}{{\varvec{d}}{\varvec{\tau}}}=24\frac{\sqrt{\left({\varvec{M}}{\varvec{m}}+{\varvec{N}}\right)}}{{\varvec{L}}}{{\varvec{F}}}_{0}{{\varvec{V}}\left({\varvec{\tau}}\right)}^{1/2}\mathbf{c}\mathbf{o}\mathbf{s}\left(\boldsymbol{\varpi }{\varvec{\tau}}\right).$$

(47)

Again differentiating (46) w. r. to ${\varvec{\tau}}$, one can determine that

$$\frac{{\varvec{d}}{\varvec{I}}}{{\varvec{d}}{\varvec{\tau}}}=36\frac{\sqrt{\left({\varvec{M}}{\varvec{m}}+{\varvec{N}}\right)}}{{{\varvec{L}}}^{2}}{{\varvec{V}}\left({\varvec{\tau}}\right)}^{1/2}\boldsymbol{ },$$

(48)

Comparing (47) and (48), it is obtained that

$$\frac{{\varvec{d}}{\varvec{V}}\left({\varvec{\tau}}\right)}{{\varvec{d}}{\varvec{\tau}}}=\frac{2{\varvec{L}}}{3}{{\varvec{F}}}_{0}\mathbf{c}\mathbf{o}\mathbf{s}\left(\boldsymbol{\varpi }{\varvec{\tau}}\right),$$

(49)

and by integrating (49), one can find

$${\varvec{V}}\left({\varvec{\tau}}\right)=\frac{2{\varvec{L}}}{3\boldsymbol{\varpi }}{{\varvec{F}}}_{0}\mathbf{s}\mathbf{i}\mathbf{n}\left(\boldsymbol{\varpi }{\varvec{\tau}}\right)+{{\varvec{V}}}_{0}.$$

(50)

where ${\varvec{\tau}}=0$, ${\varvec{V}}\left({\varvec{\tau}}\right)={{\varvec{V}}}_{0}$, and ${\varvec{V}}\left({\varvec{\tau}}\right)$ is the time-dependent velocity of IA wave propagating in the concerned plasma system. Therefore, the time-depending solution of the FZK equation can be expressed as:

$${\varvec{\uppsi}}={{\varvec{\uppsi}}}_{{\varvec{m}}}\left({\varvec{\tau}}\right){\mathbf{s}\mathbf{e}\mathbf{c}\mathbf{h}}^{2}\left(\frac{\stackrel{\sim }{{\varvec{\chi}}}}{{{\varvec{W}}}_{{\varvec{m}}}\left({\varvec{\tau}}\right)}\right).$$

(51)

where $\stackrel{\sim }{{\varvec{\chi}}}={\varvec{\xi}}{\varvec{l}}+{\varvec{\eta}}{\varvec{m}}-{\varvec{V}}\left({\varvec{\tau}}\right){\varvec{\tau}}$.

The time-depending amplitude and width of the IA soliton propagating in the concerned plasma system due to the influence of the external periodic force are obtained as:

$${{\varvec{\uppsi}}}_{{\varvec{m}}}\left({\varvec{\tau}}\right)=\frac{3{\varvec{V}}\left({\varvec{\tau}}\right)}{{\varvec{L}}{\varvec{l}}}\, {\mathrm{and}}\,{{\varvec{W}}}_{{\varvec{m}}}\left({\varvec{\tau}}\right)=2\sqrt{\frac{\left({\varvec{M}}{\varvec{m}}+{\varvec{N}}\right)}{{\varvec{V}}\left({\varvec{\tau}}\right)}},\,\mathrm{respectively}$$

This is a localized stationary solitary wave solution describing the formation and propagation of a nonlinear structure in a quantized degenerate plasma. This solution can only be obtained when nonlinearity and dispersion are balanced out.

Appendix B

The Hirota bilinear method is used to find the single- and multi-ZK soliton solution, because this method is more efficient and less complicated to obtain the multi-soliton solution. By the Hirota bilinear method (HBM), the exact solutions of the ZK equation can be determined; particularly, the multi-soliton solution can be determined by solving the system systematically with the help of the Hirota bilinear transformation. According to HBM, at first use dependent variable transformation to convert ZK equation into a couple bilinear equations and make the nonlinearity coefficient depart from the bilinear forms and become visible only as a scaling factor. The Hirota operators reduce the coupled bilinear equations into an algebraic equation and it can be solved easily. Finally, a perturbation scheme is employed for the dependent variable function, ${\varvec{f}}$, as:

$${\varvec{f}}=1+{\varvec{\epsilon}}{{\varvec{f}}}_{1}\left({\varvec{\xi}},{\varvec{\eta}},{\varvec{\tau}}\right)+{{\varvec{\epsilon}}}^{2}{{\varvec{f}}}_{2}\left({\varvec{\xi}},{\varvec{\eta}},{\varvec{\tau}}\right)+{{\varvec{\epsilon}}}^{3}{{\varvec{f}}}_{3}\left({\varvec{\xi}},{\varvec{\eta}},{\varvec{\tau}}\right)+\cdots$$

(52)

where ${\varvec{\epsilon}}$ indicates the small perturbation parameter. The ${\varvec{n}}$ (${\varvec{n}}=1,2,3,\cdots$)—solution can be found by solving the equations for different powers of ${\varvec{\epsilon}}$.The dependent variable transformation for the ZK equation exercise is [73]:

$$\begin{aligned}{{\varvec{D}}}_{{\varvec{\xi}}}^{{\varvec{p}}}{{\varvec{D}}}_{{\varvec{\eta}}}^{{\varvec{q}}}{{\varvec{D}}}_{{\varvec{\tau}}}^{{\varvec{r}}}\left({\varvec{\mu}},{\varvec{\nu}}\right)=&{\left(\frac{\partial }{\partial{\varvec{\xi}}}-\frac{\partial }{\partial {{\varvec{\xi}}}^{\boldsymbol{^{\prime}}}}\right)}^{{\varvec{p}}}{\left(\frac{\partial }{\partial{\varvec{\eta}}}-\frac{\partial }{\partial {{\varvec{\eta}}}^{\boldsymbol{^{\prime}}}}\right)}^{{\varvec{q}}}{\left(\frac{\partial }{\partial{\varvec{\tau}}}-\frac{\partial }{\partial {{\varvec{\tau}}}^{\boldsymbol{^{\prime}}}}\right)}^{{\varvec{r}}}\\&{\varvec{\mu}}\left({\varvec{\xi}},{\varvec{\eta}},{\varvec{\tau}}\right){\varvec{\nu}}\left({\varvec{\xi}},{\varvec{\eta}},{\varvec{\tau}}\right)\left|{}_{{{\varvec{\xi}}}^{\boldsymbol{^{\prime}}}={\varvec{\xi}},{{\varvec{\eta}}}^{\boldsymbol{^{\prime}}}={\varvec{\eta}},{{\varvec{\tau}}}^{\boldsymbol{^{\prime}}}={\varvec{\tau}}}\right..\end{aligned}$$

(53)

The subscripts $\left({\varvec{\xi}},{\varvec{\eta}}\right)$ in Eq. (53) indicate the ordinary derivative w. r. to ${\varvec{\xi}}$ and ${\varvec{\eta}}$. Applying the transformation (52) for Eq. (37), one can find the following system of Hirota bilinear equations [73]

$$\left[{{\varvec{D}}}_{{\varvec{\xi}}}^{2}+\frac{1}{6}{\left(\frac{{\varvec{N}}}{{\varvec{M}}}\right)}^{1/2}{{\varvec{D}}}_{{\varvec{\xi}}}{{\varvec{D}}}_{{\varvec{\eta}}}-\frac{1}{6}\frac{{\varvec{N}}}{{\varvec{M}}}{{\varvec{D}}}_{{\varvec{\eta}}}^{2}\right]{\varvec{f}}.{\varvec{f}}=0,$$

(54)

and

$$\begin{aligned}&\left[3{\varvec{M}}{{\varvec{D}}}_{{\varvec{\xi}}}^{4}-\sqrt{{\varvec{M}}{\varvec{N}}}{{\varvec{D}}}_{{\varvec{\xi}}}^{3}{{\varvec{D}}}_{{\varvec{\eta}}}+3{\varvec{N}}{{\varvec{D}}}_{{\varvec{\xi}}}^{2}{{\varvec{D}}}_{{\varvec{\eta}}}^{2}-{\varvec{N}}\sqrt{\frac{{\varvec{N}}}{{\varvec{M}}}}{{\varvec{D}}}_{{\varvec{\xi}}}{{\varvec{D}}}_{{\varvec{\eta}}}^{3}\right.\\&\quad\left.+3{{\varvec{D}}}_{{\varvec{\xi}}}{{\varvec{D}}}_{{\varvec{\tau}}}-\sqrt{\frac{{\varvec{N}}}{{\varvec{M}}}}\boldsymbol{ }{{\varvec{D}}}_{{\varvec{\eta}}}{{\varvec{D}}}_{{\varvec{\tau}}}\right]{\varvec{f}}.{\varvec{f}}=0.\end{aligned}$$

(55)

where ${{\varvec{D}}}_{{\varvec{\xi}}}$, ${{\varvec{D}}}_{{\varvec{\eta}}}$, and ${{\varvec{D}}}_{{\varvec{\tau}}}$ are the bilinear Hirota derivative operators defined as:

$${{\varvec{D}}}_{{\varvec{\xi}}}^{{\varvec{p}}}{{\varvec{D}}}_{{\varvec{\eta}}}^{{\varvec{q}}}{{\varvec{D}}}_{{\varvec{\tau}}}^{{\varvec{r}}}\left({\varvec{\mu}},{\varvec{\nu}}\right)={\left(\frac{\partial }{\partial{\varvec{\xi}}}-\frac{\partial }{\partial {{\varvec{\xi}}}^{\boldsymbol{^{\prime}}}}\right)}^{{\varvec{p}}}{\left(\frac{\partial }{\partial{\varvec{\eta}}}-\frac{\partial }{\partial {{\varvec{\eta}}}^{\boldsymbol{^{\prime}}}}\right)}^{{\varvec{q}}}{\left(\frac{\partial }{\partial{\varvec{\tau}}}-\frac{\partial }{\partial {{\varvec{\tau}}}^{\boldsymbol{^{\prime}}}}\right)}^{{\varvec{r}}}{\varvec{\mu}}\left({\varvec{\xi}},{\varvec{\eta}},{\varvec{\tau}}\right){\varvec{\nu}}\left({\varvec{\xi}},{\varvec{\eta}},{\varvec{\tau}}\right)\left|{}_{{{\varvec{\xi}}}^{\boldsymbol{^{\prime}}}={\varvec{\xi}},{{\varvec{\eta}}}^{\boldsymbol{^{\prime}}}={\varvec{\eta}},{{\varvec{\tau}}}^{\boldsymbol{^{\prime}}}={\varvec{\tau}}}\right..$$

(56)

Here, ${\varvec{p}}$, ${\varvec{q}}$, and ${\varvec{r}}$ are positive integers.

One-soliton solution: In order to determine the one-soliton solution for Eq. (37), one can assume

$${{\varvec{f}}}_{1}={{\varvec{e}}}^{\mathbf{\rm X}},$$

(57)

where $\boldsymbol{\rm X}={\varvec{k}}{\varvec{\xi}}+{\varvec{A}}{\varvec{\eta}}+{\varvec{B}}{\varvec{\tau}}$, ${\varvec{k}}$ and ${\varvec{A}}$ are the real arbitrary constants indicating the propagation constant vectors along ${\varvec{x}}$- and ${\varvec{y}}$-axes, respectively. Employing ${{\varvec{f}}}_{1}$ in ${\varvec{\epsilon}}$-order of (55) and (56), one can determine

$${\varvec{A}}=-2\sqrt{\frac{{\varvec{M}}}{{\varvec{N}}}}\boldsymbol{ }{\varvec{k}}\ \boldsymbol{ }{\varvec{a}}{\varvec{n}}{\varvec{d}}\ \boldsymbol{ }{\varvec{B}}=-5\mathbf{M}{\mathbf{k}}^{3}.$$

(58)

Expression of ${\varvec{f}}$ (given by 52) abbreviates for the choice of ${{\varvec{f}}}_{1}$ (given by Eq. (57)) and the higher order functions evaporate. With the help of ${\varvec{A}}$ and ${\varvec{B}}$, the function ${\varvec{f}}$ becomes:

$${\varvec{f}}=1+\mathbf{e}\mathbf{x}\mathbf{p}\left(\mathbf{k}{\varvec{\upxi}}-2\sqrt{\frac{\mathbf{M}}{\mathbf{N}}}{\varvec{k}}{\varvec{\eta}}-5\mathbf{M}{\mathbf{k}}^{3}{\varvec{\tau}}\right).$$

(59)

Therefore, transformation (53) gives the single-soliton solution

$${{\varvec{\Phi}}}_{{\varvec{s}}{\varvec{s}}}^{\left(1\right)}=\frac{15{\varvec{M}}}{{\varvec{L}}}{{\varvec{k}}}^{2}{\mathbf{s}\mathbf{e}\mathbf{c}\mathbf{h}}^{2}\left(\frac{\mathbf{k}}{2}{\varvec{\upxi}}-2\sqrt{\frac{{\varvec{M}}}{{\varvec{N}}}}\boldsymbol{ }{\varvec{k}}{\varvec{\eta}}-\frac{5}{2}\mathbf{M}{\mathbf{k}}^{3}{\varvec{\tau}}\right).$$

(60)

From (60), the amplitude ${{\varvec{\Phi}}}_{{\varvec{m}}}$, width ${{\varvec{W}}}_{{\varvec{m}}}=\frac{2}{\sqrt{{{\varvec{k}}}^{2}+{{\varvec{A}}}^{2}}}$, and velocity ${\varvec{v}}=\left(\frac{-{\varvec{B}}{\varvec{k}}}{{{\varvec{k}}}^{2}+{{\varvec{A}}}^{2}},\frac{{\varvec{A}}{\varvec{B}}}{{{\varvec{k}}}^{2}+{{\varvec{A}}}^{2}}\right)$ of the single-solitary wave are

$${{\varvec{\Phi}}}_{{\varvec{m}}}=\frac{15{\varvec{M}}}{{\varvec{L}}}{{\varvec{k}}}^{2},\boldsymbol{ }{{\varvec{W}}}_{{\varvec{m}}}=\frac{2\sqrt{{\varvec{N}}}}{\sqrt{\left(4{\varvec{M}}+{\varvec{N}}\right)}\left|{\varvec{k}}\right|},$$

(61)

$$\mathbf{a}\mathbf{n}\mathbf{d}\ \boldsymbol{ }{\varvec{v}}=\left({{\varvec{v}}}_{{\varvec{\xi}}},{{\varvec{v}}}_{{\varvec{\eta}}}\right)=\left(-\frac{{\varvec{M}}{\varvec{N}}{{\varvec{k}}}^{2}}{4{\varvec{M}}+{\varvec{N}}},\frac{2{\varvec{M}}{{\varvec{k}}}^{2}\sqrt{{\varvec{B}}{\varvec{C}}}}{4{\varvec{M}}+{\varvec{N}}}\right),$$

(62)

respectively.

Double-soliton solution: For double-soliton solution, let us consider

$${{\varvec{f}}}_{1}={{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}+{{\varvec{\upchi}}}_{2}}\,{\mathrm{and}}\,{{\varvec{f}}}_{2}={{\varvec{a}}}_{12}{{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}+{{\varvec{\upchi}}}_{2}}.$$

(63)

where ${{\varvec{a}}}_{12}$ is the interaction parameter,${{\varvec{\upchi}}}_{{\varvec{i}}}={{\varvec{k}}}_{\mathbf{i}}{\varvec{\upxi}}+{{\varvec{A}}}_{\mathbf{i}}{\varvec{\eta}}+{{\varvec{B}}}_{\mathbf{i}}{\varvec{\tau}}$ (${\varvec{i}}=$ 1, 2). The expression ${\varvec{f}}$ given by (52) for two solitons abbreviates at ${{\varvec{f}}}_{2}$ for the choice of ${{\varvec{f}}}_{1}$ and ${{\varvec{f}}}_{2}$ and all higher order functions disappear; therefore,

$${\varvec{f}}=1+{\varvec{\epsilon}}{{\varvec{f}}}_{1}+{{\varvec{\epsilon}}}^{2}{{\varvec{f}}}_{2}.$$

(64)

Inserting ${\varvec{f}}$ in (54) and (55) and then solving for first order of ${\varvec{\epsilon}}$, one can determine that

$${{\varvec{A}}}_{1}=-2\sqrt{\frac{{\varvec{M}}}{{\varvec{N}}}}{{\varvec{k}}}_{1},\boldsymbol{ }{{\varvec{A}}}_{2}=-2\sqrt{\frac{{\varvec{M}}}{{\varvec{N}}}}{{\varvec{k}}}_{2},\boldsymbol{ }{{\varvec{B}}}_{1}=-5{\varvec{M}}{{\varvec{k}}}_{1}^{3},\ \boldsymbol{ }\mathbf{a}\mathbf{n}\mathbf{d}\ \boldsymbol{ }{{\varvec{B}}}_{2}=-5{\varvec{M}}{{\varvec{k}}}_{2}^{3}.$$

(65)

Now comparing the terms contain ${{\varvec{\epsilon}}}^{2}$ yields,

$${{\varvec{a}}}_{12}=\frac{{\left({{\varvec{k}}}_{1}-{{\varvec{k}}}_{2}\right)}^{2}}{{\left({{\varvec{k}}}_{1}+{{\varvec{k}}}_{2}\right)}^{2}}.$$

(66)

$$\begin{aligned}\mathbf{H}\mathbf{e}\mathbf{n}\mathbf{c}\mathbf{e},=&1+{{\varvec{e}}}^{{{\varvec{k}}}_{1}{\varvec{\xi}}-2\sqrt{\frac{{\varvec{M}}}{{\varvec{N}}}}{{\varvec{k}}}_{1}{\varvec{\eta}}-5{\varvec{M}}{{\varvec{k}}}_{1}^{3}{\varvec{\tau}}}+{{\varvec{e}}}^{{{\varvec{k}}}_{2}{\varvec{\xi}}-2\sqrt{\frac{{\varvec{M}}}{{\varvec{N}}}}{{\varvec{k}}}_{2}{\varvec{\eta}}-5{\varvec{M}}{{\varvec{k}}}_{2}^{3}{\varvec{\tau}}}\\&+\frac{{\left({{\varvec{k}}}_{1}-{{\varvec{k}}}_{2}\right)}^{2}}{{\left({{\varvec{k}}}_{1}+{{\varvec{k}}}_{2}\right)}^{2}}{{\varvec{e}}}^{\left[\left({{\varvec{k}}}_{1}+{{\varvec{k}}}_{2}\right){\varvec{\xi}}-2\sqrt{\frac{{\varvec{M}}}{{\varvec{N}}}}\left({{\varvec{k}}}_{1}+{{\varvec{k}}}_{2}\right){\varvec{\eta}}-5{\varvec{M}}\left({{\varvec{k}}}_{1}^{3}+{{\varvec{k}}}_{2}^{3}\right){\varvec{\tau}}\right]},\end{aligned}$$

(67)

which gives the double-soliton solution of the ZK equation with the help of the transformation (53) as:

$${{\varvec{\Phi}}}_{{\varvec{d}}{\varvec{s}}}^{\left(1\right)}=\frac{36{\varvec{M}}}{{\varvec{L}}}{\left[{\varvec{F}}\left({{\varvec{\upchi}}}_{1},{{\varvec{\upchi}}}_{2}\right)\right]}_{{\varvec{\xi}}{\varvec{\xi}}}-\frac{12\sqrt{{\varvec{M}}{\varvec{N}}}}{{\varvec{L}}}{\left[{\varvec{F}}\left({{\varvec{\upchi}}}_{1},{{\varvec{\upchi}}}_{2}\right)\right]}_{{\varvec{\xi}}{\varvec{\eta}}},$$

(68)

where,

$${\varvec{F}}\left({{\varvec{\upchi}}}_{1},{{\varvec{\upchi}}}_{2}\right)=\mathbf{l}\mathbf{n}\left\{1+{{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}}+{{\varvec{e}}}^{{{\varvec{\upchi}}}_{2}}+{{\varvec{a}}}_{12}{{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}+{{\varvec{\upchi}}}_{2}}\right\}$$

$$\begin{aligned}&{\left[{\varvec{F}}\left({{\varvec{\upchi}}}_{1},{{\varvec{\upchi}}}_{2}\right)\right]}_{{\varvec{\xi}}{\varvec{\xi}}}\\&\quad=\frac{{{\varvec{k}}}_{1}^{2}{{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}}+{{\varvec{k}}}_{2}^{2}{{\varvec{e}}}^{{{\varvec{\upchi}}}_{2}}+\left[{\left({{\varvec{k}}}_{1}-{{\varvec{k}}}_{2}\right)}^{2}+{{\varvec{a}}}_{12}\left\{{\left({{\varvec{k}}}_{1}+{{\varvec{k}}}_{2}\right)}^{2}+{{{\varvec{k}}}_{2}^{2}{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}}+{{\varvec{k}}}_{1}^{2}{{\varvec{e}}}^{{{\varvec{\upchi}}}_{2}}\right\}\right]{{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}+{{\varvec{\upchi}}}_{2}}}{{\left(1+{{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}}+{{\varvec{e}}}^{{{\varvec{\upchi}}}_{2}}{+{\varvec{a}}}_{12}{{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}+{{\varvec{\upchi}}}_{2}}\right)}^{2}},\end{aligned}$$

$$\begin{aligned}&{\left[{\varvec{F}}\left({{\varvec{\upchi}}}_{1},{{\varvec{\upchi}}}_{2}\right)\right]}_{{\varvec{\xi}}{\varvec{\eta}}}\\&\quad=\frac{-{\varvec{l}}\left({{\varvec{k}}}_{1}^{2}{{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}}+{{\varvec{k}}}_{2}^{2}{{\varvec{e}}}^{{{\varvec{\upchi}}}_{2}}\right)-{\varvec{l}}\left[{\left({{\varvec{k}}}_{1}-{{\varvec{k}}}_{2}\right)}^{2}+{{\varvec{a}}}_{12}\left\{{\left({{\varvec{k}}}_{1}+{{\varvec{k}}}_{2}\right)}^{2}+{{{\varvec{k}}}_{2}^{2}{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}}+{{\varvec{k}}}_{1}^{2}{{\varvec{e}}}^{{{\varvec{\upchi}}}_{2}}\right\}\right]{{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}+{{\varvec{\upchi}}}_{2}}}{{\left(1+{{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}}+{{\varvec{e}}}^{{{\varvec{\upchi}}}_{2}}{+{\varvec{a}}}_{12}{{\varvec{e}}}^{{{\varvec{\upchi}}}_{1}+{{\varvec{\upchi}}}_{2}}\right)}^{2}},\end{aligned}$$

$$\begin{aligned}{\varvec{l}}=&2\sqrt{\frac{{\varvec{M}}}{{\varvec{N}}}},\boldsymbol{ }{{\varvec{\chi}}}_{{\varvec{i}}}={{\varvec{k}}}_{{\varvec{i}}}{\varvec{\xi}}-2\sqrt{\frac{{\varvec{M}}}{{\varvec{N}}}}{{\varvec{k}}}_{{\varvec{i}}}{\varvec{\eta}}-5{\varvec{M}}{{\varvec{k}}}_{{\varvec{i}}}^{3}{\varvec{\tau}}\boldsymbol{ }\left({\varvec{i}}=1,2\right)\\&\,{\mathrm{and}}\,{{\varvec{a}}}_{12}={\left(\frac{{{\varvec{k}}}_{1}-{{\varvec{k}}}_{2}}{{{\varvec{k}}}_{1}+{{\varvec{k}}}_{2}}\right)}^{2}.\end{aligned}$$

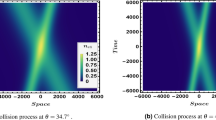
Solution (68) represents the overtaking collision of two IA solitons.

Proceeding in similar manner as above, one can determine the triple-soliton and quadruple-soliton solutions of the ZK equation.