Remarks on the Renormalization Properties of Lorentz- and CPT-Violating Quantum Electrodynamics

Abstract

In this work, we employ algebraic renormalization technique to show the renormalizability to all orders in perturbation theory of the Lorentz- and CPT-violating QED. Essentially, we control the breaking terms by using a suitable set of external sources. Thus, with the symmetries restored, a perturbative treatment can be consistently employed. After showing the renormalizability, the external sources attain certain physical values, which allow the recovering of the starting physical action. The main result is that the original QED action presents the three usual independent renormalization parameters. The Lorentz-violating sector can be renormalized by 19 independent parameters. Moreover, vacuum divergences appear with extra independent renormalization. Remarkably, the bosonic odd sector (Chern-Simons-like term) does not renormalize and is not radiatively generated. One-loop computations are also presented and compared with the existing literature.

Appendices

Appendix A: Vacuum Terms

We will discuss now the vacuum action, i.e., the action that taken account only terms depending on the sources. Since this action does not interfere with the renormalization of the sources, or with the dynamical content of the model, this discussion does not mess with the results obtained so far. However, we will not describe here all vacuum terms. We will present here only the most difficult vacuum terms which demand a careful analysis:

$$\begin{array}{@{}rcl@{}} {\Sigma}_{V}&=&\int d^{4}x\left\{\alpha_{1}\bar{A}_{\mu} \bar{A}^{\mu} \bar{A}_{\nu} \bar{A}^{\nu}+\alpha_{2}m\bar{A}_{\mu} \bar{A}^{\mu} \bar{A}_{\nu} E^{\nu}\right.\\ &&\left.+\alpha_{3}m^{2}\bar{A}_{\mu} \bar{A}^{\mu} E_{\mu} E^{\mu} +\alpha_{4}m^{2}\bar{A}_{\mu} \bar{A}_{\nu} E^{\mu} E^{\nu}\right.\\ &&\left.+\alpha_{5}m^{3} \bar{A}_{\mu} E^{\mu} E_{\nu} E^{\nu}+\alpha_{6}m^{4}E_{\mu} E^{\mu} E_{\nu} E^{\nu}\right\}\\ &&+s\int d^{4}x\left\{ \zeta\lambda_{\mu\nu\alpha}J^{\mu\beta\gamma}J^{\nu}_{\phantom{\nu} \beta\kappa}J_{\gamma}^{\phantom{\gamma}\kappa\alpha}\right.\\ &&+\left.\vartheta_{1}\bar{\kappa}_{\mu\nu\alpha\beta}\lambda^{\mu\rho\omega}J^{\nu}_{\phantom{\nu}\rho\sigma}J^{\alpha}_{\phantom{\alpha}\omega\delta}J^{\beta\sigma\delta}\right.\\ &&\left.+\vartheta_{2}T_{\mu\nu\alpha\beta}^{\phantom{\mu\nu\alpha\beta}\theta\gamma}C_{\theta\gamma}\lambda^{\mu\rho\omega}J^{\nu}_{\phantom{\nu}\rho\sigma}J^{\alpha}_{\phantom{\alpha}\omega\delta}J^{\beta\sigma\delta}\right.\\ &&+\left.\vartheta_{3}T_{\mu\nu\alpha\beta}^{\phantom{\mu\nu\alpha\beta}\tau\zeta}\eta^{\gamma\xi}\bar{\kappa}_{\tau\gamma\zeta\xi}\lambda^{\mu\rho\omega}J^{\nu}_{\phantom{\nu}\rho\sigma}J^{\alpha}_{\phantom{\alpha}\omega\delta}J^{\beta\sigma\delta}\right\}\;,\\ &=&\int d^{4}x\left\{\alpha_{1}\bar{A}_{\mu} \bar{A}^{\mu} \bar{A}_{\nu} \bar{A}^{\nu}+\alpha_{2}m\bar{A}_{\mu} \bar{A}^{\mu} \bar{A}_{\nu} E^{\nu}\right.\\\ &&\left.+\alpha_{3}m^{2}\bar{A}_{\mu} \bar{A}^{\mu} E_{\mu} E^{\mu} +\alpha_{4}m^{2}\bar{A}_{\mu} \bar{A}_{\nu} E^{\mu} E^{\nu}\right.\\ &&+\left.\alpha_{5}m^{3} \bar{A}_{\mu} E^{\mu} E_{\nu} E^{\nu}+\alpha_{6}m^{4}E_{\mu} E^{\mu} E_{\nu} E^{\nu}\right\}\\ &&+\int d^{4}x\left\{ \zeta J_{\mu\nu\alpha}J^{\mu\beta\gamma}J^{\nu}_{\phantom{\nu} \beta\kappa}J_{\gamma}^{\phantom{\gamma}\kappa\alpha}\right.\\ &&+\left.\vartheta_{1}\bar{\kappa}_{\mu\nu\alpha\beta}J^{\mu\rho\omega}J^{\nu}_{\phantom{\nu}\rho\sigma}J^{\alpha}_{\phantom{\alpha}\omega\delta}J^{\beta\sigma\delta}\right.\\ &&\left.+\vartheta_{2}T_{\mu\nu\alpha\beta}^{\phantom{\mu\nu\alpha\beta}\theta\gamma}C_{\theta\gamma}J^{\mu\rho\omega}J^{\nu}_{\phantom{\nu}\rho\sigma}J^{\alpha}_{\phantom{\alpha}\omega\delta}J^{\beta\sigma\delta}\right.\\ &&+\left.\vartheta_{3}T_{\mu\nu\alpha\beta}^{\phantom{\mu\nu\alpha\beta}\tau\zeta}\eta^{\gamma\xi}\bar{\kappa}_{\tau\gamma\zeta\xi}J^{\mu\rho\omega}J^{\nu}_{\phantom{\nu}\rho\sigma}J^{\alpha}_{\phantom{\alpha}\omega\delta}J^{\beta\sigma\delta}\right\}\;. \end{array} $$

(A.1)

The terms that depend on the electron mass are introduced in order to guarantee the quantum stability of the vacuum action. This can be easily understood by fact that the sources $\bar {A}^{\mu }$ and E ^μ suffer mix under quantum corrections. The same can be said about the sources $\bar {\kappa }_{\mu \nu \alpha \beta }$ and C _{ν μ} .

At the physical limit of the sources (3.6), the action (A.1) reduces to

$$\begin{array}{@{}rcl@{}} {\Sigma}_{Vphys}&=&\int d^{4}x\left\{\alpha_{1}a_{\mu} a^{\mu} a_{\nu} a^{\nu}+\alpha_{2}ma_{\mu} a^{\mu} a_{\nu} e^{\nu}\right.\\ &&\left.+\alpha_{3}m^{2}a_{\mu} a^{\mu} e_{\mu} e^{\mu} +\alpha_{4}m^{2}a_{\mu} a_{\nu} e^{\mu} e^{\nu}\right.\\ &&+\left.\alpha_{5}m^{3} a_{\mu} e^{\mu} e_{\nu} e^{\nu}+\alpha_{6}m^{4}e_{\mu} e^{\mu} e_{\nu} e^{\nu}+6\zeta v^{4}\right.\\ &&\left.+(8\vartheta_{3}-2\vartheta_{1})\kappa^{\alpha\mu\sigma}_{\phantom{\alpha\mu\sigma}\mu}v_{\alpha} v_{\sigma} v^{2} +\right.\\ &&+\left.8\vartheta_{2}c^{\alpha\sigma}v_{\alpha} v_{\sigma} v^{2}\right\}\;, \end{array} $$

(A.2)

which shows the nontrivial vacuum of the model. Now we can proceed as in Section 4.2 and seek for the most general counterterm compatible with Ward identities shown at (4.7):

$$\begin{array}{@{}rcl@{}} {{\Sigma}_{V}^{c}}&=&\int d^{4}x\left\{b_{1}\alpha_{1}\bar{A}_{\mu} \bar{A}^{\mu} \bar{A}_{\nu} \bar{A}^{\nu}+b_{2}\alpha_{2}m\bar{A}_{\mu} \bar{A}^{\mu} \bar{A}_{\nu} E^{\nu}\right.\\ &&\left.+b_{3}\alpha_{3}m^{2}\bar{A}_{\mu} \bar{A}^{\mu} E_{\mu} E^{\mu}+b_{4}\alpha_{4}m^{2}\bar{A}_{\mu} \bar{A}_{\nu} E^{\mu} E^{\nu}\right.\\ &&\left.+b_{5}\alpha_{5}m^{3} \bar{A}_{\mu} E^{\mu} E_{\nu} E^{\nu}+b_{6}\alpha_{6}m^{4}E_{\mu} E^{\mu} E_{\nu} E^{\nu}\right\}\\ &&+\mathcal{S}_{\Sigma}\tilde{\Delta}^{(-1)}\;. \end{array} $$

(A.3)

where

$$\begin{array}{@{}rcl@{}} \tilde{\Delta}^{(-1)}&=&\int d^{4}x\left\{b_{7}\zeta\lambda_{\mu\nu\alpha}J^{\mu\beta\gamma}J^{\nu}_{\phantom{\nu} \beta\kappa}J_{\gamma}^{\phantom{\gamma}\kappa\alpha}\right.\\ &&\left.+b_{8}\vartheta_{1}\bar{\kappa}_{\mu\nu\alpha\beta}\lambda^{\mu\rho\omega}J^{\nu}_{\phantom{\nu}\rho\sigma}J^{\alpha}_{\phantom{\alpha}\omega\delta}J^{\beta\sigma\delta}\right.\\ &&+\left.b_{9}\vartheta_{2}T_{\mu\nu\alpha\beta}^{\phantom{\mu\nu\alpha\beta}\theta\gamma}C_{\theta\gamma}\lambda^{\mu\rho\omega}J^{\nu}_{\phantom{\nu}\rho\sigma}J^{\alpha}_{\phantom{\alpha}\omega\delta}J^{\beta\sigma\delta}\right.\\ &&\left.+b_{10}\vartheta_{3}T_{\mu\nu\alpha\beta}^{\phantom{\mu\nu\alpha\beta}\tau\zeta}\eta^{\gamma\xi}\bar{\kappa}_{\tau\gamma\zeta\xi}\lambda^{\mu\rho\omega}J^{\nu}_{\phantom{\nu}\rho\sigma}J^{\alpha}_{\phantom{\alpha}\omega\delta}J^{\beta\sigma\delta}\right\}\;.\\ \end{array} $$

(A.4)

It is then straightforward to show that the most general counterterm is

$$\begin{array}{@{}rcl@{}} {{\Sigma}_{V}^{c}}&=&\int d^{4}x\left\{b_{1}\alpha_{1}\bar{A}_{\mu} \bar{A}^{\mu} \bar{A}_{\nu} \bar{A}^{\nu}+b_{2}\alpha_{2}m\bar{A}_{\mu} \bar{A}^{\mu} \bar{A}_{\nu} E^{\nu}\right.\\ &&\left.+b_{3}\alpha_{3}m^{2}\bar{A}_{\mu} \bar{A}^{\mu} E_{\mu} E^{\mu}+b_{4}\alpha_{4}m^{2}\bar{A}_{\mu} \bar{A}_{\nu} E^{\mu} E^{\nu}\right.\\ &&\left.+b_{5}\alpha_{5}m^{3} \bar{A}_{\mu} E^{\mu} E_{\nu} E^{\nu}+b_{6}\alpha_{6}m^{4}E_{\mu} E^{\mu} E_{\nu} E^{\nu}\right.\\ &&+b_{7}\zeta J_{\mu\nu\alpha}J^{\mu\beta\gamma}J^{\nu}_{\phantom{\nu}\beta\kappa}J_{\gamma}^{\phantom{\gamma}\kappa\alpha}\ \\&&+b_{8}\left.\vartheta_{1}\bar{\kappa}_{\mu\nu\alpha\beta}J^{\mu\rho\omega}J^{\nu}_{\phantom{\nu}\rho\sigma}J^{\alpha}_{\phantom{\alpha}\omega\delta}J^{\beta\sigma\delta}\right.\\ &&+\left.b_{9}\vartheta_{2}T_{\mu\nu\alpha\beta}^{\phantom{\mu\nu\alpha\beta}\theta\gamma}C_{\theta\gamma}J^{\mu\rho\omega}J^{\nu}_{\phantom{\nu}\rho\sigma}J^{\alpha}_{\phantom{\alpha}\omega\delta}J^{\beta\sigma\delta}\right.\\ &&\left.+b_{10}\vartheta_{3}T_{\mu\nu\alpha\beta}^{\phantom{\mu\nu\alpha\beta}\tau\zeta}\eta^{\gamma\xi}\bar{\kappa}_{\tau\gamma\zeta\xi}J^{\mu\rho\omega}J^{\nu}_{\phantom{\nu}\rho\sigma}J^{\alpha}_{\phantom{\alpha}\omega\delta}J^{\beta\sigma\delta}\right\}\;.\\ \end{array} $$

(A.5)

To finish the renormalizability of the vacuum term, it is needed to check the stability of the vacuum action. Thus, we have to show that

$$\begin{array}{@{}rcl@{}} {\Sigma}_{V}(J, \xi)+{\varepsilon{\Sigma}^{c}_{V}}(J,\xi)&=&{{\Sigma}_{V}^{0}}(J_{0}, \xi_{0})+\mathcal{O}(\varepsilon^{2})\;, \end{array} $$

(A.6)

where the bare parameters are defined as

$$\begin{array}{@{}rcl@{}} \xi_{0}&=&Z_{\xi}\xi\;,\;\;\;\;\;\;\;\;\xi \in \left\{\zeta,\alpha_{i},\vartheta_{j}\right\}\;. \end{array} $$

(A.7)

It is not difficult to achieve the following consistent expressions:

$$\begin{array}{@{}rcl@{}} Z_{\alpha_{1}}\!&=&\!1\!+\varepsilon\left(b_{1}\,-\,4a_{15}\!+4a_{3}\right)\;,\\ Z_{\alpha_{2}}\!&=&\!1\!+\varepsilon\left(b_{2}\,-\,a_{4}\,-\,3a_{15}\,-\,a_{10}\,+\,5a_{3}\,-\,4a_{16}\frac{\alpha_{1}}{\alpha_{2}}\right)\;,\\ Z_{\alpha_{3}}\!&=&\!1\!+\varepsilon\left(b_{3}\,-\,2a_{4}\,-\,2a_{15}\,-\,2a_{10}\,+\,6a_{3}\,-\,a_{16}\frac{\alpha_{2}}{\alpha_{3}}\right)\;,\\ Z_{\alpha_{4}}\!&=&\!1\!+\varepsilon\left(b_{4}\!-2a_{4}\!-2a_{15}\!-2a_{10}\!+6a_{3}\,-\,2a_{16}\frac{\alpha_{2}}{\alpha_{4}}\right)\;,\\ Z_{\alpha_{5}}\!&=&\!1\!+\varepsilon\left(b_{5}\!-3a_{4}\!-a_{15}\!-3a_{10}+7a_{3}-2a_{16}\left(\frac{\alpha_{3}+\alpha_{4}}{\alpha_{5}}\right)\right)\;,\\ Z_{\alpha_{6}}&=&1+\varepsilon\left(b_{6}-4a_{4}+4a_{3}-a_{16}\frac{\alpha_{5}}{\alpha_{6}}\right)\;,\\ Z_{\zeta}&=&1+\varepsilon\left(b_{7}+4a_{0}\right)\;,\\ Z_{\vartheta_{1}}&=&1+\varepsilon\left(b_{8}-a_{1}+5a_{0}\right)\;,\\ Z_{\vartheta_{2}}&=&1+\varepsilon\left(b_{9}-a_{5}-a_{6}+a_{3}+4a_{0}-a_{2}\left(\frac{\vartheta_{1}-4\vartheta_{3}}{\vartheta_{2}}\right)\right)\;,\\ Z_{\vartheta_{3}}&=&1+\varepsilon\left(b_{10}-a_{1}+5a_{0}-a_{10}\frac{\alpha_{2}}{\alpha_{3}}\right)\;. \end{array} $$

(A.8)

The proof that all other possible pure source term is also renormalizable follows the same prescription.

Appendix B: Discrete Mappings of the Sources

The coupling between the local sources and the Dirac bilinears depend on behavior of sources and Dirac bilinears under discrete mappings. Besides of the quantum numbers shown in the Table 3, the discrete mappings displayed in Table 4 will also select the allowed couplings.

Table 4 Discrete mappings of the sources

Appendix C: Feynman Rules

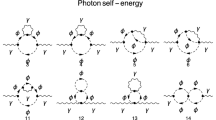
In this appendix, we provide the Feynman rules used in Section 5. Instead of dealing with the direct rules that could be extracted from the action (2.1), we opt to treat the breaking terms as insertions. Thus, the set of propagators is the usual QED propagators: For the electron

For the photon:

where p _μ is the particle momentum.

The fermion-photon vertex is given by

The Feynman rules for the Lorentz-violating QED terms are obtained by insertions of Lorentz-violating coefficients in fermion and photon propagators, namely

There is also an insertion at the fermion-photon vertex given by