1 Introduction

Transfers of non-indigenous species may potentially pose a threat to the receiving ecosystem and to the society. Organisms that mass-reproduce when they are transported and released in new environments by humans are “non-indigenous invasive species”, sometimes referred to as “alien species” (definitions and discussions of these concepts can be found in Ruiz and Carlton 2003). Ultimately, they may have serious impact on ecosystems both ecologically and economically. Ships’ ballast water is a main source of non-indigenous marine organisms and, when released, some of these species have caused dramatic and permanent damage to coastal ecosystems around the world (e.g., Bax et al. 2003; Leppäkoski et al. 2003). Since it has been impossible in practise to control and mitigate the spreading of established invasive species in “new” marine environments, efforts should focus on the prevention of introductions.

The trend in biological invasion shows an exponential increase during the last 200 years (Leppäkoski et al. 2003). Nevertheless, the problem of marine bio-invasion and the resulting environmental consequences has taken time to be recognized. One of many reasons is that unlike terrestrial ecosystems, bioinvasions in the marine environment are poorly understood since their consequences may be difficult to observe.

Many bioinvasions are considered a threat to the ecosystems, to human health as well as to the economy. The invaded ecosystems are threatened as exotic species may alter ecosystem functions and community structure. In some cases, non-indigenous species cause a dramatic decline in important marine resources by competing with the native species for food, habitat, by predation/parasitism, or due to other indirect interactions.

Biological invasions may also interact in combination with other natural and anthropogenic environmental factors such as climate change, habitat destruction and pollution to jeopardize the integrity of the ecosystem. This means that the impacts of future introductions are uncertain as well as unpredictable and current invasions may evolve into unforeseen intricate patterns. More challenges are forecast to come in handling introductions and efforts should be focused on preventing new establishments in order to protect the native biota and its diversity by means of managing human activity.

The scope of this work is to demonstrate the usefulness of the combination of hydrodynamical (HD) and agent-based models (ABM) as a tool for understanding the ecological connectivity of marine areas of the North Sea, Kattegat, and the inner Danish straits and their application for risk assessment of invasive species brought to the region (or transported within the region) by ballast water from sea vessels. Ecological connectivity mapping is proposed to provide a theoretical basis for identifying areas where ballast water could be released with the least potential risk for species to spread extensively within the region. In addition, connectivity mapping can provide knowledge on how well each specific part of the region is connected with other parts of the region.

2 Methods

2.1 Study area

The study area is the North Sea, located on the continental shelf of north-western Europe and bordered by England, Scotland, Sweden, Norway, Denmark, Germany, the Netherlands, Belgium, and France. It opens out to the Atlantic Ocean, the English Channel, and towards the less saline Baltic Sea.

The Greater North Sea (as defined by OSPAR) has a surface area of 750,000 km2 and a volume of 94,000 km3 and is separated into various areas, the relatively shallow southern North Sea (the Southern Bight and the German Bight), the central North Sea, the northern North Sea, the Norwegian Trench, and the Skagerrak, which is a shallow transition zone between the Baltic and the North Sea (OSPAR 2010).

In the eastern part of the North Sea, along the coasts of Denmark and Germany, mean winter sea surface temperature (SST) is usually less than 3 °C. The summer mean SST is 18 °C and declines to 13 °C northwards along eastern Britain (Hayward and Ryland 1995). The annual freshwater river input is ca 300 km3, about one third of that comes from the snow-melt waters of Norway and Sweden and the rest from major rivers while the main source of fresh water supply is through the Baltic Sea (Hayward and Ryland 1995).

The most prominent current circulation of the North Sea is a roughly anticlockwise flow where residual currents moves southwards along the east coast of the UK and northwards along the Western European coast. Saline water enters the Baltic Sea through Kattegat at depth while surface flow of brackish water from the Baltic Sea enters the Kattegat and North Sea (OSPAR 2010).

The North Sea, which is an economically and ecologically important marine region, is sensitive to a range of human activities. Key issues are nutrient enrichment and eutrophication, contamination with hazardous substances, overfishing, physical modification and an unfavorable biodiversity status (OSPAR 2010; HELCOM 2010). Introduction of non-indigenous species has been identified as an emerging issue.

Many areas in the North Sea are valuable habitat for marine life as well as of economic importance for the surrounding states. The shallow and productive North Sea, while being of one of the busiest seas in the world in seaborne trading, is also heavily exploited for its natural resources. Activities such as fishing, dredging, oil and gas exploration, shipping, discharges of nutrients and contaminants have polluted as well as depleted reserves in the area. Increases in awareness for the protection of the environment and resource management in the North Sea have surged during the last decades (Misund and Skjoldal 2005), and one significant issue that has been identified relatively recently is the ramifications of species introduction via ship transportation and accidental releases from aquaculture.

The most up-to-date inventory of alien species in the North Sea region lists alien aquatic species of 167 taxa (Gollasch et al. 2009). This calls for a precautionary approach to prevent future arrivals of new species. One of the key vectors in moving aquatic alien species is shipping, e.g., ballast water-mediated species introductions from ships prevail in many regions world-wide.

2.2 Hydrodynamic model

The applied hydrodynamic model is based on the MIKE 3 modeling system developed by DHI. The MIKE 3 model is a dynamic time-dependent 3D baroclinic model for free surface flows. The mathematical foundation of the model are the Reynolds-averaged Navier-Stokes equations in three dimensions, including the effects of turbulence and variable density, together with conservation equations for mass, heat, and salt, an equation of state for the density, a turbulence module and a heat exchange module. The equations are solved on a Cartesian grid by means of the finite difference techniques. The hydrodynamic model provides a full 3D model representation of the water levels, flows, salinity, temperature, and density within the modeling domain. For more information on the MIKE 3 modeling system, reference is made to DHI (2009) and DHI (2011).

2.3 Model setup

A 3D North Sea hydrodynamic model is applied as the basis for the agent-based modeling (ABM) and subsequent connectivity modeling. A period of a full year (2005) has been modeled in order to capture the seasonal and higher frequency variability of the North Sea circulation. The model represents the overall circulation patterns in the North Sea and the Belt Sea comprising of tide, meteorologically and density-driven circulation, freshwater inputs, and stratification. A local 3D hydrodynamic model resolving the Belt Sea in a higher resolution has also been applied.

The model domain includes the major part of the North Sea, the Belt Sea, and the Baltic Sea. The model applies a Cartesian grid in UTM-32 projection with a horizontal resolution of 3 nautical miles. In the vertical dimension, a 2-m resolution is used, with a maximum of 110 layers depending on the local water depth. However, the surface layer with surface elevation varying with the actual tide has a typical thickness of 5 m. For areas with depths under level −223 m, the rest of the water column is included in the lowest layer. The model domain is shown in Fig. 1.

Fig. 1
figure 1

Model domain and location of selected measurement stations. The thick black lines indicate the open boundaries of the model

Full size image

The model has been run for the period 2000–2008, but the period applied for the present purpose is the year 2005. The model runs with a hydrodynamic time step of 300 s. The model results in terms of 3D fields of, for example, current, salinity, and temperature are saved every 1 h.

The forcings on the open boundaries towards the Norwegian Sea and the English Channel include: (1) Astronomical tide along boundary (actual values for 2005), (2) salinity distribution in vertical sections (monthly climatologic from ICES), and (3) temperature distribution in vertical sections (monthly climatologic from ICES). Atmospheric forcings (e.g., wind, air pressure, air temperature, cloudiness, and precipitation (actual 2D maps with 1 h resolution)) were originally delivered by Vejr2, a former meteorological forecast service provider. The wind and air pressure are incorporated in the momentum equations, and the precipitation is used in the mass equation. Wind is also included in the turbulence module. The heat exchange module, which calculates the sea-air heat exchange, makes use of wind, air temperature and cloudiness. The runoff in terms of discharges of freshwater from land to the model domain is represented in the model by 85 source points. The runoff is based on data from SMHI’s operational HBV model and on data from Global Runoff Data Centre (GRDC). It is important to note that the applied sources are lumped sources, which means that they represent the main rivers at each location as well as the non-resolved rivers/inflows in the vicinity of the location. This means that the total runoff to the Baltic Sea/North Sea is correctly represented in the 85 model sources. Initial fields of salinity and temperature, i.e., 3D fields of salinity and temperature within the model domain, have been established based on previous model runs. The present hydrodynamic model setup is an updated version of the model used for the BANSAI project (SMHI 2006).

Since the North Sea hydrodynamic model is relatively coarse in the Belt Sea (3 nautical miles cell size), a local hydrodynamic model covering the Belt Sea and the Baltic Sea was also applied. This model has a finer resolution (down to 1 km cell size) in the Belt Sea as illustrated in Fig. 2 and thus represents the flow here in more detail. The model was developed for another purpose, but has been made available for the present purpose (FEHY 2012).

Fig. 2
figure 2

Section of the computational mesh for the hydrodynamic model covering the inner Danish waters. Colors indicate depth intervals in meters

Full size image

2.4 Agent-based modeling

Agent-based models (ABM) have been widely applied in recent years for simulating a variety of phenomena within very diverse disciplines such as biology and ecology, social sciences, industrial process optimization, traffic infrastructure planning, and the financial sector just to mention a few examples. In ecology, ABMs aim at describing the behavior and state of discrete entities such as individual organisms or groups of organisms (∼superindividuals). One key element of ABMs is the ability to simulate how individuals respond (in terms of behavior and state) to a spatially and temporarily varying environment. When studying the aquatic environment and how small individuals spread within an aquatic system, information on water movement is a fundamental need. Here, 3D hydrodynamical models describing the water currents in high temporal and spatial resolution can provide a very detailed basis for these types of studies. By defining agents as discrete entities with an explicit x-y-z coordinate at any given point in time it is possible to link this type of ABM with a hydrodynamical model and thus combine the current driven movement of agents (=advection/dispersion) with biological movement behavior processes such as horizontal swimming, vertical migration, and age-induced settling. This type of ABM is often referred to as a Lagrangian type ABM and has been applied frequently, e.g., in studies examining the spreading and migration of pelagic larvae and fish (e.g., Goodwin et al. 2001; Humston et al. 2000; Cowen et al. 2006).

To simulate the potential spread of marine invasive species deriving from ballast water an (Lagrange type) ABM was developed and applied in combination with the hydrodynamical model as described in the previous section. The ABM framework applied is an integrated part of the ecological modeling software ECO Lab, which is an open equation solver for building and executing biological and ecological models of aquatic systems.

The developed ABM is applied here to simulate the spread of agents (or organisms) in the entire model area primarily driven by advective processes predicted by the hydrodynamical model. Three model organisms are chosen to represent examples of major groups of marine organisms likely to be introduced as invasive species through the release of ballast water within the North Sea region. Here “groups of marine organisms” refer to organisms which exhibit common behavioral characteristics. The groups of organisms considered here include representatives of a: (1) planktonic species (purely passive drifters), (2) pelagic larvae of a benthic invertebrate species (passive drifters in combination with settling), and (3) fish species (passive drifters in combination with active swimming activity). We mimic the spread of these three types of model organisms in a very simplistic way by: (1) simulating passive drift in combination with a constant mortality rate, (2) simulating passive drift in combination with active settling activity triggered as a function of age, and (3) simulating passive drift in combination with active horizontal swimming behavior including mortality rate. In addition to these three simulations, as a reference, we simulate passive drifting only subject to advection/dispersion processes.

The approach described here is merely an attempt to address the spreading mechanisms and potential of small marine organisms in a general way. The approach is deliberately not addressing species-specific spreading. Also, when considering the risk of introducing invasive species in the marine environment species-specific habitat preferences, life histories and environmental tolerances are essential to understand and predict the ability of introduced species to establish a sustainable population. These issues are not addressed here. However, species-specific traits and the implication for establishing sustainable populations can be simulated by extending the current approach combining hydrodynamic modeling and ABM with habitat maps and/or classical concentration-based (Euler type) ecological modeling. The latter describing any necessary dynamical parameter affecting the organism such as salinity, temperature, dissolved oxygen, food abundance, etc.

Unlike the hydrodynamical modeling, due to the nature of the phenomena modeled neither calibration nor validation of the ABM is being considered. This means that the modeling exercise here apart from the hydrodynamical modeling is predominantly theoretical. The ABM approach can be seen as an interpreter to describe how common behavioral characteristics and traits may or may not result in significant deviations from passive drift. The results of the model approach should be evaluated as such.

2.5 ABM formulation

Selected simplistic functional behaviors and life histories used for formulation of the ABM include: (1) Movement in terms of dispersion and active swimming, (2) settling, (3) mortality, and (4) longevity. The background for and the ABM formulations used in this study are described in Appendix 1 in the Online Supplementary Material. Please note that this appendix includes additional references not cited in this paper.

2.6 Connectivity mapping

The combination of HD modeling and ABMs (or particle tracking models) has been applied in several studies addressing the degree of connectivity between specific habitats or subregions within marine regions (Cowen et al. 2003, 2006; Paris et al 2005; Christensen et al 2008; Berglunda et al. 2012) However, in most cases, the studies have focused on specific species and connectivity between the species-specific habitats, or in more general connectivity in terms of, e.g., dispersal of passively drifting larvae between specific habitats such as coral reefs, spawning sites, etc. A more general approach applying a combination of hydrodynamical modeling and simple particle tracking has been proposed to establish a framework for identifying connectivities of any sub-region within the South-Western shelf region of Australia (Condie et al. 2006). In short, the particle trajectories from the simulations are treated statistically and translated into probability maps describing the “probability of any two regions within the model domain being connected by the modeled circulation”. Probabilities were “computed for a range of dispersion times on a 0.1 degree geographical grid” covering the model domain. The connectivity statistics addresses connectivities in discrete points in time and space as well as statistics aggregated for longer periods (months or quarters). As part of the project, a web-based service was developed where users can select a “source area” from a map interface, select start time, and dispersal duration, and as a result get a connectivity probability map for the selected source area and dispersal duration.

In this study, the above-outlined approach has been further developed, e.g., by (1) including not only passive particle tracking but also biological processes by applying ABM techniques and by (2) developing an overall connectivity index or indices compiling all connectivity statistics of each local area into a single value.

In order to define “connectivity”, we discriminate between two types of connectivities: downstream connectivity and upstream connectivity (Fig. 3).

Fig. 3
figure 3

Sketch of the differences between the concepts of downstream connectivity and upstream connectivity

Full size image

Downstream connectivity we define as connectivity between donor areas (or source areas), and surrounding areas (or receiving areas). Here “areas” does not necessarily refer to computational grid cells but rather any areal division of the model domain into, e.g., a regular grid or a number of management units. During a simulation, each agent “visiting” an area at any time will have a distinct trajectory forward in time visiting other areas in the model domain. When simulating a large number of agents, the equivalent large number of trajectories forward in time can be statistically analyzed revealing the probability of areas to supply agents to other areas. This we refer to a downstream connectivity probability. Downstream connectivity answers questions such as “where do the agents go from here?”

Upstream connectivity we define as connectivity between receiving areas and source areas. Again “areas” can refer to any areal division of the model domain. During a simulation, each agent “visiting” an area at any time of the simulation will have a distinct trajectory backwards in time having visited other areas in the model domain prior to the registration of the agent in the area analyzed. When simulating a large number of agents, the equivalent large number of trajectories backwards in time can be statistically analyzed revealing the probability of areas to receive agents from other areas. This we refer to as an upstream connectivity probability. Upstream connectivity answers questions such as “where do the agents come from?”

Both upstream and downstream connectivity probabilities can be evaluated at any dispersal time ranging from seconds to years depending on the organism and dispersal phenomenon considered.

2.7 Connectivity probability

All agent trajectories stored every 6 h of the 1-year simulation period are analyzed statistically. The model domain is divided into 25 × 25 km quadratic grid cells resulting in approximately 1,000 local areas covering the sea area. This is the spatial resolution at which connectivities will be evaluated. For each agent registered in an area, the future and previous location of each agent is registered/tracked considering four dispersal times (forward and backwards in time). This is repeated for every 6 h. For details on the selection of dispersal times, see the next section.

To calculate downstream connectivity for the whole simulation period, the numbers of agents remaining in the area as well as appearing in other areas at each of the four dispersal times are counted. Downstream connectivity probabilities are calculated simply by dividing these numbers for each area by the total number of agents registered in the area analyzed. The outcome is a distribution map for each area showing the distribution of probabilities, i.e., the probability of an agent in an area to be registered sometimes in the future in the same area and in each of the surrounding areas. In cases where mortality is included in the scenario, probabilities are weighted according to the likelihood that an agent survives each of the four dispersal times.

To calculate upstream connectivity for the whole simulation period for an area, the numbers of agents originating from the same area as well as each of the surrounding areas at each of the four dispersal times backwards in time are counted. Upstream connectivity probabilities are calculated by dividing these numbers by the total number of agents registered in the area analyzed. Also here, the outcome is a distribution map for each area showing the distribution of probabilities, i.e., the probability of an agent in an area having visited each of the surrounding areas including the probability of agents that have remained in the area analyzed during the dispersal times considered.

For scenario 1 (passive drifting), scenario 2 (planktonic organism), and scenario 3 (juvenile fish) these procedures are repeated for all 25 × 25 km areas.

For scenario 4, the combination of mortality and settling was not simulated in one simulation. Since mortality is high (0.1 per day) and mean settling age is 30 days, only a very little fraction of introduced agents will reach settling age. To achieve sufficient statistical basis for the connectivity analysis, this would require a very large number of agents in the model simulation. For technical reasons, this was not desirable. Instead mortality was taken into account as part of the postprocessing of the model results.

For each agent registered in an area every 6 h, the future location where it settles is registered. For all agents registered in each area at any time for the whole simulation period, the numbers of agents settled in each of the surrounding areas, including the area analyzed, are counted and the probabilities are calculated by dividing these numbers by the total number of agents registered in the area analyzed. To account for mortality (0.1 per day), the number of agents settled in an area is adjusted using the following equation:

$$ {N}_{\mathrm{adj}} = N\times {\left(1\hbox{--}\ k\right)}^t $$
(2.1)

where:

N adj :

is the adjusted number of settled agents

N :

the number of agents settled in an area

k :

the mortality rate per day (=0.1 per day ∼0.1 daily mortality probability), and

t :

time between the time an agent is registered until it settles.

Similarly to the downstream dispersal probabilities, prior to calculating the upstream dispersal probabilities for each area in scenario 4, numbers of agent originating from each of the surrounding areas are adjusted according to the equation above, N adj now being the adjusted number of agents at the point in time where agents are discharged into the water, and t is the time between the time of discharge until the agents is settled.

For downstream connectivity probabilities in scenario 4, since agents are registered every 6 h the same agent will be registered every sixth hour starting at the time of its introduction to the model domain until it settles somewhere (on average 30 days after introduction). Every consecutive 6-h time step that the same agent is registered, the time remaining until settling decreases by 6 h. In this way, all the registrations of an agent, each time representing a time and location of release of ballast water, will correspond to the assumption that the distribution of larvae age classes is uniformly distributed in the ballast water at the time of release.

Notice that for scenario 4 while downstream connectivity probabilities reflect the assumption that all age classes are evenly represented in the ballast water at time of discharge, upstream connectivity probabilities reflect the case where organisms are age class zero at the time of discharge.

The outcome of the connectivity probability mapping for all scenarios as described above consists of connectivity probability matrices equivalent to distance matrices applied, e.g., as a look up table for distances in kilometers between major cities or locations in road atlases. Instead of distances in kilometers, the connectivity matrices include numbers representing probabilities of, in case of downstream connectivity, agents in area A ending up in area B and agents in area B ending up in area A. Contrary to a distance matrix, either direction has different probabilities. A conceptual example is shown in Table 1.

Table 1 Example of a downstream connectivity matrix for 4 areas (1–4). Table values represent probabilities of agents in one area (=source area) ending up in another area (=receiving area)
Full size table

The resulting connectivity matrices will consist of approximately two 1,000 × 1,000 matrices for downstream and upstream connectivities respectively, for each set of dispersal times. Connectivity probabilities for each area can be extracted from the two matrices to produce connectivity probability maps for downstream and upstream connectivities respectively. These approximately 2,000 maps can be referred to a multilayer connectivity maps or MCMs and are available as Online Supplementary Material.

Ideally, in cases where all agents simulated as passive drifters (as in scenario 1) and where agents are not subject to mortality, the sum of probability values within each probability map will be 1. However, when mortality is included as part of the ABM, the sum of probabilities will be less than 1, with all probabilities (in case of downstream connectivity) representing the probability of an organism being distributed to other areas a specific point in time ahead.

Since connectivity probabilities are expected to vary spatially depending on the dispersal time considered, four dispersal times were selected for each analysis in order to cover a range of dispersal situations for a given organism. These four dispersal times were selected for each analysis from three criteria: (1) ecological relevance, (2) a minimum of 10 % of agents at t = 0 remaining at any dispersal time, and (3) seasons evenly reflected in calculation results. Here “ecological relevance” refers to, e.g., that the dispersal time should lie within the expected life duration and/or the duration of the pelagic stage.

For scenario 1 (passive drifting) upstream and downstream connectivity probabilities are calculated for different sets of four dispersal times: 2, 4, 6, and 8 days, 3, 9, 15, and 21 days, and 7, 14, 21, and 28 days. The different sets of dispersal times are used for comparison with scenarios 2, 3, and 4 (see below), and in order to evaluate how selections of different dispersal times may influence the calculated connectivities. A maximum of 28 days were applied primarily to ensure that months and seasons were evenly reflected in calculation results.

For scenario 2 (planktonic species) upstream and downstream connectivity probabilities are calculated for four dispersal times: 3, 9, 15, and 21 days. These were selected for the following reasons: since a mortality of 0.1 day−1 is applied, 10 % of the agents at t = 0 remains approximately 24 days later. The 24 days were divided evenly into four time periods (0–6 days, 6–12 days, etc.) and the mean day numbers of each of four 6-day periods were selected as the four dispersal times (∼3, 9, 15, and 21 days).

For scenario 3 (fish), upstream and downstream connectivity probabilities are calculated for four dispersal times: 1, 2, 3, and 4 weeks. These were selected for the following reasons: since juvenile fish typically has much lower mortality (here, 0.003 day−1) 10 % of agents will remain after approximately 2 years. Thus, to cover the entire time span, this will require a much longer simulation than the 1-year simulation for the current study. In addition, the need to reflect months and seasons evenly results in a maximum of approximately 1 month dispersal time being selected. Based on these considerations, four weekly dispersal times were selected.

For scenario 4 (pelagic larvae of benthic invertebrate) upstream and downstream connectivity probabilities are calculated for the same four dispersal times as for scenario 2.

2.8 Connectivity indices

The primary strength of the connectivity probability matrices described in the previous section is to give detailed information on how connected any two areas are within the modeling domain integrated over time. However, more than 1,000 maps require some kind of simplification in order to provide a more overall measure on how well-connected areas are in general without necessarily providing any information on precisely which areas are interconnected. Within ballast water risk assessment, there is a need to distinguish between areas more likely to export organisms far away and/or to a larger area than other areas (∼through downstream connectivity). These areas with high dispersal potential can be perceived as high risk zones where the release of invasive species through ballast water may have an increased potential of reaching optimal habitat conditions thereby increasing the likelihood for establishing a population successfully. Here, we propose a methodology to compile all information from the downstream connectivity probability maps into one single map using a simple and transparent approach.

Similarly, in terms of upstream connectivity, it is important to identify areas more likely to receive invasive species than others, i.e., acting as sinks. These areas can be identified from upstream connectivity probability matrices as areas with high probabilities of receiving agents from far away and/or from a large area.

It is clear that the proposed simplification of connectivities through the development of connectivity indices assumes that agents are distributed randomly within the entire modeling domain which is not the case when it comes to invasive species from ballast water. However, indices will give indications on where release of ballast water may be more likely to result in a significant spread of organisms, and which areas will be more likely to receive invasive species than others. This type of information is important from a management point of view.

For calculation of connectivity indices with the term “momentum” (M) is introduced. Momentum can be calculated in several ways. The momentum can be calculated for each area and its probability map by simply summing the products of connectivity probabilities of each surrounding area and the distances to the areas:

$$ M\left(\mathrm{area}\ i\right)=\sum Prob\left(\mathrm{area}\ j\right)\times D\left(\mathrm{area}\ j\right) $$
(2.2)

This approach weights the probabilities with distance only. The results presented in this report apply this formula. However, alternative definitions of “Momentum” may be applied to include multiplication of probabilities with areal coverage instead of distance, or a combination of areal coverage and distance, where areal coverage refers to the size of the area covered by say the 90 % fractile of probabilities.

3 Results and discussion

The hydrodynamic model has been validated in terms of water level, salinity and temperature in a number of stations. The comparisons generally show a fairly good comparison between measurement and model. A few examples of this validation are given in Appendix 2 (see locations in Fig. 1). The comparisons demonstrate that the model is able to reproduce the water temperatures well within the model domain. Both the variability and the absolute values are captured by the model. The annual cycle of the thermal stratification is described well by the model. Also, the salinity conditions are described well by the model. The model captures the salinity stratification and the intrusions of saline North Sea water through the Belt Sea to the Arkona and Bornholm basins and further into the Gotland Deep in the Baltic Proper. The vertical structure of the water column in the northern North Sea is illustrated in Fig. 4b, which shows the annual mean salinity and water temperature in a vertical section between Scotland and Norway. The lower salinities of surface waters along the Norwegian coast represent the outflowing brackish Baltic water.

Fig. 4
figure 4

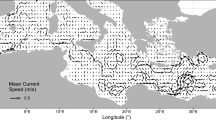
a Modeled annual (2005) mean surface currents. b Modeled annual mean water temperature in a vertical section from Scotland to Norway. c The north-south current component in the same vertical section. See Fig. 1 for the location of the vertical section

Full size image

The model includes the tidal currents as well as the meteorologically induced and the baroclinic currents. The modeled annual mean surface currents are shown in Fig. 4a. The mean current may be regarded as the residual currents, which may be expected to be important with respect to connectivity. Significant northward and northeastward residual current is observed in the southeastern and eastern part of the North Sea, whereas the western part displays relatively lower residual currents. In the Belt Sea, an outward (northward) residual surface flow is observed, which transports the brackish Baltic water out into Skagerrak. In Skagerrak, an anticlockwise gyre is observed and a residual flow along the Norwegian coast brings the Baltic surface water into the North Sea and further into the Norwegian Sea. All these features are in accordance with the literature. In the vertical, Fig. 4c shows a marked outward residual current in the upper water column along the Norwegian coast. This represents the outflow of mixed, brackish Baltic water and is consistent with the vertical salinity distribution mentioned above. In other parts of the vertical cross-section, a relatively low, southward residual current is observed.

Because the calculation procedures are repeated for each 6-h time step of the 1-year simulation time, each agent will be included multiple times as part of the statistical basis for the analyses. Thus, the total number of agents being analyzed results in a large number of agents as the basis for the statistical probability maps.

The statistical analyses of connectivity were done based on results from the ABM simulations carried out for both a regional model for the entire model domain and a local model for the Kattegat, the Belts, and the western part of the Baltic Sea. The statistical basis for the downstream connectivity of scenario 1 is shown in Figs. 5 and 6 for the two models. For the vast majority of the model domain, the statistical basis for each area is more than 1,000 agents. Smaller numbers are found close to the shorelines and in the inner Danish straits. This is partly because a part of the 25 × 25 km squares along shorelines include land and thus the area covered by water is smaller than 25 × 25 km. In addition, the smaller numbers may be a result of more agents being excluded from the simulation because agents closer to land and in shallow areas more likely hit land or seafloor boundaries.

Fig. 5
figure 5

Statistical basis for the downstream connectivity probability mapping of scenario 1. Numbers are numbers of agents available for the statistical analysis of the downstream connectivity using the regional model

Full size image
Fig. 6
figure 6

Statistical basis for the downstream connectivity probability mapping of scenario 1. Numbers are numbers of agents available for the statistical analysis of the downstream connectivity using the local model

Full size image

As described in the previous sections, these coastal areas are discarded from the statistical analyses. Also in areas located close to the open boundaries of the model domain, the statistical basis is small because of many agents crossing the open boundaries and subsequently not available for statistical analyses. Because of these issues, the robustness of the methodology based on the current simulations is strongest in the open waters of the North Sea, Kattegat, and the eastern Baltic Sea, and may be less robust in some parts of the coastal and shallow waters, and close to the open model boundaries. Robustness can be improved by applying more agents in the inner Danish straits, by improving the model describing the agent trajectories more correctly close to land and seafloor boundaries, and by extending the model domain further out in order to reduce the impact of open model boundaries on connectivity statistics. The statistical basis shown in Figs. 5 and 6 is for scenario 1 for 1 week dispersal time. Similarly, data on statistical basis can be shown for scenarios 2–4 and for each dispersal time.

3.1 Connectivity probability maps

An example of downstream connectivity probability maps for scenario 1 (simple drifting) for one selected area in the North Sea (indicated by red arrows) for four different dispersal times: 1, 2, 3, and 4 weeks is shown below (Fig. 7). Values are probability values between 0 and 1, and the sum of probabilities in each map is 1 since no mortality is considered. Only values greater than 0.01 are shown. In all maps, the probability distributions are highly influenced by north-going currents along the west coast of Jutland showing that probability values greater than 0.01 are dominating in the northern and northeastern directions. Maps also indicate that there are significant differences in probability maps depending on the dispersal time considered—the longer the dispersal time considered, the further away agents move.

Fig. 7
figure 7

Downstream connectivity probability maps for one selected area in the North Sea (indicated by red arrows) for four dispersal times: 1, 2, 3, and 4 weeks. Only probability values larger than 0.01 are shown

Full size image

Four probability maps of the four different dispersal times are combined into one probability map (Fig. 8). Because no mortality is included, each dispersal time weighted equally and probabilities for the four dispersal times are simply averaged.

Fig. 8
figure 8

Downstream connectivity probability map for one selected area (the same as in Fig. 7) in the North Sea (indicated by red arrow) with aggregated probability values for 1, 2, 3, and 4 weeks’ dispersal times

Full size image

All probability maps presented in Figs. 7 and 8 reflect the hydrodynamical variations during 2005 for scenario 1 where simple drifting is simulated. Similar maps for any area within the model domain can be extracted from the downstream connectivity matrices for scenarios 1–4 representing a given dispersal time or a combination of dispersion times. For scenarios where mortality is included, the connectivity probability maps of the combination of the four dispersal times are weighted according to the probability of agents to survive on each of the four dispersal times. This will result in an aggregated probability map where, e.g., 1 week dispersal probabilities will be weighted more than 2-, 3-, and 4-week probability values. Other dispersal times, e.g., 2, 4, 6, and 8 days, will show probability maps with a much narrower distribution of >0.01 probabilities around each area. These are not presented here.

Similarly, maps for upstream connectivity probabilities can be extracted for each area representing the probability of agents registered in an area having come from other areas. Results for the upstream analyses are not presented here.

Both upstream and downstream probability connectivity maps for scenario 1 aggregated over time for every 25 × 25 km blocks are available on Online Supplementary Material.

3.2 Connectivity indices

Downstream momentum was calculated for the four scenarios based on the aggregated connectivity probabilities (=probabilities evaluated based on multiple dispersal times). Notice that momentums for scenario 3 are based on combined 1-, 2-, 3-, and 4-week dispersal times, while for scenarios 2 and 4, momentums are based on combined 3, 9, 15, and 21 days dispersal times. For comparisons, scenario 1 will be evaluated at each of these set of time scales.

Downstream momentum for scenario 1 for 1-, 2-, 3-, and 4-weeks’ dispersal times are shown in Figs. 9 and 10.

Fig. 9
figure 9

Downstream connectivity indices (momentums) for scenario 1 (passive particle tracking). Indices are based on combined 1-, 2-, 3-, and 4-weeks’ dispersal times

Full size image
Fig. 10
figure 10

Downstream connectivity indices (momentums) for scenario 1 (passive particle tracking) presented as deviation from mean value in percentages for 1-, 2-, 3-, and 4-weeks’ dispersal times

Full size image

The greatest downstream momentum values are found in the northeastern part of the North Sea between the Danish and Norwegian coasts, along the west coast of the Netherlands and in Kattegat and the Danish belts, while large parts of the western part of the North Sea, German Bight, and the Baltic sea east of Bornholm have low connectivities.

Downstream momentum for scenario 2 for 3-, 9-, 15-, 21-days’ dispersal times are shown in Figs. 11 and 12.

Fig. 11
figure 11

Downstream connectivity indices (momentums) for scenario 2 (planktonic organisms). Indices are based on combined 3-, 9-, 15-, and 21-days’ dispersal times

Full size image
Fig. 12
figure 12

Downstream connectivity indices (momentums) for scenario 2 (planktonic organism) presented as deviation from mean value in percentages for 3-, 9-, 15-, and 21-days’ dispersal times

Full size image

Downstream momentum values of scenario 2 show a similar distribution pattern as in scenario 1. Notice that dispersal time applied for scenarios 1 and 2 are different. For more accurate comparison, see the following section.

Downstream momentum for scenario 3 for 1-, 2-, 3-, 4-weeks’ dispersal times are shown in Figs. 13 and 14.

Fig. 13
figure 13

Downstream connectivity indices (momentums) for scenario 3 (juvenile fish). Indices are based on combined 1-, 2-, 3-, and 4-weeks’ dispersal times

Full size image
Fig. 14
figure 14

Downstream connectivity indices (momentums) for scenario 3 (juvenile fish) presented as deviation from mean value in percentages for 1, 2, 3, and 4 weeks’ dispersal times

Full size image

Downstream momentum values for scenario 3 show a similar distribution pattern to that in scenario 1. For more accurate comparison see the following section.

Downstream momentums for scenario 4 for dispersal times corresponding to the time duration of the time between the registration of each organism until it settles are shown in Figs. 15 and 16.

Fig. 15
figure 15

Downstream connectivity indices (momentums) for scenario 4 (pelagic larvae). Indices are based on dispersal times corresponding to the time duration until each individual settles

Full size image
Fig. 16
figure 16

Downstream connectivity indices (momentums) for scenario 4 (pelagic larvae) presented as deviation from mean value in percentages for dispersal times corresponding to the time duration until each individual settles

Full size image

Downstream momentum values for scenario 4 show a similar overall distribution pattern to those seen in scenarios 1, 2, and 3, however with some deviation. For more accurate comparison see the following section.

3.3 Importance of dispersal time

The selection of dispersal time for evaluating connectivity between marine areas is important simply because the longer time we “follow” the dispersal of an organism, the longer distance the organism is likely to travel, given that the organism is still alive. In terms of connectivity indices, this implies that longer dispersal times give greater connectivity indices. However, in addition to the magnitude of the connectivity indices, the spatial pattern of connectivity indices may change. As an example, connectivity indices were calculated for scenario 1 for two sets of dispersal times: 2, 4, 6, 8 days, and 7, 14, 21, 28 days and deviation from the overall mean value were plotted (Fig. 17). Although the overall patterns of the two plots for the two sets of dispersal times are similar, some discrepancies are evident. Some areas show larger deviation from the mean value when evaluated on a longer time span, while others show smaller deviation from the mean value.

Fig. 17
figure 17

Downstream connectivity indices (momentums) for scenario 1 (passive particle tracking) presented as deviation from mean value in percentages for 2-, 4-, 6-, and 8-days (left) and 1-, 2-, 3-, and 4-weeks’ (right) dispersal times

Full size image

3.4 Importance of biological factors

As for the selection of dispersal time when evaluating connectivity between marine areas, biological factors including mortality, settling, etc., are important because the longer an organism lives, the longer we can “follow” the dispersal of an organism and the longer distance the organism is likely to travel if flow conditions are suitable. Thus, when applying connectivity probability maps to predict, for instance, the likelihood that an introduced organism in an area will spread to other specific areas, biological factors are important.

Biological factors may also have an effect when comparing the connectivities between areas. In Figs. 18 and 19 are shown the comparisons for scenarios 1 and 2, and scenarios 1 and 3, respectively, for the calculated deviation from the mean value of the connectivity indices. Comparisons between scenarios 1 and 2 are done for 3-, 9-, 15-, 21-days’ dispersal time, and comparisons between scenarios 1 and 3 are done for 7-, 14-, 21-, 28-days’ dispersal times. Both comparisons show a similar overall pattern in the variability of connectivity indices. However, scenario 2 shows some differences compared to scenario 1. For instance, connectivity indices in the Danish belts show significantly lower deviation from mean than in scenario 1. This indicates that when evaluating the connectivity of specific marine areas for organisms with high mortality, it may be important to consider their mortality when simulating the spread of organisms. Scenario 3 on the contrary shows very little deviation from scenario 1 indicating that swimming behavior simulated as random walk has no major effect on the spatial variability in connectivity.

Fig. 18
figure 18

Comparison of downstream connectivity indices (momentums) for scenario 1 (passive particle tracking) and scenario 2 (planktonic organism. Left panel Scenario 2 (planktonic organism). Right panel Scenario 1 (passive particle tracking). Presented as deviation from mean value in percentages for 3-, 9-, 15-, 21-days’ dispersal times

Full size image
Fig. 19
figure 19

Comparison of downstream connectivity indices (momentums) for scenario 1 (passive particle tracking) and scenario 3 (juvenile fish). Left panel Scenario 3 (juvenile fish). Right panel Scenario 1 (passive particle tracking). Presented as deviation from mean value in percentages for 1-, 2-, 3-, 4-weeks’ dispersal times

Full size image

For scenario 4, comparisons are done with scenario 2, not scenario 1, since scenario 4 is not evaluated on selected dispersal time, but rather dispersal times corresponding to the time duration from the time of registration of an agent in an area until it settles. To get an idea how settling affects the momentum, comparison of “deviations from mean” between scenario 2 and 4 are shown (Fig. 20). Differences between scenarios 2 and 4 are the settling introduced in scenario 4 and that momentums of scenario 2 are evaluated at discrete dispersal times (3, 9, 15 and 21 days). Here, as for scenarios 2 and 3, the main overall patterns in the variability of connectivity indices are maintained, with some deviations locally.

Fig. 20
figure 20

Comparison of downstream connectivity indices (momentums) for scenario 2 (planktonic organisms) and scenario 4 (pelagic larvae of benthic invertebrate). Left panel Scenario 4 (pelagic species). Right panel Scenario 2 (planktonic organism). Presented as deviation from mean value in percentages. Dispersal times evaluated for scenario 2 is 3, 9, 15, and 21 days and for scenario 4 the time duration until each individual settles

Full size image

3.5 Momentum—upstream

Upstream connectivity indices are only shortly presented here since the main focus of this study is to identify areas where the release of ballast water may have a high potential for spreading to other parts of the North Sea region. We will not go into detail on how dispersal time or biological factors may affect the outcome of the upstream connectivity analysis. However, in general, the upstream connectivity indices show similar spatial variability between areas, clearly identifying areas more likely to receive ballast-water-derived organisms from far away. Figure 21 shows the upstream connectivity indices for scenario 1 (passive particle tracking) based on 1-, 2-, 3-, 4-weeks’ dispersal times.

Fig. 21
figure 21

Upstream connectivity indices (momentums) for scenario 1 (passive particle tracking). Indices are based on combined 1-, 2-, 3-, and 4 weeks’ dispersal times

Full size image

Areas with the highest values of upstream connectivity are primarily areas of the deeper part of the waters between northwestern Jutland and Norway and along the southwestern Norwegian coast. The values are highly distinct from other marine areas and this indicates that these areas serve as major sinks or receiving water bodies of passively transported agents. Again, as for the downstream connectivity, lowest values are found in particular in the western part of the North Sea, in the German Bights and the Baltic Sea east of Bornholm. Intermediate values are found in the eastern part of the North Sea, in Kattegat, the Danish straits including Fermarn Belt, and in the western parts of the Baltic Sea.

4 Conclusions and outlook

The analyses carried out for this study show that when evaluating the connectivity of marine waters of the North Sea region including Skagerak, Kattegat, the Danish belts, and the western parts of the Baltic Sea, the hydrodynamics seem to play the most important role when considering small organisms with limited ability to perform a significant autonomic movement behavior. Despite some differences in calculated connectivities due to biological factors and the choice of dispersal time applied for the connectivity analyses, the overall pattern of the variability of connectivity indices show, at least at this preliminary stage of analysis and at a regional level, a rather unambiguous indication that biological factors and dispersal time are only of secondary importance when ranking areas according to their degree of connectivity. At the local level, however, under some conditions, biological factors as well as the choice of dispersal time applied may play an important role.

We recommend that additional biological factors that could have a potential impact on connectivity of marine areas should be identified and tested to sustain (or contradict) these conclusions. These may include: (1) simulation of diurnal vertical migration of planktonic species, (2) simulation of oriented swimming behavior of juvenile fish, and (3) analyses of differences in connectivity between seasons.

Also, the methodology proposed here for calculating connectivity (as momentums) solely depending on the distance traveled by each simulated organism during a number of dispersal time needs to be consolidated. As an example, the inclusion of the area covered by, e.g., a 90 % fractile of connectivity probabilities could be considered.

In addition to connectivity indices, the downstream connectivity probability maps for each individual area have a very high potential for predicting the probability of a ballast-water-derived organism ending up at a specific location, e.g., locations identified as being especially sensitive or at locations providing suitable habitat for specific species. Similarly, upstream connectivity probability maps for a specific area (a given habitat, Marine-Protected Areas, etc.) predict which areas may potentially contribute with ballast-water-derived organisms.

The primary aim of the methodology presented here is to demonstrate how to apply a combination of agent-based modeling and hydrodynamical modeling to describe and develop measures for the inter-connectivity of marine ecosystems systems and its potential application for ballast water risk assessment. During this work, a number of issues have been identified on how to improve the methodology: (1) the hydrodynamical model was not developed specifically to address these issues, in particular near-shore hydrodynamics are important to avoid agents being “captured” in still water which in most cases may be a model resolution artifact rather than a true hydrodynamical phenomenon, (2) agent-based models may be further developed to be species-specific including habitat preferences, environmental stresses and population dynamics, and (3) inclusion of water quality modeling will improve prediction of the effects on environmental stressors on agents.

In case our prototype tool is further developed, we foresee that it may be useful for at least three other purposes:

  1. 1.

    Data layers for assessments of cumulative human pressures and impacts (sensu Halpern et al. 2008). Mapping of cumulative pressures and impacts relies on ecologically relevant data layers, both for pressures and ecosystem components. The downstream connectivity index presented in this study could potentially be regarded as a pressure layer representing likely dispersal routes of introduced alien species. According to the EU Marine Strategy Framework Directive (Anon 2008), which is based on the Ecosystem Approach to management of human activities, all “marine” EU Member States are required to map cumulative pressures (see examples in Korpinen et al. 2012 and Andersen et al. 2013). The mapping carried out so far in Europe does not, as far as we know, take into account aliens species and their potential dispersal routes. It would in our opinion be an important step forward to full implementation of the Ecosystem Approach as both alien species and dispersal routes are included in the next generation of cumulative impact assessments

  2. 2.

    Marine Spatial Planning, including zoning and site selection, i.e., for future designation and design of Marine-Protected Areas taking the identification of so-called “Blue Corridors” into consideration (Martin et al. 2006). We foresee that the connectivity index can be modified and used for estimation of where species-specific “Blue Corridors” might be located. If so, the index developed and presented in this study could be useful for evidence-based design and designation of networks of Marine-Protected Areas in regional seas or at subregional scale.

  3. 3.

    Ballast water risk assessments, especially in regard to exemptions from the Ballast Water Management Convention (BWMC), adopted in 2004 (IMO 2004). Exemption can be granted from ships sailing routinely between specific ports or locations and is based on a risk assessment (RA) using the best available scientific information (MEPC 2007). In our opinion, the approach presented and discussed in this study potentially set a new standard for what can de done when assessing the risk. For example, the modeling setup can be modified to specific local conditions (salinity, temperature, dominating currents, etc.) and target to specific organisms of interests.

In conclusion, we have developed a prototype Decision Support Tool for modeling of risks of spreading of introduced alien species via ballast water. The prototype tool reported is based on two types of models and a postprocessing activity: Firstly, a 3D hydrodynamical model calculates the currents in the North Sea and Danish Straits. Secondly, an agent-based model estimates the dispersal of selected model organisms with the current regime calculated by the 3D model. Thirdly, scenarios of dispersal are combined into an interim estimate of connectivity within the study area.

The prototype tool should in our opinion be regarded as a platform for further development and testing. However, it can in its present form be used for interim estimates of connectivity and hence as a tool for assessment of potential risk associated to intentional or unintentional discharges of ballast water. The tool can also be used for other purposes, e.g., in regard to ecosystem-based management and the implementation of the EU Marine Strategy Framework Directive.