1 Introduction

Topological complexity is a topological invariant that was introduced by Farber [3]. It is intended to solve problems such as motion planning in robotics. To catch this aim, a computable algorithm is needed, for each pair of points of the configuration space of a mechanical or physical device, a path connecting them in a continuous way. Farber used a well-known map in algebraic topology that is a section of the path-fibration and he interpreted that algorithm in terms of this map. In 2010, Rudyak introduced a notion of higher topological complexity in [8] which is later improved by Basabe, Gonzalez, Rudyak and Tamaki in [2]. After that a discrete version of topological complexity is established by Fernandez-Ternero et al. [4].

The importance of discretisation is based on the fact that many motion planning methods transform a continuous problem into a discrete one. So the aim of the present paper is to extend the Rudyak’s approach to discrete version. Namely, we define the nth discrete topological complexity.

Before we introduce the nth discrete topological complexity, let us recall some known definitions and theorems.

Definition 1.1

Let K be a simplicial complex. An edge path in K is a finite or infinite sequence of vertices such that any two consecutive vertices span an edge. We say that K is edge path connected if any two vertices can be joined by a finite edge path.

Definition 1.2

Two simplicial maps \(\varphi , \psi : K \rightarrow L\) are said to be contiguous (denoted by \(\varphi \sim _c \psi \)) if for every simplex \(\{v_0, \dots , v_k\}\) in K, \(\{\varphi (v_0), \dots , \varphi (v_k),\psi (v_0), \dots ,\) \(\psi (v_k)\}\) constitutes a simplex in L.

Definition 1.3

Two simplicial maps \(\varphi , \psi : K \rightarrow L \) are said to be in the same contiguity class (denoted by \(\varphi \sim \psi \)) if there exists a finite sequence of simplicial maps \(\varphi _i: K \rightarrow L\) for \(i=0,1,\dots m\) such that \(\varphi = \varphi _1 \sim _c \varphi _2 \sim _c \dots \sim _c \varphi _m= \psi \).

For two simplicial complexes K and L, if there are simplicial maps \(\varphi : K\rightarrow L\) and \(\psi : L\rightarrow K\) such that \(\varphi \circ \psi \sim \textrm{1}_K\) and \(\psi \circ \varphi \sim \textrm{1}_{L}\), then K and L are said to have the same strong homotopy type, and is denoted by \(K\sim L\). If \(K\sim \{v_0\}\) where \(v_0\) be a vertex in K, then K is said to be strongly collapsible.

The cartesian product of simplicial complexes is not necessarily a simplicial complex. So a “new” product on simplicial complexes is defined to make their product into a simplicial complex. It is the categorical product of simplicial complexes and for two simplicial complexes \(K_1\) and \(K_2\), it is defined as follows.

  1. (i)

    The set of vertices is defined by \(V(K_1\prod K_2):=V(K_1)\times V(K_2)\).

  2. (ii)

    If \(p_i: V(K_1\prod K_2)\rightarrow V(K_i)\) is the projection map for \(i=1,2\), then a simplex \(\sigma \) is said to be in \(K_1\prod K_2\) if \(p_1(\sigma )\in K_1\) and \(p_2(\sigma )\in K_2\).

(for more details, see [7]).

Definition 1.4

[6] Let K be a simplicial complex. A subcomplex \(\Omega \subset K\) is said to be categorical if the inclusion \(i:\Omega \hookrightarrow K\) and a constant map \(c_{v_0}: \Omega \rightarrow K\), where \(v_0 \in K\) is some fixed vertex, are in the same contiguity class.

Definition 1.5

[6] The simplicial Lusternik-Schnirelmann category \(\textrm{scat}(K)\) is the least integer \(k\ge 0\) such that there exist categorical subcomplexes \(\Omega _0,\Omega _1,\dots , \Omega _k\) of K covering K.

Definition 1.6

[4] We say that \(\Omega \subset K^2\) is a Farber subcomplex if there is a simplicial map \(\sigma : \Omega \rightarrow K\) such that \(\Delta \circ \sigma \) \(\sim \iota _{\Omega }\) where \(\Delta : K \rightarrow K^2\), \(\Delta (v) = (v,v)\) is the diagonal map and \(\iota _{\Omega }: \Omega \hookrightarrow K^2\) is the inclusion map.

Definition 1.7

[4] The discrete topological complexity \(\textrm{TC}(K)\) of a simplicial complex K is the least non-negative integer k such that \(K^2\) can be covered by \(k+1\) Farber subcomplexes. More precisely, \(K^2 = \Omega _0 \cup \cdots \cup \Omega _k\) and there exist simplicial maps \(\sigma _j: \Omega _j \rightarrow K\) satisfying \(\Delta \circ \sigma _j \sim \iota _j\) where \(\iota _j: \Omega _j \hookrightarrow K^2\) are inclusions for each \(j = 0,\dots ,k\).

2 Higher analogues of discrete topological complexity

Proposition 2.1

If \(\varphi , \psi : K \rightarrow L\) are in the same contiguity class, then so are \(\varphi ^n\) and \(\psi ^n\).

Proof

Without loss of generality we will focus on being contiguous and show that if \(\varphi \sim _c \psi \), so is \(\varphi ^n \sim _c \psi ^n\).

Suppose that \(\varphi \sim _c \psi \). If

\(\sigma = \{(a_{11},a_{12},\dots ,a_{1m}),(a_{21},a_{22},\dots ,a_{2m}),\dots ,(a_{n1},a_{n2},\dots ,a_{nm})\}\)

is a simplex in \(K^m\), then one can say that \(\pi _1(\sigma )=\{a_{11},a_{21},\dots ,a_{n1}\}\), \(\pi _2(\sigma )=\{a_{12},a_{22},\dots ,a_{n2}\}\), \(\dots \), \(\pi _n(\sigma )=\{a_{1m},a_{2m},\dots ,a_{nm}\}\) are simplices of K. Hence, for each \(i=1,2,\dots ,m\),

\(\varphi (\pi _i(\sigma )) \cup \psi (\pi _i(\sigma )) = (\varphi (a_{1i}),\cdots ,\varphi (a_{ni}),\psi (a_{1i}),\cdots ,\psi (a_{ni}))\)

belongs to L, so that \(\varphi ^n(\sigma ) \cup \psi ^n(\sigma )\) belongs to \(L^m\). \(\square \)

Definition 2.1

We say that \(\Omega \subset K^n\) is an \(n-\)Farber subcomplex if there is a simplicial map \(\sigma : \Omega \rightarrow K\) such that \(\Delta \circ \sigma \) \(\sim \iota _{\Omega }\) where \(\Delta : K \rightarrow K^n\), \(\Delta (v) = (v,v,\dots ,v)\) is the diagonal map and \(\iota _{\Omega }: \Omega \hookrightarrow K^n\) is the inclusion map.

Definition 2.2

The nth discrete topological complexity \(\textrm{TC}_n(K)\) of a simplicial complex K is the least non-negative integer k such that \(K^n\) can be covered by \(k+1\) n-Farber subcomplexes. More precisely, \(K^n = \Omega _0 \cup \cdots \cup \Omega _k\) and there exist simplicial maps \(\sigma _j: \Omega _j \rightarrow K\) satisfying \(\Delta \circ \sigma _j \sim \iota _j\) where \(\iota _j: \Omega _j \hookrightarrow K^n\) are inclusions for each \(j = 0,\dots ,k\).

Theorem 2.1

For a subcomplex \(\Omega \subset K^n\), the followings are equivalent.

  1. (1)

    \(\Omega \) is an n-Farber subcomplex.

  2. (2)

    \((\pi _i)_|{}_\Omega \sim (\pi _j)_|{}_\Omega \) for all \(i,j\in \{1,2,\ldots ,n\}\).

  3. (3)

    One of the restrictions \((\pi _1)_|{}_\Omega , (\pi _2)_|{}_\Omega , \ldots , (\pi _n)_|{}_\Omega \) is a section (up to contiguity) of the diagonal map \(\Delta :K \rightarrow K^n\).

Proof

\((1) \Rightarrow (2)\): Suppose that \(\Omega \subset K^n\) is an \(n-\)Farber subcomplex. Then there exists a simplicial map \(\sigma : \Omega \rightarrow K \) such that \(\Delta \circ \sigma \sim \iota _\Omega \).

Observe that \(\Delta \circ \sigma \) is an n-tuple of \(\sigma \)’s, that is, \(\Delta \circ \sigma =(\sigma , \ldots , \sigma ): \Omega \rightarrow K^n\) by \(\Delta \circ \sigma (\omega )=(\sigma (\omega ), \ldots , \sigma (\omega ))\).

On the other hand, the inclusion map \(\iota _\Omega :\Omega \hookrightarrow K^n\) can be written as

$$\begin{aligned} \iota _\Omega =(\pi _1|_{\Omega }, \ldots , \pi _n|_{\Omega }). \end{aligned}$$

So we have

$$\begin{aligned} (\sigma , \ldots , \sigma )=\Delta \circ \sigma \sim (\pi _1|_{\Omega }, \ldots , \pi _n|_{\Omega }). \end{aligned}$$

Hence, \(\sigma \sim \pi _i|_{\Omega }\) for each i.

\((2) \Rightarrow (3)\): Fix \(i_0 \in \{1, 2, \ldots , n\}\) and suppose that \(\pi _i|_\Omega \sim \pi _{i_0}|_\Omega \) for all \(i\in \{1,2,\ldots ,n\}\). Then

$$\begin{aligned} \iota _\Omega =\big ( \pi _1|_\Omega , \ldots , \pi _n|_\Omega \big )\sim \big ( \pi _{i_0}|_\Omega , \ldots , \pi _{i_0}|_\Omega \big ) = \Delta \circ \pi _{i_0}|_\Omega . \end{aligned}$$

which means that one of the \(\pi _{i_0}|_\Omega \)’s is a section of \(\Delta \).

\((3) \Rightarrow (1)\): Suppose that \((\pi _i{})_|{}_\Omega \) is a section (up to contiguity) of the diagonal map \(\Delta \), for some \(i\in \{ 1,2,\ldots ,n\}\) and choose the simplicial map \(\sigma :=(\pi _i{})_|{}_\Omega :\Omega \rightarrow K\). Then \(\Omega \) is an \(n-\)Farber subcomplex. \(\square \)

Theorem 2.2

\(\textrm{TC}_m(K)\le \textrm{TC}_{m+1}(K)\).

Proof

Let \(\textrm{TC}_{m+1}(K)=\ell \). Then there exist \(\Omega _0, \ldots , \Omega _{\ell }\) \((m+1)-\)Farber subcomplexes of \(K^{m+1}\) covering \(K^{m+1}\). By Theorem 2.1,

$$\begin{aligned} (\pi _1)_|{}_{\Omega _j} \sim (\pi _2)_|{}_{\Omega _j} \sim \ldots \sim (\pi _{m+1})_|{}_{\Omega _j} \end{aligned}$$

for each \(j\in \{0,1,\ldots ,\ell \}\), where \(\pi _i:K^{m+1}\rightarrow K\) is the projection to the ith factor.

If we show that there are \(\Lambda _0, \ldots , \Lambda _{\ell }\) subcomplexes of \(K^{m}\) covering \(K^{m}\) such that \((\pi ^1)_|{}_{\Lambda _j} \sim (\pi ^2)_|{}_{\Lambda _j} \sim \ldots \sim (\pi ^{m})_|{}_{\Lambda _j}\) for each \(j\in \{0,1,\ldots ,\ell \}\), where \(\pi ^i:K^m\rightarrow K\) is the projection to the ith factor, then we are done.

For a fixed vertex \(\omega \in K\), define the simplicial map

$$\begin{aligned} g: K^m\rightarrow K^{m+1}, \hspace{0.1in} \text {by} \hspace{0.1in} g(v^1,\ldots , v^m)=(v^1,\ldots , v^m,\omega ) \end{aligned}$$

and for each \(j\in \{0,1,\ldots ,\ell \}\), define the subcomplex \(\Lambda _j:= g^{-1}(\Omega _j)\).

We have \(\pi ^i |_{\Lambda _j}=\pi _i |_{\Omega _j}\circ g: \Lambda _j \rightarrow \Omega _j \rightarrow K\), for \(i\in \{1,\ldots ,m\}\) and \(j\in \{0,1,\ldots ,\ell \}\).

For every \(j\in \{0,1,\ldots ,\ell \}\), since \((\pi _i)_|{}_{\Omega _j} \sim (\pi _{k})_|{}_{\Omega _j}\) for each \(i,k\in \{1,\ldots , m+1\}\), we have \((\pi ^i)_|{}_{\Lambda _j} \sim (\pi ^{k})_|{}_{\Lambda _j}\) for each \(i,k\in \{1,\ldots , m\}\). \(\square \)

Theorem 2.3

If \(K \sim L\), then \(\textrm{TC}_n(K) = \textrm{TC}_n(L)\), i.e., the nth discrete topological complexity is an invariant of the strong homotopy type.

Proof

We proceed in three steps.

Step 1. Let us show that if \(K\sim L\), then \(K^n \sim L^n\).

Suppose that K and L are of the same strong homotopy type, then by definition, there are simplicial maps \(\varphi , \psi \) satisfying \(\varphi \circ \psi \sim 1_L\) and \(\psi \circ \varphi \sim 1_K\). First consider the case \(\varphi \circ \psi \sim 1_L\). By Proposition 2.1, we obtain

$$\begin{aligned} \varphi ^n \circ \psi ^n =(\varphi \circ \psi )^n \sim (1_L)^n = 1_{L^n}. \end{aligned}$$

Using same arguments, we show that \(\psi ^n \circ \varphi ^n \sim 1_{K^n}\). Hence, we have \(K^n \sim L^n\).

Step 2. Next we show that if \(\Omega \subset K^n\) is an nth Farber subcomplex, then so is \((\psi ^n)^{-1}(\Omega )\subset L^n\).

There exists a simplicial map \(\sigma : \Omega \rightarrow K\) so that \(\Delta _K \circ \sigma \sim \iota _{\Omega }\) is satisfied, by definition, provided that \(\Omega \subset K^n\) is an nth Farber subcomplex.

On the other hand, from the following commutative diagram, it follows that \(\Delta _L \circ \varphi = \varphi ^n \circ \Delta _K\) and \(\Delta _K \circ \psi = \psi ^n \circ \Delta _L\).

figure a

Combining these two facts, we have the diagram

figure b

and we find out that \(\widetilde{\Omega }:=(\psi ^n)^{-1}(\Omega )\subset L^n\) is an \(n-\)Farber subcomplex as there exists a simplicial map

$$\begin{aligned} \widetilde{\sigma }:= \varphi \circ \sigma \circ (\varphi ^n)|_{\widetilde{\Omega }}: \widetilde{\Omega }\rightarrow L \end{aligned}$$

satisfing the following

$$\begin{aligned} \Delta _L \circ \widetilde{\sigma }= & {} \Delta _L \circ \varphi \circ \sigma \circ \psi ^n |_{\widetilde{\Omega }} \\= & {} \Delta _L \circ \varphi \circ \sigma \circ \psi ^n \circ \iota _{\widetilde{\Omega }} \\= & {} \varphi ^n \circ \Delta _K \circ \sigma \circ \psi ^n \circ \iota _{\widetilde{\Omega }}\\\sim & {} \varphi ^n \circ \iota _\Omega \circ \psi ^n \circ \iota _{\widetilde{\Omega }}\\= & {} (\varphi ^n \circ \psi ^n)_{|\widetilde{\Omega }}\\\sim & {} 1_{L^n} \circ \iota _{\widetilde{\Omega }}\\= & {} \iota _{\widetilde{\Omega }} \hspace{0.03in}. \end{aligned}$$

Step 3. In the last step, we show that \(\textrm{TC}_n(K) \le \textrm{TC}_n(L)\). Similarly, \(\textrm{TC}_n(K) \ge \textrm{TC}_n(L)\) can be showed and the result follows.

Let say \(\textrm{TC}_n(K) = k\). So there is a covering \(K^n = \Omega _0 \cup \cdots \cup \Omega _k\) such that each \(\Omega _j\) is an \(n-\)Farber subcomplex. From Step 2, each \(\Lambda _j = (\psi ^n)^{-1} (\Omega _j)\) is an \(n-\)Farber subcomplex for \(j\in \{ 0, \dots ,k\}\) and they cover \(L^n\). Hence, \(\textrm{TC}_n(K) \le k\). \(\square \)

Proposition 2.2

[4, Lemma 4.4] K is path-edge connected if and only if any two constant simplicial maps to K are in the same contiguity class.

Theorem 2.4

\(\textrm{scat}(K^{n-1}) \le \textrm{TC}_n(K)\) provided that K is an edge-path connected simplicial complex K.

Proof

Suppose \(\textrm{TC}_n(K)=k\). Then there exist subcomplexes \(\Omega _0, \Omega _1, \ldots , \Omega _k\) of \(K^n\) covering \(K^n\) such that each \(\Omega _i\) is \(n-\)Farber subcomplex, i.e., there exists \(\sigma _i: \Omega _i\rightarrow K\) satisfying \(\Delta _K \circ \sigma _i \sim \iota _{\Omega _i}\), where \(\iota _{\Omega _i}: \Omega _i \hookrightarrow K^n\) is the inclusion and \(\Delta _K: K\rightarrow K^n\) is the diagonal map.

For a fixed vertex \(v_1^0\), define \(\iota _0: K^{n-1}\rightarrow K^n\) by \(\iota _0(\omega )=(v_1^0,\omega )\). Set \(V_i:=\iota _0^{-1}(\Omega _i)\subset K^{n-1}\) subcomplex. Notice that \(V_0, V_1, \ldots , V_k\) cover \(K^{n-1}\). If we prove that each \(V_i\) a categorical subcomplex of \(K^{n-1}\), then we can conclude that \(\textrm{scat}(K^{n-1})\le k\), and the result follows.

For simplicity, we ignore the subscripts i. From the assumption, \(\Delta _K \circ \sigma \sim \iota _{\Omega }\), that is, there exist \(\varphi _{\bar{j}}: \Omega \rightarrow K^n\) simplicial maps, for \({\bar{j}}\in \{1, 2, \ldots , m\}\), such that \(\varphi _1=\Delta _K\circ \sigma \), \(\varphi _m=\iota _{\Omega }\) and \(\varphi _{\bar{j}}\) is contiguous to \(\varphi _{{\bar{j}}+1}:\)

$$\begin{aligned} \Delta _K \circ \sigma = \varphi _1 \sim _c \varphi _2 \sim _c \ldots \sim _c \varphi _m = \iota _{\Omega }. \end{aligned}$$

Denoting by \(\textrm{pr}_j: K^n \rightarrow K\) the projection to the jth factor, take the compositions

$$\begin{aligned} \textrm{pr}_j\circ (\Delta _K \circ \sigma ) \circ \iota _0 \circ \iota _{V}= & {} \textrm{pr}_j\circ \varphi _1 \circ \iota _0 \circ \iota _{V}\\&\sim _c&\textrm{pr}_j\circ \varphi _2 \circ \iota _0 \circ \iota _{V} \\&\sim _c&\ldots \\&\sim _c&\textrm{pr}_j\circ \varphi _m \circ \iota _0 \circ \iota _{V} \\= & {} \textrm{pr}_j\circ \iota _{\Omega }\circ \iota _0 \circ \iota _{V} \end{aligned}$$

for each \(j=1,\ldots , n\).

Notice that \(\textrm{pr}_j\circ \Delta _K \circ \sigma \circ \iota _0 \circ \iota _{V}(\omega )= \sigma (v_1^0,\omega )\in K\) for each \(j\in \{1,\ldots ,n\}\).

On the other hand

$$\begin{aligned} \textrm{pr}_1\circ (\Delta _K \circ \sigma )\circ \iota _0 \circ \iota _{V} = v_1^0 \\ \textrm{pr}_j\circ (\Delta _K \circ \sigma )\circ \iota _0 \circ \iota _{V} = \pi _{j-1} \end{aligned}$$

for \(j\in \{2,\ldots ,n\}\), where \(\pi _j:K^{n-1}\rightarrow K\) is the projection to the jth factor. Here, we can write \(\iota _{V}\) in terms of \(\pi _j\)’s. Thus,

$$\begin{aligned} \iota _{V}=\big ( \pi _1,\pi _2,\ldots , \pi _{n-1} \big ) \sim \big ( \textrm{pr}_2\circ (\Delta _K\circ \sigma )\circ \iota _0\circ \iota _{V}, \ldots , \textrm{pr}_n\circ (\Delta _K\circ \sigma )\circ \iota _0\circ \iota _{V} \big ). \end{aligned}$$

Since K is path-edge connected, by Lemma 2.2, the constant map \(c:V\rightarrow K^{n-1}\), \(c(\omega )=(v_1^0, \ldots , v_{n-1}^0)\) can be realised as another constant map \(\bar{c}: V\rightarrow K^{n-1}\), \(\bar{c}(\omega )=(v_1^0, \ldots , v_1^0)\). Therefore, \(\iota _{V}\sim c\). \(\square \)

Theorem 2.5

\(\textrm{TC}_n(K) \le \textrm{scat}(K^n)\) provided that K is an edge-path connected simplicial complex K.

Proof

Suppose that \(\textrm{scat}(K^n) = k\). Then there is a categorical covering \(\{U_0,U_1,\ldots , U_k\}\) of \(K^n\). If we show that \(U_i\) is an \(n-\)Farber subcomplex, for each \(i\in \{0,1,\ldots ,k\}\), then the proof is concluded.

Since we have \(\iota \sim c\) where \(c:U\rightarrow K^n\) is a constant map and \(\iota : U \rightarrow K^n\) is the inclusion map, there exists a sequence of simplicial maps \(h_t: V \rightarrow K^n\) for \(t\in \{1,\ldots ,m\}\) such that \(h_0=\iota \), \(h_m=c\) and \((h_{t},h_{t+1})\) are contiguous for all \(t\in \{1,2,\ldots ,m-1\}\).

Now let \(\pi _j:K^n\rightarrow K\) denote the projection map to the jth factor. Hence, \(\pi _j\circ h_{t}\) and \(\pi _j \circ h_{t+1}\) are contiguous for all \(t\in \{1,2,\ldots ,m-1\}\). From the fact that

$$\begin{aligned} \pi _j\circ \iota =\pi _j\circ h_0 \sim \pi _j\circ c, \end{aligned}$$

it follows that \(\pi _j\circ \iota \)’s are all in the same contiguity class for all j. By Theorem 2.1, U is an \(n-\)Farber subcomplex. \(\square \)

The following lemma, which can be proved by induction, is a generalisation of Theorem 5.5 in [5] and it will be used to prove the later corollary.

Lemma 2.1

For finite simplicial complexes \(K_1, K_2, \ldots , K_m\), we have

$$\begin{aligned} \textrm{scat}(K_1 \times K_2 \times \cdots \times K_m)+1 \le (\textrm{scat}K_1 +1)(\textrm{scat}K_2 +1)\cdots (\textrm{scat}K_m +1). \end{aligned}$$

Corollary 2.1

Let K be an abstract simplicial complex. Then K is strongly collapsible if and only if \(\textrm{TC}_n(K)=0\).

Proof

We have \(\textrm{scat}{K}=0\), since K is strongly collapsible. On the other hand, by Lemma 2.1, we obtain \(\textrm{scat}(K^n)+1 \le (\textrm{scat}{K}+1)^n\). Combining these two, we have \(\textrm{scat}(K^n)+1 \le 1\). Hence, \(\textrm{scat}(K^n)=0\). It follows from Theorem 2.5 that \(\textrm{TC}_n(K)=0\).

Conversely, if \(\textrm{TC}_n(K)=0\), then by Theorem 2.2\(\textrm{TC}_2(K)\le \textrm{TC}_n(K)=0\). Hence the result follows from Corollary 4.7 in [4]. \(\square \)

2.1 Geometric realisation

It is proved that \(|K^2|\approx |K|^2\) and \(|K\times K|\sim |K|^2\), see Theorem 10.21 and Proposition 15.23 in [7]. Moreover, the higher dimensional versions are also valid, as mentioned in Remark 5.2 in [5]. Combining these facts with Lemma 5.1 in [4], we get the following lemma.

Lemma 2.2

There is a homotopy equivalence \(u: |K|^n \rightarrow |K^n|\) such that the following diagram is commutative for each \(i\in \{1,\ldots ,n\}\)

figure c

where \(p_i: |K|^n \rightarrow |K|\) and \(\pi _i:K^n\rightarrow K\) are projections.

Theorem 2.6

\(\textrm{TC}_n(|K|) \leqslant \textrm{TC}_n(K)\).

Proof

Let \(\textrm{TC}_n(K) = k\). So there exist \(n-\)Farber subcomplexes \(\Omega _0, \dots \Omega _k\) of \(K^n\) covering \(K^n\). By Theorem 2.1, \(\pi _i \circ \iota _{\Omega _\ell }\) and \(\pi _j \circ \iota _{\Omega _\ell }\) are in the same contiguity class for each pair \(i,j\in \{1,2,\ldots , n\}\) and each \(\ell \in \{0,1,\ldots ,k\}\). Considering the geometric realisations of these simplicial maps, we have

$$\begin{aligned} |\pi _i \circ \iota _{\Omega _\ell }| \backsimeq |\pi _j \circ \iota _{\Omega _\ell }| \end{aligned}$$

since being in the same contiguity class can be realised as being homotopic in the continuous realm (see for details [9]).

Fig. 1
figure 1

\(\textrm{TC}_n(|K|) < \textrm{TC}_n(K)\)

Full size image

On the other hand, \( |\pi _i \circ \iota _{\Omega _\ell }| = |\pi _i|\circ |\iota _{\Omega _\ell }|\) and \(|\iota _{\Omega _\ell }|=\iota _{|\Omega _\ell |}\). Hence, we get

$$\begin{aligned} |\pi _i|\circ \iota _{|\Omega _\ell |} \backsimeq |\pi _j| \circ \iota _{|\Omega _\ell |}. \end{aligned}$$

Now consider the preimage \(F_\ell = u^{-1}(\Omega _\ell ) \subset |K|^n\) for each \(\ell =0,1,\ldots ,k\) where u is a homotopy equivalence as given in Lemma 2.2. Here, all \(F_\ell \)’s are closed and the subsets \(F_0, F_1, \ldots , F_k\) cover \(|K|^n\). Moreover,

$$\begin{aligned} p_i \circ \iota _{F_\ell } = |\pi _i|\circ u \circ \iota _{F_\ell } = |\pi _i| \circ \iota _{|\Omega _\ell |} \backsimeq |\pi _j| \circ \iota _{|\Omega _\ell |} = |\pi _j|\circ u \circ \iota _{F_\ell } = p_j \circ \iota _{F_\ell }. \end{aligned}$$

Here, the first and the last equalities follow from Lemma 2.2. This completes the proof. \(\square \)

The following is an example for the strict case of the inequality in Theorem 2.6.

Example 2.1

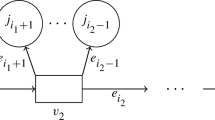
Consider the simplicial complex in Fig. 1.

As mentioned in [1], K is not strongly collapsible. By Example 3.3 in [6], \(\textrm{scat}(K)=1\). Theorem 2.4 yields that \(\textrm{scat}(K)\le \textrm{TC}_2(K)\). From Theorem 2.2, it follows that \(1\le \textrm{TC}_n(K)\) for all \(n\ge 2\). On the other hand, the geometric realisation of the simplicial complex in Fig. 1 is homeomorphic to a disc. Thus, \(\textrm{TC}_n(|K|)=0\) for any \(n\ge 2\).