Abstract
In present study, we deal with nonlinear iterative Fredholm and Volterra integral equations (Fredholm and Volterra IEs) including variable time delays. We are interested here in the investigations of the uniqueness of solutions and Ulam type stabilities of that the iterative Fredholm and the Volterra IEs. The proofs of the new outcomes of the study with regard to these concepts are done in the light of the Banach fixed point theorem (Banach FPT) and the Bielecki metric. As for new contributions of the present study, here, first time we develop the relative outcomes that can be found in the literature to certain nonlinear iterative Fredholm and Volterra IEs including several variable time delays. Finally, a concrete example is introduced at the end of the study.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We call that a Fredholm or Volterra IE is stable in the HU sense if for every function satisfying that the Fredholm IE or the Volterra IE approximately such that there is a solution of the equation that is close to it. In the relevant literature, the first result with regard to the Ulam stability of functional equations (FEs) has been originated and constructed from a significant question belonging to S.M. Ulam, (see, [28]). Following this inaugural research work of Ulam [28], up to now, several kinds of Ulam type stabilities were defined and many important and attractive results on them were formulated and proved with regard to functional differential equations (FDEs), Volterra and Fredholm IEs, Volterra and Fredholm integro-differential equations (Volterra and Fredholm IDEs), etc., in particular, see, Abbas et al. [1], Akkouchi [2], Castro and Simões [6,7,8], Chauhan et al. [9], Deep et al. [10], Egri [11], Găvruţa [12], Graef et al. [15], Janfada and Sadeghi [17], Jung [18,19,20], Khan et al. [21], Öğrekçi et al. [22], Petruşel et al. [23], Radu [24], Rassias [25], Shah et al. [26], Tunç and Biçer [27], Shah and Zada [29] and the citied references therein.
According to the data bases and the documents of the current literature, several results related to the content of this study are reported shortly in the following lines.
Egri [11] dealt with the Ulam stabilities of an iterative FDE.
Tunç and Tunç [32] dealt with the Ulam stabilities of an iterative functional IDE. In [32], the authors focused on two new results with regard to the HU and the HUR stabilities of the considered equation via the Banach FPT.
Specifically, Jung [18] interested in the Volterra IE in the below line:
The author utilized the fixed point method (FPM) for proving the uniqueness of solution and the HUR stability of this Volterra IE of the second kind. Indeed, the work of Jung [18] has been a milestone in the literature for the coming works with regard to the Ulam stabilities of IEs.
The paper of Jung [19] was devoted to an IE, where the unknown function depends on two independent variables. The author showed that the considered IE is firmly connected to the wave equation and confirmed the generalized HU stability of the equation. The main tool of [19] is the FPM.
The target of the book of Jung [20] has been to provide an overview of the stability theory of the FEs, and Jung [20] considered and discussed the stability of the several kind of the FEs.
In 2009, Castro and Ramos [6] interested in the nonlinear Volterra IE in the below:
In [6], the HU and the HUR stabilities of this IE were obtained in finite and infinite intervals cases.
In 2011, Akkouchi [2] took into consideration the Volterra IE depicted by
Using the FPM, the author established new results with regard to the HU and the HUR stabilities of this Volterra IE in the Banach spaces.
In 2010, Castro and Ramos [7] proposed a study on both the HU and the HUR stabilities for the delay Volterra IEs via the FPM:
In 2013, Castro and Guerra [5] studied the nonlinear Volterra IE including a variable delay:
The authors of [5] addressed the problem of HUR stability for this Volterra IE and obtained conditions using the Banach FPT via suitable complete metric space and the Bielecki metric. In [5], some illustrative examples are also given.
Janfada and Sadeghi [17] and Öğrekçi et al. [22] investigated the HU and the HUR stabilities of the Volterra IE depicted by
using the FPM.
In 2015, Abbas and Benchohra [1] focused on the HUR stability of the quadratic IE in a complex Hilbert space:
In [1], the existence result was also proved by using the Schauder FPT.
As for the key reference paper of this study, in 2018, Castro and Simões [8] considered the nonlinear Fredholm and Volterra IEs in the following lines, respectively:
and
In Castro and Simões [8], some very interesting and attractive results with regard to the HUR, the \(\sigma\)-semi HU and the HU stabilities of the Fredholm IE (1) and the Volterra IE (2) were built on the bounded and the unbounded intervals cases, which are integration domains. The constructed conditions of [8] were based on the use of the FPM and the Bielecki metric.
In addition, some very interesting stability problems in sense of Lyapunov for various IDEs and some other mathematical models have attracted extensively researchers’ attentions and significant results have been obtained, for example, see, Bohner and Tunç [3], Bohner et al. [4], Graef and Tunç [13, 14], Hammami and Hnia [16], Janfada and Sadeghi [17], Tunç and Tunç [30, 31], Tunç et al. [33, 34], in sense of Ulam, see, Graef et al. [15], Shah and Zada [29] and reference therein. We also refer the readers to the following very recent works on existence and uniqueness of solutions, Ulam stabilities of certain integral equations and integro-differential equations (see Tunç and Tunç ([35, 36]), Tunç et al. ([37,38,39]) and some others Khan et al. ([40, 41])
In the present paper, inspired by the study of Castro and Simões [8] and that are presented above, we will first consider the following nonlinear iterative Fredholm and Volterra IEs with variable delays, respectively:
with
and
with
where \(t, \, s, \, x \in [a, \, b],\) \(F, \, G \in C\left( {[a, \, b] \times {\mathbb{C}}^{2m + 1} ,{\mathbb{C}}} \right),\) \(K \in \left( {[a, \, b] \times [a, \, b] \times {\mathbb{C}}^{2m} ,{\mathbb{C}}} \right),\) \(a, \, b \in {\mathbb{R}},\) \(a < b,\) and \(y^{[m]}\) symbolizes mth iterate of the function \(y\) and denotes
Remark 1
In the rest of the paper, for the sake of the brevity without mentioning, instead of the representations above, we will use the following depictions and some similar ones:
and
To our knowledge, as it is seen from the literature review above, there are limited literature concentrate on the uniqueness of solutions and the Ulam type stabilities of integral equations. According to the data above, it is also easy to see that the study of the concepts mentioned deserve exploring for delay iterative Fredholm and Volterra IEs. In addition, to our knowledge, there is not any present study with regard to the same concepts for iterative Fredholm and Volterra IEs. The outcomes of this study with regard to the Ulam type stabilities are first time obtained for the iterative Fredholm and Volterra IEs including multiple variable time-delays. Therefore, our results improve or complement the results in the papers of Abbas and Benchohra [1], Akkouchi [2], Castro and Guerra [5], Castro and Ramos [6, 7], Castro and Simões [8], Janfada and Sadeghi [17], Jung [18], Öğrekçi et al. [22], etc., in some senses.
The study is systematized as in the following lines. In Sect. 2, the background definitions of the study and a reference theorem of the fixed point theory are given. In Sect. 3, the leading results of the study as the uniqueness of solutions, the HUR stability and the \(\sigma\)-semi HU stability of the iterative Fredholm IE (3) are presented. In Sect. 4, two new results of the study with regard to the uniqueness of solutions, the HUR stability and the \(\sigma\)-semi HU stability of the iterative Volterra IE (4) are established. In Sect. 5, the final main result of the study with regard to the uniqueness of solutions and the HU stability of the iterative Volterra IE (4) is provided in the infinite intervals cases. Section 6 provides an example as the numerical aptitude of the new main results of the study. Section 7 outlines the contributions of the study and allows some related statements. At the end, in Sect. 8, the conclusion of the study is designed.
2 Basic information
We now begin with some definitions with regard to the primary concepts of this study. Hence, the following definitions and the theorem are beneficial to confirm the Ulam type stability results of the study.
Definition 1.
Let \(t \in [a, \, b].\) If for each function \(y\) satisfying
where \(F\left( {\ldots} \right)\) is given together with (3) and \(\sigma \ge 0\) is a function, there is a solution \(y_0\) of the iterative Fredholm IE (3) and a \(C \in {\mathbb{R}},\) \(C > 0,\) which does not dependent \(y_0\) and \(y,\) such that
for all \(t\) in the given interval, then we say that the iterative Fredholm IE (3) has HUR stability.
Definition 2.
Let \(x \in [a, \, b].\) If for each function \(y\) satisfying.
where \(G\left( {\ldots} \right)\) is given together with (4) and \(\sigma \ge 0\) is a function, there is a solution \(y_0\) of the iterative Volterra IE (4) and a \(C \in {\mathbb{R}},\) \(C > 0,\) which does not dependent of \(y_0\) and \(y,\) such that
for all \(x\) in the given interval, then we say that the iterative Volterra IE (4) has HUR stability.
Definition 3.
Let \(t \in [a, \, b].\) If for each function \(y\) satisfying
where \(F\left( {\ldots} \right)\) is given together with (3) and \(\theta \ge 0,\) \(\theta \in {\mathbb{R}},\) there is a solution \(y_0\) of the iterative Fredholm IE (3) and a \(C \in {\mathbb{R}},\) \(C > 0,\) which does not dependent of \(y_0\) and \(y,\) so that
for all \(t\) in the given interval, then we state that the iterative Fredholm IE (3) has HU stability.
Definition 4.
Let \(t \in [a, \, b]\) and \(\sigma \ge 0\) be a function defined on the given interval. If for each function \(y\) satisfying
where \(F(\ldots)\) is given together with (3) and \(\theta \ge 0,\) \(\theta \in {\mathbb{R}},\) there is a solution \(y_0\) of the iterative Fredholm IE (3) and a \(C \in {\mathbb{R}},\) \(C > 0,\) which does not dependent \(y_0\) and \(y,\) such that
for all \(t\) in the given interval, then we state that the iterative Fredholm IE (3) has the \(\sigma\)‐semi‐HU stability.
Remark 1.
Definitions 3 and 4 can be arranged easily for the iterative Volterra IE (4). We leave out to give that definitions.
It is known that one of an effective basic technique to study the Ulam stabilities is the FPM, which depends upon suitable fixed point results and metrics. Hence, we now recall a definition of this metric on a set \(X,\) \(X \ne \emptyset .\)
Definition 5.
Let \(X\) be a nonempty set. A function \(d\) from \(X \times X\) to \([0, + \infty ]\) is called a generalized metric on the set \(X \Leftrightarrow\) the function \(d\) satisfies:
-
(M1)
\(d(x,y) = 0 \Leftrightarrow x = y;\)
-
(M2)
\(d(x,y) = d(y,x),\;\forall \;x, \, y \in X;\)
-
(M3)
\(d(x,z) \le d(x,y) + d(y,z),\;\forall \;x, \, y, \, z \in X.\)
From the information above, it is clear that the range of this metric is allowed to include the infinity, i.e., “\(\infty\)”. However, this case cannot be allowed for the usual metric. This is an important difference among the generalized and the usual metrics.
Let \(C\left( {[.],[.]} \right)\) and \(C\left( {[.]} \right)\) denote \(C\left( {[a,b],[a,b]} \right)\) and \(C\left( {[a,b]} \right),\) throughout the study, respectively.
A key fixed point background result of this work is presented in Theorem 1.
Theorem 1
(Castro and Simões [7]). Let \((X,d)\) be a generalized compete metric space and \(T\) be a strictly contractive operator from \(X\) to \(X\) with a Lipschitz constant \(L < 1.\) If there exists a \(k \in {\mathbb{Z}},\) \(k \ge 0,\) such that \(d(T^k x,T^k x) < \infty\) for some \(x \in X,\) then the following propositions can be held:
-
\(1^0 )\) The sequence \((T^n x)_{n \in {\mathbb{N}}}\) converges to a fixed point \(x*\) of \(T;\)
-
\(2^0 )\) \(x*\) is the unique fixed point of \(T\) in set \(X* = \left\{ {y \in X:d(T^k x,y) < \infty } \right\};\)
-
\(3^0 )\) if \(y \in X*,\) then
$$ d\left( {y,x*} \right) \le (1 - L)^{ - 1} d(Ty,y). $$(10)
Consider now the space continuous functions, which is represented by \(C\left( {[.]} \right)\) on \([a,b],\) equipped with a generalization of the Bielecki metric
where \(\sigma\) is a nondecreasing continuous function from the interval \([a,b]\) to the interval \((0,\infty ).\) We remember that \(\left( {C([.]),d} \right)\) is a complete metric space (see, Castro and Simões [8]).
3 The uniqueness and the HUR stability of the iterative Fredholm IE
Section 3 builds new conditions for the uniqueness of solutions, the HUR stability and the \(\sigma\)-semi HU stability of the iterative Fredholm IE (3) on a finite interval case. Hence, the first new result with regard to the uniqueness of solutions and the HUR stability of the iterative Fredholm IE (3) is presented in coming lines.
Theorem 2.
We assume that the conditions in the following lines hold:
\((As1)\) \(\tau ,\alpha \in C\left( {[.],[.]} \right)\) are variable time delay functions such that \(\tau (t) \le t\) and \(\alpha (t) \le t,\) \(\forall t \in [a,b]\) and \(\sigma \in C\left( {[.],(0,\infty )} \right).\) Furthermore, for \(\forall t \in [a,b],\) we have that there is \(\eta \in {\mathbb{R}}\) such that
\((As2)\) The continuous functions \(F:[a,b] \times {\mathbb{C}}^{2m + 1} \to {\mathbb{C}}\) and \(K:[a,b] \times [a,b] \times {\mathbb{C}}^{2m} \to {\mathbb{C}}\) allow that the following the Lipschitz conditions are held:
and
respectively, where \(M_F\) and \(M_K\) are positive constants.
Let \(y \in C([.]),\)
and
with
Then, there is a unique function \(y_0 \in C([.])\) such that
and
Hence, we infer from the conditions above that the iterative Fredholm IE (3) has the HUR stability.
Proof.
We now keep in view the operator
depicted by
According to the data of Theorem 2, we will now confirm that \(T\) is strictly contractive with regard to the metric (11). Letting \(u, \, v \in C\left( {[.]} \right),\) we get
For the next steps, letting \(u, \, v \in C\left( {[.]} \right)\) and benefiting from the mathematical induction, we derive the following outcomes, respectively:
Hence, according to the above outcomes, we can derive that
Since
then \(T\) is strictly contractive. In addition, when we utilize the Banca FPT, it follows that
which allows that the iterative Fredholm IE (3) admits the HUR.
Indeed, according to (11) and (12), we have
Hence,
and consequently (13) holds. This outcome ends the proof.
The second new outcome of this study with regard to the uniqueness of solutions and the \(\sigma\)-semi HU stability of the iterative Fredholm IE (3) is given in the below theorem.
Theorem 3.
Let \((As1)\) and \((As2)\) of Theorem 2 hold. In addition, if \(y \in C([.]),\)
where \(F\left( {\ldots} \right)\) is given together with (3), and
then there is a unique function \(y_0 \in C([.])\) such that
with
for all \(t \in [a, \, b].\)
This outcome allows that in the light of the conditions above the iterative Fredholm IE (3) has the \(\sigma\)-semi HU stability.
Proof.
We now keep in view the operator
which is depicted by
As the next steps, according to the conditions of Theorem 3, one can confirm that \(T\) is strictly contractive depending upon the metric (11) since
Hence, once again we can utilize the Banach FPT, which allows the \(\sigma\)-semi HU stability of the iterative Fredholm IE (3) with (15). This outcome is obtained via the definition of the metric (11), using (10) and (14). Thus, we verify the proof of Theorem 3.
4 The uniqueness and the HUR stability of the iterative Volterra IE in the finite interval
Section 4 deals with to build appropriate conditions for the HUR stability and the \(\sigma\)-semi HU stability of the iterative Volterra IE (4) on a finite interval, \([a,b],\) \(a,\) \(b \in {\mathbb{R}} \, {.}\) The third new outcome of this study with regard to the uniqueness of solutions and the HUR stability of iterative Volterra IE (4) is introduced in Theorem 4.
Theorem 4.
Let the conditions in the following lines hold.
\((As3)\) \(\tau ,\alpha \in C\left( {[.],[.]} \right)\) are variable delay functions such that \(\tau (t) \le t,\) \(\alpha (t) \le t,\) \(\forall t \in [a,b]\) and \(\sigma \in C\left( {[.],(0,\infty )} \right)\) is a non-decreasing function. Furthermore, we assume that there is \(\eta \in {\mathbb{R}}\) such that
\((As4)\) \(G:[a,b] \times {\mathbb{C}}^{2m + 1} \to {\mathbb{C}}\) and \(K:[a,b] \times [a,b] \times {\mathbb{C}}^{2m} \to {\mathbb{C}}\) are continuous functions allowing the Lipschitz condition:
and
respectively, where \(M_F\) and \(M_K\) are positive constants.
Let \(x \in [a, \, b],\)\(y \in C\left( {[.]} \right),\)
where \(G\left( {\ldots} \right)\) is given together with (4), and
Then, there is a unique function \(y_0 \in C\left( {[.]} \right)\) such that
and in additon
Depending on the conditions of Theorem 4, these outcomes allows that the iterative Volterra IE (4) has the HUR stability.
Proof.
Take into consideration the operator
which is depicted by
By utilizing the conditions of Theorem 4, keeping a similar way as in the proof of Theorem 2, we can conclude that the operator \(T\) is strictly contractive depending upon the metric (11). Next, letting the metric \(d\) and (16), we deduce
and consequently (17) holds.
The fourth new outcome of this study with regard to the uniqueness of solutions and the \(\sigma\)-semi HU stability of the iterative Volterra IE (4) is given in Theorem 5.
Theorem 5.
We assume that \((As3)\) and \((As4)\) of Theorem 4 hold. In addition, if \(y \in C\left( {[.]} \right)\) with.
where \(G\left( {\ldots} \right)\) is given together with (4), \(\theta > 0,\) \(\theta \in {\mathbb{R}},\) and
then there is a unique function \(y_0 \in C\left( {[.]} \right)\) such that
with
According to the conditions above, these outcomes allow that the iterative Volterra IE (4) admits the \(\sigma\)-semi HU stability.
Proof.
Take into consideration the operator
which is depicted by
By virtue of the conditions of Theorem 5, similarly keeping in mind the way in the proof of Theorem 2, we can conclude that the operator \(T\) is strictly contractive with respect to the metric (11). Hence, we can again apply the Banach FPT, which allows that the iterative Volterra IE (4) admits the \(\sigma\)-semi HU stability, i.e., the inequality (19) is satisfied via the metric \(d\) of (11), using (10) and (18). Thus, the proof of Theorem 5 is done.
5 The uniqueness and the HUR stability of the iterative Volterra IE in the infinite intervals
In Sect. 5, we will study the HU stability of the iterative Volterra IE (4) in the infinite intervals cases. Then, we will now take into consideration the intervals \([a,\infty ),\) \({ ( - }\infty {,}b{],}\) for some fixed \( \, a{, }b \in {\mathbb{R}},\) and \({\mathbb{R}} \, = { ( - }\infty {,}\infty {)}.\) Hence, we will deal with the iterative Volterra IE (4) in the infinite interval cases:
Let \(C^b \left( {\left[ {a,\infty } \right)} \right)\) be the space of bounded and continuous functions, which is equipped with the metric
The fifth and last new result of this study with regard to the HUR stability of the iterative Volterra IE (4) in the infinite interval \([a, \, \infty {)}\) is presented in Theorem 6.
Theorem 6.
Let the following conditions are fulfilled:
\((As5)\) \(\tau ,\alpha \in C\left( {\left[ {a,\infty } \right),\left[ {a,\infty } \right)} \right)\) are variable delay functions such that \(\tau (t) \le t\) and \(\alpha (t) \le t,\) \(\forall t \in \left[ {a,\infty } \right)\) and \(\sigma \in C\left( {\left[ {a,\infty } \right),(\varepsilon ,\omega )} \right)\) is a nondecreasing function with \(\varepsilon > 0, \, \omega > 0,\) \(\varepsilon , \, \omega \in {\mathbb{R}} \, {.}\) Moreover, we assume that there is \(\eta \in {\mathbb{R}}\) such that
\((As6)\) \(G:[a,\infty ) \times {\mathbb{C}}^{2m + 1} \to {\mathbb{C}}\) and \(K:[a,\infty ) \times [a,\infty ) \times {\mathbb{C}}^{2m} \to {\mathbb{C}}\) are continuous functions satisfying the Lipschitz condition in the following lines
and
respectively, where \(M_F\) and \(M_K\) are positive constants and the kernel \(\int_a^x {K(x,s,y^{[1]} (s),\ldots)ds}\) is a bounded and continuous function for any bounded continuous function \(y.\)
If \(y \in C^b \left( {\left[ {a,\infty } \right)} \right),\)
and
then there is a unique function \(y_0 \in C^b \left( {\left[ {a,\infty } \right)} \right)\) with
and
for all \(x \in [a, \, \infty {)}.\)
According to these outcomes, depending upon the conditions above, the iterative Volterra IE (4) has the HUR stability.
Proof.
Let \(I = [a,\infty ), \, a \in {\mathbb{R}},\) and \(I_n = [a,a + n],\) \(n \in {\mathbb{N}}.\) By virtue of Theorem 4, there exists a unique and bounded function \(y_{0,n} \in C[I_n ,{\mathbb{C}}]\) such that
and
Since \(y_{0,n}\) is unique, if \(x \in I_n ,\) then
Letting \(x \in [a,\infty ),\) we define \(n(x) \in {\mathbb{N}}\) by
Next, let the function \(y_0 :[a,\infty ) \to {\mathbb{C}}\) be depicted by
Hence, we claim that \(y_0\) is continuous. Following similar mathematical calculations as in Castro and Simões [8, Theorem 8], it can be shown that \(y_0 (x) = y_{0,n_1 + 1} (x)\) for all \(x \in (x_1 - \varepsilon , \, x_1 + \varepsilon )\) and since \(y_{0,n_1 + 1}\) is continuous at \(x_1 ,\) (see, Theorem 4), thus \(y_0\) is also continuous at \(x_1 ,\) \(x_1 \in {\mathbb{R}} \, .\)
We will now confirm that \(y_0\) satisfiesand in addition
For an arbitrary \(x \in [a, \, \infty {)}\) we choose \(n(x)\) such that \(x \in I_{n(x)} .\) Next, by (23) and (26), we find
Since \(n(s) \, \le \, n(x)\) for all \(x \in I_{n(x)} ,\) then from (25) we derive that
Hence, the last equality of (28) holds true. Next, from (24) and (26), it follows that
\(\forall x \in [a,\infty ),\) which is (22).
At the last step, we will prove that \(y_0\) is unique. Let \(y_1\) be another continuous and bounded function such that it satisfies (21) and (22), \(\forall x \in [a,\infty ).\) By the uniqueness of the solution on \(I_{n(x)}\) for any \( \, n(x) \in {\mathbb{N}},\) we have \(y_0 (x) = y_0 |_{I_{n(x)} } (x)\) and \(y_1 (x)\) satisfies (21) and (22), \(\forall x \in I_{n(x)} .\) Hence, we conclude that
This is the end of the proof.
Remark 2.
We can also proceed and demonstrate the idea of Theorem 6 similarly for the infinite interval cases \(I \, = { ( - }\infty {,}b{], }b \in {\mathbb{R}},\) and \({\mathbb{R}} \, = { ( - }\infty {,}\infty {)}.\)
6 Numerical application
In a particular case, we now give an example to show applications of the results.
Example 1
(Castro and Simões [8]). As a specific case of the nonlinear Volterra IE (4) with variable delays, we consider the Volterra IE:
where
We can confirm that the function \(G\left( {\ldots} \right)\) is continuous.
Let \(y \in C\left( {[0,1],{\mathbb{R}}} \right)\) and \(\sigma \in C\left( {[0,1],(0,\infty )} \right),\) which is a non-decreasing and defined by \(\sigma (x) = 0.0083x + 0.0005.\) Let \(\tau , \, \alpha \in C\left( {[0,1],[0,1]} \right).\) It is clear from (29) and (30) that \(\tau (x) = x^2 ,\) \(\alpha (x) = x^3\) such that \(\tau (x) \le x,\) \(\alpha (x) \le x,\) \(\forall x \in [0,1].\) Letting \(\eta = 0.52841,\) we derive
As for the next step, we have
and
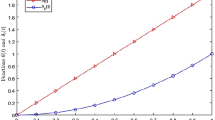
Letting \(y(x) = \frac{101x}{{100}},\) hence, we get
It can also be tested that the Volterra IE (29) has the exact solution \(y_0 (x) = x\) and the function \(y = \frac{101}{{100}}x\) approximately satisfies the Volterra IE (29). Indeed, according to the present data, it follows that
Then, according to Theorem 4, the Volterra IE (29) admits the HUR stability.
For \(x \in [0,1],\) we also have
Finally, letting \(x \in [0,1],\) we also derive that
and
respectively.
Then, according to Theorem 5, the Volterra IE (29) admits the \(\sigma\)‐semi‐HU and the HU stabilities.
7 Discussions
We will now clarify this study as summarily.
\({\text{I}}^0 )\) To our knowledge, according to the materials of the literature, there is no result on the uniqueness of solutions and Ulam type stabilities of iterative Fredholm and Volterra IEs including multiple variable time delays. This study is the first pioneer work with regard to these classes of the IEs and the concepts metioned.
-
\({\text{II}}^0 )\) In this study, we built five new theorems in connection with the HUR stability and the \(\sigma\)-semi HU stability, etc., of nonlinear iterative Fredholm and Volterra IEs, which including multiple variable time delays, on finite or infinite intervals cases. In the proof of the new outcomes we utilized the Banach FPT and the generalized Bielecki metric. The findings of this study have essential contributions to the results summarized in the begin of the study, Ulam’s qualitative theory with regard to the IEs without and with time delays and allow new advantageous for researchers working on these concepts.
-
\({\text{III}}^0 )\) We should mention that the Banach FPT and the generalized Bielecki metric are very effective tools to investigate the Ulam type stabilities of iterative Fredholm and Volterra IEs. Regarding the possible future recommendations, Ulam type stabilities of iterative fractional Fredholm and Volterra IEs are suggested as proper open problems.
-
\({\text{IV}}^0 )\) In particular cases of the considered iterative Fredholm and Volterra IEs, a numerical example was taken from the earlier data bases to provide the applications and illustrations of the results.
8 Conclusion
In this study, certain nonlinear iterative Fredholm and Volterra integral equations including variable time delays were considered. We built new sufficient conditions for the uniqueness of solutions, the HUR stability and the \(\sigma\)-semi HU stability of that iterative Fredholm and Volterra integral equations on a finite interval case. We also constructed a new qualitative result including sufficient conditions with regard to the uniqueness of solutions and the HUR stability of the iterative Volterra IE (4) on the infinite intervals cases. The outcomes of this study include five new theorems. The proofs of the new five theorems were done using the Banach FPT and the generalized Bielecki metric. In particular case, a specific example was taken from the former data bases to show the availability of the results of this study. The outcomes of this study are new and they have new contributions to the Ulam stabilities of integral equations.
Data availability
Not applicable.
References
Abbas, S., Benchohra, M.: Existence and Ulam stability results for quadratic integral equations. Lib. Math. (N. S.) 35(2), 83–93 (2015)
Akkouchi, M.: On the Hyers-Ulam-Rassias stability of a nonlinear integral equation. Appl. Sci. 21, 1–10 (2019)
Bohner, M., Tunç, O.: Qualitative analysis of integro-differential equations with variable retardation. Discrete Contin. Dyn. Syst. Ser. B 27(2), 639–657 (2022)
Bohner, M., Tunç, O., Tunç, C.: Qualitative analysis of Caputo fractional integro-differential equations with constant delays. Comput. Appl. Math. 40(6), 214 (2021)
Castro, L.P., Guerra, R.C.: Hyers-Ulam-Rassias stability of Volterra integral equations within weighted spaces. Lib. Math. (N.S.) 33(2), 21–35 (2013)
Castro, L.P., Ramos, A.: Hyers-Ulam-Rassias stability for a class of nonlinear Volterra integral equations. Banach J. Math. Anal. 3(1), 36–43 (2009)
Castro, L.P., Ramos, A.: Hyers-Ulam and Hyers-Ulam-Rassias stability of Volterra integral equations with delay. In: Constanda, C., Pérez, M.E. (eds.) Integral Methods in Science and Engineering, vol. 1, pp. 85–94. Birkhäuser Boston, Ltd., Boston (2010)
Castro, L.P., Simões, A.M.: Hyers-Ulam-Rassias stability of nonlinear integral equations through the Bielecki metric. Math. Methods Appl. Sci. 41(17), 7367–7383 (2018)
Chauhan, H.V.S., Singh, B., Tunç, C., Tunç, O.: On the existence of solutions of non-linear 2D Volterra integral equations in a Banach space. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. (RACSAM) 116(3), 101 (2022)
Deep, A., Deepmala, Tunç, C.: On the existence of solutions of some non-linear functional integral equations in Banach algebra with applications. Arab J. Basic Appl. Sci. 27(1), 279–286 (2020)
Egri, E.: Ulam stabilities of a first order iterative functional-differential equation. Fixed Point Theory 12(2), 321–328 (2011)
Găvruţa, P.: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. J. Math. Anal. Appl. 184(3), 431–436 (1994)
Graef, J.R., Tunç, C.: Continuability and boundedness of multi-delay functional integro-differential equations of the second order. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. (RACSAM) 109(1), 169–173 (2015)
Graef, J.R., Tunç, O.: Asymptotic behavior of solutions of Volterra integro-differential equations with and without retardation. J. Integral Equ. Appl. 33(3), 289–300 (2021)
Graef, J.R., Tunç, C., Şengün, M., Tunç, O.: The stability of nonlinear delay integro-differential equations in the sense of Hyers-Ulam. Nonauton. Dyn. Syst. 10(1), 20220169 (2023). https://doi.org/10.1515/msds-2022-0169
Hammami, M.A., Hnia, N.: On the stability of perturbed Volterra integro-differential equations. J. Integral Equ. Appl. 32(3), 325–339 (2020)
Janfada, M., Sadeghi, Gh.: Stability of the Volterra integro-differential equation. Folia Math. 18(1), 11–20 (2013)
Jung, S.-M.: A fixed point approach to the stability of a Volterra integral equation. Fixed Point Theory Appl. Art. ID 57064, 9 pp (2007)
Jung, S.-M.: A fixed point approach to the stability of an integral equation related to the wave equation. Abstr. Appl. Anal. Art. ID 612576, 4 pp (2013).
Jung, S.-M.: Hyers-Ulam-Rassias Stability of Functional Equations in Nonlinear Analysis. Springer Optimization and Its Applications, vol. 48. Springer, New York (2011)
Khan, H., Tunc, C., Chen, W., Khan, A.: Existence theorems and Hyers-Ulam stability for a class of hybrid fractional differential equations with p-Laplacian operator. J. Appl. Anal. Comput. 8(4), 1211–1226 (2018)
Öğrekçi, S., Başcı, Y., Mısır, A.: A fixed point method for stability of nonlinear Volterra integral equations in the sense of Ulam. Math. Methods Appl. Sci. 46(8), 8437–8444 (2023)
Petruşel, A., Petruşel, G., Yao, J.-C.: Existence and stability results for a system of operator equations via fixed point theory for non-self orbital contractions. J. Fixed Point Theory Appl. 21(3), 73 (2019)
Radu, V.: The fixed point alternative and the stability of functional equations. Fixed Point Theory 4(1), 91–96 (2003)
Rassias, T.M.: On the stability of the linear mapping in Banach spaces. Proc. Am. Math. Soc. 72(2), 297–300 (1978)
Shah, S.O., Tunç, C., Rizwan, R., Zada, A., Khan, Q.U., Ullah, I., Ullah, I.: Bielecki-Ulam’s types stability analysis of Hammerstein and mixed integro-dynamic systems of non-linear form with instantaneous impulses on time scales. Qual. Theory Dyn. Syst. 21(4), 107 (2022)
Tunç, C., Biçer, E.: Hyers-Ulam-Rassias stability for a first order functional differential equation. J. Math. Fundam. Sci. 47(2), 143–153 (2015)
Ulam, S.M.: Problems in Modern Mathematics. Science Editions John Wiley & Sons, Inc., New York (1964)
Shah, R., Zada, A.: A fixed point approach to the stability of a nonlinear Volterra integro-differential equation with delay. Hacet. J. Math. Stat. 47(3), 615–623 (2018)
Tunç, C., Tunç, O.: On the stability, integrability and boundedness analyses of systems of integro-differential equations with time-delay retardation. RACSAM 115, 115 (2021). https://doi.org/10.1007/s13398-021-01058-8
Tunç, O., Tunç, C.: Solution estimates to Caputo proportional fractional derivative delay integro-differential equations. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. 117, 12 (2023). https://doi.org/10.1007/s13398-022-01345-y
Tunç, O., Tunç, C.: Ulam stabilities of nonlinear iterative integro-differential equations. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. 117, 118 (2023). https://doi.org/10.1007/s13398-023-01450-6
Tunç, C., Tunç, O., Yao, J.-C.: On the stability, integrability and boundedness analysis of systems of integro-differential equations with time-delay. Fixed Point Theory 24(2), 753–774 (2023)
Tunç, C., Tunç, O., Wen, C.-F., Yao, J.-C.: On the qualitative analyses solutions of new mathematical models of integro-differential equations with infinite delay. Math. Methods Appl. Sci. 46, 14087–14103 (2023). https://doi.org/10.1002/mma.9306
Tunç, O., Tunç, C., On Ulam stabilities of delay Hammerstein integral equation. Symmetry. 15, 1736. (2023). https://doi.org/10.3390/sym15091736
Tunç, O., Tunç, C., Yao, J. -C.: New results on Ulam stabilities of nonlinear integral equations. Mathematics. 12, 682 (2024). https://doi.org/10.3390/math12050682
Tunç, O., Tunç, C., Yao, J. -C.: Global existence and uniqueness of solutions of integral equations with multiple variable delays and integro-differential equations: progressive contractions. Mathematics. 12(2):171. (2024) https://doi.org/10.3390/math1202017
Tunç, C., Tunç, O., Petruşel, G., Yao, J. -C.: On the Ulam stabilities of nonlinear integral equations and integro-differential equations. Math. Meth. Appl. Sci. 47, 4014–4028. (2024) https://doi.org/10.1002/mma.9800
Tunç, O., Sahu, D.R., Tunç,C.: On the Ulam type stabilities of a general iterative integro- differential equation including a variable delay. J. Nonlinear Convex Anal. 25 (2), 399-417. (2024)
Khan, H., Abdeljawad,T., Gómez-Aguilar, J. F ., Tajadodi,H., Khan, A.: Fractional order Volterra integro-differential equation with Mittag-Leffler kernel. Fractals. 29 (06), 2150154. (2021)
Khan, H., Alzabut, J.; Gulzar, H.: Existence of solutions for hybrid modified ABCfractional differential equations with p-Laplacian operator and an application to a waterborne disease model. Alexandr. Eng. J. 70, 665-672 (2023)
Funding
Open access funding provided by the Scientific and Technological Research Council of Türkiye (TÜBİTAK).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
No potential conflict of interest was reported by the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tunç, O., Tunç, C. On Ulam stabilities of iterative Fredholm and Volterra integral equations with multiple time-varying delays. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. A-Mat. 118, 83 (2024). https://doi.org/10.1007/s13398-024-01579-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13398-024-01579-y
Keywords
- Iterative Fredholm IE
- Iterative Volterra IE
- Uniqueness of solutions
- Ulam stabilities
- The Banach FPT
- The Bielecki metric