The ability to enumerate unit-cubes in 3D arrays is crucial for understanding volume and the volume formula (Battista & Clements, 1996; Smith & Barrett, 2017). However, enumerating unit-cubes in a 3D array has shown not to be an easy task for many students (Battista, 1999; Battista & Clements, 1996; Ben-Haim et al., 1985; Finesilver, 2015, 2017; Vasilyeva et al., 2013). The students need to interpret the array as a space-filling object, including units inside the array (Finesilver, 2015). This involves the use of spatial reasoning skills, as the students need to mentally manipulate the object, interpret the structural elements of the object and decompose the object into parts (Fujita et al., 2020). Limited spatial reasoning skills can lead students to count only what is visible from the drawer’s point of view, not taking the non-visible cubes into account (Battista & Clements, 1996; Ben-Haim et al., 1985; Vasilyeva et al., 2013). This may also result in a double and triple counting of unit-cubes located at the edges and corners of the array.

Research has provided a fairly comprehensive picture of students’ difficulties with enumerating units in 3D arrays. We know less about the reasons for their difficulties. Our hypothesis is that units-locating is crucial for a meaningful enumeration of units in 3D arrays. To attempt to account for this, we will investigate the role of units-locating in enumerating 3D arrays made up of cubical and spherical units, respectively. Drawing on Battista’s (2004) theoretical framework of five connected cognitive processes essential for enumerating units in a 3D array, we address the research question: What role does units-locating play in students’ strategies in enumerating units of 3D arrays and how are their units-locating processes linked to the unit-representation of the array?

We observed strategies expressed by grade 3 students, in a Norwegian school context. Before we present details of the method, we first elaborate on previous research on students’ enumeration strategies of 3D arrays and the role of representations. Then, we go through Battista’s five cognitive processes and the levels of sophistication (LoS) connected to these processes (Battista, 2004), which we will use as a framework for organizing and guiding our analyses. After presenting the method and results, we conclude by discussing implications for research and teaching, as well as pointing to issues for future research.

Previous research

We contextualize our study in a discussion of previous research on students’ enumeration strategies of 3D arrays and the role of representations. The discussion will also provide a background for our analytical approach.

Students’ strategies for enumerating cubes in 3D arrays

Ben-Haim et al. (1985) conducted a study on students’ strategies for enumerating cubes, presented in a two-dimensional (2D) representation of a 3D array, i.e. pictured on a plane piece of paper. A task from their study can be seen in Fig. 1. They found that students who experienced difficulties in enumerating cubes in the array were most often using one of the four following erroneous counting strategies: counting the number of faces visible, counting the number of faces visible and multiplying the result by two, counting the number of visible cubes or counting the number of visible cubes and multiplying the counted number by two. More recent studies have confirmed these findings (Finesilver, 2015, 2017; Kara et al., 2012; Vasilyeva et al., 2013).

Fig. 1
figure 1

Student task from Ben-Haim et al. (1985)

Full size image

Ben-Haim et al. (1985) suggested that students who counted only the visible faces interpreted the representation strictly as 2D, while students who counted the visible cubes showed more awareness of the three-dimensionality of the array since they were able to discern the unit as a 3D object. In addition, they suggested that students who multiplied their counted number by two perceived parts of the array as hidden but had not yet developed a valid strategy for properly determining the total number of units. The findings of Ben-Haim et al. (1985) point to the role of spatial visualization in enumerating 3D arrays. Spatial visualization involves mentally creating and manipulating images of 3D objects, to make it possible to reason about the objects, both when the objects are visible and when they are not (Battista et al., 2018; Fujita et al., 2020). Adding to the research of Ben-Haim et al., Battista and Clements (1996) elaborate a theoretical description of student’s solution strategies and errors. They suggest that many students are unable to correctly enumerate cubes in a 3D array due to a lack of spatial structuring skills. Spatial structuring is explained as the process of “establishing units, establishing relationships between units (…), and recognizing that a subset of the units, if repeated properly, can generate the whole set” (Battista & Clements, 1996, p. 282). They found that this process was necessary for students to be able to construct a coherent mental model of a 3D array and to correctly enumerate the array. Both spatial visualization and spatial structuring can be interpreted as parts of a student’s spatial reasoning, as they involve mentally creating and manipulating images of objects, decomposing objects into parts and using the relationships between the parts of the objects to reason about the object (Battista et al., 2018).

Enumeration strategies and different representations of 3D arrays

Previous research on students’ understanding of 3D arrays has focused on enumeration tasks with cubes as the basic unit (Smith & Barrett, 2017). Several studies have found that students might have difficulties enumerating the cubical units of the arrays both when the arrays are represented as 2D and when working with a physical 3D representation of an array (Battista, 1999; Battista & Clements, 1996; Ben-Haim et al., 1985; Finesilver, 2015, 2017; Vasilyeva et al., 2013). Finesilver (2015, 2017) found that students who tended to count only faces in enumeration tasks, i.e. ignored cubes on the inside and back of the array, moved toward a more layer-based thinking when the arrays came in different coloured layers. This implies that perceptual clues (Battista, 2010; Campbell, 1990), like colours, can help students in their spatial structuring of the 3D array. Vasilyeva et al. (2013) conducted a study where they used both gridded and non-gridded representations. They found that the students tended to apply more appropriate strategies when presented with gridded representations of 3D arrays. Hence, findings suggest that students’ enumeration strategies should not be considered as a purely cognitive issue. We need to take into account the role of unit-representation to understand students’ enumeration strategies.

The focus on cubes as the unit in previous research made us reflect on how other units might function as perceptual clues and influence students’ enumeration strategies when working with 3D arrays. To learn more about students’ strategies when enumerating units in 3D arrays, we intend to challenge students with 3D arrays that are built of cubes and spheres, respectively. We elaborate further on the tasks presented to the students after presenting our analytical approach.

Analytical approach

The analytical approach of this study is based on five cognitive processes essential for enumerating units in 3D arrays and different LoS connected to these processes (Battista, 2004).

Five underlying cognitive processes

Battista (2004) claims that five cognitive processes are essential for a meaningful enumeration of units in 3D arrays: abstraction, constructing a mental model, spatial structuring, units-locating and organizing-by-composites.

Abstraction is the process that enables individuals to purposefully interact and make sense of the physical world. In a process of abstraction, the experience of a real-world phenomenon is internalized to a mental model, a mental representation, of the phenomenon experienced.

To succeed in enumerating units in a 3D array, students need to form and use a coherent mental model of the array in question. Battista and Clements explain the concept of mental model as “a mental version of an object whose structure is identical to the structure of the perceived or conceived structure of the object it represents (…)” (Battista & Clements, 1996, p. 285).

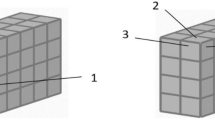
Constructing a mental model of a 3D array involves processes of spatial structuring. In particular, spatial structuring refers to the process of identifying and organizing spatial components of the array, combining components into spatial composites and establishing interrelationships between and among components and composites (Battista, 1999). For instance, the 3D array in Fig. 2 can be organized in six sides, which each, in turn, can be structured in rows or columns.

Fig. 2
figure 2

In order to locate the corner cube, students need to coordinate the different viewpoints of the array

Full size image

Two additional processes are in play in spatial structuring. Units-locating involves processes where students discern the basic units of the array and coordinate their location along the dimensions that frame the array. For instance, to understand the location of the red-coloured cube in Fig. 2, the student must discern its 3D shape and understand that it takes a position in a three-dimensional coordinate-like-structure in relation to its cube neighbours.

Organizing-by-composites is activated when students combine basic units into a more complex composite unit (a unit of units) that can be used to generate the complete array via iteration. This process is proposed to be a key to understanding volume formulas because the maximum composite will result in the first layer which, when iterated, will generate the array as in the formula base × height. (Smith & Barrett, 2017).

LoS in enumerating units in arrays

Battista (2004) suggests that the five cognitive processes can be used to describe students’ LoS when enumerating units in arrays. At the first level, students have difficulties recognizing all the units in the array and are not yet capable of organizing them into a composite unit. Next, students start to mentally organize units in groups as composite units and may use this information to determine the number of some of the hidden cubes. The third level is reached when students can coordinate orthogonal sides of a cube and differentiate between cube faces and cubes. The learner will then avoid double and triple counting but is still not able to locate all the hidden cubes in the array. At level 4, students are able to group units into a first layer, but not to iterate this layer to generate a complete array. Hence, the students are still not able to create a coherent mental model of the array. When reaching level 5, students organize units into composites which, when iterated, can lead to a correct enumeration of units in the array. Consequently, it is not until level 5 that students are able to create a coherent mental model which includes all cubes in an array. However, a lot of students on this level are not able to iterate the composites accurately, hence making enumeration errors. The ineffectiveness of the grouping also makes it difficult to generalize the pattern at this point. When students’ mental models are in terms of layers, and the students can effectively enumerate units in an array, they have reached the sixth level. The seventh and final level requires students to be able to understand the connection between “an enumeration strategy and the spatial structuring on which it is based” (Battista, 2004, p. 200).

Method

In this study, we followed the methodology of qualitative case study research (Yin, 2013), to account for details in students’ enumeration strategies.

Data collection

This study was conducted in a 3rd grade class in a small-town school in Norway. The class consisted of 22 students, aged 8 to 9, who had not been introduced to volume or had previous experience in building 3D structures. Since the students had not been formally educated on the volume of a prism, we conjectured that this could provide us the opportunity to explore a variety of enumeration strategies. The math teacher in this class had previously participated in a further education course in inquiry-based teaching. We therefore expected that the students to a certain extent were used to working in groups and putting into words their own solution strategies.

The students solved four enumeration tasks during a 45-min lesson. The students were organized in groups of two, which were selected by the class teacher to avoid unfortunate constellations that could lead to poor cooperation. During the lesson, the first and second authors served as participating observers, interacting with some of the groups in order to understand their thinking and to remind them to write down their explanations on their worksheets. Written answers from all pairs were collected and used in the analysis. The groups were numbered 1–11. Two video cameras recorded the work of groups 10 and 11, one camera per group. The choice of these two groups were made by the teacher in advance of the lesson, as she thought they would be inclined to discuss their strategies to a greater extent than the other groups.

The tasks

The students were given four tasks on enumerating units of a 3D array. The tasks were similar to the tasks used by Ben-Haim et al. (1985), as seen on Fig. 1. All four tasks had a similar phrasing: “The figure below is made up by cubes/marbles like these (picture of a single cube/marble). How many of these cubes/marbles do you need to build the figure?” On the spherical tasks, we chose the word “marbles” because “spheres” is not a concept known from students’ everyday lives. Sphere is a mathematical concept that Norwegian 3rd graders will not be familiar with. In the discussion following, however, we will use “spheres” since we believe our study concerns all spherical representations regardless of whether they are marbles, balls, balloons or similar.

In the first two tasks, the arrays followed a 3 × 3 × 3 structure. In task 1, the units were represented by cubes as shown in Fig. 3, while in task 2, they were represented by spheres as shown in Fig. 4. We chose an identical structure on these two tasks to be able to compare them and see if students would reason differently when we changed the unit-representations in the array. Our ambition was not to measure effects between different forms of unit-representations. Instead, it was supposed that the variation between the two different unit-representations would provide us rich data to explore units-locating processes and how these processes are linked to unit-representations.

Fig. 3
figure 3

Worksheet of task 1

Full size image
Fig. 4
figure 4

Worksheet for task 2

Full size image

The last two tasks are seen in Fig. 5 and involved arrays with different structures and units. Task 3 was a 3 × 3 × 4 array of spheres, while task 4 was a 2 × 5 × 4 array of cubes. We chose different structures on these two tasks to gain deeper insight into the students’ strategies, by comparing them to tasks 1 and 2. Between tasks 3 and 4, the order of the unit-representation was changed, compared to the order between tasks 1 and 2. This choice was made to see if strategies applied in the spherical situation in task 3 would be mirrored in the final cubical situation.

Fig. 5
figure 5

Worksheet for tasks 3 and 4

Full size image

Method of analysis

The analysis aimed to answer the research question: “What role does units-locating play in students’ strategies in enumerating units of 3D arrays and how are their units-locating processes linked to the unit-representation of the array?” The analysis was guided by Battista’s (2004) five cognitive processes and Battista’s LoS.

The analysis was organized in two steps. In the first step, a rough categorization of the students’ enumeration strategies was made. The analysis resulted in three categories (see Table 1). Students who applied a layer strategy were already well on their way to developing a coherent mental model of 3D arrays and thus did not provide any insight on how different unit-representations are related to the units-locating process. Therefore, we focused the second step of the analysis on the remaining two categories.

Table 1 Enumeration strategies used on each task by the groups
Full size table

In step 2, we were digging more deeply into the strategies of the students who did not manage to enumerate the arrays correctly. This part of the analysis was also guided by Battista’s (2004) five cognitive processes and the different LoS. We wanted to characterize the strategies of the students who had not developed a coherent mental model of the array. In this step of the analysis, we also searched for differences between students’ enumeration strategies, in relation to the different unit-representations.

Results

First, we will present an overview of the students’ enumeration strategies and the categorization of strategies used by the 11 student pairs in this class (Tables 1 and 2). Next, we will elaborate in more detail on how double and triple counting took place in the class, and how this can be connected to the students’ units-locating process and, in turn, how this process can be linked to the unit-representation of the array. We end the detailed analysis by elaborating on units-locating in relation to thinking in composites.

Table 2 Range of enumeration strategies on each task
Full size table

Overall patterns of enumeration strategies

We found that several students applied different enumeration strategies when the units were represented as spheres compared to when the units were represented as cubes. These different strategies can be connected to different cognitive processes and LoS and will be illustrated in the presentation of the results.

We distinguished nine categories of enumeration strategies among the students (Table 1). We labelled the first eight strategies hierarchically from A to H, with A as the most sophisticated strategy, according to Battista’s LoS, and H as the least sophisticated. Category I contains strategies which we were unable to code or understand within Battistas’ (2004) LoS. We therefore focus on category A to H.

Tables 1 and 2 show the variety of students’ enumeration strategies.

The eight strategies were grouped into three subsets: the first subset consists of strategy A and B. These strategies resulted in a correct answer to the tasks. Strategy A equals to a higher LoS because it is the most efficient strategy to determine the number of units needed to construct the array. When applying strategy B, students conceptualized the set of units as space-filling entities but did not utilize layers. Instead of iterating layers, students iterated rows or columns.

Strategies C, D and E constitute a second subset. These did not provide a correct answer, but when using one of these strategies, students managed to locate the 3D units in the array. Strategy C is the most sophisticated strategy in this subset, because organizing in composites is an important step towards a layer strategy (Battista, 2004). Students who used this strategy, however, did not iterate the composite unit a correct number of times. Thus, the strategy fails to generate the whole array. Strategy D, the doubling-strategy, indicates an awareness of the hidden units in the array. The opposite is true regarding strategy E, where students only counted the units visible in the task presentation.

The third subset consists of strategy F, G and H. Common to these are that they are strategies where students were unable to locate the unit of the array and ended up counting surfaces or the like.

In Table 2, we can see what kind of strategy each group applied on the four tasks. Interestingly, none of the groups applied less sophisticated strategies on tasks with spherical units, compared to tasks with cubical units. More often they applied more sophisticated strategies when enumerating arrays of spherical units. In the analysis, it also appeared to us that it was easier to follow students’ reasoning in tasks with spherical units. We interpret this as it was easier for the students to reason about and express their understanding in the tasks with spherical units, compared to the tasks with cubical units. Furthermore, we can see that units-locating, involved in the second subset, was more frequently used in the spherical cases (tasks 2 and 3).

Detailed analysis

Six of the 11 groups ended up with incorrect answers in both the cubical and the spherical cases. When students struggled with the tasks, they were struggling with units-locating, ending up with double and triple counting.

We start the detailed analysis by first scrutinizing how double and triple counting took place in our study. We then turn to analyse the link between units-locating and unit-representation by looking at how the spherical units seem to provide students with perceptual clues for units-locating. We will conclude the detailed analysis by elaborating on how the spherical unit-representation seems to provide perceptual clues that enable students to spatially structure the units into composite units.

Double and triple counting and the crucial role of units-locating for enumerating units in 3D arrays

Double and triple counting is a common erroneous enumeration strategy that is well documented in the research literature (Finesilver, 2015, 2017; Kara et al., 2012; Vasilyeva et al., 2013). In the present study, we not only identify double and triple counting, but we also observe how double and triple counting depends on students’ units-locating processes and, particularly, their difficulties in locating basic units when they are made up of cubes. In particular, students come to apply double and triple counting since they are not viewing the cubes as 3D units. The units they are enumerating are the visible 2D faces of the cubes. The visible 2D faces are not viewed as being part of, or making up, a coordinate-like-structure in three dimensions.

We use group 10, discussing task 4, to show how double and triple counting took place, and how students came out of this by distinguishing and locating the units in a 3D array. A visualization of the group’s counting strategy is seen in Fig. 6. Group 10 consisted of one girl (girl 10) and one boy (boy 10). We enter the work of group 10 when they approach task 4:

Boy 10:(counting cubes on right front layer; RFL) 1, 2, 3, 4, …, 20

Girl 10:And this is 20 again.

Boy 10:That means that there are 40.

Girl 10:No wait. (counting). It is 1, 2, 3, 4, 5, 6, 7, 8, 9

Fig. 6
figure 6

Visualization of group 10 counting strategy on task 4

Full size image

Girl 10 is counting the visible frame around the back and leftmost layer, reaching nine by counting the corner cube twice. She then fills in the “gap” in the frame by counting units on the right front layer (RFL) equivalent to the “hole” in the frame. The strategy is a layer strategy (A), but the counting is uncoordinated:

Girl 10:10, 11, 12, 13, 14, 15, 16, 17, 18, 19. No wait.

Girl 10 is counting another unit twice: one of the quadrilaterals is counted both as numbers 11 and 16. Her actions are not coordinated, and she fails to make a correct enumeration in her first attempt.

Group 11 consisted of two boys (boy 11a and boy 11b). They also showed initial struggles with their counting strategy on task 1:

Boy 11a:There are three inside here (pointing at the 3x3x3 array of cubes). Or, in the middle there is one. It is three down (moving his finger down the right column of RFL). So, it is three…here is nine (pointing to the surface of RFL). Nine plus three. Twelve. (…) Then there are two here (pointing at the leftmost and middle column of left front layer; LFL). That is 18. And then there are just these two (pointing at two rows furthest up left on top layer, TL). And that makes 18 plus 6.

Boy 11b: That is 24.

Boy 11a:Yes.

Boy 11b:But are there not some back there?

Boy 11a:Yes. And there are also 6 (moving his finger over RBL). We will, …no… actually… wait a minute. No, there are actually just three I can tell. And then it is 3 plus 24.

Boy 11b:27.

Boy 11a:Yes.

We note how boy 11a initially counts visible faces of the cube, strategy H. First, he identifies that the array is made out of columns of three and calculates the number of faces on the RFL, as visualized on the leftmost cube in Fig. 7. Then, when working on LFL, he has already counted a column of three and is only adding two more. Finally, he adds two rows of three for the top layer.

Fig. 7
figure 7

Visualization of group 11 counting strategy

Full size image

Not everything about this group’s counting strategy is clear. For example, it is not clear why they add three more after first concluding with 24 units. It is not obvious where these units are located. But it is evident at this point that they are not aware of the hidden units or of the 3D structure of the cubes. They have not succeeded in the process of units-locating of the 3D unit. Group 11 seems to count a 2D unit and thus end up with double and triple counting of the 3D units.

Group 6 provides a different example of double and triple counting. In task 1, group 6 counted all visible cube faces on the array and marked them with a cross. We can see their work on Fig. 8. They first identified three sides of the array, and, since each side had 9 faces, they wrote 9 + 9 + 9. They doubled this calculation to reach 9 + 9 + 9 + 9 + 9 + 9, which adds to 54. They have calculated the number of outside faces, strategy G. A simple arithmetic error gave them the sum 55. The doubling strategy is common for students who have an understanding that there must be hidden units, but who have not yet developed an efficient way of mentally structuring the array (Ben-Haim et al., 1985). By double and triple counting, group 6 discloses limitations both in their process of units-locating and of coordinating different viewpoints of the array in task 1. The students knew that they needed more cubes than those that were visible in the picture, and so, they assumed that the number of hidden units were the same as the number of visible units counted in the front. Hence, even if their perspective is 2D, group 6 orders basic units into a composite unit in their enumeration strategy.

Fig. 8
figure 8

Group 6, task 1

Full size image

The three groups presented so far have in common that they in some way applied double and/or triple counting. Differences between the groups consist of how they use this strategy: Group 10 does in fact decompose the array in a way that may indicate that they understand that not all faces should be counted. Counting a “frame” and then counting what corresponds to the “hole” in the frame will result in a valid enumeration provided that this was their strategy for counting the LBL. But a lack of coordination leads to some cubes being double counted anyway. Group 11 is counting the surface of the visible sides of the array (TL, RFL and LFL), while group 6 is counting the surface of the visible sides of the array and then doubling the counted number.

So far, we have shown some of the cases of double and triple counting within our study. Double and triple counting indicates that the student has not been able to identify the 3D unit and makes it impossible to correctly enumerate units in a 3D array. Of all the eleven groups in the class, we saw no signs of double and triple counting on tasks with spherical units. All instances of this erroneous counting strategy occurred on cubical units. This leads us to investigate whether spherical units might serve as a perceptual clue for units-locating.

Spherical units as perceptual clues for facilitating units-locating

If it is true that locating units is crucial for enumerating units in 3D arrays, there is a need to know more about how teaching can support students’ units-locating processes. Taking a detailed look at the groups of the present study, it seems as if the 3D arrays built of spherical units facilitate units-locating. In other words, it appears that the spherical form of the unit provides perceptual clues (Battista, 2010; Campbell, 1990; Vasilyeva et al., 2013) for students to distinguish the units from each other and thus avoid double and triple counting. We will use the work of groups 5 and 6 to make our point here.

Figures 9 and 10 show the worksheet of group 5 on tasks 1 and 4. They solved the tasks with cubical units by counting visible faces of the array; strategy H. Consequently, the students applied double and triple counting in tasks 1 and 4.

Fig. 9
figure 9

Group 5, task 1

Full size image
Fig. 10
figure 10

Group 5, task 4

Full size image

Moreover, they did not show any awareness of hidden cubes in the array and therefore may not see the array as 3D. Since they were counting 2D units (faces), we can tell that they had not yet developed the cognitive process of units-locating in 3D arrays.

In task 2, group 5 applied a different strategy. While solving the task, the students were asked to elaborate on their thinking and add numbers and arrows to their worksheet (Fig. 11).

Fig. 11
figure 11

Group 5, task 2

Full size image

In their response, the students explained that they had counted 9 marbles on the left side, 6 on the right side and 4 on top. Figure 12 is a visualization of their strategy.

Fig. 12
figure 12

Visualization of the enumeration strategy of group 5 in task 2

Full size image

Their strategy for task 2 was similar to the strategies they used in tasks 1 and 4, as it relied on counting what was visible. The students did still not show an awareness of the hidden units in the array. So, evidently, the students of group 5 had not yet developed a coherent mental model of the array. It is relevant to discuss whether these students perceive the array as three-dimensional. Based on Battista’s theories, we might argue that there is evidence that the students perceived the array as 3D in task 2. When counting spheres, they did not double or triple count units. Each unit was separated from a neighbour unit. This implies that the students, in the spherical case, were able to locate the unit in the array and use this as an aid in their spatial structuring process. According to Battista (1996), students have overcome double and triple counting when they recognize the unit from three different viewpoints of the array. Coordinating the three viewpoints is a sign of recognizing the unit as 3D entity. We may argue that the students’ cognitive processes have reached a higher LoS when working on the arrays built of spheres, as they are able to both locate the unit and coordinate different viewpoints of the array, even if they still not show an awareness of the spheres hidden on the back or inside of the array. We therefore categorized this as strategy E; counting only visible units. At the same time, we cannot rule out that the students were simply counting squares and circles when solving the tasks. If that is the case, students lack the ability to perceive the units as 3D, which, in turn, makes it very difficult to see the 3D structure of the array.

In the previous section, we saw group 6 utilizing double and triple counting in the cubical tasks, ending up with calculating the surface of the array. In Fig. 13, we can see a comparison of their worksheets for task 1 and task 2. In task 2, we can see that all marbles are marked with only one cross, i.e. counted exactly once. Hence, compared to the case with the cube-representations in task 1, the spherical units seemed to support the students’ units-locating process, as they moved away from double and triple counting when enumerating spheres in task 2.

Fig. 13
figure 13

Group 6, tasks 1 and 2

Full size image

Note that group 6 answered 55 on both task 1 and task 2. How could this happen? One interpretation is that the students identified structural similarities between the two arrays and that the number of units therefore should be the same. Another interpretation could be that things went a bit too fast for the students, so that they by mistake wrote the same answer to both tasks. Regardless, it is not the answers but the strategies that are of interest here and, according to that, we note how the students in task 2 distinguished composites of “threes” in the array and, based on this, formulated the expression 3 + 3 + 3 + 3 + 3 + 3. The group organized units in composites, but failed to iterate these composites a sufficient number of times; strategy C. It is interesting to note that the same group made composite units of 9 on task 1 where the structure of the array was the same (3 × 3 × 3), but the units were cubes. This indicates that the group is not only counting “circles” when encountering marbles. This group is aware of the fact that there are more units in the array than what is visible to the eye, which indicates that they perceive the array as 3D. A composite unit of three marbles is used to infer the total amount needed to construct the array. In task 2, the students have taken an important step in the development of the cognitive process of organizing-by-composites. They move away from double and triple counting and end up iterating a 3D composite unit which, if used correctly, can generate the whole array.

Supporting units-locating towards a relevant organizing-by-composites

Mastering units-locating is not enough to correctly enumerate units in a 3D array. In order to develop a coherent mental model, the students must discover a structure in the array, where the most effective understanding is layered thinking: \(\mathrm{base }\times \mathrm{ height}\). An important step towards this is organizing-by-composites (Battista, 2004). In this section, we will discuss how a spherical unit-representation might support this cognitive process.

The struggles shown in group 10 when enumerating cubical units were not present when working with the spherical units. When working with spheres, the students quickly located the units, arranged them in groups (composite units) and used this to infer the total amount of spheres. We will look at their solution on task 2.

Girl 10:3, 6, 9. (counting in rows on TL)

Boy 10:Nine. Nine (completing the calculation with pointing on Bottom Layer, BL). It is the same.

Girl 10:9, 18, 27. It is the same as the cube.

The quick and efficient decomposition of this task, as visualized in Fig. 14, may indicate that the spheres were easier to locate and arrange into a composite unit. Group 10 ends up with a layer-based strategy (A) for task 2. In both of the spherical tasks, the students had no problems identifying the 3D structure of the array.

Fig. 14
figure 14

Visualization of group 10 counting strategy on task 2

Full size image

In Fig. 15, we can see that group 6 discerned and added together composites of “sixes” on task 3. How the sixes were composed was not evident from the students’ worksheet, and unfortunately, we did not have any recorded explanation from this group that provided further insight into their reasoning. But, based on their drawings of crosses, we could see that the students counted each sphere only once and so, again, avoided double or triple counting. The written explanation indicated that the group organized the spheres into composites of six which then was iterated to enumerate the array. We also argue that the students showed an awareness of the hidden units in the array in their solution. More specifically, in the array of task 3, there are 24 units visible. So, to the students, four groups of six units were visible. However, they distinguished six groups of six units, which imply that they considered more units than only the visible ones. In addition, we argue that these composites of six spheres are relevant when enumerating this array, since they can be used to find the correct number of unit-spheres by being iterated six times. However, the students made some calculation error and ended up with 69 spheres in total.

Fig. 15
figure 15

Group 6, task 3

Full size image

For group 11, the structure of the 3D array in task 2 was immediately recognized as similar in structure to the 3D array in task 1. It is interesting to notice that this group had some initial struggles with enumerating units in the first task with cubical units and only small uncertainties on tasks with spheres as units. When encountering the third task, it seemed like the spherical units pushed the group towards a more sophisticated decomposition of the array, using composite units:

Boy 11a:And this is 36

Boy 11b:36, yes.

Boy 11a:Nine… wait a minute. Stop. This was twenty…

Boy 11b:Wait, wait. We have four up here too (pointing to the right row of RFL)

Boy 11a:Then it is 9, 9, 9. That is 27. And then there is nine on the top. 9 + 9 + 9 + 9

Figure 16 shows how group 11 decomposed the array. This counting strategy indicate that they have not yet developed an understanding of the most efficient use of layer thinking, but they are organizing units into composite units and using them correctly (strategy B). The difference in uncertainty surrounding the counting strategies for cubical and spherical tasks might imply a couple of things. It could be that they had to work through a “warm-up task” to get rid of their uncertainties and misconceptions. When working with task 1, they overcame some obstacles which made the rest of the tasks easier to solve. Another option is that the spherical units in fact invited the students in this group to locate and discern the units to a greater degree than cubical units. A third option is that the group used the 3 × 3 × 3 array with marbles as support for their answer in the first task. Since they recognized the arrays as congruent in structure, the spherical array might substantiate that their answer to the first question was correct.

Fig. 16
figure 16

Visualization of group 11 strategy on task 4

Full size image

Discussion

In this study, we addressed the research question: What role does units-locating play in students’ strategies in enumerating units of 3D arrays and how are their units-locating processes linked to the unit-representation of the array? The results of the present study show the crucial role of units-locating in enumerating units of 3D arrays and the link between units-locating and unit-representation. The findings from this study indicate that arrays built of spheres can turn students’ away from double and triple counting by facilitating students’ processes of units-locating and spatial structuring. The spherical units seem to provide students with perceptual clues (Battista, 2010; Campbell, 1990; Vasilyeva et al., 2013) that support them in developing enumeration strategies with higher LoS (Battista, 2004). In other words, the spherical unit can be of aid in the students’ spatial structuring process, helping them discern the unit, establish relationships between the units and create subsets of the units (composite units) (Battista & Clements, 1996). For example, group 6 applied double and triple counting in tasks where the unit was a cube, but not in the tasks where the unit was a sphere. This might imply that the students were able to coordinate different viewpoints of the arrays built of spheres, which according to Battista (2004) is a requirement for being able to discern the unit of which the array is constructed. Based on this, the findings show how different unit-representations can mediate different ideas and strategies in the situation of enumerating 3D arrays. Research literature has focused on children’s strategies and challenges in enumerating cubical units (Smith & Barrett, 2017). Our study suggests that we need research on the role of different unit-representations. With input from our findings, we suggest research to investigate further the following three hypotheses: (i) spherical units can turn students away from double and triple counting, (ii) spherical units can support students’ units-locating process and ability to assemble units into relevant composites and (iii) teaching of enumerating 3D arrays should start with spherical units before cubical units. We ground these three hypotheses in a discussion of implications for research and teaching.

Research implications

Previous research show how students can face difficulties in enumerating cubical units in 3D arrays (Battista & Clements, 1996; Ben-Haim et al., 1985; Finesilver, 2015, 2017; Vasilyeva et al., 2013). This study confirms many of these findings. For instance, we have found, as Ben-Haim et al. (1985) and Battista and Clements (1996), that students apply double and triple counting and that this is connected to their spatial structuring abilities, as the erroneous strategies are based on an incoherent mental model of the array. Moreover, the findings of this study also underpin the idea of Battista (2010), Finesilver (2015, 2017) and Vasilyeva et al. (2013) on how perceptual clues can support students’ reasoning when enumerating units in 3D arrays.

However, the significance of the present study should not only be understood in how it confirms findings of previous research. Instead, the significance should be understood in how the study sheds new light on the role of unit-representation in students’ enumeration strategies. For instance, it shows how students can avoid difficulties documented in the cubical case when acting on arrays built of spherical units. In particular, this study indicates that cubical units support double and triple counting to a greater extent, compared to spherical units. Additionally, according to the need of developing a coherent mental model of a 3D array (Battista, 2004), spherical units seem to support students’ processes of units-locating, spatial structuring and organizing-by-composites. The process of units-locating is essential to be able to correctly enumerate the units in the array. The ability to discern and locate units in the array show a development in students’ spatial structuring, which requires the ability to coordinate different viewpoints of the array and to be aware of the three-dimensionality of the representation of 3D units in the array (Finesilver, 2015).

This study points to the need to explore unit-representations in more detail, in order to increase the understanding of students’ difficulties and abilities to enumerate 3D arrays and to develop an understanding of the volume formula. The present study contributes to this need by illustrating how spherical units can elevate students’ way of seeing through the structure and enumerate the units of a 3D array. Our hypothesis as to why students succeed in locating units and avoid double and triple counting in the spherical case is that the spheres have no faces and do not sit together with a common side. In the context of enumerating 3D arrays, we invite further research to inquire into the role of unit-representation and, particularly, how spherical units can support students’ enumeration strategies.

Teaching implications

The present study indicates that some students find it easier to see through the structure of a 3D array built of spherical units compared to cubical units. This not only implies that the teaching of enumerating 3D arrays should provide students an opportunity to contrast between different forms of unit-representations. It also raises a question to whether students’ learning would benefit from teaching starting with spherical units before cubical units.

Through the present study, we have taken steps in understanding the crucial role of units-locating in seeing through and making sense of the mathematical structure of a 3D array. An increased ability to make sense of the mathematics of a 3D array, we claim, will put the students in a good position to not only calculate but also to understand the volume formula of prisms. Calculating the volume of prisms with understanding requires the student to see that multiplying length, width and height will generate the whole array of cubical units. This involves layer thinking, as the multiplication of two dimensions will provide the first layer of the array. Hence, when students develop a coherent mental model of a 3D array and discover that it is built of several identical layers, it can be helpful in understanding the volume formula as well. Calculating the volume of prisms accurately is not possible by enumerating spherical units, as they will leave gaps in the array. Yet, we argue that working with spherical units may facilitate students’ understanding of volume of prisms, as it seems to facilitate their process of units-locating and their ability to see through and develop efficient enumeration strategies of 3D arrays.

Conclusion

In the present study, we have focused on the role of units-locating for meaningful enumeration of units of 3D arrays and how units-locating is linked to the unit-representation of the array. Our study shows not only that students’ difficulties in enumerating units of 3D arrays can be traced to difficulties in units-locating, but also that meaningful enumeration strategies are linked to unit-representation. In other words, enumerating units of 3D arrays should not only be considered a purely cognitive process. To understand the complexity of students’ enumeration strategies, we must carefully consider the link between units-locating and unit-representation.