Skip to main content
SpringerLink
Log in

Effects of reading-oriented tasks on students’ reading comprehension of geometry proof

  • Original Article
  • Published:
Mathematics Education Research Journal Aims and scope Submit manuscript

Abstract

This study compared the effects of reading-oriented tasks and writing-oriented tasks on students’ reading comprehension of geometry proof (RCGP). The reading-oriented tasks were designed with reading strategies and the idea of problem posing. The writing-oriented tasks were consistent with usual proof instruction for writing a proof and applying it. Twenty-two classes of ninth-grade students (N = 683), aged 14 to 15 years, and 12 mathematics teachers participated in this quasi-experimental classroom study. While the experimental group was instructed to read and discuss the reading tasks in two 45-minute lessons, the control group was instructed to prove and apply the same propositions. Generalised estimating equation (GEE) method was used to compare the scores of the post-test and the delayed post-test with the pre-test scores as covariates. Results showed that the total scores of the delayed post-test of the experimental group were significantly higher than those of the control group. Furthermore, the scores of the experimental group on all facets of reading comprehension except the application facet were significantly higher than those of the control group for both the post-test and delayed post-test.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  • Alfassi, M. (1998). Reading for meaning: the efficacy of reciprocal teaching in fostering reading comprehension in high school students in remedial reading classes. American Educational Research Journal, 35(2), 309–332.

    Google Scholar 

  • Alcock, L. (2009). e-Proofs: Student experience of online resources to aid understanding of mathematical proofs. Paper presented at the 12th Conference on Research in Undergraduate Mathematics Education, Raleigh, NC. Available from http://mathed.asu.edu/crume2009/Alcock1_LONG.pdf. Accessed 25 November 2011.

  • Alcock, L. J., & Weber, K. (2005). Proof validation in real analysis: inferring and checking warrants. The Journal of Mathematical Behavior, 24(2), 125–134.

    Article  Google Scholar 

  • Anderson, R. C., & Pearson, P. D. (1984). A schema-theoretic view of basic processes in reading comprehension. In O. D. Pearson (Ed.), Handbook of reading research (pp. 255–291). NJ: Longman.

    Google Scholar 

  • Batting, W. F., & Bellezza, F. S. (1979). Organization and levels of processing. In C. R. Puff (Ed.), Memory organization and structure. New York: Academic.

    Google Scholar 

  • Chazan, D. (1993). High school geometry students’ justification for their views of empirical evidence and mathematical proof. Educational Studies in Mathematics, 24(4), 359–387.

    Article  Google Scholar 

  • Dole, J. A., Duffy, G. G., Roehler, L. R., & Pearson, P. D. (1991). Moving from the old to the new: research on reading comprehension instruction. Review of Educational Research, 61, 239–264.

    Google Scholar 

  • Duval, R. (2002). Proof understanding in mathematics: What ways for students? In: F. L. Lin (Ed.) Proceedings of the international conference on mathematics—“Understanding Proving and Proving to Understand” (pp. 61–77).

  • Ernest, P. (1989). The impact of beliefs on the teaching of mathematics. In P. Ernest (Ed.), Mathematics teaching: The state of the art (pp. 249–254). New York: Falmer Press.

    Google Scholar 

  • Furinghetti, F., & Morselli, F. (2009). Every unsuccessful problem solver is unsuccessful in his or her own way: affective and cognitive factors in proving. Educational Studies in Mathematics, 70, 71–90.

    Article  Google Scholar 

  • Garuti, R., Boero, P., & Lemut, E. (1998) Cognitive unity of theorems and difficulties of proof. In the Proceedings of the Twenty-second International Conference for thePsychology of Mathematics Education, Vol. 2, pp. 345–352.

  • Hanna, G. (2000). Proof, explanation and exploration: an overview. Educational Studies in Mathematics, 44, 5–23.

    Article  Google Scholar 

  • Harel, G. (2008). DNR perspective on mathematics curriculum and instruction, Part I: Focus on proving. ZDM-The International Journal on Mathematics Education, 40(3), 487–500.

    Article  Google Scholar 

  • Harel, G., & Sowder, L. (1998). Students’ proof schemes: Results from exploratory studies. In A. H. Schoenfeld, J. Kaput, & E. Dubinsky (Eds.), Research in Collegiate Mathematics Education III (pp. 234–283). Providence: American Mathematical Society.

    Google Scholar 

  • Healy, L., & Hoyles, C. (2000). A study of proof conception in algebra. Journal for Research in Mathematics Education, 31(4), 396–428.

    Article  Google Scholar 

  • Herbst, P. (2002). Establishing a custom of proving in American school geometry: evolution of the two-column proof in the early twentieth century. Educational Studies in Mathematics, 49, 283–312.

    Article  Google Scholar 

  • Kintsch, W. (1998). Comprehension: A paradigm for cognition. New York: Cambridge University Press.

    Google Scholar 

  • Koedinger, K. R. (1998). Conjecturing and Argumentation in High-School Geometry Students. In R. Lehrer & D. Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 319–348). Mahwah: Lawrence Erlbaum Associates.

    Google Scholar 

  • Leikin, R. (2009). Multiple proof tasks: Teacher practice and teacher education. In: F-L. Lin, F.-J. Hsieh, G. Hanna, & M. de Villiers (Eds.) Proof and proving in mathematics: ICMI Study 19 Conference proceedings, (Taipei, Taiwan), 2, 31–36.

  • Leung, A., & Lopez-Real, F. (2002). Theorem justification and acquisition in dynamic geometry: a case of proof by contradiction. International Journal of Computers for Mathematical Learning, 7, 145–165.

    Article  Google Scholar 

  • Lin, F. L., & Yang, K. L. (2007). The reading comprehension of geometric proofs: The contribution of knowledge and reasoning. International Journal of Science and Mathematics Education, 5(4), 729–754.

    Google Scholar 

  • Mariotti, M. A. (2007). Proof and proving in mathematics education. In A. Guitierrez & P. Boero (Eds.), Handbook of research on the psychology of mathematics education. Rotterdam: Sense Publishers.

    Google Scholar 

  • McNamara, D., Kintsch, E., Songer, N. B., & Kintsch, W. (1996). Are good texts always better? Interactions of text coherence, background knowledge, and levels of understanding in learning from text. Cognitive Instruction, 14, 1–43.

    Article  Google Scholar 

  • Morris, A. K. (2002). Mathematical reasoning: adults’ ability to make the inductive-deductive distinction. Cognition and Instruction, 20(1), 79–118.

    Article  Google Scholar 

  • Nassaji, H. (2002). Schema theory and knowledge-based processes in second language reading comprehension: a need for alternative perspectives. Language Learning, 52(2), 439–481.

    Article  Google Scholar 

  • Nolan, T. E. (1991). Self-questioning and prediction: combining metacognitive strategies. Journal of Reading, 35, 132–138.

    Google Scholar 

  • Norman, D. A., Gentner, S., & Stevens, A. L. (1976). Comments on learning schemata and memory representation. In D. Klahr (Ed.), Cognition and instruction. Hillsdale: Lawrence Erlbaum Associates, Inc.

    Google Scholar 

  • Paas, F., & van Merrienboer, J. (1994). Variability of worked examples and transfer of geometrical problem solving skills: a cognitive-load approach. Journal of Educational Psychology, 86, 122–133.

    Google Scholar 

  • Palincsar, A. S., & Brown, A. L. (1984). Reciprocal teaching of comprehension-fostering and comprehension-monitoring activities. Cognition and Instruction, 1(2), 117–175.

    Article  Google Scholar 

  • Pressley, M. (2000). What should comprehension instruction be the instruction of? In M. L. Kamil, P. B. Mosenthal, P. D. Pearson, & R. Barr (Eds.), Handbook of reading research (Vol. 3, pp. 545–561). Mahwah: Erlbaum.

    Google Scholar 

  • Rotnitzky, A., & Jewell, N. P. (1990). Hypothesis testing of regression parameters in semiparametric generalized linear models for cluster correlated data. Biometrika, 77, 485–497.

    Article  Google Scholar 

  • Rosenshine, B., & Meister, C. (1994). Reciprocal teaching: a review of the research. Review of Educational Research, 64, 479–531.

    Google Scholar 

  • Selden, A., & Selden, J. (2003). Validations of proofs considered as texts: aan undergraduates tell whether an argument proves a theorem? J Res Math Educ, 34, 4–36.

    Article  Google Scholar 

  • Sfard, A. (2000). On reform movement and the limits of mathematical discourse. Mathematical Thinking and Learning, 2(3), 157–189.

    Article  Google Scholar 

  • Silver, E. A. (1994). On mathematical problem posing. For the Learning of Mathematics, 14(1), 19–28.

    Google Scholar 

  • Smith, N. B. (1965). American reading instruction. Newark: International Reading Association.

    Google Scholar 

  • Solomon, Y. (2006). Deficit or difference? The role of students’ epistemologies of mathematics in their interactions with proof. Educational Studies in Mathematics, 61(3), 373–393.

    Article  Google Scholar 

  • Sweller, J., van Merriënboer, J. J. G., & Paas, F. G. W. C. (1998). Cognitive architecture and instructional design. Educational Psychology Review, 10, 251–296.

    Article  Google Scholar 

  • Yang, K. L. (2010). The Potential of Statement-Posing Tasks. For the learning of mathematics, 30(2), 22–23.

  • Yang, K. L. (2011). Structures of cognitive and metacognitive reading strategy use for reading comprehension of geometry proof. Educational Studies in Mathematics. doi:10.1007/s10649-011-9350-1.

  • Yang, K. L., & Lin, F. L. (2008). A model of reading comprehension of geometry proof. Educational Studies in Mathematics, 67(1), 59–76.

    Google Scholar 

  • Yang, K. L. & Lin, F. L. (2009). Designing innovative worksheets for improving reading comprehension of geometry proof,. In M. Tzekaki, M. Kaldrimidou, & C. Sakonidis, (Eds.), Proceedings of the 33rd Conference of the International Group for the Psychology of Mathematics Education (Vol. 5, pp. 377–384). Thessaloniki, Greece: PME.

  • Zeger, S. L., & Liang, K.-Y. (1986). Longitudinal data analysis for discrete and continuous outcomes. Biometrics, 42, 121–130.

    Article  Google Scholar 

Download references

Acknowledgments

The authors wish to thank the participating teachers and students of this study. Although this paper is about part of a research project funded by the National Science Council of Taiwan (NSC 96-2521-S-018-004-MY3), the views and opinions expressed in this paper are those of the authors and not necessarily those of the NSC.

Author information

Authors and Affiliations

  1. Department of Mathematics, National Taiwan Normal University, Taipei City, Taiwan

    Kai-Lin Yang & Fou-Lai Lin

Authors
  1. Kai-Lin Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fou-Lai Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kai-Lin Yang.

Appendices

Appendix A

The Task of Reading Proof with its Proposition

Believe me! You will be brought into a world which can make you say “Wow! How fun mathematics is! It’s quite simple!” after this class. Follow me, it’s time to start. GO!…Now, as clever as you are, please think carefully about the next questions of proof, and write down your thoughts in the following blank space:

figure a
  1. (1-1)

    What is “the given” in the above proof?

  2. (1-2)

    What is “the claim” in the above proof?

  3. (1-3)

    Thinking in the beginning of “the given” in the above proof, what can you infer in the next step?

  4. (1-4)

    Which sub-conclusion can you derive to apply “\( \overline {\text{BC}} = \overline {\text{AD}} \)” in the above proof?

  5. (2-1)

    In the above proof, which properties are written unclearly in the given?

  6. (2-2)

    In the above proof, which proof steps do you not understand? Please circle them.

  7. (2-3)

    Thinking! In the above proof, can you think which proof steps are redundant or unnecessary? Please delete them with straight lines in the above proof.

  8. (3-1)

    Now, please use brief sentences to write down the draft of the proof.

    figure b
  9. (3-2)

    Please discuss in groups. Write down the differences between drafts, and an agreed draft after the discussion.

  10. (4-1)

    If you were a teacher, which problem could you pose that would be answered by the arguments in the above proof?

  11. (4-2)

    Do you have the same answer according to the problem you devise in (4-1), (1-1), and (1-2)? What is the correct answer?

  12. (4-3)

    Please go back to check (1-3) and (1-4), and you can revise the conjecture of (1-3) and (1-4) if you need to.

  13. (4-4)

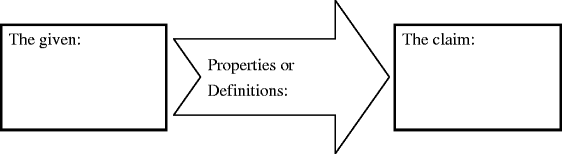
    Referring to (3-1), please describe the relationship between the given, properties or definitions, and the claim.

  14. (4-5)

    While applying the properties or definitions, what should you notice?

  15. (4-6)

    While reading mathematical proofs hereafter, how will you read for comprehending proofs?

The Statement-Posing Task

Jam read a mathematical book where some part of a page was torn to pieces. He found that a proposition was gone, but the proof of this proposition was there. Now, can you help Jam to think out what this proposition is?

figure c
figure d
  1. (1-1)

    According to the above proof, can you conjecture what this proposition is?

  2. (2-1)

    Think! In the above proof, which proof steps do you not understand? Please circle them.

  3. (2-2)

    Think! In the above proof, can you think which proof steps are redundant or unnecessary? Please cross them out in the above proof.

  4. (2-3)

    In the above proof, what do you think the key points are?

  5. (2-4)

    Which properties or definitions are used in the proof?

  6. (3-1)

    Now, please use brief sentences to write down the draft of the proof.

    figure e
  7. (3-2)

    Please discuss in groups, and write down the differences between drafts, and come up with an agreed draft after discussion.

  8. (4-1)

    Please go back to check (1-1) again. You can revise the conjecture of (1-1) if you need to.

  9. (4-2)

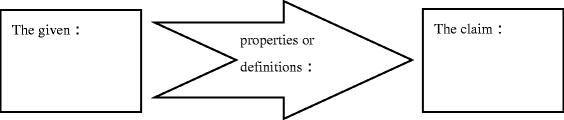
    Referring to (3-1), please describe the relationship between the given, properties or definitions, and the claim.

  10. (4-3)

    While applying the properties or definitions, what should you notice?

  11. (4-4)

    While you read mathematical proofs hereafter, how will you read to easily comprehend proofs?

Appendix B

figure f

*P# and C# respectively mean the corresponding premise and conclusion of each argument in the proof.

Answer the following questions on the basis of the proof process.

  1. (1)

    Do you agree that \( \overline {\text{BM}} = \overline {\text{CM}} \)? Explain why or why not.

  2. (2)

    Label ∠BMD in this figure as 1 and ∠CMD as 2.

  3. (3)

    If △BMD and △CMD are congruent, what is the corresponding side of \( \overline {\text{DB}} \)?

  4. (4)

    Besides the known conditions (the perpendicular bisector of \( \overline {\text{BC}} \), intersects \( \overline {\text{AB}} \) at D, and intersects \( \overline {\text{BC}} \) at M. And \( \overline {\text{DA}} = \overline {\text{DB}} \)), which conditions can be directly applied without any explanation?

  5. (5)

    If someone suggests that the proof process of lines 1, 2, 4, 3, 5, 6, 7, and 8 is correct, after lines 3 and 4 are interchanged, would you agree with his or her opinion?

  6. (6)

    If someone suggests that the proof process of lines 6, 1, 2, 3, 4, 5, 7, and 8 is correct, after the position of line 6 has been changed, would you agree with his or her opinion?

  7. (7)

    Which properties are applied in this proof?

  8. (8)

    On the basis of the question and the proof,

    1. (8-1)

      Which premises are necessarily required?

    2. (8-2)

      What final conclusion is derived from these premises?

  9. (9)

    Which statements can be validated from this proof?

  10. (10)

    From this proof process, it firstly derives an important result from the condition that the perpendicular bisector of \( \overline {\text{BC}} \), L, intersects \( \overline {\text{BC}} \) at M and other conditions.

    1. (10-1)

      What is this important result?

    2. (10-2)

      According to this important result in (10-1) and \( \overline {\text{DA}} = \overline {\text{DB}} \), one condition can be derived to confirm ∠DCA=∠DAC. What is this condition?

  11. (11)

    Choose the correct statements.

  12. (12)

    Do you agree that this proof process is correct?

  13. (13)

    Statement A: If L, the perpendicular bisector of \( \overline {\text{BC}} \) of △ABC, intersects \( \overline {\text{AB}} \) at D, and intersects \( \overline {\text{BC}} \) at M. And \( \overline {\text{DA}} = \overline {\text{DB}} \); then ∠DCA and ∠DAC must be equal.

    1. (13-1)

      Do you agree that this proof process can prove that Statement A is always correct?

    2. (13-2)

      Do you agree that this proof process can prove that Statement A is sometimes correct and sometimes incorrect?

Answer the following questions on the basis of what you know.

  1. (14)

    There is a circle with centre point P, radius \( \overline {\text{PS}} \) and \( \overline {\text{PQ}} \). If T is the midpoint of \( \overline {\text{PQ}} \), \( \overline {\text{ST}} \bot \overline {\text{PQ}} \), and S is the midpoint of \( \overline {\text{PR}} \), is △RSQ an isosceles triangle?

  2. (15)

    There are three points P, Q, and R. If S is the midpoint of \( \overline {\text{PQ}} \) and \( \overline {\text{ST}} \bot \overline {\text{PQ}} \), what conclusions can be derived?

  3. (16)

    If D is the midpoints of \( \overline {\text{AE}} \), and \( \overline {\text{BD}} \) and \( \overline {\text{AE}} \) are perpendicular to each other, and \( \overline {\text{AB}} = \overline {\text{BC}} \), then ∠AEC = 90°, is this correct?

Appendix C

figure g

*P# and C# respectively mean the corresponding premise and conclusion of each argument in this proof.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yang, KL., Lin, FL. Effects of reading-oriented tasks on students’ reading comprehension of geometry proof. Math Ed Res J 24, 215–238 (2012). https://doi.org/10.1007/s13394-012-0039-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13394-012-0039-2

Keywords

Search

Navigation