1 Introduction

Modular multiplication of large integers is the computational backbone of many applications: public-key cryptographic schemes such as RSA [26], factorization algorithms such as the elliptic curve method (ECM)  [17], or even computations of massively remote hexadecimal digits of \(\pi \) [28]. The RSA public-key algorithm is the focus of this paper because (1) increasingly large integers are required for good security and therefore faster implementations of the algorithm are of continuing interest [16]; (2) the commonly used Chinese remainder theorem (CRT) approach to decryption is vulnerable to fault-injection attacks for which countermeasures incur overhead [1]; and (3) the continuing widespread use of RSA in practice.

Throughout this paper, parallel modular multiplication refers to the simultaneous computation of several modular multiplications, each with independent inputs and moduli. Parallel modular multiplications can be realized by many separate processor cores running concurrently, e.g., with the use of libraries such as MPI [20]. Another approach, and the one adopted by this paper, is through the use of vector or single instruction multiple data (SIMD) instructions. Vector instruction sets, which simultaneously apply the same operation to multiple independent lanes of equally sized data, are now a standard offering of commodity processor vendors. In this paper, we focus on the AVX-512 instruction set recently implemented by Intel [25].

In AVX-512, each of the 32 available 512-bit registers can be utilized as 8 independent 64-bit lanes or 16 independent 32-bit lanes, with extensions to AVX-512 allowing even finer granularity. It should be noted that while many instructions targeting 64-bit lanes are available, a 64-bit \(\times \) 64-bit vector full-multiply (providing the full 128-bit result) is not one of them. The largest integer vector full-multiply available is \(32\times 32\) = 64 bits. Nonetheless, as others have recently reported, AVX-512 has the capability to outperform highly optimized multipliers based on scalar 64-bit instructions [10].

Montgomery multiplication, introduced by Peter Montgomery in 1985 [19], is a technique for performing modular multiplication that is particularly efficient on binary computers. Since then, many variants of the algorithm have been introduced that offer advantages. A good treatment of several of these variants is given by Koc [14]. Using Koc’s terminology, the Coarsely Integrated Operand Scanning (CIOS) method reduces the number of additions, reads, or writes; the Separated Operand Scanning (SOS) method allows processing using sub-quadratic methods (e.g., Karatsuba multiplication [13]); and the Finely Integrated Product Scanning (FIPS) variant can be particularly efficient on processors with hardware accumulators. The present paper introduces a block-based refinement of the FIPS technique that we denote as Block Product Scanning (BPS). BPS significantly reduces the number of loads and stores of data in practice and allows data dependencies in sequential operations to be removed, resulting in a greater degree of latency hiding. Additionally, we show that the two independent exponentiations associated with CRT-RSA decryptions can be computed simultaneously by interleaving data within the lanes of AVX-512 registers. This intermixing of data in our implementation provides protection against fault-injection attacks with no additional calculation overhead.

The contributions of this paper are (1) the introduction of the parallel BPS Montgomery multiplication variant, which, as implemented using AVX-512, demonstrates 1.9 times increased decryption throughput compared to OpenSSL and \(1.5\,\times \) increased modular exponentiation throughput compared to GMP-6.1.2 at 2048-bit modulus sizes and (2) a CRT-RSA implementation strategy whereby exponentiations modulo the two prime factors of the RSA modulus, p and q, are performed simultaneously and interleaved within AVX-512 vectors. Fault injections capable of randomizing or zeroing registers or skipping instructions at any instant during a calculation will therefore simultaneously affect both halves of the decryption, in which case no information about p or q can be extracted [1].

The rest of the paper is organized as follows. In Sect. 2, we discuss related work and present a rough taxonomy of published implementations related to the one given in this paper. Section 3 provides algorithmic detail of the BPS Montgomery multiplication variant. Section 4 discusses implementation aspects including our vectorization strategy, squaring improvements, and a timing and fault-injection resistant CRT-RSA implementation. Section 5 provides benchmarking data and Sect. 6 concludes the paper.

2 Related work

Given its broad applicability, modular multiplication has been well studied. In the work most relevant to this paper, there are four general themes, two dealing with parallelization strategies and two with low-level arithmetic approaches. All utilize Montgomery’s modular multiplication. Parallelization strategies generally fall into one of two categories: using parallel resources to accelerate a single modular multiplication at a time, or acceleration by performing several modular multiplications in parallel. Serial implementations have the advantage of lowering the latency of individual modular multiplications; parallel strategies tend to map better to SIMD architectures and therefore tend to achieve higher throughput.

Low-level arithmetic in the various implementations may use a reduced-radix approach, or not. Reduced-radix implementations encode large integers by arrays of smaller words, where each word uses fewer bits than the hardware maximum. For example, if the hardware maximum is 32 bits, large integers might be represented by arrays of 28-bit words. Doing so allows carry bits to accumulate in each word for several steps of a modular multiplication before an explicit carry propagation step becomes necessary. Reduced-radix encoding requires more array words than full-radix representations so that a drawback becomes the larger number of partial-product computations. Conversely, full-radix implementations use the full precision available in the hardware and fewer partial-product computations.

Other parallelization strategies exist as well, of course, beyond the simplistic categorization discussed here. However, we restrict our comparisons to SIMD approaches, omitting those where multiple, possibly heterogeneous compute cores process single modular multiplications in parallel.

Implementations targeting hardware on which efficient carry propagation mechanisms exist tend to use full-radix representations. Examples include general-purpose CPUs [9, 14] and GPUs [5, 6], and the first generation Xeon Phi codenamed Knight’s Corner (KNC)  [3, 15, 30]. However, the parallelization strategies differ. The GPU-accelerated modular multiplications in Emmart [5] are parallel, while the KNC’s multipliers are all serial. To our knowledge, Emmart and Zhao [30] have the best-performing modular multiplication throughput in their respective hardware platforms.

Implementations targeting Intel’s various SIMD architectures, with the exception of KNC, tend to use reduced-radix representations. In these instruction set architectures (e.g., SSE2, AVX2, and AVX-512), there are no SIMD (vector) carry flags, resulting in inefficient carry propagation. Gueron has published several works on various SIMD enhancements using reduced radix, including  [4, 9,10,11]. Orisaka et al. adopt a reduced-radix implementation in their work on Isogeny-based cryptography accelerated by AVX-512 [22]. Takahashi et al. also use reduced radix in their computation of the 100 quadrillionth hexadecimal digit of \(\pi \) [28]. Exceptions to the use of reduced-radix representations that we have found include Smart [23], Bos [2], and our work. Parallelization strategies differ here as well. Gueron’s works are serial accelerations, while Orisaka, Smart, Takahashi, and our own work are parallel. In Bos et al., a novel 2-way parallel strategy is used to accelerate serial modular multiplications.

3 Block Product Scanning technique

In the Montgomery multiplication of two k-bit integers A and B modulo a third k-bit integer M, we first choose an integer \(R = 2^{k}\) such that \(R > M\). If the inputs are then transformed via modular multiplication by R, i.e., \(\bar{A} = A \cdot R \textit{ mod } M\), then subsequent modular multiplications of transformed inputs can be computed using only shifting and masking, avoiding expensive long divisions. A Montgomery multiplication is computed via Algorithm 1.

figure a

Importantly, the output \(C \equiv (A \cdot B) \cdot R \textit{ mod M }\) is already in Montgomery form and ready for further Montgomery operations. \(M'\) is the precomputed inverse of \(M \textit{ mod } R\).

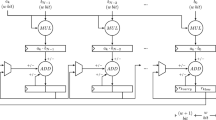
In [14], several variants of this basic algorithm are presented. The optimizations are all based on the observation that the temporary product \(U = T \cdot M' \textit{ mod } R\) only needs to be computed one word at a time, where a word is an integer in radix \(W = 2^w\). For example, in Algorithm 2 the FIPS variant of Montgomery multiplication is presented assuming operation on integers a, b, m, each composed of t w-bit words. In this variant, output words are computed and finalized one at a time, into output c, via integrated product and reduction loops. As noted in [14], the main benefit of the FIPS method is that output data can be kept in a set of three accumulation registers, denoted in Algorithm 2 by variables s[0..2], to store the double-word product summations. The notation x..y denotes indices x through y, inclusive.

figure b

With respect to Algorithm 1, the first nested loops of Algorithm 2 essentially perform column summations of all partial-product terms involved in the calculation of the lower half of T, all of U (one term at a time, via line 6 of Algorithm 2), and the lower half of \(U \cdot M\). The second nested loop then completes the upper-half calculations of T and \(U \cdot M\) while dividing by R (by storing the output into location \(c[i-t]\)).

Algorithm 2 has the unique feature of keeping frequently accessed data resident in-processor, namely, the three accumulation registers s[0..2]. Data locality is a crucial tool of software optimization and can both reduce the latency of data fetches, leading to increased instruction throughput, and lower the energy required to fetch data, leading to increased energy efficiency. The cache hierarchy present in today’s CPUs enables a considerable degree of data locality, but no storage is closer to the CPU than the register file. By partitioning the outer loops of Algorithm 2, it becomes possible to reuse not only output data registers, but input data registers as well. Consider the diagram in Fig. 1 that depicts the partial-product expansion of the full multiplication of a pair (A, B) of 512-bit integers, with the 16 w=32-bit words numbered in hexadecimal \(0-f\). All partial-product outputs b, a are numbered according to their input words. Carry propagation of the high-half product and column summations are ignored for simplicity.

Fig. 1
figure 1

Partial-product diagram of a 512-bit full product

Full size image

Blocks are identified in Fig. 1 in which (1) the accumulated output words of all partial products in each block can be kept in a small set of registers and (2) the input dependencies of all partial products in each block are limited to a relatively small set of words. There are \(n_b\) blocks of input, each with block size B. In Fig. 1, \(n_b\) and B are both equal to 4 and there are 4 columns of w-bit words in each block. There are \(2*n_b\) output block-columns numbered \(i = [0..(2*n_b-1)]\). Other block sizes are also possible as long as B divides the number of words, t, in the inputs. There are two types of blocks, full and partial. Full blocks with \(B=4\) contain 16 partial products, while partial blocks contain either 10 (on the low-side multiply) or 6 (on the high-side multiply). Within each block, we perform one set of read operations to load input data into processor registers, followed by partial-product computation and summation into a different set of processor registers. Each block reuses its four A inputs four times each and its B inputs a total of nine times, for a total savings of 21 read operations per full block. There are two write passes into the output C: one pass in each outer loop (note, the write pass in the first outer loop occurs in the BlockFinal algorithm).

figure c

In Algorithm 3, the BPS technique as applied to a Montgomery product is shown. There are two accumulators: a block accumulator, \(s[0..n_b-1]\), and a column accumulator, accum. The block accumulator stores the accumulation of each block-column is reset each outer loop iteration, after being accumulated into the column accumulator. The column accumulator folds in the results of each block-column one by one to form output words (first of U, then of the output C).

figure d
figure e
figure f
figure g

The first nested loops of Algorithm 3 perform column summations of all partial-product terms involved in the right half of Fig. 1. The first inner loop sequencing from high to low index guarantees that full block calculations always depend on earlier-computed column results. In other words, columns of blocks are computed from bottom to top in Fig. 1. Full blocks can compute their accumulations in any desired order, allowing operations to be grouped advantageously either by the compiler or manually. After the triangular partial block of inputs A and B is computed via Algorithm 5, we enter a loop to finalize each column in Algorithm 7. It is at this point where the Montgomery constant \(M'\) is folded into the accumulator, C updated, and the accumulator shifted right, similar to Algorithm 2. After the final accumulation completes for each column of the block, all inputs for the next set of blocks \((i+1)\) will be available.

The second nested loop of Algorithm 3 completes the upper-half calculations of T and \(U \cdot M\) while dividing by R (by storing the output into location \(C[i-t]\)). Column finalizations are now easier because the computation of U has been completed and the zeroth word of M is not required, allowing the final triangular partial block involving C and M to be handled by Algorithm 6. For brevity, we have substituted \(n_b\) = 4 in some loop counters and array references.

4 Implementation

In this section, we discuss implementation details of the algorithm for 64-bit processors and for processors with SIMD multiplier capability. We will show in Sect. 5 that 64-bit non-vectorized implementations of BPS can be competitive with state-of-the-art implementations like GMP, and that between similarly implemented BPS and FIPS algorithms, BPS outperforms. However, BPS is designed specifically for SIMD implementation so that multiple modular multiplications can be executed in parallel, for example using Intel’s new AVX-512 instruction set. Newly available SIMD multipliers are a straightforward way to speed up modular multiplication over heavily optimized 64-bit implementations like GMP.

There are several reasons to focus on AVX-512 specifically. First is the availability of the VPMULUDQ instruction, which is a \(32 \times 32\) = 64-bit 4-way multiplier in AVX2 or 8-way multiplier in AVX-512. The second reason we primarily target AVX-512 processors is the fact that processors with AVX-512 include double the register count of previous processor generations, to 32. With 32 wide registers available it becomes feasible to implement Algorithm 3 with block size 4 and correspondingly much greater read and write savings versus smaller block sizes. Lastly, AVX-512 includes masking operations that will be useful for carry propagation and branchless, timing-attack-resistant operation. Source code implementing the algorithms described in this paper, for both 64-bit and AVX-512 processors, is available at \(github.com/bbuhrow/avx512\_modexp\).

Compared to the \(64\times 64\) = 128-bit 1-way multiply instruction available in the same processors, an arbitrary-precision multiplier based on \(32\times 32\) = 64-bit partial products would require 4 times as many total multiplies, assuming the use of something like the \(O(t^2)\) Algorithm 2. Even if all the extra multiplies could be perfectly parallelized as SIMD operations, use of AVX2 would only match implementations based on 64-bit words. As noted in [10], AVX2 could still be beneficial if all instruction counts are considered. When considering only multiply counts, AVX-512 registers are wide enough that we can expect to see approximately a factor 2 improvement in modular multiplication over implementations using 64-bit general-purpose instructions. However, when also considering the add, read, and write counts, in addition to other overhead, a factor of 2 is difficult to achieve. In practice, we are able to show 1.5 times increased throughput over modular exponentiation in GMP 6.1.2 and 1.9 times increased decryption throughput over OpenSSL at 2048 bits. In subsequent subsections, we discuss the memory layout of the parallel multiplier and issues like register allocation, carry-handling, and enhancements available to squaring.

4.1 BPS multiplication

The bulk of BPS computation occurs in subroutine FullBlock (Algorithm 4) where the partial products of portions of four columns are computed over a subset of input words. This and all other computations are performed 8-way over 8 sets of independent inputs simultaneously. It is assumed that the w-bit words of input data have been arranged in columns of memory such that all 0th words of the 8 inputs are contiguous, followed by word 1, etc., as illustrated in Fig. 2. For example, the multiplication of all 4th words of all inputs by all 1st words of all inputs (such as required in block \(i=1, j=1\)) could be performed by the following code snippet. Here, we make use of intrinsic instructions available in several popular compilers [25].

figure h
Fig. 2
figure 2

Memory layout of 8 independent integers A–H, each with t w-bit words, such that the ith word of each integer can be loaded contiguously

Full size image

Redundant-radix representations, for example, as described in Sect. 3.1 of [10], are not used; all input words use the full precision of the register. Redundant-radix representations are typically used to help prevent bottlenecks due to carry propagation when instructions for handling carries are lacking, e.g., many SIMD instruction sets including AVX-512. Instead, in Algorithm 4 and elsewhere, a dedicated set of carry-overflow registers is used to accumulate carries in each of the four column summations. In AVX-512, carries can be generated with a single pipelinable, dual-issue instruction. Dual-issue instructions can be issued to two independent execution ports in the vector processing unit, which increases instruction throughput [8]. Carry accumulation into the dedicated register set is performed similarly. With the regrouping of operations that is permitted by Algorithm 4, the following code snippet follows each group of four independent multiplies to perform carry propagation of all four columns. Registers t0/t1, t2/t3, t4/t5,  and t6/t7 hold the column/carry summations, respectively. Registers prod[1..4] hold the results of four 64-bit products in Algorithm 4. Four sets of four products can be grouped such that each group uses independent inputs and hence may be pipelined. Mask registers c[1..4] are used in the subsequent set of masked add instructions to accumulate any generated carries. Register cv holds a constant value representing the carry.

figure i

In addition to the 13 registers used above (t[0..7], prod[1..4], and cv), Algorithm 4 further requires an additional 11 registers to hold input data for a total of 24. Algorithm 3 additionally stores the vector constant \(M'\), and two registers to hold accum and its carry, for a grand total of 27 vector registers, well within the 32 available. The grouped carry propagation into a dedicated set of registers is fast and efficient, and the full 64-bit radix available in the AVX-512 vectors is utilized throughout the calculation.

Profiling with an Advanced Hotspots Analysis in Intel’s VTune Amplifier [12] shows that the function implementing Algorithm 3 achieves an average Cycles per Instruction (CPI) rate of 0.441, or over 2 instructions retired per clock cycle, when executed on a Xeon 5122 CPU with Skylake-X microarchitecture. This CPI rate indicates the excellent pipelining and instruction concurrency of Algorithms 4, 5, and 6.

4.2 BPS squaring

Squaring an input can be implemented more efficiently than multiplication of two independent inputs because nearly half of the multiplications can be replaced with doublings (additions, or bit-shifts). This is true for Montgomery modular squaring operations as well; however, the effect is not as great because only the input can be squared, not the multiplication of U and M or of T and \(M'\). Much less has been published about squaring algorithms when using the FIPS technique versus other more commonly used algorithms such as Finely Integrated Operand Scanning (FIOS) [10]. Using 32-bit words for 2048-bit inputs in Algorithm  2, only about 24% of the total multiply operations can be replaced with doublings. Squaring in BPS is optimized by (1) input and output operand registering and re-use; (2) the allowed re-grouping of independent instructions into pipelinable, dual-issuing clusters; and (3) efficient doubling of an entire column of partial products at a time, based on ideas from [4].

To visualize the instruction savings of a squaring operation, it is again useful to consider a block diagram of all partial products, shown in Fig. 3. Here, the various terms are shaded to indicate whether or not they need to be computed. All darkly shaded terms can be skipped because their corresponding “flipped” terms are doubled. For example, the term “5,9” or the 5th word of A multiplied by the 9th word of A, can be skipped because it is the same as the term “9,5”. Simply doubling “9,5” suffices to compute both terms. Therefore, all terms in white need to be doubled. Lightly shaded terms are the square terms and need to be computed, but not doubled. In Fig. 3, it is easy to see that many entire blocks can be simply skipped. Only the butterfly-shaped region containing white or lightly shaded terms need to be calculated.

Fig. 3
figure 3

Partial-product diagram of a 512-bit full square

Full size image

Algorithm 8 presents the complete squaring algorithm when processed with the new Block Scanning approach. The FullBlock algorithm (applied to blocks that are colored entirely white in Fig. 3) does not need to be modified from its multiplication counterpart because term-doublings are handled later. The PartialBlock algorithms are applied to blocks containing shaded terms in Fig. 3 and only need minor modifications from their multiplication versions. We omit these algorithm listings but, in general, they operate by unrolling the loops and omitting terms that appear shaded in Fig. 3.

figure j

In line 6 and line 19 of Algorithm 8, the choice of PartialBlock algorithm depends on whether the loop counter i is even or odd. This branching impacts neither performance nor security. Performance-wise, we are choosing between running one large subroutine or another, and so the branch makes no practical difference. Security-wise, the branch does not depend at all on any of the inputs, only on the loop iteration counter, which is the same for all squaring operations and therefore presents no opportunity for timing attacks that reveal secret input data.

The doubling of the block accumulator, line 10 and line 23 of Algorithm 8, is accomplished with the following code snippet. Waiting until the block accumulator has been computed for an entire block-column before doubling saves significant effort, especially at larger input sizes with more blocks per block-column. Zero extra additions are required and only 4 OR’s and 8 shift operations per block-column, all of which can be pipelined and dual-issued. After the block accumulator has been doubled, any remaining square terms in the block-column are computed and accumulated into s[0..3]. The rest of Algorithm 8 is similar to Algorithm 3.

figure k

Profiling with an Advanced Hotspots Analysis in Intel’s VTune Amplifier shows that the function implementing Algorithm 8 achieves an average Cycles Per Instruction (CPI) rate of 0.398, over 2.5 instructions retired per clock cycle, when executed on a Xeon 5122 CPU with Skylake-X microarchitecture.

4.3 16-way processing for higher throughput

Our baseline implementation computes 8-way parallel modular exponentiations, as described in previous sections. However, higher throughput can be achieved by computing 16-way parallel modular exponentiations, at the expense of latency. The algorithms have the following differences. First, registers are packed with 16 parallel sets of 32-bit data instead of 8 sets. Then, the BPS sub-algorithms are run twice: first to compute 8-way products using the set of even-numbered lanes, followed by a reload and shuffling of data to compute 8-way products of the set of odd-numbered lanes. Finally, following reduction, the even and odd 32-bit results are re-interleaved and stored.

Benchmarking revealed that 16-way processing results in higher throughput, despite the extra shuffling and blending that occurs to avoid overwriting inputs with each 32x32 = 64-bit vector product. This observation is possibly a consequence of better register utilization and a corresponding overall reduction in the number of loads and stores when using 16-way processing. The latency approximately doubles, due to the two passes through each BPS algorithm. However, applications that are latency insensitive can benefit from the increased throughput.

4.4 CRT-RSA implementation

RSA decryption using the Chinese remainder theorem (CRT-RSA) provides a factor of 4 improvement in decryption speed, but is known to be vulnerable to fault-injection attacks [1]. One such class of attacks is when the attacker can inject errors with very fine-grained time resolution (down to a single clock cycle), but with coarse-grained spatial resolution (e.g., a voltage-rail associated with an entire processing core) [24]. Injected errors can zero or randomize (50% chance of flipping each of) the bits within processor registers. Such an attack model might be realistic to someone with access to the power supplies and who can perform side-channel power analysis, but either has no knowledge of the chip internals or has no access to influence them.

As described in previous sections, our vectorization strategy has been to compute 8 independent modular multiplications (or squarings) simultaneously, rather than utilize the vectors to accelerate a single multiplication. By processing in parallel, squaring and Karatsuba enhancements are more-easily realized. In addition, there are benefits when performing CRT-RSA decryptions.

CRT-RSA essentially involves the computation of two independent modular exponentiations: \(S_p = X_p^{d_p}\) \(\textit{ mod } p\) and \(S_q = X_q^{d_q} \textit{ mod } q\) for message X and key (p, q, \(d_p\), \(d_q\), \(i_q=q^{-1} \textit{ mod } p)\). Our strategy is to compute \(S_q\) and \(S_p\) simultaneously using Algorithms 8 and  3 by placing inputs in adjacent vector lanes. Four such side-by-side decryptions can therefore be performed simultaneously within the eight available vector lanes. A k-ary windowed modular exponentiation approach is used to mitigate timing attacks (for example, section 14.82 in Menezes et al. [18]). Under the stated fault-injection model, any injected fault will, with high likelihood, simultaneously corrupt both \(S_q\) and \(S_p\). After reconstructing S via CRT, taking GCD(\(S-\hat{S}, N\)) is overwhelmingly likely to produce 1 when both \(S_q\) and \(S_p\) are simultaneously faulted. The rest of this section shows that data from the two exponentiations modulo p and q remain side-by-side throughout all phases of the CRT-RSA decryption.

4.4.1 Montgomery setup

Two steps are required to set up Montgomery’s representation for each given modulus M. First, the constant \(M'\) is calculated by inverting M modulo \(2^w\). In this task, the low-order \(w=32\) bits of distinct moduli p, q are first loaded into a vector. Key loading is an avenue for fault-injection attacks, as noted by [27]. AVX-512 provides several mechanisms for loading vector data, located either contiguously in memory (VMOVDQA) or scattered in memory (VGATHERPD). We assume data is either stored as laid out in Fig. 2 or in a fashion resistant to cache timing attacks [29], so that either load instruction can be used. Simultaneously computing \(p'_0 = p^{-1} \textit{ mod } 2^w\) and \(q'_0 = q^{-1} \textit{ mod } 2^w\) is then entirely vectorizable (fault-injection attack resistant) via Newton iteration, utilizing the following instructions:

figure l

The second step involves computing \(R'_0=R^2 \textit{ mod } p\) and \(R'_1=R^2 \textit{ mod } q\), where \(R=2^{wt/2})\) so that subsequent conversions of an input A into the Montgomery domain do not require division operations. \(R'_i\) for \(0 \le i < 16\) (up to 8 pairs of p, q moduli) can be computed simultaneously using AVX-512. Begin by setting all \(R'_i = R\), followed by lg2(R) iterations of a double-and-subtract loop where all \(R'_i\) are doubled, and then p, q is conditionally subtracted if, for example, \(R_0 \ge p\) or \(R_1 \ge q\). Doubling a vector of parallel large integers held interleaved in memory (Fig. 2) and testing for 1-bit overflow at the end can be performed by entirely vectorized code in AVX-512 by utilizing masking. Intrinsic instructions used by the double-and-subtract loop include:

figure m

Prior to exponentiation, the message X needs to be reduced modulo p, q, resulting in \(X_p,X_q\). Message words \(X_i\) are loaded securely as described previously. Simultaneous reductions modulo p and q can then be accomplished using the vector division and remainder intrinsics available in Intel’s Short Vector Math (SVM) library.

figure n

4.4.2 k-ary exponentiation

Vector k-ary exponentiation proceeds by initializing accumulators \(A_i=1\), for \(0 \le i < 16\), and then processing d exponent bits at a time, where d is typically 5 or 6. For each set of exponent bits \(e_{i_d}\), A is squared d times and then multiplied by the pre-computed value \(G[e_{i_d}]\). Clearly, \(e_{i_d}\) could be different for each of the up to 16 parallel exponentiations. Therefore, 16 different pre-computed integers may need to be copied from the table G into a temporary memory location T of width 16, whence they can be loaded contiguously as required by Algorithm 3. In the worst case, this copy procedure occurs lane by lane, providing opportunity for fault-injection attacks on selected lanes, if loading \(G[e_{0_d}]\) can be distinguished from loading \(G[e_{1_d}]\). We assume the use of gather-loads from a timing-attack resistant memory space G and contiguous writes into T.

At the end of the exponentiation procedure, a final parallel Montgomery multiplication serves to translate the results out of Montgomery representation. At this point, \(S_p\) and \(S_q\) can be recombined to the final decryption result.

5 Benchmarks and comparisons

Table 1 compares benchmarks of our implementation of several modular multiplication algorithm variants using the x86-64 instruction set on an Intel Xeon 5122 Gold processor. These are compared to Algorithm 1 (Separated Operand Scanning, SOS) implemented with GMP 6.1.2 functions. The various algorithms use a common set of assembly language functions to implement inner loop full-precision multiply and add-with-carry operations, but are not hand-optimized further. Reported throughput figures are in mulmod / ms.

Table 1 Modular multiplication benchmarks using \(\times \)86–64 instruction set (mulmod/ms)
Full size table

Table 1 shows that BPS is 2.5 times faster than CIOS and 1.7 times faster than FIPS and within 10% of GMP by 2048-bit input sizes. Beyond 2048 bits, GMP starts using sub-quadratic methods for its multipliers, which our implementations do not yet use.

Table 2 compares benchmarks of our implementation of several modular squaring algorithm variants using the \(\times \) 86–64 instruction set on an Intel Xeon 5122 Gold processor. These are compared to Algorithm 1 implemented with GMP 6.1.2 functions (which detects and utilizes faster squaring algorithms when possible). The various algorithms use a common set of assembly language functions to implement inner loop full-precision multiply and add-with-carry operations, but are not hand-optimized further. Reported throughput figures are in sqrmod/ms.

Table 2 Modular squaring benchmarks using \(\times \)86–64 instruction set (sqrmod/ms)
Full size table

Table 2 shows that BPS squaring is over 15% faster than multiplication starting at 768 bits. We generally see that the ratio sqrmod/mulmod is larger for BPS than for any of CIOS, FIPS, or GMP.

Table 3 compares benchmarks of our 16-way implementation of BPS and FIPS using AVX-512 instructions on an Intel Xeon 5122 Gold processor. These are compared to Algorithm 1 implemented with GMP 6.1.2 functions (which detects and utilizes faster squaring algorithms when possible). Reported throughput figures are in mulmod/ms. The rightmost column compares the throughput of BPS squaring with BPS multiplication.

Table 3 Modular multiplication benchmarks using AVX-512 instruction set (mulmod/ms)
Full size table

Table 3 shows that BPS is at least a factor 1.17 faster than FIPS while BPS squaring is a factor 1.24 faster than FIPS starting at 1024 input bits when equivalently implemented using AVX-512. The 16-way processing of BPS results in a factor 3.2 larger throughput than GMP at 1024 bits. Orisaka et al. in [22] provide timing data for their 4-way parallel 448-bit multiplier using AVX-512 on a Skylake-X processor comparable to ours. They report 714 cycles to complete a 4-way 448-bit modular multiplication (modmul), or 178.5 cycles/modmul. In comparison, our measured throughput of 19,567 mulmod per millisecond with 512-bit inputs corresponds to 189 cycles/modmul assuming the maximum 3.7 GHz turbo clock. Scaling Orisaka’s result by a factor of \((512/448)^2\) for the difference in input size, BPS appears to be about a factor 1.23 faster on similar hardware.

Table 4 compares benchmarks of modular exponentiation implemented using BPS and AVX-512 instructions on an Intel Xeon 5122 Gold processor. These are compared to GMP 6.1.2’s mpz_powm function. Reported throughput figures are in modexp/s.

Table 4 Modular exponentiation benchmarks using AVX-512 instruction set (modexp/s)
Full size table

Table 4 shows that BPS is a factor 1.52 faster than GMP at 2048 bits. The major reason this improvement is smaller than those for multiplication and squaring is that GMP internally optimizes the mulmod and sqrmod functions when used in mpz_powm, but does not provide a separate high-level mpz interface to them. Overall, Table 1 through Table 4 shows that BPS does provide advantages over other modular multiplication approaches. The majority of the throughput improvement compared to GMP is due to SIMD processing, as designed.

Table 5 compares benchmarks of our implementation of RSA decryption versus OpenSSL 1.1.0e [21]. Both programs were compiled with Intel’s version 18.0.3 compiler (-O3 -march=skylake-avx512) and both were benchmarked on an Intel Xeon 5122 Gold processor. 4096-bit decryption throughput is over 2 \(\times \) greater when using our parallel BPS approach. Note that the latency for our method is for each batch of 4 parallel CRT-RSA decryptions. In other words, a batch of 4 decryptions can be computed in about 1.9 \(\times \) the time taken by a single OpenSSL decryption, for a resulting throughput increase of approximately 2.1 \(\times \).

Table 5 CRT-RSA Benchmarks on an Intel Xeon 5122 processor with AVX-512
Full size table

Table 6 compares benchmarks of our implementation of RSA decryption versus Zhao’s PhiRSA, which to our knowledge is the current highest throughput implementation on Xeon Phi KNC processors. Unfortunately, we could not directly compare the implementations on like platforms, as their method appears to rely on the SIMD carry propagation instructions only found in the 1st generation Xeon Phi MIC instruction set. Our attempt to implement their VCPC-based decryptions on a 2nd generation KNL processor using emulated SIMD add-with-carry instructions achieved less than half the throughput of our BPS-based code. This is a consequence of Intel removing SIMD carry propagation in KNL’s AVX-512, versus KNC’s IMIC instruction set. In Table 6, we measure latency for each batch of 4096 parallel decryptions on 256 threads of a 7210 KNL processor, using our 16-way implementation (16 decryptions/thread). We achieve roughly 36% higher throughput, but at an expense in latency due to the large batch size. For applications that are latency insensitive, the throughput increase is significant.

We also include recent modular exponentiation results reported on GPUs, and scale them appropriately for doing CRT-RSA decryptions (e.g., 1024-bit decryption throughput estimated by dividing the reported 512-bit modular exponentiation throughput by 2). The estimates show that the GPUs used in [6] and [7] outperform Knight’s Corner Xeon Phi and our results on a model 7210 Knight’s Landing CPU. The larger core counts and higher clock frequencies on, for example, model 7290 Knight’s Landing CPUs would likely more closely match GPU performance. In addition, it is not clear that GPU implementations have the same protections from fault-injection attacks as our approach.

Table 6 Benchmarks on massively parallel hardware
Full size table

6 Conclusion

In conclusion, this paper presents a new block-based variant of Montgomery multiplication, Block Product Scanning (BPS), together with implementation details to optimize parallel operations using AVX-512. A branch-free and constant-time modular exponentiation approach combined with an interleaved strategy for computing CRT-RSA decryptions provides resistance to both timing and fault-injection attacks. We demonstrate \(1.9\,\times \) increased throughput of modular exponentiation and CRT-RSA decryption relative to OpenSSL 1.1.0e, and \(1.4\,\times \) increased throughput relative to previous-generation Intel Xeon Phi results. We also demonstrate a factor \(3.2\,\times \) increased throughput of modular multiplication and a factor \(1.5\,\times \) increased throughput of modular exponentiation relative to GMP-6.1.2 on processors with AVX-512 capability.