Abstract
We study how the presence of dependencies between risks in a population of prospective insurance customers translates into risk exposure for an insurance company, depending on the company’s market share on the various risks. It turns out that the dependency structure in the insurer’s portfolio may differ significantly from the dependency structure of those risks in the general population, even when policyholders for different risks are selected independently. We obtain an upper bound for the difference between the ruin probability and its estimate based on the company’s portfolio marginal distributions. Under certain conditions, dependencies between risks in the portfolio of a company with small market shares are mild. We characterize the optimal loadings and market shares, assuming generic demand functions for the different risks.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is widely recognized that dependencies between different risks may have a significant impact in the aggregate risk exposure and the outcomes of risk management in a insurance company. Dependencies may take many forms with different impacts on various aspects of actuarial industry. Thus, the published literature covers a wide range of topics, namely, optimal choice of insurance or reinsurance treaties [11, 17, 32, 33, 47], optimal investment-reinsurance strategies [8, 10, 46], choice of premia and ratemaking [1, 9], capital allocation [25], ruin probabilities [15, 24, 27, 45], and effects on various risk measures [15, 22]. For a comprehensive study of problems arising from risk dependencies, see e.g. [18].
We are interested in the mechanisms by which the dependency structure between the risks constituting the insurance portfolio of an insurance company can be changed by changing the exposure to these risks, and the effect of these changes on the company’s financial stability. In this context, a risk corresponds to a particular type of insurance policy sold by the company. Thus, the exposure to a given risk is accurately measured by the number of policies of that particular type sold by the company. For simplicity, we ignore the possibility of reinsurance or other risk-sharing arrangements that might reduce this underlying exposure. By dependencies we understand, naturally, dependencies between the (random) value of claims filed under different risks. Recall that the concept of dependence is distinct and far more rich than the concept of correlation [22]. In this work, we will consider a broad class of dependencies.
To measure financial stability, we use the probability of eventual ruin, that is, the probability of the company’s total reserve going below zero in finite time. This is a classical measure of risk and there are several excellent books dedicated to ruin problems or containing extensive chapters dedicated to such problems (see e.g. [3, 19, 30, 41]). Portfolios can be compared by the corresponding ruin probabilities, but no absolute meaning should be attached to this measure, since it does not represent the actual probability that the insurer will go bankrupt sometime in the future. Indeed, the expected time to ruin, given that ruin occurs, may be quite long, and we can not expect the data used to compute the ruin probability will remain valid for a long time, due to the natural evolution of circumstances, management decisions, etc. Further, it can be argued that events in the very distant future have little bearing in present decisions. Due to this, there have been attempts to replace the ruin probability by a more “realistic” measure, like the finite time ruin probability. This choice introduces the somewhat arbitrary choice of the time horizon T. More importantly, it allows for hiding existing problems beyond the time T. That is, it is possible to have simultaneously a very low probability of ruin up to time T and a very high probability of ruin in a short time after T. Other popular risk measures, like VaR or CTE, suffer from the same inconvenients. Notice that a low ruin probability means that the company is likely to survive until any time horizon T and furthermore it is highly likely to continue thriving thereafter. Further, in order to have a low ruin probability, the insurer’s reserves must be expected to increase sufficiently fast, that is, the company must be sufficiently profitable. Thus, the ruin probability has a built-in balance between safety and profitability. Finally, for multidimensional risk processes, there are many alternative definitions of ruin probability, according to the rules that may apply to capital transfers between different lines of business. Such rules depend on the structure of the particular company being considered. For simplicity, we consider that no such rules apply and therefore capital can be freely shifted to cover losses on different risks.
We consider a market populated by a large number of identical individuals, all equally exposed to the same risks, which are potential customers of an insurance company. The collective claim process of this population is modeled by a multidimensional compound Poisson process featuring common shocks, i.e., it can be represented as a sum of independent compound Poisson processes with some of them causing simultaneous claims in more than one risk. The dependency structure in these common shocks is described by joint distributions which we do not require to meet any particular assumption. This type of process was studied in [7]. Particular cases were studied in several other papers [10, 17, 32, 46, 47].
In this setting, the insurer’s risk exposure results from the proportion of individuals in the market buying insurance for each risk or combination of risks, from that particular company. It turns out that the dependency structure in the company’s portfolio may differ markedly from the dependency structure in the market, even if customers for different risks are picked independently.
We expect the number of policies that the insurer can sell to depend on the premium charged for that risk. Since the premium and number of policies determine the insurer’s revenue and the size and characteristics of its portfolio, the problem of choosing the optimal loadings arises naturally, provided the demand function is known.
The relation between premia and the size of the company’s portfolio has been extensively studied, namely in game-theoretic settings. These settings feature both games between a single company and many customers [4, 13, 44] and competitive games between several companies [5, 6, 21, 23, 31, 34, 35, 43]. A few papers feature models involving a large number of customers and a few insurers [38, 40]. Most of these studies concern markets for a single risk. Literature concerning markets with more than one risk is quite sparse.
We consider the optimization problem for a generic (nonspecified) demand function. Some of the publications listed above contain a (unidimensional) demand function in the respective models, which can be plugged in our optimization problem. Multidimensional demand functions can be assembled from unidimensional ones using copulas, as explained in Sect. 4.4.
Finally, we mention some limitations of our work. First, we present only the 2-risks case. This is just for the sake of simplicity and readability, since all theoretical results can be readily extended to any number of risks, though numerical computations may become exceedingly laborious. Second, the class of processes considered in this paper includes a broad range of dependencies between risks, but it does not include processes where dependencies are due to some form of joint modulation of the claim numbers intensities, like in Cox processes [2, 12, 16, 24, 27], or in Hawkes processes [12, 24, 28]. We will address some of these later classes in a forthcoming paper.
The paper is organized as follows: Sect. 2 contains some background material about ruin probabilities in the Lundberg process and aggregation of compound Poisson processes. In Sect. 3, we present a characterization of the optimal premium loading and risk exposure, given any particular demand function for insurance. This section is not about dependencies but the result is, to our knowledge, new and contrasts notably with the result in Sect. 4.4. Section 4 contains the main results. Section 4.1 describes the company’s risk process, depending on its market shares. In Sect. 4.2 we give an upper bound for the difference between the ruin probability and its estimate based on the company’s portfolio marginal distributions. In Sect. 4.3, this estimate is used to show that, under certain conditions, companies with small market shares are expected to hold portfolios with weak dependencies. In Sect. 4.4 we characterize the optimal loadings and exposure in the dependent case. Section 5 contains a numerical illustration. A numerical scheme to compute the ruin probabilities is given in the Appendix.
2 Preliminaries
2.1 Claim and surplus processes
The Lundberg risk model describes the evolution of the capital of an insurance company and assumes that exposure is constant in time, losses follow a compound Poisson process, and premia arrive at a fixed continuous rate
where u is the initial surplus, c is the gross premium rate net of expenses, \(N_t\) is a time homogeneous Poisson process with intensity parameter \(\lambda \), and \(Y_i\) are i.i.d. random variables independent of \(N_t\), representing the severity of claim \(i \in {\mathbb {N}}\). Here it is assumed that \(Y_i\) are positive. In the following sections, Y denotes an arbitrary random variable with the same distribution as any \(Y_i\). The severity distribution function is denoted by F and the severity survival function by \({\overline{F}}=1-F\). \(S_t\) is a compound Poisson process and thus \(X_t\) is a stochastic process (sometimes called the surplus process) representing the insurer’s wealth or reserve at time t. \(X_t\) increases due to earned premia and decreases when claims occur. When the capital of an insurance company hits zero, the insurance company is said to be ruined. Formally, the ruin probability is defined as follows.
Definition 2.1
(Probability of Ruin) The probability of (eventual) ruin is the function \(V: {\mathbb {R}} \mapsto [0,1]\) defined as
Sometimes it is useful to use the survival (non-ruin) probability, defined as \({\overline{V}}(x) = 1-V(x)\). The ruin probability can be calculated using the following integro-differential equation [26].
Proposition 2.1
Assume that \(X_t\) is defined as above and the premium rate satisfies \(c > \lambda {{\,\mathrm{\mathbb {E}}\,}}[Y]\). If \(V \in C^1(]0, \infty [),\) then the probability of ruin with infinite time horizon satisfies the following equation
with the following boundary condition
Furthermore, the probability of non-ruin satisfies the following equation
for \(0< \epsilon \le x < + \infty \) with the following boundary condition
A numerical scheme solving Eq. (2.2) can be found in Appendix.
2.2 Accounting for claim dependencies
Consider the k-dimensional surplus process \({\user2{X}} = (X_t^{(1)},\ldots ,X_t^{(k)}) \) where
If these processes are independent, they can be combined into a single compound Poisson process
where \(N_t\) is a Poisson r.v. with \(\lambda = \lambda _{1} + \cdots + \lambda _{k}\) and \(Y_i\) are i.i.d. random variables with distribution \(F(x) = \sum _{j = 1}^{k} \frac{\lambda _j}{\lambda } F_j(x)\) (see e.g. [30, Theorem 3.4.1]). This property allows us to use the integro-differential equation (2.1) to calculate the ruin of multiple surplus processes.
If the risks are not independent, then we can use the fact that compound Poisson processes are characterized by their Lévy measure to decompose the claim process into independent processes to which the aggregation property can be applied. In particular, for \(n = 2\) risks, we obtain the decomposition
where \(S^{1\perp }\) and \(S^{2\perp }\) are compound Poisson processes accounting for events concerning only risk 1 and risk 2, respectively. \(S^{\parallel }\) is a compound Poisson process accounting for events concerning both risks simultaneously. Furthermore, \(S^{1\perp }\), \(S^{2\perp }\) and \(S^{\parallel }\) are mutually independent.
In this section, we briefly explain how this can be achieved. Further details can be found in [42]. We will use the following definitions.
Definition 2.2
The tail integral of a Lévy measure \(\nu \) on \([0, \infty ]^2\) is given by a function \(U:[0, \infty ]^2 \mapsto [0, \infty ]\)
Definition 2.3
(Lévy copula for processes with positive jumps) A two-dimensional Lévy copula for Lévy processes with positive jumps, or for short, a positive Lévy copula, is a 2-increasing grounded function \({\mathcal {C}}: [0,\infty ]^2 \rightarrow [0, \infty ]\) with uniform margins, that is, \({\mathcal {C}}(x,\infty ) = {\mathcal {C}}(\infty ,x) = x\).
Similarly to Sklar’s theorem for ordinary copulas [36], it has been shown that the dependency structure of \((X_t^{(1)},X_t^{(2)})\) can be characterized by a Levy copula \({\mathcal {C}}\) such that \({\mathcal {C}}(U_1(x_1), U_2(x_2))\) where \(U_1\) and \(U_2\) are the marginal tail integrals for \(X_t^{(1)}\) and \(X_t^{(2)}\). If \(U_1\) and \(U_2\) are absolutely continuous, this Lévy copula is unique, otherwise it is unique on \(Range(U_1)\times Range(U_2)\), the product of ranges of one-dimensional tail integrals, [14, Theorem 5.4]
Consider a two dimensional claim process
where \(N_t\) is a Poisson process with intensity \(\lambda \) and \(Y_i = (Y_i^{(1)},Y_i^{(2)})\), \(i \in {\mathbbm {N}}\) are independent random variables with common joint distribution \(F_Y\). The components of S, \(S^{(1)}\) and \(S^{(2)}\), are one-dimensional compound Poisson processes with intensities \(\lambda _1\) and \(\lambda _2\) and severity distributions \(F_{ Y^{(i)}}(x) = \frac{{{\,\mathrm{{\mathbb {P}}}\,}}\left\{ 0 < Y^{(i)} \le x \right\} }{{{\,\mathrm{{\mathbb {P}}}\,}}\left\{ Y^{(i)}>0 \right\} }\), \(i=1,2\), respectively. We wish to obtain a decomposition
where \(\sum _{i = 0}^{N_t^{1\perp }} Y_i^{(1\perp )}\),\(\sum _{i = 0}^{N_t^{2\perp }} Y_i^{(2\perp )}\) and \(\sum _{i = 0}^{N_t^{\parallel }}(Y_i^{(1\parallel )}, Y_i^{(2\parallel )})\) are independent compound Poisson processes with intensities \(\lambda _1^\perp \), \(\lambda _2^\perp \), \(\lambda ^\parallel \) and severity distributions \(F_{Y^{1\perp }}\),\(F_{Y^{2\perp }}\),\(F_{Y^{\parallel }}\), respectively. In the above, we set
A compound Poisson process, S, is a Lévy process with Lévy measure \(\nu (dx) = \lambda dF(x)\), with tail integral
The components \(S^{(1)}\) and \(S^{(2)}\) are independent if and only if \(U(x_1, x_2) = 0\) for every \((x_1, x_2) \in ]0, + \infty [^2\), i.e., if and only if \(\lim _{x_1 \rightarrow 0^{+}, x_2 \rightarrow 0^{+}} U(x_1, x_2) = 0 \).
The (marginal) Lévy measures of the processes \(S^{(i)}\), \(i = 1,2\), have tail integrals
Taking Eq. (2.5) into account, one obtains
The severity distributions \(F_{Y^{1\perp }}\), \(F_{Y^{2\perp }}\), and \(F_{Y^{\parallel }}\) can be recovered from the tail integrals
If the dependency between \(S^{(1)}\) and \(S^{(2)}\) is characterized by a Lévy copula, \({\mathcal {C}}\), i.e. \(U(x_1, x_2) = {\mathcal {C}}(U_1(x_1), U_2(x_2))\) for \((x_1, x_2) \in [0, +\infty [^2\), then the relations above can be written using the Lévy copula and one-dimensional tail integrals
Using the above methodology, the surplus process can be represented as
where \(u = u_1 + u_2\), \(c = c_1 + c_2\), \(N^{*}\) is a Poisson process with intensity \(\lambda = \lambda _1^\perp + \lambda _2^\perp + \lambda ^\parallel \) and \(Y_i^{*}\) are i.i.d. random variables with distribution
where
The approach above can be extended in a straightforward way to any number \(k \in {\mathbb {N}}\) of dependent risks. However, such extension can be computationally challenging, since the right-hand side term of decomposition (2.4) will be, in general, a sum of \((2^k-1)\) terms.
3 The optimal loading for a single risk
An insurer can control the volume of its business through the premium loading \(\theta \). A reasonable assumption is that the higher the loading, the smaller the number of contracts in its portfolio, which means that the claim intensity (or business volume) will decrease. Therefore, both the claim intensity \({{\,\mathrm{\mathbb {E}}\,}}^\theta [N_1]\), and the premium income rate \(c(\theta )\), will depend on \(\theta \). It is reasonable to assume that \({{\,\mathrm{\mathbb {E}}\,}}^\infty [N_1] = 0\), as abnormal premium rates will not attract customers [29]. To capture these concepts let
Here \(\lambda \) is the average number of claims per unit of time for the whole market, and \(p(\theta )\) is the probability that a potential claim is filed as an actual claim to the particular insurer under consideration. In other words, \(p(\theta )\) reflects the demand or the market share sensitivity to the loading parameter \(\theta \). \(p(\theta )\) can be interpreted as a probability that a customer buys an insurance product. The particular form of the function p is not important in the following, since the results hold for every sufficiently regular p. For example, p may be derived from any model of customer’s behaviour, possibly taking into account competition from other insurers. It may also be obtained by various econometric estimation methods (see e.g. [37]). Assuming that the company has some fixed costs \(r>0\), independent of the risk exposure, the expression for the net premium income becomes
Let \(V(x,\theta )\) denote the probability of eventual ruin given the initial reserve x, assuming that the premium loading remains constant and equal to \(\theta \).
Proposition 3.1
\(V(x,\theta )\) is strictly increasing with respect to the parameter \(\alpha = \frac{ {{\,\mathrm{\mathbb {E}}\,}}^\theta [N_1]}{c(\theta )}.\)
Proof
It is possible to integrate Eq. (2.1) on the interval ]0, x] to obtain
To prove the proposition, we will study equations of the general form
where \(\alpha \) is a given real constant, \(g:[0,+\infty [ \mapsto {\mathbb {R}}\) is a given measurable locally bounded function, and the solution \(u:[0,+\infty [ \mapsto {\mathbb {R}}\) is also required to be measurable and locally bounded.
We introduce the operator \(\Psi \), acting on measurable locally bounded functions \(h:[0, +\infty ] \mapsto {\mathbbm {R}}\), as
Notice that the transformation \(h \mapsto \Psi h\) is linear and for every h, the function \(\Psi h : [0, + \infty [ \mapsto {\mathbbm {R}}\) is continuous, hence measurable and locally bounded. Thus, powers of the operator \(\Psi \) are defined in the usual way.
Let, \(\left\Vert h\right\Vert _{[0,x]} = \sup _{z \in [0,x]} |h(z)| \). Then
If the inequality
holds, for some \(n \in {\mathbbm {N}}\), then
Thus, by induction, (3.6) holds for every \(n \in {\mathbb {N}}\). Therefore, for every \(x \in [0, \infty [\), fixed, there is some \(n \in {\mathbb {N}}\) such that \(\Psi ^n\) is a contraction in the space of measurable and bounded functions \(h:[0,x] \mapsto {\mathbbm {R}}\). It follows from the contraction principle that Eq. (3.3) has one unique solution. Further, \(\lim _{n \rightarrow \infty } (\alpha ^n \Psi ^n) h = 0\), uniformly in [0, x] for any given h and any fixed \(x \in [0, +\infty [\).
Let \(u_{\alpha , g}\) be the solution of Eq. (3.4) for given g and \(\alpha \). Then,
Since \(\lim _{n \rightarrow \infty } \alpha ^n \Psi ^n u_{\alpha ,g}(x) = 0\), this shows that \(u_{\alpha ,g}\) admits the series representation
which converges uniformly with respect to \(\alpha \) on compact intervals. Thus, we can differentiate term by term and obtain
where the last equality results from applying (3.7) to the function \({\tilde{g}} = u_{\alpha , g}\). For any \(h:[0,x] \mapsto {\mathbbm {R}}\) locally absolutely continuous function
Thus, \(h>0\) implies \((\Psi h)>0\), which implies \((\Psi ^n h)>0\), \(\forall n \in {\mathbbm {N}}\), and therefore \(u_{\alpha ,h}>0\) for any \(\alpha >0\). This argument shows that \(\frac{d}{d\alpha } V =\frac{1}{\alpha ^2} u_{\alpha ,V} >0\) as \(V >0\). Therefore V is strictly increasing with \(\alpha \). \(\square \)
According to Proposition 3.1, in order to find \(\theta \) minimizing the probability of ruin, it is sufficient to find \(\theta \) minimizing \(\frac{{\mathbb {E}}^\theta [N_1]}{c(\theta )}\). In particular, if p is differentiable, then the optimal loading \(\theta _{ruin}\) satisfies \(\left. \left( \frac{\partial }{\partial \theta } \frac{{\mathbb {E}}^\theta [N_1]}{c(\theta )}\right) \right| _{\theta = \theta _{ruin}} =0\). Using equalities (3.1) and (3.2), this is \(\left. \left( \frac{\partial }{\partial \theta } \frac{\lambda p(\theta )}{(1+\theta ) \lambda p(\theta ) {\mathbb {E}}[Y] - r} \right) \right| _{\theta =\theta _{ruin}}=0\), which reduces to
Notice that the variable x does not appear in Eq. (3.8). Hence, the optimal loading and exposure do not depend on the company’s initial reserves. Further, (3.8) depends on the losses’ distribution only through the expected value \(\lambda {\mathbb {E}}[Y]\) of the total losses in the market. Thus, two different processes yield the same optimal loading if the demand function p, the fixed cost r and the expected loss \(\lambda {\mathbb {E}}[Y]\) are the same, albeit the optimal ruin probability is expect to depend on the whole distribution rather than the first moment only.
Under our risk model, the expected profit is the function \(L(\theta ) = \lambda {\mathbb {E}}[Y] \theta p(\theta ) -r\). Thus, \(\frac{\partial L (\theta )}{\partial \theta } = \lambda {\mathbb {E}}[Y] (p(\theta ) + \theta p^\prime (\theta ))\). From this and (3.8), it is easy to check that
This shows that the loading which maximizes the expected profit, \(\theta _{profit}\), is always lower than \(\theta _{ruin}\).
For example, we may consider that demand is described by a logit model [37], i.e.,
where \(\beta _1\) is a positive number so that \(p\rightarrow 0\) when \(\theta \rightarrow \infty \) and \(p\rightarrow 1\) when \(\theta \rightarrow -\infty \). In this case, (3.8) yields the simple expression
while \(\theta _{profit}\) is the unique solution of
4 The multiple risk case
In this section, we explore how dependencies between risks available in an insurance market translate into risk exposure for a company through its market shares on the different risks. It turns out that this mechanism is non trivial when the risks are dependent. For the sake of simplicity, we assume that the company offers insurance for two risks in a market constituted by identical individuals, all of them exposed to both risks. Using the notation in Eqs. (2.3) and (2.4) to denote the market claim process, \(S_t = (S_t^{(1)}, S_t^{(2)})\) is the vector of the total (accumulated) amount of claims of each risk that occurred in the market, up to time t. The marginal distributions of \(S^{(1)}\) and \(S^{(2)}\) are characterized by claim intensities \(\lambda _1\) and \(\lambda _2\) and the severity distributions \(F_{Y^{(1)}}\), \(F_{Y^{(2)}}\) and their dependency structure is characterized by a parameter \(\lambda ^\parallel \in [0, \min (\lambda _1, \lambda _2)]\) and a joint distribution \(F_{(Y^{1\parallel },Y^{2\parallel })}\), as explained in Sect. 2.
4.1 Risk exposure as a function of market shares
To extend the approach outlined in Sect. 3, we consider a vector of market shares \(p=(p_1,p_2) \in [0,1]^2\), where \(p_i\) denotes the proportion of individuals in the market holding a policy for risk i. Let \(p^{(1,0)}\) be the proportion of individuals in the market holding a policy for risk 1 and no policy for risk 2. Similarly, \(p^{(0,1)} \) and \(p^{(1,1)} \) denote the proportion of individuals holding a policy only for risk 2 and for both risks, respectively. Obviously, \(p_1=p^{(1,1)}+p^{(1,0)}\) and \(p_2=p^{(1,1)}+p^{(0,1)}\). If the acquisition of polices for different risks is independent, then
Under this model, the company’s surplus process is
where \(\tilde{N}_t^{1\perp }\), \(\tilde{N}_t^{2\perp }\), and \(\tilde{N}_t^{\parallel }\) count the number of claims received by the company, concerning only risk 1, only risk 2, and both risks, respectively. Their intensities are, respectively,
The distribution of the single risk claim amounts \(\tilde{Y}^{1\perp }\) (resp., \(\tilde{Y}^{2\perp }\)) is a mixture of the distributions \(Y^{1\perp }\) and \(Y^{1\parallel }\) (resp., \(Y^{2\perp }\) and \(Y^{2\parallel }\))
This is because some customers insure risk 1, but not risk 2 and vice-versa. Therefore, the aggregate process for the insurer is
where \(\tilde{N}_t\) is a Poisson process with intensity
and \(\tilde{Y}_i\), \(i \in {\mathbb {N}}\) are i.i.d random variables with distribution
Thus, if the risks in the market are independent (i.e. if \(\lambda ^\parallel = 0\)), then the risk in the company’s portfolio is just a sum of the risks \(S^{(1)}\) and \(S^{(2)}\), weighted by the respective market shares, \(p_1\) and \(p_2\), irrespective of any dependency between sales of policies for different risks. However, if the risks in the market are dependent (\(\lambda ^\parallel \ne 0\)), then the company’s risk is not, in general, a weighted sum of \(S^{(1)}\) and \(S^{(2)}\). Further, this effect persists even in the case where sales of different policies are independent (i.e., \(p^{(1,1)} = p_1 p_2\)). On the other hand, equalities (4.1) and (4.2) show that in the (unlikely) situation where clients always buy insurance for only one risk, the risk exposure of the insurer is accurately computed using only the marginal distributions of each risk (i.e. assuming that the risks are independent). This is due to homogeneity of our mode, i.e., the intensities \(\lambda _1^\perp \), \(\lambda _2^\perp \) and \(\lambda ^\parallel \) are constants and therefore the model does not account for events that increase temporarily the frequency of claims, like weather phenomena, natural catastrophes, or collective behaviour of customers. If \(\lambda _1\) and \(\lambda _2\) are stochastic processes, like in multidimensional Cox [16] or Hawkes [28] processes, then some (possibly very important) dependencies remain even if \(\lambda ^\parallel \) is identically zero. This is work in progress.
4.2 The impact of dependencies on ruin probability
From the discussion above and Proposition 2.1, it follows that the ruin probability of a company with market shares (\(p_1\), \(p_2\), \(p^{(1,1)}\)) solves the equation
with \(\tilde{\lambda }\) and \(F_{\tilde{Y}}\) given by Eqs. (4.1) and (4.2).
Since estimating the dependency structure may pose substantial difficulties, we may wish to have an a-priori bound for the error introduced by neglecting dependencies, that is, by substituting the probability \(V_{ind}(x)\) for V(x), where \(V_{ind}(x)\) solves the equation.
where \(\hat{\lambda } = \lambda _1p_1 + \lambda _2p_2\) and \(F_{\hat{Y}}(x) = \frac{\lambda _1 p_1 F_{Y^{(1)}} + \lambda _2 p_2 F_{Y^{(2)}}}{\hat{\lambda }}\). Notice that \(\hat{\lambda } {{\,\mathrm{\mathbb {E}}\,}}[\hat{Y}] = \tilde{\lambda } {{\,\mathrm{\mathbb {E}}\,}}[\tilde{Y}]\) and therefore the boundary condition for (4.5) is again (4.4).
The discussion in Sect. 4.1 shows that the difference \(V(x) - V_{ind}(x)\) is expected to be small when \(p^{(1,1)}\) is small compared to \(p_1 + p_2\). The following proposition gives a precise meaning for this statement.
Proposition 4.1
With the notation above,
for every amount of initial reserve \(x \ge 0\).
Proof
Integration of Eqs. (4.3) and (4.5) with boundary condition (4.4), yields the following versions of Eq. (3.3)
From these equalities, using the decompositions of \({\tilde{\lambda }}\), \({\hat{\lambda }}\), \(F_{\tilde{Y}}\) and \(F_{{\hat{Y}}}\), and rearranging terms one obtains
Notice that for every distribution function \(G:[0, +\infty [ \mapsto [0,1]\)
Since \(V_{ind}\) is a monotonically decreasing function, both terms in this sum are non-positive for every \(z \ge 0\). Further,
Thus the estimate
holds for every \(x \ge 0\) and every distribution function G. Therefore, (4.6) implies
(the coefficient 2x in the first term takes into account the fact that, having opposite sign, the first term of (4.6) partially cancels the second and third terms). Thus, the result follows by Grönwall’s inequality [20]. \(\square \)
4.3 The impact of dependencies on small companies
Now, we proceed with the argument above to explore how dependencies affect companies of different size. We measure the size of the company by it’s expected total value of claims, \(\tilde{\lambda } {{\,\mathrm{\mathbb {E}}\,}}[\tilde{Y}]\) and, to make comparisons meaningful, we consider that the total revenue is proportional to the company’s size, i.e.
Similarly, we consider the initial reserve to be proportional to size, i.e.
In this setting, Proposition 4.1 yields the following estimate
Notice that the right-hand side of (4.7) has the same asymptotic behaviour as
Further, if the sales of policies for different risks to the same individual are independent, then \(p^{(1,1)} = p_1 p_2\) goes to zero faster than \(\tilde{\lambda } {{\,\mathrm{\mathbb {E}}\,}}[\tilde{Y}] = p_1 \lambda _1 {{\,\mathrm{\mathbb {E}}\,}}[Y^{(1)}] + p_2 \lambda _2 {{\,\mathrm{\mathbb {E}}\,}}[Y^{(2)}]\), when \((p_1 + p_2 )\rightarrow 0\). Thus, a small company selling policies for different risks independently is relatively immune to the effects of dependencies between the risks, contrary to a large company (it is obvious that a monopolistic company is fully exposed to the dependencies between risks). This immunity to risk’s dependencies may persist even when sales of policies for different risks are not independent, provided the dependency in sales is sufficiently mild. For example, \(\lim _{(p_1 + p_2) \rightarrow 0} \frac{p^{(1,1)}}{p_1 + p_2} = 0\) if the dependency between sales is modelled by a Clayton or a Frank copula in (4.4). However, small companies are not specially protected from risk dependencies if the dependency between sales is modelled by a Pareto or a Gumbel copula.
4.4 Optimal loadings and market shares
Now, we assume that the market shares are functions of the premium loadings \(\theta = (\theta _1, \theta _2)\). A possible economic interpretation of these functions is as follows. Suppose that every individual in the market (a potential client) is provided with a vector of bid prices (\(b_1\), \(b_2\)). The client acquires the insurance for risk i if \(b_i \ge \theta _i\) (for convenience, we consider prices net of the pure premium). The distribution of the price vectors in the market is modelled by a random vector \(B = (B_1, B_2)\). Thus, \(p_i(\theta ) = p_i(\theta _i) = {{\,\mathrm{{\mathbb {P}}}\,}}\big ( B_i \ge \theta _i \big )\) is the company’s market share for the insurance of risk i at equilibrium, given the loadings \(\theta = ( \theta _1, \theta _2)\). Dependency between the acquisition of different risks can be introduced by considering dependent random variables \( (B_1, B_2)\). In particular, if the joint distribution of B is characterized by an ordinary copula \(C: [0,1]^2 \mapsto [0,1]\), then, according to Sklar’s theorem [36] \(F_B(\theta _1, \theta _2) = C(F_{B_1}(\theta _1), F_{B_2}(\theta _2))\) and therefore
Notice that in this particular case, the market share in each risk, \(p_i\) depends only on the premium loading charged on that risk. However, other more complex interactions can be analysed in the present framework. Like in Sect. 3, we do not prescribe any specific form for these functions and our results hold for any sufficiently regular \(p^{(1,1)}\), \(p^{(1,0)}\) and \(p^{(0,1)}\).
In the framework above, the net premium income generated by each risk is
where \(\lambda _i\) and \(Y^{(i)}\) are as in Sect. 2.2, and \(r_i>0\) is a fixed cost assigned to risk i but independent of the exposure to that risk. The total net premium income is \(c(\theta ) = c^{(1)}(\theta ) + c^{(2)}(\theta ) \). It is convenient to extend the notation introduced in the proof of Proposition 3.1: for any distribution function \(G:[0, +\infty [ \mapsto [0,1]\), we consider the operator \(h \mapsto \Psi _G h\) of type (3.5)
Thus, the 2-risk version of Eq. (3.3) can be written as
where
Notice that Eq. (4.8) differs fundamentally from Eq. (3.3) in that the right-hand side of (3.3) depends on \(\theta \) only through the coefficient \(\frac{{\tilde{\lambda }}_\theta }{c(\theta )}\) while the right-hand side of (4.8) depends also through the distribution function \(F_\theta \). Thus, Proposition 3.1 can not be generalized to models with multiple risks. However, it is possible to provide optimality conditions for the loadings \(\theta = (\theta _1, \theta _2)\) minimizing the ruin probability.
Since \(\frac{\lambda _1^\perp }{\tilde{\lambda }_\theta } p_1(\theta ) + \frac{\lambda _2^\perp }{\tilde{\lambda }_\theta }p_2(\theta ) + \frac{\lambda ^\parallel }{\tilde{\lambda }_\theta } p^{(1,0)}(\theta ) + \frac{\lambda ^\parallel }{\tilde{\lambda }_\theta } p^{(0,1)}(\theta ) + \frac{\lambda ^\parallel }{\tilde{\lambda }_\theta } p^{(1,1)}(\theta ) = 1\), (4.8) becomes
We write this in abbreviated form
where \(\alpha (\theta )\) is the vector
\(\Gamma (x)\) is the vector function
\(\Psi \) is the vector of operators
and \(\langle \cdot , \cdot \rangle \) is the usual inner product in \({\mathbbm {R}}^5\). Notice that \(\alpha = \alpha (\theta )\) does not depend on x and \(\Gamma =\Gamma (x)\) does not depend on \(\theta \).
Using the argument in the proof of Proposition 3.1, we see that \(V_\theta \) admits the series representation
Similarly, any vector \(\gamma \in {\mathbbm {R}}^5\) and any bounded measurable function \(g:[0, +\infty [ \mapsto {\mathbbm {R}}\) define one unique function
This function is analytic with respect to \(\gamma \), with partial derivatives
Taking into account the chain rule for derivatives, this proves the following proposition.
Proposition 4.2
If \(\theta \mapsto \alpha (\theta )\) is differentiable, then \(\theta \mapsto V_\theta (x)\) is differentiable for every \(x \ge 0\) and
By Proposition 4.2, the optimal loadings satisfy the equation
Notice that here, the coefficients of the partial derivatives \(\frac{\partial \alpha _j}{\partial \theta _i}\) depend jointly on \((x,\theta )\) and are not, in generical, multiples of the same function. Thus, the optimal loadings are, in general, dependent on the initial reserve x, contrary to what happens in the single risk case (3.8). This holds even if the risks are perfectly independent. To see this, notice that in the independent case we have \(\lambda ^\parallel =0\) and \(\alpha (\theta ) = \frac{1}{c(\theta )} \left( \lambda _1p_1(\theta ),\lambda _2p_2(\theta ),0,0,0 \right) \). However, the function \(u_{\alpha (\theta ), \Gamma _2+\Psi _2V_\theta }\) is not, in general, a multiple of \(u_{\alpha (\theta ), \Gamma _1+\Psi _1V_\theta }\). Thus, separate management of each risk is generally not optimal, even in cases when the risks are perfectly independent (the obvious exception is the case \(F_{Y^{(1)}}=F_{Y^{(2)}}\), i.e., when both risks have the same claim severity distributions).
Contrary to the single-risk case, the odds of finding explicit solutions for Eq. (4.9) seem very low, even in simple cases. However, (4.9) can be numerically solved by Newton’s algorithm, the second-order partial derivatives being
Notice that the expected profit is
Thus, it depends only on the marginal distribution of the claim processes \(S^{(1)}\), \(S^{(2)}\), being independent of the dependency structure. It follows that the loadings maximizing the joint profit coincide with the loadings maximizing the profit on each risk, separately. That is, a pricing strategy that completely focuses on expected profit completely fails to take both dependencies between risks and dependencies between sales of policies into account.
5 Numerical results
In this section, some numerical examples are used to illustrate results from the previous sections.
Our base-line case is (rather arbitrarily) a risk with claim intensity \(\lambda =10^4\) and claim severity Y, a gamma random variable with shape and scale parameters \(a=2\), \(k=\frac{1}{2}\), respectively. Thus, \({\mathbb {E}}[Y]=ak=1\). The demand function is a logit function (3.9) with parameters \(\beta _0=\ln 2 - \frac{3}{2}\) and \(\beta _1=30\), and the fixed cost (3.2) is \(r=\frac{5}{12}\times 10^2\). From this, we choose two variants. The first variant differs from the baseline in the distribution parameters \((\lambda , a,k)\), preserving the value \(\lambda {\mathbb {E}}[Y]=10^4\). The second variant differs from the base-line in the parameter \(\beta _1\), controlling the sensitivity of demand for insurance to the price (loading). In Sect. 5.1, we compare the optimal loadings and ruin probabilities for these three cases in a single-risk model, as explained in Sect. 3. In Sect. 5.2, we combine the base-line risk with the first variant in a two-risk model, as described in Sect. 4.4. We consider three different dependency structures, thus exploring the effect of dependencies combined with risks with different distributions. In Sect. 5.3, we combine the base-line risk with the second variant in a two-risk model, considering the same dependency structures as in Sect. 5.2, to explore the effect of dependencies combined with different sensibilities to price.
The programming language R [39] was used. The code can be found at https://github.com/ragnarlevi/RuinDependency.
5.1 The single risk case
First, we consider a risk with the parameters described above. By (3.11), profit is maximized by \(\theta _{profit}=\frac{1}{20}\) with a market share \(p\left( \frac{1}{20} \right) =\frac{1}{3}\). By (3.10), the ruin probability is minimized by \(\theta _{ruin} =\frac{1}{20} \left( 1 + \frac{2}{3} \ln 4 \right) \approx 0.096\), corresponding to a market share \(p(\theta _{ruin})=\frac{1}{9}\). The graphs of the profit and ruin probabilities as functions of the loading \(\theta \) are shown in Fig. 1. The profit has a maximum at \(\theta _{profit}\) and it drops by about \(37\%\) at \(\theta _{ruin}\). In this case, the minimal ruin probability is quite sensitive to the amount of initial surplus, at least for modest values of surplus.
Sensitivity of the ruin probability to claim distribution is illustrated by considering the case when the claim intensity is \(\lambda = \frac{10^4}{3}\), and Y is gamma distributed with parameters \(a =3\) and \(k=1\). Other parameters are identical to the example in Fig. 1. Since \(\lambda {\mathbb {E}}[Y]=10^4\) is identical in both cases, \(\theta _{profit}\) and \(\theta _{ruin}\) remain unchanged, but we can see in Fig. 2 that the ruin probability is higher for all values of loading yielding a positive expected profit.
To illustrate further the sensitivity of the (optimal) ruin probability to the claim distribution, consider Fig. 3, where the minimal probability of ruin is plotted as a function of the scale parameter k in the distribution of Y. The shape parameter is \(a=\frac{1}{k}\), such that \({\mathbb {E}}[Y]=1\) in all cases, and all other parameters are the same as in Fig. 1 (thus, \(\theta _{profit}\) and \(\theta _{ruin}\) remain the same). Larger values of k correspond to heavier tails of the distribution of Y. As expected, we see that the probability of ruin is higher for heavier tailed distributions.
Figure 4 shows the expected profit and ruin probabilities for the same claim process as in Fig. 1 with higher sensitivity of insurance demand to price. The price sensitivity parameter is increased to \(\beta _1= \frac{75}{2}\), such that the expected profit is maximized by \(\theta _{profit}=\frac{1}{25} \), corresponding to the same market share \(p(\theta _{profit})= \frac{1}{3}\). The fixed cost is changed to \(r=\frac{10^2}{3}\) such that the ratio between fixed cost and maximal expected profit remains the same. All other parameters are the same as in Fig. 1. In this case, the expected profit is lower and the loss of profit due to charging \(\theta _{ruin} =\frac{1}{25} \left( 1+\frac{2}{3} \ln 4 \right) \approx 0.077\) instead of \(\theta _{profit}\) is relatively larger (\(\approx 48\%\)), compared to Fig. 1. Also, the minimal ruin probabilities for the same level of initial surplus are higher in this case.
The same process as in Fig. 1, with higher price sensitivity
Figure 5 further illustrates the effect of different price sensitivities on optimal profit and ruin probability. The parameters for this example are the same as in Fig. 1, except the price sensitivity parameter, \(\beta _1\), which now takes values between 2 and 50. We can see that both optimal loadings \(\theta _{profit}\) and \(\theta _{ruin}\) decrease with increasing sensitivity to price, with \(\theta _{ruin}\) having the sharper decline. As expected, the maximal profit decreases and the minimal ruin probability increases with increased price sensitivity. Comparing the curves of minimal ruin probabilities as functions of \(\beta _1\) for different levels of initial surplus, we see that not only the level of these curves decreases with initial surplus (as expected), but also the shape of the curve changes with different levels of initial surplus.
5.2 Two risks with different distributions
Now, we consider a claim process with two risks. Risk 1 and risk 2 have the same parameters as the risks considered in Figs. 1 and 2, respectively. Thus, when considered separately, both risks have the same optimal loadings but risk 2 leads to higher probability of ruin than risk 1. For these risks, we consider three scenarios: (a) the risks are independent; (b) the risks are dependent but customers buy insurance for each risk independently; (c) the risks are dependent and customers who buy insurance for one risk are more likely to buy for the other risk too. Dependence between risks is modeled by a Clayton Lévy copula [42] with parameter \(\nu =1\) (see Sect. 2.2), while dependence in the purchase of insurance is modeled by a Gumbel copula, as described in Sect. 4.4. Recall from the discussion following Proposition 4.2 that in this case we expect the optimal loadings \(\theta _{ruin}\) to depend on the initial surplus, contrary to the single-risk case.
Figure 6 plots the optimal loadings and the corresponding expected profit as functions of the initial surplus. The parameter of the Gumbel copula (dependence in acquisition of insurance for different risks) is set at \(\omega =\frac{5}{3}\), corresponding to Kendall’s \(\tau =0.4\). We see that the dependence on the initial surplus is quite strong, but only when the initial surplus is small. The optimal loading for risk 1 (lighter tail) is lower than the optimal loading when we consider this risk isolated (\(\approx 0.096\), Fig. 1), while the optimal loading for risk 2 (heavier tail) is higher than in the single risk case (also \(\approx 0.096\), Fig. 2). Further, the optimal loading for risk 1 decreases with increasing initial surplus, while \(\theta _{2,ruin}\) increases with initial surplus. The expected (total) profit corresponding to \(\theta _{ruin}\) decreases with initial reserves. Thus, in these cases, the safest strategy for a company with small reserves is to bet on higher profitability (thus, allowing the expected reserves to grow faster), even at the cost of taking more risk. This effect is seen in all three scenarios but it is stronger when the risks and the acquisitions are both dependent (case (c)) and weaker when risks and acquisitions are both independent.
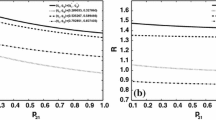
Figure 7 shows the optimal ruin probabilities in the same scenarios, as functions of the initial surplus. As expected, the ruin probabilities are lower in the independent risks case and higher in the dependent risks and dependent acquisitions case. Notice that the difference between the cases (a) and (b) is smaller than the difference between cases (b) and (c), that is, in this example dependence between acquisitions has a stronger effect on ruin probability than dependence between the risks.
Figure 8 plots the optimal loadings \(\theta _{ruin} = (\theta _{1,ruin},\theta _{2,ruin})\) in the plane \((\theta _1,\theta _2)\), for the three scenarios under consideration and various amounts of initial surplus. We see that, for the same initial surplus, the optimal loadings in the case of dependent risks and independent acquisitions are higher for both risks than in the case of independent risks. In the case of dependent risks and dependent acquisitions, the optimal loading for risk 1 is lower than in the case of independent risks and the optimal loading for risk 2 is higher than in the case of dependent risks with independent acquisitions.
In Fig. 9, we see how the optimal loadings and ruin probability change with increasing dependence between acquisition of insurance for different risks. To make interpretation easier, we plot these values as functions of Kendall’s \(\tau \). Recall that Kendal’s \(\tau \) is related with the Gumbel copula parameter by the relation \(\omega _{Gumbel}= \frac{1}{1-\tau }\). The initial surplus is fixed at \(x=9\). As already suggested by Fig. 8, the optimal loading for risk 1 decreases with increasing dependence, while the optimal loading for risk 2 increases. The optimal ruin probability increases slightly with increasing dependence.
5.3 Two risks with different price sensitivities
Finally, we consider a claim process with two risks, where risk 1 and risk 2 have the same parameters as the risks considered in Figs. 1 and 4, respectively. Thus, the risks differ in their demand sensitivities to price, with demand for risk 2 being more sensitive. The dependency scenarios ((a), (b), (c)) are the same as in Sect. 5.2.
Figure 10 plots the optimal loadings and the corresponding expected profit as functions of the initial surplus. It should be compared to Fig. 6, where the dependency parameters are the same. Since both risks have the same distribution, the optimal loadings \(\theta _{ruin}\) in the case of independent risks (a) do not depend on the initial surplus, as noted after Proposition 4.2. The optimal loading for risk 1 (less sensitive to price) is lower than the optimal loading when we consider this risk isolated (\(\approx 0.096\), Fig. 1), while the optimal loading for risk 2 (more sensitive to price) is higher than in the single risk case (\(\approx 0.077\), Fig. 4). In the scenarios with dependencies ((b) and (c)), the optimal loadings depend on the initial surplus, as expected, albeit this effect is weaker than in Fig. 6. In the case of dependent risks with independent insurance acquisition, the optimal loading increases with initial reserves for both risks, while in the case with dependent risks and dependent acquisitions, the optimal loading for risk 1 (less sensitive to price) is decreasing with increasing initial reserve.
Figure 11 shows the optimal ruin probabilities in the same scenarios, as functions of the initial surplus. This is similar to Fig. 7, but the probabilities of ruin are lower, as should be expected from the fact that in this case, risk 1 is the same and risk 2 has a lighter tail.
Figure 12 plots the optimal loadings \(\theta _{ruin} = (\theta _{1,ruin},\theta _{2,ruin})\) in the plane \((\theta _1,\theta _2)\), for the three scenarios under consideration and various amounts of initial surplus. In image (a), we use the same dependency parameters as in Fig. 8 (Sect. 5.2). The case with independent risks reduces to a single point, since in this case the optimal loadings are independent of the initial surplus. If the acquisition of insurance for different risks is independent, then the loadings for both risks increase with initial reserve and the increase seems to follow approximately a fixed proportion (i.e., the dots fall along an almost straight line).
In the case when the acquisition of insurance for different risk is dependent (Gumbel copula parameter \(\omega =\frac{5}{3}\), Kendall’s \(\tau =0.4\), like in Fig. 8), the behaviour is quite different: the optimal loading for risk 2 increases with initial reserve, while the optimal loading for risk 1 is maximal for initial surplus of \(\approx 0.5\), decreasing for larger surpluses. To give some further insight about how the optimal loadings change with the intensity of dependence between acquisition of insurance for different risks, we show on Image (b) the results for a weaker dependence (Gumbel’s copula parameter \( \omega =\frac{100}{85}\), Kendall’s \(\tau =0.15\)).
We plot Figs. 8 and 12 on the same scale to show that the relative sensibilities of the optimal loadings to the initial surplus are much smaller in Fig. 12. Also, the positions of the points \((\theta _{1,ruin},\theta _{2,ruin})\) relative to the case when the risks are considered separately are quite different.
In Fig. 13, we see how the optimal loadings and ruin probability change with increasing dependence between acquisition of insurance for different risks. The dependence between risks and the initial surplus are the same as in Fig. 9. It is interesting to see that for weak dependence between acquisitions of different risks, we have \(\theta _{1,ruin}> \theta _{2,ruin}\), i.e., the company minimizes its probability of ruin by charging a higher premium for the risk with demand less sensitive to price, as it is intuitively expectable. However, if the dependence between acquisitions of different risks is strong, then we have the inverse relation \(\theta _{1,ruin}<\theta _{2,ruin}\).
References
Andrade e Silva JM, de Lourdes Centeno M (2017) Ratemaking of dependent risks. ASTIN Bull 47(3):875–894. https://doi.org/10.1017/asb.2017.16
Asmussen S (1989) Risk theory in a Markovian environment. Scand Actuar J 1989(2):69–100. https://doi.org/10.1080/03461238.1989.10413858
Asmussen S, Albrecher H (2010) Ruin probabilities, 2nd edn. World Scientific, Singapore
Asmussen S, Christensen BJ, Taksar M (2013) Portfolio size as function of the premium: modelling and optimization. Stochastics 85(4):575–588. https://doi.org/10.1080/17442508.2013.797426
Asmussen S, Christensen BJ, Thøgersen J (2019) Nash equilibrium premium strategies for push–pull competition in a frictional non-life insurance market. Insurance Math Econ 87:92–100. https://doi.org/10.1016/j.insmatheco.2019.02.002
Asmussen S, Christensen BJ, Thøgersen J (2019) Stackelberg equilibrium premium strategies for push-pull competition in a non-life insurance market with product differentiation. Risks 7(2):49. https://doi.org/10.3390/risks7020049
Avanzi B, Cassar LC, Wong B (2011) Modelling dependence in insurance claims processes with Lévy copulas. ASTIN Bull 41(2):575–609. https://doi.org/10.2143/AST.41.2.2136989
Bäuerle N, Blatter A (2011) Optimal control and dependence modeling of insurance portfolios with Lévy dynamics. Insurance Math Econ 48(3):398–405. https://doi.org/10.1016/j.insmatheco.2011.01.008
Bäuerle N, Müller A (1998) Modeling and comparing dependencies in multivariate risk portfolios. ASTIN Bull 28(1):59–76. https://doi.org/10.2143/AST.28.1.519079
Bi J, Chen K (2019) Optimal investment-reinsurance problems with common shock dependent risks under two kinds of premium principles. RAIRO Oper Res 53(1):179–206. https://doi.org/10.1051/ro/2019010
Cai J, Wei W (2012) Optimal reinsurance with positively dependent risks. Insurance Math Econ 50:57–63. https://doi.org/10.1016/j.insmatheco.2011.10.006
Cao J, Landriault D, Li B (2020) Optimal reinsurance-investment strategy for a dynamic contagion claim model. Insurance Math Econ 93:206–215. https://doi.org/10.1016/j.insmatheco.2020.04.013
Christensen BJ, Parra-Alvarez JC, Serrano R (2021) Optimal control of investment, premium and deductible for a non-life insurance company. Insurance Math Econ 101:384–405. https://doi.org/10.1016/j.insmatheco.2021.07.005
Cont R, Tankov P (2004) Financial modelling with jump processes. Chapman & Hall/CRC, Boca Raton
Cossette H, Marceau E (2000) The discrete-time risk model with correlated classes of business. Insurance Math Econ 26(2):133–149. https://doi.org/10.1016/S0167-6687(99)00057-8
Cox DR (1955) Some statistical methods connected with series of events. J R Stat Soc Ser B (Methodol) 17(2):129–157. https://doi.org/10.1111/j.2517-6161.1955.tb00188.x
de Lourdes Centeno M (2005) Dependent risks and excess of loss reinsurance. Insurance Math Econ 37(2):229–238. https://doi.org/10.1016/j.insmatheco.2004.12.001
Denuit M, Dhaene J, Goovaerts M, Kaas R (2005) Actuarial theory for dependent risks. Measures, orders and models. Wiley, New York
Dickson DCM (2017) Insurance risk and ruin, 2nd edn. Cambridge University Press, Cambridge
Dragomir SS (2003) Some Gronwall type inequalities and applications. Nova Science, New York
Dutang C, Albrecher H, Loisel S (2013) Competition among non-life insurers under solvency constraints: a game-theoretic approach. Eur J Oper Res 231:702–711. https://doi.org/10.1016/j.ejor.2013.06.029
Embrechts P, McNeil AJ, Straumann D (2002) Correlation and dependence in risk management: properties and pitfalls. In: Dempster M (ed) Risk management: value at risk and beyond. Cambridge University Press, Cambridge, pp 176–223. https://doi.org/10.1017/CBO9780511615337.008
Emms P (2007) Dynamic pricing of general insurance in a competitive market. Astin Bull 37(1):1–34. https://doi.org/10.2143/AST.37.1.2020796
Fu K-A, Liu Y (2021) Ruin probabilities for a multidimensional risk model with non-stationary arrivals and subexponential claims. Probab Eng Inf Sci. https://doi.org/10.1017/S0269964821000085
Furman E, Landsman Z (2008) Economic capital allocations for non-negative portfolios of dependent risks. ASTIN Bull 38(2):601–619. https://doi.org/10.2143/AST.38.2.2033355
Grandell J (2012) Aspects of risk theory. Springer Science & Business Media, New York
Guo JY, Yuen KC, Zhou M (2007) Ruin probabilities in Cox risk models with two dependent classes of business. Acta Math Sin Engl Ser 23(7):1281–1288. https://doi.org/10.1007/s10114-005-0819-7
Hawkes AG (1971) Spectra of some self-exciting and mutually exciting point processes. Biometrika 58:83–90
Hipp C (2004) Stochastic control with application in insurance. In: Frittelli M, Runggaldier W (eds) Stochastic methods in finance. Springer, Berlin, pp 127–164
Kaas R, Goovaerts M, Dhaene J, Denuit M (2008) Modern actuarial risk theory: using R. Springer Science & Business Media, New York
Li D, Li B, Shen Y (2021) A dynamic pricing game for general insurance market. J Comput Appl Math 389:113349. https://doi.org/10.1016/j.cam.2020.113349
Liang Z, Yuen KC (2016) Optimal dynamic reinsurance with dependent risks: variance premium principle. Scand Actuar J 2016(1):18–362. https://doi.org/10.1080/03461238.2014.892899
Lu Z, Meng S, Liu L, Han Z (2018) Optimal insurance design under background risk with dependence. Insurance Math Econ 80:15–28. https://doi.org/10.1016/j.insmatheco.2018.02.006
Mouminoux C, Dutang C, Loisel S, Albrecher H (2022) On a Markovian game model for competitive insurance pricing. Methodol Comput Appl Probab 24(2):1061–1091. https://doi.org/10.1007/s11009-021-09906-1
Mourdoukoutas F, Boonen TJ, Koo B, Pantelous AA (2021) Pricing in a competitive stochastic insurance market. Insurance Math Econ 97:44–56. https://doi.org/10.1016/j.insmatheco.2021.01.003
Nelsen RB (2007) An introduction to copulas. Springer Science & Business Media, New York
Ohlsson E, Johansson B (2010) Non-life insurance pricing with generalized linear models. Springer, Berlin
Polborn MK (1998) A model of an oligopoly in an insurance market. Geneva Pap Risk Insur Theory 23:41–48. https://doi.org/10.1023/A:1008677913887
R Core Team (2021) R: a language and environment for statistical computing. R Foundation for Statistical Computing. https://www.R-project.org
Ramsay CM, Oguledo VI (2012) Insurance pricing with complete information, state-dependent utility, and production costs. Insurance Math Econ 50:462–469. https://doi.org/10.1016/j.insmatheco.2012.02.004
Schmidli H (2008) Stochastic control in insurance. Springer, Berlin
Tankov P (2016) Lévy copulas: review of recent results. In: Podolskij M, Stelzer R, Thorbjørnsen S, Veraart AED (eds) The fascination of probability, statistics and their applications. Springer, Berlin, pp 127–151
Taylor GC (1986) Underwriting strategy in a competitive insurance environment. Insurance Math Econ 5:59–77. https://doi.org/10.1016/0167-6687(86)90009-0
Thøgersen J (2016) Optimal premium as a function of the deductible: customer analysis and portfolio characteristics. Risks 4(4):42. https://doi.org/10.3390/risks4040042
Yang Y, Wang K, Konstantinides DG (2014) Uniform asymptotics for discounted aggregate claims in dependent risk models. J Appl Probrobab 51:669–684. https://doi.org/10.1239/jap/1409932666
Yu Y, Hui M, Hui C (2021) Mean-variance problem for an insurer with dependent risks and stochastic interest rate in a jump-diffusion market. Optimization. https://doi.org/10.1080/02331934.2021.1887179
Yuen KC, Liang Z, Zhou M (2015) Optimal proportional reinsurance with common shock dependence. Insurance Math Econ 64:1–13. https://doi.org/10.1016/j.insmatheco.2015.04.009
Acknowledgements
M. Guerra A. B. Moura acknowledge financial support from FCT—Fundação para a Ciência e Tecnologia (Portugal), national funding, through research grant UIDB/05069/2020.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Numerical scheme for Eq. (2.2)
Appendix: Numerical scheme for Eq. (2.2)
Consider the process
where \(Y_i\) are iid continuous random variables and \(N_t\) is a \(Poisson(\lambda t)\). To approximate Eq. (2.2), take a grid of points \(\epsilon =x_0<x_1<\cdots x_n\), \(x_i \in {\mathbbm {R}}, \forall i \in {\mathbbm {N}}, \epsilon >0\), with equal interval lengths, \(h = x_{i}- x_{i-1}\). A linear approximation is used to approximate \(\bar{V}(x)\)
where \( \frac{\bar{V}(x_j)- \bar{V}(x_{j-1})}{h}\) is an approximation of the derivative, \(\bar{V}'(x_{j-1})\), using the so-called forward difference
Let \(\bar{V}_i\) denote the approximation of \(\bar{V}(x_i)\). Let \(\bar{S}(x) = \int _0^x \bar{F}(y)dy\) and \(\bar{\bar{S}}(x) = \int _0^x \bar{S}(y)dy\). For each \(x_i, i>0\) solve the following equation
The goal is to develop a recursive method from \(x_0\) as the value of \(\bar{V}_0\) is known.
\({if} \quad i =0\)
Set \(\bar{V}_0 = 1-\frac{\lambda }{c}{{\,\mathrm{\mathbb {E}}\,}}[Y]\)
\({if \quad i =1}\)
Calculate
\({if \quad i >1}\)
Calculate

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gudmundarson, R.L., Guerra, M. & Moura, A.B. On some effects of dependencies on an insurer’s risk exposure, probability of ruin, and optimal premium loading. Eur. Actuar. J. 13, 341–373 (2023). https://doi.org/10.1007/s13385-022-00326-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13385-022-00326-0