Skip to main content
SpringerLink
Log in

Selection effect modification to the Lee-Carter model

  • Original Research Paper
  • Published:
European Actuarial Journal Aims and scope Submit manuscript

Abstract

Although other risk factors can be used, depending on feasibility, marketing, and data availability, age and gender are the two most common risk factors considered in life insurance products. Previous studies have shown that the newly insured, who passed certain health examinations, tend to have lower mortality rates than those already insured. Insurance companies often use select and ultimate tables to handle mortality discrepancies between the insured in different policy years (i.e., the selection effect). However, the selection effect is easily confused with mortality improvement, and its estimate is likely to be influenced by the annual reduction in mortality rates. In this study, we propose modifying the Lee-Carter model, including the selection effect and mortality improvement. We first use a simulation to evaluate the parameter estimation of the proposed approach and then apply it to experienced data from Taiwan’s largest insurance company, Cathay Life Insurance Company Ltd. The results of our simulation and empirical studies support the newly proposed approach, which provides stable and accurate estimates of the selection effect and mortality improvement. We also find that the size of the selection effect concerning policy year was larger than the difference in mortality rates between smokers and non-smokers; this is particularly noticeable for older age groups.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Availability of data and material

The empirical data are the property of the Cathay Life Insurance Co. and are not open to the public.

Code availability

The code is open source and is written in R statistical software.

Notes

  1. In 2011, the European Court of Justice ruled that using gender to calculate premiums and benefits was inconsistent with the European Charter.

  2. Conversely, the selection effect would be overestimated if the insured were ex-smokers.

  3. Mortality improvement is an important factor for modeling mortality rates today; however, it was not considered until the late 1990s.

  4. IFRS 17 is an International Financial Reporting Standard, and is expected to be effective in 2023. In 2021, the Taiwan government decided to delay the effective date to 2026.

  5. The selection effect can also exist in health insurance products. For example, cancer insurance is a popular product in Taiwan, and insurance claims occur when the insured is diagnosed with cancer for the first time. Thus, we can plug the incidence rates into the population's proposed model to evaluate a selection effect. Note that the proportion of initial disease cases is defined as an incidence rate.

  6. We also tried singular value decomposition for the parameter estimation, and the results were similar.

  7. The estimates of parameters \({\alpha }_{x}\), \({\beta }_{x}\), \({\kappa }_{t}\), and \({C}_{xs}\) are derived from the “StMoMo” package. The estimates obtained from the “ilc” package are extremely similar to those from “StMoMo.” The \({\alpha }_{x}\) estimates from “ilc” are also negatively biased at the 1st iteration.

References

  1. Bowers N, Gerber H, Hickman J, Jones D, Nesbitt C (1997) Actuarial mathematics, 2nd edn. Society of Actuaries, Chicago

    MATH  Google Scholar 

  2. Brouhns N, Denuit M, Vermunt JK (2002) A Poisson log-bilinear regression approach to the construction of projected life-tables. Insur Math Econ 31(3):373–393. https://doi.org/10.1016/S0167-6687(02)00185-3

    Article  MATH  Google Scholar 

  3. Butt Z, Haberman S, Shang HL (2014) The ilc package in R: Generalized Lee-Carter models using iterative fitting algorithms. https://cran.r-project.org/web/packages/ilc/vignettes/ilc.pdf. Retrieved June 06, 2021

  4. Carriere JF (1994) A select and ultimate parametric model. Trans Soc Actuar 46:75–97

    Google Scholar 

  5. Gerber HU (1995) Life insurance mathematics, 2nd edn. Swiss Association of Actuaries, Zürich. Springer

  6. Kirkeleit J, Riise T, Bjørge T, Christiani DC (2013) The healthy worker effect in cancer incidence studies. Am J Epidemiol 177(11):1218–1224. https://doi.org/10.1093/aje/kws373

    Article  Google Scholar 

  7. Klein AM, Krysiak ML (2014) Select period mortality survey. Society of Actuaries

  8. Last JM (2000) A Dictionary of epidemiology, 4th edn. Oxford University Press, Oxford

    Google Scholar 

  9. Lee RD, Carter LR (1992) Modeling and forecasting US mortality. J Am Stat Assoc 87(419):659–671. https://doi.org/10.1080/01621459.1992.10475265

    Article  MATH  Google Scholar 

  10. Lew EA, Garfinkel L (1987) Differences in mortality and longevity by sex, smoking habits and health status. Trans Soc Actuar 39:107–130

    Google Scholar 

  11. London RL (1985) Graduation: The revision of estimates. ACTEX Publication

  12. McCarthy D, Mitchell OS (2003) International adverse selection in life insurance and annuities. NBER Working Papers 9975. National Bureau of Economic Research

  13. Renshaw AE, Haberman S (1997) Dual modelling and select mortality. Insur Math Econ 19(2):105–126. https://doi.org/10.1016/S0167-6687(96)00016-9

    Article  MATH  Google Scholar 

  14. Renshaw AE, Haberman S (2006) A cohort-based extension to the Lee-Carter model for mortality reduction factors. Insur Math Econ 38(3):556–570. https://doi.org/10.1016/j.insmatheco.2005.12.001

    Article  MATH  Google Scholar 

  15. Renshaw AE, Haberman S (2008) On simulation-based approaches to risk measurement in mortality with specific reference to Poisson Lee-Carter modelling. Insur Math Econ 42(2):797–816. https://doi.org/10.1016/j.insmatheco.2007.08.009

    Article  MATH  Google Scholar 

  16. Richards SJ (2020) A Hermite-spline model of post-retirement mortality. Scand Actuar 2020(2):110–127

    Article  MathSciNet  MATH  Google Scholar 

  17. SCOR (2016) Proposed “08” series mortality tables, CMI, vol CMI Working Paper 92

  18. Villegas AM, Kaishev VK, Millossovich P (2018) StMoMo: An R package for stochastic mortality modeling. J Stat Softw. https://doi.org/10.18637/jss.v084.i03

  19. Waldron I, Hughes ME, Brooks TL (1996) Marriage protection and marriage selection—prospective evidence for reciprocal effects of marital status and health. Soc Sci Med 43(1):113–123. https://doi.org/10.1016/0277-9536(95)00347-9

    Article  Google Scholar 

  20. Wang HC, Yue JC (2015) Mortality, health, and marriage: a study based on Taiwan’s population data. North Am Actuar J 19(3):187–199. https://doi.org/10.1080/10920277.2015.1019518

    Article  MathSciNet  MATH  Google Scholar 

  21. Wang HC, Yue CJ, Chong CT (2018) Mortality models and longevity risk for small populations. Insur Math Econ 78:351–359. https://doi.org/10.1016/j.insmatheco.2017.09.020

    Article  MathSciNet  MATH  Google Scholar 

  22. Yue CJ, Huang H (2011) A study of incidence experience for Taiwan life insurance. Geneva Pap Risk Insur Issues Pract 36(4):718–733. https://doi.org/10.1057/gpp.2011.28

    Article  Google Scholar 

  23. Yue JC, Wang HC, Leong YY, Su WP (2018) Using Taiwan National Health Insurance Database to model cancer incidence and mortality rates. Insur Math Econ 78:316–324. https://doi.org/10.1016/j.insmatheco.2017.09.016

    Article  MathSciNet  MATH  Google Scholar 

  24. Yue JC, Wang H, Wang T (2021) Using graduation to modify the estimation of Lee-Carter model for small populations. North Am Actuar J 25(sup1)(sup. 1):S410–S420. https://doi.org/10.1080/10920277.2019.1650288

Download references

Funding

Not applicable.

Author information

Authors and Affiliations

  1. Department of Statistics, National Chengchi University, Taipei, 11605, Taiwan, ROC

    Jack C. Yue

  2. Center for Fundamental Science, and Research Center for Nonlinear Analysis and Optimization, Kaohsiung Medical University, Kaohsiung, 80708, Taiwan, ROC

    Jack C. Yue

  3. Cathay Life Insurance Co., Ltd., Taipei, 10693, Taiwan, ROC

    Chao-Ting Lin, Yu-Lin Yang, Yi-Chun Chen & Wan-Chen Tsai

  4. Department of Risk Management and Insurance, Feng Chia University, Taichung, 40724, Taiwan, ROC

    Yin-Yee Leong

Authors
  1. Jack C. Yue
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chao-Ting Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yu-Lin Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yi-Chun Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Wan-Chen Tsai
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Yin-Yee Leong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yin-Yee Leong.

Ethics declarations

Conflict of interest

We declare that we have no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

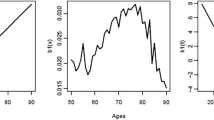
Appendix: Estimates and Monte Carlo Confidence Intervals of \({\alpha }_{x}\), \({\beta }_{x}\), and \({\kappa }_{t}\) (Simulation)

Bias of \(\alpha_{x}\) Estimates

See Fig. 7

Fig. 7
figure 7

Bias of Estimates for Parameter \(\alpha_{x}\)(1st and 15th iteration)

Full size image

Bias of βx Estimates

See Fig. 

Fig. 8
figure 8

Bias of Estimates for Parameter βx (1st and 15th iteration)

Full size image

8

Bias of \(\kappa_{t}\) Estimates

See Fig. 

Fig. 9
figure 9

Bias of Estimates for Parameter \(\kappa_{t}\)(1st and 15th iteration)

Full size image

9

Estimates of Selection Effect

See Fig. 

Fig. 10
figure 10

Estimates of Selection Effect (15th iteration)

Full size image

10

Parameters \(\alpha_{x}\),\(\beta_{x}\), and \(\kappa_{t}\) with the Monte Carlo 95% Confidence Intervals

See Tables

Table 8 Parameters \(\alpha_{x}\) and \(\beta_{x}\) with their Monte Carlo 95% Confidence Intervals
Full size table

8 and

Table 9 Parameters \(\kappa_{t}\) with their Monte Carlo 95% Confidence Intervals
Full size table

9

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yue, J.C., Lin, CT., Yang, YL. et al. Selection effect modification to the Lee-Carter model. Eur. Actuar. J. 13, 213–234 (2023). https://doi.org/10.1007/s13385-022-00312-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13385-022-00312-6

Keywords

Search

Navigation