Current developments in German pension schemes: What are the benefits of the new target pension?

Abstract

We analyze the newly introduced German occupational pension scheme called target pension (“Zielrente”), which links the beneficiaries’ benefits during the retirement phase to the mortality experienced among the pension beneficiaries and the performance of the financial market, from a pension beneficiary’s perspective. We model the contract payoffs related to the target pension according to the new enhancement law on German occupational law. Specifically, we include two parameters in the plan design, one to control the surplus participation and one to control the loss participation. These parameters are chosen in such a way that the initial wealth of the retiree equals the initial value of the target pension. With the help of expected lifetime utility and wealth equivalent, we find that the target pension provides a meaningful supplement to the first and third pillar. Further, we find some comparative advantages of the target pension over the traditional pure defined benefit and some defined contribution plans from a policyholder’s point of view. Our analysis with reasonable parameter choices shows that target pension plans can be outperformed by defined contribution plans with variable annuities, while the latter are accompanied by a considerably higher ruin probability.

1 Introduction

One of the major societal challenges is the changing demographics due to our aging society. While birth rates remain low, life expectancy has been increasing continuously for several decades, leading to high costs for social security systems. A shrinking working population has to support pensions of an increasing retiring population, which destroys an effective functioning of the statutory pay-as-you-go system. At the same time due to current low interest and highly volatile stock markets, it becomes more difficult to build up capital reliably over long time horizons. How to provide pension security and how to deal with an aging society is a very challenging task in contemporary social security, both in developed industrial and developing countries. Diverse measures have been taken to provide better pension security. In Germany, the role of occupational and private pension plans, the second and third pillar of the pension system, has been substantially enhanced. According to the new law of occupational pension plans (Betriebsrentenstärkungsgesetz), a new occupational pension plan, so called target pension (“Zielrente”, TP), was introduced and implemented in 2018. Due to the complexity of the pension system, it is not easy to come up with a thorough solution which solves all the problems resulting from the demographic changes.

In the majority of developed countries, defined contribution (DC) and defined benefit (DB) pension schemes are still the two main types of occupational retirement plans ([13]). In DC schemes, employers and their employees make payments to a pension fund which invests the contributions in the financial market. The benefits at retirement are highly dependent on the performance of the investment returns experienced during the membership, i.e. the employee carries the investment risk. In a DB scheme, employers promise their employees a guaranteed pension payment and carry the investment risk. From the year 2000 on, there has been a shift from DB towards DC schemes in the majority of developed countries ([13]). [1] provide a discussion of further causes responsible for this shift. For further details on DB and DC schemes, see also [14] and for DB schemes see additionally [2]. An overview of stochastic methods for analyzing pensions can be found in [6]. [3] compare occupational pension schemes to private life annuities. Further articles connected with the design and development of pension schemes include, but are not limited to [15, 16, 8] and [11].

Although the new pension scheme TP is technically not the same as a pure DC scheme¹, it is the first occupational pension scheme in Germany that does not offer any guaranteed benefits to the policyholders. This feature has created a lot of skepticism in the German population. The question arises whether the new scheme is beneficial to the employees, whether the newly introduced scheme can be a meaningful supplement to the first and third pillar, and whether the TP is better than pure DB or pure DC plans for the pension beneficiaries. This article aims to answer this question by analyzing the benefits of a TP in an expected utility framework assuming no bequest motive.

Following the new enhancement law on occupational pensions, the TP contains a collective risk sharing scheme: The retirement benefits are adjusted on a yearly basis, based on the performance of the financial market and the mortality experienced among the members in the pension plan. After each year, the pension benefits can increase, decrease or remain the same as in the previous year. To control the magnitude of the increase and reduction in the pension benefits, we introduce a surplus participation and a loss participation parameter. We rely on risk-neutral pricing techniques to determine the initial value of the TP for a fixed up-front premium of the retiree. The surplus and loss participation parameters are determined in such a way that financial fairness is achieved.

We assume that the retiree has access to all three pillars with a pay-as-you-go first pillar, occupational pensions as a second pillar, and private pensions as a third pillar. In this paper, for simplicity, we assume that the pension payments each retiree obtains from the first and third pillar are merged to a constant whole-life annuity. In this article, there are two objectives: (1) We want to find out whether a TP can be a meaningful supplement to the first and third pillar, and (2) whether the TP can bring some added value within the second pillar, especially compared to the DC and DB scheme. To answer these questions, we assume that the retiree splits her initial wealth between some occupational pension scheme and a constant annuity resulting from the first and third pillar. The wealth is split in such a way that her expected discounted lifetime utility is maximized. If the TP then generates a higher level of expected utility than an alternative occupational pension scheme, the TP is superior to this alternative. First, we perform these analyses in a rather simple model where we disregard systematic mortality risk. We then check the results obtained for robustness by additionally considering a model setup which takes the systematic mortality risk and safety loadings into account. To assess the added value which an individual gains by joining a TP scheme, we consider the wealth equivalent derived from the expected utility, which is the initial wealth level required for a TP to achieve the same expected utility level as some other pension scheme with some fixed initial wealth level.

In both model frameworks, we find that individuals with different degrees of relative risk aversion invest positive fractions of their wealth in a TP, suggesting that the TP forms a meaningful supplement to the first and third pillar. The more risk-averse a retiree is, the lower the optimal fraction of wealth invested in the TP becomes, as retirees with a higher risk aversion desire more stable payments during the retirement phase. Furthermore, our results suggest that a TP is likely to be a more beneficial occupational pension scheme than some DC and DB schemes, as the resulting wealth equivalents are below the initial wealth invested in the DC and DB schemes. However, we also find DC plans with variable annuities which make the wealth equivalent higher than the initial wealth invested in the DC scheme. The disadvantage of this DC structure is, though, that it leads to a default with certainty, whereas the TP provides ruin probabilities near zero under reasonable parameter choices. Under the more realistic model which takes account of the systematic mortality risk, the qualitative results remain widely similar to the case with no systematic mortality risk. For the majority of investors, the inclusion of risk loading in this setting can lead to an even higher attractiveness of the TP scheme over some DC and DB schemes under a prudent investment strategy, whereas more risky investment strategies underlying the TP lower its attractiveness compared to the setting with no loadings. Again, DC plans with variable annuities we analyze outperform the TP but lead again to a certain default in contrast to the TP under reasonable parameter choices.

The remainder of this article is organized as follows: In Sect. 2, we describe the fundamental model setup used throughout the article. In particular, we describe how the preferences of the retirees are modeled, the financial market, the structure and design of the TP pension plan and the valuation of it. In Sect. 3, we disregard systematic longevity risk and determine the optimal fraction of wealth invested in each occupational pension scheme, and determine the wealth equivalent of the TP for the DB and two DC plans. In Sect. 4, we include the systematic mortality risk and perform similar analyses as in Sect. 3. Section 5 concludes the article.

2 Model setup

Consider a retiree who is currently x years old and has a total initial wealth of $x_0$. The future lifetime of the retiree is denoted by $\zeta$ which is assumed to be independent of the financial market risk.

2.1 Stochastic model

The TP has a collective risk sharing component: The individual payments from the TP depend on the number of surviving pension beneficiaries as well as on the performance of the financial market. We assume that there are in total n retirees who can be seen as identical copies of each other. Each of the retirees contributes the same initial wealth $x_0$ to the collective, resulting in a collective initial wealth level of $X_0 = n x_0$.

We consider a stochastic basis ($\Omega , \mathcal {F}, \{\mathcal {F}_t\}_{t \ge 0}, P$) satisfying the usual hypothesis. Let $\{ W_t \}_{t \ge 0}$ be a standard Brownian motion. There are two assets traded in the market, a risky asset S following a geometric Brownian motion and a risk-free asset B earning a constant interest rate r:

$$\begin{aligned} d S_t&= \mu S_t dt + \sigma S_t d W_t, S_0 = s \\ d B_t&= r B_t dt, B_0 = 1. \end{aligned}$$

Here we assume that $\mu -r > 0$ and $\sigma >0$. Assuming that the pension beneficiaries’ future lifetimes are independent, the number of living pension beneficiaries at time t is given by $N_t \sim \text {Bin}(n,{}_t p_x)$. In the following, we assume that the filtration $\{ \mathcal {F}_t \}_{t \ge 0}$ is defined by $\mathcal {F}_t = \sigma (\mathcal {H}_t \cup \mathcal {G}_t)$, where $\mathcal {G}_t = \sigma \{N_s,\, s \le t \}$ and the filtration $\{\mathcal {H}_t\}_{t \ge 0}$ is the standard filtration of the standard Brownian motion $\{ W_t \}_{t \ge 0}$. That is, the filtration $\{ \mathcal {F}_t \}_{t \ge 0}$ contains all the relevant information about the payoff of the TP: $\{ \mathcal {G}_t \}_{t \ge 0}$ contains the information about the deaths occurring over time and $\{\mathcal {H}_t\}_{t \ge 0}$ contains the information about the stock price.

2.2 Expected utility

Assume that the retiree is situated in a three-pillar pension system with a pay-as-you-go first pillar, an occupational pension as a second pillar, and a private pension as a third pillar. The main purpose of the paper is to find out whether the second pillar is a meaningful supplement to the first and third pillar, and whether the specific form of TP as the second pillar brings some added value compared to the traditional pure DB and pure DC pension plans. Typically, the pension obtained from the first pillar is annuity-like, i.e. a fixed periodic whole-life payment. Concerning the third pillar, the retiree can voluntarily access the life and pension, stock market or real estate market etc. to ensure supplementary provisions for their old age. In this paper, for simplicity, we assume that the pension payments each retiree obtains from the first and third pillar are merged to a constant whole-life annuity.² The up-front premium of this annuity constitutes a $1-\phi$ fraction of the retiree’s initial wealth $x_0$, where $\phi \in [0,1]$. The remaining wealth $\phi x_0$ is used to purchase the occupational pension plan. Note that if we want to emphasize that that the pension from the first pillar is statutory and the retiree is ensured with at least this part of pension, we shall adjust the upper bound of $\phi$ from 1 to $0\le \bar{\phi }<1$. For our analysis below, this can be incorporated straightforwardly. However, as the level $\bar{\phi }$ can vary substantially for different persons, we stick to the case with $\phi \in [0,1]$. Let us use L to denote the periodic annuity payment if $x_0$ is fully used to purchase the annuity, and $\{L_k\}_{k=0,1,\ldots }$ be the periodic payment from investing in the occupational pension plan if $x_0$ is fully used to invest in the second pillar. In other words, the retiree who invests $(1-\phi ) x_0$ in the annuity and $\phi x_0$ in the second pillar as described above, obtains $\phi L_k + (1-\phi )L$ at $k=0, 1, \ldots$, if she is alive.

The retiree measures utility by using a constant relative risk aversion (CRRA) utility function given by $u(y) = \frac{y^{1-\gamma }}{1-\gamma }$, where $\gamma >0$, $\gamma \ne 1$ is the coefficient of relative risk aversion. Consequently, the expected lifetime utility is given by

$$\begin{aligned} U\left( \{ \phi L_k + (1-\phi ) L \}_{k=0,1,\ldots } \right)&= \mathbb {E} \left[ \sum _{k=0}^{\infty } e^{-\rho k} \mathbb {1}_{\{\zeta>k\}} u(\phi L_k + (1-\phi )L) \right] \nonumber \\&= \sum _{k=0}^{\infty } e^{-\rho k} \mathbb {E} \left[ \mathbb {1}_{\{\zeta>k\}} u(\phi L_k + (1-\phi )L) \right] \nonumber \\&= \sum _{k=0}^{\infty } e^{-\rho k} \cdot {}_k p_x \cdot \mathbb {E} \left[ u(\phi L_k + (1-\phi )L) \mid \zeta > k \right] \end{aligned}$$

(1)

where we have used the usual actuarial notation $P(\zeta > k ) = {}_k p_x$ and $\rho$ is the subjective discount factor of the retiree. We assume that the policyholder determines $\phi$ in such a way that the expected lifetime utility (1) is maximized.

• If we can find a $\phi >0$ that delivers a higher expected lifetime utility than that of $\phi =0$ (constant annuity), the second pillar provides a beneficial supplementary retirement plan in addition to constant annuities. Note that the expected lifetime utility of a constant annuity can be determined explicitly:

  $$\begin{aligned} U(\{ L \}_{k=0,1,\ldots })&= \mathbb {E} \left[ \sum _{k=0}^{\infty } e^{-\rho k} \mathbb {1}_{\{\zeta >k\}} u(L) \right] \\&= u(L) \sum _{k=0}^{\infty } e^{-\rho k} {}_k p_x =: u(L) \ddot{a}_x(\rho ) . \end{aligned}$$

• Note that the aggregate periodic pension payments are identical for two cases: $\phi =0$ and $L_k=L$ for all k. The latter case can result from a fixed annuity payment from the first and third pillar together with a DB plan which also pays out a fixed payment. In this sense, if $\phi >0$ turns out optimal for $L_k$ unequal to L for at least one k, we show that a DB pension plan is outperformed by other occupational plans.

• Given $\phi >0$, we can compare various occupational pension plans by specifying and analyzing concrete payment streams for $L_k$.

As the emphasis of the paper is laid on analyzing the newly developed occupational pension plan TP in Germany, we will specify $L_k$ to meet the descriptions of the TP stipulated in the enhancement law on occupational pensions in the remainder of this section and subsequently in the numerical section compare it with alternative pension schemes.

2.3 Payoff mechanism of TP

Below we describe the payoff mechanism of a TP. In the following, we consider a run-off scheme, i.e. we assume that there is a finite number of initial members and that no new members will enter the system in the future.

• Annuity payments of in total $N_k L_{k}$ to the survivors at time k occur annually in advance, that is, at times $k=0,1,2,\ldots$. As we assume that the retirees are identical copies of each other, they all receive the same annual annuity benefit.

• After the annuity payments are subtracted from the account, the remainder is invested in financial assets. Within one year, the total assets are assumed to develop according to the following stochastic differential equation (SDE) under P:

  $$\begin{aligned} d X_t = \left( r + \pi (\mu -r) \right) X_t dt + \sigma \pi X_t d W_t \, , \quad t \in [k,k+1] \,, \end{aligned}$$

  (2)

  where $\pi$ is the fraction of the account value invested in the risky asset, i.e. the asset strategy is a constant mix strategy, and the initial investment is given by $X_0' = X_0 - nL_0$. The solution to the above SDE is given by

  $$\begin{aligned} X_t = X_{k} \exp \left( \left( r+\pi (\mu -r) - \frac{\pi ^2 \sigma ^2}{2} \right) (t-k) + \pi \sigma (W_t - W_{k}) \right) \end{aligned}$$

  (3)

  for $t \in [k,k+1]$. As long as $X_t > 0$, the TP can provide payments to the beneficiaries. If $X_t = 0$ for some t, no further payments can be made and the account value remains at zero. In case of a TP, the pension beneficiaries do not obtain a guaranteed payment as in a DB plan, i.e. no protection is provided by the pension guarantee fund, when the sponsoring company or the pension fund defaults. In other words, we assume that the TP has a limited liability, and it does not pay out more than the fund’s asset value. That is why $X_t$ cannot be negative.

• At the end of each year, we determine the funding ratio which indicates the ratio between the available assets and the future pension liabilities. Mathematically spoken, it is given by

  $$\begin{aligned} F_{k} = \frac{\text {Assets}_{k}}{\text {Liabilities}_{k}} = \frac{X_{k}}{N_k \, L_{k-1} \, \ddot{a}_{x+k}(r)} , \end{aligned}$$

  where $\ddot{a}_{x+k}(r) = \sum _{j=0}^{\infty } {}_j p_{x+k} \cdot v^j$ is the present value of a lifelong annuity-due with $v = e^{-r}$ being the annual discount factor.

• According to the enhancement law on occupational pensions, the pension payments of the TP shall be adjusted according to the realization of the funding ratio. If the funding ratio falls out of the interval [1, 1.25], the annuity payments $L_{k}$ shall be adjusted. To be precise, let $N_t$ be the number of the survivors at time t.

  • $L_0=X_0/(n \ddot{a}_x(r))$, i.e. the funding ratio $F_0$ at time 0 equals 1.

  • At time 0, the first pension payment is made. The remainder $X_0'= X_0- nL_0$ is invested in financial assets and evolves according to (2) which delivers $X_1$.

  • The second individual pension payment $R_1$ is based on the funding ratio $F_1=X_1/ (N_1 L_0 \ddot{a}_{x+1}(r))$ at time 1 :

    $$ L_{1} = \left\{ {\begin{array}{*{20}l} {L_{0} ,} & {{\text{if}}\; F_{1} \in [1,1.25]} \\ {L_{0} + \frac{\alpha }{n}(X_{1} - N_{1} L_{0} \ddot{a}_{{x + 1}} (r)),} & {{\text{if}}\;F_{1} > 1.25} \\ {\max \left\{ {L_{0} + \frac{\beta }{n}(X_{1} - N_{1} L_{0} \ddot{a}_{{x + 1}} (r)),0} \right\},} & {{\text{if}}\; F_{1} > 1.25} \\ \end{array} } \right. $$

    If the fund performs extremely well ($F_1 > 1.25$), some surpluses are given to the retirees in the second case. If the fund performs extremely badly ($F_1 < 1$), the pension payment will be cut. Both $\alpha$ and $\beta$ are in (0, 1). In a good performance, some reserves are set up. In a bad performance, not all the deficits are covered by the retiree. After the annuity payments are made, the remainder $X_1' = X_1 - N_1 L_1$ is invested in financial assets.

  • The k-th individual pension payment $L_k$ is based on the funding ratio at time k which is given by $F_k=X_k/ (N_k L_{k-1} \ddot{a}_{x+k}(r))$:

    $$L_{k} = \left\{ {\begin{array}{*{20}l} {L_{{k - 1}} ,} & {{\mkern 1mu} {\text{if}}\;F_{k} \in [1,1.25]} \\ {_{{k - 1}} + \frac{\alpha }{n}(X_{k} - N_{k} L_{{k - 1}} \ddot{a}_{{x + k}} (r)),} & {{\text{if}}\;F_{k} > 1.25} \\ {ax\left\{ {L_{{k - 1}} + \frac{\beta }{n}(X_{k} - N_{k} L_{{k - 1}} \ddot{a}_{{x + k}} (r)),0} \right\},} & {{\text{if}}\;F_{k} < 1} \\ \end{array} } \right.$$

    (4)

    In the second case, some surpluses are given to the retirees. In the third case, the pension payment will be cut. If $L_{k} = 0$ for some k in (4), one final payment of $L_k := X_k/N_k$ is made to each retiree who is still alive at time k. After that, the account value is zero and, consequently, no further retirement benefits can be paid out. If $L_{k} > 0$ in (4), after the annuity payments are made, the remainder $X_k' = X_k - N_k L_k$ is invested in financial assets.

To achieve fairness (see subsequent subsection), we assume additionally that the TP pays out a death benefit in case no living policyholders remain but the assets are not yet depleted. For a given t, the death benefit is zero if there are still some policyholders alive. In this sense, we shall note that this event that all the policyholders pass away plays a negligible role in a large portfolio, which is e.g. the case in our numerical analyses. In addition to the survival benefits $L_k$, we assume that the remainder is split equally among all the policyholders. We define $T:= \inf \{ k \in \mathbb {N} \mid N_k = 0 \}$ as the first time when there are no policyholders left. This leads to the following payoff structure:

$$\begin{aligned} Z(k) = L_k \mathbb {1}_{ \{\zeta > k \} } + \frac{X_T}{n} \mathbb {1}_{\{ T = k \}}. \end{aligned}$$

Note that we assume that the death benefit does not contribute to the policyholder’s expected lifetime utility (1). Since the death benefit is zero with positive probability, we have decided not to include it in the expected utility of the policyholder, since a payoff potentially equal to zero would turn the overall expected utility equal to $- \infty$ for $\gamma >1$, which does not allow us to analyze the real retirement benefits generated by the TP to the pension beneficiaries. We could restrict our analysis to $\gamma \in (0,1)$, where the mentioned problem does not appear. However, we believe it is more important to study the impact of the risk aversion where more realistic risk aversion levels larger than 1 can be chosen as well. An alternative approach would also be to use a different type of utility function for the death benefit, which does not lead to a utility level of $-\infty$. However, in this case, we would be adding two different types of utility functions which would lead to inconsistent results. Therefore, we have decided to compare the different retirement plans considered in Section 3 solely based on their corresponding survival benefits.

2.4 Valuation of TP

The question is how to set the parameters $\alpha$ and $\beta$, where $\alpha$ can be considered as a surplus participation coefficient, while $\beta$ as a loss participation coefficient. A contract is fair for a policyholder if the initial market value of the contract payoff equates her initial investment.

To address the fair contract, we shall determine the initial market value of the TP. We rely on the risk-neutral pricing technique. The insurer chooses, for pricing purposes, a risk neutral probability Q among the infinitely many risk-neutral measures existing in incomplete arbitrage-free markets. The probability Q then accounts for both diversifiable and systematic mortality risk inherent to this portfolio. The financial uncertainty in our model is only due to assets randomness. In this benchmark setting, we first assume that no systemic mortality risk is existent and the portfolio is sufficiently large so that the unsystematic risk can be neglected, i.e.

$$\begin{aligned} P(\zeta>k)= Q(\zeta >k). \end{aligned}$$

(5)

We start with this simple setting as we want to single out the effect of the systematic mortality risk by adding it explicitly in a later section. Beyond the natural requirement that financial and demographic risk are independent, we assume the dynamics of the stock market under Q to be given by

$$\begin{aligned} d S_t = S_t \left( r dt + \sigma d W^Q_t \right) , \quad t\ge 0. \end{aligned}$$

To determine the initial value of the TP, we first note that the event $\{T=k\}$ is for all $k \in \mathbb {N}$ equivalent to the event $\{N_k \le 0 < N_{k-1} \}$. Further, note that

$$\begin{aligned} P(N_k \le 0 < N_{k-1})&= P(N_{k-1}> 0) - P(N_k > 0) \nonumber \\&= 1- P(N_{k-1} \le 0) - (1 - P(N_k \le 0)) \nonumber \\&= 1 - (1- {}_{k-1} p_x)^n - (1- (1-{}_k p_x)^n) \nonumber \\&= (1-{}_k p_x)^n - (1- {}_{k-1} p_x)^n. \end{aligned}$$

(6)

According to the fair contract principle and using (6), we obtain the fair value $V_0 = V_0(\{L_k\}_{k=0,1,\ldots })$ as

$$\begin{aligned} V_0&= \mathbb {E}_Q \left[ \sum _{k=0}^{\infty } \left( \mathbb {1}_{\{\zeta> k \} } v^k L_k + v^k \cdot \frac{X_k}{n} \mathbb {1}_{\{ T=k \}} \right) \right] \nonumber \\&= \sum _{k=0}^{\infty } \left( v^k \mathbb {E}_Q \left[ \mathbb {1}_{\{\zeta> k \} } L_k \right] + \frac{v^k}{n} P(T = k) \mathbb {E}_Q \left[ X_k \mid T=k \right] \right) \nonumber \\&= \sum _{k=0}^{\infty } \left( {}_k p_x \, v^k \, \mathbb {E}_Q \left[ L_k \mid \zeta> k \right] \right. \nonumber \\&\quad \left. + \frac{v^k}{n} \left( (1-{}_k p_x)^n - (1- {}_{k-1} p_x)^n \right) \mathbb {E}_Q \left[ X_k \mid T=k \right] \right) \nonumber \\&= \sum _{k=0}^{\infty } {}_k p_x \, v^k \, \mathbb {E}_Q \left[ L_k \mid \zeta > k \right] \nonumber \\&\quad + \sum _{k=1}^{\infty } \left( \frac{v^k}{n} \left( (1-{}_k p_x)^n - (1- {}_{k-1} p_x)^n \right) \mathbb {E}_Q \left[ X_k \mid T=k \right] \right) \nonumber \\&= x_0. \end{aligned}$$

(7)

3 Analyzing the utility of TP

In this section, we first aim to assess whether the addition of an occupational pension plan is beneficial to a single policyholder, with the aid of TP. Further, we compare the TP with pure DB and DC pension plans.

Table 1 Base case parameters

Table 1 provides the parameter setup for our numerical analyses. Below are a few remarks regarding our base case parameters:

• For our numerical analyses, we have chosen the Gompertz law to describe the force of mortality, due to its reputation for being the best description of senior population’s future lifetimes (see e.g. [7, 12] and [10]). In this section, we consider an actuarially fair pricing framework, and adopt the parameters calibrated to real-world data directly from [10]. Later in Sect. 4, when we explicitly consider safety loadings, we calibrate the Gompertz parameters to DAV 2004R life table which is used in Germany to price retirement products. That is to say, we assume that ${}_t p_x = e^{e^{\frac{x-m}{b}} \big (1-e^{\frac{t}{b}} \big )}$ with modal age at death m and dispersion coefficient b. The parameters are taken from [10], where the parameters for Germans are estimated as $m=88.12$, $b=9.09$ for females and $m=83.57$, $b=9.90$ for males. Hence, our study focuses on the perspective of a female retiree, but could of course be changed to the male perspective without drastic changes in the results.³

• The maximum age is 122 which is based on the publicly available German life table DAV 2004R which assumes 121 as maximum age.

• The retiree is aged 67 (which is the current typical retirement age in Germany) and the continuous risk-free interest rate is $r = 1 \%$ based on [17].

• The constant-mix investment strategy $\pi =0.2$ is more realistic for the situation in Germany. German insurance companies and pension funds are not allowed to invest more than a (rather low) prescribed percentage of their capital in risky assets. The higher fraction 0.6 could be applicable to the United States or Switzerland, where less conservative bounds are prescribed.

We start our numerical analysis in Tables 2 and 3 by giving some insights on the behavior of the initial value $V_0$ depending on $\alpha$ and $\beta$ for two investment strategies $\pi \in \{0.2,0.6\}$.

Table 2 Initial value $V_0$ depending on the two parameters $\alpha$ and $\beta$

Table 3 Initial value $V_0$ depending on the two parameters $\alpha$ and $\beta$

We observe the following:

• We see that an increase in $\alpha$ has no monotone effect on the initial value, but does decrease the initial value once it exceeds the value 0.4. The reason for this is that a higher $\alpha$ leads to more surpluses being distributed to the policyholders, leaving less capital to be invested in the capital market to build reserves for the future.

• We observe that $\beta$ has no monotone effect on the initial value. Instead, its effects strongly depend on the choice of the surplus participation $\alpha$.

• Most importantly, we observe that the condition (7) is approximately, e.g. to the nearest whole number, fulfilled for many combinations of $\alpha$ and $\beta$. Among these, we choose the combination which delivers the lowest ruin probability,⁴ i.e. $\alpha =0.05$ and $\beta = 0.4$, as we will see in Sect. 3.3. Note that, as the pension payments are proportional to the initial investment $x_0$, the resulting $\alpha$ and $\beta$ sets are also approximately fair, when another initial wealth level is applied.

3.1 Comparison of TP and DB

In this section, we want to compare the optimal TP to the DB scheme. To compare the resulting utility level of the TP to that of a conventional annuity with constant annual payments, we consider the wealth equivalent, which is the initial wealth level WE invested in the optimal TP which makes the retiree indifferent between the TP and DB scheme, where the initial value of the DB scheme is given by $x_0$. Let $U\left( \{ \phi L_k + (1-\phi ) L \}_{k=0,1,\ldots } \right)$ be the expected utility resulting from a TP with initial wealth $x_0$ as given in (1), and let $U\left( \{ L \}_{k=0,1,\ldots } \right)$ be the expected utility resulting from the DB scheme with initial wealth $x_0$. As the payments of the TP and the constant annuity are proportional to the initial wealth level, we obtain the wealth equivalent mathematically as

$$\begin{aligned}&\left( \frac{\text {WE}}{x_0} \right) ^{1-\gamma } U\left( \{ \phi L_k + (1-\phi ) L \}_{k=0,1,\ldots } \right) = U\left( \{ L \}_{k=0,1,\ldots } \right) \nonumber \\ \Leftrightarrow&\quad \text {WE} = x_0 \left( \frac{U\left( \{ L \}_{k=0,1,\ldots } \right) }{U\left( \{ \phi L_k + (1-\phi ) L \}_{k=0,1,\ldots } \right) } \right) ^{\frac{1}{1-\gamma }}. \end{aligned}$$

(8)

In the first equation, we need to add $\left( \frac{\text {WE}}{x_0} \right) ^{1-\gamma }$ to change the pension payoffs starting from $x_0$ to WE, as $\{ \phi L_k + (1-\phi ) L \}_{k=0,1,\ldots }$ is originally defined for a stream of payoffs starting with an initial wealth $x_0$.

In Table 4, we provide the optimal fraction $\phi$ invested in the TP, and the wealth equivalent defined in (8), in dependence of the risk aversion $\gamma$. If the wealth equivalent is greater (smaller) than the initial wealth $\text {WE} >(<) x_0$, then the DB scheme is more (less) beneficial than the TP. Note that the initial wealth for the DB plan is equal to $x_0 = 100$, $(\text {WE}-100)/100$ can be considered as the percentage of initial wealth which is additionally required if $(\text {WE}-100)/100>0$, or may be taken away from the investment in the TP if $(\text {WE}-100)/100<0$, to achieve the same expected utility as in the DB scheme.

Table 4 Wealth equivalent along with the optimal fraction of initial wealth invested in the TP compared to the DB scheme ($\phi = 0$) depending on the relative risk aversion parameter

We observe that the wealth equivalent is lower than 100 which implies that the TP is more beneficial than a pure constant annuity. The wealth equivalent is increasing in the risk aversion, meaning that the TP is more beneficial the less risk-averse an individual is. The optimal fraction of wealth invested in the TP is larger than zero for all risk aversion parameters and decreases in the risk aversion. For the lowest risk aversion $\gamma =0.5$, the policyholder even invests all of her initial wealth in the TP and nothing in the annuity. These results suggest that a TP can be a beneficial supplement to constant annuities. The reason for this is that, through its collective risk sharing component and the returns earned through the risky asset (which are higher than the risk-free interest rate), the TP offers more upside potential than a constant annuity to the policyholders. In this place, the investment strategy $\pi$ does not seem to play a major role in the attractiveness of the TP, since the individuals can adjust the fraction of wealth invested in the TP accordingly. Riskier strategies lead to lower fractions of wealth invested in the TP. Only the retiree with the lowest risk aversion $\gamma =0.5$ benefits significantly from a more risky investment strategy. For all the other risk aversions, the wealth equivalent changes only negligibly.

3.2 Comparison of TP and DC

As already pointed out in the model section, $\phi >0$ implies also that the TP is more beneficial to the retiree than a pure DB pension plan. In what follows, we will compare the TP with a pure DC pension plan. As mentioned in the introduction of this article, a DC scheme pays out the accumulated earnings of the contributions paid during the pre-retirement phase. Typically, this payoff can be paid as a lump sum payment or converted to an annuity. In the latter case, if it deals with a constant annuity, the DC scheme would simply be equal to the DB scheme. That is why we focus on two cases: In the first one, the retiree consumes the whole benefit received from the DC scheme at time 0. In the second case, the DC scheme pays out variable annuity payments resulting from an investment in the financial market. The magnitude of the lump sum payment is set in such a way that the initial value of the overall payments is equal to $x_0$. In other words, the retiree simply sets aside a fraction of her initial wealth $\phi x_0$ which is immediately consumed while the remainder $(1-\phi )x_0$ is invested in the first and third pillar yielding a constant annuity. This leads to a payment stream of $\phi x_0 + (1-\phi )L$ at time 0 and $(1-\phi )L$ at all times $k \ge 1$. The expected discounted lifetime utility is given by

$$\begin{aligned}&U (\phi x_0 + (1-\phi )L, L,L,\ldots ) \\&\quad = \mathbb {E} \left[ u(\phi x_0 + (1-\phi )L) + \sum _{k=1}^{\infty } e^{-\rho k} \mathbb {1}_{\{\zeta >k\}} u((1-\phi )L) \right] \\&\quad = u(\phi x_0 + (1-\phi )L) + u((1-\phi )L) \sum _{k=1}^{\infty } e^{-\rho k} {}_k p_x \\&\quad = u(\phi x_0 + (1-\phi )L) + u((1-\phi )L) a_x(\rho ), \end{aligned}$$

following the standard actuarial notation.⁵ In this case, the optimal fraction of wealth invested in the DC scheme $\phi$ can be determined explicitly. Consider the following optimization problem:

$$\begin{aligned} \max _{\phi \in [0,1]} u(\phi (x_0-L) + L) + u((1-\phi )L) a_x(\rho ). \end{aligned}$$

The first-order condition yields the optimal fraction of wealth set aside:

$$\begin{aligned}&u'(\phi (x_0-L) + L) \cdot (x_0-L) - u'((1-\phi )L) \cdot L \cdot a_x(\rho ) = 0 \\&\quad \Leftrightarrow (\phi (x_0-L) + L) \cdot (x_0-L)^{-\frac{1}{\gamma }} = (1-\phi )L \cdot ( L \cdot a_x(\rho ))^{-\frac{1}{\gamma }} \\&\quad \Leftrightarrow \phi (x_0-L)^{1-\frac{1}{\gamma }} + \phi L ( L \cdot a_x(\rho ))^{-\frac{1}{\gamma }} = L ( L \cdot a_x(\rho ))^{-\frac{1}{\gamma }} - L (x_0-L)^{-\frac{1}{\gamma }} \\&\quad \Leftrightarrow \phi ^* = \frac{ L ( L \cdot a_x(\rho ))^{-\frac{1}{\gamma }} - L (x_0-L)^{-\frac{1}{\gamma }} }{(x_0-L)^{1-\frac{1}{\gamma }} + L ( L \cdot a_x(\rho ))^{-\frac{1}{\gamma }}} \\&\quad = \frac{ L^{1-\frac{1}{\gamma }} \left( a_x(\rho )^{-\frac{1}{\gamma }} - a_x(r)^{-\frac{1}{\gamma }} \right) }{(x_0-L)^{1-\frac{1}{\gamma }} + L ( L \cdot a_x(\rho ))^{-\frac{1}{\gamma }}}, \end{aligned}$$

where we have used $x_0 - L = L \ddot{a}_x(r) - L = L a_x(r)$ in the last equation. There are three different cases for $\phi ^*$:

• $\rho = r$: In this case, $a_x(\rho )^{-\frac{1}{\gamma }} = a_x(r)^{-\frac{1}{\gamma }}$ and thus $\phi ^* = 0$, i.e. it is optimal to annuitize all the initial wealth. This result is well-known since [18].

• $\rho > r$: In this case, $a_x(\rho )^{-\frac{1}{\gamma }} > a_x(r)^{-\frac{1}{\gamma }}$ and thus $\phi ^* > 0$. If early consumption is preferred, i.e. the subjective discount rate exceeds the risk-free interest rate, an advantage can result by immediately consuming some wealth.

• $\rho < r$: In this case, $a_x(\rho )^{-\frac{1}{\gamma }} < a_x(r)^{-\frac{1}{\gamma }}$ and thus $\phi ^* < 0$ which we do not allow. In this case, the minimal $\phi$ that can be chosen is simply 0. If later consumption is preferred, i.e. the subjective discount rate is exceeded by the risk-free interest rate, it is thus again optimal to annuitize all the initial wealth.

It is already mentioned in [18] that the optimal consumption is increasing if the subjective discount rate is smaller than the risk-free interest rate and decreasing if the subjective discount rate exceeds the risk-free interest rate. Furthermore, it is well-known that constant annuities are suboptimal for individuals whose subjective discount factor differs from that of the insurer (cf. [19]), which is why the above results are rather natural. In our base case, we have chosen $\rho = r$, i.e. in this case no wealth from the DC scheme is immediately consumed and all the initial wealth is invested in the first and third pillar. In other words, the DC scheme coincides with the DB scheme and is outperformed by the TP.

In order to make a proper comparison between TP and DC, some results related to $\rho > r$ are shown in the following as well. We choose $\rho = 0.03$. Table 5 shows the resulting wealth equivalents defined analogously to (8) for the DC instead of the DB scheme:

$$\begin{aligned} \text {WE} = x_0 \left( \frac{U (\phi x_0 + (1-\phi )L, L,L,\ldots )}{U\left( \{ \phi L_k + (1-\phi ) L \}_{k=0,1,\ldots } \right) } \right) ^{\frac{1}{1-\gamma }}. \end{aligned}$$

Table 5 Wealth equivalent along with the optimal fraction of initial wealth invested in the TP and the DC scheme depending on the relative risk aversion parameter

We observe that the TP outperforms the DC scheme for all risk aversion coefficients considered. As only a small fraction of the initial wealth is immediately consumed, the results are rather similar to those in Table 4 and the wealth equivalent increases in the risk aversion. While for the TP, the optimal fraction of initial wealth increases drastically as the risk aversion becomes smaller, the fraction of wealth immediately consumed from the DC scheme remains rather low for all risk aversions. Compared to Table 4, the optimal fraction invested in the TP is slightly smaller than for the case $\rho = r$. In other words, the TP loses more of its attractiveness compared to the constant annuity if the subjective and risk-free discount rate differ. The differences in Tables 4 and 5 are only moderate, though. Compared to Table 4, we observe that all investors benefit (at least slightly) from a more risky investment strategy if the subjective discount factor exceeds the risk-free interest rate. The reason for this is that the TP’s assets are depleted more quickly under a more risky investment strategy, leading to higher payments at younger ages.

3.3 DC scheme with variable annuities

In this section, we consider the DC scheme with variable annuity payments. We assume that the DC plan pays out a life-long (non-constant) annuity adjusted as follows. The payoff streams (as long as the fund is not yet depleted) can be expressed in the following way:

• $L_0= X_0/(n \ddot{a}_x)$. At time 0, the first pension payment is made. The remainder $X_0'= X_0- nL_0$ is invested in financial assets and evolves according to (2) which delivers $X_1$.

• The second individual pension payment is $L_1= X_1/(N_1 \ddot{a}_{x+1})$, which usually differs from $L_0$. The remainder $X_1' = \max \{X_1 - N_1 L_1,0 \}$ is invested in financial assets.

• The k-th individual pension payment is given by $L_k = X_k/(N_{k}\ddot{a}_{x+k})$. After the annuity payments are made, the remainder $X_k' =\max \{ X_k - N_k L_k,0 \}$ is invested in financial assets.

Unlike in the target pension case, the pension payment in the DC plan does not specifically depend on the funding ratio. In case all policyholders have died before the account value is depleted, i.e. $N_k = 0$ but $X_k >0$, there is an additional death benefit of $X_k/n$ to all retirees. We can compute the initial value similarly to the TP in (7). Tables 6 and 7 provide the wealth equivalents defined analogously to (8) for the alternative DC scheme.

Table 6 Wealth equivalent along with the optimal fraction of initial wealth invested in the TP compared to the DC scheme depending on the relative risk aversion parameter

Table 7 Wealth equivalent along with the optimal fraction of initial wealth invested in the TP compared to the DC scheme depending on the relative risk aversion parameter

In both tables, we observe that the DC scheme with variable annuity payments manages to outperform the TP scheme, since the wealth equivalent is above 100 for all risk aversions. If a more risky investment strategy is chosen, the wealth equivalent increases, especially for the lower risk aversions $\gamma = 1/2,2,4$. From $\gamma =2$ onward, the wealth equivalent decreases in the risk aversion for both investment strategies as the retiree invests more of her initial wealth in the constant annuity as the risk aversion increases. This makes the overall retirement incomes obtained from the TP and the constant annuity or the DC scheme and the constant annuity more similar to each other. Compared to the DC scheme with variable annuity payments, the pension payments for the target pension are less volatile. Our results here, on some level, demonstrate that the retirees, to a certain extent, do enjoy taking on higher risks coupled with higher expected returns.

To extend our comparison of TP and DC with variable annuities, we define the ruin time of the pension fund as the first time that the collective asset value is depleted while there are still members alive, i.e. $\tau :=\inf \{t>0 \mid X_{t} = 0, {N(t)>0} \}$. Due to the collective risk-sharing, the ruin event is not defined on an individual but on a collective level. Apparently, we shall consider this risk measure under the physical probability measure P:

$$\begin{aligned} \Psi (\omega - x) := P(\tau <\omega -x {\mid \zeta \ge \omega -x}). \end{aligned}$$

(9)

where $\omega$ is maximal age reachable by the retirees. Note that we determine the ruin probability under the assumption that there is one policyholder who reaches the maximum age $\omega$ with certainty (which is not unrealistic under extremely large pool sizes). Tables 8 and 9 provide the ruin probabilities of the TP for different parameter combinations of the surplus and loss participation rate $\alpha$ and $\beta$.

Table 8 Ruin probability $\Psi$ depending on the two parameters $\alpha$ and $\beta$

Table 8 provides a justification for our choice of $\alpha$ and $\beta$ in the previous numerical analyses, since this combination provides the lowest ruin probability among the combinations considered.

Table 9 Ruin probability $\Psi$ depending on the two parameters $\alpha$ and $\beta$

In Table 9, we observe that a more risky trading strategy which allocates more capital to the risky asset leads to a higher ruin probability for all combinations of $\alpha$ and $\beta$ considered. Note that the ruin probability of the DC scheme is equal to 1 for both investment strategies $\pi \in \{0.2,0.6\}$, because all of its surplus is directly distributed to all the surviving beneficiaries, meaning that the account value of the DC scheme will hit zero with certainty, if at least one policyholder lives long enough. This is an advantage that the TP has against the DC scheme, as the goal of an occupational pension scheme should be to provide a life-long retirement income to all of its pension beneficiaries.

4 Systematic mortality risk

4.1 A simple stochastic mortality model and risk loadings

In this section, we incorporate uncertainty in the mortality law in a similar way as [9] by applying a random shock $\epsilon$ to the survival probabilities such that the shocked survival probabilities are given by ${}_t p_x^{1-\epsilon }$, where $\epsilon$ is assumed to be a continuous random variable taking values in $(-\infty ,1)$. By this assumption, we make sure that the shocked survival probabilities ${}_t p_x^{1-\epsilon }$ are still between 0 and 1. We use the notation $N_t(\epsilon )$ and $\zeta (\epsilon )$ to emphasize the dependence of the number of living policyholders in a TP and the remaining lifetime of a single policyholder on this shock. Note that, assuming the conditional independence of the remaining lifetimes of the retirees, it holds $(N_t(\epsilon ) \mid \epsilon ) \sim \text {Bin}(n,{}_t p_x^{1-\epsilon })$. The special case in which no shock is applied is obtained by setting $\epsilon = 0$.

To account for this unhedgeable risk, the insurer applies a prudent pricing measure to determine the initial value of the retirement plans. That is, under Q, the survival probabilities are larger than the survival probabilities under P, i.e.

$$\begin{aligned} \mathbb {E} \left[ \mathbb {1}_{\{\zeta (\epsilon )> t\}} \right] = P(\zeta (\epsilon )> t) < Q(\zeta (\epsilon )> t) = \mathbb {E}_Q \left[ \mathbb {1}_{\{\zeta (\epsilon ) > t\}} \right] . \end{aligned}$$

One way to achieve this is by choosing the original survival curve prudently, i.e. ${}_t \tilde{p}_x > {}_t p_x$, where ${}_t \tilde{p}_x$ is the survival curve under Q and ${}_t p_x$ is the survival curve under P. Additionally, we assume that the longevity shock $\epsilon$ follows the same distribution under P and Q. The survival curves $({}_t \tilde{p}_{x})_{t\ge 0}$ and $({}_t p_{x})_{t\ge 0}$, result from the deterministic mortality model. $\mathbb {E}_P[({}_tp_{x})^{1-\epsilon }]$ and $\mathbb {E}_Q[({}_t \tilde{p}_{x})^{1-\epsilon }]$ resulting from the shocked model can be considered the survival probabilities from the internal model, under the real world measure P and the risk-neutral pricing measure Q. For our numerical analyses, we have again chosen the Gompertz law for the deterministic part and follow [4] to model the shock part. Due to this specific structure, we can calibrate the parameters in the deterministic force of mortality part first and then estimate the parameters of the shock afterwards:

• In the first step, we estimate the parameters in the Gompertz law, where the force of mortality and the survival probabilities are parameterized as

  $$\begin{aligned} \widetilde{\mu }_{x+t}=&\frac{1}{\widetilde{b}}e^{\frac{x+t-\widetilde{m}}{\widetilde{b}}},\,\\ {}_t \widetilde{p}_x =&e^{e^{\frac{x-\widetilde{m}}{\widetilde{b}}} \big (1-e^{\frac{t}{\widetilde{b}}} \big )} \end{aligned}$$

  with $\widetilde{b}>0$ being the dispersion coefficient and $\widetilde{m}$ being the modal age at death under safety loadings. We do this by calibrating these two parameters to the observed survival probabilities using the DAV 2004R table for a 67-year female born in 1953. We obtain $\widetilde{m}=98.899$ and $\widetilde{b}=9.162$.

• Using the estimated $\widetilde{m}=98.899$ and $\widetilde{b}=9.162$ from the first step, in the second step, we estimate the parameters for $\epsilon$, where $\epsilon$ is assumed to follow a truncated normal distribution with a mean $\mu _{\epsilon }$ and a variance $\sigma _{\epsilon }^2$, following [4]. As the DAV 2004R table is a life table used for calculating prices for annuity products in practice, the table is constructed based on prudent pricing, i.e. it does not deal with actuarially fair premiums, but loaded ones. Hence, we calibrate $\mathbb E_Q[({}_t \tilde{p}_x)^{1-\epsilon }]$ to the observed survival probability. We obtain $\mu _{\epsilon }=-0.0686$ and $\sigma _{\epsilon }=0.386$.

• For the calibration, we follow the criterion of minimizing the sum of the squared errors between $_t \tilde{p}_x$ and the observed survival probabilities, and between $\mathbb {E}_Q[({}_t \tilde{p}_{x})^{1-\epsilon }]$ and the observed survival probabilities on a discrete grid $t=0,1,\ldots ,\omega -x$, i.e.

  $$\begin{aligned}&\min _{\widetilde{m},\widetilde{b}} \sum ^{\omega - x}_{t=0} \left( _t \tilde{p}^{observed}_x-{}_t \tilde{p}_{x} \right) ^2, \nonumber \\&\min _{\mu _{\epsilon }, \sigma _{\epsilon }} \sum ^{\omega - x}_{t=0} \left( _t \tilde{p}^{observed}_x-\mathbb {E}_Q[({}_t \tilde{p}_{x})^{1-\epsilon }] \right) ^2. \end{aligned}$$

  (10)

  In (10), we have used the calibrated $\widetilde{m}$ and $\widetilde{b}$ to compute $\mathbb {E}_Q[({}_t\widetilde{p}_{x})^{1-\epsilon }]$.

• Our estimated mortality parameters under Q and those parameters under P taken from [10] allow us to compute the loading incorporated in various retirement products. Taking a regular constant annuity in advance as an example, we obtain a loading of $42\%$ computed by the following formula:

  $$\begin{aligned} \delta = \frac{\sum _{t=0}^{\omega -x} e^{-r t}\mathbb {E}_Q[({}_t \tilde{p}_{x})^{1-\epsilon }]}{\sum _{t=0}^{\omega -x} e^{-r t}\mathbb {E}_P[({}_tp_{x})^{1-\epsilon }]} -1. \end{aligned}$$

  Here we have used an interest rate of 1%. The high loading reflects that German annuity providers price the annuity products in a very prudent way.

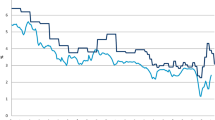
In Fig. 1, we provide the survival curve ${}_t \tilde{p}_x^{observed}$ taken from the DAV 2004R table, the calibrated survival curve ${}_t \tilde{p}_x$ under the Gompertz law and the calibrated internal survival curve $\mathbb E_{Q}[({}_t\tilde{p}_x)^{1-\epsilon }]$ obtained under the shocked Gompertz law using the above parameters.

Fig. 1

Survival curve ${}_t \tilde{p}_x$ taken from the DAV 2004R table, the calibrated survival curve ${}_t \tilde{p}_x$ under the Gompertz law and the calibrated internal survival curve $\mathbb E_{Q}[({}_t\tilde{p}_x)^{1-\epsilon }]$ obtained under the shocked Gompertz law

While the Gompertz law without shock appears to be closer to the shorter survival probabilities taken from the DAV 2004R table, the shocked Gompertz law is significantly closer to the longer survival probabilities. This is why, in total, the shocked Gompertz law delivers a lower minimum squared error than the Gompert law.

4.2 Analyzing the utility of TP

To assess the benefits of a TP, we perform similar analyses as in Sect. 3. In addition to the parameters in Table 1, we use the parameters derived above, which are again summarized in Table 10.

Table 10 Base case parameters in addition to Table 1

While the definition of the ruin probability remains unchanged compared to Sect. 3, the initial value of the TP and the constant annuity change. We define $T(\epsilon ) := \inf \{ k \in \mathbb N : N_k(\epsilon ) = 0 \}$ as the first time at which there remain no surviving policyholders. Note that the event $\{ T(\epsilon ) = k\}$ is, for a given $\epsilon$, equivalent to $\{N_k(\epsilon ) \le 0 < N_{k-1}(\epsilon ) \}$ with probability

$$\begin{aligned} P(N_k(\epsilon ) \le 0 < N_{k-1}(\epsilon ) \mid \epsilon )&= P(N_{k-1}(\epsilon )> 0 \mid \epsilon ) - P(N_k(\epsilon ) > 0 \mid \epsilon ) \\&= 1- P(N_{k-1}(\epsilon ) \le 0 \mid \epsilon ) - (1 - P(N_k(\epsilon ) \le 0 \mid \epsilon )) \\&= 1 - (1- {}_{k-1} p_x^{1-\,\epsilon } )^n - (1- (1- {}_{k} p_x^{1-\,\epsilon } )^n ) \\&= (1- {}_{k} p_x^{1-\,\epsilon } )^n - (1- {}_{k-1} p_x^{1-\,\epsilon } )^n. \end{aligned}$$

The initial value of the TP can thus be obtained as

$$\begin{aligned} V_0&= V_0(\{L_k\}_{k=0,1,\ldots }) = \mathbb {E}_Q \left[ \sum _{k=0}^{\infty } \mathbb {1}_{\{\zeta (\epsilon )> k \} } v^k L_k(\epsilon ) + \sum _{k=1}^{\infty } v^k \cdot \frac{X_k}{n} \mathbb {1}_{\{ T(\epsilon )=k \}} \right] \nonumber \\&= \sum _{k=0}^{\infty } v^k \mathbb {E}_Q \left[ \mathbb {1}_{\{\zeta (\epsilon )> k \} } L_k(\epsilon ) \right] + \sum _{k=1}^{\infty } \frac{v^k}{n} \mathbb {E}_Q \left[ X_k \mathbb {1}_{\{ T(\epsilon )=k \}} \right] \nonumber \\&= \sum _{k=0}^{\infty } v^k \mathbb {E}_Q \left[ \mathbb {E}_Q \left[ \mathbb {1}_{\{\zeta (\epsilon )> k \} } L_k(\epsilon ) \mid \epsilon \right] \right] + \sum _{k=1}^{\infty } \frac{v^k}{n} \mathbb {E}_Q \left[ \mathbb {E}_Q \left[ X_k \mathbb {1}_{\{ T(\epsilon )=k \}} \mid \epsilon \right] \right] \nonumber \\&= \sum _{k=0}^{\infty } \, v^k \, \mathbb {E}_Q \left[ {}_k \tilde{p}_x^{1-\epsilon } \mathbb {E}_Q \left[ L_k(\epsilon ) \mid \zeta (\epsilon ) >k, \epsilon \right] \right] \nonumber \\&\quad + \sum _{k=1}^{\infty } \frac{v^k}{n} \mathbb {E}_Q \left[ \left( (1- {}_{k} \tilde{p}_x^{1-\,\epsilon } )^n - (1- {}_{k-1} \tilde{p}_x^{1-\,\epsilon } )^n \right) \mathbb {E}_Q \left[ X_k \mid T(\epsilon )=k, \epsilon \right] \right] = x_0. \end{aligned}$$

(11)

The initial value of the constant annuity is given by

$$\begin{aligned} \tilde{\ddot{a}}_x(r,\epsilon ) = \mathbb {E}_Q \left[ \sum _{k=0}^{\infty } \mathbb {1}_{\{\zeta (\epsilon )> k\}} v^k \right] = \sum _{k=0}^{\infty } v^k \mathbb {E}_Q \left[ \mathbb {1}_{\{\zeta (\epsilon ) > k\}} \right] = \sum _{k=0}^{\infty } v^k {}_k \tilde{p}_x \, m_{\epsilon }(-\ln {}_k \tilde{p}_x), \end{aligned}$$

where $m_{\epsilon }(s)=\mathbb {E}\left[ e^{s\epsilon }\right]$ for $s\in \mathbb {R}$ is the moment generating function of $\epsilon$.

Before we can analyze the utility resulting from different compositions of the TP and the constant annuity, we need to find a new combination $(\alpha , \beta )$ which fulfills the condition (7). In Tables 11 and 12, we analyze the behavior of the initial value and the ruin probability depending on the parameters $\alpha$ and $\beta$ for two investment strategies $\pi \in \{ 0.2,0.6 \}$. For the ruin probability, we simulate the evolution of the account under the real-world measure P, while for the initial value, we simulate it under Q. Note that in both simulations, the actuarial present value $\tilde{\ddot{a}}_x(r,\epsilon )$ (determined under Q) is used.

Table 11 Initial value $V_0$ and ruin probability $\Psi$ depending on the two parameters $\alpha$ and $\beta$. The parameters are chosen as in Tables 1 and 10 with $\pi =0.2$

Table 12 Initial value $V_0$ and ruin probability $\Psi$ depending on the two parameters $\alpha$ and $\beta$. The parameters are chosen as in Tables 1 and 10 with $\pi =0.6$

We observe the following:

• We see that an increase in $\alpha$ leads to an increase in the ruin probability. The reason for this is that a higher $\alpha$ leads to more surplus being distributed to the policyholders, leaving less capital to be invested in the capital market to build reserves for the future. The effect of $\alpha$ on the initial value is rather similar to Tables 2 and 3.

• We observe that $\beta$ has no monotone effect on the initial value. Instead, its effects strongly depends on the choice of the surplus participation $\alpha$. In the current parameter setup, an increase in $\beta$ leads to an increase in the ruin probability.

• Most importantly, we observe that the condition (7) is again approximately (rounded to the nearest whole number) fulfilled for $\alpha = 0.05$ and $\beta =0.4$. We choose the same parameters as in Section 3 to ease the interpretation of our results.

• Comparing Tables 11 and 12, we observe that an increase in the fraction invested in the risky asset leads to higher or equal ruin probabilities, whereas the effect of the investment strategy on the initial value of the TP is not monotone.

4.2.1 Comparison of TP and DB

The expected lifetime utility resulting from both the TP and a constant annuity is determined as follows:

$$\begin{aligned}&U\left( \{ \phi L_k + (1-\phi ) L \}_{k=0,1,\ldots } \right) \\&\quad = \mathbb {E} \left[ \sum _{k=0}^{\infty } \mathbb {1}_{\{\zeta (\epsilon )> k \} } e^{-\rho k} u\left( \phi L_k(\epsilon ) + (1-\phi ) L \right) \right] \nonumber \\&\quad = \sum _{k=0}^{\infty } e^{-\rho k} \mathbb {E} \left[ \mathbb {1}_{\{\zeta (\epsilon )> k \} } u\left( \phi L_k(\epsilon ) + (1-\phi ) L \right) \right] \nonumber \\&\quad = \sum _{k=0}^{\infty } e^{-\rho k} \mathbb {E} \left[ \mathbb {E} \left[ \mathbb {1}_{\{\zeta (\epsilon )> k \} } u\left( \phi L_k(\epsilon ) + (1-\phi ) L \right) \mid \epsilon \right] \right] \nonumber \\&\quad = \sum _{k=0}^{\infty } \, e^{-\rho k} \, \mathbb {E} \left[ {}_k p_x^{1-\epsilon } \mathbb {E} \left[ u\left( \phi L_k(\epsilon ) + (1-\phi ) L \right) \mid \zeta (\epsilon ) >k, \epsilon \right] \right]. \end{aligned}$$

Note that the expected utility is computed under the real-world measure P, i.e. using the survival curve ${}_k p_x$ instead of ${}_k \tilde{p}_x$.

The wealth equivalents along with the optimal fractions of initial wealth invested in the annuity under the new stochastic mortality model are provided in Table 13.

Table 13 Wealth equivalent along with the optimal fraction of initial wealth invested in the TP compared to the DB scheme ($\phi = 0$) depending on the relative risk aversion parameter

Similar to Table 4, we observe that the wealth equivalent is always smaller than 100 and that the optimal fraction of wealth invested in the TP is always larger than zero, which suggests again that the TP can be an attractive supplement to constant annuities. The wealth equivalent is again increasing and the optimal fraction is again decreasing in the risk aversion, since retirees with a higher risk aversion seek more stable payments during their retirement phase. Note that the optimal level of initial wealth invested in the TP is, for all degrees of risk aversion, smaller than in Table 4, except for $\gamma =1/2$ which is equal for $\pi =0.2$. The reason for this is the relatively higher premium of the annuity resulting from the risk-neutral pricing measure Q due to the longevity shock $\epsilon$ which leaves less capital to be invested in the TP to achieve the same level of constant retirement income. Further, we observe that a riskier investment strategy now influences the wealth equivalent more strongly. The higher fraction invested in the risky asset forces the retirees to invest more in the constant annuity which is, due to the risk loading, more expensive than in Sect. 3 leading to losses in utility.

4.2.2 Comparison of TP and DC

We consider the same DC scheme setup as in Section 3. The expected discounted lifetime utility is given by

$$\begin{aligned}&U (\phi x_0 + (1-\phi )L, L,L,\ldots ) \\&\quad = \mathbb {E} \left[ u(\phi x_0 + (1-\phi )L) + \sum _{k=1}^{\infty } e^{-\rho k} \mathbb {1}_{\{\zeta (\epsilon )>k\}} u((1-\phi )L) \right] \\&\quad = u(\phi x_0 + (1-\phi )L) + u((1-\phi )L) \sum _{k=1}^{\infty } e^{-\rho k} {}_k p_x \cdot m_{\epsilon }(-\ln {}_k p_x) \\&\quad = u(\phi x_0 + (1-\phi )L) + u((1-\phi )L) a_x(\rho ,\epsilon ), \end{aligned}$$

following the standard actuarial notation. The optimal fraction of wealth invested in the DC scheme $\phi$ can again be determined explicitly. Consider the following optimization problem:

$$\begin{aligned} \max _{\phi \in [0,1]} u(\phi (x_0-L) + L) + u((1-\phi )L) a_x(\rho ,\epsilon ). \end{aligned}$$

Similarly to Sect. 3, we can derive the optimal level of initial wealth set aside explicitly as

$$\begin{aligned} \phi ^* = \frac{ L ( L \cdot a_x(\rho ,\epsilon ))^{-\frac{1}{\gamma }} - L (x_0-L)^{-\frac{1}{\gamma }} }{(x_0-L)^{1-\frac{1}{\gamma }} + L ( L \cdot a_x(\rho ,\epsilon ))^{-\frac{1}{\gamma }}} = \frac{ L^{1-\frac{1}{\gamma }} \left( a_x(\rho ,\epsilon )^{-\frac{1}{\gamma }} - \tilde{a}_x(r,\epsilon )^{-\frac{1}{\gamma }} \right) }{(x_0-L)^{1-\frac{1}{\gamma }} + L ( L \cdot a_x(\rho ,\epsilon ))^{-\frac{1}{\gamma }}}, \end{aligned}$$

where we have used $x_0 - L = L \tilde{\ddot{a}}_x(r,\epsilon ) - L =: L \tilde{a}_x(r,\epsilon )$ in the last equation. In addition to the discount rate, the actuarial present values $a_x(\rho ,\epsilon )$ and $\tilde{a}_x(r,\epsilon )$ differ in the survival curve used. Assuming ${}_t \tilde{p}_x > {}_t p_x$, we obtain the following special cases:

• $\rho \ge r$: In this case,

  $$\begin{aligned} a_x(\rho ,\epsilon )^{-\frac{1}{\gamma }}&= \left( \sum _{k=0}^{\infty } e^{-\rho k} {}_k p_x \, m_{\epsilon }(-\ln {}_k p_x) \right) ^{-\frac{1}{\gamma }}\\&> \left( \sum _{k=0}^{\infty } e^{-rk} {}_k \tilde{p}_x \, m_{\epsilon }(-\ln {}_k \tilde{p}_x) \right) ^{-\frac{1}{\gamma }} = \tilde{a}_x(r,\epsilon )^{-\frac{1}{\gamma }} \end{aligned}$$

  because $e^{-\rho k} {}_k p_x \, m_{\epsilon }(-\ln {}_k p_x) < e^{-rk} {}_k \tilde{p}_x \, m_{\epsilon }(-\ln {}_k \tilde{p}_x)$ for all k, and thus, $\phi ^* >0$. Due to the differences in the survival curve and the discount rate, the annuity is overpriced from the retiree’s perspective and, therefore, some fraction of the initial wealth is immediately consumed.

• $\rho < r$: In this case, we have $e^{-\rho k} > e^{-rk}$ and ${}_k p_x \, m_{\epsilon }(-\ln {}_k p_x) < {}_k \tilde{p}_x \, m_{\epsilon }(-\ln {}_k \tilde{p}_x)$. Hence, we cannot draw general conclusions on the relation between $a_x(\rho ,\epsilon )^{-\frac{1}{\gamma }}$ and $\tilde{a}_x(r,\epsilon )^{-\frac{1}{\gamma }}$.

In Table 14, we now compare the DC scheme to the TP under the assumption that $\rho \ne r$. Similar to Sect. 3, we choose $\rho = 0.03$.

Table 14 Wealth equivalent along with the optimal fraction of initial wealth invested in the TP and the DC scheme depending on the relative risk aversion parameter

From Table 14, we can basically draw the same conclusions as from Table 5, where we have considered the case without longevity shock. The main difference is that the TP loses attractiveness if the more risky investment strategy is used, similarly to Table 13. Nevertheless, the TP outperforms the DC scheme for both investment strategies under consideration.

4.2.3 DC scheme with variable annuities

We assume that the DC plan pays out a life-long annuity designed in a similar way as in Sect. 3.3. The results are provided in Tables 15 and 16.

Table 15 Wealth equivalent along with the optimal fraction of initial wealth invested in the TP compared to the DC scheme depending on the relative risk aversion parameter

Table 16 Wealth equivalent along with the optimal fraction of initial wealth invested in the TP compared to the DC scheme depending on the relative risk aversion parameter

From Tables 15 and 16, we can see that the DC scheme again generates a higher expected lifetime utility than the TP for both investment strategies. Compared to Tables 6 and 7, the wealth equivalents have increases substantially, implying that the superiority of the DC scheme compared to the TP is even more pronounced in the presence of loadings. Note that the wealth equivalent is decreasing for both investment strategies, where the decrease starts after $\gamma =2$ for the investment strategy $\pi =0.2$. The reason for this is that, for a risk aversion of $\gamma =1/2$, the optimal fraction of wealth invested in the TP is 1 for $\pi =0.2$ but 0.725 for $\pi =0.6$, making the difference between the TP and DC scheme more pronounced in the second case than in the first case. However, the DC scheme has again a ruin probability of 1 and is therefore likely not to deliver a life-long retirement income to its beneficiaries, whereas the TP has a ruin probability of only 0.01 and 0.33 for $\pi =0.2$ and $\pi =0.6$, respectively (see Tables 11 and 12).

5 Conclusion

This paper analyzes the potential of the newly introduced German pension scheme TP, a pension plan which links the pension payments to the beneficiaries to the mortality experienced and the performance of the financial market. Each year, the pension payments are adjusted based on the funding ratio of the pension fund. We include two parameters in the design of the product: One which controls the surplus participation and another one which controls the loss participation. The two parameters are chosen in such a way that the initial value of the TP is equal to the initial wealth of the retiree. We consider occupational pension schemes like the TP as an additional source of retirement income to constant annuity payments resulting from the first and third pillar, compute the optimal fraction of initial wealth allocated to the TP, a DC or a DB scheme and then compare the resulting optimal levels of expected utility of these three pension schemes. This analysis is carried out in two different model setups: First, we consider an actuarially fair pricing framework disregarding systematic longevity risk, and, secondly, we include systematic longevity risk in the model and assume that risk loadings are charged from the retirees. Our numerical results show that a TP can outperform some DC and the DB scheme for all the risk aversions considered and suggest that the newly introduced TP is a beneficial supplementary retirement plan to constant annuities (obtained from the first and third pillar). However, the DC scheme with variable annuities outperforms the TP for all risk aversions under consideration. The disadvantage of this DC scheme is, on the other hand, that it defaults with certainty under reasonable parameter choices, whereas the TP can deliver a ruin probability which is close to zero.

Note that in this paper, we only analyze the benefits of a TP as an additional source of retirement income in addition to fixed income retirement plans from the first and third pillar. That is, when convincing employees to join a TP scheme, it should be emphasized that the TP is not able to provide a guaranteed retirement income and that additional retirement plans are needed if a hard minimum guaranteed income shall be achieved throughout the retirement phase.

A main assumption for the attractiveness of a TP is a well-performing market which is, in our numerical analysis, ensured by the choice of the market price of risk $\eta = \frac{\mu - r}{\sigma }$. These allow the TP more upside potential than traditional retirement plans which rely on the constant (and currently low) interest rate. In this sense, our results support the current trend that less capital should be invested in financial products which provide guarantees, as they are difficult to finance in the current low interest rate environment.

Another main assumption made in this paper is the homogeneous cohort of retirees, in particular the assumption that all the retirees have the same age x. In practice, there are retirees who have different ages and they might be pooled even though their ages are not identical. Therefore, an analysis with different cohorts allowing for different ages of the retirees would be a natural extension to our model setup.