Long-term insurance products and volatility under the Solvency II Framework

Abstract

Solvency II will become the new regulatory framework for insurance companies in Europe. It sets the capital requirements in function of the insurer’s risk exposure at a one-year time horizon. The objective of the paper is to quantify the cost of the volatility in the required capital induced by the Solvency II liability valuation methodology. First, we show that Solvency II will induce large variation in the required capital for illiquid long-term products with guarantees. The volatility of the required capital is larger for policies with a larger maturity. We then introduce a different liability valuation technique specifically for illiquid liabilities. The volatility of the required capital in this model is lower since it only depends on the default component of the credit spread of the backing assets. We prove that this model is market consistent. We conclude by estimating the cost of the option, which an insurer could buy to eliminate the extra induced capital volatility. Such option will generate the cash flow necessary to supply the extra required capital resulting from a change in illiquidity spread.

1 Introduction

The key difficulty in establishing a market consistent framework for the insurance business is the lack of a market where insurance liabilities are traded. While the market value of assets can readily be determined using a mark-to-market approach, for liabilities one has to rely on the mark-to-model approach. The difficulty thus lies in valuing liabilities that are not traded, with a market consistent model constructed in such a way that the (implicit) model assumptions do not contradict the characteristics of the insurance liability.

1.1 Illiquid long-term insurance products with guarantees

Long-term insurance products have long maturities which can reach 40 years or more for certain pension and annuity products. Historically, asset liability management and capital management of these products has centered around its long maturity. Insurers often invest the premiums in fixed income instruments in such a way that the fixed income cash flows replicate the liability cash flow runoff. This allows the insurer to honor the payout that it guaranteed to its policyholder. The risk carried by the insurer with this investing strategy is the risk of default of the fixed income instrument.

The Solvency II Directive [6], which will take effect on 1/1/2016, creates a risk-based regulatory framework for capital requirements and risk management of insurance undertakings and is built around the undertaking’s risk exposure at the 1 year time horizon. The Solvency II liability valuation model consists of discounting the liability cash flows at the risk-free rate to obtain its value. This valuation method implies that the liabilities are valued as risk-free (non-defaultable) bonds.

For long-term insurance products this liability valuation technique combined with the one-year time horizon led to several issues. Indeed, credit spread variations in the financial markets will affect the asset side of the balance sheet, but not the liability side. This results in a high volatility of the net asset value of the balance sheet. Moreover, this approach overestimates the volatility and the risk since it captures the entire credit spread risk, which includes more than the risk of default. Spread risk includes liquidity risk in addition to default risk [8]. Indeed, if the asset and liability cash flows are matched and the liability cash flow is sufficiently stable, then the insurance undertaking is not exposed to the illiquidity of the market since the insurer can wait for maturity of the instrument.

Two conditions have to be fulfilled for an insurer not to be exposed to liquidity risk. First, asset and liability cash flows have to be matched. Indeed, imagine that the cash flows are not matched as the insurance liability has to be paid out before the fixed income asset matures. In such case the asset will have to be sold before maturity to pay out the liability. Selling the asset will happen at the market price. The insurer is hence exposed to the risk that the market is illiquid at that time, resulting in a lower market value. If, on the other hand, the asset cash flow matches the liability cash flow then the insurer does not need to sell in the secondary market, but can wait for the instrument to mature.

The second condition which needs to be fulfilled for the insurer not to be exposed to liquidity risk, is that the cash flow of the insurance liability has to be sufficiently stable. Even when the insurance liability is cash flow matched, if the policyholder has the right to redeem the policy early, the insurer will have to sell the backing asset at market price which exposes the insurer again to the full credit spread risk. In practice, many long-term insurance product have stable cash flow runoffs. For example, a pension product where the policyholder receives a lump sum upon reaching a set retirement age. The policyholder cannot choose to reach that retirement age early. Moreover, there are legal and/or fiscal hurdles in many European countries to an early redemption of a pension product. If the policyholder is allowed to transfer the product from one insurer to another, a market value adjuster clause in the contract can specify that the client carries the market risk under such a transfer before maturity of the product. Annuities is another example of a product class which often has a stable runoff. Long-term insurance products with a stable cash flow are often referred to as illiquid liabilities.¹

In this paper we will consider a valuation technique that takes into account the illiquidity of the liability in a market consistent way. To that end, we will work with a mathematical toy example that stylizes the two key properties discussed above. We will assume a perfect cash flow matching and we will assume the product to have an entirely stable cash flow. The entirely stable cash flow implies that the policyholder has no option to redeem or trade the policy, as such the policy cannot be converted into cash before maturity. This toy example has first been introduces in [14] to study similar questions. Our analysis differs from [14] since we allow the illiquidity spread to be time-dependent, which will provide us with different conclusions.

1.2 The matching adjustment and volatility adjustment

To address the issues of volatility discussed in the previous section and the procyclicality this would entail, the Solvency II Draft Implementing Measures[5] from 31 October 2011 included a mechanism, the Matching Premium, designed to alleviate these issues. This mechanism modifies the standard Solvency II valuation method for liabilities which satisfy a set of precise conditions. The valuation method now allows for the discounting of the liability cash flow at the risk-free rate plus an excess spread. This excess spread is linked with the illiquidity component of the credit spread of the backing assets.

The conditions for an insurance product to qualify for application of the Matching Premium were in broad lines based on the two key conditions identified in the previous section. These qualification conditions are binary, either a product does qualify for the use of the Matching Premium or it does not. In practice, a very limited number of long-term products satisfies all required conditions. An extensive discussion between the industry and the European authorities ensued and alternative proposals were launched. The trilogue parties comprised of the European Parliament, the European Commission and the Council of the European Union agreed in July 2012 to an assessment of the different proposed solutions in the form of the Long-Term Guarantee Assessment (LTGA).²

In its final report on the LTGA [4], EIOPA expressed a preference for maintaining the more restrictive conditions on the Matching Adjustment.³ Shortly thereafter a new mechanism, the volatility adjuster, was proposed for products which cannot satisfy the Matching Adjustment conditions. While this new mechanism originally might have been inspired by the Matching Adjustment, it is merely an adjustment of the risk-free curve. There is no link with the type of liability nor with the backing asset. Whether a liability has a stable cash flow runoff or not, the mechanism applies in equal amount. The Volatility Adjuster can thus be seen as part of the definition of the risk-free curve under Solvency II.

1.3 A valuation model for illiquid long-term insurance products

To come to a better understanding of the valuation of illiquid insurance liabilities and its practical implementation, there are three topics that have to be analyzed. First, a market consistent valuation technique has to be derived which takes the long-term nature of the liability combined with its illiquidity into account. In [14] the Matching Adjustment valuation model is analyzed and it is proven that this model is not market consistent (see section 2.4 of [14]). The main aim of this paper is to propose a valuation model which is market consistent, while taking into account the specific features of illiquid long-term insurance products with guarantees.

Second, a key ingredient to be able to account for illiquidity, is measuring the illiquidity component in credit spreads. This paper does not address how to differentiate the real world default probability and the illiquidity spread. This is an interesting and complex issue dealt with in a rapidly growing body of literature (see [2, 10] or [8] for corporate debt and [7] for government bonds).

Third, as discussed earlier, two key conditions have to be satisfied for the insurer to be solely exposed to default risk. To apply the valuation technique in practice, one has to translate these key conditions into practical conditions that a product has to satisfy. The conditions for application of the Matching Adjustment in the Draft Implementing Measures [5] is one such translation. One could envision, instead of the binary conditions of the Draft Implementing Measures, where you either qualify to apply the Matching Adjustment or do not qualify, conditions which take the degree of illiquidity into account in a more gradual way.

As this paper aims to contribute to the first topic by working out a different valuation technique, we will argue that an illiquid policy is different from a risk-free non-defaultable bond and that this difference plays an essential role in the valuation. The difference between a risk-free bond and a long-term insurance product can be illustrated from the insurer’s perspective, as well as from the policyholder’s point of view.

First, imagine a potential policyholder planning to invest savings in either a highly rated bond or a pension product with equal payout and maturity. The pension product locks in the money until retirement without the possibility of early redemption, while the bond can be sold before maturity. If both options would have the same value, there would be no reason to buy the pension product. Indeed, the bond has the advantage that it can traded before maturity. The value of the pension product should thus deviate from the value of the bond.

Now consider an insurer planning to buy another insurance company. The insurer is interested in two insurance companies as takeover targets. Both of these companies have underwritten similar policies for a very similar population of policyholders. There is one major difference. Policyholders of the first undertaking are allowed to redeem their policy, while the policyholders of the second undertaking cannot redeem. In this case, we argue that the price for takeover (irrespective of possible capital requirements) of the first undertaking should be lower, accounting for the risk premium that an unexpected amount of policyholders might execute the redemption option in the policy. Indeed, a policy with redemption option is more similar to a bond, where liquidity is available to the investor via the secondary market. The absence of this embedded option, the illiquidity, lowers the value of the policy.

A insurance liability model should be able to account for the price difference illustrated in the previous paragraphs. Models based on the efficient market hypothesis presume that all priced instruments are readily tradable in a deep and liquid market. However, by design, our illiquid insurance contract is non-tradable. As such, we argue that a model that applies the efficient market hypothesis alone is not able to price such instrument.

1.4 Organization of the paper

The paper is organized as follows. Section 2 reviews the balance sheet model developed by MV Wüthrich [14]. We extend the model to include a time-variable spread and insurance products with a longer maturity.

In Sect. 3, we show that the market consistent solvency analysis as presented in Sect. 2.3 of [14] leads to volatility in the consumption stream. Insurers will be exposed to the daily variation of the spread risk of the bond market. This effect is more pronounced for longer-term insurance products.

In Sect. 4, we derive a model which uses a different definition for the market value of an insurance liability. We show that this model still satisfies the no arbitrage condition. However, crucially, the consumption stream of this model is less volatile.

Section 5 focuses on the downside risk of having a negative consumption stream. We analyze the option that an insurance company could buy to insure themselves against the downside risk. We conclude by estimating the behavior of the option price for insurance products with a longer maturities.

2 Market-consistent solvency analysis

In this section we set up the theoretical framework which we will use throughout the paper. We start from the example presented in [14]. We proceed to extend this model to include a time-dependent illiquidity spread. This extension will allow us to investigate the impact of a variable credit spread. We then extend the model to a multi-period model to study the impact of longer-term maturities.

We note that throughout this paper, we use the deflators formalism with (real world) measure $\mathbb {E}[\ldots ]$. One could translate the assumptions and calculations to the risk neutral measure $\tilde{\mathbb {E}}[\ldots ]$, since the deflator formalism is fully equivalent to the risk neutral formalism. However, for the derivations of the volatility and probability of negative consumption in the sections below, one has to use the real world measure since we are interested in real world volatilities and probabilities.

2.1 Insurance balance sheet model

In this section we review in detail the example presented in [14].

2.1.1 State price deflator and pricing of zero-coupon bonds

The example is constructed in a filtered probability space $(\Omega , \mathcal {F}, \mathbb {P}, \mathbb {F})$ with finite time horizon $n \ge 2$ and discrete time filtration $\mathbb {F} = (\mathcal {F})_{t=0,\ldots ,n}$ with $\mathcal {F}_0 = \{\emptyset , \Omega \}$ We construct the state price deflator $\varvec{\varphi } = (\varphi _t)_{t=0,\ldots ,n}$ using two strictly positive and $\mathbb {F}$-adapted stochastic processes $\varvec{\psi } = (\psi _t)_{t=0,\ldots ,n}$ and $\varvec{\chi } = (\chi _t)_{t=0,\ldots ,n}$. We take $\psi _0 = 1$ and assume that $\chi _t$ is independent from $\sigma \{ \mathcal {F}_{t-1}, \varvec{\psi }\}$ with $\mathbb {E}[\chi _t] = 1$ for all $t$:

$$\begin{aligned} \varphi _t = \psi _t \prod ^{t}_{u=0} \chi _u \, . \end{aligned}$$

(1)

The decoupling property of the state price deflator $\varvec{\varphi }$ into a “global market state price deflator”, $\varvec{\psi }$, and “idiosyncratic distortions”, $\varvec{\chi }$, will be crucial.

The price of a default-free zero-coupon bond is given by

$$\begin{aligned} P (t,m) = \frac{1}{\varphi _t} \, \mathbb {E}[ \varphi _m | \mathcal {F}_{t} ] = \frac{1}{\psi _t} \, \mathbb {E}[ \psi _m | \mathcal {F}_{t} ] \, . \end{aligned}$$

(2)

The proof of the second equation is given in [14] and makes use of the independence of $\chi _t$ from $\sigma \{ \mathcal {F}_{t-1}, \varvec{\psi }\}$ and the condition $\mathbb {E}[\chi _t] = 1$.

To compute the price of defaultable zero-coupon bonds we introduce a default process $\varvec{\Gamma } = (\Gamma _t)_{t=0,\ldots ,n}$, where $\varvec{\Gamma }$ is a non-increasing process with $\Gamma _0 = 1$ and $\Gamma _t = 0$ if the bond has defaulted in $[0,t]$ otherwise $\Gamma _t = 1$. We assume the process $\varvec{\Gamma }$ to be $\mathbb {F}$-adapted and independent of $\varvec{\psi }$. In addition, we assume for all $t > 0$

$$\begin{aligned} \mathbb {E}[\Gamma _t | \mathcal {F}_{t-1}, \varvec{\psi }]&= (1-p)\, \Gamma _{t-1} \end{aligned}$$

(3)

$$\begin{aligned} \mathbb {E}[\chi _t \, \Gamma _t | \mathcal {F}_{t-1}, \varvec{\psi }]&= (1-p) \, (1 - s) \, \Gamma _{t-1} \end{aligned}$$

(4)

for fixed $p \in (0,1)$ parameterizing the real world probability of default and $s \in [0,1)$ which represents the illiquidity spread. We can now compute the price of a defaultable zero-coupon bond:

$$\begin{aligned} B(t,m) = \frac{1}{\varphi _t} \, \mathbb {E}[ \varphi _m \Gamma _m | \mathcal {F}_{t} ] = P (t,m) \, (1-p)^{m-t} \, (1-s)^{m-t} \, \Gamma _t \, . \end{aligned}$$

(5)

The proof of the second equation is given in [14]. The price of a defaultable zero-coupon bond conditional on the fact that the bond survived at least up to time $k$ (with $k \le t \le m$) is given by

$$\begin{aligned} B^{(k)}(t,m) = \frac{1}{\varphi _t} \, \mathbb {E}[ \varphi _m \Gamma ^{(k)}_m | \mathcal {F}_{t} ] = P (t,m) \, (1-p)^{m-t} \, (1-s)^{m-t} \, \Gamma ^{(k)}_t \, . \end{aligned}$$

(6)

with $\Gamma ^{(k)}_t$ the default process conditional on the fact the $\Gamma _k = 1$.

2.1.2 Solvency analysis of a simple insurance liability

Following [14], we now study the balance sheet of an insurance company. We consider an insurance liability given by a default-free cash flow of size $M = 1$ at time $m=2$. Strictly speaking this is not an insurance contract since we consider a completely predictable liability cash flow. As discussed in Sect.  1.1 of the introduction, many long-term insurance products have stable cash flows and are, as such, close to this stylized mathematical toy example. The time series of the market-consistent value of the liability of the balance sheet is given by

$$\begin{aligned} L_0= P (0,2), \quad L_1= P (1,2), \quad L_2= P (2,2) = 1 \;\;\; \mathrm {and} \;\;\; L_{t \ge 3} = 0 \, . \end{aligned}$$

(7)

We now briefly review the analysis of [14].

Time t = 0 The value of the insurance contract is $L_0 = P (0,2)$. The policyholder is thus charged a (single pure risk) premium of $\pi = L_0$. We assume the insurer chooses to invest the premium income in a defaultable zero-coupon bond of the same maturity as the liability:

$$\begin{aligned} A_0 = \pi = (1 - p)^{-2} \, (1 - s)^{-2} \, B(0, 2) \end{aligned}$$

(8)

For this operation, the insurer does not need extra available capital, nor does it generate available capital. The capital consumption is

$$\begin{aligned} C_0 = A_0 - \pi = 0 \, . \end{aligned}$$

(9)

Time t = 1 The asset and liability values have evolved to:

$$\begin{aligned} A_0&\rightarrow A^{-}_1 = (1-p)^{-1} \, (1-s)^{-1} \, \Gamma _1 \, P (1,2) \end{aligned}$$

(10)

$$\begin{aligned} L_0&\rightarrow L_1 \; = P (1,2) \end{aligned}$$

(11)

To reinstate $A_1 = L_1 = P (1,2)$, the insurer will either need to inject capital in case the asset defaulted or the asset will have created capital which becomes available. As in [14], we assume that the injection of new capital is done through new (defaultable) bonds that have not defaulted yet. The capital consumption is:

$$\begin{aligned} C_1 = A^{-}_1 - A_1 = \left[ (1-p)^{-1} \, (1-s)^{-1} \, \Gamma _1 - 1\right] \, P (1,2) \, . \end{aligned}$$

(12)

Time t = 2 Assets and liabilities are now:

$$\begin{aligned} A_1&\rightarrow A^{-}_2 = (1-p)^{-1} \, (1-s)^{-1} \, \Gamma ^{(1)}_2 \, P (2,2)\end{aligned}$$

(13)

$$\begin{aligned} L_1\rightarrow L_2 \; = 1 \end{aligned}$$

(14)

To pay out the policyholder $A_2 = L_2 = 1$, the insurer faces the following capital consumption:

$$\begin{aligned} C_2 = A^{-}_2 - A_2 = \left[ (1-p)^{-1} \, (1-s)^{-1} \, \Gamma ^{(1)}_2 - 1\right] \end{aligned}$$

(15)

The consumption stream is thus given by

$$\begin{aligned} C_0&= 0 \end{aligned}$$

(16)

$$\begin{aligned} C_1&= \left[ (1-p)^{-1} \, (1-s)^{-1} \, \Gamma _1 - 1\right] \, P (1,2) \end{aligned}$$

(17)

$$\begin{aligned} C_2&= \left[ (1-p)^{-1} \, (1-s)^{-1} \, \Gamma ^{(1)}_2 - 1\right] \end{aligned}$$

(18)

One can show that the value $Q_0[\varvec{C}]$ of the consumption stream at time 0 is given by

$$\begin{aligned} Q_0[\varvec{C}] = \sum ^{2}_{u=0} \mathbb {E}[ \varphi _u \, C_u] = 0 \end{aligned}$$

(19)

which implies that there exists no arbitrage strategy for this insurance product since the pure risk premium was correctly chosen.

2.2 Extension of the model with a time-dependent spread

2.2.1 Deflator and zero-coupon bonds with time-dependent spread

We will extend the example introduced in Sect. (2.1.2) with a time-dependent correlation between $\varvec{\chi }$ and $\varvec{\Gamma }$. We therefore replace the time-invariant assumptions (3)–(4) with the conditions that for all $t > 0$,

$$\begin{aligned} \mathbb {E}[ \Gamma _t | \mathcal {F}_{t-1}, \varvec{\psi }]&= (1-p) \, \Gamma _{t-1} \end{aligned}$$

(20)

$$\begin{aligned} \mathbb {E}[ \chi _t \, \Gamma _t | \mathcal {F}_{t-1}, \varvec{\psi }]&= (1-p) \, (1-\tilde{s}_{t-1}) \, \Gamma _{t-1} \end{aligned}$$

(21)

$$\begin{aligned} \mathbb {E}[(1-\tilde{s}_{t})^{k} \chi _t \, \Gamma _t | \mathcal {F}_{t-1}, \varvec{\psi }]&= (1-p) \, (1-\tilde{s}_{t-1})^{k+1} \, \Gamma _{t-1}, \forall k: 0 \le k \le n-t \end{aligned}$$

(22)

where the illiquidity spread $\tilde{\varvec{s}} = (\tilde{s}_t)_{t=0,\ldots ,n}$ with $\tilde{s}_t \in [0,1), \forall t$ is now a $\mathbb {F}$-adapted stochastic process independent of $\varvec{\psi }$. Note that since $\tilde{s}_t$ is $\mathcal {F}_{t}$-measurable, but not $\mathcal {F}_{t-1}$-measurable, we cannot take the term $(1-\tilde{s}_{t})^{k}$ outside the expectation $\mathbb {E}[\ldots ]$ in (22). Given these assumptions, defaultable bonds have a price at time $t$, with $t \le m$, given by

$$\begin{aligned} B(t,m)&= \frac{1}{\varphi _t} \, \mathbb {E}[ \varphi _m \, \Gamma _m | \mathcal {F}_{t} ] = \frac{1}{\psi _t} \, \mathbb {E}\left[ \psi _m \prod ^{m-1}_{u=t+1} \chi _u \, \mathbb {E}[\chi _m \, \Gamma _m | \mathcal {F}_{m-1}, \varvec{\psi } ] \bigg | \mathcal {F}_{t} \right] \nonumber \\&= (1-p) \frac{1}{\psi _t} \, \mathbb {E}\left[ \psi _m \prod ^{m-2}_{u=t+1} \chi _u \, \mathbb {E}[(1-\tilde{s}_{m-1}) \, \chi _{m-1} \, \Gamma _{m-1}| \mathcal {F}_{m-2}, \varvec{\psi } ] \bigg | \mathcal {F}_{t} \right] \nonumber \\&= (1-p)^2 \frac{1}{\psi _t} \, \mathbb {E}\left[ \psi _m \prod ^{m-3}_{u=t+1} \chi _u \, \chi _{m-2} \, (1-\tilde{s}_{m-2})^2 \, \Gamma _{m-2} \bigg | \mathcal {F}_{t} \right] \nonumber \\&= \ldots = (1-p)^{m-t} \, (1-\,\tilde{s}_{t})^{m-t} \, \Gamma _t \, P (t,m) \, . \end{aligned}$$

(23)

We see that with the new assumptions (20)–(22), our asset universe now includes a set of bonds with different maturities $0 \le m \le n$, with a constant default probability per time step $p$, and with a variable illiquidity spread $\tilde{s}_t$, which under our assumptions is independent from the maturity $m$ of the bond. For example, taking $n = 2$, we have a set of 3 bonds with different maturities with the following market values $B(t,m)$ (where $q = 1 - p$):

	$t = 0$	$t = 1$	$t = 2$
$m = 0$	$1$
$m = 1$	$q \, (1-\,\tilde{s}_{0}) \, P (0,1)$	$\Gamma _1 \, P (1,1)$
$m = 2$	$q^{2} \, (1-\,\tilde{s}_{0})^{2} \, P (0,2)$	$q \, (1-\,\tilde{s}_{1}) \, \Gamma _1 \, P (1,2)$	$\Gamma _2 \,P (2,2)$

If one would add another set of defaultable bonds to our asset universe, we would introduce another default process, $\varvec{\Gamma '}$, that characterizes these bonds. Using this new default process, one can compute the associated default probability $p'$ and illiquidity spread $\tilde{s}'_t$:

$$\begin{aligned} \mathbb {E}[\Gamma '_t | \mathcal {F}_{t-1}, \varvec{\psi }]&= (1-p')\, \Gamma '_{t-1}\end{aligned}$$

(24)

$$\begin{aligned} \mathbb {E}[\chi _t \, \Gamma '_t | \mathcal {F}_{t-1}, \varvec{\psi }]&= (1-p') \, (1-\tilde{s}'_{t-1}) \, \Gamma '_{t-1} \end{aligned}$$

(25)

Note that it is, for example, possible to have two sets of bonds with the same default probability $p' = p$, but another spread process $\tilde{s}'_t \ne \tilde{s}_t$.

For the rest of the paper, we will redefine the spread process as

$$\begin{aligned} 1-\,\tilde{s}_{t} = e^{-s_{t}} \in (0,1] \, , \end{aligned}$$

(26)

with $s_{t} \in [0,\infty )$. The assumptions (20)–(22) are thus rewritten as

$$\begin{aligned} \mathbb {E}[ \Gamma _t | \mathcal {F}_{t-1}, \varvec{\psi }]&= (1-p) \, \Gamma _{t-1} \end{aligned}$$

(27)

$$\begin{aligned} \mathbb {E}[e^{-k\,s_t} \chi _t \, \Gamma _t | \mathcal {F}_{t-1}, \varvec{\psi }]&= (1-p) \, e^{-(k+1)\,s_{t-1}} \, \Gamma _{t-1}, \quad \forall k: 0 \le k \le n-t \end{aligned}$$

(28)

and we have

$$\begin{aligned} B(t,m) = (1-p)^{m-t} \, e^{-(m-t)\,s_{t}} \, \Gamma _t \, P (t,m) \, . \end{aligned}$$

(29)

Note that this paper does not address the question on how to measure the real world default probability $p$ and the illiquidity spread $s_t$.

2.2.2 Solvency analysis with varying spread

We now revisit the insurance balance sheet from Sect.2.1.2 and work out the consumption stream.

Time t = 0 The insurance company invests the premium $\pi = L_0 = P (0,2)$ in a defaultable zero-coupon bond with the same maturity.

$$\begin{aligned} A_0 = \pi = (1 - p)^{-2} \, e^{2s_0} \, B(0, 2) \end{aligned}$$

(30)

The consumption is

$$\begin{aligned} C_0 = A_0 - \pi = 0 \, . \end{aligned}$$

(31)

Time t = 1 We now have:

$$\begin{aligned} A_0&\rightarrow A^{-}_1 = (1 - p)^{-2} \, e^{2s_0} \, B(1, 2) = (1 - p)^{-1} \, e^{2s_0-s_1} \, \Gamma _1 \, P (1, 2) \end{aligned}$$

(32)

$$\begin{aligned} L_0&\rightarrow L_1 = P (1,2) \end{aligned}$$

(33)

and

$$\begin{aligned} C_1 = A^{-}_1 - A_1 = \left[ (1-p)^{-1} \, e^{2s_0-s_1} \, \Gamma _1 - 1\right] \, P (1,2) \end{aligned}$$

(34)

such that $A_1 = L_1$. Notice that if the bond has defaulted ($\Gamma _1 = 0$) then $C_1 < 0$. This is similar to the constant spread model. However, unlike the constant spread model, we can have $C_1 < 0$ without default ($\Gamma _1 = 1$):

$$\begin{aligned} e^{-s_1} < (1-p) \, e^{-2s_0} \, . \end{aligned}$$

(35)

Time t = 2 We get

$$\begin{aligned} A_1&\rightarrow A^{-}_2 = (1 - p)^{-1} \, e^{s_1} \, B^{(1)}(2, 2) = (1-p)^{-1} \, e^{s_1} \, \Gamma ^{(1)}_2 \, P (2,2)\end{aligned}$$

(36)

$$\begin{aligned} L_1&\rightarrow L_2 = 1 \end{aligned}$$

(37)

with consumption

$$\begin{aligned} C_2 = A^{-}_2 - A_2 = \left[ (1-p)^{-1} \, e^{s_1} \, \Gamma ^{(1)}_2 - 1\right] \, . \end{aligned}$$

(38)

The total consumption stream is:

$$\begin{aligned} C_0&= 0 \end{aligned}$$

(39)

$$\begin{aligned} C_1&= \left[ (1-p)^{-1} \, e^{2s_0-s_1} \, \Gamma _1 - 1\right] \, P (1,2) \end{aligned}$$

(40)

$$\begin{aligned} C_2&= \left[ (1-p)^{-1} \, e^{s_1} \, \Gamma ^{(1)}_2 - 1\right] \end{aligned}$$

(41)

and the no arbitrage condition, $Q_0[\varvec{C}] = 0$, is still satisfied.

2.3 Extension of the model to long-term insurance products

One can easily extend the derivation of Sect. 2.2.2 to a larger maturity $m$. The consumption stream is given by

$$\begin{aligned} C_0&= 0 \end{aligned}$$

(42)

$$\begin{aligned} C_t&= \left[ (1-p)^{-1}\,e^{- (m-t)\,(s_{t} - s_{t-1})}\,e^{s_{t-1}}\,\Gamma ^{(t-1)}_t - 1\right] \, P (t,m) \end{aligned}$$

(43)

with $1 \le t \le m$. For $t > 0$, we can compute

$$\begin{aligned} & \mathbb {E}[ \varphi _t \, C_t] \nonumber \\&\quad = \mathbb {E}\left[ \psi _t \chi _0 \ldots \chi _{t-1} \chi _t (1 - p)^{-1} e^{- (m-t)s_{t}} e^{(m-t+1)s_{t-1}} \Gamma ^{(t-1)}_t P(t,m) - \varphi _t P(t,m) \right] \nonumber \\ &\quad= \mathbb {E}\left[ \psi _t \chi _0 \ldots \chi _{t-1} (1 - p)^{-1} e^{(m-t+1)s_{t-1}} P(t,m) \mathbb {E}\big [\chi _t e^{- (m-t)s_{t}} \Gamma ^{(t-1)}_t \big | \mathcal {F}_{t-1}, \varvec{\psi } \big ] \right] \nonumber \\& \quad \quad- \mathbb {E}\Big [ \varphi _t P(t,m) \Big ] \nonumber \\ &\quad= 0 \end{aligned}$$

(44)

and thus the no arbitrage condition, $Q_0[\varvec{C}] = 0$, holds.

3 Analysis of the consumption stream volatility

As we noticed in Sect. 2.2.2, there are two possible reasons for a negative consumption $C_t$. If the assets defaults, then $C_t < 0$. If the asset does not default, then having

$$\begin{aligned} e^{-(m-t)\,(s_{t} - s_{t-1})} < (1-p) e^{-s_{t-1}} \end{aligned}$$

(45)

also leads to a negative consumption. Given that $m-t$ can easily be of the order of $30$ (or higher) for long-term insurance products, this condition can be satisfied for relatively smaller spread increases.

Let us estimate the volatility of the consumption $C_1$ at time 1. We remind ourselves that we compute the volatility using the real world measure $\mathbb {E}[\ldots ]$, since we are interested in real world volatilities. We compute

$$\begin{aligned} \mathbb {E}[C_1]&= e^{s_0} \, \mathbb {E}\big [ e^{-(m-1)\,(s_1-s_0)} \big ] \, \mathbb {E}\big [ P (1,m) \big ] - \mathbb {E}\big [ P (1,m) \big ] \nonumber \\&\\&\quad+ \, (1-p)^{-1} \, e^{s_0} \, \mathrm {Cov}\big [e^{-(m-1)\,(s_1-s_0)}, \Gamma _1 \big ] \, \mathbb {E}\big [ P (1,m) \big ] \, , \end{aligned}$$

(46)

$$\begin{aligned} \mathbb {E}[C^2_1]&= (1-p)^{-1} \, e^{2s_0} \, \mathbb {E}\big [e^{-2(m-1)\,(s_1-s_0)} \big ] \, \mathbb {E}\big [ P^2(1,m) \big ] + \mathbb {E}\big [ P^2(1,m) \big ] \nonumber \\&\quad- \, 2\, e^{s_0} \, \mathbb {E}\big [ e^{-(m-1)\,(s_1-s_0)} \big ] \, \mathbb {E}\big [ P^2(1,m) \big ] \nonumber \\&\quad+ \, (1-p)^{-2} \, e^{2s_0} \, \mathrm {Cov}\big [e^{-2(m-1)\,(s_1-s_0)}, \Gamma _1 \big ] \, \mathbb {E}\big [ P^2(1,m) \big ] \nonumber \\&\quad- \, 2\, (1-p)^{-1} \, e^{s_0} \, \mathrm {Cov}\big [ e^{-(m-1)\,(s_1-s_0)}, \Gamma _1 \big ] \, \mathbb {E}\big [ P^2(1,m) \big ] \, . \end{aligned}$$

(47)

We find that

$$\begin{aligned}\mathbb {V}\mathrm {ar}[C_1] &= \ldots \nonumber \\&= e^{2s_0} \frac{\mathbb {E}^2[P (1,m)]}{\mathbb {E}[\Gamma ^2_1]} \mathbb {V}\mathrm {ar}\big [e^{-(m-1)\,(s_1-s_0)} \big ] \nonumber \\&\quad+ \, e^{2s_0} \frac{\mathbb {E}^2[P (1,m)]}{\mathbb {E}^2[\Gamma _1]} \mathbb {E}^2\big [ e^{-(m-1)\,(s_1-s_0)} \big ] \mathbb {V}\mathrm {ar}[\Gamma _1] \nonumber \\&\quad + \, \bigg ( 1 - 2\, e^{s_0} \, \mathbb {E}\big [ e^{-(m-1)\,(s_1-s_0)}\big ] + \frac{e^{2s_0}}{\mathbb {E}[\Gamma ^2_1]} \mathbb {E}\big [ e^{-2(m-1)\,(s_1-s_0)} \big ] \bigg ) \,\end{aligned}$$

(48)

The first term is due to the volatility in the spread, the second term due to the volatility in the default process and the third term is linked with the volatility of the term structure which determines the price of non-defaultable zero-coupon bonds. The last term, $A$, is the cross term with all the covariance terms:

$$\begin{aligned} A&= e^{2s_0} \frac{\mathbb {E}[P^2(1,m)]}{\mathbb {E}^2[\Gamma _1]} \, \mathrm {Cov}\big [ e^{-2(m-1)\,(s_1-s_0)}, \Gamma _1 \big ] \nonumber \\&\quad- \, e^{2s_0} \frac{\mathbb {E}^2[P(1,m)]}{\mathbb {E}^2[\Gamma _1]} \, \mathrm {Cov}^2\big [ e^{-(m-1)\,(s_1-s_0)}, \Gamma _1 \big ] \nonumber \\&\quad- \, 2 \, e^{2s_0} \frac{\mathbb {E}^2[P(1,m)]}{\mathbb {E}[\Gamma ^2_1]} \mathbb {E}\big [ e^{-(m-1)\,(s_1-s_0)} \big ] \, \mathrm {Cov}\big [ e^{-(m-1)\,(s_1-s_0)}, \Gamma _1 \big ] \nonumber \\&\quad- \, 2 \, e^{s_0} \frac{1}{\mathbb {E}[\Gamma ^2_1]} \, \mathrm {Cov}\big [ e^{-(m-1)\,(s_1-s_0)}, \Gamma _1 \big ] \, \mathbb {V}\mathrm {ar}\big [ P(1,m) \big ] \, . \end{aligned}$$

(49)

If we consider a bond with maturity $m$ and approximate the associated spread process $(s_1-s_0)$ with a normal distribution $\mathcal {N}\big (\mu = 0; \sigma (m)\big )$ where we parametrize $\sigma (m)$ with an empirical formula which exhibits a decaying volatility with maturity ($m \gg 1$),

$$\begin{aligned} \sigma ^2(m) = \sigma ^2_0 + \sigma ^2_1 \frac{1}{(m-1)^2} \, , \end{aligned}$$

(50)

then we obtain:

$$\begin{aligned} \mathbb {V}\mathrm {ar}\Big [e^{-(m-1)\,(s_1-s_0)} \Big ]&= \Big (e^{(m-1)^2\, \sigma _0^2 + \sigma _1^2} - 1 \Big ) e^{(m-1)^2\, \sigma _0^2 + \sigma _1^2} \end{aligned}$$

(51)

$$\begin{aligned} \mathbb {E}\Big [e^{-(m-1)\,(s_1-s_0)} \Big ]&= e^{\frac{1}{2}(m-1)^2\, \sigma _0^2 + \frac{1}{2} \sigma _1^2} \, . \end{aligned}$$

(52)

We can see in formula (48) that the illiquidity spread term dominates the volatility terms coming from the default process and from the term structure for large $m$. The first term of (49) has the dominant $m$-dependence among the cross terms. Its $m$-dependence is equal to that of the illiquidity spread term. We conclude that the volatility of the consumption stream, $\mathbb {V}\mathrm {ar}[C_1]$, increases exponentially with the maturity of the insurance product. Moreover, this rapid increase is entirely due to time-dependent illiquidity spread. Indeed, if we assume a constant illiquidity spread $s$, then we see that the first term in (48) and all cross terms disappear. The $m$-dependence of the volatility of the consumption stream then becomes implicit through the term structure $P(1,m)$.

4 Impact of the definition of the market value of non-tradable liabilities on the capital flow volatility

4.1 Reduced time grid

Let us now reconsider the example from Sect. 2.2.2. We will alter the time grid by leaving out the odd times. The consumption stream is now given by

$$\begin{aligned} \widetilde{C}'_0&= 0 \end{aligned}$$

(53)

$$\begin{aligned} \widetilde{C}'_2&= \left[ (1-p)^{-2} \, e^{2s_0} \, \Gamma _2 - 1\right] \end{aligned}$$

(54)

In this example there still is no over-consumption of capital which would violate market consistency and the no arbitrage condition holds:

$$\begin{aligned} Q_0[\widetilde{\varvec{C}}'] = \sum ^{1}_{u=0} \mathbb {E}[ \varphi _{2u} \, \widetilde{C}'_{2u}] = 0 \, . \end{aligned}$$

(55)

It is crucial to note that the policyholder does not have any arbitrage opportunity either, given the specific characteristics of the policy which is non-redeemable and non-tradable. The consumption stream only depends on the default in this case, not on spread movements. Indeed, $\widetilde{C}'_2 < 0$ implies that $\Gamma _2 = 0$. The volatility of the consumption stream is smaller compared to the volatility of the example from Sect. 2.2.2.

We could extend this example again to larger maturities $m$. This would lead us to the same conclusion. Indeed, since we only have consumption streams on even times, we will find that the volatility of this consumption stream is lower than a situation with a consumption stream every time step as in Sect. 2.3. The spread term in the volatility [see equation (48)] will be less dominant over the volatility term from the default process. One could think of this reduced time grid example as an example of Solvency II, but with a 2 year time horizon instead of a one-year horizon.

There is another equivalent point of view to interpret this reduced time grid example. Recall that given the absence of insurance contract trading, liabilities have to be valued using a mark-to-model approach respecting market consistency. Leaving out the odd time step in the above example is equivalent to imposing $\widetilde{C}'_1 = 0$, or defining the market value of the liability in the model at time 1 to be equal to $L_1 = A^-_1 = A_1$.

We also note that the policyholder in the reduced time grid example receives exactly the same payout as in the example of Sect. 2.2.2. The difference between both examples is the definition of the market value of the liability.

4.2 Reduced consumption stream

The reduced time grid example is merely a theoretical example, since it contains a serious flaw from a practical point of view. If the bond defaults at time $1$ ($\Gamma _1 = 0$ and thus $A^-_1 = A_1 = 0$), no capital is injected at $t = 1$. The policyholder relies entirely on the consumption stream at $t = 2$ to back the liability. In this section, we will develop a market consistent model with a reduced consumption stream at $t = 1$ which is always $\widetilde{C}_1 = 0$ unless a default occurs.

Time t = 0 Just as in the previous examples, the insurance company invests the premium $\pi = L_0 = P(0,2)$ in a defaultable zero-coupon bond with the same maturity.

$$\begin{aligned} A_0 = \pi = (1 - p)^{-2} \, e^{2s_0} \, B(0, 2) \end{aligned}$$

(56)

The consumption is

$$\begin{aligned} \widetilde{C}_0 = A_0 - \pi = 0 \, . \end{aligned}$$

(57)

Time t = 1 The value of the bond has evolved to:

$$\begin{aligned} A_0&\rightarrow A^{-}_1 = (1 - p)^{-2} \, e^{2s_0} \, B(1, 2) = (1 - p)^{-1} \, e^{2s_0-s_1} \, \Gamma _1 \, P(1, 2) \, . \end{aligned}$$

(58)

We now impose a consumption stream that only injects cash if a default occurred:

$$\begin{aligned} \widetilde{C}_1 = A^-_1 - A_1 = - (1 - \Gamma _1) P(1,2) \, . \end{aligned}$$

(59)

We thus, implicitly, defined the market value of the liability as

$$\begin{aligned} L_1 = A_1&= \left[ (1 - p)^{-1} \, e^{2s_0-s_1} \, \Gamma _1 - \Gamma _1 + 1\right] \, B^{(1)}(1,2) \, (1-p)^{-1} \, e^{s_1} \, . \end{aligned}$$

(60)

On the other hand, when a default happens we inject capital through the consumption stream [see Eq. (59)], and restore $L_1 = A_1 = P(1,2)$.

Time t = 2 We get

$$\begin{aligned} A_1 \rightarrow A^{-}_2&= (1 - p)^{-2} \, e^{2s_0} \, \Gamma _2 + (1-p)^{-1} \, e^{s_1} \, (1 - \Gamma _1) \, \Gamma ^{(1)}_2 \end{aligned}$$

(61)

where we used that $\Gamma _1 \Gamma ^{(1)}_2 = \Gamma _2$. The consumption is thus:

$$\begin{aligned} \widetilde{C}_2 = A^{-}_2 - A_2 = (1 - p)^{-2} \, e^{2s_0} \, \Gamma _2 + (1-p)^{-1} \, e^{s_1} \, (1 - \Gamma _1) \, \Gamma ^{(1)}_2 - 1 \, , \end{aligned}$$

(62)

with $A_2 = L_2 = 1$.

The total consumption stream is:

$$\begin{aligned} \widetilde{C}_0&= 0 \end{aligned}$$

(63)

$$\begin{aligned} \widetilde{C}_1&= - (1 - \Gamma _1) P(1,2) \end{aligned}$$

(64)

$$\begin{aligned} \widetilde{C}_2&= (1 - p)^{-2} \, e^{2s_0} \, \Gamma _2 + (1-p)^{-1} \, e^{s_1} \, (1 - \Gamma _1) \, \Gamma ^{(1)}_2 - 1 \end{aligned}$$

(65)

We now confirm that this model is market consistent by checking that the no arbitrage condition is still satisfied:

$$\begin{aligned} Q_0[\widetilde{\varvec{C}}]&= \mathbb {E}[\varphi _1 \, (\Gamma _1 - 1) P(1,2)] + \mathbb {E}[\varphi _2 \, (1 - p)^{-2} \, e^{2s_0} \, \Gamma _2] \nonumber \\&\quad+ \, \mathbb {E}[\varphi _2 \, (1-p)^{-1} \, e^{s_1} \, (1 - \Gamma _1) \, \Gamma ^{(1)}_2] - \mathbb {E}[\varphi _2] \nonumber \\&= \mathbb {E}[\psi _2 \chi _0 \chi _1 \, (\Gamma _1 - 1) ] + \mathbb {E}[\varphi _2] + \, \mathbb {E}[\psi _2 \chi _0 \chi _1 \, (1 - \Gamma _1)] - \mathbb {E}[\varphi _2] \nonumber \\&= 0 \, . \end{aligned}$$

(66)

4.3 Analysis of the reduced consumption stream model

The liability value at time 1 in the reduced consumption stream model is given by equation (60). If the backing bond defaulted ($\Gamma _1 = 0$), then we have $L_1 = P(1,2)$. If the bond did not default, then the market value is given by $L_1 = (1 - p)^{-1} \, e^{2s_0-s_1} \, P(1,2)$. In the latter case, the liability value is asset-dependent. Indeed, since the liability is non-tradable at $t = 1$ for the policyholder, the market consistent price can vary with the backing assets. This phenomena reflects the reality that two policyholders with identical contracts purchased with different insurers can end up with a different payout in case the policyholder is allowed to terminate the contract before maturity with a market value adjustment clause. In such case, the potential loss incurred by the insurer due to the early sale of the backing assets is borne by the policyholder.

Notice that the liability value, in absence of a default,

$$\begin{aligned} L_1 = (1 - p)^{-1} \, e^{2s_0-s_1} \, P(1,2) = \frac{P(0,2)}{B(0,2)} \, B^{(1)}(1,2) \end{aligned}$$

(67)

can both be bigger, as well as smaller than its Solvency II value, $P(1,2)$. If the illiquidity spread $s_1$ has not increased significantly compared to $s_0$, then $L_1$ will be bigger than $P(1,2)$. This would, in reality, allow insurers to give profit sharing to the policyholder. If, on the other hand, the illiquidity spread $s_1$ increased significantly, though without a default, then we have $L_1 < P(1,2)$. For the special case $s = s_0 = s_1$ studied in [14], we find that $(1-p)^{-1} > 1$ and $e^{2s_0-s_1} \ge 1$. Indeed, in [14], this excess return generates a positive consumption stream at time 1. Notice that in the proposed reduced consumption stream model there is never any upstreaming of capital at time 1, even if $L_1 > P(1,2)$, instead we have $\widetilde{C}_1 = 0$, or $\widetilde{C}_1 < 0$ in case of a default.

The policyholder is not at risk since we impose in the model that $L_2 = P(2,2) = 1$. This is achieved via the consumption stream backing the liability. However, in providing this backing, the shareholder does not run an illiquidity spread risk. Indeed, both $\widetilde{C}_1$ and $\widetilde{C}_2$ are only negative in case a default is realized in the respective time step. We also note that, contrary to time step 1, there is upstreaming of capital at time 2 ($\widetilde{C}_2 > 0$), as long as no default occurred at $t = 2$.

In reality, the illiquidity spread process $e^{-s_t}$ and the default process $\Gamma _t$ are often positively correlated. Indeed, as the spreads on certain government bonds increased significantly during the recent European sovereign-debt crisis, it was the shareholders, who are liable for the consumption stream, that grew increasingly worried as insurers’ ratings decreased, forcing insurers to reorient their asset portfolios. This would correspond in our model to replacing the bond $A$ at time 1 with another bond $A'$ where $A_1 \,<\, A'_1$. This necessitates a cash injection $A'_1 - A_1$ at time 1 to maintain the liability backing ($L'_1 = A'_1$). Just as in the case of default (see equation (59)), we impose $A'_1 = P(1,2)$. Indeed, by executing this transaction, the insurer assumes the full spread risk. Shareholders would tend to prefer such known cash injection over the possibly bigger and unknown consumption stream needed to back the liability in case of a default at a later time.

On the other hand, when economic conditions are good, the opposite transaction where $A_1 > A'_1 = P(1,2)$ could be executed. In this case, capital is released which could be upstreamed, allocated as profit sharing or used to supply an additional countercyclical reserve as suggested in [1]. Another regulatory approach could be the restrict (full) consumption when $A_1 > P(1,2)$. This case corresponds to the reduced consumption stream model with $L_1 > P(1,2)$ as if a countercyclical reserve is built into the liability valuation.

5 Downside risk and exotic options as protection

5.1 Probability of a negative consumption

Following [3], we will analyze the probability of a negative consumption. Let us first consider the example from 2.2.2.

$$\begin{aligned} \mathbb {P}\mathrm {rob}[C_1 < 0]&= \mathbb {P}\mathrm {rob}\Big [(1-p)^{-1} \, e^{2s_0-s_1} \, \Gamma _1 - 1 < 0 \Big ] \nonumber \\&= p + \mathbb {P}\mathrm {rob}\Big [e^{-s_1} < (1-p) \, e^{-2s_0} \Big | \Gamma _1 = 1 \Big ] \nonumber \\&\ge p \end{aligned}$$

(68)

$$\begin{aligned} \mathbb {P}\mathrm {rob}[C_2 < 0]&= \mathbb {P}\mathrm {rob}\Big [(1-p)^{-1} \, e^{s_1} \, \Gamma ^{(1)}_2 - 1 < 0 \Big ] \nonumber \\&= \mathbb {P}\mathrm {rob}\Big [\Gamma ^{(1)}_2 < (1-p) \, e^{-s_1} \Big ]\nonumber \\&= p \,. \end{aligned}$$

(69)

Let us now do the same exercise for the reduced consumption stream:

$$\begin{aligned} \mathbb {P}\mathrm {rob}[\widetilde{C}_1 < 0]&= \mathbb {P}\mathrm {rob}\Big [ - (1 - \Gamma _1) < 0 \Big ] \nonumber \\&= p \end{aligned}$$

(70)

$$\begin{aligned} \mathbb {P}\mathrm {rob}[\widetilde{C}_2 < 0]&= \mathbb {P}\mathrm {rob}\Big [ (1 - p)^{-2} \, e^{2s_0} \, \Gamma _2 + (1-p)^{-1} \, e^{s_1} \, (1 - \Gamma _1) \, \Gamma ^{(1)}_2 - 1 < 0 \Big ] \nonumber \\&= p \,. \end{aligned}$$

(71)

The total probability to have a negative consumption in the original example is bigger than $2p$, while it is exactly equal to $2p$ with the reduced consumption stream. Indeed, in the original example it might happen that at time 1 the spreads have risen such that the asset value went down enough to necessitate a capital injection ($C_1 < 0$ with $\Gamma _1 = 1$). However, at time 2 the bond did not default ($\Gamma _2 = 1$) so that the claim can be paid out and the remaining asset value, including the capital injected at $t = 1$, is released via a positive consumption stream ($C_2 > 0$). In the reduced consumption stream case, such scenario would not provoke a negative consumption at time 1.

5.2 An option as protection against the downside spread risk

Let us now consider an insurance company for which the shareholders are willing to support the reduced consumption stream (see equations (63)–(65)), but where the Solvency II condition $A_1 \ge P (1,2)$ has to be respected, as in the example in Sect.  2.2.2. The reduced consumption stream at $t = 1$ is non-zero if a default occurred. If there is no default, the consumption stream is zero. However, if, in that case, the illiquidity spread led to a bond value less than $P (1,2)$, an additional cash injection will be needed to comply with the condition $A_1 \ge P (1,2)$.

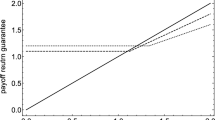
The insurer could decide to buy an option which guarantees exactly this additional cash flow, to protect against this specific downside risk. Another solution, suggested in [1], is for the insurer to hold an additional reserve. This additional reserve would be used to supply the additional cash flow. Both solutions come at a cost, either the cost of buying the option, or the cost to remunerate the capital in the additional reserve. The insurance premium increase necessary to cover the cost of remunerating the additional buffer was estimated at $10$ to $15\%$ in [12] compared to current premium levels.

In this section, we consider the option that would generate the additional cash flow. The price of this option is exactly the price to comply with the Solvency II condition $A_1 \ge P (1,2)$, while operating with a reduced consumption stream. In the example in Sect. 2.2.2, we obtained the consumption stream $C_1$ by requiring $A_1 = P(1,2)$. To safeguard $A_1 \ge P(1,2)$, we thus need a cash flow injection of $(-C_1)^+ = \max (-C_1,0)$, since a cash injection equals a negative consumption stream. The payoff from the option $\Delta _1 (\ge 0)$ necessary to preserve $A_1 \ge P(1,2)$ is then given by:

$$\begin{aligned} (-C_1)^+ \le -\widetilde{C}_1 + \Delta _1 \, , \end{aligned}$$

(72)

or,

$$\begin{aligned} \Delta _1&= \left( \widetilde{C}_1 + (-C_1)^{+} \right) ^{+} \end{aligned}$$

(73)

$$\begin{aligned}&= \Bigg \{ \begin{array}{ll} \widetilde{C}_1 - C_1 &{} \quad \text{ if } C_1 < \widetilde{C}_1 < 0\,; \\ 0 &{} \quad \text{ otherwise. } \end{array}\end{aligned}$$

(74)

$$\begin{aligned}&= \Big [ 1 - (1-p)^{-1} \, e^{2s_0-s_1} \Big ]^+ \Gamma _1 P (1,2) \, . \end{aligned}$$

(75)

We see that the payout is indeed zero if the bond has defaulted at $t=1$, since in that case the reduced consumption stream $\widetilde{C}_1$ is used as capital injection. Notice that no additional option is needed at maturity ($t=2$) since the reduced consumption stream already ensures that $L_2 = P (2,2) = 1$.

For insurance contracts with a long-term character, an option at each time step will be required to cover the downside risk associated with the illiquidity spread. Extending the formalism to larger $m$, one can find the dependency of the option price on $m$, using option pricing theory. Given Eq. (43), the price has an exponential behavior in $m$, rendering these options expensive for long-term insurance contracts.

6 Conclusions

In Sect. 2, we extended the model for defaultable bonds developed in [14] to include longer maturities and a time-varying illiquidity spread process.

In Sect. 3, we applied the liability valuation rules of Solvency II to a long-term insurance contract. We showed that it will induce a volatile required capital. The volatility is composed of three contributions and their cross terms: a term linked with the volatility of the term structure, another term originating from the default process and a final term coming from the illiquidity spread. The illiquidity spread term grows quickly with the maturity of the insurance product, making it the dominant volatility source for long-term insurance products.

In Sect. 4, we introduced a liability valuation technique, the reduced consumption stream model, which is applicable for illiquid insurance products. It does lead to a liability valuation which becomes asset-dependent once the contract is underwritten. This does not result in an arbitrage possibility since the product is non-redeemable and non-tradable. We proved the market consistency of the model.

As detailed in the introduction, while our mathematical example exhibits the stylized features of a perfect cash flow matching and an entirely stable liability cash flow runoff, in practice many annuity and pension products do have a high degree of illiquidity. As such, we believe that this valuation technique has practical applications for such products on the condition that they are cash flow matched.

We can now compare this proposed valuation model with the Matching Adjustment valuation model. Both techniques take into account the illiquid nature of the insurance liability and reduce the volatility of the required capital. If we extend the reduced consumption stream model to larger maturities $m$, one can prove that its capital volatility is lower than the Solvency II volatility computed in Sect. 3. Indeed, the volatility in Sect. 3 is dominated by the spread, while the volatility of the reduced consumption stream is dominated by the default process, due to its intrinsic construction. As proven in [14], the Matching Adjustment valuation is not market consistent, whereas our proposed methodology is market consistent. Moreover, it does not change the (initial) price of the insurance product, nor does it recognize upfront gains from the illiquidity spread.

In Sect. 5, we verified that the probability of needing a capital injection is higher under the Solvency II valuation rules than in the reduced consumption model. The additional capital injection at time 1 under the Solvency II valuation rules is due when the illiquidity spread increases without having a realized default. An insurer could either opt to constitute a reserve from which this additional cash injection could be sourced, or it could opt to buy an option which would cover this risk. The price of such option corresponds to the exact additional cost linked with the Solvency II liability valuation method. We find that the price of this option increases rapidly with the maturity of the insurance contract.