Abstract
We present some recent stability results concerning the isoperimetric inequality and other related geometric and functional inequalities. The main techniques and approaches to this field are discussed.
Similar content being viewed by others
1 Introduction
The isoperimetric inequality is probably one of the most beautiful and at the same time one of the most powerful tools of modern mathematics. Despite the fact that the isoperimetric property of the circle among all planar figures was already well known in ancient times, the first rigorous proofs of this fact have been only obtained at the beginning of last century. In particular Hurwitz proved in 1901 that given a simple, closed curve \(\gamma \subset \mathbb {R}^2\) of length L enclosing an area A, then
with equality holding if and only if \(\gamma \) is a circle. His proof, see [86], used the Gauss–Green formula and Wirtinger inequality that is the one-dimensional Sobolev–Poincaré inequality with the sharp constant. This is not surprising since in higher dimension the connections of the isoperimetric inequality with the divergence theorem and with the Sobolev inequality are even more evident.
Passing to higher dimensions was not an easy task for the mathematicians of last century, also because it was clear that proving the isoperimetric inequality in full generality would require a deeper understanding of the concept of surface measure. In the end, three main directions were followed to this purpose. The first one, and maybe the simplest, was based on the Brunn–Minkowski inequality, see for instance [29, Th. 8.1.1], stating that if \(H,K\subset \mathbb {R}^n\) are compact sets then
From this inequality one gets easily that if \(K\subset \mathbb {R}^n\) is compact then
where \(B_r\) is a ball of the same volume as K and \(\sigma (\partial K)\) denotes the outer Minkowski content of the boundary of K, defined as
where \({\bar{B}}\) is the closed unit ball. Note that if K is the closure of a bounded smooth open set, then \(\sigma (\partial K)\) coincides with the usual measure of the surface \(\partial K\). Therefore (1.3) can be viewed as a generalized version of the classical isoperimetric inequality.
Another approach to the isoperimetric inequality comes from Calculus of Variations. Provided that an isoperimetric set exists and is a smooth bounded open set, by taking small variations of this set one immediately sees that its boundary must have constant mean curvature. This observation led people to prove that the ball is the only smooth open set in \(\mathbb {R}^n\) whose boundary has constant mean curvature, a result that was eventually obtained by Aleksandrov in 1958, see [2].
A third approach was followed by De Giorgi in his celebrated paper [53] of 1958. He used an observation going back to Steiner: the surface area of a set E, or more generally its perimeter P(E), decreases under Steiner symmetrization, see Theorem 2.7. The isoperimetric property of balls then follows, since they are the only sets that are invariant under Steiner symmetrization in every direction. The formulation given by De Giorgi in the framework of the theory of sets of finite perimeter is the most general one. It states that if \(E\subset \mathbb {R}^n\) is a Lebesgue measurable set with the same volume as a ball \(B_r\) then
with the equality holding if and only if E is a ball.
Other proofs of the isoperimetric inequality have been proposed more recently. Among them we shall discuss the one given by Gromov in [100], see Sect. 5.1, which uses ideas related to mass transportation and ultimately reduces the isoperimetric inequality to the divergence theorem and the arithmetic-geometric mean inequality. Finally, an elegant and short proof has been given by Cabré in [30] using the properties of solutions of the Neumann problem for the Laplacian. We cannot pursue here the history of all proofs and formulations of the isoperimetric inequality, but we refer the interested reader to the survey paper of Ossermann [104] and to the book of Chavel [37].
Let us go back to the isoperimetric inequality in the plane. In the 1920’s Bonnesen obtained a series of improved versions of (1.1), later on named by Osserman [105] Bonnesen type inequalities, of the form
where the quantity d on the right hand side is a nonnegative geometrically significant expression vanishing if and only if \(\gamma \) is a circle. In particular in 1924 Bonnesen [21] proved the following sharp and elegant estimate.
Theorem 1.1
(Bonnesen) Given a closed, simple curve \(\gamma \subset \mathbb {R}^2\) enclosing a convex set C of area A, there exist two concentric circles \(C_1 \subset C\subset C_2\) of radii \(r_1\) and \(r_2\), respectively, such that
This inequality has the feature of being sharp, since the constant \(4\pi \) at the denominator cannot be increased, and of having an elementary proof. It provides a nice example of quantitative isoperimetric inequality, i.e., an inequality where a suitable distance of a set E from a ball of the same volume is controlled in terms of the difference of the perimeter of E and the perimeter of the ball.
It was only in 1989 that Fuglede extended this result to convex sets in higher dimension. Indeed, he proved in [72] that given a convex body K with the same volume as the unit ball B one can always measure the Hausdorff distance of a translate of K from B by a suitable power of the isoperimetric deficit of K, i.e., the difference \(P(K)-P(B)\), see Theorem 3.2.
His result was the starting point of modern investigations on the stability of isoperimetric inequality. In fact only a few years later Fuglede’s result was extended to general sets of finite perimeter in \(\mathbb {R}^n\) in two papers by Hall et al. [84] and by Hall [82]. Precisely, in the last paper it was proved that if \(E\subset \mathbb {R}^n\) is a measurable set with the same volume as the unit ball B, then
where C(n) is a positive constant depending only on the dimension. Note that in dealing with general sets one has to replace the Hausdorff distance with the weaker one given by the measure of the symmetric difference between a translated of the set E and B. This is unavoidable if one thinks that by adding to B some long thin spikes the volume and the perimeter of the resulting set change very little while its Hausdorff distance from B goes to infinity. Note also that in (1.5) the power 4 on the left hand side is independent of the dimension, though Hall suggested in [82] that it should be replaced with the optimal power 2, see the discussion at the beginning of Sect. 4.
Inequality (1.5) with the power 2 was proved in [76] by Maggi, Pratelli and the author using symmetrization arguments. This result was not the end of the story. On the contrary it initiated a series of papers where other proofs of the same inequality were given or similar stability results were obtained for other inequalities such as the Sobolev, the Faber–Krahn, the Brunn–Minkowski and the isodiametric inequalities, see Sects. 5 and 6.
The aim of this paper is to present the results, the techniques and the main ideas developed in this context. Three different approaches are now available if one wants to study these stability issues: a first one using symmetrization, another one via mass transportation and a third one based on the regularity theory for minimal surfaces and other PDEs.
The paper is organized as follows. After quickly recalling some basic tools from De Giorgi’s theory of sets of finite perimeter and from Geometric Measure Theory, in Sect. 3 we present Fuglede’s proof of the quantitative isoperimetric inequality for convex sets and for nearly spherical sets, that are sets close to a ball in \(C^1\) sense. In rewriting the original proofs of [72] we have tried to simplify some unnecessarily complicated parts and to highlight some ideas contained therein that have been successfully used later by various authors in different contexts.
In Sect. 4 we present the proof of the quantitative isoperimetric inequality via symmetrization given in [76], with some simplifications introduced by Maggi in [94]. Although a shorter proof has been given later by Cicalese and Leonardi [45] using the regularity theory for area minimizing sets of finite perimeter, the proof by symmetrization uses no deep results from geometric and functional analysis, is geometrically intuitive and can be adapted to other situations where a complete regularity theory is not available.
The stability proofs via mass transportation and via regularity are presented in Sect. 5. Not all the details of the proofs are given, but we have tried to explain the main ideas and the novel techniques. In this section we discuss also several generalizations of the quantitative isoperimetric inequality to higher codimension, to non local perimeters and to non Euclidean settings such as the Gauss space.
Finally, Sect. 6 gives an account on how the techniques developed for the isoperimetric inequality have been successfully applied to study the stability of other related inequalities. The quantitative versions of the Sobolev inequality and of the Faber–Krahn inequality for the first eigenvalue of the Laplacian are discussed with some details. Reference to other inequalities are given in the last section. But at that point we had to stop since for some of them new developments are foreseen in the next years.
2 Notation and preliminary results
In the following we denote by \(B_r(x)\) the ball with radius \(r>0\) and center x and we use the following simplified notation
The measure of the unit ball B will be denoted by \(\omega _n\).
Though most of the results that we are going to present could be given first for smooth sets and then extended to sets of finite perimeters via the approximation Theorem 2.4 below, we have preferred to state them in full generality. However the reader who is not familiar with the theory of sets of finite perimeter may still read the statements and the proofs without problems by simply pretending that all sets involved are smooth. For the basic properties of sets of finite perimeter and related results we refer to [8, 59]. We start by recalling the definition. Let \(\Omega \) be an open set in \(\mathbb {R}^n\) and \(E\subset \mathbb {R}^n\) a measurable set. The perimeter of E in \(\Omega \) is defined as
If E is smooth we can use the classical divergence theorem to find that
thus, taking the supremum over all \(\varphi \) as in the definition, we get
Note that if \(P(E;\Omega ) < + \infty \) the map
is linear and continuous, so by means of Riesz’s theorem, we can find a vector valued Radon measure \(\mu = (\mu ^1,\ldots , \mu ^n)\) such that
Thus \(\mu = - D{\chi _{_{E}}}\), where \(D{\chi _{_{E}}}\) is the distributional derivative of \({\chi _{_{E}}}\) and the above formula can be rewritten as
So, E has finite perimeter in \(\Omega \) if and only if \(D{\chi _{_{E}}}\) is a Radon measure with values in \(\mathbb {R}^n\) and finite total variation. In fact, from the definition we immediately get that
Recalling Besicovitch differentiation theorem, we also have that for \(|D{\chi _{_{E}}}|\)-a.e. \(x \in \text{ supp }|D{\chi _{_{E}}}|\), there exists
We shall denote by \(\partial ^*E\) the set of all points in \(\text{ supp }|D{\chi _{_{E}}}|\) where (2.3) holds. The set \(\partial ^*E\) is called the reduced boundary of E, while the vector \(\nu ^E(x)\) is the generalized exterior normal at x. From (2.3) we have that the measure \(D{\chi _{_{E}}}\) is obtained by integrating \(-\nu ^E\) with respect to \(|D{\chi _{_{E}}}|\), i.e.,
Thus (2.2) can be rewritten as
Since \(\partial ^*E \subset \text{ supp }|D{\chi _{_{E}}}| \subset \partial E\), the reduced boundary of E is a subset of the topological boundary. The next result (see e.g. [59, Sect. 5.7] or [8, Th. 3.59]) describes the structure of sets of finite perimeter. Here and in the sequel by \({\mathcal H}^k\), \(k=0,1,\ldots ,n\), we denote the k-dimensional Hausdorff measure in \(\mathbb {R}^n\). For the definition and the basic properties of rectifiable sets see [8, Ch. 2].
In the following the perimeter of E in \(\mathbb {R}^n\) will be denoted by P(E). If \(P(E)<\infty \) we say that E is a set of finite perimeter.
Theorem 2.1
(De Giorgi) Let \(E \subset \mathbb {R}^n\) be a measurable set of finite perimeter, then the following hold:
-
(i)
\(\partial ^*E \) is countably \((n-1)\)-rectifiable, i.e., \(\partial ^*E = \bigcup _{i}K_i \cup N_0\), where \({\mathcal H}^{n-1}(N_0)= 0\) and \(K_i\) are compact subsets of \(C^1\) manifolds \(M_i\) of dimension \(n-1\);
-
(ii)
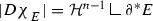, in particular \(P(E;\Omega )={\mathcal H}^{n-1}(\partial E^*\cap \Omega )\) for any open set \(\Omega \subset \mathbb {R}^n\); -
(iii)
for \( {\mathcal H}^{n-1}\)-a.e. \(x \in K_i \), the generalized exterior normal \(\nu ^{E}(x)\) is orthogonal to the tangent hyperplane to the manifold \(M_i\) at x;
-
(iv)
for all \(x \in \partial ^*E, \frac{|E\cap B_r(x)|}{B_r(x)} \rightarrow \frac{1}{2}\) as \(r\rightarrow 0\);
-
(v)
for all \(x \in \partial ^*E, {\lim \nolimits _{r \rightarrow 0} \frac{{\mathcal H}^{n-1}(\partial ^*E \cap B_r(x))}{\omega _{n-1}r^{n-1}} = 1}\).
, in particular From (ii) above we have that (2.4) can we rewritten as
Another characterization of the reduced boundary is contained in the following result. To this aim we recall that if \(E\subset \mathbb {R}^n\) is a measurable set E has density \(t\in [0,1]\) at a point \(x\in \mathbb {R}^n\) if
We shall denote by \(E^{(t)}:=\{x\in \mathbb {R}^n:\,D(E;x)=t\}\). Then the measure theoretic boundary of E is defined as \(\partial ^ME:=\mathbb {R}^n{\setminus }(E^{(0)}\cup E^{(1)})\). For the proof of the next theorem see [8, Th. 3.61].
Theorem 2.2
(Federer) Let E be a set of finite perimeter in \(\mathbb {R}^n\). Then
Let \(E_h\) be a sequence of measurable subsets of \(\mathbb {R}^n\). We say that the sets \(E_h\) converge in measure to a set \(E\subset \mathbb {R}^n\) in an open set \(\Omega \subset \mathbb {R}^n\) if \({\chi _{_{E_h}}}\rightarrow {\chi _{_{E}}}\) in \(L^1(\Omega )\). The local convergence in measure is defined accordingly. Note that from the definition (2.1) of perimeter it follows immediately that the perimeter is lower semicontinuous with respect to the local convergence in measure, i.e. if the sets \(E_h\) converge locally in measure in \(\Omega \) to a set E, then \(P(E;\Omega )\le \liminf _{h}P(E_h;\Omega )\). Note also, as a consequence of Rellich–Kondrachov theorem, that sets of finite perimeter are compact with respect to the convergence in measure, see [8, Th. 3.39].
Theorem 2.3
Let \(E_h\) be a sequence of measurable subsets of \(\mathbb {R}^n\) such that \(\sup _h P(E_h;\Omega )<\infty \). Then, there exists a subsequence \(E_{h_k}\) locally converging in measure in \(\Omega \) to a set E of finite perimeter in \(\Omega \). Moreover,
Another useful property of sets of finite perimeter is stated in the next approximation result.
Theorem 2.4
Let E be a set of finite perimeter in \(\Omega \). Then there exists a sequence of smooth, bounded open sets \(E_h \subset \mathbb {R}^n\) such that \(E_h \rightarrow E\) in measure in \(\Omega \) and \(P(E_h;\Omega ) \rightarrow P(E;\Omega ) \).
Note also that in Theorem 2.4 one may replace the smooth sets \(E_h\) with polyhedra, i.e. bounded open sets obtained as the intersection of finitely many half-spaces.
The next result is a special case of the coarea formula for rectifiable sets, see [8, Th. 2.93]. To this aim, given \(k=1,\ldots ,n-1\), we set \(x=(x^\prime ,y)\in \mathbb {R}^{n-k}\times \mathbb {R}^k\). Similarly, given a vector \(v=(v_1,\ldots ,v_n) \in \mathbb {R}^n\) we set \(v_{x^\prime }=(v_1,\ldots ,v_{n-k})\), \(v_y=(v_{n-k+1},\ldots ,v_n)\), and given a measurable set \(E\subset \mathbb {R}^n\) we denote the section of E over \(x^\prime \in \mathbb {R}^{n-k}\) by \(E_{x^\prime }:=\{y\in \mathbb {R}^k:\,(x^\prime ,y)\in E\}\).
Theorem 2.5
Let E be a set of finite perimeter in \(\mathbb {R}^n\). Given \(k\in \{1,\ldots ,n-1\}\), for \({\mathcal H}^{n-k}\)-a.e. \(x^\prime \in \mathbb {R}^{n-k}\) the slice \(E_{x^\prime }\) is a set of finite perimeter in \(\mathbb {R}^k\) and \({\mathcal H}^{k-1}(\partial ^*(E_{x^\prime })\Delta (\partial ^*E)_{x^\prime })=0\). Moreover if \(g: \mathbb {R}^n \rightarrow [0, + \infty ]\) is a Borel function we have
Fix k and a measurable set \(E\subset \mathbb {R}^n\). Let \(v_E:\mathbb {R}^{n-k}\rightarrow [0,\infty )\) be the function measuring the k-dimensional slices of E, i.e.,
Note that \(v_E\) is \({\mathcal H}^{n-k}\)-measurable. Moreover, if E is a set of finite perimeter, \(v_E\) is a function of bounded variation (BV-function) and even a Sobolev function if the reduced boundary of E has no vertical parts. For the definition and the main properties of BV functions we refer to [8, Ch. 3]. The following result is a consequence of Lemma 3.1 and Propositions 3.4 and 3.5 of [11].
Theorem 2.6
Let E be a set of finite perimeter with finite measure and \(k\in \{1,\ldots ,n-1\}\). Then the function \(v_E\) defined in (2.5) belongs to \(BV(\mathbb {R}^{n-k})\). Moreover if \({\mathcal H}^{n-1}(\{(x\in \partial ^*E:\,\nu ^E_y(x)=0\})=0\), then \(v_E\in W^{1,1}(\mathbb {R}^{n-k})\). In addition, if \(U\subset \mathbb {R}^{n-k}\) is a Borel set
where \(\nabla v_E\) and \(D^sv_E\) are the absolutely continuous part and the singular part, respectively, of the gradient measure \(Dv_E\) with respect to Lebesgue measure in \(R^{n-k}\) and for \({\mathcal H}^{n-k}\)-a.e. \(x^\prime \in \mathbb {R}^{n-k}\) we have set \(p_E(x^\prime ):={\mathcal H}^{k-1}(\partial ^*(E_{x^\prime }))\).
Given a measurable set \(E\subset \mathbb {R}^n\) and \(k\in \{1,\ldots ,n-1\}\) we define the essential projection of E over the first \(n-k\) coordinate hyperplanes by setting
If \(x^\prime \in \pi (E)^+\) we denote by \(r_E(x^\prime )\) the radius of a k-dimensional ball with \({\mathcal H}^k\)-measure equal to the one of \(E_{x^\prime }\). Then the Steiner symmetral of E of codimension k with respect to the subspace \(\{y=0\}\) is defined by setting
Note that by definition \(v_E(x^\prime )=v_{E^S}(x^\prime )\) for \({\mathcal H}^{n-k}\)-a.e. \(x^\prime \in \mathbb {R}^{n-k}\), hence \(|E|=|E^S|\). On the other hand perimeter decreases under Steiner symmetrization. Precisely, we have the following result whose proof can be found for instance in [11, Section 3].
Theorem 2.7
Let \(E\subset \mathbb {R}^n\) be a set of finite perimeter and \(E^S\) its Steiner symmetral with respect to to first \(n-k\) coordinate hyperplanes. Then \(E^S\) is a set of finite perimeter and for any Borel set \(U\subset \mathbb {R}^{n-k}\) we have
Moreover,
Let us apply the above formula to a set of finite perimeter E, axially symmetric with respect to the \(x_n\) axis and let us set \(v(t):={\mathcal H}^{n-1}(\{x'\in \mathbb {R}^{n-1}:\,(x',t)\in E\})\). For any open set \(U\subset \mathbb {R}\) we have
provided \(n\ge 3\) or \(n=2\) and \(v>0\) in U.
A characterization of the equality cases in the perimeter inequality (2.6), under suitable assumptions on the set E, has been given in [38] for the case \(k=1\) and in [11] for the higher codimension case. The complete characterization of the equality cases for the codimension 1 case has been recently proven in [33].
We conclude this section by recalling the coarea formula for functions. Though it holds more generally for functions of bounded variations, we are going to apply it only to Sobolev functions. In this case we have, see for instance [8, Th. 3.40].
Theorem 2.8
Let \(\Omega \subset \mathbb {R}^n\) be an open set and \(f\in W^{1,1}_{loc}(\Omega )\). Then, for every Borel function \(g:\Omega \rightarrow [0,\infty ]\) we have
3 The Fuglede’s approach
3.1 Nearly spherical sets
In this section, following Fuglede [72], we consider a nearly spherical set, that is a set \(E\subset \mathbb {R}^n\) whose boundary can be written as a graph over the boundary of the ball with the same volume and the same barycenter as E. Thus, up to a translation and a dilation, we shall assume that there exists a Lipschitz function \(u:\mathbb {S}^{n-1}\rightarrow (-1, 1)\) such that
that \(|E|=|B|\) and that E has barycenter at the origin.
Fuglede’s result states that if E is sufficiently close to B, then the isoperimetric deficit, that is the difference between P(E) and P(B), controls the \(L^2\) norm of the tangential gradient \(\nabla _\tau u\).
Theorem 3.1
There exists \(\varepsilon (n)>0\) such that if E is as in (3.1), \(|E| = |B|\), the barycenter of E is the origin and \(\Vert u\Vert _{W^{1,\infty }(\mathbb {S}^{n-1})} \le \varepsilon \), then
Proof
Step 1 Let us prove that if E is as in (3.1) then
In fact, from the area formula we have that
where \(J_{n-1}\varphi \) is the \((n-1)\)-dimensional Jacobian of the map \(\varphi (x)=x(1+u(x))\), \(x\in \mathbb {S}^{n-1}\). Recall that, if \(T_x\mathbb {S}^{n-1}\) is the tangential plane to \(\mathbb {S}^{n-1}\) at x, then \(J_{n-1}\varphi =\sqrt{\mathrm{det}((d_x\varphi )^*\circ d_x\varphi })\), where the linear map \(d_x\varphi :T_x\mathbb {S}^{n-1}\mapsto \mathbb {R}^n\) is the tangential differential of \(\varphi \) at x and \((d_x\varphi )^*:\mathbb {R}^n\mapsto T_x\mathbb {S}^{n-1}\) denotes the adjoint of the differential.
Since for any \(\tau \in T_x\mathbb {S}^{n-1}\) we have \(d_x\varphi (\tau )=\tau (1+u(x))+xD_\tau u(x)\), the coefficients of the matrix \(d_x\varphi \) relative to an orthonormal base \(\{\tau _1,\ldots ,\tau _{n-1}\}\) of \(T_x\mathbb {S}^{n-1}\) and to the standard base \(\{e_1,\ldots ,e_n\}\) are \(\tau _i\cdot e_h(1+u(x))+x_hD_{\tau _i} u\), for \(i=1,\ldots ,n-1, h=1,\ldots ,n\). Thus, for all \(i,j\in \{1,\ldots ,n-1\}\) the coefficients \(a_{ij}\) of the matrix \((d_x\varphi )^*\circ d_x\varphi \) are given by
where in the last equality we have used the fact that \(\tau _i\cdot \tau _j=\delta _{ij}\) and \(\tau _i\cdot x=0\) for all \(i,j=1,\ldots ,n-1\). Hence, recalling that for \(a,b\in \mathbb {R}^k\) one has \(\mathrm{det}(I+a\otimes b)=1+a\cdot b\), we have that
and thus (3.3) follows immediately from (3.4). Let us extend u by setting u(x) : u(x / |x|) for all \(x\not =0\). Then \(E=\Phi (B)\), where \(\Phi :B\rightarrow E\) is the map defined by setting \(\Phi (x):=x(1+u(x))\). Note that \(D\Phi (x)=(1+u(x))I+x\otimes Du\) and that \(x\cdot Du(x)=0\) for all \(x\not =0\). Thus, we conclude that the n-dimensional Jacobian of \(\Phi \) is given by \((1+u(x))^n\). Hence, the assumptions \(|E|=|B|\) and \(\int _Ey\,dy=0\) can be rewritten as follows
Step 2 Using (3.3) we have
From the Taylor expansion of the square root it follows that for \(t>0\) sufficiently small \(\sqrt{1+t}\ge 1+\frac{t}{2}-\frac{t^2}{7}\). Hence from the smallness assumption \(\Vert u\Vert _{W^{1,\infty }(\mathbb {S}^{n-1})}<\varepsilon \) we get
Note that the first equation in (3.5), that is the assumption \(|E|=|B|\), implies that
that is
From this identity, recalling again that \(\Vert u\Vert _{L^\infty (\mathbb {S}^{n-1})}<\varepsilon \), we have
Therefore, using this last inequality and the smallness assumption, we may estimate
In conclusion, recalling (3.6), we have proved that if \(\Vert u \Vert _{W^{1,\infty }(\mathbb {S}^{n-1})} \le \varepsilon \), then
Step 3 Now, for any integer \(k \ge 0\), let us denote by \(y_{k,i}\), \(i= 1, \ldots , G(n,k)\), the spherical harmonics of order k, i.e., the restriction to \(\mathbb {S}^{n-1}\) of the homogeneous harmonic polynomials of degree k, normalized so that \(|| y_{k,i} ||_{L^2(\mathbb {S}^{n-1})}=1\), for all k and for \(i \in \{ 1,\ldots , G(n,k) \}\). For instance, since \(\int _{\mathbb {S}^{n-1}}1 d{\mathcal H}^{n-1} = n\omega _n\) and, for \(i= 1,\ldots n\), \(\int _{\mathbb {S}^{n-1}}x_i^2 d{\mathcal H}^{n-1} =n^{-1} \int _{\mathbb {S}^{n-1}} |x|^2 d{\mathcal H}^{n-1} = \omega _n\), we have \(y_0=1/\sqrt{n\omega _n}\) and \(y_{1,i} = x_i/\sqrt{\omega _n}\), respectively. The functions \(y_{k,i}\) are eigenfunctions of the Laplace–Beltrami operator on \(\mathbb {S}^{n-1}\) and for all k and i
Therefore if we write
we have
Observe that from formula (3.7) we have
hence
Similarly, from the second equality in (3.5), that is the assumption that the barycenter of E is at the origin, using the equality \( \int _{\mathbb {S}^{n-1}}x_i =0\), we immediately get that for all \(i= 1, \ldots , n\),
Therefore, from (3.9) we get
But since for \(k \ge 2\), \(k(k+n-2) \ge 2n\), from (3.9) we have
and thus, recalling (3.8) and choosing \(\varepsilon \) sufficiently small, in dependence on n, we get
This proves the first inequality in (3.2). To get the second inequality we observe that, choosing again \(\varepsilon \) sufficiently small
Therefore, from the last inequality of (3.10) we conclude that
\(\square \)
3.2 Convex sets
We shall now discuss the case of convex sets for which Fuglede in [72] proved a quantitative estimate where the distance from a ball is measured in terms of the Hausdorff distance. To this aim we recall that if E, F are any two sets in \(\mathbb {R}^n\) the Hausdorff distance between E, F is defined as
In this section we shall always assume that K is a closed convex set with non empty interior and \(|K|=|B|\). For such a set we define the isoperimetric deficit \(\mathcal {D}(K)\) and the asymmetry index \(\mathcal {A}(E)\) as
respectively. With these definitions in hand the result proved in [72, Th. 2.3] reads as follows.
Theorem 3.2
(Fuglede) Let \(n \ge 2\). There exist \(\delta , C\), depending only on n, such that if K is convex, \(|K| = |B|\), and \(\mathcal {D}(K) \le \delta \), then:
To be precise, in his paper [72] Fuglede only deals with the case \(n\ge 3\), since when \(n=2\) the result was already known with a better estimate and a more elementary proof. Indeed, the case of planar convex sets was already studied by Bernstein [13] in 1905 and by Bonnesen [21] in 1924, see Theorem 1.1 in Sect. 1. Note that the estimates (3.11) are sharp with respect to the order of magnitude as \(\mathcal {D}(K)\rightarrow 0\), see [72, Sect. 3].
The proof of Theorem 3.2 is based on the quantitative estimate proved in the previous section. The key point is the observation that a convex sets K with the same volume as the unit ball and small isoperimetric deficit is nearly spherical. Indeed, the boundary of K can be written as the graph of a Lipschitz function u over the boundary of the sphere centered at the barycenter of K with \(\Vert u\Vert _{W^{1,\infty }}\) small. This is precisely the content of the next lemma.
Lemma 3.3
For all \( \varepsilon > 0\), there exists \( \delta _{\varepsilon } > 0\) such that if K is a closed convex, \(|K| = |B|\), the barycenter of K is the origin and \(\mathcal {D}(K) < \delta _{\varepsilon }\), then there exists a Lipschitz function \(u:\mathbb {S}^{n-1}\rightarrow (0,\infty )\), with \(\Vert u\Vert _{W^{1,\infty }(\mathbb {S}^{n-1})}\le \varepsilon \), such that
Proof
Note that if K is any closed convex set with barycenter at the origin and nonempty interior, then K can be always represented as in (3.12) for some Lipschitz function \(u:\mathbb {S}^{n-1}\rightarrow (0,\infty )\). The point here is to show that the \(W^{1,\infty }\) norm of u is small when \(\mathcal {D}(K)\) is small.
Step 1 We start by proving a weaker statement, namely that for any \(\varepsilon >0\) there exists \(\delta _\varepsilon >0\) such that if K is a closed convex set with barycenter at 0, \(|K|=|B|\) and \(\mathcal {D}(K)<\delta _\varepsilon \), then K can be represented as in (3.12) for some Lipschitz function u with \(\Vert u\Vert _{L^\infty (\mathbb {S}^{n-1})}\le \varepsilon \).
To prove this we argue by contradiction assuming that there exist \(\varepsilon > 0\) and a sequence of closed convex sets \(K_j\) such that \(|K_j| =|B|\), the barycenter of \(K_j\) is the origin, \(\mathcal {D}(K_j) \rightarrow 0\), but \(||u_j||_{L^{\infty }(\mathbb {S}^{n-1})} \ge \varepsilon _0\), where \(u_j\) is the function representing \(K_j\) as in (3.12).
The following fact is well known, see for instance [58, Lemma 4.1]. If \(n\ge 2\) there exists C(n) such that for any convex set K with non empty interior
Using this inequality we deduce that the sets \(K_j\) are equibounded and so, up to a not relabeled subsequence, we may assume that they converge in the Hausdorff distance to a closed set K. Note that K is convex and that \(|K_j\Delta K|\rightarrow 0\) as \(j\rightarrow \infty \). Therefore, by the lower semicontinuity of the perimeter we have that \(P(K)\le \liminf _{j\rightarrow \infty }P(K_j)\). Therefore, since \(\mathcal {D}(K_j ) \rightarrow 0\), we conclude that \(P(K)=P(B)\) and thus that K is the closed unit ball centered at the origin. This gives a contradiction, since it is not possible that the sets \(K_j\) converge in the Hausdorff sense to \(\bar{B}\), while \(||u_j||_{L^{\infty }(\mathbb {S}^{n-1})} \ge \varepsilon _0\) for all j.
Step 2 Let us now assume that \(\Vert u\Vert _{L^\infty (\mathbb {S}^{n-1})}\le \varepsilon \) for some \(\varepsilon <1/2\). To conclude the proof of the lemma we show that if this is the case, then the following stronger inequality holds
To prove this estimate we observe that if K is represented as in (3.12), then it is not too hard to show that for \({\mathcal H}^{n-1}\)-a.e. \(x\in \mathbb {S}^{n-1}\) the exterior normal \(\nu ^K(y(x))\) to \(\partial K\) at the point \(y(x)=x(1+u(x))\) is given by
Thus, if \(x\in \mathbb {S}^{n-1}\) is a point where u is differentiable from the previous equality we have that
where we used the fact that \(x\cdot \nabla _\tau u(x)=0\). Then, denoting by z(x) the projection of the origin on the tangent plane to K at y(x), the triangle with vertices \(0,\,z(x),\,y(x)\) is rectangle at z(x) and the angle at the origin is equal to the angle formed by the vectors x and \(\nu ^K(y(x))\), see Fig. 1. Therefore \(|z(x)|=|y(x)|(x\cdot \nu ^K(y(x)))\). Observe also that
where the last inequality follows from the convexity of K, and thus
from which we get
thus concluding
whence (3.13) follows. \(\square \)
The construction in Lemma 3.3
The proof of Theorem 3.2 now follows quite easily from the lemma we have just proved and from the next interpolation result, whose proof is given in [72, Lemma 1.4].
Lemma 3.4
If \(v \in W^{1, \infty } (\mathbb {S}^{n-1})\) and \( \int _{\mathbb {S}^{n-1}} v = 0 \), then
where the constant C(n) depends only on the dimension and e is the Neper number.
Proof of Theorem 3.2
Fix \(\varepsilon >0\). Thanks to Lemma 3.3 we may assume that K is a convex set represented as in (3.12) by means of a function u such that \(\Vert u\Vert _{W^{1,\infty }}<\varepsilon \). Set \(v := \frac{(1+u)^n - 1}{n}\). From the volume constraint \(|K| =|B|\) we have, see the first equality in (3.5),
Moreover, since
if \(\varepsilon > 0\) is small enough we have
Assume now, to fix the ideas, that \(n\ge 4\). If \(\varepsilon \) is smaller than or equal to the one provided by Theorem 3.1, from the interpolation Lemma 3.4 and (3.13) we have
hence \(\Vert u\Vert _{\infty }\le C(n)\Vert \nabla _\tau u\Vert _2^{\frac{4}{n+1}}\). Thus, recalling the first inequality in (3.2), we may conclude that
The cases \(n=2,3\) are proved in the same way. \(\square \)
When passing from a convex set to a general set E of finite perimeter one cannot expect to estimate the isoperimetric deficit with the Hausdorff distance from a ball, see the discussion at the beginning of the next section. However, this is still possible if some additional structure is imposed on the set E. At this regard we mention two results that have been recently obtained in this direction. The first one, proved in [73], deals with sets satisfying a uniform interior cone condition at the boundary. To simplify the statement we shall assume as before that E is a set with the same volume as the unit ball. The general case can be recovered by suitably rescaling all the relevant quantities, see [73, Theorem 1.1].
Given \(x\in \mathbb {R}^n\), \(r>0\) and \(\nu \in \mathbb {S}^{n-1}\) the spherical sector with vertex at x, axis of symmetry parallel to \(\nu \), radius r and aperture \(\pi /2\) is defined as
Then, we say that a closed set E satisfies the interior cone condition at the boundary with radius r and aperture \(\pi /2\) if for any \(x\in \partial E\), there exists \(\nu _x\in \mathbb {S}^{n-1}\) such that \(S_{\nu _x,r}(x)\subset E\) and we denote by \({\mathcal {C}}_r\) the family of all closed sets E, with \(|E|=|B|\), satisfying the interior cone condition at the boundary with radius r. It can be easily checked [73, Lemma 2.9], that if \(E\in {\mathcal {C}}_r\) and \(\mathcal {D}(E)\) is sufficiently small then E is compact.
The interior cone condition at the boundary is a rather mild regularity condition. In fact, given any \(\varrho >0\) and any \(\theta \in (0,\pi /2)\) one may construct a set \(E\in {\mathcal {C}}_r\) which does not satisfy the standard interior cone condition with height \(\varrho \) and aperture \(\theta \), see [73, Example 2.3]. On the other hand, a set in \({\mathcal {C}}_r\) has always finite perimeter [73, Prop. 2.4], but the \({\mathcal H}^{n-1}\)-measure of its topological boundary may be strictly larger than its perimeter, [73, Example 2.6]. The main result proved in [73] then reads as follows.
Theorem 3.5
For any \(r>0\) there exist \(\delta , C\), depending only on n and r, such that if \(E\in {\mathcal {C}}_r\) and \(\mathcal {D}(E) \le \delta \), then:
We observe that the powers appearing in (3.15) are the same as in Theorem 3.2. Another estimate with the same powers has been also obtained by Rajala and Zhong in [106, Th. 1.5] for John domains whose complement with respect to a suitable ball is also a John domain. Note that though the sets considered in [106] do not necessarily belong to \({\mathcal {C}}_r\), they cannot have singularities such as inward cusps, which are instead admissible for sets in \({\mathcal {C}}_r\).
4 The quantitative isoperimetric inequality: the approach via symmetrization
We now discuss the quantitative isoperimetric inequality for general sets of finite perimeter. In this case it is clear that we cannot use the Hausdorff distance to measure the asymmetry of a set. Think for instance of a set which is the union of a large ball and a far away tiny one. For this reason we replace the asymmetry index considered in the previous section with an \(L^1\)-type distance, the so-called Fraenkel asymmetry, which is defined for a measurable set E, as the minimum of the symmetric difference between E and any ball with the same measure
We shall refer to a ball minimizing \(\alpha (E)\) as to an optimal ball. Note that an optimal ball needs not to be unique. Note also that \(\alpha (E)\) is scaling invariant. It is convenient to define the isoperimetric deficit of a set E also in a scaling invariant way by setting
where again r is the radius of a ball with the same measure of E.
The first quantitative estimate for sets of finite perimeter was obtained in 1992 by Hall [82]. Using some previous results proved in collaboration with Hayman and Weitsman [84], he showed that there exists a constant C(n) such that for all measurable sets of finite measure
It is interesting to observe that the power 4 on the left hand side of this estimate does not depend on the dimension, while in Fuglede’s Theorem 3.2 it does. However, in his paper Hall conjectured that the right power should be 2 and actually proved that (4.2) holds with the exponent 2 if E is an axially symmetric set, see [82, Th. 2]. Moreover he observed that one cannot expect a power smaller than 2. To see this, take \(\varepsilon > 0\) and consider in any dimension \(n \ge 2\) the ellipsoid
It can be proved, see Proposition 4.3, that \(\alpha (E_{\varepsilon }) = |E_{\varepsilon } \Delta B| \). Then one can show that
In 2008 Maggi, Pratelli and the author proved in [76] the following quantitative isoperimetric inequality with the sharp exponent.
Theorem 4.1
There exists a constant \(\gamma (n)\) such that for any measurable set E of finite measure
Note that inequality (4.3) can be rewritten in the following equivalent way: if \(|E|=|B_r|\),
Thus the asymmetry index \(\alpha (E)\) can be viewed as a quantity estimating the second order term in the Taylor expansion of P(E) around \(P(B_r)\). This point of view has been exploited in the proof of Theorem 3.1 where the idea is precisely to view the perimeter of E as an integral functional over the sphere depending on the function u and then to write the second order Taylor expansion of that functional.
In this section we will present the proof of the quantitative isoperimetric inequality given in [76] which is mostly based on symmetrization arguments. Though different and even shorter proofs can be given, based on completely different strategies, the one we present here has the advantage of not using any sophisticate technical tool, it is geometrically intuitive and can be adapted to other contexts where symmetry plays a fundamental role. Other proofs of the quantitative isoperimetric inequality will be discussed in the Sect. 5.
Let us now give a short description of how the proof goes. The main idea is to reduce the problem, by means of suitable geometric constructions, to the case of more and more symmetric sets, namely to axially symmetric sets that are also symmetric with respect to n orthogonal hyperplanes. For these sets one may either use the already mentioned result by Hall [82, Th. 2], or simpler ad hoc arguments.
Observe that both the asymmetry and the isoperimetric deficit are scaling invariant. Therefore, throughout all this section we will only deal with sets with the same measure of the unit ball B and with small isometric deficit. In fact, since \(\alpha (E)\) is always smaller than 2 inequality (4.3) becomes trivial when D(E) is large.
The first step in the proof is to reduce to sets that are confined in a sufficiently large cube. This step is needed in order to take advantage of the compactness properties of bounded sets with equibounded perimeter. This first reduction is achieved by using the concavity property of the isoperimetric function which is the function that associates to every \(t>0\) the perimeter \(n\omega ^{1/n}t^{(n-1)/n}\) of the ball of measure t, see Lemma 4.2.
The second step in the proof is to reduce to the case of n-symmetric sets. We say that E is n-symmetric if E is symmetric with respect to all coordinate hyperplanes. This reduction is the most delicate part the proof. On the other hand, when restricted to n-symmetric sets, the proof of (4.3) will be relatively easy. The reason is that while in general it can be be quite hard to find an optimal ball, when E is n-symmetric the ball centered at the center of symmetry of E plays the same role of the optimal ball, even if it is not optimal. Indeed, if E is n-symmetric and \(|E|=|B|\), Lemma 4.4 states that if \(B(x_0)\) is an optimal ball then
a simple, but very useful property.
The next step is to pass from an n-symmetric to an axially symmetric set. This further reduction is achieved by proving, see Proposition 4.9, that if E is n-symmetric and \(E^*\) denotes its Steiner symmetral with respect to an axis passing through its center of symmetry, then we have
for some positive constant C depending only on n, provided that \(n=2\) or \(n\ge 3\) and the quantitative isoperimetric inequality holds true in dimension \(n-1\). To conclude the proof one has only to show that (4.3) holds true for the axially symmetric and n-symmetric set \(E^*\), i.e.
Then, (4.3) for E follows at once by combining this inequality with (4.4) and recalling that \(D(E^*)\le D(E)\), see Theorem 2.7.
4.1 Reduction to n-symmetric sets
As we said before the first step is to reduce to the case where the set E is contained in a cube of fixed edge length. To this aim, given \(l>0\) we denote be \(Q_l\) the open cube \((-l,l)^n\). Thus, we may state the following result, proved in [76, Lemma 5.1].
Lemma 4.2
There exist two constants, \(l,C>0\) depending only on n with the following property: given a measurable set \(E\subset \mathbb {R}^n\), with \(|E|=|B|\), it is possible to find a new set \(F\subset Q_l\), such that \(|F|=|B|\) and
Proof
By rotating E a little if necessary, we may assume that
Thus, Theorem 2.6 applied with \(k=n-1\) yields that the function
belongs to \(W^{1,1}(\mathbb {R})\). Hence, \(v_E\) is continuous. Set \(E^-_t=\{x\in E:\,x_1<t\}\) for all \(t\in \mathbb {R}\) and recall that if F is a set of finite perimeter, then by Theorem 2.2 we have \({\mathcal H}^{n-1}(F^{(1/2)}{\setminus }\partial ^*F)=0\). Therefore from (4.6) we have that for \({\mathcal H}^1\)-a.e. \(t\in \mathbb {R}\)
Let us now define a function \(g:\mathbb {R}\rightarrow \mathbb {R}^+\) as
From Fubini’s theorem it follows that g is a non-decreasing absolutely continuous function such that \(g'(t)=v_E(t)/\omega _n\) for \({\mathcal H}^1\)-a.e. \(t\in \mathbb {R}\). Therefore there exist \(-\infty \le a<b\le +\infty \) such that \(\{t:\ 0<g(t)<1\}=(a,b)\). Fix any \(t\in (a,b)\) and note that by definition
Therefore, by the isoperimetric inequality (1.4) \(P(g(t)^{-1/n} E_t^-)\ge P(B)\), hence
Similarly,
Therefore, from (4.7) we get that
for all \(t\in (a,b)\). On the other hand, from the definition of isoperimetric deficit we have \(P(E)=P(B)(1+D(E))\), and thus
Let us now define a function \(\psi :[0,1]\rightarrow \mathbb {R}^+\) as
Note that \(\psi (0)=\psi (1)=0\) and that \(\psi \) is a concave function attaining its maximum at 1 / 2, \(\psi (1/2)=2^{1/n}-1\). Therefore,
We may assume, without loss of generality, that \(2D(E)< \psi (1/2)\). Otherwise, since \(\alpha (E)\le 2\), the assertion immediately follows by choosing \(F=B\) and \(C=4/\psi (1/2)\). Then, let \(a<t_1<t_2<b\) be two numbers such that \(g(t_1)=1-g(t_2)\) and \(\psi (g(t_1))=\psi (g(t_2))=2D(E)\); therefore,
and by (4.9)
Thanks to (4.8) and (4.10), for \(\mathcal {H}^1\)-a.e. \(t_1\le t\le t_2\) we have
Therefore, recalling that \(v_E(t)=\omega _ng'(t)\),
for some constant \(\alpha =\alpha (n)\). Let us now set
Note that \(\tau _1\) and \(\tau _2\) are well defined since \(v_E\) is continuous and \(v_E(a)=v_E(b)=0\) and that by (4.10) and (4.12) \(v_E(\tau _1)=v_E(\tau _2)=(n\omega _nD(E))/2\). Moreover, from (4.11), we have
and a similar estimate holds for \(\tau _2-t_2\).
Let us now set \({\widetilde{E}}=E\cap \{x:\tau _1<x_1<\tau _2\}\). From the above estimate and (4.13), we have that \(\tau _2-\tau _1<\beta (n)\). Moreover, (4.11), the definition of \(\tau _1,\tau _2\) and (4.7) immediately yield
Let us now assume that \(D(E)<(2^{1/n}-1)/4\) and set
Clearly, \(|F|=|B|\) and F is contained in a strip \(\{\tau '_1<x_1<\tau '_2\}\), with \(\tau '_2-\tau '_1\le \beta '\), where \(\beta '\) is a constant depending only on n. Let us now show that F satisfies (4.5) for a suitable constant C depending only on n.
To this aim, note that since we are assuming D(E) small, from (4.14) we get that \(1\le \sigma \le 1+C_0D(E)\), with \(C_0=C_0(n)\). Thus, from (4.14), we get
Hence, the first inequality in (4.5) follows. To prove the second inequality, let us denote by B(x) an optimal ball for F. From the first inequality in (4.14), we then get
Thus, the set F satisfies (4.5). Starting from this set, we may repeat the same construction with respect to the \(x_{n-1}\) axis, thus getting a new set, still denoted by F, uniformly bounded with respect to the first two coordinate directions and satisfying (4.5) with a new constant, still depending only on n. Thus, the assertion follows by repeating this argument with respect to all remaining coordinate directions. \(\square \)
The next step is to show that we may reduce to a n-symmetric set. To this aim, following the terminology introduced in [76] we say that \(E\subset \mathbb {R}^n\) is an n-symmetric set if it is symmetric with respect to the n coordinate hyperplanes. Note that for an n-symmetric set it is not true in general that the optimal ball for the Fraenkel asymmetry is the one centered at the center of symmetry, see Fig. 2. However, this is true if the set E is convex as shown in the next result that was proved in [11, Lemma 5.9].
The optimal ball of a n-symmetric set is not always centered at the origin
Proposition 4.3
Let \(E \subset \mathbb {R}^n\) be an n-symmetric bounded convex set with \(|E| =|B_r|\). Then
Proof
Given \(F,G\subset \mathbb {R}^n\), consider their Steiner symmetral \(F^S\), \(G^S\) with respect to any coordinate hyperplane. Then, it is easily checked that \(|F^S\cap G^S|\ge |F\cap G|\). Since E is n-symmetric and convex, E is stable under the Steiner symmetrization with respect to any coordinate hyperplane. Hence for any \(x\in \mathbb {R}^n\) we have
from which (4.15) immediately follows. \(\square \)
On the other hand, though for n symmetric sets the ball centered at the origin is not always a minimizer for the Fraenkel asymmetry, yet it is ‘optimal’ up to a constant.
Lemma 4.4
Let E be n-symmetric, \(|E| = |B_r|\). Then
Proof
Let \(B_r(x_0)\) be an optimal ball for E. Since E is n-symmetric, also \(B_r(-x_0)\) is optimal. Thus, using twice the triangular inequality and the inequality \(|B_r(x_0) \Delta B_r|\le |B_r(x_0) \Delta B_r(-x_0)|\), we have
\(\square \)
Remark 4.5
The same argument used to prove the above lemma, shows that if E is symmetric with respect to k orthogonal hyperplanes \(H_1,\ldots ,H_k, k=1,\ldots ,n\), and \(H=\cap _{i=1}^kH_i\), then
The next theorem is the key point of the whole proof of the quantitative isoperimetric inequality via symmetrization.
Theorem 4.6
There exist \(\delta \) and C, depending only on n, such that if \(E \subset Q_l\), \(|E| =|B|\), \(D(E) \le \delta \), then there exists an n-symmetric set F such that \(F \subset Q_{2l}\), \(|F| = |E|\) and
Construction of \(E^+\) and \(E^-\)
The proof of Theorem 4.6 is quite tricky. In order to explain the strategy we start with some definitions. Given a hyperplane H, we consider the two half spaces \(H^+,H^-\) in which \(\mathbb {R}^n\) is divided by H and denote by \(r_H\) the reflection about H. Let E be a measurable set divided by the hyperplane H in two parts of equal volume. Then consider the two halves in which E is divided by H: \(E\cap H^+\) and \(E\cap H^-\) and the sets obtained by adding to each half its symmetral with respect to H, i.e.,
The construction is illustrated in Fig. 3. By construction, \(|E^+|=|E^-|=|E|\). Moreover, using Theorem 2.2 it is not too hard to show that
with the first inequality possibly being strict. Thus, if for some universal constant C(n) one had
iterating this estimate we would immediately get (4.17). Unfortunately, (4.20) is false, as shown by the example in Fig. 4, where we have \(\alpha (E) > 0\), but \(\alpha (E^+) = \alpha (E^-) =0.\)
Counterexample to (4.20)
The following proposition provides the right strategy in order to deal with such unpleasant situation.
Proposition 4.7
There exist \(\delta _0, C_0>0\) such that if E is a measurable set with finite measure and \(D(E) \le \delta _0\), given any two orthogonal hyperplanes \(H_1\), \(H_2\) dividing E in four parts of equal measure and the four sets \(E_1^{\pm }\), \(E_2^{\pm }\) defined as in (4.18) with H replaced by \(H_1\) and \(H_2\), respectively, we have that at least one of them, call it \(\widetilde{E}\), satisfies the estimate
In other words, even if some of the sets \(E_i^\pm \) have a small asymmetry (or even zero asymmetry as in Fig. 4), at least one of them must have a sufficiently large asymmetry, compared to the one of E. To convince oneself that indeed this is the case, observe that if we symmetrize the set of the previous example in the horizontal direction we get a larger asymmetry, see Fig. 5.
A different symmetrization may give a bigger asymmetry
Before proving Proposition 4.7 let us show the continuity of the asymmetry index with respect to the isoperimetric deficit which is a simple consequence of the compactness properties of sets of finite perimeter.
Lemma 4.8
Let \(l>0\). For any \(\varepsilon >0\) there exists \(\delta >0\) such that if \(E\subset Q_l\), \(|E|=|B|\), and \(D(E)\le \delta \) then \(\alpha (E)\le \varepsilon \).
Proof
We argue by contradiction. If the assertion is not true, there exist \(\varepsilon >0\) and a sequence of sets \(E_j\subset Q_l\), with \(|E_j|=|B|\), \(D(E_j)\rightarrow 0\) and \(\alpha (E_j)\ge \varepsilon >0\) for all \(j\in \mathbb {N}\). Since the sets \(E_j\) are all contained in \(Q_l\), thanks to Theorem 2.3 we may assume that up to a subsequence the \(E_j\) converge in measure to some set \(E_\infty \) of finite perimeter. Thus \(|E_\infty |=|B|\), and by the lower semicontinuity of the perimeters \(P(E_\infty )\le P(B)\), so \(E_\infty \) is a ball. However the convergence in measure of \(E_j\) to \(E_\infty \) immediately implies that \(|E_j\Delta E_\infty |\rightarrow 0\), against the assumption \(\alpha (E_j)\ge \varepsilon \). The contradiction concludes the proof. \(\square \)
Following [94, Th. 6.1] we may now give the proof of Proposition 4.7.
Proof of Proposition 4.7
Step 1 Without loss of generality we may assume \(|E|=|B|\). Let \(E^+_1\), \(E^-_1\), \(E^+_2\), \(E^-_2\), be the four sets obtained by reflecting E around the two orthogonal hyperplanes \(H_1\) , \(H_2\) dividing E in parts of equal measure. For \(i=1,2\) let \(B^\pm _i\) four balls of radius one such that
Observe that for \(i=1,2\), from the definition of \(B^\pm _i\) and the triangular inequality we have
To conclude the proof it is enough to show that if D(E) is sufficiently small at least one of the following two inequalities
holds. Indeed, if for instance the first inequality is true, from (4.22) applied with \(i=1\), recalling the definition of \(B^\pm _1\) and (4.16), we get
thus proving (4.21) with \(C_0=54\) and \(\widetilde{E}\) equal to \(E^+_1\) or \(E^-_1\).
Step 2 To prove (4.23) we argue by contradiction assuming that
and introduce the following unions of half balls
Then, by (4.24) we get that
The contradiction will be achieved if we show that
provided D(E) is sufficiently small. To this aim, recall that given \(\varepsilon >0\), Lemma 4.8, (4.16) and the second inequality in (4.19) yield that there exists \(\delta _0>0\) such that if \(D(E)<\delta _0\), then
Note that this inequality tells us that E is close in the sense of convergence in measure to its optimal balls. Similarly, also the balls \(B^\pm _i\) are close to the sets \(E^\pm _i\) in the same sense. Hence the centers of these balls are all close to each other and to the center of an optimal ball for E which in turn is close to the ball of radius 1 centered at the intersection of \(H^1\) and \(H^2\). Therefore all the four regions \(H_1^\pm \cap H_2^\pm \) contain almost one quarter of the balls \(B^\pm _i\). Therefore we may choose \(\varepsilon \) so small, and \(\delta _0\) accordingly, that for all possible choices of the \(\sigma ,\tau \in \{+,-\}\) we have
Thus, recalling the definition of \(S_1\) and \(S_2\), we have
From this inequality we have in particular that
and in a similar way that \(|B^+_2\cap B^-_2|<16|S_1\Delta S_2|\), thus proving the desired contradiction (4.25). \(\square \)
At this point we have all the ingredients for the proof of Theorem 4.6.
Proof of Theorem 4.6
Take \(\delta _1 = \delta _0 2^{-(n-1)}\), where \(\delta _0\) is chosen as in Proposition 4.7. By applying this proposition \(n-1\) times to different pairs of orthogonal directions and recalling (4.19) we find a set \(\widetilde{E}\), with \(|\widetilde{E}|=|B|\) such that
Moreover, by translating \(\widetilde{E}\) and relabeling the coordinate axes, if needed, we may assume without loss of generality that \(\widetilde{E}\) is symmetric about all the coordinate hyperplanes \(\{x_1=0\},\ldots ,\{x_{n-1}=0\}\). In order to get the last symmetry we take a hyperplane H orthogonal to \(e_n\) and dividing \(\tilde{E}\) into two parts of equal measure and consider the corresponding sets \(\widetilde{E}^+\), \(\widetilde{E}^-\). Again, by translating \(\widetilde{E}\) in the direction of \(e_n\), if necessary, we may assume that \(H=\{x_n=0\}\). As before we have
To control the asymmetry of \(\widetilde{E}^\pm \) observe that since \(\widetilde{E}\) is symmetric with respect to the first \(n-1\) coordinate hyperplanes, \(\widetilde{E}^+\) and \(\widetilde{E}^-\) are both n-symmetric so we can use Lemma 4.4 to get
Thus, at least one of the sets \(\widetilde{E}^\pm \) has asymmetry index greater than \(\frac{1}{3}\alpha (\widetilde{E})\). Therefore, denoting by F this set, we have
Finally, the inclusion \(F\subset Q_{2l}\) follows immediately from the construction performed in the proof of Proposition 4.7 and the one performed here. \(\square \)
4.2 Reduction to axially symmetric sets
From the results obtained in the previous section it is clear that in order to prove the quantitative isoperimetric inequality (4.3) we may assume without loss of generality that there exist \(\delta _0\in (0,1)\) and \(l>0\) such that
In fact, since \(\alpha (E)\le 2\) it is clear that if \(D(E)\ge \delta _0\) (4.3) follows immediately with \(\gamma (n)=4/\delta _0\). Thus, if \(\delta _0\) is sufficiently small Lemma 4.2 and Theorem 4.6 tell us that we may assume without loss of generality that E is contained in some cube of fixed size and that it is n-symmetric. Therefore, throughout this section we shall always assume that E satisfies the above assumptions (4.26).
The next step consists in reducing the general case to the case of an axially symmetric set, i.e., a set E having an axis of symmetry such that every non-empty cross section of E perpendicular to this axis is an \((n-1)\)-ball. To this aim we recall that the Schwarz symmetral of a measurable set E with respect to the \(x_n\) axis is defined as
where \(r_{E}(t)\) is the radius of the \((n-1)\)-dimensional ball having the same measure of the section \(E_t\), that is \({\mathcal H}^{n-1}(E_t)=\omega _{n-1}r_E(t)^{n-1}\). Note that \(E^*\) coincides with the Steiner symmetral of E with respect to the line \(\{x^\prime =0\}\). Therefore, from Theorem 2.7 we have that \(P(E^*)\le P(E)\). Moreover the properties stated in Theorems 2.6 and 2.7 apply to the functions defined for \({\mathcal H}^1\)-a.e. \(t\in \mathbb {R}\) as \(v_E(t):={\mathcal H}^{n-1}(E_t)\) and \(p_E(t):={\mathcal H}^{n-2}(\partial ^*E_t)\).
Proposition 4.9
Let E satisfy assumptions (4.26). If \(n=2\) or if \(n \ge 3\) and the quantitative isoperimetric inequality (4.3) holds true in \(\mathbb {R}^{n-1}\), then there exist a constant C(n) such that
Proof
The second inequality in (4.27) follows immediately from the fact that \(|E^*|=|E|\) and \(P(E^*)\le P(E)\). In order to prove the first inequality in (4.27) we start by assuming that
Thus, from Theorem 2.6 we have that \(v_E\) is an absolutely continuous function in \(\mathbb {R}\). We use Theorem 2.6 again and Theorem 2.7 to estimate
where the inequality before the last one follows from Hölder’s inequality. Since \(D(E) \le \delta _0< 1\), we have \(P(E^*) \le P(E) \le 2P(B)\). Therefore we get, observing that \(p_E\ge p_{E^*}\),
for some constant c depending only on n. Now assume that \(n \ge 3\) and observe that since \((E^*)_t\) is a \((n-1)\)-dimensional ball of radius \(r_E(t)\) with \({\mathcal H}^{n-1}\) measure equal to \({\mathcal H}^{n-1}(E_t)\), the ratio
is precisely the isoperimetric deficit in \(\mathbb {R}^{n-1}\) of \(E_t\). Since by assumption, the quantitative isoperimetric inequality (4.3) holds true in \(\mathbb {R}^{n-1}\), we have
where \(\alpha _{n-1}(E_t)\) is the \((n-1)\)-dimensional Fraenkel asymmetry of \(E_t\). But \(E_t\) is an \((n-1)\)-symmetric set in \(\mathbb {R}^{n-1}\) and \((E^*)_t\) is the ball centered at the center of symmetry of \(E_t\). Therefore from Lemma 4.4 we get
Inserting this inequality in (4.29) we then get
where the inequality before the last one follows from the inclusion \(E\subset Q_l\) and the last equality is just Fubini’s theorem. This proves (4.27). Hence the assertion follows when \(n\ge 3\).
If \(n=2\), since E is 2-symmetric, either \(E_t\) is a symmetric interval (hence \(E_t = E_t^*\)) or \(E_t\) is the union of at least two intervals with no endpoints in common, hence \(p_E(t) \ge 4\), while \(p_{E^*}(t) =2\). Moreover, since \(E\subset Q_l\), then \( {\mathcal H}^1(E_t \Delta E_t^*) \le 2l\) for all \(t\in \mathbb {R}\). Therefore, from (4.29) we get
thus concluding the proof also in this case.
Finally, if (4.28) does not hold, we approximate E in measure by a sequence of sets \(E_h\) obtained by rotating a little E so that (4.28) holds true for each \(E_h\). Then, the conclusion follows by observing that also \(E_h^*\) converge to \(E^*\) in measure and that (4.27) holds for all the sets \(E_h\). \(\square \)
For an axially symmetric set the proof of the quantitative isoperimetric inequality was given by a direct argument in [82, Th. 2]. A different proof can be also found in [76, Th. 4.2]. However both proofs are technically a bit complicate. Here we shall give a third proof due to Maggi [94, Sec. 7.2]. This last proof has two interesting features. First, it is based on a further and very natural reduction argument, which was not exploited in the original proof of (4.3) given in [76], the reduction to a connected set. This further reduction, is again a consequence of the strict concavity of the isoperimetric function. Another interesting feature is the use of some ideas from the mass transportation argument of Gromov’s proof of the isoperimetric inequality, to which we will come back in the next section. So, let us start with the reduction lemma proved in [94, Th. 4.4].
Lemma 4.10
There exists two positive constants, \(\delta \) and C, depending only on the dimension n, such that if E is a bounded open set of class \(C^\infty \) with \(D(E)\le \delta \) there exists a connected component F of E such that \(|F|>|E|/2\),
Proof
Without loss of generality we may assume \(|E|=|B|\). Since E is a smooth bounded open set, if E is not connected we may decompose it as the union of finitely many connected components \(E_h\), \(h\in I\subset \mathbb {N}\). Moreover, \(P(E)=\sum _{h\in I}P(E_h)\). From the isoperimetric inequality (1.4) we have
where \(a_h:=|E_h|/|B|\). Observe that \(\sum _{h\in I}a_h=1\) and assume that the \(a_h\) are arranged in decreasing order. If \(a_1>1/2\), from inequality (4.9) we have
hence \(|E{\setminus } E_1|\le C_0D(E)\), with \(C_0=\omega _n/ 2(2^{1/n}-1)\). Thus, we set \(F=E_1\) and we have, denoting by r the radius of the ball with the same measure of F,
From this inequality, since \(\omega _n(1-r^n)=|E{\setminus } E_1|\le C_0D(E)\) and \(\omega _nr^n=|F|>{|B|/2}\), we easily get
for some possibly bigger constant, still depending only on n. Similarly, denoting by \(B_r(x_0)\) an optimal ball for \(\alpha (F)\) we get
thus completing the proof of (4.30).
To conclude the proof of the lemma it is enough to show that if \(\delta \) is sufficiently small, in dependence on n, then \(a_1>1/2\). In fact, suppose that \(a_1\le 1/2\) and denote by \(N\ge 2\) the smallest integer such that \(\sum _{h< N}a_h\le 1/2\). Then, using again (4.9) and arguing as in the proof of (4.31), we have
Adding up these two inequalities we then conclude that
which is impossible if we choose \(\delta <2/(2^{1/n}-1)\). \(\square \)
We may now proceed to the proof of the quantitative isoperimetric inequality. As we already said before, for the final argument, i.e. the proof of (4.3) for an axially and n-symmetric set, we follow the argument of Maggi [94].
Proof of Theorem 4.1
Step 1 As we observed at the beginning of this section, it is enough to prove the quantitative inequality (4.3) only when E satisfies the assumptions (4.26) for a sufficiently small \(\delta _0\), depending only on the dimension, that will be specified during the proof. Observe that we may also assume without loss of generality that E is a bounded open set of class \(C^\infty \). Otherwise, by a standard approximation procedure, see for instance the proof of [8, Th. 3.42], we may find a sequence of n-symmetric smooth open sets \(E_h\) converging in measure to E, \(|E_h|=|E|\) for all h, \(P(E_h)\rightarrow P(E)\), satisfying the assumptions (4.26) with l possibly replaced by 2l. Then the quantitative isoperimetric inequality for E will follow from the same inequality for \(E_h\).
Finally, observe that we may also assume that E is connected. In fact if E were not connected, taking \(\delta _0\) sufficiently small we could apply Lemma 4.10 and consider the open connected component F of E such that \(|F|>|E|/2\), satisfying (4.30). Observe that also this connected component is n-symmetric. Indeed, consider for instance the hyperplane \(H=\{x_1=0\}\) and assume by contradiction that there exists \(x\in F\) such that its reflection \(r_H(x)\not \in F\). Then \(F\cap H=\emptyset \), since otherwise x and \(r_H(x)\) would belong to the same connected component of E, hence both would belong to F. Since E is n-symmetric, also \(r_H(F)\) is contained in E. However, this is not possible since F is contained either in \(H^+\) or in \(H^-\) and thus \(|F\cup r_H(F)|=2|F|>|E|\). This proves that \(r_H(F)=F\). By repeating this argument for all the coordinate hyperplanes, we conclude that F is n-symmetric. Thus, we may replace E by \(\lambda F\), where \(\lambda >0\) is such that \(\lambda ^n|F|=|B|\). The set \(\lambda F\) is now a bounded, smooth, open and connected set satisfying all the assumptions in (4.26), with l possibly replaced by 2l.
Consider the strips \(S=\{x:\,|x_n|<\sqrt{2}/2\}\) and \(S^\prime =\{x:\,|x_1|<\sqrt{2}/2\}\). Since \(B\subset S\cup S^\prime \) one of the two strips must contain at least one half of the measure of \(B{\setminus } E\). To fix the ideas, let us assume that S does it, that is \(|(B{\setminus } E)\cap S|\ge |B{\setminus } E|/2\). Therefore,
Denote by \(E^*\) is the Schwartz symmetral of E with respect to the \(x_n\) axis. We claim that if \(D(E^*)\) is sufficiently small, then
Note that the conclusion of the proof will follow immediately from (4.33). Indeed, assume \(n=2\) or \(n\ge 3\) and that (4.3) holds true in \(\mathbb {R}^{n-1}\). Then, if D(E) is sufficiently small, from Lemma 4.4, and (4.27), (4.32) and (4.33) we get
The rest of the proof will be devoted to prove (4.33).
Step 2 Set \(v(t):={\mathcal H}^{n-1}(E^*\cap \{x_n=t\})\). From our assumptions and Theorem 2.6 we have that \(v\in BV(\mathbb {R})\), v is symmetric with respect to 0 and \(\{v>0\}=(-a,a)\) for some \(a>0\). Observe that we may also assume without loss of generality that \(v\in W^{1,1}(\mathbb {R})\). Otherwise, we split v as \(v=v^a+v^s\) where \(v^a\) and \(v^s\) are nonnegative, symmetric with respect to 0, \(v^a\in W^{1,1}(\mathbb {R})\) and \(v^s\) is purely singular, see [8, Sect. 3.2], and we approximate \(v^s\) in \(L^1(\mathbb {R})\) with a sequence \(w_h\in C^1_c(\mathbb {R})\), with \(w_h\) nonnegative and symmetric with respect to 0, \(w_h>0\) in an interval \((-a',a')\) and such that \(\int _{-a}^a|w_h'|\rightarrow |Dv^s|(\mathbb {R})\) as \(h\rightarrow \infty \). Then denoting by \(E^*_h\) the axially symmetric sets such that \(v_{E^*_h}=v^a+w_h\), from (2.7) we get immediately that the \(E^*_h\) converge to \(E^*\) in measure and that \(P(E^*_h)\rightarrow P(E^*)\). Thus we prove (4.33) for \(E^*_h\) and then pass to the limit as \(h\rightarrow \infty \).
So, let us assume that \(v\in W^{1,1}(\mathbb {R})\) and in particular that it is continuous. We first show that if \(D(E^*)\) is sufficiently small, then the strip S contains a fairly large amount of the mass of \(E^*\). Precisely, we are going to show that there exist \(c_0\) and \(\delta _0\), depending only on the dimension n such that if \(D(E*)\le \delta _0\), then
In order to prove this inequality we compare the distribution function v of \(E^*\) with the distribution function w of B, defined as \(w(t):={\mathcal H}^{n-1}(B\cap \{x_n=t\})\).
We set \(c_0(n)=w(4/5)/3\) and then argue by contradiction. If (4.34) is not true, there exists \(t_0\in (-\sqrt{2}/{2},\sqrt{2}/{2})\subset (-4/5,4/5)\) such that \(v(t_0)<c_0\). Then, there exist \(t_1<t_0<t_2\) such that \((t_1,t_2)\) is the largest interval containing \(t_0\), contained in \((-4/5,4/5)\) and such that
By the definition of \(c_0\), recalling Lemma 4.4, we immediately have
Then Lemma 4.8 implies that \(t_2-t_1\) is small if \(D(E^*)\) is small. Therefore the closed interval \([t_1,t_2]\) is contained in \((-4/5,4/5)\) and thus in particular \(v(t_1)=v(t_2)=2c_0\). Now we compare \(E^*\) with the axially symmetric set whose distribution function \(v_F\) coincides with v outside the interval \((t_1,t_2)\) and such that \(v_F\equiv 2c_0\) in \((t_1,t_2)\). Then, setting \(\Sigma :=\mathbb {R}^{n-1}\times (t_1,t_2)\),
Clearly \(P(F;\Sigma )=c_1(n)(t_2-t_1)\) with \(c_1(n)\) depending only on \(c_0(n)\) and from (2.7) we have
Thus, from the above inequalities, observing that \(|F|\ge |E^*|=|B|\) and using the isoperimetric inequality, we get
Since by (4.35) \(t_2-t_1\rightarrow 0\) as \(D(E^*)\rightarrow 0^+\), from this inequality we get a contradiction if \(D(E^*)\) is sufficiently small.
Step 3 Recall that \(\{v>0\}=(-a,a)\) for some \(a>0\). Observe that (4.34) implies that \(a>\sqrt{2}/2\). Then, we define a function \(\tau :(-a,a)\rightarrow (-1,1)\) which associates to every sublevel \(E^*\cap \{x_n<t\}\) the sublevel \(B\cap \{x_n<\tau (t)\}\) with the same measure. Precisely, for all \(t\in (-a,a)\) we define \(\tau (t)\) as the unique number in \((-1,1)\) such that
Note that \(\tau \) is a strictly increasing \(C^1(-a,a)\) function and for all \(t\in (-a,a)\)
Since \(v\in W^{1,1}(\mathbb {R})\) the above equality implies that \(\tau \in W^{2,1}_{loc}(-a,a)\). Moreover, since w is locally Lipschitz in \((-1,1)\), setting \(I:=(-\sqrt{2}/2,\sqrt{2}/2)\), we get from (4.36)
for some constant C(n) depending only on the Lipschitz constant of w in I. Note that in the last inequality we have used the fact that since \(\tau (0)=0\) by the n-symmetry of E, then \(|t-\tau (t)|\le \int _I|1-\tau '|\). Thus, to achieve the proof of (4.33) we only need to show that
To this aim we introduce the map \(T:(-a,a)\times \mathbb {R}^{n-1}\mapsto \mathbb {R}^n\) defined as
Note that T maps every level set \(E^*\cap \{x_n=t\}\) into the level set \(B\cap \{x_n=\tau (t)\}\), and it is a one-to-one continuous map between the open sets \(E^*\) and B. Moreover for all \(0<b<a\), \(T\in W^{1,1}(E^*\cap (\mathbb {R}^{n-1}\times (-b,b));B)\). It is also easily checked that for a.e. \(x\in E^*\cap (\mathbb {R}^{n-1}\times (-a,a))\)
where we used that the function \(s\rightarrow s+(n-1)s^{-1/(n-1)}\) has a strict minimum at \(s=1\) for \(s>0\). Therefore, using the divergence theorem in the sets \(E^*\cap (\mathbb {R}^{n-1}\times (-b,b))\) and observing that \(\lim _{b\rightarrow a-}v(\pm b)=0\), we have
Therefore we have by Fubini’s theorem
where we used the elementary inequality \(n-1+t^n-nt\ge n(t-1)^2/2\) for all \(t>0\) and \(n\ge 2\). Then from the previous chain of inequalities we get, setting \(\sigma (t):=\tau ^\prime (t)^{1/(n-1)}\),
where the last inequality follows by observing that, since \(\int _{-a}^a\tau ^\prime dt=2\), \(\int _{-a}^a v dt=|E^*|=|B|\) and \(v\le (2l)^{n-1}\) by assumption (4.26), if \(n\ge 3\) we have
A similar estimate holds also when \(n=2\). To conclude the proof we observe that there exists a constant \(\lambda (n)\in (0,1)\) such that
To this aim, note that
for some positive constant \(c_2(n)\), provided that \(D(E^*)\), hence \(\alpha (E^*)\) is sufficiently small. On the other hand, by the very definition of \(\tau \), we have
Combining the two previous inequalities we get that \(1-\tau (\sqrt{2}/2)\ge c_3(n)\) for a suitable positive constant depending only on n, hence \(\tau (\sqrt{2}/2)\le 1-c_3(n)\). Since a similar inequality can be proved for \(\tau (-\sqrt{2}/2)\), (4.39) follows. Observe that (4.39), together with (4.36) implies that \(\sup _{t\in I}|\tau ^\prime (t)|\le C(n)\) for a suitable constant depending only on n. Then, recalling (4.34) and (4.38) we may conclude that
thus proving (4.37). \(\square \)
5 Other proofs and extensions
5.1 Isoperimetric inequality via mass transport
In the previous section we have presented the proof of the the quantitative isoperimetric inequality given in [76]. As we have seen, that proof was based on symmetrization arguments. The same approach has been used in several other papers to obtain quantitative versions of the Sobolev inequality, of the isoperimetric inequality in Gauss space and of other relevant geometric and functional inequalities, see for instance [43, 44, 75, 78]. On the other hand there are situations where one considers inequalities which are realized by non symmetric sets or functions.
This is the case of the anisotropic isoperimetric inequality. In order to state it let us fix some notation. Let \(\varphi :\mathbb {R}^n\rightarrow [0,\infty )\) be a positively 1-homogeneous, continuous function such that \(\varphi (x)>0\) for all \(x\not =0\). To the function \(\varphi \) we may associate the anisotropic perimeter, defined for any set E of finite perimeter as
It is well known that the isoperimetric sets for \(P_\varphi \) are the homothetic and translated of the so called Wulff shape set associated to \(\varphi \) which is given by
Then, the anisotropic isoperimetric inequality states that
for all sets of finite perimeter such that \(|E|=|W_\varphi |\), with equality holding if and only if E is a translated of the Wulff shape set \(W_\varphi \) (see [69, 70] and also [50] for a proof in two dimensions). Note that as in the case of the standard euclidean perimeter we have \(P_\varphi (W_\varphi )=n|W_\varphi |\). However, differently from the usual perimeter, \(P_\varphi \) is not invariant under the action of either O(n) or SO(n). Moreover, in general \(P_\varphi (E)\not =P_\varphi (\mathbb {R}^n{\setminus } E)\) unless \(\varphi \), hence \(W_\varphi \), is symmetric with respect to the origin.
The quantitative version of the anisotropic isoperimetric inequality is a remarkable result proved by Figalli et al. in [67]. It states that there exists a constant C, depending only on n, such that for any set of finite perimeter E such that \(|E|=r^n|W_\varphi |\)
where
denote the anisotropic asymmetry index and the anisotropic isoperimetric deficit, respectively.
Since the Wulff shape \(W_\varphi \) can be any bounded open convex set, it is clear that no symmetrization argument can be used to prove the anisotropic isoperimetric inequality or its quantitative counterpart (5.1). And in fact the strategy used in [67] is completely different from the one we have seen in the last section, since it relies on an optimal mass transportation argument and on the proof of a very general trace inequality.
To simplify even further the presentation of the main ideas used in the proof of Figalli et al. we shall only consider the case of the standard perimeter where inequality (5.1) reduces to the more familiar quantitative isoperimetric inequality (4.3). The starting point is a variant of Gromov’s proof of the classical isoperimetric inequality where the Knothe map originally used in [100, App. 1] is replaced by the Brenier map. Its main properties are stated in the next theorem, which follows from the results in [26, 93].
Theorem 5.1
Let \(\mu \) and \(\nu \) be two probability measures on \(\mathbb {R}^n\) with \(\mu \) absolutely continuous with respect to Lebesgue measure. Then there exists a convex function \(\varphi :\mathbb {R}^n\rightarrow \mathbb {R}\), such that the map \(T:=\nabla \varphi \) transports \(\mu \) onto \(\nu \), that is for every Borel function \(h:\mathbb {R}^n\rightarrow [0,\infty ]\)
Observe that (5.2) can be restated by saying that the map T pushes forward the measure \(\mu \) onto \(\nu \) (for the definition of the push forward of a measure see for instance [8, Sect. 1.5]). In the particular case that E is a set of finite perimeter with \(|E| = |B|\), setting \(\mu =\frac{1}{\omega _n}{\chi _{_{E}}}dx\) and \(\nu =\frac{1}{\omega _n}{\chi _{_{B}}}dx\), from the above theorem we may conclude (see also [97, Sect. 2.1]), that there exists a convex function \(\varphi :\mathbb {R}^n\rightarrow \mathbb {R}\) such that, setting \(T:=\nabla \varphi \), then \(T(x)\in B\) for a.e. \(x\in \mathbb {R}^n\) and for every Borel function \(h:B\rightarrow [0,\infty ]\)
Note that there is a regularity issue here, since \(\varphi \) is convex, hence T is defined only a.e. and it is just a BV map. However, in order to avoid technical complications, see the discussion in [67, Sect. 2.2], let us assume that T is a Lipschitz map. Under this extra assumption, by a change of variable, one easily gets from (5.3) that \(\mathrm{det}\nabla T(x)=1\) for a.e. \(x\in E\). Then we can give the
Gromov’s proof of the isoperimetric inequality
For every \(x\in E\) denote by \(\lambda _i(x)\), \(i=1,\ldots ,n\), the eingenvalues of the symmetric matrix \(\nabla T(x)\). Using the geometric–arithmetic mean inequality and the divergence theorem, we have
Observe that if \(P(E) = P(B)\) then \(\lambda _1(x) = \lambda _2(x) = \cdots = \lambda _n(x) = 1\) for a.e. \(x\in E\), since \(\mathrm{det} \,\nabla T(x) = 1\). Hence, up to a translation, T is the identity map and E is a ball.
\(\square \)
Let us try to exploit this argument to prove the quantitative isoperimetric inequality. Since, by definition,
from the inequalities above we immediately get that
It is not too difficult to show (see [67, Corollary 2.4]) that (5.4) implies that there exists a constant C depending only on n such that, if \(D(E)\le 1\), then
where I stands for the identity matrix. Let us assume for a moment that the set E is so good to satisfy a Poincaré inequality for some universal constant depending only on n and let us see what information we may deduce from (5.6). Indeed, it can be proved that if D(E) is smaller than some positive \(\delta \) depending only on n one may remove from E a small critical set, whose measure is controlled by D(E), such that outside this critical set a Poincaré inequality holds true with a constant depending only on n. Therefore, by a reduction argument, we may assume that
Therefore, by translating E we have from (5.6) that
Therefore, given \(\varepsilon >0\), from the previous inequality we get
Minimizing the right hand side of this inequality with respect to \(\varepsilon \) we then get
that is the quantitative isoperimetric inequality with the not optimal exponent 4. Note however that this argument can never lead to a proof of the quantitative isoperimetric inequality: firstly, because even if E is a connected open set the constant of the Poincaré inequality may blow up in presence of small cusps; secondly because in the above argument we are not taking into account the information contained in the inequality (5.5) derived from Gromov’s proof.
Indeed the strategy followed in [67] is more subtle. Namely, one can show that if E has small deficit, then (see [67, Th. 3.4 and Lemma 3.1]), up to removing a small critical set from E whose measure is controlled by D(E), one may assume that E satisfies the following trace inequality
for some constant \(\tau \) depending only on n. Then, by applying the previous inequality to the map \(T-Id\), up to translating E conveniently, we have, recalling (5.6),
Combining this inequality with (5.5), we obtain, assuming \(D(E)\le 1\),
The proof of the quantitative isoperimetric inequality (4.3) then immediately follows from this estimate since, see [67, Lemma 3.5], there exists a constant C(n) such that, see Fig. 6,
Beside providing an alternative proof of the quantitative isoperimetric inequality in the wider framework of anisotropic perimeter, the paper by Figalli et al. contains several interesting results. In particular, Theorem 3.4 which states that given any set of finite perimeter E with small deficit one may always extract from E a maximal set for which a trace inequality holds with a universal constant. This is a new and deep result that may have several applications. Moreover, the mass transportation approach used in [67] has been also successfully used to obtain the quantitative versions of other important inequalities, see [43, 66, 68].
\(|E \Delta B_1| \le C\int _{\partial ^*E} \big | 1-|x| \big |\)
5.2 Quantitative isoperimetric inequality via regularity
Another very interesting proof of the quantitative isoperimetric inequality has been recently given by Cicalese and Leonardi in [45]. The starting point is the quantitative inequality (3.2) proved by Fuglede for nearly spherical sets and the observation that all known examples suggest that the quantitative inequality becomes really critical only when the set E is a small perturbation of a ball. Therefore their idea is to reduce the general case to the case of nearly spherical sets via a contradiction argument. Precisely, they start by assuming that there exists a sequence of sets \(E_j\), converging in measure to the unit ball, for which the quantitative inequality does not hold. Then they replace it with a different sequence of sets \(F_j\), still not satisfying the quantitative inequality, but converging to B in \(C^1\), thus contradicting Fuglede’s Theorem 3.1 for nearly spherical sets. The sets \(F_j\) are constructed as the solutions of certain minimum problems and their convergence in \(C^1\) to the unit ball is a consequence of the a priori estimates for perimeter almost minimizers established in the theory of minimal surfaces.
Though the approach of Cicalese and Leonardi to the quantitative isoperimetric inequality is based on the results of a difficult and deep theory, it has the advantage of providing a short proof that has been successfully applied to several other inequalities, see [1, 18, 19, 24, 47, 48, 74]. The proof we are going to present here is a further simplification of the original proof by Cicalese and Leonardi which has been developed in a more general context by Acerbi et al. in [1]. To this aim, let us quickly recall the definition and the regularity properties of the perimeter almost minimizers.
Let \(\omega , r_0\) be positive numbers. A set F of finite perimeter is an \((\omega ,r_0)\)-almost minimizer if, for all balls \(B_r(x)\) with \(r<r_0\) and all measurable sets G such that \(F \Delta G \subset \subset B_r(x)\), we have
see (Fig. 7). Thus, an almost minimizer locally minimizes the perimeter up to a higher order error term. The main properties of almost minimizers are contained in the following statement which is essentially due to Tamanini, see [114, Sect. 1.9 and 1.10] and also [95, Th. 26.5 and 26.6].
A perimeter almost minimizer F
Theorem 5.2
If E is an \((\omega , r_0)\)-almost minimizer, then \(\partial ^*E\) is a \(C^{1,1/2}\) manifold, \(\partial E{\setminus }\partial ^*E\) is relatively closed in \(\partial E\) and \({\mathcal H}^s(\partial E {\setminus } \partial ^* E)=0\) for all \(s> n-8\). Moreover, if \(E_j\) is a sequence of equibounded \((\omega , r_0)\)-almost minimizers converging in measure to a \(C^2\) open set E, then for j large each \(E_j\) is of class \(C^{1,1/2}\) and the sequence \(E_j\) converges to E in \(C^{1,\alpha }\) for all \(0<\alpha <1/2\).
As we said above the starting point of the proof is the Fuglede estimate for nearly spherical sets. Recall that Theorem 3.1 states that there exist two positive constants \(\varepsilon (n)\), \(c_0(n)\) such that if E is an open set with \(|E|=|B|\), the barycenter of E is at the origin and \(\partial E = \{ x + u(x): x \in \partial B\}\) for a Lipschitz function u such that \(\Vert u\Vert _{W^{1,\infty }(\mathbb {S}^{n-1})}< \varepsilon \), then the following estimate holds
We also need the following simple lemma.
Lemma 5.3
If \(\Lambda > n\), the unique solution up to translations of the problem
is the unit ball.
Proof
By the isoperimetric inequality it follows that in order to minimize the functional in (5.9), we may restrict to the balls \(B_r\). Thus the above problem is equivalent to minimizing in \([0,\infty )\) the function \(r\rightarrow nr^{n-1}+\Lambda |r^n-1|\), which has a unique minimum for \(r=1\), if \(\Lambda >n\). \(\square \)
We are now ready to give the proof of the quantitative isoperimetric inequality (4.3) via regularity. Before that we need also to introduce the non-rescaled asymmetry index by setting for any measurable set E of finite measure
Proof of the quantitative isoperimetric inequality via regularity
Step 1 Thanks to Lemma 4.2 we may assume, without loss of generality, that \(|E|=|B|\) and that \(E\subset B_{R_0}\), for some \(R_0\) depending only on n. As we have already observed in the previous section, in order to prove (4.3) it is enough to show that
Claim There exists \(\delta _0>0\) such that if \(E\subset B_{R_0}\), \(|E|=|B|\) and \(P(E)-P(B)\le \delta _0\), then
where \(c_0\) is the constant in (5.8).
To this aim we argue by contradiction assuming that there exist a sequence \(E_j \subset B_{R_0}, |E_j| = |B|\), with \(P(E_j) \rightarrow P(B)\) and
Since \(P(E_j) \rightarrow P(B)\), by the compactness Theorem 2.3 we may assume that up to a subsequence the sets \(E_j\) converge in measure to some set E. Then, by the lower semicontinuity of the perimeter we get that \(P(E)=P(B)\). Thus E is a ball of radius 1 and we may conclude that \(A(E_j)\rightarrow 0\) as \(j\rightarrow \infty \). Now, to achieve the proof of (5.10), we would like to replace the \(E_j\) with a sequence of sets converging to B in \(C^1\) and contradicting inequality (5.8).
To build this new sequence, for every j we consider a minimizer \(F_j\) of the problem:
where \(\Lambda >n\) is a fixed constant. Using again the compactness Theorem 2.3 we may assume that the sets \(F_j\) converge in measure to a set F. Moreover, the lower semicontinuity of the perimeter immediately yields that F is a minimizer of the problem:
Therefore by Lemma 5.3 we may conclude that the sequence \(F_j\) converge in measure to a ball \(B(x_0)\). Let us now show that this convergence holds indeed in \(C^1\). To this aim, by Theorem 5.2 it is enough to prove that each \(F_j\) is an \(\left( \omega , R_0 \right) \)-almost minimizer for some \(\omega >0\). To prove this take a ball \(B_r(x)\) with \(r<R_0\) and a set G such that \(F_j \Delta G \subset \subset B_r(x)\). Two cases may occur.
Case 1 \(G \subset \bar{B}_{R_0}\). Then, by the minimality of \(F_j\) we get
Case 2 \(|G {\setminus } \bar{B}_{R_0}| > 0\). In this case we split G as follows
Since \(G \cap B_{R_0} \subset B_{R_0}\), as before we have
while
by the isoperimetric inequality. Therefore we may conclude that the sets \(F_j\) are all \(\left( (\Lambda + 1)\omega _n, R_0 \right) \)-almost minimizers and that they converge to a ball \(B(x_0)\) in \(C^{1,\alpha }\) for all \(\alpha <1/2\).
Step 2 By the minimality of the \(F_j\), recalling (5.11) and using Lemma 5.3, we get
Therefore, we have that \(|A(F_j) - A(E_j)| \le \frac{c_0}{2}A(E_j)^2\) and since \(A(E_j)\rightarrow 0\) we get that \(A(F_j)/A(E_j)\) \(\rightarrow 1\) as \(j\rightarrow \infty \).
To conclude the proof we need only to adjust the volumes of the sets \(F_j\). For this reason we set \(\tilde{F}_j = \lambda _j F_j\), where \(\lambda _j\) is chosen so that \(|\tilde{F}_j| = |B|\). Note that \(\lambda _j\rightarrow 1\) since the \(F_j\) are converging in \(C^1\) to \(B(x_0)\). Observe also that, since \(P(F_j)\rightarrow P(B)\) and \(\Lambda >n\), for j large we have \(P(F_j)<\Lambda |F_j|\). Therefore for j large we have
From this estimate, recalling (5.13) we get that
However, since \(A(F_j)/A(E_j)\rightarrow 1\) as \(j\rightarrow \infty \) we have \(A(E_j)^2<2 A(\tilde{F}_j)^2\) for j large. Therefore, from (5.14) we obtain
which is a contradiction to (5.8) since, up to translations, the sets \(\tilde{F}_j\) have all barycenter at the origin and are converging in \(C^1\) to the unit ball. This contradiction proves the Claim, thus concluding the proof of the quantitative inequality. \(\square \)
5.3 An improved version of the quantitative isoperimetric inequality
Let E be a nearly spherical set and let us look back at the estimate (3.2) stated in Fuglede’s Theorem 3.1. Observe that in the previous argument we have only used part of the information provided by (3.2), since we have not exploited the presence of the full norm of u in \(H^1(\mathbb {S}^{n-1})\).
The fact that in the quantitative isoperimetric inequality (4.3) we are throwing away some valuable information encoded in the isoperimetric deficit D(E) can be understood by looking at the two sets E and F in Fig. 8. Indeed, E and F have the same measure, the same Fraenkel asymmetry, but \(D(E) << 1\), while \(D(F) >> 1\). Therefore the quantitative inequality (4.3) gives a sharp information on E while it is useless when applied to F. The reason is that the isoperimetric deficit depends strongly on the oscillation of the boundary of the set, while the Fraenkel asymmetry only looks at the distance in measure of a set from a ball.
E and F have the same measure and the same asymmetry
This suggests that we should introduce a more precise index which takes into account also the oscillation of the normals. To this aim, given a set of finite perimeter E and a ball \(B_r(y)\) with the same volume as E, we are going to measure the distance from E to the ball in the following way, see Fig. 9. For every point \(x\in \partial ^*E\) we take the projection \(\pi _{y,r}(x)\) of x on the boundary of \(B_r(y)\) and consider the distance \(|\nu ^E(x)-\nu ^{r,y}(\pi _{y,r}(x))|\) from the exterior normal to E at the point x to the exterior normal to \(B_r(y)\) at the projection point \(\pi _{y,r}(x)\). Then, we take the \(L^2\) norm of this distance and minimize the resulting norm among all possible balls, thus getting
We shall refer to \(\beta (E)\) as to the oscillation index (or excess) of the set E.
The construction of the oscillation index
Observe that Fuglede’s Theorem 3.1 provides indeed an estimate for the oscillation index. In fact, if E is a nearly spherical set satisfying (3.1), \(|E|=|B|\) and the \(W^{1,\infty }\) norm of u is sufficiently small, by (3.14) at every point \(x\in \partial ^*E\) the exterior normal to E is given by
where \(z=x/|x|\) and thus \(x=z(1+u(z))\). Hence, from (3.2) we have
for some constant \(\widetilde{C}\) depending only on n. The next result, proved by Julin and the author in [74], is an improved version of the quantitative isoperimetric inequality.
Theorem 5.4
There exists a constant \(\kappa (n)\), such that for any set of finite perimeter E, with \(|E|=|B_r|\) for some \(r>0\),
Inequality (5.17) is stronger than (4.3), since a Poincaré type inequality shows that the asymmetry index \(\alpha \) is always controlled by \(\beta \), see Proposition 5.5. Before proving this, let us give a closer look to the new index. Observe that by the divergence theorem we immediately have
Therefore, we may write
where we have set
If \(y\in \mathbb {R}^n\) is the center of an optimal ball for \(\beta (E)\) then y maximizes the integral on the right hand side of (5.19). Such a point will be called a center for the set E. Note that in general such a center is not unique. The next result is contained in [74, Prop. 1.2].
Proposition 5.5
There exists a constant C(n) such that if E is a set of finite perimeter, with \(|E|=|B_r|\) for some \(r>0\), then
Proof
Let E be a set of finite perimeter. Without loss of generality we may assume that \(|E| = |B|\) and that E is centered at the origin, i.e.,
Since \(\beta (B)=0\), hence \(P(B)=(n-1)\int _E\frac{1}{|x|}dx\), from the equality above and (5.18) we have
Let us estimate the last two terms in (5.20). Since \(|E| = |B|\) we have
Denote by \(A(R,1) = B_R {\setminus } B_1\) and \(A(1,r) = B_1 {\setminus } B_r\) two annuli such that \(|A(R,1)| = |A(1, r)| =a\). Hence,
By construction \(|A(R,1)| = |E {\setminus } B|\). Therefore, since \(\frac{1}{|x|}\) is radially decreasing,
Similarly, we have
Therefore we may estimate (5.20) by
The function \(f(t) = (1 + t)^{\frac{n-1}{n}}\) is uniformly concave in \([-1,1]\) and there exists a positive constant c(n) such that for all \(s,t\in [-1,1]\)
Therefore, recalling (5.21), we may estimate (5.22) by
Hence, the assertion follows. \(\square \)
The strategy for proving inequality (5.17) is the same that we have seen in the previous section and the starting point is again Fuglede’s inequality (3.2) which implies in particular (5.17) if E is a nearly spherical set sufficiently close in \(W^{1,\infty }\) to the unit ball. However, beside using the regularity properties of perimeter almost minimizers, we need to introduce another notion of minimality. We say that a set of locally finite perimeter E is an area \((K, r_0)\) -quasi-minimizer if for every F, such that \( F \Delta E \subset \subset B_{r}(x)\), with \(r \le r_0\), the following inequality holds
We observe that this definition is the counterpart in the framework of sets of finite perimeter of the notion of quasi-minimum introduced by Giaquinta and Giusti in [79] in the context of variational integrals. Therefore it is not surprising that although quasi-minimality is a very weak property, yet area quasi-minimizers have some kind of mild regularity. This is indeed the content of the next result which was first proved by David and Semmes in [51] and then extended by Kinnunen et al. [88] to the metric spaces setting.
Theorem 5.6
Suppose that E is an area \((K, r_0)\)-quasi-minimizer. Then there exists \(C>1\) such that for any \(0 < r< r_0\) and every \(x \in \partial E\) there are points \(y,z \in B_r(x)\) for which
We are now ready to prove the main result of this section.
Proof of Theorem 5.4
Step 1 As in the previous section, we start by observing that in order to prove (5.17) it is enough to assume \(|E|=|B|\) and that D(E) is smaller than a given constant \(\delta _0\) to be chosen later. Moreover, the same reduction argument used to prove Lemma 4.2 shows that also in this case we may assume without loss of generality that \(E\subset B_{R_0}\), where the radius \(R_0\) depends only on the dimension n, see [74, Lemma 3.2].
Let \(c_0>0 \) be a constant which will be chosen at the end of the proof. From what we have just observed it is enough to show that there exists \(\delta _0>0\) such that, if \(D(E) \le \delta _0\), \(E\subset B_{R_0}\) and \(|E|=|B|\), then
We argue by contradiction assuming that there exists a sequence of sets \(E_j \subset B_{R_0}\) such that \(|E_j| = |B|\), \(D(E_j) \rightarrow 0\) and
By the compactness Theorem 2.3 it follows that, up to a subsequence, \( E_j \rightarrow E_{\infty }\) in measure and by the lower semicontinuity of the perimeter we immediately conclude that \( E_{\infty }\) is a ball of radius one. It is easily checked that the functional \(\gamma \) defined in (5.19) is continuous with respect to the convergence in measure. Therefore, since the \(E_j\) are converging to a ball of radius one and \(P (E_j) \rightarrow P(B)\), we have that
As in the previous section we replace each set \(E_j\) by a minimizer \(F_j\) of the following problem
for some fixed \(\Lambda > n\). It is not too hard to show that the above functional is lower semicontinuous with respect to the convergence in measure, see [74, Lemma 3.4], and therefore a minimizer exists. Moreover, up to a subsequence, we may assume that \(F_j \rightarrow F_{\infty }\) in measure. From the minimality of \(F_j\), (5.23) and Lemma 5.3 we have that
Hence \(| \beta (F_j)^2 -\beta (E_j)^2| \le 4 c_0 \beta (E_j)^2\), which implies \(\beta (F_j) \rightarrow 0\) and
Therefore \(F_{\infty }\) is a minimizer of the problem
Thus from Lemma 5.3 we conclude that \(F_{\infty }\) is a ball \(B(x_0)\), for some \(x_0\in \mathbb {R}^n\).
Step 2 We claim that for any \(\varepsilon >0\), \(B_{1- \varepsilon }(x_0) \subset F_j \subset B_{1+\varepsilon }(x_0) \) for j large enough.
To this aim we show that the sets \(F_j\) are area \((K, r_0)\)-quasi-minimizers and use Theorem 5.6. Let \(G\subset \mathbb {R}^n\) be such that \(G \Delta F_j \subset \subset B_r(x)\), \(r \le r_0\).
Case 1 Suppose that \(B_r(x) \subset B_{R_0}\). By the minimality of \(F_j\) we obtain
Assume that \(\beta (F_j)\ge \beta (G)\) (otherwise the argument is similar) and denote by \(y_G\) a center of G. Then we get
Therefore, from (5.25) we get
From the above inequality the \((K, r_0)\)-quasi-minimality immediately follows observing that
and choosing \(r_0 \) sufficiently small.
Case 2 If \( |B_r(x) {\setminus } B_{R_0} | >0\), we may write
From Case 1 we have that this term is less than \((K-1) P(G \cap B_{R_0}; B_r(x))\) which in turn is smaller than \((K-1) P(G; B_r(x))\). Hence, all \(F_j\) are \((K, r_0)\)-quasi-minimizers with uniform constants K and \(r_0\). The claim then follows from the theory of \((K, r_0)\)-quasi-minimizers and the fact that \(F_j \rightarrow B(x_0)\) in \(L^1\). Indeed, arguing by contradiction, assume that there exists \(0<\varepsilon _0<2r_0\) such that for infinitely many j one can find \(x_j\in \partial F_j \) for which
Let us assume that \(x_j \in B_{1- \varepsilon _0}(x_0)\) for infinitely many j (otherwise, the argument is similar). From Theorem 5.6 it follows that there exist \(y_j \in B_{\frac{\varepsilon _0}{2}}(x_j)\) such that \(B_{\frac{\varepsilon _0}{2C}}(y_j) \subset B(x_0) {\setminus } F_j\). This implies
which contradicts the fact that \(F_j\rightarrow B(x_0)\) in \(L^1\), thus proving the claim.
Step 3 Let us now translate \(F_j\), for j large, so that the resulting sets, still denoted by \(F_j\), are contained in \(B_{R_0}\), have their barycenters at the origin and converge to B. We are going to use Theorem 5.2 to show that the \(F_j\) are \(C^{1,1/2}\) and converge to B in \(C^{1, \alpha }\) for all \(\alpha <1/2\). To this aim, fix a small \(\varepsilon >0\). From Step 2 we have that for j large
We want to show that when j is large \(F_j\) is a \((\Lambda ',r_0)\)-almost minimizer for some constants \(\Lambda ',r_0\) independent of j. To this aim, fix a set \(G\subset \mathbb {R}^n\) such that \(G \Delta F_j \subset \subset B_r(y) \), with \(r<r_0\).
If \(B_r(y) \subset B_{1- \varepsilon }\), from (5.26) it follows that \(G \Delta F_j \subset \subset F_j\) for j large enough. This immediately yields \(P(F_j) \le P(G)\).
If \(B_r(y) \not \subset B_{1- \varepsilon }\), choosing \(r_0\) and \(\varepsilon \) sufficiently small we have that
Denote by \(y_{F_j}\) and \(y_G\) the centers of \(F_j\) and G, respectively. If \(\varepsilon \) is sufficiently small, from (5.26) and Lemma 5.7 below we have that for j large
By the minimality of \(F_j\) we have
which immediately implies
We may estimate the last term simply by
and
Therefore, recalling (5.27) and (5.28), we have
From this estimate and inequality (5.29) we may then conclude that
Hence, the sets \(F_j\) are \((\Lambda ', r_0)\)- almost minimizers with uniform constants \(\Lambda '\) and \( r_0\).
Thus, Theorem 5.2 yields that the \(F_j\) are \(C^{1, 1/2}\) and that, for j large,
for some \(u_j\in C^{1,1/2}(\partial B)\) such that \(u_j \rightarrow 0\) in \(C^{1}(\partial B_1)\).
Step 4 By the minimality of \(F_k\), (5.23) and (5.24) we have
We are almost in a position to use (5.16) to obtain a contradiction. We only need to rescale the \(F_j\) so that the volume constraint is satisfied. Thus, set \(F_j' := \lambda _j F_j\), where \(\lambda _j\) is such that \(\lambda _j ^n|F_j| = |B|\). Then \(\lambda _j \rightarrow 1 \) and also the sets \(F_j' \) converge to B in \(C^1\) and have their barycenters at the origin. Therefore, since \(\Lambda >n\), \(P(F_j)\rightarrow n|B|\) and \(|F_j|\rightarrow |B|\), we have that for j sufficiently large
which contradicts (5.16) if \(2c_0/(1-4c_0)<1/{\widetilde{C}}\) and j is large. \(\square \)
Lemma 5.7
For every \(\varepsilon >0\) there exists \(\delta >0\) such that if \(F \subset B_{R_0}\) and \(|F \Delta B| < \delta \), then \(|y_F| < \varepsilon \) for every center \(y_F\) of F.
Proof
We argue by contradiction and assume that there exist \(F_j \subset B_{R_0}\) such that \(F_ j\rightarrow B\) in measure and \(y_{F_j} \rightarrow y_0\) with \(|y_0| \ge \varepsilon \), for some \(\varepsilon >0\). Then we would have
Letting \(j \rightarrow \infty \), by the dominated convergence theorem the left hand side converges to \(\int _{B} \, \frac{1}{|x|} \, dx\), while the right hand side converges to \(\int _{B} \, \frac{1}{|x - y_0|} \, dx\). Thus we have
By the divergence theorem we conclude that
and this inequality may only hold if \(y_0=0\), thus leading to a contradiction. \(\square \)
We conclude this section quoting a recent paper by Neumayer [103] dealing with the same kind of improved quantitative estimate that we have discussed here, but in the case of the anisotropic perimeter. It turns out that if the function \(\varphi \) which defines the anisotropic perimeter is of class \(C^2\) and satisfies a suitable form of ellipticity, then one can prove an inequality of the type (5.17) with \(\beta \) replaced by a suitable anisotropic oscillation index. In this case, see [103, Th. 1.5] one may get the stability estimate with the exponent 2 and a constant depending on the function \(\varphi \). In the general case, i.e., when no assumptions on \(\varphi \) are made, a stability estimate is still obtained with a constant depending only on the dimension, but with a not optimal power [103, Th. 1.1].
5.4 The isoperimetric inequality in higher codimension
The isoperimetric inequality in higher codimension goes back to a celebrated paper by Almgren [3]. In that paper he proved the manifold counterpart of the classical isoperimetric inequality established by De Giorgi in [53]. Though stated in the framework of currents, in the particular case of a smooth \((n-1)\)-dimensional manifolds \(\Gamma \subset \mathbb {R}^{n+k}\) without boundary, spanning an area minimizing smooth surface M, his inequality states that
where D is an n-dimensional flat disk with the same area as M. Moreover equality occurs if and only if \(\Gamma \) is the boundary of a flat disk. The stability of this inequality has been addressed, in the context of currents, in a recent paper by Bögelein et al. [18]. In order to describe the result we restrict to the case of smooth \((n-1)\)-dimensional closed surfaces \(\Gamma \) in \(\mathbb {R}^{n+k}\) and give the definitions of the quantities that come into play.
Denoting by \(Q(\Gamma )\) an area minimizing n-dimensional surface with boundary \(\Gamma \) the isoperimetric deficit is defined as
where \(D_r\) is an n-dimensional flat disk in \(\mathbb {R}^{n+k}\) with the same area as \(Q(\Gamma )\), i.e., \({\mathcal H}^n(D_r)= {\mathcal H}^n(Q(\Gamma ))\). Note that the area minimizing surface \(Q(\Gamma )\) may have singularities even if \(\Gamma \) is smooth. It is then clear why the use of currents with finite mass becomes unavoidable even to give the basic definitions. This is even more true in the case of the asymmetry index \(\varvec{\alpha }(\Gamma )\) whose precise definition is more technical and requires the use of a certain seminorm defined for integer multiplicity currents [18, Sect. 2]. However, the underlying geometric idea is easy to describe. Given any flat disk \(D_r\) with the same area as \(Q(\Gamma )\), first one considers an area minimizing cylindric type surface \(\Sigma (D_r)\) spanned by the boundary components \(\Gamma \) and \(\partial D_r\), and afterwards one takes the infimum of the surface area \({\mathcal H}^n(\Sigma (D_r))\) among all possible disks \(D_r\):
With these definitions in hand we may state the following quantitative isoperimetric inequality proved in [18, Th. 2.1].
Theorem 5.8
Let \(n\ge 2\) and \(k\ge 0\). There exists a constant \(C=C(n,k)>0\) such that for any \((n-1)\)-dimensional closed surface \(\Gamma \subset \mathbb {R}^{n+k}\) the following inequality holds:
Note that if \(\Gamma \) is the boundary of a smooth open set E contained in an n-dimensional hyperplane, then the asymmetry index \(\varvec{\alpha }(\Gamma )\) coincides with the Fraenkel asymmetry index \(\alpha (E)\) defined in (4.1). Hence, (5.32) reduces to (4.3). In particular this shows that the exponent 2 on the left hand side of the inequality cannot be improved, since we know that it is already optimal for (4.3).
As in the two previous sections the strategy to prove Theorem 5.8 is to show first a Fuglede type inequality and then to reduce the general case to it via a regularity argument. However, here the situation is more delicate and involved due to the higher codimension. First of all, the analogue of Fuglede’s result deals with a spherical graph over \(\mathbb {S}^{n-1}\) in \(\mathbb {R}^{n+k}\), i.e., a manifold \(\Gamma \) which can be parametrized by a map \(X:\mathbb {S}^{n-1}\rightarrow \mathbb {R}^{n+k}\) of the form
where \(u\in C^1(\mathbb {S}^{n-1})\) and \(v\in C^1(\mathbb {S}^{n-1},\mathbb {R}^k)\) have both small \(C^1\)-norms. In the present case a substantial difficulty arises from the fact that, beside imposing the volume constraint \({\mathcal H}^n(Q(\Gamma ))=\omega _n\) and that the barycenter of \(\Gamma \) is at the origin, we have also to fix some second order quantities. This can be done for instance by assuming that they are all equal to zero, i.e.,
for any choice of \(i=1,\ldots ,n\) and \(j=n+1,\ldots ,n+k\). Differently from the case \(k=0\) considered in Sect. 3, in which v does not appear, the conditions (5.33) play a crucial role in the estimation of the \(n\cdot k\) first order Fourier coefficients of v. Instead, the bounds on the first order Fourier coefficients of u and the zero order Fourier coefficient of v follow from the barycenter condition, while the zero order Fourier coefficient of u is controlled by using the constraint \({\mathcal H}^n(Q(\Gamma ))=\omega _n\). Then, under the above assumptions on u and v one has the following inequality, see [18, Th. 4.1],
where c(n) is a constant depending only on n, provided the \(C^1\) norms of u and v are sufficiently small. Note also that
Combining this inequality with (5.34) one then gets the quantitative isoperimetric inequality (5.32) in this case.
The next step is to reduce the general case to the previous one by the same contradiction argument that we have seen in Sect. 5.2. Beside the technical complications due to the fact that one is now dealing with higher codimension, the main ingredients come from the theory of currents that ‘almost’ minimize certain elliptic variational integrals. The regularity results needed in the proof were obtained in [20, 54].
5.5 The isoperimetric inequality on the sphere
The isoperimetric property of geodesic balls on the sphere and in hyperbolic spaces goes back to Schmidt [108]. Before stating it, let us fix some basic notation. Recall that if x, y are two points in the n-dimensional sphere \(\mathbb {S}^n\subset \mathbb {R}^{n+1}\), \(n\ge 1\), the geodesic distance between them is given by
Thus, the open geodesic ball with center at a point \(p\in \mathbb {S}^n\) and radius \(\vartheta \in (0,\pi )\) is defined by setting
We just write \(B_{\vartheta }\) if the center of the geodesic ball is at the north pole \(e_{n+1}\). Then, the isoperimetric inequality on the sphere states that if \(E\subset \mathbb {S}^n\) is a Borel set such that \({\mathcal H}^n(E)={\mathcal H}^n(B_{\vartheta })\) then
with the equality occurring if and only if E is a geodesic ball. Here, \(\mathbf {P}(E)\) denotes the perimeter of E on the sphere, see the definition below, which coincides with the \({\mathcal H}^{n-1}\)-measure of the (relative) boundary of E on the sphere if E is a \(C^1\) manifold. Note that from (5.35) we immediately have that if \(E\subset \mathbb {S}^n\) is a set of finite perimeter such that \(\mathbf {P}(E)=\mathbf {P} (B_{\vartheta })\) for some \(0<\vartheta <\pi \), then
Also in this case equality occurs if and only if E is a geodesic ball.
We recall that if \(E\subset \mathbb {S}^n\) is a Borel set, the perimeter of E on the sphere can be defined similarly to the euclidean case by setting
If \(\mathbf {P}(E)<\infty \) by Riesz’s representation theorem it follows that the tangential gradient of \({\chi _{_{E}}}\) can be represented as a vector valued Radon measure \(D_\tau {\chi _{_{E}}}\). Thus, as in the euclidean case one may consider the set \(\partial ^*E\) of all points in \(\mathbb {S}^n\) such that the following limit exists
and satisfies \(|\nu _E(x)|=1\) and \(\nu _E(x)\in T_x\mathbb {S}^n\), where \(T_x\mathbb {S}^n\) stands for the tangential space to \(\mathbb {S}^n\) at the point x. Then the De Giorgi structure theorem on the sphere states that \(\partial ^*E\) is countably \((n-1)\)-rectifiable and that the total variation measure \(|D_\tau {\chi _{_{E}}}|\) coincides with 
. Moreover, if g is a \(C^1\) tangential vector-field on \(\mathbb {S}^n\) we have the following Gauss–Green formula, see [110, (7.6)]
Note that when E is a smooth open subset of \(\mathbb {S}^n\), the unit vector \(\nu _E(x)\in T_x\mathbb {S}^n\) coincides with the outer unit normal vector to \(\partial E\) at x. In the case of a geodesic ball \(B_{\vartheta }(p)\) it can be easily checked that the outer unit normal vector field along its boundary is given by
In view of the results that we have seen in Sect. 4, the natural counterpart of (4.3) would be the inequality
where now the Fraenkel asymmetry index is defined by
When compared with (4.3) inequality (5.38), even if it looks similar, has a completely different nature. In fact (4.3) is scaling invariant while there is no scaling at all on \(\mathbb {S}^n\). It would be quite easy to adapt one of the different arguments that we have seen in Sect. 4 and in Sect. 5.2 in order to prove (5.38) with a constant depending additionally on the volume of the set E, but possibly blowing up as \(\vartheta \downarrow 0\). Indeed, the difficult case is when the set E has a small volume sparsely distributed over the sphere. In this situation a localization argument aimed to reduce the problem to the flat Euclidean estimate (4.3) does not work. However, as in Sect. 5.3 one can prove a stronger inequality by replacing \(\varvec{\alpha }(E)\) with an oscillation index which is the counterpart in our new setting of the one defined in (5.15).
The idea is the same as in the euclidean case. Given a geodesic ball \(B_\vartheta (p)\) with the same \({\mathcal H}^n\)-measure of E, for every point \(x\in \partial ^*E\) we want to measure the distance between \(\nu _E(x)\) and the unit normal vector \(\nu _{B_\vartheta (p)}(\pi _{\vartheta ,p}(x))\), where \(\pi _{\vartheta ,p}(x)\) is the closest point in \(\partial B_\vartheta (p)\) in the sense of geodesic distance. However, since the two normals \(\nu _E(x)\) and \(\nu _{B_\vartheta (p)}(\pi _{\vartheta ,p}(x))\) lie in two different tangent spaces in order to measure their distance correctly we have to parallel transport the normal \(\nu _{B_\vartheta (p)}(\pi _{\vartheta ,p}(x))\) to the tangent space \(T_x\mathbb {S}^n\). Since the parallel transport on the sphere is just translation along great circles, the normal \(\nu _{B_\vartheta (p)}(\pi _{\vartheta ,p}(x))\) is thus carried into the normal \(\nu _{B_{\vartheta (x)}(p)}(x)\) at the point x to the geodesic ball with center p and radius \(\vartheta (x):=\mathrm{dist}_{\mathbb {S}^n}(x,p)\). So, as in Sec. 5.3, we measure the \(L^2\) distance between the normals \(\nu _E(x)\) and \(\nu _{B_{\vartheta (x)}(p)}(x)\) and then minimize the resulting norm among all possible geodesic balls having the same measure of E. This leads to the following definition of oscillation index for the set E
The quantitative isoperimetric inequality proved in [19, Th. 1.1] reads as follows.
Theorem 5.9
There exists a constant c(n) such that for any Borel set \(E\subset \mathbb {S}^n\) with \({\mathcal H}^n(E)={\mathcal H}^n(B_\vartheta )\) for some \(\vartheta \in (0,\pi )\), the following inequality holds
As in the euclidean case, see the discussion made in Sect. 5.3, inequality above implies (5.38), since a Poincaré type inequality still holds in the case, allowing to control \(\varvec{\alpha }(E)\) by the oscillation index \(\varvec{\beta }(E)\), see [19, Lemma 2.7].
Lemma 5.10
There exists a constant \(c=c(n)>0\) such that for any Borel set \(E\subset \mathbb {S}^n\) with \({\mathcal H}^n(E)={\mathcal H}^n(B_\vartheta )\) for some \(\vartheta \in (0,\pi )\) there holds
As in Sect. 5.3 the starting point for the proof of Theorem 5.9 is a Fuglede-type stability result aimed to establish (5.39) in the special case of sets \(E\subset \mathbb {S}^n\) whose boundary can be written as a radial graph over the boundary of a geodesic ball \(B_\vartheta (p)\) with the same volume. To establish such a result one could follow in principle the strategy used in the euclidean case in Theorem 3.1. However, to deduce (5.39) for radial graphs with a constant not depending on the volume needs much more care in the estimations, see the proof of Theorem 3.1 in [19]. The main difficulty arises when passing from the special situation of radial graphs to arbitrary sets. To deal with this issue one needs to change significantly the strategies that we have seen in the previous sections.
To explain where the major difficulties come from, we observe that as in the euclidean case the oscillation index can be re-written as the difference of \(\mathbf {P}(E)\) and a suitable potential on E. To this aim, note that
To proceed further, we recall (5.37) and set
Note that X is a tangential vector field, that is \(X(x)\cdot x=0\) for all \(x\in \partial ^*E\). Hence, by the Gauss–Green formula (5.36) we have
Computing the tangential divergence \(\mathrm{div}_{\mathbb {S}^n}X\) we obtain, denoting by \(\{\tau _1,\ldots ,\tau _n\}\) an orthonormal base for \(T_x\mathbb {S}^n\),
Inserting this equality in the formula above, we conclude that
where
From this formula it is clear that the core of the proof is to provide estimates independent of the volume of E for the potential
and for its maximum with respect to p. This requires some technically involved ideas and strategies. In particular, in the contradiction argument used to deduce (5.39) for general sets from the case of a radial graph we need to show that all the constants are independent of the volume of E. The arguments become particularly delicate when the volume of E is small. In this case inequality (5.39) shows a completely different nature depending on the size of the ratio \(\varvec{\beta }^2(E)/\mathbf {P}(B_\vartheta )\). In fact, if \({\mathcal H}^n(E)\rightarrow 0\) and also \(\varvec{\beta }^2(E)/\mathbf {P}(B_\vartheta )\rightarrow 0\), then E behaves asymptotically like a flat set, i.e., a set in \(\mathbb {R}^n\) and inequality (5.39) can be proven by reducing to the euclidean case, rescaling and then arguing as when E has large volume. However, the most difficult situation to deal with is when \({\mathcal H}^n(E)\rightarrow 0\) and \(\varvec{\beta }^2(E)/\mathbf {P}(B_\vartheta )\) converge to a strictly positive number. This case has to be treated with ad hoc estimates for the potential (5.40).
5.6 The fractional perimeter
The fractional s-perimeter has recently attracted the interest of several authors. In particular, Caffarelli et al. have initiated in [31] the study of Plateau-type problems in the fractional setting, see also [32]. Recall that for \(s\in (0,1)\) and a Borel set \(E\subset \mathbb {R}^n\), \(n\ge 2\), the fractional s-perimeter is defined by setting
Note that if \(P_s(E)<\infty \), then
for \(p\ge 1\) and \(\sigma p=s\), where \([{\chi _{_{E}}}]^p_{W^{\sigma ,p}(\mathbb {R}^n)}\) denotes the Gagliardo \(W^{\sigma ,p}\)-seminorm of the characteristic function of E. The functional \(P_s(E)\) can be thought as a \((n-s)\)-dimensional perimeter in the sense that \(P_s(\lambda E)=\lambda ^{n-s}P_s(E)\) for any \(\lambda >0\). Note that since for \(s\in (0,1)\) \(BV(\mathbb {R}^n)\) is imbedded in \(W^{\frac{s(n-1)}{n-s},\frac{n-s}{n-1}}(\mathbb {R}^n)\), see [81, Theorem 1.4.4.1], the s-perimeter of E is finite if E has finite (standard) perimeter and finite measure. On the other hand, \(P_s(E)\) can be finite even if the Hausdorff dimension of \(\partial E\) is strictly greater than \(n-1\), see for instance [107]. Observe also that if E, F are two bounded sets of non trivial and finite s-perimeter in general
However, the s-perimeter provides an approximation of the standard euclidean perimeter since it can be shown that for any bounded set of finite perimeter E
Formula (5.41) originates from a paper by Bourgain, Brezis and Mironescu [23, Th. 3’ and Rem 4]. It was completed by Dávila [52], see also [115] for a simpler proof. Subsequently, the same formula was proved in [32] and [7] under additional smoothness assumptions on E. On the other hand, as a consequence of [98, Th. 3], we have that, for any set E of finite measure and finite s-perimeter for all \(s\in (0,1)\),
Also for the s-perimeter balls are the isoperimetric sets, since it can be proved that if \(E\subset \mathbb {R}^n\) is a measurable set with \(|E|=|B_r|\) for some \(r>0\), then
with equality holding if and only if E is a ball. Inequality (5.42) can be deduced from a symmetrization result due to Almgren and Lieb [4], while the cases of equality have been determined in [71]. Note also, see for instance [62, (2.11)], that the s-perimeter of the unit ball is given by
where \(\Gamma \) is the so-called gamma function. In order to state a quantitative version of the isoperimetric inequality (5.42), if E is a measurable set such that \(|E|=|B_r|\) and \(s\in (0,1)\), we define the s -isoperimetric deficit as
The next result has been proven in [62, Th. 1.1].
Theorem 5.11
For every \(n\ge 2\) and \(s_0\in (0,1)\) there exists a positive constant \(C(n,s_0)\) such that
whenever \(s\in [s_0,1]\) and E has positive, finite measure.
The interesting feature of inequality (5.43) is that it holds uniformly with respect to s, at least if s is bounded away from zero. Therefore, thanks to (5.41), it implies in particular the quantitative inequality (4.3) for the standard perimeter. As we have seen in the previous sections, the starting point is a Fuglede type result, see [62, Th. 2.1], which now states that there exist two positive constants \(\varepsilon , c_0\), depending only on n, such that if E is a nearly spherical set as in Theorem 3.1, with \(\Vert u\Vert _{W^{1,\infty }(\mathbb {S}^{n-1})}<\varepsilon \), then for all \(s\in (0,1)\)
where the Gagliardo seminorm \([u]_{H^{\frac{1+s}{2}}(\mathbb {S}^{n-1})}\) is given by
Since it can be proved, see [23, Cor. 2] and also [62, (8.4)] for a different proof, that
one immediately recovers the Fuglede’s estimate (3.2) from (5.44). As we have seen already in different situations, in order to pass from a nearly spherical set to a general set of finite perimeter one has to use the right notion of perimeter almost minimizer and the right regularity results. The definition of perimeter almost minimizer given in (5.7) can be immediately extended to the s-perimeter in the obvious way and the counterpart in this new setting of Theorem 5.2 has been proved by Caputo and Guillen in [34]. However, in order to prove Theorem 5.11 one needs to show that all the regularity estimates needed in the proof are in fact independent of s, at least if s is bounded away from zero. This requires the use of more technically involved arguments and of more delicates estimates, see Sect. 4 in [62].
5.7 The isoperimetric inequality in Gauss space
The Gauss space is the space \(\mathbb {R}^n\), \(n\ge 1\), endowed with the measure \(\gamma \) given by
for any Lebesgue measurable set \(E\subset \mathbb {R}^n\). Note that \((\mathbb {R}^n,\gamma )\) is a probability space, since \(\gamma (\mathbb {R}^n)=1\). Clearly, \(\gamma \) is invariant under a rotation around the origin, while is not invariant under translation. Similarly to what we do in the euclidean space, if E is measurable and \(\Omega \subset \mathbb {R}^n\) is an open set we define the Gaussian perimeter of E in \(\Omega \) as
It turns out that if E has finite Gaussian perimeter in \(\Omega \) then it has also locally finite perimeter in \(\Omega \) in the Euclidean sense and
The perimeter of E in \(\mathbb {R}^n\) will be simply denoted by \(P_\gamma (E)\).
The isoperimetric inequality in the Gauss space asserts that among all subsets of \(\mathbb {R}^n\) with prescribed Gaussian measure, half-spaces have the least Gaussian perimeter. Precisely, for any \(\nu \in \mathbb {S}^{n-1}\) and \(s\in \mathbb {R}\) denote by \(H_{\nu ,s}\) the half space
Then we have \(\gamma (H_{\nu ,s})=\Phi (s)\) and \(P_\gamma (H_{\nu ,s})=e^{-\frac{s^2}{2}}\), where \(\Phi \) is the strictly decreasing function defined for all \(s\in \mathbb {R}\) by setting
Then the analytic form of the Gaussian isoperimetric inequality states that if \(\gamma (E)=\gamma (H_{\nu ,s})=\Phi (s)\) for some \(s\in \mathbb {R}\), then
with the equality holding if and only if \(E=H_{\nu ,s}\) for some \(\nu \in \mathbb {S}^{n-1}\). This inequality was independently established by Borell in [22] and by Sudakov and Cirel’son in [112]. However, the characterization of half-spaces as the unique minimizers in the isoperimetric Gaussian problem is a relatively recent result of Carlen and Kerce [36], relying on the theory of rearrangements as well as on probabilistic techniques involving the Mehler semigroup of contractions. A different proof has been recently given in [44], where the Ehrhard symmetrization [55] plays the same role of Steiner symmetrization in De Giorgi’s proof [53] of the isoperimetric inequality.
The stability of the isoperimetric property of half spaces in (5.45) has been addressed for the first time in [44]. In order to state the result proved therein we introduce the Gaussian isoperimetric deficit \(D_\gamma (E)\) and the Gaussian asymmetry \(\alpha _\gamma (E)\) by setting, respectively,
whenever E is a measurable set with \(\gamma (E)=\Phi (s)\), \(n\ge 1\). With this definitions in hand, the stability result proved in [44, Th. 1.1] reads as follows.
Theorem 5.12
Let \(n\ge 2\). For any \(0<\lambda <1\) there exists a positive constant \(C(n,\lambda )\) depending only on n and \(\lambda \) such that
for every measurable set \(E\subset \mathbb {R}^n\) such that \(\gamma (E)=\lambda \).
Note that also in (5.46) the power 2 is sharp. To see this one can consider in dimension 2 the family of sets constructed in [44, Lemma 6.1]. When \(n=1\), the quantitative version of the isoperimetric inequality (5.46) takes a somewhat different form. In fact one can prove that if \(n=1\), for any \(0<\lambda <1\) there exists a positive constant \(C(\lambda )\) such that
for every measurable set \(E\subset \mathbb {R}\) such that \(\gamma _1(E)=\lambda \). Also in this case the result is sharp, in the sense that the left hand side of (5.47) cannot be replaced by any function of \(\alpha _\gamma (E)\) decaying slower as \(\alpha _\gamma (E)\rightarrow 0\), see the sets defined in [44, Lemma 3.5].
As in the proof of (4.3) that we discussed in Sect. 4, the strategy to prove (5.46) is to reduce, via subsequent simplifications, to classes of sets E enjoying special additional geometric properties. A first reduction consists in showing that it suffices to prove (5.46) for \((n-1)\)-symmetric sets E, namely sets which are symmetric about \((n-1)\) mutually orthogonal hyperplanes containing the origin. This is obtained by proving a counterpart of Theorem 4.6 in the Gaussian setting. Once this reduction is performed, in order to prove (5.46) in dimension \(n=2\) it is enough to deal only with sets that are symmetric with respect to one of the two coordinate axes. In this case the proof follows by using ad hoc geometric constructions, together with a careful study of a particular class of almost optimal sets. Finally, by combining Ehrhard symmetrization with the reduction result to \((n-1)\)-symmetric sets, one may pass from a generic set E to a Cartesian product of \(\mathbb {R}^{n-2}\) times an epigraph in \(\mathbb {R}^2\). Thanks to the tensorial properties of the Gaussian density, this class of sets can be handled by the two-dimensional result.
The fact that the Gaussian isoperimetric inequality (5.45) is independent of the dimension suggests that also the constant in the quantitative inequality (5.46) should only depend on \(\lambda \). Beside its intrinsic mathematical interest, having a constant independent of n in (5.45) would have some interesting applications in probability, as pointed out in [101, Sect. 1.4]. Indeed in [101] a stability estimate with a non sharp logarithmic dependence on the isoperimetric deficit \(D_\gamma (E)\) was proven, but with a dimension free constant. This last result was later on greatly improved by Eldan [56] who proved inequality (5.46), actually an even stronger one, with a dimensionless constant and an almost optimal dependence on \(D_\gamma (E)\), actually just a logarithm below the optimal growth. However, it was only a very recent paper by Barchiesi et al. [10] that settled the issue in a complete and satisfactory way.
To state properly their result we have to introduce a sharper index, which in the gaussian context plays the role of the one that we have introduced in Sect. 5.3. To this aim, for any measurable set \(E\subset \mathbb {R}^n\) we define the non-renormalized barycenter of E by setting \(b(E):=\int _Ex\,d\gamma \). Then, following [10] we define a strong asymmetry by setting
In [10] the following result is proved.
Theorem 5.13
There exists an absolute constant C such that for every \(s\in \mathbb {R}\) and for every set \(E\subset \mathbb {R}^n\) with \(\gamma (E)=\Phi (s)\) the following estimate holds
Observe that this inequality is extremely interesting for several reasons. First, the constant C is dimension free, second, the dependence on the mass of E through s is also optimal, see [10, Rem. 1]. Moreover, a Poincaré type inequality shows that for any measurable set E with \(\gamma (E)=\Phi (s)\) then
Finally, the new asymmetry index is clearly related to the Gaussian counterpart of the oscillation index defined in (5.15) since one can prove that
The key point in the proof of Theorem 5.13 is to study the minimization problem
and to show that for \(\varepsilon \) sufficiently small, and \(\Lambda \) large, the only minima are the half spaces \(H_{\nu ,s}\). A part from the penalization term that eventually forces the minimizers to have mass equal to \(\Phi (s)\), the other two terms in the energy functional are somewhat of opposite nature. Indeed, for a given mass, half spaces minimize the Gaussian perimeter while maximize the absolute value of the barycenter. The reason why proving that the half spaces \(H_{\nu ,s}\) minimize the above functional leads to the quantitative inequality (5.48) can be understood on observing that \(b(H_{\nu ,s})=e^{-\frac{s^2}{2}}\nu /\sqrt{2\pi }\). Therefore, from the minimality of \(H_{\nu ,s}\) one has that if \(\gamma (E)=\Phi (s)\), then
from which is not difficult to deduce (5.48), see the argument at the beginning of Section 4 of [10].
The proof that half spaces are minimizers of the above problem is based on a PDE rigidity argument that is certainly new in this context. The idea in [10] is to derive the second variation for the above functional and then to deduce the minimality of a half space by a powerful and elegant choice of the test function, see Step 3 of the proof of the main result contained in Sect. 4 of [10].
We conclude this section by observing that while the result by Barchiesi et al. proves the quantitative Gaussian isoperimetric inequality with an optimal dependence on the dimension and on the mass, the dependence on the dimension of the constant \(\gamma (n)\) which appears in (4.3) is not known. However, inequality (3.2) implies that for a nearly spherical set E sufficiently close to a ball one has
This suggests that \(\gamma (n)\) should grow like n as \(n\rightarrow \infty \). Unfortunately, looking more carefully at the proof of the quantitative isoperimetric inequality (4.3) given in Sect. 4 one gets a constant growing exponentially fast with n, while the contradiction argument used in the Sect. 5.2 gives no clue about \(\gamma (n)\). However, in [67, (1.12)] it is observed that \(\gamma (n)\) has at most a polynomial growth, though the power that one obtains with their methods, even if one may be possibly improve it a bit, seems still far away from being optimal. The value of the constant in dimension \(n=2\) for small values of the asymmetry was first given by Hall et al. in [83, 84] in the convex case, and then extended by Cicalese and Leonardi in [45] for general sets of finite perimeter. Their result states that
Other, interesting estimates of the quantitative isoperimetric constant in dimension 2 for special classes of convex sets, not necessarily with small asymmetry, are studied in [6, 46].
6 Other functional inequalities
6.1 Stability of Sobolev inequality
In this section we shall discuss the stability of Sobolev inequality, which states that if \(n\ge 2\), \(1\le p<n\) and \({p^*}=np/(n-p)\), then
for every function f in the homogeneous Sobolev space \(W^{1,p}(\mathbb {R}^n)\). Throughout this section by the homogeneous Sobolev space we mean the completion of \(C_c^1(\mathbb {R}^n)\) with respect to the \(L^{p}(\mathbb {R}^n)\) norm of the gradient.
If \(p=1\) it is well known that (6.1) is equivalent to the isoperimetric inequality, see [59, p. 192], and thus \(S(1,n)=n\omega _n^{1/n}\). Indeed, a simple approximation argument shows that if f is a function in \(BV(\mathbb {R}^n)\), the homogeneous space of all functions in \(L^{\frac{n}{n-1}}(\mathbb {R}^n)\) whose distributional gradient is a measure with finite total variation, then
where \(|Df|(\mathbb {R}^n)\) denotes the total variation, with equality holding if and only if f is the characteristic function of a ball. If \(p>1\) the best constant in (6.1) was found independently by Aubin [9] and Talenti [113] and it turns out to be equal to
In this case the family of extremals in (6.1) is given by the functions \(g_{a,b,x_0}\) defined as
for some \(a\ne 0\), \(b>0\), \(x_0\in \mathbb {R}^n\), where \(p'=p/(p-1)\). When \(p=2\), as a consequence of a celebrated result by Gidas et al. [80] applied to the Euler equation of the functional \(\Vert \nabla f\Vert _{L^2(\mathbb {R}^n)}\big /\Vert f\Vert _{L^{2^\star }(\mathbb {R}^n)}\), one can show that the above functions are the only ones for which equality holds in (6.1). However if \(p>1, p\not =2\) the characterization of the functions of the form (6.2) as the only ones attaining equality in (6.1) was shown much later by Cordero-Erausquin et al. [49] with a proof of the Sobolev inequality (6.1) via mass transportation in the same spirit of Gromov’s proof of the isoperimetric inequality that we have seen in Sect. 5.1. We reproduce here their proof.
Proof of the sharp Sobolev inequality via mass transport
Observe that in order to prove (6.1) it is enough to assume that f is nonnegative since \(|\nabla |f||=|\nabla f|\). Therefore, if f and g are two nonnegative functions from \(W^{1,p}(\mathbb {R}^n)\) such that \(\Vert f\Vert _{p^*}=\Vert g\Vert _{p^*}=1\), by applying Theorem 5.1 with \(\mu =f^{p^*}dx\) and \(\nu =g^{p^*}dy\) we find that there exists a convex function \(\varphi :\mathbb {R}^n\rightarrow \mathbb {R}\) such that, setting \(T:=\nabla \varphi \) one has
for all nonnegative Borel functions h. To avoid some technical details that could make the idea of the proof less clear, let us assume that f and g have compact support and that T is Lipschitz. Then from the above formula we deduce that
From this inequality, using the geometric-arithmetic mean inequality, we have that for a.e. x in the support of f
where \(\mathrm{Tr}\,(T)\) denotes the trace of T. Multiplying both sides of this inequality by \(f^{p^*}(x)\) and integrating by parts we get
Using Hölder inequality and recalling (6.3) again we have
Combining this inequality with (6.4) and recalling (6.3) we then conclude that
Now we take \(b=1\) and \(a>0\) such that the function \(h_p:=g_{a,1,0}\) has \(L^{p^*}\) norm in \(\mathbb {R}^n\) equal to 1 and we argue as before, choosing \(f=g=h_p\). Since in this case the map T is just the identity map, the above argument simplifies a lot and one can easily check that all previous inequalities are indeed equalities. Therefore we conclude by getting that
From this equality, recalling (6.5) one gets that if \(\Vert f\Vert _{p^*}=\Vert h_p\Vert _{p^*}=1\), then
This inequality, as one can check with a few computations is precisely the Sobolev inequality (6.1) with the sharp constant S(n, p). \(\square \)
In the argument above we have chosen to put ourself in the simple situation when the functions f and g have compact support and T is Lipschitz. With a bit of technical adjustments, see [49, Sect. 4] the above argument can be justified also in the general case. Thus, if f and g are two functions for which inequality (6.5) holds as an equality one can prove [49, Prop. 6], that there exist two positive constants \(\alpha \) and \(\lambda \) such that \(f(x)=\alpha g(\lambda (x-x_0))\) for some \(x_0\in \mathbb {R}^n\). From this the characterization of the functions in (6.2) as the only extremals in the Sobolev inequality immediately follows.
In [27, (c) p. 75] Brezis and Lieb raised the following stability problem: ‘is there a way to bound \(\Vert \nabla f\Vert _2-S(2,n)\Vert f\Vert _{2^*}\) from below in terms of a ‘distance’ of f from the set of optimal functions (6.2)?’ The answer to this question was provided a few years later in a nice paper by Bianchi and Egnell [16]. Given a function f in the homogeneous Sobolev space \(W^{1,2}(\mathbb {R}^n)\) they considered the distance \(\mu \) from f to the manifold \(\mathcal {M}\) made up by all the functions \(g_{a,b,x_0}\) given by (6.2) with \(p=2\):
They proved the following result.
Theorem 6.1
There exist a positive constant c(n) depending only on n such that for all \(f\in W^{1,2}(\mathbb {R}^n)\)
Note that in inequality (6.7) the power 2 is optimal, since it cannot be replaced, up to a rescaling, by any smaller power. The key point in the proof is a lemma, see [16, Lemma 1], where they show the inequality when \(\mu (f)\) is sufficiently small. The proof of this lemma is elegant and simple. Given a function f, they consider the function \(g_{a,b,x_0}\) minimizing \(\mu (f)\). Due to the Hilbert structure of \(W^{1,2}(\mathbb {R}^n)\), one immediately has that \(f-g_{a,b,x_0}\) is orthogonal to the tangent space \(T{\mathcal {M}}_{g_{a,b,x_0}}\). Then the proof consists in relating \(T{\mathcal {M}}_{g_{a,b,x_0}}\) to the first and second eigenspace of the operator \(g_{a,b,x_0}^{2-2^*}\Delta \) on the weighted \(L^2\) space in \(\mathbb {R}^n\) with weight \(g_{a,b,x_0}^{2-2^*}\).
The situation is completely different when dealing with \(p\not =2\), where one cannot take advantage of the Hilbert structure of the space. Indeed, the results proved in this case in [43, 75] are weaker and not completely satisfactory. Let us first describe the content of the last paper, where the case \(1<p<n\) is consider. The first big difference between the result proved by Bianchi and Egnell and the one proved in [43] is that one has to replace the distance considered in (6.6) with a weaker kind of distance or asymmetry. Indeed, given a function f in the homogeneous Sobolev space \(W^{1,p}(\mathbb {R}^n)\) one sets
A part from the rescaling factor at the denominator and the constraint \(\Vert g_{a,b,x_0}\Vert _{p^*}=\Vert f\Vert _{p^*}\), the new distance \(\lambda (f)\) is clearly controlled from above by \(\mu (f)\) due to the Sobolev inequality itself. Indeed, if one goes back to the asymmetry indices defined in Sects. 4 and 5, it is clear that \(\lambda (f)\) and \(\mu (f)\) play the role of the indices \(\alpha (E)\), see (4.1), and \(\beta (E)\), see (5.15), respectively. Moreover in the quantitative estimate proved in [43, Th. 1] the power is far from being optimal.
Theorem 6.2
Let \(n\ge 2\) and let \(1<p<n\). There exist two positive constants \(\alpha \) and \(\kappa \), depending only on p and n, such that for every \(f\in W^{1,p}(\mathbb {R}^n)\)
The power \(\alpha \) in (6.9) can be retrieved from [43, (2.54), Cor. 4, (4.1) and the proof of Th. 1], but it is clearly non optimal. A comparison with the statement of Theorem 6.1 above and the statement of Theorem 3.3 in [43] suggests that the optimal power could be \(\alpha =\max \{2,p\}\), but we have no examples in this direction. Observe also that (6.9) can be rewritten in equivalent way as
We shall refer to the term \(\delta (f)\) at the right hand side of the previous equation as to the Sobolev deficit of the function f. Note also that in order to have an inequality of the type (6.10) both the asymmetry \(\lambda (f)\) and the deficit \(\delta (f)\) must be rescaling invariant. However we observe that the constraint in definition of \(\lambda (f)\) is not really needed. Indeed one could define a smaller asymmetry by setting
Observe that \(\widetilde{\lambda }(f)\le \lambda (f)\le 2^{p^*}\widetilde{\lambda }(f)\), hence we could indifferently use one of the two asymmetries.
The proof of the inequality follows a strategy very similar to the one used in Sect. 4 aimed to reduce the general case in (6.9) to the case where f is a more and more symmetric function. But before discussing that proof in more detail, let us recall the notion of spherically symmetric decreasing rearrangement of a function \(f:\mathbb {R}^n\rightarrow [0,\infty )\) such that \(|\{x:\,f(x)>t\}|<\infty \) for all \(t>0\). If f has this property, for every \(x\in \mathbb {R}^n\) we set
Note that \(f^\star \) is a decreasing function depending on the norm of x and that from the definition it follows that \(|\{f^\star >t\}|=|\{f>t\}|\). Thus, in particular, one has that
Moreover, the Pólya–Szegö principle states that if f is a nonnegative function from \(W^{1,p}(\mathbb {R}^n)\), with \(p\ge 1\), then also \(f^\star \) belongs to \(W^{1,p}(\mathbb {R}^n)\) and moreover, see for instance [28, 87],
The proof of this inequality is a simple application of the coarea formula for functions (2.8) and of the isoperimetric inequality.
Proof of the Pólya–Szegö inequality (6.12)
Let f be a nonnegative function from the homogeneous Sobolev space \(W^{1,p}(\mathbb {R}^n)\) and assume without proving it that also \(f^\star \) is in \(W^{1,p}(\mathbb {R}^n)\) (see [92, Th. 73]). We set for all \(t>0\)
The function \(\mu \) is called the distribution function of f. Since by construction the level sets of f and \(f^\star \) have the same measure, the two functions share the same distribution function \(\mu \). Note that \(\mu \) is a decreasing function. Moreover, an easy application of the coarea formula (2.8) shows that for a.e. \(t>0\)
and that
see for instance [41, Lemmas 2.4 and 2.6]. Note that in (6.14) we have implicitly used the fact that \(|\nabla f^\star |\) is constant on \(\{f^\star =t\}\). Then from coarea formula (2.8), (6.14), the fact that \(|\nabla f^\star |\) is constant on \(\{f^\star =t\}\) and the isoperimetric inequality applied to the sublevel sets of f, we have
From this inequality, using (6.15), Hölder inequality and coarea formula again we get
thus concluding the proof. \(\square \)
Note that from the above proof it is clear that when equality holds in (6.12) then for a.e. \(t>0\)
However this information is not enough to conclude that f coincides with \(f^*\) up to a translation, see Fig. 10. The equality cases in the Pólya–Szegö inequality have been fully characterized first by Brothers and Ziemer in [28], see also [41, 61]. Their result reads as follows.
An example showing the necessity of condition (6.16) to deduce that f is a translated of \(f^\star \)
Theorem 6.3
Let \(p>1\) and \(f\in W^{1,p}(\mathbb {R}^n)\) a nonnegative function such that
If equality holds in (6.12), then there exists \(x_0\in \mathbb {R}^n\) such that \(f(x)=f^\star (x-x_0)\) for all \(x\in \mathbb {R}\).
We observe that if \(|\{\nabla f=0\}\cap \{0<f<\mathrm{ess}\sup f\}|=0\), then (6.16) holds. The reverse implication is not in general true.
As we already observed, it may happen that \(\Vert \nabla f\Vert _p\) almost agrees with \(\Vert \nabla f^\star \Vert _p\) without f being close to any translated of \(f^\star \). The presence of large sets where \(|\nabla f|\) is zero or very small is responsible of this phenomenon. Therefore the quantitative versions of (6.12) available require either a control on the size of the set where \(|\nabla f|\) is small, see [40, 42], or further assumptions on the class of functions under consideration, see [12, Th. 1.3].
Going back to the Sobolev inequality, it is clear the role played by the Pólya–Szegö inequality (6.12). Indeed observe that we may always assume, without loss of generality, that \(f\ge 0\). In fact, replacing f by |f| changes neither the \(L^p\) norm of the function nor the \(L^p\) norm of the gradient, since \(|\nabla |f|(x)|=|\nabla f(x)|\) for a.e. \(x\in \mathbb {R}^n\). Therefore, if one wants to find the equality cases in the Sobolev inequality it is clear that these will be realized by spherically symmetric and decreasing functions. Thus Pólya–Szegö inequality plays in the proof of the quantitative Sobolev inequality given in [43] the same role played by the perimeter inequality for Schwartz symmetrization in the proof of (4.3) that we have seen in Sect. 4.
Let us describe briefly how the proof of inequality (6.9) goes. The idea is to reduce to spherically symmetric decreasing functions exactly as in Sect. 4 we reduced the proof of the quantitative isoperimetric inequality to axially symmetric sets. Observe that if \(f\in W^{1,p}(\mathbb {R}^n)\) is nonnegative, spherically symmetric and decreasing, then there exists a decreasing function \(u\in W^{1,p}_{loc}(\mathbb {R})\) such that \(f(x)=u(|x|)\). In this case the Sobolev inequality (6.1) is equivalent to the one-dimensional Bliss inequality [17]
for every decreasing, locally absolutely continuous function \(u:[0,\infty )\rightarrow [0,\infty )\). The extremals in (6.17) are the one dimensional profiles of the functions defined in (6.2), see for instance [17, 49, 113], that is
for some \(a> 0\), \(b>0\). Moreover, if we set for a measurable function \(w:(0,\infty )\rightarrow \mathbb {R}\),
and for every nonnegative function u in \((0,\infty )\) we define
Theorem 6.2 for spherically symmetric functions is equivalent to the following quantitative Bliss inequality.
Theorem 6.4
Let \(n\ge 2\) and let \(1<p<n\). Then there exist constants \(\beta \) and \(\kappa \), depending only on p, n, such that
for every decreasing, locally absolutely continuous function \(u:[0,\infty )\rightarrow [0,\infty )\).
The proof of this theorem is a bit long and technically involved, but the underlying idea is quite simple. First of all, by an approximation, rescaling and normalization argument one may always assume that u is a nonnegative decreasing function with support in [0, 1] such that
Then, one tries to compare this function with the function \(v:=v_{a,1}\), where a is chosen in such a way that also
In order to compare the two functions, following the argument that we have seen in the proof of the Sobolev inequality given above, one defines a transport map \(T:[0,1)\rightarrow [0,\infty )\) by setting
From this definition one gets immediately that T is a \(C^1(0,1)\) strictly increasing function such that \(T(0)=0\), \(\displaystyle \lim _{r\rightarrow 1^-}T(r)=\infty \), and
In particular, Eq. (6.19) implies that
for every Borel function \(h:[0,\infty )\rightarrow [0,\infty ]\). Therefore the function T can be regarded as a transport map carrying the measure \(u(r)^{p^*} r^{n-1}dr\) into \(v(r)^{p^*} r^{n-1}dr\).
Note that when \(T(r)=kr\) for some \(k>0\), one has \(u(r)=k^{(n-p)/p}v(kr)\), thus proving that u is an extremal function in the Bliss inequality (6.17). Thus, the idea is to show that when the difference between the two sides of the Bliss inequality is small, then an interval \([r_1,r_2]\subset [0,1]\) can be chosen in such a way that T(r) is close to some linear function kr for \(r\in [r_1,r_2]\), and simultaneously the integral of \(u(r)^{p^*} r^{n-1}\) outside \([r_1,r_2]\) is small. These facts lead to conclude that u is close to \(k^{(n-p)/p}v(kr)\) in in the quantitative way stated in (6.18).
As observed in [43, (2.54)] one can in fact choose \(\beta \) in (6.18) to be the (non optimal) exponent
The next step in the proof of Theorem 6.2 is to take advantage of the quantitative Bliss inequality (6.18) to reduce the general case to the case of a spherically symmetric and decreasing function, via the Pólya–Szegö inequality (6.12). In fact, from that inequality, recalling also (6.11), one has
for every \(f\in W^{1,p}(\mathbb {R}^n)\). The idea at this point is to estimate from below the difference between the \(L^p\) norm of \(\nabla f\) and \(\nabla f^\star \) in terms of the \(L^{p^*}\) distance of f from a suitable translated of \(f^\star \). Unfortunately, as we already observed, it is not possible in general to control the distance between f and \(f^\star \) in terms of the left hand side of (6.21), since if the measure of the set \(\{\nabla f=0\}\) is large the \(L^p\) norms of \(\nabla f\) and \(\nabla f^\star \) may be equal, without f or \(f^*\) being close. However, if f belongs to a sufficiently rigid class of functions, this estimate is still possible. Indeed, this is the case of n-symmetric functions, for which it is not too hard to show, see [43, Th. 3], the following stability result for the Pólya-Szegö inequality.
Theorem 6.5
Let \(n\ge 2\) and let \(1<p<n\). Set \(q=\max \{p,2\}\). Then a positive constant C exists such that
for every nonnegative \(f\in W^{1,p}(\mathbb {R}^n)\) which is symmetric with respect to the coordinate hyperplanes.
The proof of this theorem consists in a careful revisitation of the proof of the Pólya–Szegö inequality that we have given above, using the quantitative isoperimetric inequality (4.3) in place of the standard isoperimetric inequality and taking advantage of the fact that since f is n-symmetric then also the level sets \(\{f>t\}\) are n-symmetric and thus their asymmetry \(\alpha (\{f>t\})\) is equivalent to the symmetric difference with the ball centered at the origin with the same measure, see Lemma 4.4. As a consequence of this theorem and of the quantitative Bliss inequality (6.18) one can easily deduce (6.9).
Proposition 6.6
Let \(n\ge 2\) and let \(1<p<n\). Then there exists a constant \(\kappa >0\) such that (6.9) holds for every nonnegative n-symmetric function \(f\in W^{1,p}(\mathbb {R}^n)\), with \(\alpha =\beta \), \(\beta \) as in (6.20).
Proof
As we already observed (6.9) is equivalent to (6.10). To prove this last one, since both \(\delta (f)\) and \(\lambda (f)\) are invariant by rescaling and multiplication by a constant, we may assume, without loss of generality, that \(\Vert f\Vert _{L^{p^*}(\mathbb {R}^n)}=1\). Observe also that \(\lambda (f)\le 2^{p^*}\), hence we may also assume that \(\delta (f)\le 1/S(p,n)\), since otherwise (6.10) follows with \(\kappa (n)=1/(2^{\alpha p^*} S(n,p))\). Then, from (6.11) and (6.12) we have
We have
for some constant C, where the first inequality is just a consequence of the triangle inequality, and the second one follows from Theorems 6.4 and 6.5. Inequalities (6.22) ensure that
for some constant C. Combining (6.23), (6.24), and (6.21) yields
for some constant C. Hence, inequality (6.9) follows with \(\alpha =\beta \), since by (6.20) one has \(\beta >q\). \(\square \)
At this point the full proof of Theorem 6.2 follows from a reduction argument of the same kind of the one we stated in Theorem 4.6. However, the reduction to n-symmetric functions although related to a similar construction employed in Sect. 4, entails the overcoming of new serious obstacles in the present setting, mainly due to the nonlinear growth of the functional \(\Vert \nabla f\Vert _{L^p(\mathbb {R}^n)}^p\). The precise statement of the reduction theorem reads as follows, see [43, Th. 6].
Theorem 6.7
Let \(n\ge 2\) and let \(1<p<n\). There exists a positive constant C, depending only on n and p such that for every \(f\in W^{1,p}(\mathbb {R}^n)\) there exists a nonnegative n-symmetric function \({\tilde{f}}\) with the property that
where \(\beta \) is given by (6.20).
We conclude this discussion on the quantitative Sobolev inequality for \(1<p<n\) by noting that, in view of the results of [16, 75], the question arises of the optimal exponent \(\alpha \) in equality (6.9). Furthermore, the result of [16] also leaves open the problem of whether the distance of f from the family of extremals in \(L^{{p^*}}(\mathbb {R}^n)\) can be replaced by the distance in \(W^{1,p}(\mathbb {R}^n)\) in Theorem 6.2.
In the special case \(p=1\) the Sobolev inequality (6.1) takes the form
for all f in the homogeneous Sobolev space \(W^{1,1}(\mathbb {R}^n)\). Here \(n':=n/(n-1)\) stands for the Sobolev exponent \(1^*\). By approximation it can be readily extended to the homogenous space \(BV(\mathbb {R}^n)\). For these functions it takes the form
As we already observed, the above inequality is equivalent to the isoperimetric inequality, Indeed if E is a set of finite measure, taking \(f={\chi _{_{E}}}\) in the inequality above one gets exactly the isoperimetric inequality. It is well-known that equality holds in (6.25) if and only if \(f=a{\chi _{_{B_r(x_0)}}}\) for some \(a\in \mathbb {R}\), \(x_0\in \mathbb {R}^n\) and \(r>0\). Therefore, in analogy with (6.8) it is natural to introduce the asymmetry of a function \(f\in BV(\mathbb {R}^n)\) by setting
Indeed, it can be proved that the above infimum is attained, see [75, Lemma B.1]. In the case \(p=1\) the quantitative version of the Sobolev inequality (6.25) has been obtained with the sharp exponent 2 [75, Th. 1.1].
Theorem 6.8
There exists a dimensional constant \(C=C(n)\) such that
for every \(f\in BV(\mathbb {R}^n)\).
The proof of this result follows the same pattern of the proof of the quantitative isoperimetric inequality that we have seen in Sect. 4. A part from a series of technical difficulties due to the fact that one deals with functions instead of sets, the only point where the proof really differs from the one we have already seen is when one has to show inequality (6.26) for a spherically symmetric and decreasing function, see [75, Sect. 3].
I would like also to point out that very recently Figalli et al. in [68] proved a similar stability estimate for the anisotropic Sobolev (and log-Sobolev) inequality for functions of bounded variation. Also in this case the stability estimate is obtained with the sharp exponent 2, see [68, Th. 1.1]. The proof combines symmetrization arguments with the Gromov’s idea for proving the isoperimetric inequality, and thus also the Sobolev inequality for BV functions, with a mass transport argument.
The Morrey–Sobolev imbedding theorem states that if \(p>n\) a function from the homogeneous Sobolev space \(W^{1,p}(\mathbb {R}^n)\) is essentially bounded and actually Hölder continuous. In particular, if the support of f is bounded the following inequality holds
where \(\mathrm{supp}\,f\) denotes the support of f and the sharp constant S(n, p) is given by
In this case the extremals are given by the family of functions
for some \(a\in \mathbb {R}\), \(b\ge 0\) and \(x_0\in \mathbb {R}^n\). The stability for (6.27) has been proved by Cianchi and stated in terms of the \(L^\infty \) distance from the extremals. Precisely, see [39, Th. 1.1], we have the following quantitative estimate, where \(\delta (f)\) is defined as in (6.10) for \(p=\infty \).
Theorem 6.9
Let \(n\ge 2\) and \(p>n\). There exist two positive constants \(\alpha \) and C, depending only on p and n, such that for every \(f\in W^{1,p}(\mathbb {R}^n)\)
6.2 The Faber–Krahn inequality
The Faber–Krahn inequality goes back to Lord Rayleigh who in 1877 in his book ‘The theory of sound’ [111] conjectured that the gravest principal tone of a vibrating membrane is obtained by a circular one. In other words, if \(\Omega \subset \mathbb {R}^n\) is an open set with \(|\Omega |=|B_r|\) for some \(r>0\) then
with the equality holding if and only if \(\Omega \) is a ball. Here by \(\lambda (\Omega )\) we denote the first eigenvalue of the Laplacian which is defined as
Note that a function f realizing the minimum on the right hand side is called an eigenfunction for the Laplacian and satisfies the equation
Inequality (6.28) was proved in two dimensions by Faber [60] and extended for any \(n\ge 2\) by Krahn [91]. Indeed, it can be proved as an immediate consequence of the Pólya–Szegö inequality (6.12) by observing that if f is a minimizer in \(H^1_0(\Omega )\) of the above variational problem then
The characterization of the equality cases in (6.28) can be also easily recovered using Theorem 6.3. Observing that \(\lambda (r\Omega )=r^{-2}\lambda (\Omega )\), inequality (6.28) may be rewritten in the following scaling invariant form
The stability of balls with respect to this inequality has been investigated by several authors. As for the quantitative isoperimetric inequality people tried first to understand the convex case. In particular, it was proved by Melas in [99] that if \(\Omega \subset \mathbb {R}^n\) is a bounded, convex open set then one can find two balls \(B'\subset \Omega \subset B''\) such that
is controlled by a suitable power, depending on n, of the Faber–Krahn deficit
A similar result was later on obtained by Hansen and Nadirashivili in [85] where the inner and the outer radius of a convex set are used to control the distance from a ball in terms of the Faber–Krahn deficit. For a general open set, it was conjectured by Bhattacharya and Weitsman in [15] and by Nadirashvili in [102] that the following quantitative Faber–Krahn inequality holds
for any open set \(\Omega \subset \mathbb {R}^n\) of finite measure, where \(\alpha \) is the Fraenkel asymmetry index defined in (4.1). An inequality of this kind, dealing with general open sets, was obtained first in dimension two by Bhattacharya in [14] with the exponent 3 in place of 2 and in any dimension n by Maggi et al. in [77] with the exponent 4. Indeed, in [77] a more general inequality was proved, related to the first eigenvalue of the p-Laplacian, \(p>1\) which is defined, similarly to (6.29), by setting for any open set \(\Omega \) with finite measure
Note that the same argument used to show Faber–Krahn inequality (6.32) implies that for any open set of finite measure one has
Then, the following quantitative estimate was proved in [77, Th. 1].
Theorem 6.10
Let \(n\ge 2\) and \(p>1\). There exists a positive constant c(n, p) such that for every open set \(\Omega \subset \mathbb {R}^n\) of finite measure
The proof of the above inequality makes use of the following observation. Assuming for the sake of simplicity that \(p=2\) and that \(\Omega \) has the same measure of the unit ball B, let \(f\in H^1_0(\Omega )\) be the function minimizing the right hand side of (6.29). Then, recalling (6.31), one has that
In turn, denoting as in the previous section by \(\mu \) the distribution function of f defined as in (6.13) one has, see [77, (32)],
for some positive constant c(n). Therefore, one may conclude that
This inequality shows indeed that the Faber–Krahn deficit controls in an integral form the asymmetry of the level sets of the eigenfunctions. However, to recover from this information the sharp quantitative estimate of the asymmetry for \(\Omega \) does not seem easy.
The above conjecture on the optimal power in inequality (6.34) has been proved in a recent paper by Brasco et al. [24]. Here is their result.
Theorem 6.11
There exists a positive constant C(n) such that (6.34) holds true for every open set \(\Omega \subset \mathbb {R}^n\) of finite measure.
The proof is deep and technically involved. However, we shall try to explain the main ideas. The first key point of their strategy is to prove a sharp quantitative estimate for a weaker inequality related to the torsional rigidity. To explain this inequality we have to introduce, for an open set \(\Omega \) of finite measure, the following quantity
Note that the function \(f_\Omega \) minimizing the integral functional on the right hand side coincides with the unique solution of the Dirichlet problem
Therefore, multiplying the above equation by \(f_\Omega \) and integrating by parts one gets
From this equality one easily gets a reformulation of \(E(\Omega )\) as
The maximum of the integral on the right hand side of the previous formula is the torsional rigidity of \(\Omega \). Observe that E satisfies the scaling law: \(E(r\Omega )=r^{-n-2}E(\Omega )\) for all \(r>0\) and all open sets \(\Omega \) with finite measure. Then, the same argument used to show inequality (6.28) immediately yields the following inequality
with the equality holding if and only if \(\Omega \) is a ball. A deeper inequality, due to Kohler-Jobin, see [89, 90], relates the first eigenvalue of the Laplacian to the torsional rigidity.
Theorem 6.12
For every open set \(\Omega \subset \mathbb {R}^n\) of finite measure we have
with the equality holding if and only if B is a ball.
As we already said, the first key point is to observe that in view of (6.36) one can deduce (6.34) from a quantitative version of (6.35), see [24, Prop. 2.1].
Proposition 6.13
Assume that there exists a constant \(c_0(n)\) such that for every open set \(\Omega \subset \mathbb {R}^n\) of finite measure
Then, there exists another constant \(c_1(n)\) such that one has also
Proof
Assume \(|\Omega |=|B|\) and observe that from the Kohler-Jobin inequality (6.36) we have
Since \(E(\Omega )\) is a negative quantity, from (6.35) we have that \(E(B)/E(\Omega )\ge 1\). Therefore, if the ratio \(E(B)/E(\Omega )\ge 2\), from (6.38) we get
On the other hand, if \(1\le E(B)/E(\Omega )\le 2\), from (6.38) and the assumption (6.37) we have
where c(n) is such that \(t^{\frac{2}{n+2}}-1\ge c(n)(t-1)\) for all \(t\in [1,2]\). \(\square \)
With this proposition in hands it is now clear that the strategy followed in [24] is to prove a stability inequality for \(E(\Omega )\) of the type (6.37). Namely they follow the pattern that we have discussed in Sect. 5.2 of proving first the stability estimate for nearly spherical sets and then to extend it to general open sets by a contradiction argument via regularity. The proof for nearly spherical sets is essentially a second variation argument and it leads to the following Fuglede type result, see [24, Th. 3.3].
Theorem 6.14
Let \(\sigma \in (0,1]\). There exists a positive constant \(\delta \), depending only on n and \(\gamma \), such that if \(\Omega \) is a nearly spherical set as in (3.1), \(|\Omega |=|B|\), the barycenter of \(\Omega \) is at the origin and \(\Vert u\Vert _{C^{2,\sigma }(\mathbb {S}^{n-1})}\le \delta \), then
As for Fuglede’s estimate (3.2) this inequality immediately implies (6.37) for nearly spherical sets. Note however that the perimeter deficit controls the \(H^1\) norm of u, while the difference \(E(\Omega )-E(B)\), hence the Faber–Krahn deficit (6.33), only controls the weaker \(H^{1/2}\) norm of u. This is not surprising if one thinks that one may easily find open sets \(\Omega _h\) for which the perimeter \(P(\Omega _h)\) goes to \(\infty \) while the first eigenvalue of the Laplacian \(\lambda (\Omega _h)\) remains bounded. Indeed it is enough to take
with \(u_h:\mathbb {S}^{n-1}\rightarrow (-1,1)\) chosen so that \(\Vert u_h\Vert _{H^{1/2}(\mathbb {S}^{n-1})}\) is bounded and \(\Vert u_h\Vert _{H^{1}(\mathbb {S}^{n-1})}\rightarrow \infty \).
Coming to the proof of the stability of the functional E, after proving Theorem 6.14 one would like to argue as we did in Sect. 5.2. So let us try to imitate the contradiction argument used in Sect. 5.2 by assuming that there exists a sequence \(\Omega _j\) of open sets with \(|\Omega _j|=|B|\), \(E(\Omega _j)\rightarrow E(B)\) and
for some big constant \(C_0\) to be chosen later. Then, one would like to replace the sets \(\Omega _j\) with a sequence of sets, say \(U_j\), minimizing a functional of the type we introduced in (5.12)
to show that they still satisfy a ‘wrong’ inequality as (6.40) and that they converge in \(C^{2,\sigma }\) to the a ball, so to get a contradiction to (6.39). This is the point where the proof in [24] becomes really complicate and requires some new ideas and deep arguments. To understand why observe that minimizing the functional above is equivalent to finding a minimizer \(f_j\) of the functional
among all functions with a support of finite measure. It turns out that to get the desired regularity one has to modify in a non trivial way the theory developed by Alt and Caffarelli in [5]. But even this is not enough. In fact the functional in (6.41) is not sufficiently smooth to ensure that the support of the minimizers \(f_j\) are of class \(C^{2,\sigma }\). Well, one could replace it with an essentially equivalent and smoother one, such as
but even this functional would not work. And the reason is that the Fraenkel asymmetry is not smooth enough. So, another delicate point in [24] is the replacement of the asymmetry index with a new distance which on one side dominates the square of the Fraenkel asymmetry, on the other side is much smoother since it behaves like the square of an \(L^2\) norm.
6.3 Further results
In the previous sections we have seen the natural extension of the ideas developed for the study of the stability of the quantitative isoperimetric inequality to two important inequalities. Indeed, several other inequalities have been investigated in the last years in this direction. For instance, in [77] the same argument used to prove Theorem 6.10 is also used to derive a quantitative inequality for the isocapacitary inequality stating that for any open set of finite measure \(\Omega \) one has
where the p capacity of \(\Omega \), for \(p\in (1,n)\), \(n\ge 2\) is defined as
Quantitative inequalities for the so called Cheeger constant have been also obtained in [77] as a limit case of Theorem 6.10 and in [65] with the optimal exponent. To this aim we recall that if \(\Omega \) is an open set with finite measure, \(n\ge 2\), and
then the m-Cheeger constant of \(\Omega \) is defined by setting
When \(m=1\) a set E minimizing the right hand side is called a Cheger set of \(\Omega \). The Cheeger inequality states that balls minimize the Cheeger constant among all open sets with the same measure. Thus, taking into account the right scaling factor, we have that
with the equality holding if and only if \(\Omega \) is a ball. Using the quantitative isoperimetric inequality it has been shown by Figalli et al. in [65] that the following stability estimate holds. Given \(m>1/n'\), there exist a positive constant \(\kappa (m,n)\) such that for every open set \(\Omega \) of finite measure one has
The results discussed in the previous section have been extended by Brasco and Pratelli in [25] to the second eigenvalue of the Laplacian. To this aim, we recall that if \(\Omega \) is an open set with finite measure the second eigenvalue \(\lambda _2(\Omega )\) is defined by minimizing the Dirichlet integral among all functions that are orthogonal to the first eigenfunctions. Precisely, denoting by \(f_\Omega \) a non trivial eigenfunction, that is a nontrivial solution to Eq. (6.30). We have
Then Krahn–Szegö inequality states that among all open sets of given measure the unique minimizer of \(\lambda _2\) is given by the union of two disjoint balls of equal measure. In other words, setting \(\Theta :=B'\cup B''\) where the balls \(B'\) and \(B''\) are disjoint and \(|B'|=|B''|=|B|/2\) we have, taking into account the rescaling law,
with the equality holding if and only if \(\Omega \) is the union of two disjoint balls of equal measure. As a consequence of Theorem 6.11 and of [25, Th. 3.5 and Rem. 3.6] one has
Theorem 6.15
There exists a constant \(\kappa (n)\) depending only on the dimension such that for any open set \(\Omega \) of finite measure one has
where
It is not known whether the power \(n+1\) in the statement of Theorem 6.15 is optimal, though it is clear that in this case the optimal power must depend on the dimension.
Things are better understood with the second, or the first non trivial, eigenvalue of the Laplacian under Neumann boundary conditions \(\mu _2(\Omega )\) which is defined by setting for every open set \(\Omega \) of finite measure
In this case the Szegö–Weinberger inequality states that among all open sets of given measure the unique maximizer of \(\lambda _2\) is given by a ball. This inequality can be written in a scaling invariant form as
It turns out that a quantitative version of this inequality can be proved as well, see [25, Th. 4.1].
Theorem 6.16
There exists a constant \(\kappa (n)\) depending only on the dimension such that for every open set with Lipschitz boundary one has
It is interesting to observe that in the inequality above the exponent 2 is sharp. The proof of this inequality uses a simple geometric argument. However proving the sharpness of the exponent 2 is harder, see [25, Sect. 6].
We conclude this section by quickly quoting a few other inequalities for which stability results have been obtained recently.
We recall that the Brunn–Minkowski inequality (1.2) states that if \(H,K\subset \mathbb {R}^n\) are compact sets then
with the equality holding if and only if: \(|H+K|=0\), either H or K consists of a single point, H and K are two convex bodies homothetic to each other, i.e., there exist \(x_0\in \mathbb {R}^n\) and \(\lambda >0\) such that \(H=x_0+\lambda K\), see [29, Th. 8.1.1]. A quantitative version of the inequality above, in the case when H and K are convex bodies, has been obtained in [66] and with an improved constant in [109]. See also a recent paper by Eldan and Klartag [57]. The general case of measurable sets is still open apart from a very recent result by Figalli and Jerison [64].
The isodiametric inequality states that among all sets of given diameter the ball is the one enclosing the biggest volume. Equivalently, if E is a measurable set of finite measure in \(\mathbb {R}^n\) then
with the equality holding if and only if E is a ball. The stability of this inequality has been studied by Maggi et al. in [96] where the following result is proved.
Theorem 6.17
If \(E\subset \mathbb {R}^n\) is a set with \(\mathrm{diam\,}(E)=2\), there exists a ball B(x) such that
for some positive constant \(\kappa \) depending only on the dimension n.
Paper [63] is devoted to the stability of the relative isoperimetric inequality in a cone while [11] contains a characterization of the equality cases in the perimeter inequality for Steiner symmetrization in any codimension, as well as a stability result for this inequality for a class of convex sets. A similar stability result, concerning concave and log-concave functions has been proved in [12]. Finally, a quantitative version of the Gagliardo–Sobolev–Nirenberg inequality, has been recently proved by Carlen and Figalli in [35], starting from the Bianchi and Egnell stability result that we have discussed in Sect. 6.1.
References
Acerbi, E., Fusco, N., Morini, M.: Minimality via second variation for a nonlocal isoperimetric problem. Commun. Math. Phys. 322, 515–557 (2013)
Aleksandrov, A.D.: Uniqueness theorems for surfaces in the large. V (Russian). Vestnik Leningr. Univ. 13, 5–8 (1958)
Almgren, F.: Optimal isoperimetric inequalities. Indiana Univ. Math. J. 35, 451–547 (1986)
Almgren, F.J., Lieb, E.H.: Symmetric decreasing rearrangement is sometimes continuous. J. Am. Math. Soc. 2, 683–773 (1989)
Alt, H.W., Caffarelli, L.A.: Existence and regularity for a minimum problem with free boundary. J. Reine Angew. Math. 325, 105–144 (1981)
Alvino, A., Ferone, V., Nitsch, C.: A sharp isoperimetric inequality in the plane. J. Eur. Math. Soc. 13, 185–206 (2011)
Ambrosio, L., De Philippis, G., Martinazzi, L.: Gamma-convergence of nonlocal perimeter functionals. Manuscr. Math. 134, 377–403 (2011)
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Mathematical Monographs. The Clarendon Press, New York (2000)
Aubin, T.: Problèmes isopérimétriques et espaces de Sobolev. J. Differ. Geom. 11, 573–598 (1976)
Barchiesi, M., Brancolini, A., Julin, V.: Sharp dimension free quantitative estimates for the Gaussian isoperimetric inequality. Ann. Probab. arXiv:1409.2106v1 (2015, to appear)
Barchiesi, M., Cagnetti, F., Fusco, N.: Stability of the Steiner symmetrization of convex sets. J. Eur. Math. Soc. 15, 1245–1278 (2013)
Barchiesi, M., Capriani, G.M., Fusco, N., Pisante, G.: Stability of Pólya–Szegö inequality for log-concave functions. J. Funct. Anal. 267, 2264–2297 (2014)
Bernstein, F.: Über die isoperimetriche Eigenschaft des Kreises auf der Kugeloberflache und in der Ebene. Math. Ann. 60, 117–136 (1905)
Bhattacharya, T.: ome observations on the first eigenvalue of the \(p\)-Laplacian and its connections with asymmetry. Electron. J. Differ. Equ. 35, 15 (2001)
Bhattacharya, T., Weitsman, A.: Estimates for Greens function in terms of asymmetry. AMS Contemp. Math. Ser. 221, 31–58 (1999)
Bianchi, G., Egnell, H.: A note on the Sobolev inequality. J. Funct. Anal. 100, 18–24 (1991)
Bliss, G.A.: An integral inequality. J. Lond. Math. Soc. 5, 40–46 (1930)
Bögelein, V., Duzaar, F., Fusco, N.: A sharp quantitative isoperimetric inequality in higher codimension. Rend. Lincei Mat. Appl. 26, 309–362 (2015)
Bögelein, V., Duzaar, F., Fusco, N.: A quantitative isoperimetric inequality on the sphere. http://cvgmt.sns.it/paper/2146/ (2013)
Bombieri, E.: Regularity theory for almost minimal currents. Arch. Ration. Mech. Anal. 78, 99–130 (1982)
Bonnesen, T.: Über die isoperimetrische Defizit ebener Figuren. Math. Ann. 91, 252–268 (1924)
Borell, C.: The Brunn–Minkowski inequality in Gauss space. Invent. Math. 30, 207–216 (1975)
Bourgain, J., Brezis, H., Mironescu, P.: Another look at Sobolev spaces. In: Menaldi, J.L., Rofman, E., Sulem, A. (eds.) Optimal Control and Partial Differential Equations, pp. 429–455. IOS Press, Amsterdam (2001)
Brasco, L., De Philippis, G., Velichkov, B.: Faber–Krahn inequalities in sharp quantitative form. Duke Math. J. 164, 1777–1831 (2015)
Brasco, L., Pratelli, A.: Sharp stability of some spectral inequalities. Geom. Funct. Anal. 22, 107–135 (2012)
Brenier, Y.: Polar factorization and monotone rearrangement of vector-valued functions. Commun. Pure Appl. Math. 44, 375–417 (1991)
Brezis, H., Lieb, E.H.: Sobolev inequalities with remainder terms. J. Funct. Anal. 62, 73–86 (1985)
Brothers, J., Ziemer, W.: Minimal rearrangements of Sobolev functions. J. Reine. Angew. Math. 384, 153–179 (1988)
Burago, Y.D., Zalgaller, V.A.: Geometric Inequalities. Springer, Berlin (1988)
Cabré, X.: Partial differential equations, geometry and stochastic control (Catalan). Butl. Soc. Catalana Mat. 15, 7–27 (2000)
Caffarelli, L., Roquejoffre, J.M., Savin, O.: Non-local minimal surfaces. Commun. Pure Appl. Math. 63, 1111–1144 (2010)
Caffarelli, L., Valdinoci, E.: Uniform estimates and limiting arguments for nonlocal minimal surfaces. Calc. Var. Partial Differ. Equ. 41, 203–240 (2011)
Cagnetti, F., Colombo, M., De Philippis, G., Maggi, F.: Rigidity of equality cases in Steiner’s perimeter inequality. Anal. PDE 7, 1535–1593 (2014)
Caputo, M.C., Guillen, N.: Regularity for non-local almost minimal boundaries and applications. arXiv:1003.2470 (2010)
Carlen, E.A., Figalli, A.: Stability for a GNS inequality and the log-HLS inequality, with application to the critical mass Keller–Segel equation. Duke Math. J. 162, 579–625 (2013)
Carlen, E.A., Kerce, C.: On the cases of equality in Bobkov’s inequality and Gaussian rearrangement. Calc. Var. Partial Differ. Equ. 13, 1–18 (2001)
Chavel, I.: Isoperimetric Inequalities. Cambridge Tracts in Mathematics, vol. 145. Cambridge University Press, Cambridge (2001)
Chlebík, M., Cianchi, A., Fusco, N.: The perimeter inequality under Steiner symmetrization: cases of equality. Ann. Math. 162, 525–555 (2005)
Cianchi, A.: Sharp Morrey–Sobolev inequalities and the distance from extremals. Trans. Am. Math. Soc. 360, 4335–4347 (2008)
Cianchi, A., Esposito, L., Fusco, N., Trombetti, C.: A quantitative Pólya–Szegö principle. J. Reine Angew. Math. 614, 153–189 (2008)
Cianchi, A., Fusco, N.: Functions of bounded variation and rearrangements. Arch. Ration. Mech. Anal. 165, 1–40 (2002)
Cianchi, A., Fusco, N.: Dirichlet integrals and Steiner asymmetry. Bull. Sci. Math. 130, 675–696 (2006)
Cianchi, A., Fusco, N., Maggi, F., Pratelli, A.: The sharp Sobolev inequality in quantitative form. J. Eur. Math. Soc. 11, 1105–1139 (2009)
Cianchi, A., Fusco, N., Maggi, F., Pratelli, A.: On the isoperimetric deficit in the Gauss space. Am. J. Math. 133, 131–186 (2011)
Cicalese, M., Leonardi, G.P.: A selection principle for the sharp quantitative isoperimetric inequality. Arch. Ration. Mech. Anal. 206, 617–643 (2012)
Cicalese, M., Leonardi, G.P.: Best constants for the isoperimetric inequality in quantitative form. J. Eur. Math. Soc. 15, 1101–1129 (2013)
Cicalese, M., Leonardi, G.P., Maggi, F.: Sharp stability inequalities for planar double bubbles. arXiv:1211.3698v2 (2012)
Cicalese, M., Leonardi, G.P., Maggi, F.: Improved convergence theorems for bubble clusters. I. The planar case. arXiv:1409.6652v2 (2014)
Cordero-Erausquin, D., Nazaret, B., Villani, C.: A mass-transportation approach to sharp Sobolev and Gagliardo–Nirenberg inequalities. Adv. Math. 182, 307–332 (2004)
Dacorogna, B., Pfister, C.E.: Wulff theorem and best constant in Sobolev inequality. J. Math. Pures Appl. 71, 97–118 (1992)
David, G., Semmes, S.: Quasiminimal surfaces of codimension 1 and John domains. Pac. J. Math. 183, 213–277 (1998)
Dávila, J.: On an open question about functions of bounded variation. Calc. Var. Partial Differ. Equ. 15, 519–527 (2002)
De Giorgi, E.: Sulla proprietà isoperimetrica dell’ipersfera, nella classe degli insiemi aventi frontiera orientata di misura finita (Italian). Atti Accad. Naz. Lincei. Mem. Cl. Sci. Fis. Mat. Nat. Sez. I (8) 5, 33–44 (1958)
Duzaar, F., Steffen, K.: Optimal interior and boundary regularity for almost minimizers to elliptic variational integrals. J. Reine Angew. Math. 546, 73–138 (2002)
Ehrhard, A.: Symétrisation dans l’espace de Gauss. Math. Scand. 53, 281–301 (1983)
Eldan, R.: A two-sided estimate for the Gaussian noise stability deficit. Invent. Math. 201, 561–624 (2015)
Eldan, R., Klartag, B.: Dimensionality and stability. Ann. Sc. Norm. Super. Pisa Cl. Sci. 13, 975–1007 (2014)
Esposito, L., Fusco, N., Trombetti, C.: A quantitative version of the isoperimetric inequality: the anisotropic case. Ann. Sc. Norm. Super. Pisa Cl. Sci. 4, 619–651 (2005)
Evans, L.C., Gariepy, R.F.: Measure Theory and Fine Properties of Functions. CRC Press Inc, Boca Raton (1992)
Faber, C.: Beweis dass unter allen homogen Membranen von gleicher Fläche und gleicher Spannung die kreisförmige den tiefsten Grundton gibt, Sitzungsber, pp. 169–172 . Bayer. Akad. der Wiss. Math.-Phys., Munich (1923)
Ferone, A., Volpicelli, R.: Minimal rearrangements of Sobolev functions: a new proof. Ann. Inst. H. Poincaré Anal. Non Linéaire 20, 333–339 (2003)
Figalli, A., Fusco, N., Maggi, F., Millot, V., Morini, M.: Isoperimetry and stability properties of balls with respect to nonlocal energies. Commun. Math. Phys. 336, 441–507 (2015)
Figalli, A., Indrei, E.: A sharp stability result for the relative isoperimetric inequality inside convex cones. J. Geom. Anal. 23, 938–969 (2013)
Figalli, A., Jerison, D.: Quantitative stability for sumsets in \(\mathbb{R}^n\). J. Eur. Math. Soc. 17, 1079–1106 (2015)
Figalli, A., Maggi, F., Pratelli, A.: A note on Cheeger sets. Proc. Am. Math. Soc. 137, 2057–2062 (2009a)
Figalli, A., Maggi, F., Pratelli, A.: A refined Brunn–Minkowski inequality for convex sets. Ann. Inst. H. Poincaré Anal. Non Linéaire 26, 2511–2519 (2009b)
Figalli, A., Maggi, F., Pratelli, A.: A mass transportation approach to quantitative isoperimetric inequalities. Invent. Math. 182, 167–211 (2010)
Figalli, A., Maggi, F., Pratelli, A.: Sharp stability theorems for the anisotropic Sobolev and log-Sobolev inequalities on functions of bounded variation. Adv. Math. 242, 80–101 (2013)
Fonseca, I.: The Wulff theorem revisited. Proc. R. Soc. Lond. 432, 125–145 (1991)
Fonseca, I., Müller, S.: A uniqueness proof for the Wulff theorem. Proc. R. Soc. Edinb. 119A, 125–136 (1991)
Frank, R.L., Seiringer, R.: Non-linear ground state representations and sharp Hardy inequalities. J. Funct. Anal. 255, 3407–3430 (2008)
Fuglede, B.: Stability in the isoperimetric problem for convex or nearly spherical domains in \(\mathbb{R}^n\). Trans. Am. Math. Soc. 314, 619–638 (1989)
Fusco, N., Gelli, M.S., Pisante, G.: On a Bonnesen type inequality involving the spherical deviation. J. Math. Pures Appl. 98, 616–632 (2012)
Fusco, N., Julin, V.: A strong form of the quantitative isoperimetric inequality. Calc. Var. Partial Differ. Equ. 50, 925–937 (2014)
Fusco, N., Maggi, F., Pratelli, A.: The sharp quantitative Sobolev inequality for functions of bounded variation. J. Funct. Anal. 244, 315–341 (2007)
Fusco, N., Maggi, F., Pratelli, A.: The sharp quantitative isoperimetric inequality. Ann. Math. 168, 941–980 (2008)
Fusco, N., Maggi, F., Pratelli, A.: Stability estimates for certain Faber–Krahn, isocapacitary and Cheeger inequalities. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 8, 51–71 (2009)
Fusco, N., Millot, V., Morini, M.: A quantitative isoperimetric inequality for fractional perimeters. J. Funct. Anal. 261, 697–715 (2011)
Giaquinta, M., Giusti, E.: Quasi-minima. Ann. Inst. H. Poincaré Anal. Non Linéaire 1, 79–107 (1984)
Gidas, B., Ni, W.M., Nirenberg, L.: Symmetry and related properties via the maximum principle. Commun. Math. Phys. 68, 209–243 (1979)
Grisvard, P.: Elliptic Problems in Non Smooth Domains. Monongraphs and Studies in Mathematics. Pitman, Boston (1985)
Hall, R.R.: A quantitative isoperimetric inequality in \(n\)-dimensional space. J. Reine Angew. Math. 428, 161–176 (1992)
Hall, R.R., Hayman, W.K.: A problem in the theory of subordination. J. Anal. Math. 60, 99–111 (1993)
Hall, R.R., Hayman, W.K., Weitsman, A.W.: On asymmetry and capacity. J. Anal. Math. 56, 87–123 (1991)
Hansen, W., Nadirashvili, N.: Isoperimetric inequalities in potential theory. In: Proceedings from the International Conference on Potential Theory (Amersfoort, 1991). Potential Analysis, vol. 3, pp. 1–14 (1994)
Hurwitz, A.: Sur le problème des isopérimètres. C. R. Acad. Sci. Paris 132, 401–403 (1901)
Kawohl, B.: Rearrangements and Convexity of Level Sets in PDE. Lecture Notes in Mathematics, vol. 1150. Springer, Berlin (1985)
Kinnunen, J., Korte, R., Lorent, A., Shanmugalingam, N.: Regularity of sets with quasiminimal boundary surfaces in metric spaces. J. Geom. Anal. 23, 1607–1640 (2013)
Kohler-Jobin, M.T.: Une méthode de comparaison isopérimétrique de fonctionnelles de domaines de la physique mathématique. I. Une démonstration de la conjecture isopérimétrique \(P\lambda ^2\ge \pi j_0^4/2\) de Polýa et Szegö. Z. Angew. Math. Phys. 29, 757–766 (1978)
Kohler-Jobin, M.T.: Symmetrization with equal Dirichlet integrals. SIAM J. Math. Anal. 13, 153–161 (1982)
Krahn, E.: Über Minimaleigenschaft des Kugel in drei und mehr Dimensionen. Acta Comment. Univ. Tartu Math. A9, 1–44 (1926)
Leoni, G.: A First Course in Sobolev Spaces. Graduate Studies in Mathematics. American Mathematical Society, Providence (2009)
McCann, R.J.: Existence and uniqueness of monotone measure-preserving maps. Duke Math. J. 80, 309–323 (1995)
Maggi, F.: Some methods for studying stability in isoperimetric type problems. Bull. Am. Math. Soc. 45, 367–408 (2008)
Maggi, F.: Sets of Finite Perimeter and Geometric Variational Problems. An Introduction to Geometric Measure Theory. Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge (2012)
Maggi, F., Ponsiglione, M., Pratelli, A.: Quantitative stability in the isodiametric inequality via the isoperimetric inequality. Trans. Am. Math. Soc. 366, 1141–1160 (2014)
Maggi, F., Villani, C.: Balls have the worst best Sobolev inequalities. J. Geom. Anal. 15, 83–121 (2005)
Maz’ya, V., Shaposhnikova, T.: On the Bourgain, Brezis, and Mironescu theorem concerning limiting embeddings of fractional Sobolev spaces. J. Funct. Anal. 195, 230–238 (2002) (Erratum, J. Funct. Anal. 201, 298–300 (2003))
Melas, A.: The stability of some eigenvalue estimates. J. Differ. Geom. 36, 19–33 (1992)
Milman, V.D., Schechtman, G.: Asymptotic Theory of Finite-Dimensional Normed Spaces. With an Appendix by M. Gromov. Lecture Notes in Mathematics, vol. 1200. Springer, Berlin (1986)
Mossel, E., Neeman, J.: Robust dimension free isoperimetry in Gaussian space. Ann. Probab. 43, 971–991 (2015)
Nadirashvili, N.: Conformal maps and isoperimetric inequalities for eigenvalues of the Neumann problem. In: Proceedings of the Ashkelon Workshop on Complex Function Theory, pp. 197–201 (1996), Israel Mathematical Conference Proceedings, vol. 11. Bar-Ilan University, Ramat Gan (1997)
Neumayer, R.: A strong form of the quantitative Wulff inequality. arXiv:1503.06705 (2015)
Osserman, R.: The isoperimetric inequality. Bull. Am. Math. Soc. 84, 1182–1238 (1978)
Osserman, R.: Bonnesen-style isoperimetric inequalities. Am. Math. Mon. 86, 1–29 (1979)
Rajala, K., Zhong, X.: Bonnesen’s inequality for John domains in \(\mathbb{R}^n\). J. Funct. Anal. 263, 3617–3640 (2012)
Runst, T., Sickel, W.: Sobolev Spaces of Fractional Order, Nemytskij Operators, and Nonlinear Partial Differential Equations. de Gruyter Series in Nonlinear Analysis and Applications. Walter de Gruyter & Co., Berlin (1996)
Schmidt, E.: Beweis der isoperimetrischen Eigenschaft der Kugel im hyperbolischen und sphärischen Raum jeder Dimensionszahl. Math. Z. 49, 1–109 (1943)
Segal, A.: Remark on stability of Brunn–Minkowski and isoperimetric inequalities for convex bodies. In: Geometric Aspects of Functional Analysis. Lecture Notes in Mathematics, vol. 2050, pp. 381-391. Springer, Heidelberg (2012)
Simon, L.: Lectures on geometric measure theory. In: Proceedings of the Centre for Mathematical Analysis, Australian National University, vol. 3. Australian National University, Centre for Mathematical Analysis, Canberra (1983)
Strutt, J.W. (Lord Rayleigh): The Theory of Sound. 2nd edn. Dover Publications, New York (1945)
Sudakov, V.N., Cirel’son, B.S.: Extremal properties of half-spaces for spherically invariant measures (Russian). In: Problems in the Theory of Probability Distributions, II. Zap. Naučn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) vol. 41, pp. 14–24 (1974)
Talenti, G.: Best constant in Sobolev inequality. Ann. Mat. Pura Appl. 110, 353–372 (1976)
Tamanini, I.: Regularity results for almost minimal oriented hypersurfaces. Quaderni del Dipartimento di Matematica dell’Università di Lecce, Lecce. http://cvgmt.sns.it/paper/1807/ (1984)
Van Schaftingen, J., Willem, M.: Set transformations, symmetrizations and isoperimetric inequalities, Nonlinear analysis and applications to physical sciences, 135–152. Springer Italia, Milan (2004)
Acknowledgments
Part of this work has been carried on at the University of Jyväskylä and supported by the FiDiPro project 2100002028. The friendly atmosphere of the Mathematics and Statistics Department of Jyväskylä is warmly acknowledged. I would also thank Marco Barchiesi, Laura Bufford and Matteo Rinaldi who did some of the pictures and Marco Barchiesi for carefully reading the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Ari Laptev.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fusco, N. The quantitative isoperimetric inequality and related topics. Bull. Math. Sci. 5, 517–607 (2015). https://doi.org/10.1007/s13373-015-0074-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13373-015-0074-x