A modified viscosity iterative method for implicit midpoint rule for optimization and fixed point problems in CAT(0) spaces

Abstract

In this paper, we introduce a proximal point-type of viscosity iterative method with double implicit midpoint rule comprising of a nonexpansive mapping and the resolvents of a monotone operator and a bifunction. Furthermore, we establish that the sequence generated by our proposed algorithm converges strongly to an element in the intersection of the solution sets of monotone inclusion problem, equilibrium problem and fixed point problem for a nonexpansive mapping in complete CAT(0) spaces. In addition, we give a numerical example of our method each in a finite dimensional Euclidean space and a non-Hilbert space setting to show the applicability of our method . Our results complement many recent results in the literature.

1 Introduction

A curve c (or simply a geodesic path) joining x to y is an isometry $c:I=[0,d(x,y)] \rightarrow X$ such that $c(0)=x$, $c(d(x,y))=y$ and $d(c(t),c(t'))=|t-t'|$ for all $t,t'\in I$. The image of a geodesic path is called the geodesic segment, which is denoted by [x, y] whenever it is unique. We say that a metric space X is a geodesic space if for every pair of points $x,y \in X$, there is a minimal geodesic from x to y. A geodesic triangle $\Delta (x_1,x_2,x_3)$ in a geodesic metric space (X, d) consists of three vertices (points in X) with unparameterized geodesic segment between each pair of vertices. For any geodesic triangle, there is a comparison (Alexandrov) triangle $\bar{\Delta }\subset \mathbb {R}^2$ such that $d(x_i,x_j)=d_{\mathbb {R}^2}(\bar{x}_i,\bar{x}_j)$ for $i,j\in \{1,2,3\}$. A geodesic space X is a CAT(0) space if the distance between arbitrary pair of points on a geodesic triangle $\Delta$ does not exceed the distance between its pair of corresponding points on its comparison triangle $\bar{\Delta }$. If $\Delta$ is a geodesic triangle and $\bar{\Delta }$ is it comparison triangle in X, then $\Delta$ is said to satisfy the CAT(0) inequality for all points x, y of $\Delta$ and $\bar{x},\bar{y}$ of $\bar{\Delta }$, if

$$\begin{aligned} d(x,y)=d_{\mathbb {R}^2}(\bar{x},\bar{y}). \end{aligned}$$

(1.1)

Let x, y, z be points in X and $y_0$ be the midpoint of the segment [y, z], then the CAT(0) inequality implies

$$\begin{aligned} d^2(x,y_0)\le \frac{1}{2}d^2(x,y)+\frac{1}{2}d^2(x,z)-\frac{1}{4}d(y,z). \end{aligned}$$

(1.2)

Inequality (1.2) is known as CN inequality of Bruhat and Titus [12]. A geodesic space X is said to be a CAT(0) space if all geodesic triangles satisfy the CAT(0) inequality. Equivalently, X is called a CAT(0) space if and only if it satisfies the CN inequality. Examples of CAT(0) spaces includes Hilbert space, Hadamard manifold, $\mathbb {R}$-trees [28], pre-Hilbert space [11], hyperbolic spaces [42], and Hilbert ball [21].

Monotone operator theory remains one of the most important aspects of nonlinear and convex analysis. It plays essential role in optimization, variational inequalities, semigroup theory and evolution equations. One of the vital problems in monotone operator theory is the following nonlinear stationary problem:

$$\begin{aligned} \text {Find}~x\in \mathbb {D}(A)~\text {such that}~0\in ~A(x), \end{aligned}$$

(1.3)

where A is a monotone operator and $\mathbb {D}(A)$ is the domain of A defined by $\mathbb {D}(A) = \{x \in X : Ax \ne \emptyset \}.$ Problem (1.3) is called Monotone Inclusion Problem (MIP) and its solution set denoted by $A^{-1}(0)$ is closed and convex. The MIP is known to be very useful in solving some well known problems like the minimization problem and variational inequality problem. Therefore, it is of great importance in convex and nonlinear analysis, and optimization theory.

An equally significant optimization problem is the Equilibrium Problem (EP) which also extends and unifies other optimization problems such as the minimization problems, variational inequality problems, Nash equilibrium problems, complementarity problems, fixed point problems among others (see [2, 3, 38, 39, 48] and the references therein). Thus, the EPs are of high importance in optimization theory. Let D be a nonempty subset of X and $f : D \times D \rightarrow \mathbb {R}$ be a bifunction. The EP for f is to find $x^*\in D$ such that

$$\begin{aligned} f(x^*, y) \ge 0,~\forall ~y \in D. \end{aligned}$$

(1.4)

The point $x^*$ for which (1.4) is satisfied is called an equilibrium point of f and we denote the solution set of problem (1.4) by EP(f, D). Several types of bifunctions for EPs have been studied extensively in Hilbert, Banach and topological vector spaces, as well as in Hadamard manifolds by many researchers (see [10, 13, 14, 22, 35, 40, 49] and other references therein). In an attempt to study the EP in complete CAT(0) spaces, Kumam and Chaipunya [30] introduced the resolvent of the bifunction f associated with the EP (1.4) (see also [23]). Define a perturbed bifunction $\bar{f}_{\bar{x}}: D \times D \rightarrow \mathbb {R}$ of f by

$$\begin{aligned} \bar{f}_{\bar{x}}(x, y) := f(x, y) - \langle \overrightarrow{x\bar{x}},\overrightarrow{xy}\rangle ,~x,y \in D~\text {and}~\bar{x}\in X. \end{aligned}$$

The perturbed bifunction $\bar{f}_{\bar{x}}$ has a unique equilibrium called the resolvent operator $J^f : X \rightarrow 2^D$ defined by

$$\begin{aligned} J^f(x) := EP(\bar{f}_{\bar{x}}) = \{ z \in D : f(z, y) - \langle \overrightarrow{zx},\overrightarrow{zy}\rangle \ge 0,~y \in D \}, ~x \in X. \end{aligned}$$

(1.5)

It was established in [30] that $F(J^f) = EP(f, D),$ $J^f$ is well defined, single valued and $\mathbb {D}(J^f) = X,$ under some assumptions.

The Proximal Point Algorithm (PPA) is one of the most effective methods for finding solutions of optimization problems. The PPA was introduced by Martinet [33] in Hilbert spaces. Later, Rockafellar [43] developed it and proved that it converges weakly to a zero of a monotone operator. The PPA was first studied by Bačák [7] in complete CAT(0) spaces to find minimizers of proper, convex and lower semicontinuous functionals and he established the $\Delta$-convergence of the PPA. Khatibzadeh and Ranjbar [27] also studied the PPA in complete CAT(0) spaces for approximating solutions of (1.3). They established that the PPA involving a monotone operator $\Delta$-converges to a zero of the monotone operator in complete CAT(0) spaces. Very recently, Dehghan et al. [15] proposed a Halpern-type PPA for approximating a common solution of a finite family of MIPs. They proved that the proposed PPA converges strongly to an element in the set of solutions of the MIPs. The PPA was also studied by Kumam and Chaipunya [30] for approximating solutions of (1.4) in CAT(0) spaces.

The Viscosity Iterative Method (VIM) is another reliable iterative method because of it advantage over other iterative methods. In fact, the Halpern iterative method is a particular case of the VIM. In 2000, the VIM was introduced by Moudafi [34] in a real Hilbert space where he used a strict contraction to regularize a nonexpansive mapping for the sole aim of obtaining a fixed point of the nonexpansive mapping. Since then, many researchers have also obtained convergence results with the use of VIM in some more general spaces than Hilbert spaces (see for example [24, 26, 31, 56] and other references therein). The VIM have also been studied extensively in the framework of complete CAT(0) spaces (see [5, 23, 46, 53, 54]). Like other types of iterative methods, the PPA type of VIM have also been studied in the setting of CAT(0) spaces. For instance in [19], Eskandani and Raeisi studied the PPA type of VIM associated with product of finitely many resolvents of monotone operators to find a common zero of a finite family of monotone operators. They obtained the strong convergence of the PPA under appropriate conditions. Also in [23], Izuchukwu et al. introduced a PPA type of VIM, which comprises of a nonexpansive mapping and a finite sum of resolvent operators associated with monotone bifunctions. They proved a strong convergence theorem for approximating solutions of a finite family of equilibrium problems and fixed point problem for a nonexpansive mapping in a complete CAT(0) space.

In the same vein, the Implicit Midpoint Rule (IMR) is one of the most potent techniques for solving differential algebraic equations and Ordinary Differential Equations (ODE) due to it ability to eliminate stability errors of system of ODE (see [6, 8, 44, 47, 52] for details). Therefore, the implicit midpoint rule is known to improve numerical method by adding a midpoint in the step which increases the accuracy by one order. Consider an ODE

$$\begin{aligned} x'(t) = g(t)~\text {with initial condition}~x(t) = x(0), \end{aligned}$$

(1.6)

where $g:\mathbb {R}^N \rightarrow \mathbb {R}^N$ is a continuous function. The IMR (see [4]) is a recursion procedure that generates the sequence $\{x_n\}$ by

$$\begin{aligned} x_{n+1} = x_n + hg\Big (\frac{x_n + x_{n+1}}{2} \Big ),~n>0, \end{aligned}$$

(1.7)

where $h > 0$ is the step size. It is generally known that if g is Lipschitz continuous and sufficiently smooth, then the sequence $\{x_n\}$ converges to an exact solution of (1.6) as $h\rightarrow 0$ uniformly over $t\in [0,T]$ for any fixed $T > 0.$ In 2015, Xu et al. [57] introduced a unification of the VIM and IMR associated with a nonexpansive mapping in a real Hilbert space. They established that the sequence generated from the unification converges to a fixed point of the nonexpansive mapping which is also a unique solution of some variational inequality problem. Based on the work of Xu et al. [57], Zhao et al. [58] proposed a VIM for IMR in complete CAT(0) spaces as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_1 \in D,\\ x_{n} = \alpha _n g(x_n) \oplus (1 - \alpha _n) T\big ( \frac{x_n \oplus x_{n+1}}{2} \big ), ~\forall ~n\ge 1. ~\forall ~n \in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(1.8)

where g is a contraction, $\alpha _n \in (0, 1)$ and T is a nonexpansive mapping on D. They established that (1.8) converges to a fixed point of the nonexpansive mapping T. Ahmad and Ahmad [1] also proposed a VIM type of IMR as follows: For arbitrary initial point $x_1\in D,$ the sequence $\{x_n\}$ is generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} w_n = \frac{x_n \oplus x_{n+1}}{2,}\\ y_n = \alpha _n (w_n) \oplus \beta _n g(w_n) \oplus \gamma _n T(w_n),\\ x_{n+1} = T(y_n), ~~n\ge 1, \end{array}\right. } \end{aligned}$$

(1.9)

where $\{\alpha _n\}, \{\beta _n\}$ and $\{\gamma _n\}$ are sequences in (0, 1),  g is a contraction with a coefficient $\theta \in [0, 1)$ and T is a nonexpansive mapping on D. They also obtained that (1.9) converges strongly to a fixed point of the nonexansive mapping which is also the unique solution of some variational inequality.

Motivated by the results of Khatibzadeh and Ranbar [27], Kumam and Chaipunya [30], Izuchukwu et al. [23], Zhao et al. [58], Ahmad and Ahmad [1], we introduce a PPA-type of VIM with a double IMR comprising of a nonexpansive mapping and the resolvents of a monotone operator and a bifunction. With a double midpoint in our method, it tends to have better accuracy than (1.8) and (1.9). We establish that the sequence generated by our proposed algorithm converges strongly to an element in the intersection of the solution sets of MIP, EP and fixed point problem for nonexpansive mapping in complete CAT(0) spaces. In addition, we give a numerical example of our method each in a finite dimensional Euclidean space and a non-Hilbert space setting to show the applicability of our method. Our results complement many recent results in the literature.

2 Preliminaries

We state some known and useful results which will be needed in the proof of our main results, (see [36, 51] for details). In the sequel, we denote strong and $\Delta$-convergence by “$\rightarrow$” and “$\rightharpoonup$” respectively.

Definition 2.1

Let $\{x_n\}$ be a bounded sequence in X and $r(\cdot , \{x_n\}): X\rightarrow [0, \infty )$ be a continuous functional defined by $r(x, \{x_n\}) = \limsup \limits _{n\rightarrow \infty }d(x, x_n).$ The asymptotic radius of $\{x_n\}$ is given by $r(\{x_n\}):= \inf \{r(x, \{x_n\}): x\in X\},$ while the asymptotic center of $\{x_n\}$ is the set $A(\{x_n\}) = \{x\in X : r(x, \{x_n\})= r(\{x_n\})\}.$ It is well known that in an Hadamard space X,  $A(\{x_n\})$ consists of exactly one point. A sequence $\{x_n\}$ in X is said to be $\Delta -$convergent to a point $x\in X$ if $A(\{x_{n_k}\}) = \{x\}$ for every subsequence $\{x_{n_k}\}$ of $\{x_n\}.$ In this case, we write $\Delta -\lim \limits _{n\rightarrow \infty }x_n = x.$

Remark 2.2

The notion of $\Delta -$convergence is weaker than usual metric convergence but it is equivalent to the weak convergence in Hilbert spaces.

Definition 2.3

[9] Let a pair $(a,b)\in X\times X$, denoted by $\overrightarrow{ab},$ be called a vector in $X\times X$. The quasilinearization map $\langle .,.\rangle :(X\times X)\times (X\times X)\rightarrow \mathbb {R}$ is defined by

$$\begin{aligned} \langle \overrightarrow{ab},\overrightarrow{cd}\rangle =\frac{1}{2}(d^2(a,d)+d^2(b,c)-d^2(a,c)-d^2(b,d)), \forall ~ a,b,c,d \in X. \end{aligned}$$

(2.1)

It is easy to see that $\langle \overrightarrow{ba}, \overrightarrow{cd}\rangle =-\langle \overrightarrow{ab}, \overrightarrow{cd}\rangle ,~\langle \overrightarrow{ab}, \overrightarrow{cd}\rangle =\langle \overrightarrow{ae}, \overrightarrow{cd}\rangle +\langle \overrightarrow{eb}, \overrightarrow{cd}\rangle$ and $\langle \overrightarrow{ab}, \overrightarrow{cd}\rangle =\langle \overrightarrow{cd}, \overrightarrow{ab}\rangle$ for all $a,b,c,d,e\in X$. Furthermore, a geodesic space X is said to satisfy the Cauchy-Schwarz inequality if

$$\begin{aligned} \langle \overrightarrow{ab},\overrightarrow{cd}\rangle \le d(a,b)d(c,d)~\forall ~a, b, c, d \in X. \end{aligned}$$

It is known from [18] that a geodesically connected space is a CAT(0) space if and only if it satisfies the Cauchy-Schwarz inequality.

The notion of duality in CAT(0) space was introduced by Kakavandi and Amini [25] as follows:

Definition 2.4

Let (X, d) be a complete CAT(0) space. Consider the map $\Theta :\mathbb {R}\times X\times X\rightarrow C(X, \mathbb {R})$ defined by

$$\begin{aligned} \Theta (t,a,b)(x)&=t\langle \overrightarrow{ab},\overrightarrow{ax}\rangle ~\forall ~t\in \mathbb {R},~a,b,x\in X, \end{aligned}$$

(2.2)

where $C(X,\mathbb {R})$ is the space of all continuous real-valued functions on X. The pseudometric space $(\mathbb {R}\times X\times X, \mathcal {D})$ is a subspace of the pseudometric space $(Lip(X, \mathbb {R}),L)$ of all real-valued Lipschitz functions. Also, $\mathcal {D}$ defines an equivalence relation on $(\mathbb {R}\times X\times X)$, where the equivalence class of (t, a, b) is

$$\begin{aligned} {[}t\overrightarrow{ab}]&=\{s\overrightarrow{cd}:t\langle \overrightarrow{ab},\overrightarrow{xy}\rangle =s\langle \overrightarrow{cd},\overrightarrow{xy}\rangle ~\forall ~x,y\in X\}. \end{aligned}$$

(2.3)

The set $X^*=\{[t\overrightarrow{ab}]:(t,a,b)\in \mathbb {R}\times X\times X \}$ is a metric space with metric $\mathcal {D}$, and the pair $(X^*,\mathcal {D})$ is the dual space of X.

Definition 2.5

Let (X, d) be a metric space and D be a nonempty closed and convex subset of X. Let T be a nonlinear mapping on D into itself. Denote by $F(T) = \{x \in D: Tx = x\}$ the set of fixed points of T. The mapping T is said to be nonexpansive, if

$$\begin{aligned} d(Tx, Ty) \le d(x, y)~~\forall ~ x, y~\in X, \end{aligned}$$

and firmly nonexpansive (see [27]), if

$$\begin{aligned} d^2(Tx,Ty)\le \langle \overrightarrow{TxTy},\overrightarrow{xy}\rangle ~~\forall ~x,y\in X. \end{aligned}$$

Definition 2.6

Let X be a complete CAT(0) space and $X^*$ be its dual space. A multivalued operator $A:X\rightarrow 2^{X^*}$ is monotone, if for all $x,y\in \mathbb {D}(A)$ with $x\ne y,$ we have

$$\begin{aligned} \langle x^*-y^*,\overrightarrow{yx}\rangle&\ge 0,~\forall ~~x^*\in Ax,~y^*\in Ay. \end{aligned}$$

(2.4)

The graph of the operator $A:X\rightarrow 2^{X^*}$ is the set

$$\begin{aligned} Gr(A) =\{(x,x^*)\in X\times X^*: x^*\in A(x)\}. \end{aligned}$$

The monotone operator A is called a maximal monotone operator if Gr(A) is not properly contained in the graph of any other monotone operator.

Definition 2.7

[41] Let X be a complete CAT(0) space and $X^*$ be its dual space. The resolvent of a monotone operator A of order $\lambda >0$ is the multivalued mapping $J^A_{\lambda }: X\rightarrow 2^X$ defined by

$$\begin{aligned} J_{\lambda }^A(x):=\big \{z\in X:\big [\frac{1}{\lambda }\overrightarrow{zx}\big ]\in Az\big \}. \end{aligned}$$

(2.5)

The multivalued operator A is said to satisfy the range condition if $\mathbb {D}(J_{\lambda }^A)=X,$ for every $\lambda >0.$

The following results depict the relationship between monotone operators and their resolvents in the settings of CAT(0) spaces.

Lemma 2.8

[27] Let X be a CAT(0) space and $J^A_\lambda$ be the resolvent of a multivalued mapping A of order $\lambda .$ Then

• (i) for any $\lambda > 0,~R(J^A_\lambda ) \subset \mathbb {D}(A)$ and $F(J^A_\lambda ) = A^{-1}(0),$ where $R(J^A_\lambda )$ is the range of $J^A_\lambda ,$

• (ii) if A is monotone, then $J^A_\lambda$ is a single-valued and firmly nonexpansive mapping,

• (iii) if $0 < \lambda _1 \le \lambda _2,$ then $d(J^A_{\lambda _2} x, J^A_{\lambda _1} x) \le \frac{\lambda _2 - \lambda _1}{\lambda _2 + \lambda _1}~d(x, J^A_{\lambda _2} x),$ which implies that $d(x, J^A_{\lambda _1} x) \le 2d(x, J^A_{\lambda _2} x)~~\forall ~x \in X.$

Remark 2.9

If X is a CAT(0) space and $A : X \rightarrow 2^{X^*}$ is a multivalued monotone mapping, then

$$\begin{aligned} d^2(J^A_\lambda x, x) \le d^2(x, v) - d^2(J^A_\lambda x, v) \end{aligned}$$

(2.6)

for all $v \in A^{-1}(0), ~x \in \mathbb {D}(J^{A}_\lambda )$ and $\lambda > 0$ (see [50]);

and

(2.7)

Definition 2.10

Let X be a CAT(0) space and D be a nonempty closed and convex subset of X. A function $f : D \times D \rightarrow \mathbb {R}$ is called monotone if

$$\begin{aligned} f(x, y) + f(y, x) \le 0~~\forall ~ x, y~\in D. \end{aligned}$$

Lemma 2.11

[30] Let D be a nonempty closed and convex subset of a CAT(0) space X. Suppose that f is monotone and $\mathbb {D}(J^f) \ne \emptyset .$ Then, the following properties hold:

• (i) $J^f$ is single-valued.

• (ii) If $\mathbb {D}(J^f) \supset D,$ then $J^f$ is nonexpansive restricted to D.

• (iii) If $\mathbb {D}(J^f) \supset D$ then $F(J^f) = EP(f, D).$

Remark 2.12

[23] It follows easily from (1.5) that the resolvent $J^f_\mu$ of the bifunction f and order $\mu > 0$ is given as

$$\begin{aligned} J^f_\mu (x) := EP (\bar{f}_x,D) = \{z \in D : f(z, y) + \frac{1}{\mu }\langle \overrightarrow{xz},\overrightarrow{zy}\rangle \ge 0,~y\in D\},~~x\in X, \end{aligned}$$

(2.8)

where $\bar{f}$ is defined in this case as

$$\begin{aligned} \bar{f}_{\bar{x}}(x, y) := f(x, y) + \frac{1}{\mu }\langle \overrightarrow{\bar{x}x},\overrightarrow{xy}\rangle ,~\forall ~x,y \in D,~\bar{x}\in X. \end{aligned}$$

(2.9)

Lemma 2.13

[23] Let D be a nonempty, closed and convex subset of a complete CAT(0) space X and $f : D \times D \rightarrow \mathbb {R}$ be a monotone bifunction such that $D \subset \mathbb {D}(J^f_\mu )$ for $\mu > 0.$ Then, the following hold:

• (i) $J^f_\mu$ is firmly nonexpansive restricted to D.

• (ii) If $F(J_\mu ) \ne \emptyset ,$ then

  $$\begin{aligned} d^2(J^f_\mu x, x) \le d^2(x, v) - d^2(J^f_\mu x, v) ~\forall ~x \in D,~v \in F(J^f_\mu ). \end{aligned}$$

• (iii) If $0 < \mu _1 \le \mu _2,$ then $d(J^f_{\mu _2} x, J^f_{\mu _1} x) \le \sqrt{1 - \frac{\mu _1}{\mu _2}}d(x, J^f_{\mu _2} x),$ which implies that $d(x, J^f_{\mu _1} x) \le 2d(x, J^f_{\mu _2} x)~~\forall ~x \in D.$

Theorem 2.14

[30, Theorem 5.2] Let D be a nonempty, closed and convex subset of a complete CAT(0) space X. Suppose that f has the following properties

• (i) $f(x, x) = 0$ for all $x \in D,$

• (ii) f is monotone,

• (iii) for each $x \in D,$ $y \mapsto f(x, y)$ is convex and lower semicontinuous.

• (iv) for each $x \in D,$ $f(x, y) \ge \limsup _{t\downarrow 0} f((1 - t)x \oplus tz, y)$ for all $x, z \in D.$

Then $\mathbb {D}(J^f) = X$ and $J^f$ single-valued.

Remark 2.15

[23] If the bifunction f satisfies assumption (i)-(iv) of Theorem 2.14, then the conclusions of Lemma 2.13 hold in the whole of X.

Definition 2.16

Let D be a nonempty closed and convex subset of a CAT(0) space X. The metric projection is a mapping $P_D:X\rightarrow D$ which assigns to each $x\in X,$ the unique point $P_Dx\in D$ such that

$$\begin{aligned} d(x,P_Dx)=\inf \{d(x,y):y\in D\}. \end{aligned}$$

Lemma 2.17

[18, 36] Let X be a CAT(0) space. Then for all $x,y,z \in X$ and all $t, s \in [0,1],$ we have

• (i) $d(tx\oplus (1-t)y,z)\le td(x,z)+(1-t)d(y,z),$

• (ii) $d^2(tx\oplus (1-t)y,z)\le td^2(x,z)+(1-t)d^2(y,z)-t(1-t)d^2(x,y),$

• (iii) $d^2(z, t x \oplus (1-t) y)\le t^2 d^2(z, x)+(1-t)^2 d^2(z, y)+2t (1-t)\langle \overrightarrow{zx}, \overrightarrow{zy}\rangle ,$

• (iv) $d(tw \oplus (1 - t)x, ty \oplus (1 - t)z) \le td(w, y) + (1 - t)d(x, z),$

• (v) $d(tx \oplus (1 - t)y, sx \oplus (1 - s)y) \le |t - s|d(x, y).$

Lemma 2.18

[36] Every bounded sequence in a complete CAT(0) space has a $\Delta$-convergent subsequence.

Lemma 2.19

[16] Let D be a nonempty, closed and convex subset of a CAT(0) space X,  $x\in X$ and $u\in D.$ Then $u=P_{D}x$ if and only if $\langle \overrightarrow{xu},\overrightarrow{yu}\rangle \le 0$ for all $y\in D.$

Definition 2.20

Let D be a nonempty, closed and convex subset of a complete CAT(0) space X. A mapping $T : D \rightarrow D$ is said to be $\Delta$-demiclosed, if for any bounded sequence $\{x_n\}$ in X,  such that $\Delta -\lim \limits _{n\rightarrow \infty }x_n = x$ and $\lim \limits _{n\rightarrow \infty }d(x_n, Tx_n) = 0,$ then $x = Tx$.

Lemma 2.21

[17] Let X be a complete CAT(0) space and $T:X\rightarrow X$ be a nonexpansive mapping. Then T is $\Delta$-demiclosed.

Lemma 2.22

[55] Let $\{a_{n}\}$ be a sequence of non-negative real numbers satisfying

$$ a_{n+1}\le (1-\alpha _{n})a_{n}+\delta _{n},~~n\ge 0,$$

where $\{\alpha _{n}\}$ and $\{\delta _{n}\}$ satisfy the following conditions:

• (i) $\{\alpha _n\}\subset [0,1],~\Sigma _{n=0}^{\infty }\alpha _{n}=\infty$,

• (ii) $\limsup _{n\rightarrow \infty }\frac{\delta _{n}}{\alpha _n}\le 0$ or $\Sigma _{n=0}^{\infty }|\delta _{n}|<\infty .$

Then $\lim _{n\rightarrow \infty }a_{n}=0.$

3 Main results

We begin with the following Lemma which is crucial in establishing our main result.

Lemma 3.1

Let D be a nonempty, closed and convex subset of a complete CAT(0) space X. Let $X^*$ be the dual space of X and $A : X \rightarrow 2^{X^*}$ be a multivalued monotone operator which satisfies the range condition. Let $f : D \times D \rightarrow \mathbb {R}$ be a bifunction satisfying assumptions (i)-(iv) of Theorem 2.14 and $T: X \rightarrow X$ be a nonexpansive mapping. If $F(T) \cap F(J^A_{\lambda _2}) \cap F(J^f_{\mu _2}) \ne \emptyset ,$ then for $0 < \lambda _1 \le \lambda _2$ and $0 < \mu _1 \le \mu _2,$ we have that $F(T\circ J^A_{\lambda _2}\circ J^f_{\mu _2}) = F(T) \cap F(J^A_{\lambda _1}) \cap F(J^f_{\lambda _1}).$

Proof

It is obvious that $F(T) \cap F(J^A_{\lambda _1}) \cap F(J^f_{\mu _1}) \subseteq F(T\circ J^A_{\lambda _2}\circ J^f_{\mu _2}) .$ We only need to show that $F(T\circ J^A_{\lambda _2}\circ J^f_{\mu _2}) \subseteq F(T) \cap F(J^A_{\lambda _1}) \cap F(J^f_{\mu _1}).$ Let $x \in F(T\circ J^A_{\lambda _2}\circ J^f_{\mu _2})$ and $y \in F(T) \cap F(J^A_{\lambda _2}) \cap F(J^f_{\mu _2}).$ Then by nonexpansivity of T, we have

$$\begin{aligned} d(x, y)= & {} d(T(J^A_{\lambda _2}(J^f_{\mu _2}x)), y)\nonumber \\\le & {} d(J^A_{\lambda _2}(J^f_{\mu _2}x), y). \end{aligned}$$

(3.1)

From (2.6) and (3.1), we have

$$\begin{aligned} d^2(J^A_{\lambda _2}(J^f_{\mu _2}x), J^f_{\mu _2}x)\le & {} d^2(J^f_{\mu _2}x, y) - d^2(J^A_{\lambda _2}(J^f_{\mu _2}x), y) \\\le & {} d^2(x, y) - d^2(J^A_{\lambda _2}(J^f_{\mu _2}x), y) \\\le & {} d^2(J^A_{\lambda _2}(J^f_{\mu _2}x), y) - d^2(J^A_{\lambda _2}(J^f_{\mu _2}x), y), \end{aligned}$$

which implies

$$\begin{aligned} J^A_{\lambda _2}(J^f_{\mu _2}x) = J^f_{\mu _2}x. \end{aligned}$$

(3.2)

Similarly, from Lemma 2.13(ii), (3.1) and (3.2) we have

$$\begin{aligned} d^2(J^f_{\mu _2}x, x)\le & {} d^2(x, y) - d^2(J^f_{\mu _2}x, y) \\= & {} d^2(x, y) - d^2(J^A_{\lambda _2}(J^f_{\mu _2}x), y) \\\le & {} d^2(J^A_{\lambda _2}(J^f_{\mu _2}x), y) - d^2(J^A_{\lambda _2}(J^f_{\mu _2}x), y), \end{aligned}$$

which implies

$$\begin{aligned} J^f_{\mu _2}x = x. \end{aligned}$$

(3.3)

From (3.2) and (3.3), we obtain that

$$\begin{aligned} x = J^A_{\lambda _2}(J^f_{\mu _2}x) = J^A_{\lambda _2}x, \end{aligned}$$

(3.4)

which implies that

$$\begin{aligned} x = T(J^A_{\lambda _2}(J^f_{\mu _2}x)) = Tx. \end{aligned}$$

(3.5)

Furthermore, from (2.8) and Lemma 2.11 we have

$$\begin{aligned} f(J^f_{\mu _1}x, J^f_{\mu _2}x) + \frac{1}{\mu _1}\langle \overrightarrow{xJ^f_{\mu _1}x}, \overrightarrow{J^f_{\mu _1}xJ^f_{\mu _2}x}\rangle\ge & {} 0 \end{aligned}$$

(3.6)

and

$$\begin{aligned} f(J^f_{\mu _2}x, J^f_{\mu _1}x) + \frac{1}{\mu _2}\langle \overrightarrow{xJ^f_{\mu _2}x}, \overrightarrow{J^f_{\mu _2}xJ^f_{\mu _1}x}\rangle\ge & {} 0. \end{aligned}$$

(3.7)

Adding (3.6) and (3.7), and using the fact that f is monotone, we obtain

$$\begin{aligned} \langle \overrightarrow{J^f_{\mu _1}xx}, \overrightarrow{J^f_{\mu _2}xJ^f_{\mu _1}x}\rangle\ge & {} \frac{\mu _1}{\mu _2} \langle \overrightarrow{J^f_{\mu _2}xx}, \overrightarrow{J^f_{\mu _2}x J^f_{\mu _1}x}\rangle . \end{aligned}$$

(3.8)

Using the quasilinearization properties on (3.8), we obtain

$$\begin{aligned} \Big (\frac{\mu _1}{\mu _2} + 1\Big ) d^2(J^f_{\mu _2}x, J^f_{\mu _1}x) \le \Big (1 - \frac{\mu _1}{\mu _2} \Big ) d^2(x, J^f_{\mu _2}x) + \Big (\frac{\mu _1}{\mu _2} - 1\Big ) d^2(x, J^f_{\mu _1}x). \end{aligned}$$

Since $\frac{\mu _1}{\mu _2} \le 1,$ we have that

$$\begin{aligned} \Big (\frac{\mu _1}{\mu _2} + 1\Big ) d^2(J^f_{\mu _2}x, J^f_{\mu _1}x) \le \Big (1 - \frac{\mu _1}{\mu _2} \Big ) d^2(x, J^f_{\mu _2}x), \end{aligned}$$

which implies that

$$\begin{aligned} d^2(J^f_{\mu _2}x, J^f_{\mu _1}x) \le \sqrt{1 - \frac{\mu _1}{\mu _2}} d^2(x, J^f_{\mu _2}x). \end{aligned}$$

(3.9)

By triangle inequality and (3.9), we obtain that

$$\begin{aligned} d(x, J^f_{\mu _1}x) \le 2 d(x, J^f_{\mu _2}x). \end{aligned}$$

(3.10)

Therefore from (3.3), we obtain that $x \in F(J^f_{\mu _1}).$ By similar argument as in (3.6)–(3.10), we obtain that $x \in F(J^A_{\lambda _1})$ and then we have that $F(T\circ J^A_{\lambda _2}\circ J^f_{\mu _2}) \subseteq F(T) \cap F(J^A_{\lambda _1}) \cap F(J^f_{\mu _1}).$ Hence, this completes the proof. $\square$

Theorem 3.2

Let D be a nonempty, closed and convex subset of a complete CAT(0) space X, $X^*$ be the dual space of X and $A : X \rightarrow 2^{X^*}$ be a multivalued monotone operator satisfying the range condition. Let $f: D \times D \rightarrow \mathbb {R}$ be a bifunction satisfying assumption (i)-(iv) in Theorem 2.14. Let $T: X \rightarrow X$ be nonexpansive mapping and $g: X \rightarrow X$ be a contraction mapping with coefficient $\theta \in (0, 1).$ Suppose that $\Gamma : = F(T) \cap A^{-1}(0) \cap EP(f, D) \ne \emptyset$ and for arbitrary $x_1 \in X,$ the sequence $\{x_n\}$ is generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=J^A_{\lambda _n}\circ J^f_{\mu _n}\Big (\frac{x_n\oplus x_{n+1}}{2}\Big ),\\ x_{n+1}=\alpha _n g\Big (\frac{x_n\oplus x_{n+1}}{2}\Big )\oplus (1-\alpha _n)Ty_n~~ \forall ~ n \ge 1, \end{array}\right. } \end{aligned}$$

(3.11)

where $\{\alpha _n\} \in (0,1)$ and $\{\lambda _n\},~\{\mu _n\}$ are sequences in $(0,\infty )$ such that the following conditions are satisfied:

• (A1) $\lim \limits _{n \rightarrow \infty } \alpha _n = 0$ and $\sum \limits ^{\infty }_{n=1}\alpha _n=\infty ,$

• (A2) $\sum \limits _{n=1}|\alpha _{n+1}-\alpha _n| <\infty ,$

• (A3) $0< \lambda _{n-1} \le \lambda _n,~\sum \limits _{n=1}^\infty \left( \sqrt{1-\frac{\lambda _{n-1}}{\lambda _n}}\right) <\infty$ and $0< \mu _{n-1} \le \mu _n, ~\sum \limits _{n=1}^\infty \left( \sqrt{1-\frac{\mu _{n-1}}{\mu _n}}\right) <\infty ~\forall ~n \ge 1.$

Then, the sequence $\{x_n\}$ converges to a point $\bar{x}$ in $\Gamma$ which is also a unique solution of the following variational inequality

$$\begin{aligned} \langle \overrightarrow{\bar{x}g(\bar{x})},\overrightarrow{p\bar{x}} \rangle \ge 0,~~\forall ~p\in \Gamma . \end{aligned}$$

Remark 3.3

With a midpoint at each step of our method, it tends to have better accuracy than (1.8), (1.9) and other methods with single or no midpoint rule.

Proof

STEP 1: We show that $\{x_n\}$ is bounded. Let $p\in \Gamma ,$ then by Lemma 2.17(i) and (3.11) we have

$$\begin{aligned} d(x_{n+1},p)&=d\left( \alpha _n g\left( \frac{x_n\oplus x_{n+1}}{2}\right) \oplus (1-\alpha _n)Ty_n,p\right) \\&\le \alpha _n d\left( g\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,p\right) +(1-\alpha _n)d(Ty_n,p)\\&\le \alpha _n d\left( g\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,p\right) +(1-\alpha _n)d\left( \frac{x_n\oplus x_{n+1}}{2},p\right) \\&\le \alpha _n \theta d\left( \frac{x_n\oplus x_{n+1}}{2},p\right) +\alpha _n d(g(p),p)+(1-\alpha _n)d\left( \frac{x_n\oplus x_{n+1}}{2},p\right) \\&=\big (1-\alpha _n(1-\theta )\big )d\left( \frac{x_n\oplus x_{n+1}}{2},p\right) +\alpha _n d(g(p),p)\\&\le \Big (\frac{1-\alpha _n(1-\theta )}{2}\Big )(d(x_n,p)+d(x_{n+1},p))+\alpha _n d(g(p),p).\\ \end{aligned}$$

This implies that

$$\begin{aligned} d(x_{n+1},p)&\le \frac{1-\alpha _n(1-\theta )}{1+\alpha _n(1-\theta )}d(x_n,p)+\frac{2\alpha _n}{1+\alpha _n(1-\theta )}d(g(p),p)\\&= 1-\frac{2\alpha _n(1-\theta )}{1+\alpha _n(1-\theta )} d(x_n,p)+\frac{2\alpha _n(1-\theta )}{1+\alpha _n(1-\theta )}\left( \frac{1}{(1-\theta )}d(g(p),p)\right) \\&\le \left\{ d(x_n,p),\frac{1}{(1-\theta )}d(g(p),p)\right\} , \end{aligned}$$

which implies by mathematical induction that

$$\begin{aligned} d(x_{n+1},p) \le \left\{ d(x_1,p),\frac{1}{(1-\theta )}d(g(p),p)\right\} ,~~ \forall ~~n\in \mathbb {N}. \end{aligned}$$

Thus, $\{x_n\}$ is bounded. Consequently $\{y_n\},$ $\{Ty_n\}$ and $\left\{ g\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right\}$ are also bounded.

STEP 2: We show that $\lim \limits _{n \rightarrow \infty }d(x_{n+1},x_n)=0.$ From Lemma 2.17(iv),(v) and (3.11) we have

$$\begin{aligned} d(x_{n+1},x_n)&=d\left( \alpha _n g\left( \frac{x_n \oplus x_{n+1}}{2}\right) \oplus (1-\alpha _n)Ty_n,~\alpha _{n-1} g\left( \frac{x_{n-1} \oplus x_n}{2}\right) \oplus (1-\alpha _{n-1})Ty_{n-1}\right) \nonumber \\&\le d\left( \alpha _n g\left( \frac{x_n \oplus x_{n+1}}{2}\right) \oplus (1-\alpha _n)Ty_n,~\alpha _{n-1} g\left( \frac{x_{n} \oplus x_{n+1}}{2}\right) \oplus (1-\alpha _{n-1})Ty_n\right) \nonumber \\&\quad +d\left( \alpha _{n-1} g\left( \frac{x_{n} \oplus x_{n+1}}{2}\right) \oplus (1-\alpha _{n-1})Ty_n,~\alpha _{n-1} g\left( \frac{x_{n-1} \oplus x_n}{2}\right) \oplus (1-\alpha _{n-1})Ty_{n-1}\right) \nonumber \\&\le |\alpha _n-\alpha _{n-1}|~d\left( g\left( \frac{x_n \oplus x_{n+1}}{2}\right) ,~Ty_n\right) +\alpha _{n-1}d\left( g\left( \frac{x_n \oplus x_{n+1}}{2}\right) ,~g\left( \frac{x_{n-1} \oplus x_n}{2}\right) \right) \nonumber \\&\quad +(1-\alpha _{n-1})~d(Ty_n,~Ty_{n-1}) \nonumber \\&\le |\alpha _n-\alpha _{n-1}|~d\left( g\left( \frac{x_n \oplus x_{n+1}}{2}\right) ,Ty_n\right) +\alpha _{n-1}\theta d\left( \frac{x_n \oplus x_{n+1}}{2},\frac{x_{n-1} \oplus x_n}{2}\right) \nonumber \\&\quad +(1-\alpha _{n-1})~d(y_n,y_{n-1}) \nonumber \\&= |\alpha _n-\alpha _{n-1}|~d\left( g\left( \frac{x_n \oplus x_{n+1}}{2}\right) ,Ty_n\right) +\alpha _{n-1}\theta d\left( \frac{x_n \oplus x_{n+1}}{2},\frac{x_{n-1} \oplus x_n}{2}\right) \nonumber \\&\quad +(1-\alpha _{n-1})d\left( J^A_{\lambda _n}\circ J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) , J^A_{\lambda _{n-1}}\circ J^f_{\mu _{n-1}}\left( \frac{x_{n-1}\oplus x_n}{2}\right) \right) \end{aligned}$$

(3.12)

Again, from (2.7) and (3.9) we obtain that

$$\begin{aligned} d(y_n, y_{n-1})&\le d\left( J^A_{\lambda _n}\left( J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right) ,~J^A_{\lambda _{n-1}}\left( J^f_{\mu _{n-1}}\left( \frac{x_n\oplus x_{n+1}}{2}\right) \right) \right) \nonumber \\&\quad +d \left( J^A_{\lambda _{n-1}}\left( J^f_{\mu _{n-1}}\left( \frac{x_n\oplus x_{n+1}}{2}\right) \right) ,~J^A_{\lambda _{n-1}}\left( J^f_{\mu _{n-1}}\left( \frac{x_{n-1}\oplus x_n}{2}\right) \right) \right) \nonumber \\&\le d\left( J^A_{\lambda _n}\left( J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right) ,~J^A_{\lambda _{n-1}}\left( J^f_{\mu _n}\left( \frac{x_n\oplus x_{n+1}}{2}\right) \right) \right) \nonumber \\&\quad + d\left( J^A_{\lambda _{n-1}}\left( J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right) ,~J^A_{\lambda _{n-1}}\left( J^f_{\mu _{n-1}}\left( \frac{x_n\oplus x_{n+1}}{2}\right) \right) \right) \nonumber \\&\quad +d\left( \frac{x_n\oplus x_{n+1}}{2}, \frac{x_{n-1}\oplus x_n}{2}\right) \nonumber \\&\le \sqrt{1 - \frac{\lambda _{n-1}}{\lambda _n}}~d\left( J^f_{\mu _n}\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,J^A_{\lambda _n}\left( J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right) \right) \nonumber \\&\quad +d\left( J^f_{\mu _n}\left( \frac{x_n\oplus x_{n+1}}{2}\right) , J^f_{\mu _{n-1}}\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right) +d\left( \frac{x_n\oplus x_{n+1}}{2},\frac{x_{n-1} \oplus x_n}{2}\right) \nonumber \\&\le \sqrt{1 - \frac{\lambda _{n-1}}{\lambda _n}}~d\left( J^f_{\mu _n}\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,J^A_{\lambda _n}\left( J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right) \right) \end{aligned}$$

(3.13)

$$\begin{aligned}&\quad +\sqrt{1-\frac{\mu _{n-1}}{\mu _n}}~d\left( \frac{x_n\oplus x_{n+1}}{2},J^f_{\mu _n}\left( \frac{x_n\oplus x_{n+1}}{2}\right) \right) + d\left( \frac{x_n\oplus x_{n+1}}{2}, \frac{x_{n-1}\oplus x_n}{2} \right) \nonumber \\&\le \sqrt{1 - \frac{\lambda _{n-1}}{\lambda _n}}~d\left( J^f_{\mu _n}\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,J^A_{\lambda _n}\left( J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right) \right) \nonumber \\&\quad +\sqrt{1-\frac{\mu _{n-1}}{\mu _n}}~d\left( \frac{x_n\oplus x_{n+1}}{2},J^f_{\mu _n}\left( \frac{x_n\oplus x_{n+1}}{2}\right) \right) + \big [d\left( x_n,~x_{n-1})+ d(x_{n+1},~x_n\right) \big ] . \end{aligned}$$

(3.14)

Substituting (3.13) in (3.12) we have

$$\begin{aligned}&\quad d(x_{n+1},~x_n) \le |\alpha _n-\alpha _{n-1}|~d\left( g\left( \frac{x_n \oplus x_{n+1}}{2}\right) , ~Ty_n\right) \nonumber \\&\quad +(1-\alpha _{n-1}(1-\theta ))~d\left( \frac{x_n\oplus x_{n+1}}{2}, ~\frac{x_{n-1}\oplus x_n}{2}\right) \nonumber \\&\quad +(1-\alpha _{n-1})\left[ \sqrt{1-\frac{\lambda _{n-1}}{\lambda _n}}~d\left( J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) ,~J^A_{\lambda _n}\left( J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right) \right) \right] \nonumber \\&\quad +(1-\alpha _{n-1})\left[ \sqrt{1-\frac{\mu _{n-1}}{\mu _n}}~d\left( \frac{x_n \oplus x_{n+1}}{2}, ~J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right) \right] \nonumber \\&\qquad \le |\alpha _n-\alpha _{n-1}|~d\left( g\left( \frac{x_n \oplus x_{n+1}}{2}\right) , ~Ty_n \right) \nonumber \\&\quad +\frac{(1-\alpha _{n-1}(1-\theta ))}{2}~\big [d\left( x_n,~x_{n-1})+ d(x_{n+1},~x_n\right) \big ]\nonumber \\&\quad +(1-\alpha _{n-1})\left[ \sqrt{1-\frac{\lambda _{n-1}}{\lambda _n}}~d\left( J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) ,~J^A_{\lambda _n}\left( J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right) \right) \right] \nonumber \\&\quad +(1-\alpha _{n-1})\left[ \sqrt{1-\frac{\mu _{n-1}}{\mu _n}}~d\left( \frac{x_n \oplus x_{n+1}}{2}, ~J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right) \right] \nonumber \\&\qquad \le \left[ |\alpha _n-\alpha _{n-1}|+\sqrt{1-\frac{\lambda _{n-1}}{\lambda _n}} +\sqrt{1-\frac{\mu _{n-1}}{\mu _n}}\right] B +\frac{(1-\alpha _{n-1}(1-\theta ))}{2}\nonumber \\&\quad \big [d\left( x_n,~x_{n-1})+ d(x_{n+1},~x_n\right) \big ] \end{aligned}$$

(3.15)

where

$$\begin{aligned} B \ge \max \Bigg \{\sup _{n \ge 1} \left\{ d\left( g\left( \frac{x_n \oplus x_{n+1}}{2}\right) ,~Ty_n\right) \right\} , ~\sup _{n \ge 1}\left\{ d\left( \frac{x_n \oplus x_{n+1}}{2},~J^f_{\mu _n}\left( \frac{x_n \oplus x_{n+1}}{2}\right) \right) \right\} ,\\ \sup _{n\ge 1}\left\{ d\left( J^f_{\mu _n}\left( \frac{x_n\oplus x_{n+1}}{2}\right) , ~J^A_{\lambda _n}\left( J^f_{\mu _n}\left( \frac{x_n\oplus x_{n+1}}{2}\right) \right) \right) \right\} \Bigg \}. \end{aligned}$$

It implies from (3.15) that

$$\begin{aligned} d(x_{n+1},x_n)&\le \frac{(1-\alpha _{n-1}(1-\theta ))}{(1+\alpha _{n-1}(1-\theta ))}d(x_n,x_{n-1}) \\&\qquad +\left[ |\alpha _n-\alpha _{n-1}|+\sqrt{1-\frac{\lambda _{n-1}}{\lambda _n}}+\sqrt{1-\frac{\mu _{n-1}}{\mu _n}}\right] \frac{2B}{1+\alpha _{n-1}(1-\theta )}\\&\quad = \left[ 1-\frac{2\alpha _{n-1}(1-\theta )}{1+\alpha _{n-1}(1-\theta )}\right] d(x_n,x_{n-1}) \\&\qquad + \left[ |\alpha _n-\alpha _{n-1}|+\sqrt{1-\frac{\lambda _{n-1}}{\lambda _n}}+\sqrt{1-\frac{\mu _{n-1}}{\mu _n}}\right] \frac{2B}{1+\alpha _{n-1}(1-\theta )}. \end{aligned}$$

Then, by Lemma 2.22, conditions (A2) and (A3),  we obtain that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }d(x_{n+1},x_n)=0. \end{aligned}$$

(3.16)

STEP 3: We show that $\lim \limits _{n \rightarrow \infty }d(\bar{x}_n,T\bar{x}_n)=0=\lim \limits _{n \rightarrow \infty }d(\bar{x}_n,Ty_n),$ where $\bar{x}_n=\frac{x_n\oplus x_{n+1}}{2}.$ From Lemma (2.17)(ii) we have

$$\begin{aligned}{} & {} d^2(x_{n+1}, p) \le \alpha _nd^2(g(\bar{x}_n),p) + (1 - \alpha _n)d^2(y_n, p)\nonumber \\{} & {} \quad \le \alpha _nd^2(g(\bar{x}_n),p) + d^2(y_n, p). \end{aligned}$$

(3.17)

Also, from (2.6), we have that

$$\begin{aligned} d^2(y_n,~p)&\le ~ d^2(J^f_{\mu _n}\bar{x}_n,~p) - d^2(y_n,~J^f_{\mu _n}\bar{x}_n). \end{aligned}$$

(3.18)

Substituting (3.18) in (3.17), we obtain

$$\begin{aligned} d^2(x_{n+1}, p)\le & {} \alpha _nd^2(g(\bar{x}_n),p) + d^2(J^f_{\mu _n}\bar{x}_n,~p) - d^2(y_n,~J^f_{\mu _n}\bar{x}_n), \end{aligned}$$

(3.19)

which implies

$$\begin{aligned} d^2(y_n,~J^f_{\mu _n}\bar{x}_n)\le & {} \alpha _nd^2(g(\bar{x}_n),p) + d^2(J^f_{\mu _n}\bar{x}_n,~p) - d^2(x_{n+1}, p)\nonumber \\\le & {} \alpha _nd^2(g(\bar{x}_n),p) + d^2(\bar{x}_n,~p) - d^2(x_{n+1}, p)\nonumber \\\le & {} \alpha _nd^2(g(\bar{x}_n),p) + \frac{1}{2}\big [d^2(x_n,~p) - d^2(x_{n+1}, p)\big ]\nonumber \\\le & {} \alpha _nd^2(g(\bar{x}_n),p) + \frac{1}{2}\big [\big (d(x_n,x_{n+1}) + d(x_{n+1} ~p)\big )^2 - d^2(x_{n+1}, p)\big ]\nonumber \\= & {} \alpha _nd^2(g(\bar{x}_n),p) + \frac{1}{2}d^2(x_n,x_{n+1}) + d(x_n,x_{n+1})d(x_{n+1}, p). \end{aligned}$$

(3.20)

Then from (3.16) and condition (A1), we obtain that

$$\begin{aligned} \lim \limits _{n \rightarrow \infty }d^2(y_n,~J^f_{\mu _n}\bar{x}_n)=0. \end{aligned}$$

(3.21)

Similarly, from Lemma 2.13(ii) we have that

$$\begin{aligned} d^2(J^f_{\mu _n}\bar{x}_n,~p)&\le d^2(\bar{x}_n,~p) - d^2(J^f_{\mu _n}\bar{x}_n,~\bar{x}_n). \end{aligned}$$

(3.22)

Again, substituting (3.22) in (3.19), we have

$$\begin{aligned} d^2(x_{n+1}, p)\le & {} \alpha _nd^2(g(\bar{x}_n),p) + d^2(\bar{x}_n,~p) - d^2(J^f_{\mu _n}\bar{x}_n,~\bar{x}_n) - d^2(y_n,~J^f_{\mu _n}\bar{x}_n)\nonumber \\\le & {} \alpha _nd^2(g(\bar{x}_n),p) + d^2(\bar{x}_n,~p) - d^2(J^f_{\mu _n}\bar{x}_n,~\bar{x}_n), \end{aligned}$$

(3.23)

which also implies

$$\begin{aligned} d^2(J^f_{\mu _n}\bar{x}_n,~\bar{x}_n)\le & {} \alpha _nd^2(g(\bar{x}_n),p) + d^2(\bar{x}_n,~p) - d^2(x_{n+1}, p). \end{aligned}$$

(3.24)

By the same argument as in (3.20), we obtain that

$$\begin{aligned} \lim \limits _{n \rightarrow \infty }d^2(J^f_{\mu _n}\bar{x}_n,~\bar{x}_n)=0. \end{aligned}$$

(3.25)

Hence, from (3.21) and (3.25) we obtain that

$$\begin{aligned} d(y_n,~\bar{x}_n)&\le d(y_n, ~J^f_{\mu _n}\bar{x}_n) + d(J^f_{\mu _n}\bar{x}_n,~\bar{x}_n) \longrightarrow 0,~\text {as}~n\rightarrow \infty . \end{aligned}$$

(3.26)

Also, from (3.16), we have that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }d(\bar{x}_n,~x_n) = 0. \end{aligned}$$

(3.27)

Then from (3.16), (3.26), (3.27) and condition (A1), we obtain that

$$\begin{aligned}&d(\bar{x}_n,T\bar{x}_n) \le d(\bar{x}_n, x_n) + d(x_n,x_{n+1})+d(x_{n+1},Ty_n)+d(Ty_n,T\bar{x}_n)\nonumber \\&\quad \le d(\bar{x}_n, x_n) +d(x_n,x_{n+1})+\alpha _n d(g(\bar{x}_{n}),Ty_n)+d(y_n,\bar{x}_n)~~ \rightarrow 0, ~~ \text {as}~~ n \rightarrow \infty . \end{aligned}$$

(3.28)

Also, from (3.26) and (3.28) we have

$$\begin{aligned} d(\bar{x}_n,Ty_n)&\le d(\bar{x}_n,T\bar{x}_n)+d(T\bar{x}_n,Ty_n) \nonumber \\&\le d(\bar{x}_n,T\bar{x}_n)+d(\bar{x}_n,y_n)~~ \rightarrow 0~~ \text {as}~~ n \rightarrow \infty . \end{aligned}$$

(3.29)

STEP 4: We show that $\limsup \limits _{n \rightarrow \infty }\langle \overrightarrow{g(x^{*})x^{*}},\overrightarrow{x_nx^{*}}\rangle \le 0,$ where $x^{*}=P_{\Gamma }g(x^{*}).$

Since $\{x_n\}$ is bounded and X is a complete CAT(0) space, then we obtain from Lemma 2.18 that there exists a subsequence $\{x_{n_i}\}$ of $\{x_n\}$ such that $\Delta -\lim \limits _{i\rightarrow \infty }x_{n_i}=\bar{z}.$ Thus, by (3.27), we obtain that $\Delta -\lim \limits _{i\rightarrow \infty }\bar{x}_{n_i}=\bar{z}.$ Also, since $T\circ J^A_{\lambda _n}\circ J^f_{\mu _n}$ is nonexpansive, then it implies from Lemma 2.21 that it is demiclosed. Therefore, from Lemma 2.11(iii), Lemma 2.8(i), Lemma 3.1 and (3.29) we obtain that $\bar{z}\in F(T\circ J^A_{\lambda _n}\circ J^f_{\mu _n})\subseteq F(T)\cap F(J^A_{\lambda })\cap F(J^f_{\mu })=\Gamma .$ Since $\{x_n\}$ is bounded, we can choose without loss of generality, $\{x_{n_i}\}$ of $\{x_n\}$ such that

$$\begin{aligned} \limsup \limits _{n \rightarrow \infty }\langle \overrightarrow{g(x^{*})x^{*}},\overrightarrow{x_nx^{*}}\rangle= & {} \lim \limits _{i\rightarrow \infty }\langle \overrightarrow{g(x^{*})x^{*}},\overrightarrow{x_{n_i}x^{*}}\rangle . \end{aligned}$$

Now, using this and Lemma 2.19 we obtain that

$$\begin{aligned} \limsup \limits _{n \rightarrow \infty }\langle \overrightarrow{g(x^{*})x^{*}},\overrightarrow{x_nx^{*}}\rangle= & {} \langle \overrightarrow{g(x^{*})x^{*}},\overrightarrow{\bar{z}x^{*}}\rangle \le 0. \end{aligned}$$

(3.30)

STEP 5: Finally, we show that $x_n\rightarrow x^{*}~~ \text {as}~~n \rightarrow \infty$ and then $x^{*}$ is also the unique fixed point of the contraction $P_{\Gamma }\circ g.$ From Lemma 2.17(iii) and (3.11), we have

$$\begin{aligned}&d^2(x_{n+1},x^{*}) =d^2\left( \alpha _n g\left( \frac{x_n \oplus x_{n+1}}{2}\right) \oplus (1-\alpha _n)Ty_n,~x^{*}\right) \\&\quad \le {\alpha _n}^2 d^2\left( g\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,~x^{*}\right) +(1-\alpha _n)^2d^2(Ty_n,~x^{*}) \\&\qquad +2\alpha _n(1-\alpha _n)\Big \langle \overrightarrow{g\left( \frac{x_n\oplus x_{n+1}}{2}\right) x^{*}},~\overrightarrow{Ty_nx^{*}}\Big \rangle \\&\quad \le {\alpha _n}^2 d^2\left( g\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,~x^{*}\right) +(1-\alpha _n)^2d^2(y_n,~x^{*}) \\&\qquad +2\alpha _n(1-\alpha _n)\Big \langle \overrightarrow{g\left( \frac{x_n\oplus x_{n+1}}{2}\right) x^{*}},~\overrightarrow{Ty_nx^{*}}\Big \rangle \\&\quad \le {\alpha _n}^2 d^2\left( g\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,~x^{*}\right) +(1-\alpha _n)^2d^2(y_n,x^{*})\\&\qquad +2\alpha _n(1-\alpha _n)\Big \langle \overrightarrow{g\left( \frac{x_n\oplus x_{n+1}}{2}\right) g(x^{*})},~\overrightarrow{Ty_nx^{*}}\Big \rangle \\&\qquad +2\alpha _n(1-\alpha _n)\langle \overrightarrow{g(x^{*})x^{*}},~\overrightarrow{Ty_nx^{*}}\rangle \\&\quad \le {\alpha _n}^2 d^2\left( g\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,~x^{*}\right) +(1-\alpha _n)^2d^2(y_n,~x^{*})\\&\qquad +2\alpha _n(1-\alpha _n)d\left( g\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,~g(x^{*})\right) d(Ty_n,~x^{*})\\&\qquad +2\alpha _n(1-\alpha _n)\langle \overrightarrow{g(x^{*})x^{*}},~\overrightarrow{Ty_nx^{*}}\rangle \\&\quad \le {\alpha _n}^2 d^2\left( g\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,~x^{*}\right) +(1-\alpha _n)^2d^2(y_n,~x^{*})\\&\qquad +2\theta \alpha _n(1-\alpha _n)d\left( \frac{x_n\oplus x_{n+1}}{2},x^{*}\right) d(y_n,~x^{*})\\&\qquad +2\alpha _n(1-\alpha _n)\langle \overrightarrow{g(x^{*})x^{*}},~\overrightarrow{Ty_nx^{*}}\rangle \\&\quad \le {\alpha _n}^2 d^2\left( g\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,~x^{*}\right) +(1-\alpha _n)^2d^2\left( \frac{x_n\oplus x_{n+1}}{2},~x^{*}\right) \\&\qquad +2\theta \alpha _n(1-\alpha _n)d\left( \frac{x_n\oplus x_{n+1}}{2},~x^{*}\right) d(\frac{x_n\oplus x_{n+1}}{2},~x^{*})\\&\qquad +2\alpha _n(1-\alpha _n)\langle \overrightarrow{g(x^{*})x^{*}},~\overrightarrow{Ty_nx^{*}}\rangle \\&\quad =(1-\alpha _n)(1-\alpha _n+2\theta \alpha _n)d^2\left( \frac{x_n\oplus x_{n+1}}{2},x^{*}\right) +C_n, \end{aligned}$$

where

$$\begin{aligned} C_n:=\alpha _n^2d^2\left( g\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,x^{*}\right) +2\alpha _n(1-\alpha _n)\langle \overrightarrow{g(x^{*})x^{*}},~\overrightarrow{Ty_nx^{*}}\rangle . \end{aligned}$$

(3.31)

Then

$$\begin{aligned} d^2(x_{n+1},x^{*})&\le \frac{1}{2}(1-\alpha _n)(1-\alpha _n+2\theta \alpha _n)\left[ d^2(x_n,~x^{*})+d(x_{n+1},~x^{*})\right] +C_n, \end{aligned}$$

which implies that

$$\begin{aligned} d^2(x_{n+1},x^{*})&\le \frac{\frac{1}{2}(1-\alpha _n)(1-\alpha _n+2\theta \alpha _n}{1-\frac{1}{2}(1-\alpha _n)(1-\alpha _n+2\theta \alpha _n)}d^2(x_n,x^{*})+D_n, \end{aligned}$$

(3.32)

where

$$\begin{aligned} D_n=\frac{C_n}{1-\frac{1}{2}(1-\alpha _n)(1-\alpha _n+2\alpha _n)}. \end{aligned}$$

(3.33)

Let $k:(0,\infty )\rightarrow \mathbb {R}$ be a function defined by

$$\begin{aligned} k(t)=\frac{1}{t}\left\{ 1-\frac{\frac{1}{2}(1-t)(1-t+2\theta t)}{1-\frac{1}{2}(1-t)(1-t+2\theta t)}\right\} ~~~ \text {for all}~~~t>0. \end{aligned}$$

Then $\lim \limits _{t \rightarrow 0}k(t)=4(1-\theta ).$ Let $\delta >0$ such that $0<t<\delta$ and $\epsilon =4(1-\theta )>0.$ Then

$$\begin{aligned} \frac{1}{t}\left\{ 1-\frac{\frac{1}{2}(1-t)(1-t+2\theta t)}{1-\frac{1}{2}(1-t)(1-t+2\theta t)}\right\} ~~~ >\epsilon \end{aligned}$$

(3.34)

which implies that

$$\begin{aligned} 1-\alpha _n\epsilon >\frac{\frac{1}{2}(1-\alpha _n)(1-\alpha _n+2\theta \alpha _n)}{1-\frac{1}{2}(1-\alpha _n)(1-\alpha _n+2\theta \alpha _n)}. \end{aligned}$$

Since $\alpha _n \rightarrow 0$ as $n \rightarrow \infty ,$ there exists an integer $n\in \mathbb {N}$ such that $\alpha _n <\delta$ for $n\ge \mathbb {N}.$

From (3.15) and (3.16) we obtain

$$d^2(x_{n+1},~x^{*})\le (1-\alpha _n\epsilon )d^2(x_n,~x^{*})+D_n.$$

From (3.31) we have

$$\begin{aligned} \frac{C_n}{\alpha _n}=\alpha _nd^2\left( g\left( \frac{x_n\oplus x_{n+1}}{2}\right) ,~x^{*}\right) +2(1-\alpha _n)\langle \overrightarrow{g(x^{*})x^{*}},\overrightarrow{y_nx^{*}}\rangle . \end{aligned}$$

Then by (3.30) and condition (A1) we obtain that

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty }\frac{C_n}{\alpha _n}\le 0. \end{aligned}$$

Similarly, from (3.30) and condition (A1) we obtain that

$$\begin{aligned} \limsup \limits _{n\rightarrow \infty }\frac{D_n}{\alpha _n} \le 0. \end{aligned}$$

(3.35)

By Lemma 2.22, (3.35), and condition (A1) we obtain that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }d^2(x_{n+1},x^{*})=0. \end{aligned}$$

(3.36)

Hence, (3.36) implies that $x_n\rightarrow x^{*}$ as $n \rightarrow \infty .$ Therefore $\{x_n\}$ converges to $x^{*} \in \Gamma .$ $\square$

By setting $J^f_{\mu _n} \equiv I$ (where I is an identity mapping) in Theorem 3.2, we obtain the following result:

Corollary 3.4

Let X be a complete CAT(0) space, $X^*$ be the dual space of X and $A : X \rightarrow 2^{X^*}$ be a multivalued monotone operator satisfying the range condition. Let $T: X \rightarrow X$ be nonexpansive mapping and $g: X \rightarrow X$ be a contraction mapping with coefficient $\theta \in (0, 1).$ Suppose that $\Gamma : = F(T) \cap A^{-1}(0)\ne \emptyset$ and for arbitrary $x_1 \in X,$ the sequence $\{x_n\}$ is generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=J^A_{\lambda _n}\Big (\frac{x_n\oplus x_{n+1}}{2}\Big ),\\ x_{n+1}=\alpha _n g\Big (\frac{x_n\oplus x_{n+1}}{2}\Big )\oplus (1-\alpha _n)Ty_n~~ \forall ~ n \in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(3.37)

where $\{\alpha _n\} \in (0,1)$ and $\{\lambda _n\}$ is a sequence in $(0,\infty )$ such that the following conditions are satisfied:

• (A1) $\lim \limits _{n \rightarrow \infty } \alpha _n = 0$ and $\sum \limits ^{\infty }_{n=1}\alpha _n=\infty ,$

• (A2) $\sum \limits _{n=1}|\alpha _{n+1}-\alpha _n| <\infty ,$

• (A3) $0 < \lambda _{n-1} \le \lambda _n$ and $\sum \limits _{n=1}^\infty \left( \sqrt{1-\frac{\lambda _{n-1}}{\lambda _n}}\right) <\infty ~\forall ~n \ge 1.$

Then, the sequence $\{x_n\}$ converges to a point $\bar{x}$ in $\Gamma$ which is also a unique solution of the following variational inequality

$$\begin{aligned} \langle \overrightarrow{\bar{x}g(\bar{x})},\overrightarrow{p\bar{x}} \rangle \ge 0,~~\forall ~p\in \Gamma . \end{aligned}$$

The following corollaries are single and non-implicit midpoint rule cases of Theorem 3.2.

Corollary 3.5

Let D be a nonempty, closed and convex subset of a complete CAT(0) space X, $X^*$ be the dual space of X and $A : X \rightarrow 2^{X^*}$ be a multivalued monotone operator satisfying the range condition. Let $f: D \times D \rightarrow \mathbb {R}$ be a bifunction satisfying assumption (i)-(iv) in Theorem 2.14. Let $T: X \rightarrow X$ be nonexpansive mapping and $g: X \rightarrow X$ be a contraction mapping with coefficient $\theta \in (0, 1).$ Suppose that $\Gamma : = F(T) \cap A^{-1}(0) \cap EP(f, D) \ne \emptyset$ and for arbitrary $x_1 \in X,$ the sequence $\{x_n\}$ is generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=J^A_{\lambda _n}\circ J^f_{\mu _n}(x_n),\\ x_{n+1}=\alpha _n g\big (\frac{x_n+x_{n+1}}{2}\big )\oplus (1-\alpha _n)Ty_n~~ \forall ~ n \in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(3.38)

where $\{\alpha _n\} \in (0,1)$ and $\{\lambda _n\},~\{\mu _n\}$ are sequences in $(0,\infty )$ such that the conditions (A1) - (A3) of Theorem 3.2 are satisfied. Then, the sequence $\{x_n\}$ converges to a point $\bar{x}$ in $\Gamma$ which is also a unique solution of the following variational inequality

$$\begin{aligned} \langle \overrightarrow{\bar{x}g(\bar{x})},\overrightarrow{p\bar{x}} \rangle \ge 0,~~\forall ~p\in \Gamma . \end{aligned}$$

Corollary 3.6

Let D be a nonempty, closed and convex subset of a complete CAT(0) space X, $X^*$ be the dual space of X and $A : X \rightarrow 2^{X^*}$ be a multivalued monotone operator satisfying the range condition. Let $f: D \times D \rightarrow \mathbb {R}$ be a bifunction satisfying assumption (i)-(iv) in Theorem 2.14. Let $T: X \rightarrow X$ be nonexpansive mapping and $g: X \rightarrow X$ be a contraction mapping with coefficient $\theta \in (0, 1).$ Suppose that $\Gamma : = F(T) \cap A^{-1}(0) \cap EP(f, D) \ne \emptyset$ and for arbitrary $x_1 \in X,$ the sequence $\{x_n\}$ is generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=J^A_{\lambda _n}\circ J^f_{\mu _n}(x_n),\\ x_{n+1}=\alpha _n g(x_n)\oplus (1-\alpha _n)Ty_n~~ \forall ~ n \in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(3.39)

where $\{\alpha _n\} \in (0,1)$ and $\{\lambda _n\},~\{\mu _n\}$ are sequences in $(0,\infty )$ such that the conditions (A1) - (A3) of Theorem 3.2 are satisfied. Then, the sequence $\{x_n\}$ converges to a point $\bar{x}$ in $\Gamma$ which is also a unique solution of the following variational inequality

$$\begin{aligned} \langle \overrightarrow{\bar{x}g(\bar{x})},\overrightarrow{p\bar{x}} \rangle \ge 0,~~\forall ~p\in \Gamma . \end{aligned}$$

Let X be a CAT(0) space. A function $h : X \rightarrow (-\infty , \infty ]$ is called convex, if

$$\begin{aligned} h(\lambda x \oplus (1-\lambda )y) \le \lambda h(x) + (1-\lambda )h(y)~\forall ~ x, y \in X,~\lambda \in (0, 1). \end{aligned}$$

h is proper, if $\mathbb {D}(h) := \{x \in X : h(x) < +\infty \} \ne \emptyset .$ The function $h:\mathbb {D}(h)\subseteq X \rightarrow (-\infty , \infty ]$ is said to be lower semicontinuous at a point $x \in \mathbb {D}(h),$ if

$$\begin{aligned} h(x) \le \liminf \limits _{n\rightarrow \infty }h(x_n), \end{aligned}$$

for each sequence $\{x_n\} \in \mathbb {D}(h),$ such that $\lim \limits _{n\rightarrow \infty }x_n = x.$ h is said to be lower semicontinuous on $\mathbb {D}(h)$ if it is lower semicontinuous at any point in $\mathbb {D}(f).$ For any $\mu > 0,$ the resolvent of a proper, convex and lower semicontinuous function h in X is defined as (see [7]) $J^h_{\mu } (x) = \arg \min \limits _{y \in X} \big [h(y) + \frac{1}{2\mu }d^2(y, x)\big ].$

A minimization problem is to find $x \in X$ such that $h(x) = \min \limits _{y\in X} h(y).$ The solution set of such problem is denoted by $\arg \min \limits _{y\in X}h (y).$

Suppose we replace the bifunction f with a proper, convex and lower semicontinuous function h and $g(x_n)$ with u for a fixed $u\in X$ in Corollary 3.6, we have the following result as a consequence.

Corollary 3.7

Let X be a complete CAT(0) space, $X^*$ be the dual space of X and $A : X \rightarrow 2^{X^*}$ be a multivalued monotone operator satisfying the range condition. Let $h:X\rightarrow [-\infty , +\infty )$ be a proper, convex and lower semicontinuous function and $T: X \rightarrow X$ be nonexpansive mapping. Suppose that $\Gamma : = F(T) \cap A^{-1}(0) \cap \arg \min \limits _{y\in X}f (y) \ne \emptyset$ and for arbitrary $x_1 \in X,$ the sequence $\{x_n\}$ is generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=J^A_{\lambda _n}\circ J^h_{\mu _n}(x_n),\\ x_{n+1}=\alpha _n u\oplus (1-\alpha _n)Ty_n~~ \forall ~ n \in \mathbb {N}, \end{array}\right. } \end{aligned}$$

(3.40)

where $\{\alpha _n\} \in (0,1)$ and $\{\lambda _n\},~\{\mu _n\}$ are sequences in $(0,\infty )$ such that the conditions (A1) - (A3) of Theorem 3.2 are satisfied. Then, the sequence $\{x_n\}$ converges to a element x in $\Gamma .$

4 Numerical example

In this section, we present some numerical experiments to illustrate the applicability of the proposed algorithms.

Example 4.1

Let $X = \mathbb {R}^2,$ endowed with the Euclidean norm. For each $\bar{x} \in X,$ we define a mapping T as follows:

$$\begin{aligned} T\bar{x} = (-x_1,~x_2). \end{aligned}$$

Then, T is nonexpansive. Let $A : \mathbb {R}^2 \rightarrow \mathbb {R}^2$ be defined by

$$\begin{aligned} A(\bar{x}) = (4x_1 - 3x_2, ~x_1 + 2x_2). \end{aligned}$$

(4.1)

Then A is a monotone. We note from [16] that $[t\overrightarrow{ab}] \equiv t(b - a),$ for all $t \in \mathbb {R}$ and $a, b \in \mathbb {R}^2$ (see [25]). Therefore, for each $\bar{x} \in \mathbb {R}^2$ we have

$$\begin{aligned} J^A_{\lambda _n}(\bar{x}) = \bar{z},\Longleftrightarrow ~\frac{1}{\lambda _n}(\bar{x} - \bar{z}) = A\bar{z},\Longleftrightarrow \bar{x} = (I + \lambda _n A)\bar{z},~\Longleftrightarrow \bar{z} = (I + \lambda _n A)^{-1}\bar{x.} \end{aligned}$$

Computing $\bar{z} = J^A_{\lambda _n}(\bar{x})$ for (4.1), we have

$$\begin{aligned} J^{A}_{\lambda _n} (\bar{x})= & {} \left( \begin{bmatrix} 1&{} 0\\ 0 &{} 1 \end{bmatrix}+\begin{bmatrix} 4\lambda _n &{} -3\lambda _n\\ \lambda _n &{} 2\lambda _n \end{bmatrix}\right) ^{-1}\begin{bmatrix} x_1\\ x_2 \end{bmatrix}\\\\= & {} {\begin{bmatrix} 1+4\lambda _n &{} -3\lambda _n\\ \lambda _n &{} 1+2\lambda _n \end{bmatrix}}^{-1}\begin{bmatrix} x_1\\ x_2 \end{bmatrix}\\\\= & {} \frac{1}{1+6\lambda _n +5\lambda _n^2} \begin{bmatrix} 1+2\lambda _n &{} 3\lambda _n \\ -\lambda _n &{} 1+4\lambda _n \end{bmatrix} \begin{bmatrix} x_1\\ x_2 \end{bmatrix}\\\\= & {} \left( \frac{(1+2\lambda _n)x_1 + 3\lambda _n x_2}{1+6\lambda _n +5\lambda _n^2}, ~\frac{-\lambda _n x_1 +(1+4\lambda _n) x_2}{1+6\lambda _n +5\lambda _n^2}\right) . \end{aligned}$$

Thus

$$\begin{aligned} J^A_{\lambda _n}(\bar{x}) = \left( \frac{(1+2\lambda _n)x_1 + 3\lambda _n x_2}{1+6\lambda _n +5\lambda _n^2}, ~\frac{-\lambda _n x_1 +(1+4\lambda _n) x_2}{1+6\lambda _n +5\lambda _n^2}\right) . \end{aligned}$$

Also, let $f : D \times D \rightarrow \mathbb {R}$ be a bifunction defined by

$$\begin{aligned} f(\bar{z}, \bar{y}) = \bar{z}\bar{y} + 8\bar{y} + 8\bar{z} - \bar{z}^2. \end{aligned}$$

(4.2)

Then, (4.2) satisfies assumption (i)-(iv) in Theorem 2.14. Let $\mu _n = 1~\forall ~n\ge 1,$ then

$$\begin{aligned} J^f_1(\bar{x}):= \{ \bar{z} \in D : f(\bar{z}, \bar{y}) + \langle \overrightarrow{\bar{x}\bar{z}},\overrightarrow{\bar{z}\bar{y}}\rangle \ge 0,~y \in D \}. \end{aligned}$$

(4.3)

Computing $\bar{z} = J^f_{1}(\bar{x})$ for (4.2), we have

$$\begin{aligned} J^f_{1}(\bar{x})&= \bar{z}\bar{y} + 8\bar{y} - 8\bar{z} - \bar{z}^2 + \langle \overrightarrow{\bar{x}\bar{z}},~\overrightarrow{\bar{z}\bar{y}}\rangle = 0\\&= \bar{z}(\bar{y} - \bar{z}) + 8(\bar{y} - \bar{z}) + \langle \overrightarrow{\bar{x}\bar{z}},~\overrightarrow{\bar{z}\bar{y}}\rangle = 0\\&\le (\bar{z} + 8)(y - \bar{z}) + d(\bar{z}, \bar{x}) d(\bar{y}, \bar{z}) = 0\\&= (\bar{z} + 8) + (\bar{z} - \bar{x}) = 0, \end{aligned}$$

which implies that $\bar{z} = \frac{1}{2}(\bar{x} - 8).$ Hence, $J^f_{1}(\bar{x}) = \frac{1}{2}(x_1 - 8,~x_2 - 8).$

Let $g : \mathbb {R}^2 \rightarrow \mathbb {R}^2$ be defined by $g(\bar{x}) = \frac{3}{5}\bar{x}.$ We choose $\alpha _n = \frac{1}{100n+1}$ then conditions (A1)-(A3) of Theorem 3.2 are satisfied. Hence, for $x_1 \in \mathbb {R}^2,$ Algorithm 3.11 becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=J^A_{\lambda _n}\Big ( J^f_{1}\Big (\frac{x_n + x_{n+1}}{2}\Big )\Big ),\\ x_{n+1}= \frac{1}{100n+1}~g\Big (\frac{x_n + x_{n+1}}{2}\Big ) + (1 - \frac{1}{100n+1})Ty_n~~ \forall ~ n \in \mathbb {N}. \end{array}\right. } \end{aligned}$$

(4.4)

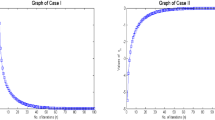
Case 1: Take $x_1=[0.5,~0.25]^T$ and $\lambda _n=1.$

Case 2: Take $x_1=[2,~-3]^T$ and $\lambda _n=1.$

Case 3: Take $x_1=[0.5,~0.25]^T$ and $\lambda _n=\frac{4n+1}{n+4}.$

Case 4: Take $x_1=[2,~-3]^T$ and $\lambda _n=\frac{4n+1}{n+4}.$

Fig. 1

Errors vs Iteration numbers(n): Case 1 (top left); Case 2 (top right); Case 3 (bottom left); Case 4 (bottom right)

Matlab version R2019a is used to obtain the graphs of errors against number of iterations.

Remark 4.2

Using different choices of the initial points $x_1$ and $\lambda$ (that is, Case 1-Case 4), we obtain the above numerical results (Fig. 1). We see that the error values converge to 0 which implies that choosing arbitrary starting points, the sequence $\{x_n\}$ converges to an element in the solution set $\Gamma .$

In the following example, we consider a numerical example of our method in a non-Hilbert space setting.

Example 4.3

[15] Let $Y =\mathbb {R}^2$ be an $\mathbb {R}-$tree with the radial metric $d_r,$ where $d_r(x, y) = d(x, y)$ if x and y are situated on a Euclidean straight line passing through the origin and $d_r(x, y) = d(x, \textbf{0}) + d(y, \textbf{0}) := \Vert x\Vert + \Vert y\Vert$ otherwise. Let $p = (1, 0)$ and $X = B \cup C,$ where

$$\begin{aligned} B = {(h, 0) : h \in [0, 1]} ~\text {and}~C = {(h, k) : h + k = 1, h \in [0,1)}. \end{aligned}$$

Then X is an Hadamard space. Thus, for each $[\overrightarrow{tab}]\in X^*,$ we obtain that

$$\begin{aligned} {[}{\overrightarrow{tab}}]= \left\{ \begin{array}{l} s{\overrightarrow{cd}}:c,d\in B,s\in \mathbb {R}, t(\Vert b\Vert -\Vert a\Vert )=s(\Vert d\Vert -\Vert c\Vert ),~a,b\in B, \\ s{\overrightarrow{cd}}:c,d\in C\cup \{\textbf{0}\},s\in \mathbb {R}, t(\Vert b\Vert -\Vert a\Vert )=s(\Vert d\Vert -\Vert c\Vert ),~c,d\in C\cup \{\textbf{0}\}, \\ t{\overrightarrow{ab}},~a\in B, b\in C. \end{array}\right. \end{aligned}$$

Now, define $A : X \rightarrow 2^{X^*}$ by

$$\begin{aligned} A(x)= {\left\{ \begin{array}{ll} \{{[}\overrightarrow{\textbf{0}p}]\},~x\in B \\ \{{[}\overrightarrow{\textbf{0}p}], [\overrightarrow{\textbf{0}x}]\},~x\in C. \end{array}\right. } \end{aligned}$$

Then A is a multivalued monotone operator and

$$\begin{aligned} J_{\lambda _n}^A(x)= {\left\{ \begin{array}{ll} \{z=(h-\lambda _n, 0)\},~x=(h,0)\in B, \\ \{z=(h', k')\in C: (1+\lambda _n)^2(h'^2+k'^2=h^2+k^2)\},~x=(h,k)\in C. \end{array}\right. } \end{aligned}$$

5 Conclusion

In this paper, we introduce a proximal point-type of viscosity iterative method with double implicit midpoint rule comprising of a nonexpansive mapping and the resolvents of a monotone operator and a bifunction in Hadamard spaces. Furthermore, we prove a strong convergence result under some mild conditions and provide some numerical experiments to show the accuracy and efficiency of the proposed method in a finite dimensional space and a non-Hilbert space. This improves some existing methods on implicit midpoint point rule in the literature.