The Seismic Response Evaluation of an Existing Multi-span Reinforced Concrete Highway Bridge in the Presence of Linear and Nonlinear Viscous Dampers

Abstract

It’s crucial to keep bridges safe and operational all the time. Before or after an earthquake, they may require immediate seismic retrofitting. In this situation, adopting both isolation systems and viscous dampers could be used as a solution. Therefore, the seismic performance of a RC bridge with linear and nonlinear viscous dampers at both pier tops and abutments is investigated. The selected bridge model is the Incesu Bridge in Artvin province in north–eastern Turkiye. In the bridge model, elastomer bearings (EBs) and viscous dampers (VDs) are added to the abutments and the tops of the piers (i.e., the bridge deck connection points). The results revealed that the maximum bending moment of two piers could be significantly reduced compared with the case where the pier’s tops are fixed to its deck. However, a large level of a viscous damper coefficient added to a bridge could cause structural damage to its deck under a strong design earthquake.

1 Introduction

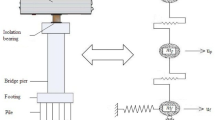
As earthquake disasters have become more frequent in recent years and are responsible for direct and indirect losses, an in-depth understanding of earthquakes is required (see [1,2,3,4]). Before and after earthquakes, it is essential to maintain the transportation and safety of bridges. In some cases, they need immediate retrofitting, especially in the case of damaged or deficient bridges (e.g., Fig. 1). There are several traditional methods to strengthen bridges such as external post-tensioning, steel plate bonding, Fiber Reinforced Polymer (FRP) strengthening, concrete jacketing [5]. Apart from these methods, using bearings and dampers, which are two of emerging methods, are also widely investigated in the literature.

Fig. 1

Partially damaged bridge due to ground failure during February 6, 2023, Kahramanmaraş earthquakes in Turkiye

To limit the seismic reaction of the structure and preserve an elastic response during earthquakes, a significant percentage of the seismic energy is directed to seismic isolation devices or/and dampers installed in the structure. Seismic isolation technology has currently been included into standards in the US, Japan, and Europe. It is also specified in the guidelines for the seismic design of highway bridges in China and Turkiye. The goal of seismic isolations (e.g., bearings) is to change the seismic dynamic characteristics [6,7,8,9] or dynamic effects of the structure by reducing the seismic responses. Damping systems altering the durability, stiffness, or energy dissipation capacity has been widely adopted in literature [10] for the vibration control of buildings [11,12,13,14,15,16] and bridges [17,18,19,20].

For the seismic isolation design of small- and medium-sized bridges, the literature offers some examples of the combination of fluid viscous dampers (FVDs) and lead rubber bearings (LRB) [21,22,23,24]. The advantages of adding FVDs to bridges are widely proved. For examples, Zhen, et al. [21] performed numnerical simulations to evaluate a high-speed multi-span continuous beam bridge with lead-rubber bearings in addition to supplemented viscous dampers under earthquake. They found that the longitudinal seismic response of multi-span continuous girder bridges is well controlled by the FVD. Khedmatgozar Dolati, et al. [22] showed that the response of the bridge with LRBPs (Laminated Rubber Bearing Pads) and LRBPs with viscous dampers. They found that the relative displacement of the bridge with respect to the substructure was decreased by up to 60%. Moreover, LRBPs with viscous dampers lessened the post-earthquake residual displacements. Makris and Zhang [25] investigated the seismic response of highway overcrossing equipped with elastomeric bearings and fluid dampers accounting for the effects of soil–structure interaction at its end abutments.

The aforementioned studies use viscous dampers, which are placed in either abutments or piers’ tops. The seismic performance of an abutment-only isolated RC bridge with linear and nonlinear viscous dampers in both piers’ top and abutments is not widely investigated. Therefore, this study aims to investigate an existing multi-span continuous reinforced concrete highway bridge, whose piers are originally fixed to its deck. The bridge is modified with removing the fixed joints between piers and deck, and replacing with bearings. Also, to limit bearing movements under large earthquakes, fluid VDs are added to the bridge in both piers’ top and abutments.

2 Fluid Viscous Damper

Dampers are frequently employed to reduce a building’s response to earthquakes. They have demonstrated a high capability for dissipating energy under dynamic loads. In most cases, dampers absorb energy as a result of material yielding [26], or the movement of viscous liquid through orifices [27, 28]. Viscous dampers are one type of damper that has demonstrated excellent performance under dynamic loads. This kind of damper regulates motion by applying an opposing force or torque proportionate to the motion’s velocity. Viscous dampers have been extensively used in seismic-resistant bridge construction (e.g., Fig. 2). The use of the viscous damper in long-span bridges [17, 21, 22], including suspension [29, 30] and cable-stayed bridges [19], has been extensively studied. Zhu, et al. [31] investigated the seismic effects of the fluid viscous damper (FVD), based on Maxwell model, for a cable-stayed bridge considered soil-pile interaction under randomly generated earthquake excitation. The results indicated that the FVD is very efficient in reducing the displacement response of the cable-stayed bridge and the bending moment of the tower while simultaneously limiting the shear force in the tower. It is obtained that the nonlinear FVD performs better in reducing the seismic response of the cable-stayed bridge when compared to the linear FVD. The bridge components such as elastomeric bearings, piers and abutment possess different damping ratios, stiffnesses, and lumped masses. Therefore, the design of supplemental viscous dampers corresponding to a desired system-damping ratio in highway bridges is important. This is why, Hwang and Tseng [17] derived the design formulas, based on the concept of composite damping ratio, for supplemental viscous dampers for highway bridges. Fu, et al. [32] studied a benefit-cost approach for bridges based on probabilistic resilience. The cost-effectiveness of seven retrofit measures, such as steel jackets, seat extenders, and elastomeric isolation bearings, is evaluated in the model by applying them to the bridge as built. The findings indicated that one of the most cost-effective retrofit solutions is elastomeric isolation bearings, and that the cost-effectiveness of retrofit measures vary with the degree of ground motion. The Canakkale 1915 Bridge [33], which is situated in a seismically active region, is a well-known example of a practical implementation of this kind of damper. The structural components (superstructure and substructure) are protected during an earthquake by the employment of suitable viscous dampers. The damper force, which opposes the motion of the structure, is given in Eq. (1).

$${\text{F}}_{d} = C_{d} \times |\dot{\delta }|^{\alpha } \times \;{\text{sgn}}\left( {\dot{\delta }} \right)$$

(1)

where ${C}_{d}$ is the damping coefficient, $\dot{\delta }$ is the velocity between two end of damper and $\alpha$ is velocity exponent that can range from 0.3 to 2 [34]. sgn () is the sign function returning + 1 or − 1. The cross-section of a typical viscous damper is shown in Fig. 3. The damper force has an exponential variation with velocity exponent $\alpha$, as given in Eq. (1). Fig. 4a displays the force-velocity curve for various $\alpha$ values. Linear VD is presented with a pure ellipse. The value of 0.3 represents nonlinear VD. The force-dashpot displacement relationship of VD with equal to 1 and 0.3 is shown in Fig. 4b.

Fig. 2

The view of VD application in abutment, a 91/I5 Anaheim overcrossing in California, reproduced from Hwang and Tseng [17] and pier, b the Dong-Yun Bridge reproduced from Infanti, et al. [40]

Fig. 3

Typical longitudinal cross section of fluid VD [41]

Fig. 4

a Force-velocity relation of VD and b typical force-deflection relation of linear and nonlinear viscous dampers

3 Materials and Method

3.1 Bridge Model

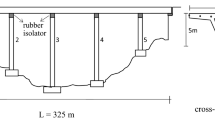
The selected bridge model is the Incesu Bridge located in Artvin province in north–eastern Turkiye (see Fig. 5). The bridge has a total length of 80 m and three spans. The main span is 50 m, two equal side spans are 15 m. The cross-section of the deck is 8.40 m in width and 1.2m in depth as illustrated in Fig. 6a. The bridge is supported by two circular piers with a diameter of 2.20 m whose lengths are 18.10 m and 13.55 m length, respectively, as can be seen in Fig. 6a, b. The deck of the bridge is designed as a continuous two-interior concrete box girder. The bridge has gravity-type abutments. The back wall is 4.6m wide and 1.44 m high (Fig. 6c). The elastomer bearings, given in Fig. 6d, have a size of 600×600×50 mm whereas the seating pads, which elastomer bearings seat on them, in the abutments are 800×800×24 mm. The end bearings are seated on the gravity-type abutments given in Fig. 6d. The elastomer bearing only exists in abutment girders in the project. Piers’ tops are fixed to the girders. I.e., in the existing project, there is no bearing between the connection points of piers and girder.

Fig. 5

Artvin Incesu bridge

Fig. 6

a The deck and pier cross section, b elevation data of the model, c abutment cross section, and d the view of EB on the abutment plan (unit: cm)

3.2 Modelling of Elastomer Bearings

The details of elastomeric bearing (EB) considered in this study is given in Fig. 7. Following the experimental test in laboratory, the properties of 100 % pure neoprene EB are defined and given in Table 1. In the model, the EB is modelled as a link element. The stiffnesses of the link element are calculated by means of Eqs. (2–4) as recommended by Warn and Ryan [35] and Erhan and Dicleli [36]. Bearing movements are allowed in all directions (i.e., horizontal, longitudinal, and transverse) based on the effective stiffness of the elastomer bearings, which is described in Fig. 8 and Table 2. The EBs are modelled as a pinned support at the connection nodes of the deck, abutments, and top of the piers as recommended by Pan, et al. [37] and Erhan and Dicleli [36]. i.e., moments are not transferred from EBs to the piers or abutment beams. As recommended in the study of Pan, et al. [37], multilinear plastic link elements are used in this study to model the EBs of the bridge.

$${\text{K}}_{{\text{H}}} = {\text{k}}_{{\text{eff,bearing}}} = \frac{{{\text{G}}_{{{\text{eff}}}} {\text{A}}}}{{{\text{H}}_{{\text{r}}} }}$$

(2)

$${\text{K}}_{{\text{V}}} = \frac{{{\text{E}}_{{\text{c}}} {\text{A}}}}{{\text{H}}}$$

(3)

$${\text{K}}_{\uptheta } = \frac{{{\text{EI}}}}{{{\text{H}}_{{\text{r}}} }}$$

(4)

Fig. 7

The detail of elastomeric bearing a cross section and b three-dimensional view

Table 1 The properties of EBs

Fig. 8

a The components of the link element, b behaviour model of EB

Table 2 The calculated stiffness values of EB

The elastomeric pads’ horizontal (${\text{K}}_{\text{H}})$, vertical (${\text{K}}_{\text{V}})$, and rotational (${\text{K}}_{\uptheta })$ stiffnesses, which are depicted in Fig. 8a, are calculated using Eqs. (2–4) and the calculated stiffness values of EB are given in Table 2. The EB hysteresis loop is represented as a bilinear curve, where ${\text{k}}_{\text{eff}}$ is the effective stiffness of an EB that exhibits nonlinear behaviour, ${\text{k}}_{\text{u}}$ and ${\text{k}}_{\text{d}}$ are the initial elastic and the post-yield stiffnesses of the EB, respectively. ${\text{F}}_{\text{y}}$ and ${\text{d}}_{\text{u}}$ are the yield strength and yield deformation of the bearing, respectively. ${\text{F}}_{\text{max}}$ and ${\text{d}}_{\text{i}}$ are the maximum force and displacement of the EB, respectively, as depicted in Fig. 8b. The bridge is free to react in all three directions. In other words, elastomeric pads can move or rotate depending on their stiffness. As can also be seen from Table 2, the vertical and rotational stiffnesses are 539 and 23 times of horizontal stiffness, respectively. I.e., the vertical and rotational movements are negligible compared with horizontal movements of EBs.

3.3 Modelling of Superstructure

A three- and two-dimensional finite element model of the bridge, which is modelled in CSIBridge [38] (version 23) software is presented in Fig. 9a, b, c. Since the deck represents the effective stiffness and mass distribution characteristics of the bridge, it is treated as a single line of elastic beam components as used by Khedmatgozar Dolati, et al. [22] and Pan, et al. [37] as well. It is expected that the bridge superstructure will remain essentially elastic throughout typical earthquake ground motions. Nonlinear behaviour has been considered for both the substructure (e.g., bottom of piers) and the link between the superstructure and supporting column (i.e., EBs). Spring-supported continuous beam elements are used to model the abutments as shown in Fig. 9d. The foundation springs are fixed to the ground by assuming that the existing foundation is adequate for such an assumption. The continuously supported beam elements connect to the girder bottom only. The EBs are connected to the deck by a rigid link element (e.g., the stiffness of the link elements $(\text{k})$ equals to $1{0}^{11}\text{ kN}/\text{m}$) in all six-degree movements (e.g., three displacements and three rotations). The piers are assumed to be fixed to the ground as shown in Fig. 9e. The boundary conditions of the horizontal and longitudinal directions are free, whereas those of the transverse direction are fixed at the top of the piers. In other words, transverse /vertical movement of the top of the piers is not allowed by simply assuming that the vertical resistance of piers is sufficient under loads.

Fig. 9

a and b The 3D view of the bridge, details of c two-dimensional finite-element of the bridge, d the abutment and e the pier

In the bridge model, a variety of loads are considered, which are described as live loads (e.g., cars), dead loads (e.g., asphalt, pavements, guardrails, self-weight of the deck), surcharge loads, braking forces, shrinkage-creep temperature loads, and pedestrian loads. The total live and dead load of the bridge (including the self-weight of the deck) are calculated as 402 kN/m in the study.

3.4 Verification of System With a Simplified Model

For verifying the period of the bridge with the software outputs, the bridge system is simplified into two separate single-degree-of-freedom (SDOF) systems due to having differing heights in piers. The EBs are represented by linear spring elements in the simplification. Since bridge superstructures contribute significantly to the mass participation in seismic cases, it is assumed that the superstructure’s total mass is located at the pier’s top.

3.4.1 The Case of Fixed System (no EB on the Piers)

The period of fixed system is compared with the simplified models which is shown in Fig. 10.

Fig. 10

Simplified model of the bridge for fixed system

From the concrete core testing of the bridge, it is found that C20/25 concrete material exist in the Incesu Bridge, and its elasticity modulus is 3×10⁷ kN/m². The bridge model has two circular piers with a diameter of 2.20 m and with different elevations. The moment of inertia of the piers (I) are calculated as 1.1499 m⁴. The linear stiffness of piers ${(\text{k}}_{\text{sub }})$ is calculated using Eq. (5) as follows.

$${\text{k}}_{{{\text{sub}}}} = \frac{{{\text{3EI}}}}{{{\text{H}}^{{3}} }}$$

(5)

The stiffness of pier 1 ${(\text{k}}_{\text{sub1 }})$ with 18.1 m height is 17452 kN/m, while that of pier 2 ${(\text{k}}_{\text{sub2 }})$ with 13.55 m height is 41599 kN/m. Since there are four EBs in each abutment, the total lateral stiffness of the EBs (${\text{k}}_{\text{abut}}$) can be also calculated by multiplying one elastomer bearing’s stiffness with the number of elastomers as follows in Eq. (6). The stiffness of each abutment ${(\text{k}}_{\text{abut1}}$ and ${\text{k}}_{\text{abut2 }})$ is calculated as 33104 kN/m.

$${\text{k}}_{{{\text{abut1}}}} = {\text{k}}_{{{\text{abut2}}}} = {\text{n}} \times {\text{k}}_{{\text{eff,bearing}}} = {\text{n}}\frac{{{\text{G}}_{{{\text{eff}}}} {\text{A}}}}{{{\text{H}}_{{\text{r}}} }}$$

(6)

The total lateral stiffness of the bridge (${\text{K}}_{\text{T}}$) is calculated by summing up all stiffnesses as follows in Eq. (7) and ${\text{K}}_{\text{T}}$ is equal to 124658 kN/m

$${\text{K}}_{{\text{T}}} { = }\sum {\text{k}} { = }\sum {{\text{k}}_{{{\text{sub1}}}} {\text{ + k}}_{{{\text{sub2}}}} {\text{ + k}}_{{{\text{abut1}}}} {\text{ + k}}_{{{\text{abut2}}}} }$$

(7)

The combined superstructure mass (i.e., self-weight of deck and additional loads) and half of the substructure (i.e., self-weight of piers) constitute the participated mass in a seismic situation. Cross section area of pier₁ and pier₂ is calculated as $3.8013$ m², and weight per unit volume is defined as $25$ kN/m³. The total weight is calculated by summing up half of pier₁ self-weight ($0.5{\text{W}}_{\text{sub1}}$), half of pier₂ self-weight ($0.5{\text{W}}_{\text{sub2}}$) and supper structure line loads (${\text{W}}_{\text{sup},\text{line}};$ including deck self-weight and other additional live and dead loads coming from cars, people, etc. $\text{L}$ is 50 m; length of bridge). ${\text{W}}_{\text{sup},\text{line}}$ and ${\text{W}}_{\text{sub}}$ are 402 kN/m³ and 25 kN/m³, respectively. The total mass of the system (${\text{M}}_{\text{T}})$ is calculated with Eq. (8), by dividing the calculated total weight to gravity (g). ${\text{M}}_{\text{T}}$ is obtained as 2202 ton.

$${\text{M}}_{{\text{T}}} = \frac{{{\text{W}}_{{\text{sup,line}}} {\text{L}} + {0}{\text{.5W}}_{{{\text{sub1}}}} + {0}{\text{.5W}}_{{{\text{sub2}}}} }}{{\text{g}}}$$

(8)

The fundamental period of the fixed bridge model (${\text{T}}_{\text{k}})$ is calculated as 0.84s with Eq. (9) as follows

$${\text{T}}_{{\text{k}}} = {2}\pi \sqrt {\frac{{{\text{M}}_{{\text{T}}} }}{{{\text{K}}_{{\text{T}}} }}}$$

(9)

3.4.2 The case of isolated system (with EB on the piers)

The isolated system has one bearing at the top of each pier, unlike the case of the fixed system as shown in Fig. 11. As it was stated above, in the present Incesu Bridge model, elastomer bearings only exist in the abutments. In this study, the piers are also isolated from the deck. The mathematical representation of the isolated system is depicted in Fig. 11 as follows

Fig. 11

Simplified model of the bridge for the isolated system

The stiffnesses of the piers and the total stiffness of four EBs on abutments were calculated in previous section. The total bearing stiffnesses of piers’ head ${(\text{k}}_{\text{pierhead }})$ are determined in Eq. (10). ${\text{k}}_{\text{pierhead}}$ is calculated as 8276 kN/m.

$${\text{k}}_{{{\text{pierhead1}}}} = {\text{k}}_{{{\text{pierhead2}}}} = {\text{n}} \times {\text{k}}_{{\text{eff,bearing}}} = {\text{n}}\frac{{{\text{G}}{}_{{{\text{eff}}}}{\text{A}}}}{{{\text{H}}_{{\text{r}}} }}$$

(10)

The effective linear stiffness 1 (${\text{K}}_{\text{eff}1}$) consists of the stiffnesses of ${\text{k}}_{\text{sub1}}$ and ${\text{k}}_{\text{pierhead1}}$, while the effective linear stiffness 2 (${\text{K}}_{\text{eff}2}$) consists of the stiffnesses of ${\text{k}}_{\text{sub2}}$ and ${\text{k}}_{\text{pierhead2 }}.$ The effective linear stiffnesses of ${\text{K}}_{\text{eff}1}$ and ${\text{K}}_{\text{eff}2}$ are calculated by using Eqs. (11–12) as follows and they are 5614 kN/m and 6903 kN/m, respectively.

$${\text{K}}_{{{\text{eff1}}}} = \frac{{{\text{k}}_{{{\text{sub1}}}} {\text{k}}_{{{\text{pierhead1}}}} }}{{\left( {{\text{k}}_{{{\text{sub2}}}} {\text{ + k}}_{{{\text{pierhead1}}}} } \right)}}$$

(11)

$${\text{K}}_{{{\text{eff2}}}} = \frac{{{\text{k}}_{{{\text{sub2}}}} {\text{k}}_{{{\text{pierhead2}}}} }}{{\left( {{\text{k}}_{{{\text{sub2}}}} + {\text{k}}_{{{\text{pierhead2}}}} } \right)}}$$

(12)

Total lateral stiffness of the bridge (${\text{K}}_{\text{T}}$), which is calculated in Eq. (13), is the sum of effective linear stiffness of pier 1 (${\text{k}}_{\text{eff}1}$), pier 2 (${\text{k}}_{\text{eff}2}$) and elastomer stiffness on each abutment (${\text{k}}_{\text{abut1}}$ and ${\text{k}}_{\text{abut2}}$). ${\text{K}}_{\text{T}}$ is calculated as 78724 kN/m.

$${\text{K}}_{{\text{T}}} { = }\sum {\text{k}} { = }\sum {{\text{k}}_{{{\text{eff}}}} + {\text{k}}_{{{\text{eff2}}}} + {\text{k}}_{{{\text{abut1}}}} + {\text{k}}_{{{\text{abut2}}}} }$$

(13)

The fundamental period of the isolated system (${\text{T}}_{\text{k}})$ is calculated as 1.05s with Eq. (9), which is given above.

3.4.3 The Comparison for the Cases of the Fixed Model and the Isolated Model

The exact results obtained from CSIBridge software and the approximate analysis results obtained from the simplified model are compared in Table 3.

Table 3 Numerical results

It was determined that the fundamental period of the isolated model is longer than the period of the fixed model, according to CSIBridge results. Note that there is not much different between these two models, because elastomer bearings are added only to the top of the piers. The bridge piers have quite larger lateral stiffness than the elastomeric bearing stiffness of piers’ head. Thus, to use the elastomeric bearings reduce the effective stiffness of the system in the bridge model.

3.5 Modelling of Viscous Damper

The Incesu RC bridge, located in Artvin, Turkiye, has four bearings in each abutment. In the present design of the bridge in the field, the top of the piers was fixed to the deck (i.e., no bearings). To examine the bridge responses of the system supported on elastomer bearings with linear viscous damper (LVD) and nonlinear viscous damper (NVD) under different ground motions, in this study, elastomer bearings, which have the same properties, and viscous dampers added both on the top of piers and abutments. In this section, the bridge responses of the system supported on with EBs& NVDs bearing (concisely, ${S}_{ys1}$) and EBs&LVDs bearing (concisely, ${S}_{ys2}$) are evaluated.

The behaviour of the VD is based on the damping coefficient and power factor, and it has a velocity-dependent mechanism. The VD is modelled as a link damper-exponential element in the direction of excitation (U1 only) [34]. Each column functions as a vertical cantilever beam for longitudinal motion. Hence, the most damaging direction for causing damage to the bridge components is longitudinal motions. The VDs in the piers are designed to act only in the longitudinal direction (y-axis) as can be seen in Fig. 12. However, the dampers in the abutments are angled at 45 degrees to the deck as depicted in Fig. 13. It is aimed to allow a designer not only the freedom of adding more dampers in the longitudinal direction (y-axis) but also to reduce bearing displacements in the horizontal direction (x-axis) in the case of horizontal direction-based design. Two factors, ${C}_{d}$ and $\alpha$, characterise the damper’s behaviour. Different damper parameters can have different impacts on the bridge seismic behaviour. To compare the seismic performance of the bridge with LVD ($\alpha$=1.0) and NVD ($\alpha =0.3)$ under different earthquakes, in this study, one damper (Fig. 12) is installed at each pier’s top while eight dampers (Fig. 13) are placed at the each abutment. The damping coefficients of all dampers (8 dampers) at abutments are updated by using sequential formula given in Eq. 14. I.e., all eight dampers (at abutments) have the same ${C}_{d}$ value. The same equation is also used to calculate for pier’s damping coefficient.

$${\text{C}}_{{\text{d}}}^{{\text{n + 1}}} = {\text{C}}_{{\text{d}}}^{{\text{n}}} \left( {\frac{{\Delta_{{{\text{max}}}}^{{\text{n}}} }}{{\Delta_{{{\text{target}}}} }}} \right)$$

(14)

where ${\Delta }_{\text{max},\text{i}}^{\text{n}}$ and ${\Delta }_{\text{target}}$ are the maximum drift at the piers’ top and each abutment computed at the nth iteration and the target drift, respectively; ${\text{C}}_{\text{d}}^{\text{n}}$ and ${\text{C}}_{\text{d}}^{\text{n}+1}$ are the damping coefficients of the LVD and NVD installed at the abutments and the top of the piers at two subsequent iterations n and n + 1. ${\Delta }_{\text{target}}$ is set as 4.5 cm (as it is EBs maximum allowable drift value). Since target drift is defined, Eq.14 is used for the iterations under KOB excitation, which has one of the largest spectral acceleration, as shown in Fig. 14. Following those iterative simulations, the damping coefficients used in this study are determined under y-axis excitation (transverse direction) and are given in Table 4.

Fig. 12

Simplified application of viscous damper to the bridge

Fig. 13

The view of VD distribution in each abutment and the top of the piers in the bridge model

Fig. 14

Acceleration spectra of natural records

Table 4 Identified the damping coefficients by using Eq.14 (under y-axis excitation)

3.6 Selected Ground Motions

The ground motion records with various primary frequency ranges are chosen from the Pacific Earthquake Engineering Research Center [39] ground motion database for the study. The information on the selected ground motions is given in Table 5 and, acceleration response spectra of those are depicted in Fig. 14. The fundamental periods of the bridge for the fixed system and the isolated system are 0.84 s and 1.06 s, respectively.

Table 5 The selected ground motion information

4 Seismic Performance of ${{\varvec{S}}}_{{\varvec{y}}{\varvec{s}}1}$ and ${{\varvec{S}}}_{{\varvec{y}}{\varvec{s}}2}$

4.1 The Bridge Response Under Different Ground Motions

In the study, the bridge is exposed to different ground excitations with the same damping coefficients, which are given in Table 4. The obtained maximum bearing drifts of ${S}_{ys1}$ are scaled to the case of ${S}_{ys2}$ in piers and abutments. Also, the maximum shear force and maximum bending moment of ${S}_{ys1}$ and ${S}_{ys2}$ in abutment and piers are scaled to the case of the fixed model.

4.1.1 KOB Ground Motion (Design Earthquake)

The seismic performance of ${S}_{ys1}$ and ${S}_{ys2}$ are evaluated under the design KOB earthquake. As mentioned in Section 3.5, the damping coefficients of viscous dampers in ${S}_{ys1}$ and ${S}_{ys2}$ are set to have the same drift in abutments and piers (Fig. 15a) before the two system seismic performance evaluations (${S}_{ys1}$ and ${S}_{ys2}$). The maximum shear-force ratio (${S}_{ys1}$/${S}_{ys2}$) of the deck in the 1st and 3rd span of the bridge for the cases of ${S}_{ys1}$ and ${S}_{ys2}$ are depicted in Fig. 15b. The maximum shear-force ratio (${S}_{ys1}$/${S}_{ys2}$) of the piers are given in Fig. 15c. The maximum bending moment in the bottom of the piers are shown in Fig. 15d, for the cases of ${S}_{ys1}$ and ${S}_{ys2}$. The study compares the maximum shear forces of the deck in only two spans (i.e., span 1 and span 3) as spans 2 has the smallest forces.

Fig. 15

a Maximum bearing drift, b shears force of the deck, c shear forces of the piers and, d bending moments of the piers for ${ }S_{ys1}$ and ${S}_{ys2}$

As expected, the maximum shear forces of the deck increased in both systems (${S}_{ys1}$ and ${S}_{ys2}$) compared with the pier fixed system due to viscous dampers’ force. In the 1st and 3rd span, ${S}_{ys1}$ increased the deck shear forces by 117% and 260%, whereas ${S}_{ys2}$ resulted in just 55% and 150%, respectively. Since the maximum deck shears force of the bridge happened in 1st span (see Table 6), the results of 1st span can be considered to sum up the discussion. To recall the above discussion, ${S}_{ys2}$ increased the force of pier fixed system by only 55%, whereas ${S}_{ys1}$ resulted in a significant increase of 117%. The maximum shear force and bending moments of both piers are given in Fig. 15c and d. The shear forces in pier 1 and pier 2 is, respectively, reduced by 86% and 90.4% in the case of ${S}_{ys1}$, whereas ${S}_{ys2}$ reduced the forces by 88% and 89.6% respectively. The maximum bending moment of pier 1 and pier 2 is reduced by 84% and 89% in the case of ${S}_{ys1}$ and 86% and 88% in the case of ${S}_{ys2}$, respectively. Note that maximum shear force and maximum bending moment at pier 1 occur in the case of ${S}_{ys1}$, while these at pier 2 occur in the case of ${S}_{ys2}$. To summarize the results of Fig. 15c, d, it can be said that compared with pier fixed system, ${S}_{ys2}$ generally performed better than ${S}_{ys1}$ due to increasing the shear force of the deck by only 55% (whereas ${S}_{ys1}$ was 117%.) and reducing the moment of the pier by 88% (whereas the ${S}_{ys1}$ was 84%).

Table 6 Main results of the bridge with different systems subjected to seismic records

Figures 16 and 17 give a general overview of the VD and EB forces acting on both abutments and piers. The hysteresis loops of the LVD and EB, both in the abutment and top of pier 1, are shown in Fig. 16. Similarly, the force-displacement relationship of the NVD and EB, both in the abutment and top of pier 1, is given in Fig. 17. Also, these results are only for one damper and one EB. The damper forces at the top of pier 1 are less than the bearing forces, yet the damper forces in the abutment are noticeably bigger than the bearing forces, as shown in Figs. 16 and 17. In this context, it can be argued that damping forces at the abutment may cause greater damage to the deck than those at the pier if the damping forces exceed the deck’s shear force resistance.

Fig. 16

Hysteresis loop of the LVD and the EB for a the abutment and b the top of the pier 1

Fig. 17

Hysteresis loop of the NVD and the EB a for the abutment, b for the top of the pier 1

The relationship between time history-shear force for the 1st span of the deck in the cases of ${\text{S}}_{\text{ys}1}$, ${\text{S}}_{\text{ys}2}$, and fixed system are given in Fig. 18. It can be seen that the peak shear forces in the cases of the ${\text{S}}_{\text{ys}1}$ and fixed system almost occurred at the same time (i.e., points 1 and 3), whereas the peak shear force in the case of ${\text{S}}_{\text{ys}2}$ happened at a much earlier time (i.e., point 2), which means that ${\text{S}}_{\text{ys}2}$ forces are partically out of phase with ${\text{S}}_{\text{ys}1}$ forces.

Fig. 18

Showing the time history of the deck shear forces of span 1 for pier1 fixed, ${S}_{ys1}$ and ${S}_{ys2}$

The time history-displacement of the top of the pier is depicted in Fig. 19 for pier fixed, ${\text{S}}_{\text{ys}1}$ and ${\text{S}}_{\text{ys}2}$. The relative displacement of the pier fixed system was slightly over 45 cm, whereas that of ${S}_{ys1}$ and ${S}_{ys2}$ was limited to 8.2 cm and 7.2 cm, respectively.

Fig. 19

The time history of displacement of pier 1 top (relative to fixed ground) under KOB earthquake

4.1.2 KOB2 Ground Motion

The bridge is exposed to KOB2 excitation with the same damping coefficients as KOB. Fig. 20 Reference source not found. compares the results in terms of maximum bearing drift, maximum deck shear force, maximum pier shear forces and maximum bending moment. Fig. 20a shows that the maximum bearing drift, which resulted from ${S}_{ys1}$, was 34% smaller than the ${S}_{ys2}$ in the abutment, yet in piers 1 and 2, the ${S}_{ys1}$ was 18% and 11% larger than ${S}_{ys2}$, respectively. Note that all these bearing drifts are still below the maximum allowable value (i.e., 4.5 cm). When it comes to maximum deck shear forces shown in Fig. 20b, ${S}_{ys1}$ increased the forces of spans 1 and 3 by 155% and 186%, respectively, whereas ${S}_{ys2}$ only increased 77% and 90%, respectively. As the maximum shear forces happed in span 1, the above discussion can be recalled that the ${S}_{ys2}$ was better than the ${S}_{ys1}$ due to increasing the shear force by only 77% whereas the ${S}_{ys2}$ was 155%.

Fig. 20

a Maximum bearing drift, b shears force of the deck, c shear forces of the piers and, d bending moments of the piers for ${S}_{ys1}$ and ${S}_{ys2}$

In comparison with the fixed system (Fig. 20c) the ${S}_{ys1}$ reduced the maximum shear forces of the piers 1 and 2 by 81% and 85%, respectively, whereas these values were 85% (pier 1) and 86% (pier 2) for the ${S}_{ys2}$. In this discussion, the most effected column was pier 2 as a result, the ${S}_{ys2}$ was only 1% (86%–85%) better than the ${S}_{ys1}$ in pier shear force. In the maximum bending moments of piers 1 and 2 (Fig. 20d), the ${S}_{ys1}$ reduced that by 77% and 83%, respectively, whereas these reductions were 82% (pier 1) and 84% (pier 2) for ${S}_{ys2}$. The biggest moment happened in pier 1 for both ${S}_{ys1}$ and ${S}_{ys2}$, and as a result, the ${S}_{ys2}$ was 5% (82%–77%) better than the ${S}_{ys1}$.

4.1.3 CAP Ground Motion

The bridge is subjected to CAP earthquake by adopting damping coefficients given in Table 4. The results are discussed in Fig. 21. When the responses of two systems (${S}_{ys1}$ and ${S}_{ys2}$) are compared with each other, ${S}_{ys1}$ resulted in 52% less drift than ${S}_{ys2}$ in both the abutment and pier 1, whereas this value was 22% less in pier 2. Note that these bearing drifts are still far below the maximum allowable value (i.e., 4.5 cm), which means that they are safe. The maximum deck shear forces of ${S}_{ys1}$ and ${S}_{ys2}$ (Fig. 21b), which is scaled to the pier fixed model, showed that ${S}_{ys1}$ increased the force of spans 1 and 3 by 79% and 218%, respectively, whereas the ${S}_{ys2}$ increased the force by only 33% (span 1) and 128% (span 3), respectively. As the maximum shear forces of the ${S}_{ys1}$ and ${S}_{ys2}$ occur in span 1 (see Table 6), the discussion can be rewritten so that ${S}_{ys2}$ is 46% (i.e., 79%–33%) less than ${S}_{ys1}$ in terms of increasing the shear force of the deck. The maximum shear forces of ${S}_{ys1}$ and ${S}_{ys2}$ (Fig. 21c) in piers 1 and 2 resulted in a reduction of 87.5% on average. As can be seen in Fig. 21d, a similar situation exists in terms of bending moments, namely, the reduction was 85.5% on average in all piers for ${S}_{ys1}$ and ${S}_{ys2}$.

Fig. 21

The comparison of a the maximum bearing drift, b shear forces of the deck, c shear forces and d bending moment of piers

4.1.4 PAR Ground Motion

In the bridge model, PAR excitation with the same damping coefficients (as given in Table 4) is considered to evaluate obtained responses of the piers and abutment. The obtained results are presented in Fig. 22. The maximum bearing drifts are depicted in Fig. 22a, and it is observed that ${S}_{ys1}$ was 78%, 70%, and 56% better than ${S}_{ys2}$ in the abutments, pier 1 and pier 2, respectively. The drift of the bearings is still below the allowable value (e.g., 4.5 cm) for PAR earthquake. However, for the maximum deck shear force (Fig. 22b), the opposite situation exists. Namely, ${S}_{ys1}$ increased the force of fixed system by 70% and 124% at span 1 and span 3, respectively, whereas ${S}_{ys2}$ increased the force by only 17% for span 1 and 52% for span 3. The maximum pier shear forces are illustrated in Fig. 22c for ${S}_{ys1}$ and ${S}_{ys2}$. It is obtained that ${S}_{ys1}$ reduced the force in pier 1 and pier 2 by 93% and 91%, respectively, whereas these values were 93% for pier 1 and 92% for Pier 2 in the case of ${S}_{ys2}$. Besides, the maximum pier bending moments are depicted in Fig. 22c for the ${S}_{ys1}$ and ${S}_{ys2}$. It is determined that the bending moment of pier 1 and pier 2 reduced by 92% and 89% for ${S}_{ys1}$, whereas those were 92% and 90.5% for ${S}_{ys2}$, respectively. Since the maximum bending moment for the cases of 1 and 2 occurred in pier 2 (see Table 6), ${S}_{ys2}$ was only 1.5% (90.5%–89%) better than ${S}_{ys1}$. As can be seen from Table 6, the results of this earthquake are the lowest of all four excitations, which means that it is not concerning regarding bridge safety compared with the KOB earthquake. However, the importance of this outcome is that it is consistent with the findings of KOB excitation, which is that the deck shear force of ${S}_{ys2}$ is less than that of ${S}_{ys1}$.

Fig. 22

Comparing a the maximum bearing drift, b shear force of the deck, c shear and d moment of piers under PAR earthquake

4.2 Energy Dissipation for the Dampers

Fig. 23 discusses the dissipated energy by LVD and NVD dampers. It can be said that the largest energy dissipation is observed under KOB earthquake as shown in Fig. 23a, yet the LVD is only 8% better than NVD.

Fig. 23

The time history of energy dissipation for dampers under KOB earthquake

4.3 The Damper Forces on Bridge Members

Fig. 24 compares the required maximum damper force at abutments (only one damper value, i.e., eight dampers are used at abutment), piers 1 and 2 under different ground motions. As shown in Fig. 24, for abutment, piers 1 and 2, the required maximum damper force is set as 1800 kN (red dash-line), 200 kN (black dash-line) and 1000 kN (green dash-line), respectively. it can be said that the maximum damper force happens under KOB earthquake. The required damper force for NVD at pier 1 is almost the same as LVD, yet at abutment, NVD requires 4% larger damping force than LVD. At pier 2, the damper force required by LVD is 36% larger than NVD.

Fig. 24

Maximum damper forces under a KOB, b KOB2, c CAP and d PAR earthquakes. Please see the online version of this article for an interpretation of this figure

5 Conclusions

This study considers an existing multi-span continuous reinforced concrete highway bridge, whose piers were originally fixed to the deck. The bridge model is modified with adding EBs at piers ‘top. The bridge is also equipped with viscous dampers (linear and nonlinear) in both the abutments and the piers’ top to limit the sliding between the EBs and the deck. The damping coefficient of the dampers is set under design earthquake KOB by limiting the maximum drift of EBs to 4.5 cm. The efficiency of ${S}_{ys1}$ (EBs & NVDs) and ${S}_{ys2}$ (EBs&LVDs) are investigated in this paper. The investigation verifies the bridge period obtained from the software with hand calculation results. The main findings of this research work can be summarised as follows:

• The fundamental period of the “pier fixed”, and “pier isolated”. Which were obtained results from the software perfectly matched the results of the simplified model.

• Compared with the ”pier fixed” system (i.e., the piers are fixed to the deck) under a set of earthquakes, ${S}_{ys1}$ reduced the maximum bending moment of the most affected pier from 77% to 89% whereas, for ${S}_{ys2}$, it was 82% to 90.5%, respectively. When it comes to the maximum deck shear force, ${S}_{ys1}$ increased the forces ranging from 70% to 155% whereas, for ${S}_{ys2}$, it increased the forces varying from only 17% to 77%. In summary, ${S}_{ys2}$ performed better than ${S}_{ys1}$ in terms of both reducing bending moment of the piers and the having smaller deck shear forces than ${S}_{ys1}$, yet the main performance difference between ${S}_{ys1}$ and ${S}_{ys2}$ is the resulted maximum deck shear forces.

• The results show that under several earthquakes, reducing bending moments as well as limiting maximum bearing drifts below safety level (i.e., max 4.5 cm at EBs) is achievable, yet large damping forces in the abutments result in an increase in the deck shear forces. It is possible to limit or/ reduce the deck shear forces alongside both reducing pier shear forces and limiting bearing drifts by changing the type of bearings and reducing damper forces at the abutments. Instead of selecting a simple elastomer bearing, Lead Rubber Bearing (LRB) may be used since it has a high capacity for horizontal motions and has a high-energy damping.

• From all results, it can be said that ${S}_{ys2}$, which consists of EBs and LVD, should be selected instead of ${S}_{ys1}$, yet adding large damping forces to the bridge might damage the bridge deck. Therefore, if there is a concern regarding the safety of the deck, then a limited amount of VD damping should be added to the RC bridge.

6 Future Studies

As was discussed above, the RC bridge equipped with bearings and VDs significantly reduced maximum displacements and pier shear forces. However, adding VDs increased deck shear forces. To limit this force, VD forces must be limited. Therefore, further investigations are needed. A future study will investigate an optimal bearing stiffness (EBs or LRBs) with an optimal VD damping coefficient selection in RC bridge.