1 Introduction

The human skin is a protective layer, and its applications in development of the human body thermoregulation plays a key role in biological functioning. The thermoregulation process in warm-blooded animals or homeotherms resembles and might be considered based on a common study. The human structure is sophisticated from this perspective and is of use to recognize the rest system whatsoever. Among supreme significant biological limitations that affect the progress of a human organ is known as thermoregulation. This procedure acts to hold or permit the body temperature to a cold environment than the body to prevent hypothermia and acts to eliminate heat of the body in a hot environment than the body to prevent hyperthermia.

Over a couple of decades, the mathematical formation of bio-heat transfer system in body core soft tissue owing to the usual and unusual environmental surroundings has gained significance in the current research area; thus in 1948 Penne’s proposed bio-heat transfer model [1] has become an influential article and referred to as Penne’s equation. Penne’s proposed research work was based on the forearm, and the model estimated the radial temperature distribution and led a board review of the skin temperature of the forearm and measured the temperature of the brachial and rectal arteries. Heat transfer procedures confine the presentation of atmosphere components and schemes, and the course has a vast variety of applications. In this modern era, the bio-heat transfer research field has cleared a key establishment in cryogenic surgery, thermal diagnosis, hyperthermia cancer therapy, etc. [2, 3]; for example, for years, the presence of bio-heat equation (Penne’s, H. H., 1948) has numerous models on the temperature in several skin parts of a human body that has been presented recently, see [4,5,6].

The bio-heat transfer model is a much more suitable model for estimating the temperature variation in the body owing to its computational simplicity. The possessions of bloodstream are based on a heat allocation in active core tissue, and these have stayed studied lasted over a decade as the physiological value and atmospherically conditions [7], the study of heat scald injury found on Henrique’s model [8], the human dermal region exposed to an exterior heat cause [9], the heat transfer model in a triple-covered skin [10], a sensitivity and the inverse problem occurs in the bio-heat equation [11], the electromagnetic energy couple to human bodies and animals [12], the temperature distributions carried in human dermal parts [13], the atmosphere parameter and the tissue culture [14], heat transmission process in tissues of human skin by thermal therapy [15], the thermal biological system and can expand to applications, clinical treatment, and temperature field reform [16], the temperature transmission in skin-subcutaneous tissues [17], tumors at various angular and axial situations of the dermal layers of a limb [18], the temperature distribution in the human skin resulting from various exercises [19].

The temperature distribution of the dermal region might be defined in terms of Penne’s equation with appropriate boundary conditions. The bio-heat transfer equation has been solved by numerous methods like the finite difference method [20], homotopy perturbation method [21], lattice Boltzmann method [22], Sinc Collocation technique [23], Legendre computation method (LCM) [24], variational element method [25], Laplace transform [26], and boundary element method [27].

In the literature concerning bio-heat equation, it is detected by just deterministic solvers that are enforced to evaluate its dynamics and no one has utilized stochastic optimization. In recent years, the stochastic approach on the bases of the artificial intelligence approach is effectually utilized to determine the solutions for both integer and fractional derivatives involved in differential equations with suitable conditions [28,29,30,31,32]. Such as, a couple of feasible stochastic technique applications are the solutions of the Lane–Emden schemes rising in the astrophysics model [33], nonlinear Troesch’s model arising in a plasma physics [34], pantograph DE (differential equation) arising in a model of cell-growth [35], Blasius equation [36], Falkner–Skan equations [37], nonlinear MHD Jeffery–Hamel’s blood flow model [38, 39].

Usually, the most merged stochastic solvers are found on bio-inspired artificial intelligence (AI) by genetic algorithms (GAs) which are sort of an actual global methodology and GAs have been utilized widely to figure out various problems got up in multiple applications of the physiologic sciences [40,41,42,43,44]. The affluence of talent and the scope of curiosity has been involved in this region as a magnet for authors. The significance of these suitable methodologies is reflected in the ease of the concept, extensive applicability, comfort in application processes, stability, avoidance of divergence, and reliability, and all these properties make them splendid to utilize this proposed methodology for stimulating models like bio-heat equation (BHE). The consequence of the current research is a phase onward in scheming learning algorithms so long as the solution of a nonlinear singular system for bio-heat equation determines thermoregulation at dermal layers.

The basic purpose of the proposed current research is to originate a model to evaluate thermoregulation in the human dermal region by using the stochastic technique.

2 Proposed Model for Singular Nonlinear Bio-Heat Equation

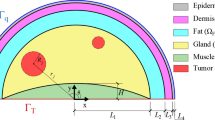
An illustrative diagram of a singular nonlinear BHE is demonstrated in Fig. 1 in which thermal conductivity is taken as a function of temperature [17]. This research work intends to solve the bio-heat model of the human dermal region characterized through one-dimensional nonlinear singular bio-heat equation (BHE) by utilizing the stability of artificial intelligence (AI) algorithms. The most significant form of the BHE is given as:

$$\rho_{a} c_{a} \frac{\partial E}{{\partial t}} = \nabla (k(E)\nabla .E) + H.$$
(1)
Fig. 1
figure 1

Neural network scheme of BHE

Full size image

The parameters \(\rho_{a}\), \(c_{a}\), and \(k\) are density, the specific heat of blood, and the thermal conductivity. Severally, \(H\) is termed as heat generation which is the function of a temperature defined as \(H = h(37 - E)\), and \(\nabla\) is a first-order partial derivative operator of \(E\) that represents the temperature. By using all assumptions and linear transformation, we have

$$x = E - E_{H} \quad {\text{and}}\quad t = \frac{r}{R},\quad 0 < t < 1.$$
(2)

where R is an outer radius and r is an inner radius, and the governing equation is given as:

$$\frac{{{\text{d}}^{2} x}}{{{\text{d}}t^{2} }} + \left( \frac{2}{t} \right)\left( {\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right) + \frac{1}{x}\left( {\frac{{{\text{d}}x}}{{{\text{d}}t}}} \right)^{2} + \left( {\frac{{(37 - x - E_{H} )}}{x}} \right)\beta = 0,$$
(3)

with the boundary condition, given as,

$$\frac{{{\text{d}}x}}{{{\text{d}}t}}(0) = 0,x(1) = 0,\quad 0 < t < 1.$$
(4)

where the term thermal diffusivity is defined as \(\beta = \frac{{hR^{2} }}{{k_{0} }}\).

3 Design Methodology

The proposed design methodology for nonlinear singular BHE defined in Eq. (3) is designed to calculate the approximate solution by utilizing feed-forward ANN technique and the derivatives of the proposed model, constructed by utilizing the log sigmoid function and then formulating the fitness function with a combination of these appropriate networks. And rest of the paper is based on numerical experimentations and results for different scenarios of BHE. The graphical representation and basic comparative studies through statistical analysis are given in the next sections.

3.1 Differential Equation Utilizes the Artificial Neural Networks

The differential derivatives by using ANNs for nonlinear singular first-order BHE are given in Eq. (4) and are composed in such a way that the solution and its derivatives are given below as a continuous mapping:

$$\begin{aligned} x(t) & = \sum\limits_{i = 1}^{N} {\delta_{i} f(\mu_{i} t + \nu_{i} } ), \\ \frac{{{\text{d}}x(t)}}{{{\text{d}}t}} & = \sum\limits_{i = 1}^{N} {\delta_{i} \frac{{\text{d}}}{{{\text{d}}t}}\left[ {f(\mu_{i} t + \nu_{i} )} \right]} , \\ \end{aligned}$$
(4)
$$\begin{gathered} \frac{{{\text{d}}^{2} x(t)}}{{{\text{d}}t^{2} }} = \sum\limits_{i = 1}^{N} {\delta_{i} \frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }}} \left[ {f(\mu_{i} t + \nu_{i} )} \right]\,, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,. \hfill \\ \frac{{{\text{d}}^{M} x(t)}}{{{\text{d}}t^{M} }} = \sum\limits_{i = 1}^{N} {\delta_{i} \frac{{{\text{d}}^{N} }}{{{\text{d}}t^{N} }}} \left[ {f(\mu_{i} t + \nu_{i} )} \right]. \hfill \\ \end{gathered}$$
(5)

In the set of Eq. (5), typically the activation functions in the most hidden layer utilized as log-sigmoid functions and derivatives as given below:

$$x(t) = \sum\limits_{i = 1}^{N} {\frac{{\delta_{i} }}{{1 + e^{{ - (\mu_{i} t + \nu_{i} )}} }}} ,$$
$$\frac{{{\text{d}}x(t)}}{{{\text{d}}t}} = \sum\limits_{i = 1}^{N} {\frac{{\delta_{i} \mu_{i} e^{{ - (\mu_{i} t + \nu_{i} )}} }}{{(1 + e^{{ - (\mu_{i} t + \nu_{i} )}} )^{2} }}} ,$$
(6)
$$\frac{{{\text{d}}^{2} x(t)}}{{{\text{d}}t^{2} }} = \sum\limits_{i = 1}^{N} {\delta_{i} \mu_{i}^{2} \left[ {\frac{{ - 2e^{{ - (\mu_{i} t + \nu_{i} )}} }}{{(1 + e^{{ - (\mu_{i} t + \nu_{i} )}} )^{3} }} - \frac{{e^{{ - (\mu_{i} t + \nu_{i} )}} }}{{(1 + e^{{ - (\mu_{i} t + \nu_{i} )}} )^{2} }}} \right]} .$$

Here, \(\mu_{i} ,\nu_{i} ,\) and \(\delta_{i}\) are optimization weights. The structural scheme using ANN based on three main layers designed for the BHE is shown in Fig. 1.

3.2 Fitness Function

Fitness function is defined as the sum of mean square error. Assume the sum of two-mean square error as \(\xi_{r}\). Let \(\xi_{{r_{1} }}\) and \(\xi_{{r_{2} }}\) be the mean square errors and then the \(\xi_{r}\) is defined as:

$$\xi_{r} = \xi_{{r_{1} }} + \xi_{{r_{2} }} .$$
(7)

where \(\xi_{{r_{1} }}\) is fitness error function, related to second order on linear differential equation represented in Eq. (3), which can be written as:

$$\xi_{{r_{1} }} = \frac{1}{N}\sum\limits_{i = 1}^{M} {\left[ {\frac{{d^{2} x_{i} }}{{dt^{2} }} + \frac{2}{{t_{i} }}\frac{{dx_{i} }}{dt} + \frac{1}{{x_{i} }}\left( {\frac{{dx_{i} }}{dt}} \right)^{2} + \frac{{\alpha (37 - x_{i} - T_{H} )}}{{x_{i} }}} \right]}^{2} ,$$
(8)

And \(\xi_{{r_{2} }}\) is also a fitness error function resulting from the boundary conditions.

$$\xi_{{r_{2} }} = \frac{1}{2}\left[ {(x_{0} - 1)^{2} + (x_{1} - 0)^{2} } \right].$$
(9)

where \(N = \frac{1}{h}\,\,,x_{i} = x(t_{i} )\,\,\,\,{\text{and}}\,\,\,(t_{i} ) = ih\,.\)

3.3 Algorithm and Flowchart of Optimization Methodology

The global optimization task is to calculate the minimum value of a fitness function by specific constraints. The proposed model utilizes global optimization solvers to approximate the appropriate solution. The selected optimization solvers are pattern search (PS) and genetic algorithm (GA) hybridized with AST, IPT, and SQP techniques. The selected solvers aptitudes to be efficient solvers deal with all sorts of constrained and unconstrained problems. The pattern search (PS)/direct search has a demonstrable aptitude to converge via a determinist iterating approach.

The genetic algorithm (GA) handles random numbers and holds stochastic iterations that take a reasonable time to converge. The pattern search (PS) algorithms are well discussed to calculate multiple applications problems like dispatch problems of combined heat and power (CHP) [45], the hazardous material problem [46], some heat transfer properties [47], strain shape and frequency of dynamical model [48], adaptive rood [49], nonlinear power system [50], and radiotherapy design [51]. GAs have been utilized efficiently as a splendid optimization technique in various fields some as optics, electronics, controls, electromagnetism, robotics, digital communication, chemical industry, astrophysics materials, nuclear power system, signal processing, economics, bioinformatics, and financial mathematics [50, 52,53,54]. Some significant applications of GA include spacecraft control guidance [55], bicycle-sharing models [56], arch bridges [57], the density of heat pumps [58], robotic manipulator tracking [59], gas diffusion with curved fibers [60], face recognition, comparison of watermarking techniques, and management of warehouses energy consumption [61]. The GAs and PSs are implemented by using built-in MATLAB functions for optimization. GAs and PSs are hybridized through AST, IPT, and SQP for global search. In such a way, hybridized optimization techniques are established for ANNs training weights, which depend on GAs and PSs; these are integrated through AST, IPT, and SQP to approximate the best accurate solution of BHE. The flowchart of detailed research work is suggested in terms of the BHE, optimization procedure, and the numerical outcomes and comparison obtainable in Fig. 2.

Fig. 2
figure 2

Graphical abstract of proposed methodology

Full size image

The research work has been implemented with built-in functions in an optimization tool of MATLAB by PSs and GAs solvers. PSs and GAs are hybridized with AST, IPT, and SQP for fast convergence. Active set technique in optimization calculates the constraints that influence the optimum result, whereas the interior point technique is some sort of algorithm that evaluates the convex optimization of linear and nonlinear problems. The MATLAB built-in optimization toolbox is found on the FMINCON function by the local modification technique hybridized with PSs and GAs. The research work designed the governing relation of singular nonlinear BHE. The workflow is based on mathematical modeling of the BHE model, selected AI type of ANN, and optimization with PSs, GAs, AST, IPT, and SQP. The parameterized setting of the proposed scheme is given in Table 1. These parameterized settings have been carefully selected. Subsequently, extensive testing and adjustment of these parameterized settings have greatly raised the convergence rate. The effect of environmental temperature on human dermal region thermoregulation by utilizing second-order singular nonlinear bio-heat equation (BHE) is examined through the designed solvers because the dermal region is sensitive to different environments, temperatures, and touch in the form of four different scenarios.

Table 1 Pattern search (PS) and genetic algorithm (GA) OPTIM parameter setting
Full size table

In the hybridized optimization, the PSs algorithm specifies the size, expansion factor, constraint factor of the mesh, maximum number of the function estimations, and iterations. If it meets the given criteria, then stop the execution; otherwise, set the initial point that constructs the pattern vectors and generates the points, and then calculates the mesh points. If the poll is successful, they go back to the termination criterion condition and then execute it. Choose the best global initial weight bounds for hybrid, set optimum parameters for AST, IPT, and SQP, and again evaluate fitness function; if it meets the convergence criteria, then execute it to the next level. If it does not meet the given criteria, then reproduce the weights of each iteration of the selected optimization solver. Approximate the best solution for the proposed problem. These sorts of simulations are applied to lead the statistical analysis.

Firstly, GAs individuals are initiated by using real-bounded random values. Now, choose log-sigmoid as a network transfer function for proposed model. Then, assign the weights to all linkages and by using input and linkage find the activation function rate of the hidden layer. By an activation rate of the hidden layer and linkage to the output node, find the activation rate of an output node. The objective function is calculated for individual chromosome of the defined population by utilizing defined fitness function equations. If it attains the selected genetic algorithm optimum for the proposed model, then jump to the next step; otherwise, again update the bounds, declarations, etc. It is called a reproduction cycle. Similarly, as in PSs choose the best global initial weight bounds for hybrid, set optimum parameters for AST, IPT, and SQP, and again evaluate fitness function; if it meets the convergence criteria, then execute it to next level. If it does not meet the given criteria, then reproduce the weights of each iteration of the selected optimization solver. Approximate the best solution for proposed problem. These kinds of simulations are applied to lead the statistical analysis.

figure a

4 Numerical Handling of the Problems

The experimental numerical results will be discussed for the solution of the nonlinear singular BHE by taking four scenarios under consideration to estimate the numerical results over the PSs and GAs hybridization with local search techniques as in below presented scenarios. These parameters will remain the same for all scenarios:

$$\begin{aligned} T_{H} & = 33.03 + 0.14(T_{a} - 10),\,k_{0} = 0.00009T_{H} (37 - T_{H} )^{ - p} \\ p & = \frac{1}{3},\,q = 0.000002T_{H}^{2} ,n = 10,\,{\text{N = 3}}0,\\ &\quad {\text{ h}} = 0.{1},t_{i} = ih,x_{i} = x(t_{i} ) \end{aligned}$$
(10)

Scenario 1:

The proposed case selects the environmental temperature as, \(T_{a} = 0\) with parameters setting as given in Eq. (10). Thus, Eqs. (3–4) become:

$$\frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }}x(t) + \frac{2}{t}\frac{{{\text{d}}x}}{{{\text{d}}t}} + \frac{1}{x}\left( {\frac{{\text{d}}}{{{\text{d}}t}}x(t)} \right)^{2} + \frac{(5.37 - x)}{x}(0.1308) = 0,\,$$
(11)

with boundary conditions,

$$\frac{{{\text{d}}x}}{{{\text{d}}t}}(0) = 0,x(1) = 0.$$
(12)

The fitness error function Eqs. (8–9), related to second-order nonlinear singular BHE Eqs. (11–12), can be written as:

$$\xi_{{r_{1} }} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left[ {\frac{{{\text{d}}^{2} x_{i} }}{{{\text{d}}t^{2} }} + \frac{2}{{t_{i} }}\frac{{{\text{d}}x_{i} }}{{{\text{d}}t}} + \frac{1}{{x_{i} }}\left( {\frac{{{\text{d}}x_{i} }}{{{\text{d}}t}}} \right)^{2} + \frac{{(5.37 - x_{i} )}}{{x_{i} }}(0.1308)} \right]}^{2} ,$$
(13)

And \(\xi_{{r_{2} }}\) is also a fitness error function resulting from the boundary conditions.

$$\xi_{{r_{2} }} = \frac{1}{2}\left[ {(x_{0} - 1)^{2} + (x_{1} - 0)^{2} } \right].$$
(14)

Figure 3 shows the graphical set of best 3-D weights of optimum solvers PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA having fitness function \(1.8 \times 10^{ - 2} ,\,3.97975 \times 10^{ - 3} ,9.1631 \times 10^{ - 7}\)\(,\,\,3.9480 \times 10^{ - 7} ,\,\,3.9271 \times 10^{ - 4} ,\,\,1.15547 \times 10^{ - 4} ,\,\,2.1601 \times 10^{ - 5} ,\,8.3563 \times 10^{7}\), for scenario 1 of BHE, respectively, for \(t \in \left[ {0,1} \right]\) with h = 0.1. The sorted and unsorted runs are shown in Figs. 4 and 5, which shows the X-scale as number of runs and Y-scale as numerical values for PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA optimum solvers. By utilizing all three weights of each proposed optimum solvers, in Eq. (6) the solution for each \(t \in \left[ {0,1} \right]\) with step size of 0.1 for scenario 1 is given in Table 2. The numerical results are plotted graphically in Fig. 6 where X-scale is shown as parameter t and Y-scale is shown as numerical results for singular nonlinear bio-heat equation (BHE) for proposed solvers PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA.

Fig. 3
figure 3

3-D display of proposed optimum weights

Full size image
Fig. 4
figure 4

Sorted runs for scenario 1

Full size image
Fig. 5
figure 5

Unsorted runs for scenario 1

Full size image
Table 2 Derived solution scenario 1 of BHE
Full size table
Fig. 6
figure 6

Numerical results for scenario 1 of BHE

Full size image

The residual error of PS, GA, AST-PS, AST -GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA obtained from these numerical results shows that the results lie between \(10^{ - 10}\) and \(10^{ - 4}\), \(10^{ - 10}\) and \(10^{ - 4}\), \(10^{ - 12}\) and \(10^{ - 3}\), \(10^{ - 13}\) and \(10^{ - 5}\), \(10^{ - 12}\) and \(10^{ - 4}\), \(10^{ - 9}\) and \(10^{ - 4}\), \(10^{ - 9}\) and \(10^{ - 3}\), \(10^{ - 14}\) and \(10^{ - 4}\) for \(t \in \left[ {0,1} \right]\) with step size h = 0.1. These numerical results are convergent and more precise in the case of second-order singular nonlinear bio-heat equation (BHE). The residual error is shown graphically in Fig. 7 that presents the residual numerical values for \(t \in \left[ {0,0.8} \right]\) with step size h = 0.1.

Fig. 7
figure 7

Residual error for scenario 1

Full size image

Scenario 2: Environmental temperature as \(T_{a} = 10\).

The proposed case selects the environmental temperature as \(T_{a} = 10\) with parameters setting as given in Eq. (10). Thus, Eqs. (3–4) take the form as given below:

$$\frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }}x(t) + \frac{2}{t}\frac{{{\text{d}}x}}{{{\text{d}}t}} + \frac{1}{x}\left( {\frac{{\text{d}}}{{{\text{d}}t}}x(t)} \right)^{2} + \frac{(3.97 - x)}{x}(0.1849) = 0,$$
(15)

and with boundary conditions

$$\frac{{{\text{d}}x}}{{{\text{d}}t}}(0) = 0,x(1) = 0.$$
(16)

The fitness error function Eqs. (8–9), related to second-order nonlinear singular BHE Eqs. (14–15) can be written as:

$$\xi_{{r_{1} }} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left[ {\frac{{{\text{d}}^{2} x_{i} }}{{{\text{d}}t^{2} }} + \frac{2}{{t_{i} }}\frac{{{\text{d}}x_{i} }}{{{\text{d}}t}} + \frac{1}{{x_{i} }}\left( {\frac{{{\text{d}}x_{i} }}{{{\text{d}}t}}} \right)^{2} + \frac{{(3.97 - x_{i} )}}{{x_{i} }}(0.1849)} \right]}^{2} ,$$
(16)

And \(\xi_{{r_{2} }}\) is also a fitness error function resulting from the boundary conditions.

$$\xi_{{r_{2} }} = \frac{1}{2}\left[ {(x_{0} - 1)^{2} + (x_{1} - 0)^{2} } \right].$$
(17)

Figure 8 shows the graphical set of best 3-D weights of optimum solvers PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA having fitness function 1.79 \(\times \,\,10^{ - 2}\), 1.16 \(\times \,\,10^{ - 2}\), 4.4756 \(\times \,\,10^{ - 6}\), 1.4513 \(\times \,\,10^{ - 5}\), 1.2 \(\times \,\,10^{ - 3}\), 9.3454 \(\times \,\,10^{ - 6}\), 3.2208a \(\times \,\,10^{ - 5}\), 1.7609 \(\times \,\,10^{ - 6}\), for scenario 1 of BHE, respectively, for the inputs \(t \in \left[ {0,1} \right]\) with step size h = 0.1.

Fig. 8.
figure 8

3-D display of proposed optimum weights

Full size image

Figures 9 and 10 show the X-scale as number of runs and Y-scale as numerical values for PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA optimum solvers. By utilizing all three weights of each proposed optimum solvers, in Eq. (6) the proposed solution for each \(t \in \left[ {0,1} \right]\) for scenario 1 is given in Table 3. The numerical results are plotted graphically in Fig. 11, where X-scale is shown as parameter t and Y-scale is shown as numerical results for singular nonlinear bio-heat equation (BHE) for proposed solvers PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA. The residual error of PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA obtained from these numerical results shows that the results lie between \(10^{ - 10}\) and \(10^{ - 4}\), \(10^{ - 8}\) and \(10^{ - 4}\), \(10^{ - 10}\) and \(10^{ - 4}\), \(10^{ - 11}\) and \(10^{ - 4}\), \(10^{ - 9}\) and \(10^{ - 4}\), \(10^{ - 10}\) and \(10^{ - 4}\), \(10^{ - 11}\) and \(10^{ - 4}\), \(10^{ - 11}\) and \(10^{ - 4}\) for \(t \in \left[ {0,1} \right]\) with a step size as h = 0.1. These results are relatively more accurate and convergent for second-order singular nonlinear bio-heat equation (BHE). The residual error is shown graphically in Fig. 12 that presents the residual numerical values for \(t \in \left[ {0,0.8} \right]\) with step size h = 0.1.

Fig. 9
figure 9

Sorted runs for scenario 2

Full size image
Fig. 10
figure 10

Unsorted runs for scenario 2

Full size image
Table 3 Derived solution scenario 2 of BHE
Full size table
Fig. 11
figure 11

Graphical illustration of numerical results for scenario 2 of BHE

Full size image
Fig. 12
figure 12

Residual error for scenario 2

Full size image

Scenario 3: Environmental Temperature as \(T_{a} = 21\).

The proposed case selects the environmental temperature as \(T_{a} = 21\), with parameters setting as given in Eq. (10). Thus, Eqs. (3–4) take the form:

$$\frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }}x(t) + \frac{2}{t}\frac{{{\text{d}}x}}{{{\text{d}}t}} + \frac{1}{x}\left( {\frac{{\text{d}}}{{{\text{d}}t}}x(t)} \right)^{2} + \frac{(2.43 - x)}{x}(0.1270) = 0$$
(18)

and with boundary conditions

$$\frac{{{\text{d}}x}}{{{\text{d}}t}}(0) = 0,x(1) = 0$$
(19)

The fitness error function Eqs. (8–9), related to second-order nonlinear singular BHE Eqs. (18–19), can written as:

$$\xi_{{r_{1} }} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left[ {\frac{{{\text{d}}^{2} x_{i} }}{{{\text{d}}t^{2} }} + \frac{2}{{t_{i} }}\frac{{{\text{d}}x_{i} }}{{{\text{d}}t}} + \frac{1}{{x_{i} }}\left( {\frac{{{\text{d}}x_{i} }}{{{\text{d}}t}}} \right)^{2} + \frac{{(2.43 - x_{i} )}}{{x_{i} }}(0.1270)} \right]}^{2} ,$$
(20)

And \(\xi_{{r_{2} }}\) is also a fitness error function resulting from the boundary conditions.

$$\xi_{{r_{2} }} = \frac{1}{2}\left[ {(x_{0} - 1)^{2} + (x_{1} - 0)^{2} } \right].$$
(21)

Figure 13 shows the graphical set of best 3-D weights of optimum solvers PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA having fitness function 4.2 \(\times \,\,10^{ - 4}\), 6.8594 \(\times \,\,10^{ - 4}\), 9.9167 \(\times \,\,10^{ - 7}\), 4.3130 \(\times \,\,10^{ - 7}\), 3.7123 \(\times \,\,10^{ - 5}\), 1.1262 \(\times \,\,10^{ - 4}\), 2.5590 \(\times \,\,10^{ - 5}\), 1.2813 \(\times \,\,10^{ - 6}\), for scenario 1 of BHE, respectively, for the inputs \(t \in \left[ {0,1} \right]\) with step size h = 0.1.

Fig. 13.
figure 13

3-D display of proposed optimum weights

Full size image

Figures 14 and 15 show the X-scale as number of runs and Y-scale as numerical values for PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA optimum solvers. By utilizing all three weights of each proposed optimum solvers, in Eq. (6) the proposed solution for \(t \in \left[ {0,1} \right]\) for scenario 1 is given in Table 4. The numerical results are plotted graphically in Fig. 16 where X-scale is shown as parameter t and Y-scale is shown as numerical results for singular nonlinear bio-heat equation (BHE) for proposed solvers PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA. The residual error of PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA obtained from these numerical results shows that the results lie between \(10^{ - 11}\) and \(10^{ - 5}\), \(10^{ - 10}\) and \(10^{ - 5}\), \(10^{ - 11}\) and \(10^{ - 5}\), \(10^{ - 10}\) and \(10^{ - 4}\), \(10^{ - 14}\) and \(10^{ - 5}\), \(10^{ - 9}\) and \(10^{ - 5}\), \(10^{ - 11}\) and \(10^{ - 5}\), \(10^{ - 11}\) and \(10^{ - 5}\) for \(t \in \left[ {0,1} \right]\) with step size h = 0.1. These results are relatively more accurate and convergent for second-order singular nonlinear bio-heat equation (BHE). The residual error is shown graphically in Fig. 17 that presents the residual numerical values for \(t \in \left[ {0,0.8} \right]\) with a step size as h = 0.1.

Fig. 14
figure 14

Sorted runs for scenario 3

Full size image
Fig. 15
figure 15

Unsorted runs for scenario 3

Full size image
Table 4 Derived solution scenario 3 of BHE
Full size table
Fig. 16
figure 16

Graphical illustration of numerical results for scenario 3 of BHE

Full size image
Fig. 17
figure 17

Residual error for scenario 3

Full size image

Scenario 4: Environmental Temperature as \(T_{a} = 25\).

The proposed case selects the environmental temperature as \(T_{a} = 21\), with parameters setting as given in Eq. (10). Thus, Eqs. (3–4) take the form as given below:

$$\frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }}x(t) + \frac{2}{t}\frac{{{\text{d}}x}}{{{\text{d}}t}} + \frac{1}{x}\left( {\frac{{\text{d}}}{{{\text{d}}t}}x(t)} \right)^{2} + \frac{(1.87 - x)}{x}(0.4175) = 0\,,$$
(22)

and with boundary conditions

$$\frac{{{\text{d}}x}}{{{\text{d}}t}}(0) = 0,x(1) = 0.$$
(23)

The fitness error function Eqs. (8–9), related to second-order nonlinear singular BHE Eqs. (22–23), can be written as:

$$\xi_{{r_{1} }} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left[ {\frac{{{\text{d}}^{2} x_{i} }}{{{\text{d}}t^{2} }} + \frac{2}{{t_{i} }}\frac{{{\text{d}}x_{i} }}{{{\text{d}}t}} + \frac{1}{{x_{i} }}\left( {\frac{{{\text{d}}x_{i} }}{{{\text{d}}t}}} \right)^{2} + \frac{{(1.87 - x_{i} )}}{{x_{i} }}(0.4175)} \right]}^{2} ,$$
(24)

And \(\xi_{{r_{2} }}\) is also a fitness error function resulting from the boundary conditions.

$$\xi_{{r_{2} }} = \frac{1}{2}\left[ {(x_{0} - 1)^{2} + (x_{1} - 0)^{2} } \right].$$
(25)

Figure 18 shows the graphical set of best 3-D weights of optimum solvers PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA having fitness function 3.5 \(\times \,\,10^{ - 3}\), 2.8 \(\times \,\,10^{ - 3}\), 7.2387 \(\times \,\,10^{ - 7}\), 7.2316 \(\times \,\,10^{ - 6}\), 1.9717 \(\times \,\,10^{ - 4}\), 4.9973 \(\times \,\,10^{ - 4}\), 4.1926 \(\times \,\,10^{ - 8}\), 1.3874 \(\times \,\,10^{ - 7}\), for scenario 1 of BHE, respectively, for the inputs \(t \in \left[ {0,1} \right]\) with step size h = 0.1.

Fig. 18.
figure 18

3-D display of proposed optimum weights

Full size image

Figures 19 and 20 show the X-scale as number of runs and Y-scale as numerical values for PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA optimum solvers. By utilizing all three weights of each proposed optimum solvers, in Eq. (6) the proposed solution for each \(t \in \left[ {0,1} \right]\) for scenario 1 is given in Table 5. The numerical results are plotted graphically in Fig. 21 where X-scale is shown as parameter t and Y-scale is shown as numerical results for singular nonlinear bio-heat equation (BHE) for proposed solvers PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA. The residual error of PS, GA, PS-AST, GA-AST, PS-IPT, GA-IPT, PS-SQP, and GA-SQP obtained from these numerical results lies between \(10^{ - 12}\) and \(10^{ - 5}\), \(10^{ - 10}\) and \(10^{ - 6}\), \(10^{ - 12}\) and \(10^{ - 5}\), \(10^{ - 13}\) and \(10^{ - 6}\), \(10^{ - 12}\) and \(10^{ - 5}\), \(10^{ - 11}\) and \(10^{ - 6}\), \(10^{ - 11}\) and \(10^{ - 5}\), \(10^{ - 11}\) and \(10^{ - 6}\). These results are quite more precise and convergent for second-order singular nonlinear bio-heat equation (BHE). The residual error is shown graphically in Fig. 22 that presents the residual numerical values for \(t \in \left[ {0,0.8} \right]\) with step size h = 0.1.

Fig. 19
figure 19

Sorted runs for scenario 4

Full size image
Fig. 20
figure 20

Unsorted runs for scenario 4

Full size image
Table 5 Derived solution scenario 4 of BHE
Full size table
Fig. 21
figure 21

Graphical illustration of numerical results for scenario 4 of BHE

Full size image
Fig. 22
figure 22

Residual error for scenario 4

Full size image

4.1 Statistical Analysis

In this section, we have presented the one-way ANOVA with 95 present confidence level to compare the hybrid and global designed optimization solvers that are more accurate, reliable, and efficient. Moreover, the significance of the solvers is examined through P values.

Hsu Simultaneous Tests for Level Mean–Largest of Other Level Means

Difference of levels

Difference of means

SE of difference

95% CI

T-value

P Value

PS-AST—PS

− 0.001563

0.000533

(− 0.002837, 0.000000)

− 2.93

0.013

GA-AST—PS

− 0.001805

0.000533

(− 0.003080, 0.000000)

− 3.39

0.004

PS-IPT—PS

− 0.001376

0.000533

(− 0.002651, 0.000000)

− 2.58

0.032

GA-IPT—PS

− 0.001539

0.000533

(− 0.002814, 0.000000)

− 2.89

0.015

PS-SQP—PS

− 0.001655

0.000533

(− 0.002930, 0.000000)

− 3.11

0.008

GA-SQP—PS

− 0.001796

0.000533

(− 0.003070, 0.000000)

− 3.37

0.004

Difference of levels

Difference of MEANS

SE of difference

95% CI

T-Value

P Value

PS-AST—GA

− 0.001698

0.000580

(− 0.003086, 0.000000)

− 2.93

0.013

GA-AST—GA

− 0.001640

0.000580

(− 0.003027, 0.000000)

− 2.83

0.017

PS-IPT—GA

− 0.001444

0.000580

(− 0.002832, 0.000000)

− 2.49

0.040

GA-IPT—GA

− 0.001416

0.000580

(− 0.002804, 0.000000)

− 2.44

0.045

PS-SQP—GA

− 0.001788

0.000580

(− 0.003176, 0.000000)

− 3.08

0.009

GA-SQP—GA

− 0.001612

0.000580

(− 0.003000, 0.000000)

− 2.78

0.020

Difference of levels

Difference of means

SE of difference

95% CI

T-Value

P Value

PS-AST—PS

− 0.000978

0.000185

(− 0.001421, 0.000000)

− 5.28

0.000

GA-AST—PS

− 0.001051

0.000185

(− 0.001494, 0.000000)

− 5.67

0.000

PS-IPT—PS

− 0.000793

0.000185

(− 0.001237, 0.000000)

− 4.28

0.000

GA-IPT—PS

− 0.000844

0.000185

(− 0.001287, 0.000000)

− 4.55

0.000

PS-SQP—PS

− 0.001002

0.000185

(− 0.001446, 0.000000)

− 5.41

0.000

GA-SQP—PS

− 0.001048

0.000185

(− 0.001491, 0.000000)

− 5.65

0.000

figure b
figure c
figure d

5 Conclusion

The research study has presented the computing approach on artificial intelligence (AI) to approximate the solution of singular nonlinear second-order 1-D bio-heat equation (BHE) with boundary conditions. Numerous artificial neural networks (ANNs) are constructed to handle the proposed model based on several scenarios. The hybridization includes the pattern search (PS) and genetic algorithm (GA) solvers with AST, IPT, and SQP. Comparative study of the research model approximates the solution by taking 5–7 decimal places. The following annotations provide the final remarks on the proposed study:

  • The proposed scenarios of the second-order singular nonlinear bio-heat equation (BHE) concludes that in scenario 1, GA-SQP solver gives more accurate and efficient numerical solution as compared to other selected optimum solvers. In scenario 2, PS-SQP solver gives more accurate and efficient numerical approximated solution from other selected optimum solvers. In scenario 3, GA-IPT solver gives more accurate and efficient numerical approximated solution from other selected optimum solvers, whereas, in scenario 4, PS-AST solver gives more accurate and efficient numerical approximated solution as compared to other optimization solvers based on residual error results.

  • The convergence and stability of all the designed solvers are analyzed through the fitness numerical values corresponding to the number of independence runs that is completely illustrated by sorted and unsorted data plots for all four scenarios of BHE.

  • The statistical analysis is presented for detail explanation of accuracy and efficiency of all scenarios.

  • The P value < 0.05 for all the scenarios of BHE with 95% confidence level explains that hybrid solvers provide statistically significant results.

  • The computational intricacy of the anticipated stochastic numerical techniques is compared by various scenarios of local, global, and hybridized optimization solvers, but this feature is dominated on the basis of recent computing stages through advanced computing strategies.

  • PS, GA, AST-PS, AST-GA, IPT-PS, IPT-GA, SQP-PS, and SQP-GA studied human dermal region thermoregulation based on various environmental temperatures by utilizing second-order singular nonlinear bio-heat equation (BHE) through solvers.

In future, the novel attitude offered here might be utilized for further advances in the study of BHE or its groupings for progressive skills. The authors are also interested in applying the proposed methodology on higher-order, nonlinear, and singular partial differential equations [62,63,64,65].