1 Introduction

Several base fluids like water, glycol and alcohol have rather low viscosity, thermal conductivity and may not be used independently in several applications, the suspension containing nanoparticles combined with the base fluid [1]. A special type of fluid known as nanofluid has been introduced, to overcome this weakness. Due to the extreme essential properties of heat transfer, such nanofluids are commonly used for macroscopic cooling [2]. In everyday life, implementations such as portable computer processors, lubricant processing, coolants, air conditioning, freezers and nanotechnology, the single-phase flow model of nanofluids is of considerable significance [3]. Narla et al. have presented the pumping of electroosmotic nanofluid past a curved channel [4]. A very simple and environment friendly conversion method of ultraviolet irradiance to heat energy is identified as a solar collector, used in the industrial sector [5]. In such collectors, different fluids like water and glycol are being used to improve their power and performance [7]. Sheikholeslami et al. have analyzed the hydrothermal analysis of nanofluids with wavy pipe absorber [6]. Recently, both numerically and experimentally, Li et al. [8] have presented the use of nanofluids in certain kinds of solar collectors. Oke [9] has discussed and numerically analyzed a special type of nanofluid known as gold-water nanofluid and presented the obtained results.

There is another classification of nanofluids obtained by dispersing two or more types of nanoparticles in conventional fluid, termed as hybrid nanofluids [10]. Hybrid nanofluids are essential because they are potential heat transfer fluids that possess more enhanced thermophysical properties and better thermal performance than base fluids and nanofluids having single type of nanoparticles [11]. Algehyne et al. [12] have presented the BVP of Maxwell hybrid nanofluid and its thermophysical performances. Khan et al. [13] have investigated a fractional model on hybrid nanofluids with porous medium. The use of nanoparticles for imaging and sensing purposes in bio-medical field has become very important for advance applications [12]. This growth in the field of nanoparticles is directly linked with designing new materials at nanoscale level along with innovations in imaging technologies to measure and manipulate nanomaterials [14]. The ternary MHD hybrid nanofluid flow past a rotating surface is treated numerically by Oke [15]. The production, usage and disposal of synthesized nanoparticles will cause expulsion of air, sand, soil and water systems. Harmful effects are to be expected; therefore, minimization and quantification of these negative effects on ecological health are of great importance [16]. Therefore, true information about chemical and physical properties of nanoparticles in consideration of realistic circumstances is necessary to predict their toxicity, fate and behavior in normal aquatic environment [17].

The phrase thin film is widely used to describe flow that is defined by the thickness of a layer of material ranging from nanometer scale to the several micrometers. In one dimension (one or two dimensions), the flow spectra are significantly less than the other [18]. It is a property that may be utilized to simplify Navier–Stokes equations [19]. The structural importance of flow problems with thin films (flow) is significant [20]. Thin-film flow problems in regular activities range from simple to sophisticated effects, such as transmitting a rain drop on an airplane window [21]. Siddiqui et al. [22] implemented the He’s homotopy method for third-grade TFF fluid flow. It is true that thin-film flow is used in a variety of industrial processes [23]. The Casson hybrid nanofluid based on TFF is analyzed by Alhussain and Tassaddiq [24]. Researchers are interested in working on this topic because of its extensive applications in sectors such as coating material, industrial processes, chemical engineering, cooling and the lubrication of thermal changer fins into contact lens motion, dam breaking wave simulation and nuclear reactor fluid dynamics that are among the most significant industrial applications [25]. The TFF flow past a stretching sheet is numerically tackled by Kamis et al. [26]. The representation of TFF dynamics is similar to tear films in the eye and membranes in the biophysics field [27]. The most prevalent fluid properties are thin-film flow and flow characteristics. Furthermore, in this advanced and fast-paced era, thin film allows all those involved to monitor the output of paints in surface flow coverings, plan the layout of nuclear reactors and reduce the structure of equipment such as lubricating fluid [28]. TFF’s biological uses are similar to red blood cells flowing via veins, eyes and lungs [18]. A neuro-heuristic intelligent algorithm is utilized by Ahmad et al. [29] to evaluate TFF model.

Many engineering systems involving electro-magnetic accelerators and magnetohydrodynamic (MHD) power generators work on high temperatures; therefore, the understanding of MHD nanofluidic flow past has become very essential in production of appropriate equipment [31]. Thus, problems regarding nanofluids and magnetohydrodynamics (MHD) have become mechanically more important [32]. The modified Eyring Powell MHD fluid flow is presented and numerically solved by Oke [33]. The concept of using nanofluids in magnetohydrodynamic (MHD) flows over different flow geometries (specifically stretching sheets) has been presented due to the stability, enhanced heat transfer and effective thermal conductivity of these kinds of fluids [34]. Thermal conductivity of the nanofluids contributes in better performance, high energy proficiency and subordinate operating costs, discussed by Ijaz and Ayub in [35].

Lobatto IIIA based on finite difference method is a version of bvp4c method. The numerical code bvp4c in MATLAB, which is a finite difference technique, implements the 3-stage Lobatto IIIA formula that is a collocation technique having accuracy of order four. In the literature usually, the symbol III is associated with Lobatto methods because symbols I and II are held in reserve for two kinds of Radau methods [36]. A collocation method based on Lobatto IIIA technique is utilized by Oke et al. [37] for numerical solution of transformed ordinary differential equations. Lobatto IIIA method has a strong point to tackle extremely nonlinear systems of ordinary differential equations (ODEs) [38]. Implementation of Lobatto IIIA method to attain better approximation and rapid convergence is an inventive effort, used by Ahmad et al. [39].

The salient features of the proposed techniques are itemized as follows:

  • A novel investigation is presented to examine the heat transfer and thermal performance of nanofluidic transportation of nanofluids and hybrid nanofluids toward stretching surfaces by Lobatto IIIA techniques.

  • The governing physical flow systems are modeled mathematically in curvilinear coordinates and simplified by using appropriate transformations.

  • The simplified systems of nonlinear differential equations are numerically treated to investigate the influences of emerged physical parameters on temperature, pressure and velocity profiles.

  • A comparative dynamical analysis of nanofluids and hybrid nanofluids under the influence of emerging parameters is presented through tables and graphs which ascertain the worth of the scheme as an effective and viable computing solver.

  • The conceptual simplicity, smoothness and stability are the hallmarks of the proposed study.

The framework of rest of the manuscript is structured as follows: Mathematical development and modeling of the problems is provided in Section two, results obtained by computational technique are presented graphically as well as in tabulated form in Section three, while the Section four includes the conclusion and future research study.

2 Mathematical Development

This section is held in reserve to the mathematical development and numerical simulation of axisymmetric flow of \(\hbox {SiO}_2/\hbox {EG}\)-based nanofluid and hybrid \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\)-based nanofluid on a radially stretched surface under consideration of magnetic field effect along with the internal heat absorption/generation. Lobatto IIIA is employed for computational exploration of governing flow model. Here ethylene glycol is taken as base fluid, molybdenum sulfide (\(\hbox {MoS}_2\)) and silicon dioxide (\(\hbox {SiO}_2\)) as ultra-fine nanoparticles. Hybrid nanofluid is prepared by inserting the nanoparticles of \(\hbox {MoS}_2\) and \(\hbox {SiO}_2\) in ethylene glycol.

Fig. 1
figure 1

Physical demonstration of \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) flow

Full size image

2.1 Mathematical Modeling

A porous infinite radially stretched disk is considered for electrically conducting and incompressible nanofluidic flow. This opted disk is placed at the plane where \({\bar{z}}=0\). Nanocomposite \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) fluid flow is taking place above a half space \({\bar{z}}>0\). This hybrid nanofluidic mixture contains 1% of \(\hbox {SiO}_2\) volumetric fraction (\(\phi _1\)), while \(\hbox {MoS}_2\) volumetric fraction (\(\phi _2\)) varies from 1 up to 5%. Equation (1) determines the nanoparticles volumetric fraction \(\phi _{\mathrm{hnf}}\) of the hybrid \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) nanofluid.

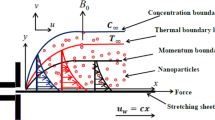
$$\begin{aligned} \phi _{\mathrm{hnf}}=\frac{V_{\mathrm{MoS}_2}+V_{\mathrm{SiO}_2}}{V_{\mathrm{total}}}=\phi _1+\phi _2. \end{aligned}$$
(1)

Magnetic field \(B_0\) having uniform intensity is applied in axial direction, and magnetic induction is unnoticed assuming the sufficiently weak magnetic field. The current analysis is done in cylindrical coordinates (\({\bar{r}},{\bar{\theta }},{\bar{z}}\)). Moreover, the flow is generated due to the reason of stretching of the surface along radial direction. This flow has uniform velocity \(U_{\mathrm{w}}\left( {\bar{r}}\right) =c{\bar{r}}\), where real number c is nonnegative. Surface of the porous disk is incorporated with heat transfer along with internal heat generation. Furthermore, lower surface is assumed to be heated through convection using a warm fluid having temperature \(T_{\mathrm{f}}\). Temperature \(T_{\mathrm{f}}\) is more than that of constant ambient temperature \(T_{\infty }\) and gives a heat-transfer coefficient \(h_{\mathrm{f}}\). The physical structure of governing flow model is demonstrated in Fig. 1.

The derivatives regarding \({\bar{\theta }}\) are absent because of axial symmetry of the leading engineering problem. Using above considerations together with boundary-layer approximations, the principal equations can be coupled into the subsequent forms.

$$\begin{aligned}&\frac{\partial u}{\partial {\bar{r}}}+\frac{u}{{\bar{r}}}+\frac{\partial w}{\partial {\bar{z}}}=0, \end{aligned}$$
(2)
$$\begin{aligned}&u\frac{\partial u}{\partial {\bar{r}}}+w\frac{\partial u}{\partial {\bar{z}}}=\frac{\mu _{\mathrm{hnf}}}{\rho _{\mathrm{hnf}}}\frac{\partial ^2u}{\partial {\bar{z}}^2}-\frac{\sigma ^2_{\mathrm{hnf}}\beta ^2}{\rho _{\mathrm{hnf}}}u, \end{aligned}$$
(3)
$$\begin{aligned}&u\frac{\partial T}{\partial {\bar{r}}}+w\frac{\partial T}{\partial {\bar{z}}}=\alpha _{\mathrm{hnf}}\frac{\partial ^2T}{\partial {\bar{z}}^2}+\frac{Q}{\left( \rho c_p\right) _{\mathrm{hnf}}}\left[ T-T_{\infty }\right] . \end{aligned}$$
(4)

along with related boundary conditions

$$\begin{aligned} u= & {} U_{\mathrm{w}}\left( {\bar{r}}\right) =c{\bar{r}},\ w=-f_{\mathrm{w}}\left( {\bar{r}}\right) ,\ \\&-k_{\mathrm{hnf}}\frac{\partial T}{\partial {\bar{z}}}=h_{\mathrm{f}}\left( T_{\mathrm{f}}-T\right) ,\ \hbox {at}\ {\bar{z}}=0, \end{aligned}$$
$$\begin{aligned} u\rightarrow 0,\ T\rightarrow T_{\infty }\ \hbox {as}\ {\bar{z}}\rightarrow \infty . \end{aligned}$$
(5)

where u and w are components of velocity along \({\bar{r}}\) and \({\bar{z}}\)-axis, correspondingly. Furthermore, \(\mu _{\mathrm{hnf}}\), \(\rho _{\mathrm{hnf}}\) and \(\sigma _{\mathrm{hnf}}\) indicate hybrid nanofluidic dynamic viscosity, density and electrical conductivity, respectively. \(f_{\mathrm{w}}\left( {\bar{r}}\right) \) is injection/suction velocity over the radial disk’s surface.

Fig. 2
figure 2

Graphical abstract of \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) flow

Full size image

2.2 Numerical Simulation of Model

Numerical exploration of temperature and velocity profiles for the hybrid \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) nanofluidic flow over a porous infinite radially stretched surface is done by employing Lobatto IIIA technique according to process illuminated in Fig. 2. Moreover, thermo-physical properties of ethylene glycol, \(\hbox {SiO}_2\) and \(\hbox {MoS}_2\) are listed in Table 1.

Table 1 Numerical values of nanoparticles and base fluid
Full size table

Similarity transformations as well as dimensionless variable \(\zeta \) and \(f\left( \zeta \right) \) are accustomed to more assist and simplify the current investigation.

$$\begin{aligned} u= & {} c{\bar{r}}f'\left( \zeta \right) ,\ w=-2\sqrt{c\nu _{\mathrm{f}}}f\left( \zeta \right) ,\ \nonumber \\&\zeta ={\bar{z}}\sqrt{\frac{c}{\nu _{\mathrm{f}}}},\ \theta \left( \zeta \right) =\frac{T_{\mathrm{f}}-T}{T_{\mathrm{f}}-T_{\infty }}. \end{aligned}$$
(6)

After simplification, system of PDEs Eqs. (2–5) for proposed physical problem is reduced into equivalent transformed system of nonlinear coupled ODEs Eqs. (7–9)

$$\begin{aligned} \frac{1}{\Omega _1}f'''+2ff''-f'^2-\frac{1}{\Omega _2}M^2f'=0, \end{aligned}$$
(7)
$$\begin{aligned} \frac{1}{\Omega _3}\frac{k_{\mathrm{hnf}}}{k_{\mathrm{f}}}\theta ''+2Prf\theta '+\lambda \frac{\left( \rho c_p\right) _{\mathrm{f}}}{\left( \rho c_p\right) _{\mathrm{hnf}}}=0, \end{aligned}$$
(8)
$$\begin{aligned} f\left( 0\right) =S,\ f'\left( 0\right) =1,\ \theta '\left( 0\right) =-Bi\frac{k_{\mathrm{f}}}{k_{\mathrm{hnf}}}\left( 1-\theta \left( 0\right) \right) , \end{aligned}$$
$$\begin{aligned} f'\left( \zeta \right) \rightarrow 0,\ \theta \left( \zeta \right) \rightarrow 0\ \hbox {as } \zeta \rightarrow \infty . \end{aligned}$$
(9)

in which

$$\begin{aligned}&\Omega _1=\frac{\nu _{\mathrm{f}}}{\nu _{\mathrm{hnf}}}=\left( 1-\phi _1\right) ^{2.5}\left( 1-\phi _2\right) ^{2.5} \nonumber \\&\quad \times \left[ \left( 1-\phi _2\right) \left\{ \left( 1-\phi _1\right) +\phi _1\left( \dfrac{\rho _{s_1}}{\rho _{\mathrm{f}}}\right) \right\} +\phi _2\dfrac{\rho _{s_2}}{\rho _{\mathrm{f}}}\right] , \end{aligned}$$
(10)
$$\begin{aligned}&\Omega _2=\frac{\rho _{\mathrm{hnf}}}{\rho _{\mathrm{f}}}=\left( 1-\phi _2\right) \left[ \left( 1-\phi _1\right) +\phi _1\left( \dfrac{\rho _{s_1}}{\rho _{\mathrm{f}}}\right) \right] +\phi _2\dfrac{\rho _{s_2}}{\rho _{\mathrm{f}}}, \end{aligned}$$
(11)
$$\begin{aligned}&\Omega _3=\frac{\left( \rho c_p\right) _{\mathrm{hnf}}}{\left( \rho c_p\right) _{\mathrm{f}}}=\left( 1-\phi _2\right) \left[ \left( 1-\phi _1\right) +\phi _1\left( \dfrac{\left( \rho c_p\right) _{s_1}}{\left( \rho c_p\right) _{\mathrm{f}}}\right) \right] \nonumber \\&\quad +\phi _2\left( \dfrac{\left( \rho c_p\right) _{s_2}}{\left( \rho c_p\right) _{\mathrm{f}}}\right) . \end{aligned}$$
(12)

where the condition \(f\left( 0\right) =S\) with \(S>0\) indicates the injection case, while \(S<0\) implies suction.

Furthermore, the dimensionless parameters arising in above set of ODEs, e.g., Hartman number M, heat generation parameter \(\lambda \), Prandtl number Pr and Biot number Bi, can be defined as

$$\begin{aligned} M= & {} \frac{\sigma _{\mathrm{hnf}}B_{0}^{2}}{c\rho _{\mathrm{f}}},\ \lambda =\frac{Q}{c\left( \rho c_p\right) _{\mathrm{f}}},\ \hbox {Pr}=\frac{\mu _{\mathrm{f}}\left( c_p\right) _{\mathrm{f}}}{k_{\mathrm{f}}},\ \nonumber \\&\hbox {Bi}=h_{\mathrm{f}}k_{\mathrm{f}}\sqrt{\frac{\nu _{\mathrm{f}}}{c}},\ S=\frac{f_{\mathrm{w}}}{2\sqrt{c\nu _{\mathrm{f}}}}. \end{aligned}$$
(13)

Local Nusselt number Nu\(_{{\bar{r}}}\) and skin friction coefficient \(C_{\mathrm{f}}\) are concerned physical quantities, which are defined as

$$\begin{aligned} Nu_{{\bar{r}}}=\frac{{\bar{r}}q_{\mathrm{w}}}{k_{\mathrm{hnf}}\left( T_{\mathrm{w}}-T_{\infty }\right) },\ C_{\mathrm{f}}=\frac{\tau _{\mathrm{w}}}{\frac{1}{2}\rho _{\mathrm{hnf}}u_{w}^{2}}. \end{aligned}$$
(14)

where \(q_{\mathrm{w}}\) and \(\tau _{\mathrm{w}}\) are

$$\begin{aligned} \begin{aligned} q_{\mathrm{w}}=\left. -k_{\mathrm{hnf}}\left( \frac{\partial T}{\partial {\bar{z}}}\right) \right| _{{\bar{z}}=0},\\ \tau _{\mathrm{w}}=\left. \mu _{\mathrm{hnf}}\left( \frac{\partial u}{\partial {\bar{z}}}\right) \right| _{{\bar{z}}=0}. \end{aligned} \end{aligned}$$
(15)

In sight of Eq. (6), expression, which is labeled in Eqs. (14) and (15), gives the dimensionless local Nusselt Nu\(_{{\bar{r}}}\) and skin friction \(C_{\mathrm{f}}\) as

$$\begin{aligned} Nu_{{\bar{r}}}=-\frac{k_{\mathrm{hnf}}}{k_{\mathrm{f}}}\theta '\left( 0\right) ,\ C_{\mathrm{f}}=\frac{f''\left( 0\right) }{\left( 1-\phi \right) ^{2.5}}. \end{aligned}$$
(16)

where Nu\(_{{\bar{r}}}\) and \(C_{\mathrm{f}}\) are reduced Nusselt number and skin friction, respectively.

The system of nonlinear coupled ODEs Eqs. (7–9) is then converted into system of first-order ODEs for Lobatto IIIA. In this investigation, mesh points are fixed at 900, while relative error tolerance varies as \(10^{-3}\), \(10^{-6}\), \(10^{-9}\) and \(10^{-12}\). Approximated velocity and temperature profiles of the hybrid nanofluidic system are determined under consideration of dimensionless quantities, e.g., Hartman number M, heat generation parameter \(\lambda \), Prandtl number Pr and Biot number Bi-based scenarios. At the end stability, accuracy and convergence analysis are performed.

3 Results and Discussion

In proceeding section, numerically computed impacts for evolving physical constraints on nanofluidic motion and temperature of \(\hbox {SiO}_2/\hbox {EG}\) nanofluid and hybridized \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) nanofluid are explained. Hartman number M, suction parameter S, nanoparticles volumetric fractions \(\phi _1\) and \(\phi _2\), heat absorption/generation parameter \(\lambda \), Biot number Bi and shape factors m are several influential constraints of interest in this exploration. Graphical and numerical outcomes are designed for both categories of nanofluids to provide comparative study. Dotted curves illustrate outcomes achieved for \(\hbox {SiO}_2/\hbox {EG}\) nanofluid, whereas solid curves explain outcomes for hybridized \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) nanofluid. For exploration the default numerical values of evolving parameters are presented as: \(M=2.5,\ S=0.05,\ \lambda =-3,\ m=3,\ \hbox {Bi}=2,\ \hbox {Pr}=203.63,\ \phi _1=0.01,\ \phi _2=0.01.\)

Six scenarios each with three cases of the evolving constraints for both nanofluids are shown in Tables 2, 3, 4, 5, 6, 7 and 8. In these tables different values are given to sundry variables in different cases. We have 6 scenarios and 3 cases for each scenario, which demonstrates variation of each parameter. Numerical calculations for different tolerance rates like (\(10^{-3}\), \(10^{-6}\), \(10^{-9}\) and \(10^{-12}\)) show the adequate accuracy and better convergence obtained by computing scheme. Mesh points used for solutions of each case of 6 scenarios are revealed in Table 2. Table 3 indicates stopping criteria depending on maximum residual obtained for different cases of each scenario, during problem evaluation. Complexity analysis of numerical method Lobatto IIIA to obtain required values of residual error is performed in terms of number of evaluated ODEs and BCs. Number of evaluated ODEs to develop the desired residual is given in Table 4 for different scenarios and cases. The evaluated boundary conditions for the specified accuracy given in Table 3 during different cases of each scenario are presented in Table 5. Table 6 offers skin friction coefficients attained during different cases of sundry scenarios. Nusselt numbers against five different shape factors are calculated for both nanofluids during each case of different scenarios, provided in Tables 7 and 8.

Table 2 Number of mesh points taken for solution of model
Full size table
Table 3 Maximum residual during different scenarios and cases of model
Full size table
Table 4 Number of evaluated ODEs during solution of model
Full size table
Table 5 Number of evaluated BCs during solution of model
Full size table

The impacts of suction and magnetic constraints on fluidic motion are displayed in Fig. 3. From Fig. 3a it is determined that suction parameter decelerates flow past of both nanofluids and works as an opposing force. This decreasing trend is caused by the suction taking place at porous stretched surface that interrupts the boundary layer fluid flow and leads to descend fluidic velocity. Similarly rising values of magnetic parameter reduce rate of fluid’s flow as can be perceived in Fig. 3b. Existence of magnetic field in directed flows is significant. Moreover, perpendicularly applied magnetic field to the nanofluidic flow direction has dominant effects in opposing manner. Therefore, parameter M acts as a drag force and retards the movement of nanofluids. Deceleration of flow due to suction and magnetic constraints is observed leading for \(\hbox {SiO}_2/\hbox {EG}\) nanofluid. Furthermore, in Table- 6 skin friction coefficient which is also termed as velocity gradient rises using positively increasing values of both suction and magnetic constraints.

Fig. 3
figure 3

Influence of suction and magnetic parameters on \(f'\left( \zeta \right) \)

Full size image
Fig. 4
figure 4

Influence of Biot number on \(f'\left( \zeta \right) \) and \(f\left( \zeta \right) \)

Full size image

Biot number (sheet convection) gives influence on nanofluidic velocity and \(f\left( \zeta \right) \) which is presented in Fig. 4. Nanofluidic flow under up surging values of Biot number possesses ascending behavior, while graphs for \(f\left( \zeta \right) \) exhibit descending behavior as demonstrated in Fig. 4a, b, respectively. Moreover, leading rise is appeared for hybridized \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) nanofluid, while leading drop is found for \(\hbox {SiO}_2/\hbox {EG}\) nanofluid.

Figure 5 reveals the effects for volumetric concentrations of \(\hbox {SiO}_2\) and \(\hbox {MoS}_2\)–\(\hbox {SiO}_2\) in ethylene glycol on nanofluidic velocity and \(f\left( \zeta \right) \). It is noticed that a marginal rise in volumes of nanoparticles accelerates the flow and raises the graphs for \(f\left( \zeta \right) \) as given in Fig. 5a, b, respectively. Since usage of nanoparticles in conventional fluid decreases its viscosity which helps the fluid flow to accelerate. Faster increase in velocity and \(f\left( \zeta \right) \) is observed for hybridized nanofluid. Furthermore, greater values of \(\phi _1\) and \(\phi _2\) increase the skin friction coefficient which is more leading for \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) as given in Table 6.

Table 6 Skin friction numbers \(-C_{\mathrm{f}}\) for both nanofluids of model
Full size table
Table 7 Nusselt numbers Nu for nanofluid of model
Full size table
Fig. 5
figure 5

Influence of volumetric fractions on \(f'\left( \zeta \right) \) and \(f\left( \zeta \right) \)

Full size image
Fig. 6
figure 6

Influence of volumetric fractions on \(\theta \left( \zeta \right) \) against m

Full size image

Figures 6, 7 and 8 are plotted to explain the influence of some evolving constraints such as volumetric fractions, Biot number and heat absorption/generation parameter with each against five shape factors on profiles of temperature for both fluids. Sphere, hexahedron, tetrahedron, column and lamina are five considered shapes of nanoparticles. Figure 6 is devoted to inspect the thermal performance of nano and hybrid nanofluid by submerging nanoparticles of both categories up to 5% of volume. Figure 6a, b demonstrates that increasing volume of nanoparticles raises the temperature of both fluids. For hybrid nanofluid 1% volume of \(\hbox {SiO}_2\) nanoparticles is reserved fix. Moreover, both nanofluids holding lamina shape of nanoparticles offer maximum temperature for variation of \(\phi _1\) and \(\phi _2\). On comparing Fig. 6a, b, it is also visualized that the temperature of hybrid nanofluid leads the temperature of nanofluid.

Table 8 Nusselt numbers Nu for hybrid nanofluid of model
Full size table
Fig. 7
figure 7

Influence of Biot number on \(\theta \left( \zeta \right) \) against m

Full size image

Thermal behavior of nano and hybrid nanofluid subject to rising sheet convection constraint is pictured in Fig. 7. Biot number (sheet convection) is defined as a quotient of heat transmission resistances within and above the conductive surface that measures the temperature difference by means of applied thermal gradient over the conductive surface. Therefore, upsurge in this quotient raises the temperature curves for both \(\hbox {SiO}_2/\hbox {EG}\) and \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) nanofluids. Moreover, high temperature is measured by submerging nanoparticles with lamina shape into the both fluid categories. Tables 7 and 8 validate that Nusselt numbers for both fluids are increased using greater values of Bi while decreased using greater values of shape factors.

Fig. 8
figure 8

Influence of parameter \(\lambda \) on \(\theta \left( \zeta \right) \) against m

Full size image

Impressions of heat absorption/generation constraint on temperature curves are provided in Fig. 8. Since \(\lambda <0\) is heat absorption case, so descending \(\lambda \) values decrease the temperature graphs as well. This behavior is perceived for both \(\hbox {SiO}_2/\hbox {EG}\) and \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) nanofluids. Lowest temperature is achieved for spherical nanoparticles. In Tables 7 and 8, it is witnessed that Nusselt numbers for both fluids are increased using smaller values of \(\lambda \) while decreased using greater values of shape factors.

4 Conclusion

In this work, a novel approach is presented to numerically examine the nanofluidic and hybrid nanofluidic systems \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\), through designed computing scheme. In the proposed model, axisymmetric flow of \(\hbox {SiO}_2/\hbox {EG}\) nanofluid as well as \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) hybrid nanofluid over a radially stretched disk under influential impacts of magnetic field, suction, internal heat absorption/generation, sheet convection and volumetric fractions is investigated in detail. The foremost judgments of presented work are:

  • It is determined that \(\hbox {MoS}_2\)–\(\hbox {SiO}_2/\hbox {EG}\) hybrid nanofluid holds better thermal abilities because its temperature upsurges more rapidly with rising Biot number and volume fractions as matched to \(\hbox {SiO}_2/\hbox {EG}\) nanofluid.

  • High magnetic field and suction of porous disk decelerate flow past both nanofluids inside the boundary; on the other hand, volumetric fractions accelerate it.

  • Lowest nondimensional temperature is witnessed for nanoparticles of sphere shape, whereas peak temperature is perceived for lamina shape.

  • In case of heat absorption constraint, negative impacts on thermal performance of both nanofluids are observed.

  • Skin friction coefficient of both nanofluids gain rises, when subject to the influence of suction, magnetic and volumetric fraction constraints and leads in hybrid nanofluidic case.

  • Constraints of heat absorption and sheet convection raise the Nusselt number of both nanofluidic categories, but shape factors are a cause to decrease its values.

In future, one may exploit artificial intelligence-based numerical computing paradigm [40,41,42,43] for dynamical analysis of hybrid nanoparticles (\(\hbox {MoS}_2\)–\(\hbox {SiO}_2\), \(\hbox {TiO}_2\)–\(\hbox {CuO}\)) on the fluid toward stretched surfaces with the influential impacts of evolving constraints such as slip condition, nanoparticles shape factors, heat generation, thermal radiation and applied transverse magnetic field.