Skip to main content
SpringerLink
Log in

A web of confocal parabolas in a grid of hexagons

  • Original Paper
  • Published:
Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry Aims and scope Submit manuscript

Abstract

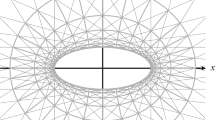
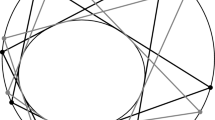
If one erects regular hexagons upon the sides of a triangle T, several surprising properties emerge, including: (i) the triangles which flank said hexagons have an isodynamic point common with T, (ii) the construction can be extended iteratively, forming an infinite grid of regular hexagons and flank triangles, (iii) a web of confocal parabolas with only three distinct foci interweaves the vertices of hexagons in the grid. Finally, (iv) said foci are the vertices of an equilateral triangle.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Notes

  1. This pencil is known as the Schoutte pencil (Johnson 1917).

  2. This is the double-length reflection about the barycenter \(X_2\).

References

  • Akopyan, A.: Private communication (2021)

  • Casey, J.: A Sequel to the First Six Books of the Elements of Euclid, 5th edn. Hodges, Figgis & Co., Dublin (1888)

    Google Scholar 

  • Čerin, Z.: Regular hexagons associated to triangles with equal centroids. Elem. Math. 53, 112–118 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  • Čerin, Z.: Loci related to variable flanks. Forum Geometricorum 2, 105–113 (2002)

    MathSciNet  MATH  Google Scholar 

  • Dosa, T.: Some triangle centers associated with the excircles. Forum Geometricorum 7, 151–158 (2007)

    MathSciNet  MATH  Google Scholar 

  • Dragović, V., Radnović, M.: Bicentennial of the great Poncelet theorem (1813–2013): current advances. Bull. Amer. Math. Soc. (N.S.) 51(3), 373–445 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  • Fukuta, J.: Problem 10514. Am. Math. Mon. 103 (1996) (Solution: vol. 104 (1997), p. 775)

  • Fukuta, J.: Problem 1493. Math. Mag. 69 (1996) (Solution: 70 (1997), pp. 70–73)

  • Grinberg, D.: Private communication (2021)

  • Hoehn, L.: Extriangles and excevians. Math. Mag. 74, 384–388 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  • Johnson, R.: Directed angles and inversion with a proof of Schoute’s theorem. Am. Math. Mon. 24, 313–317 (1917)

    Article  MathSciNet  MATH  Google Scholar 

  • Johnson, R.A.: Advanced Euclidean Geometry, 2nd edn. Dover, New York (1960). (Editor John W. Young)

  • Kimberling, C.: Encyclopedia of triangle centers. https://bit.ly/2GF4wmJ (2019). Accessed 16 June 2022

  • Lamoen, Fv.: Friendship among triangle centers. Forum Geometricorum 1, 1–6 (2001)

    MathSciNet  MATH  Google Scholar 

  • Martini, H.: On the theorem of Napoleon and related topics. Mathematische Semesterberichte 43, 47–64 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  • Morozov, E., Nilov, F.: Squares around affine regular and affine semi-regular polygons. Kvant. To appear (in Russian) (2022)

  • Reznik, D., Garcia, R.: Related by similarity II: Poncelet 3-periodics in the homothetic pair and the Brocard porism. Intl. J. Geom. 10(4), 18–31 (2021)

    MATH  Google Scholar 

  • Stachel, H.: Napoleon’s theorem and generalizations through linear maps. Beiträge zur Algebra und Geometrie 43(2), 433–444 (2002)

    MathSciNet  MATH  Google Scholar 

  • Weisstein, E.W.: CRC Concise Encyclopedia of Mathematics, 2nd edn. Chapman and Hall, Boca Raton (2002)

    Book  MATH  Google Scholar 

Download references

Acknowledgements

We thank Arseniy Akopyan for contributing crucial insights and discovering the web of parabolas in the grid. Darij Grinberg lend us an attentive ear and proved the stationarity of \(X_{16}\). Clark Kimberling was kind enough to include our early observations on the Encyclopedia of Triangle Centers.

Author information

Authors and Affiliations

  1. Moparmatic Inc., Worcestershire, England

    Peter Moses

  2. Data Science Consulting Ltd., Rio de Janeiro, Brazil

    Dan Reznik

Authors
  1. Peter Moses
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dan Reznik
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dan Reznik.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A: Explicit formulas

Appendix A: Explicit formulas

To facilitate computational reproduction of our results, we provide code-friendly expressions for a few objects. In the expressions below a, b, c refer to sidelengths and x, y, z are barycentric coordinates.

1.1 A-parabola

It is given implicitly by:

figure a

The B- and C-parabolas can be obtained by cyclic permutations, i.e., \((a,b,c)\rightarrow (b,c,a)\), and \((a,b,c)\rightarrow (c,a,b)\), respectively.

1.2 The two “skip-1” parabolas

The skip-1 parabola through B is given by:

figure b

The skip-1 parabola through C is obtained with a bicentric substitution, i.e., \((a,b,c,x,y,z)\rightarrow (a,c,b,x,z,y)\).

1.3 Center (at infinity) of the A-parabola group

The A-parabola and BC skip-1 pair of parabolas have parallel axes through \(f_a,f_b,f_c\), therefore their axes will cross the line at infinity at the same point given by the following barycentrics;

figure c

1.4 Directrix of the A-parabola

Is is the line given by:

figure d

The other two directrices can be obtained via cyclic substitution.

1.5 Directrix equilateral

The barycentrics x, y, z of the A-vertex of the directrix equilateral (Proposition 12) are given by:

figure e

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Moses, P., Reznik, D. A web of confocal parabolas in a grid of hexagons. Beitr Algebra Geom 64, 669–688 (2023). https://doi.org/10.1007/s13366-022-00651-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13366-022-00651-1

Keywords

Mathematics Subject Classification

Search

Navigation