Abstract
Euclid uses an undefined notion of “equal figures”, to which he applies the common notions about equals added to equals or subtracted from equals. This notion does not occur in modern geometrical theories such as those of Hilbert or Tarski. Therefore to account for Euclid in modern geometry, one must somehow replace Euclid’s “equal figures” with a defined notion. In this paper we present a new solution to this problem, and moreover we argue that “Euclid could have done it”. That is, it is based on mathematics that was available in Euclid’s time, including ideas related to Euclid’s Proposition I.44. The proof uses the theory of proportions. Hence we also discuss the “early theory of proportions”, which has a long history.





























Similar content being viewed by others
Notes
It does occur in English translation in Prop. I.35, but in the context parallelogrammic areas, which according to Heath’s commentary, is intended mainly to emphasize that only four-sided figures are meant, i.e., regular polygons of more than four sides with opposite sides parallel are not meant.
But Heron, in his Metrica of 50 CE (Alexandrinus 1903), did use the word
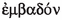 which is translated as “area”, and explains it this way: “A cubit area is called when a square plot has each side of one cubit.” The tile of Metrica shows Heron’s concern with techniques for actually calculating areas; he even gives a numerical procedure for computing approximate square roots. He also has no problem multiplying four lengths and then taking the square root to get an area. But that answer was a number, not a geometric length. The identification of line segments with numbers was not a part of Greek mathematics.
which is translated as “area”, and explains it this way: “A cubit area is called when a square plot has each side of one cubit.” The tile of Metrica shows Heron’s concern with techniques for actually calculating areas; he even gives a numerical procedure for computing approximate square roots. He also has no problem multiplying four lengths and then taking the square root to get an area. But that answer was a number, not a geometric length. The identification of line segments with numbers was not a part of Greek mathematics.This could now be explained using set theory, as set-theoretic union and difference, but that is a development only of the past century, and the verifications of Euclid’s common notions for this notion still involve real numbers as well as sets.
Actually, Euclid needed one more property: halves of equal figures are equal, used in Prop. I.39. The step that (implicitly) uses that property occurs in Euclid’s text without justification.
For example, see (Vieta 1646), p. 86, where Vieta writes A cubus + B quad. in A, equetur B quad.in Z, or in modern symbols, \(A^3 + B^2A = B^2Z\) instead of \(x^3 + px = q\). See Hartshorne (2022) for further discussion. Incidentally, one sees both Viète and Vieta, the French and Latin spellings of the name.
We have not defined AB : AC as a function taking four points, or two segments; the use of the equality symbol and colon in informal writing is just an abbreviation for the 8-argument relation. Bernays in his Supplement II to (Hilbert 1899) does define a : b for segments a, b to be, in effect, the angle whose tangent is b/a; but he never makes any use of that definition other than to verify that the equality of such angles implies the definition of proportionality we give here.
Euclid I.7 is quite a bit more difficult to prove than Euclid thought; it is hard to prove that an angle cannot be both equal to and less than another angle. Hilbert avoided the difficulty by including uniqueness in his angle-copying axiom.
There is a related precise question: Is the equal-figure axiom that ABC and BAC are equal figures redundant? That is, can it be derived from the rest of the axioms in the system of Beeson et al. (2019)? We do not know the answer.
In Propositions I.37, I.38, and I.48
Except of course, that we still need to show how to develop the theory of proportion with techniques from Book I.
Thus “early” refers to the logical status of the work, i.e., not relying on the later parts of Euclid that need Archimedes, and not to the chronology, since this work was done in the nineteenth century.
Kupffur gave two proofs of the interchange theorem in 1893. Mollerup gave proofs in 1902 (Mollerup 1902), emphasizing that Archimedes’s axiom was not used. Bernays gave a proof in 1956, identical to Kupffur’s first proof, that Bernays attributed to Federigo Enriques’s 1911 book (Enriques 1911). The relevant material is in a chapter written by someone else, namely Giovanni Vailati. On p. 239, Vailati gives Kupffur’s second proof, with credit and citation, and mentions his first proof, but then says that the first proof is actually due to Weierstrass, who (Vailati says) was the first to develop proportion theory without the axiom of Archimedes. But Vailati gives no citation to support this claim, and I could not pick up the trail.
Euclid III.20 and III.21 need repairs both in statement and proof. Some of these problems have been known for centuries (see Heath’s commentary Euclid 1956). But Heath does not remark on the step in Euclid’s proof of III.20 for which Euclid gives no justification, but which is difficult to prove formally, and the final “Therefore etc.” obscures the difficult proof that the two cases Euclid presents (and the one he does not present) are actually exhaustive.
References
Alexandrinus, H.: Opera Quae Supersunt Omnia, volume iii. Teubner, Leipzig. Editor: Hermann Schöne. English translation by Henry Mendell available on the Web (1903)
Baldwin, J.: Axiomatizing changing conceptions of the geometric continuum I: Euclid-Hilbert. Philos. Math. 26(3), 346–374 (2018)
Beeson, M.: Euclid after computer proof-checking. Am. Math. Mon. (2022). https://doi.org/10.1080/00029890.2022.2069985
Beeson, M., Narboux, J., Wiedijk, F.: Proof-checking Euclid. Ann. Math. Artif. Intell. 85(2), 213–257 (2019)
Bolzano, B.: Beiträge zu einer begründeteren Darstellung der Mathematik. Caspar Widtmann, Prague English translation in [Ewald (1996)], pp. 174–224 (1810)
Enriques, F.: Fragen der Elementargeometrie, I. Teil. Hermann Thieme (1911)
Euclid: the Thirteen Books of The Elements. Dover, New York. Three volumes. Includes commentary by the translator, Sir Thomas L. Heath (1956)
Ewald, W.: Philosophy of Logic. Elsevier, Amsterdam (1996)
Giovannini, E.N., Haeusler, E.H., Lassalle-Casaneve, A., Veloso, P.A.S.: De Zolt’s postulate: an abstract approach. Rev. Symbol. Logic 15(1), 197–224 (2022)
Hartshorne, R.: Geometry: Euclid and Beyond. Springer, New York (2000)
Hartshorne, R.: Francois Viète–life. https://math.berkeley.edu/~robin/Viete/work.html (2022)
Hilbert, D.: Foundations of Geometry (Grundlagen der Geometrie). Open Court, La Salle, Illinois, 1960. Second English edition, translated from the tenth German edition by Leo Unger. Original publication date (1899)
Kupffer, K.: Die Darstellung einiger Kapitel der Elementarmathematik. Sitzungsberichte der Dorpater Naturforschergesellschaft, pp. 373 (1893)
Mollerup, J.: Die Lehre von den geometrischen Proportionen. Math. Ann. 56(2), 277–280 (1902)
Pasch, M.: Vorlesung über Neuere Geometrie. Teubner, Leipzig (1882)
Schur, F.: Zur Proportionslehre. Math. Ann. 57(2), 205–208 (1903)
Vieta, F.: Opera Mathematica. Lugduni Batavorum, Leiden (1646)
Acknowledgements
I would like to thank Victor Pambuccian and Vincenzo De Risi for their help with the history of this subject. I would like to thank the anonymous referee for an extremely careful reading and many helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix: Listing of the equal-figures axioms
This formal listing is intended for reference. Only ASCII symbols are used, to facilitate cut-and-paste to computer-readable files. Polish notation can be found in Beeson et al. (2019).
Congruent triangles are equal.

Triangles with the same vertices are equal.

Triangle equality is a symmetric relation

Quadrilaterals with the same vertices are equal

Halves of equals are equal

Equal quadrilaterals is a symmetric relation

Equal quadrilaterals is a transitive relation

Equal triangles is a transitive relation

Cutting off equal triangles from equal triangles yields equal quadrilaterals

Cutting off equal triangles from equal quadrilaterals yields equal quadrilaterals

Pasting equal triangles yields equal triangles

Cutting off a triangle makes an unequal triangle

Cutting off a quadrilateral makes an unequal triangle

Pasting equal triangles to equal quadrilaterals yields equal quadrilaterals

Pasting equal triangles to equal triangles yields equal quadrilaterals

Pasting equal quadrilaterals yields equal quadrilaterals

Appendix: Where the equal-figures axioms are used
The following listing shows all the lines in the formal development of Beeson et al. (2019) that are justified by the equal-figure axioms other than the axioms ETpermutation, EFpermutation, and the axioms asserting that ET and EF are equivalence relations. The middle entry in each line is the statement justified; in most cases, the reader will be able to identify the corresponding line in Euclid’s own proof, which will either be justified by a common notion, or not justified at all. To decode the statements: for example in EFADGBFEGC, the initial EF means “equal figures” and the statement means that ADGB and FEGC are equal quadrilaterals.

Rights and permissions
About this article
Cite this article
Beeson, M. On the notion of equal figures in Euclid. Beitr Algebra Geom 64, 581–625 (2023). https://doi.org/10.1007/s13366-022-00649-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13366-022-00649-9





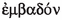 which is translated as “area”, and explains it this way: “A cubit area is called when a square plot has each side of one cubit.” The tile of Metrica shows Heron’s concern with techniques for actually calculating areas; he even gives a numerical procedure for computing approximate square roots. He also has no problem multiplying four lengths and then taking the square root to get an area. But that answer was a number, not a geometric length. The identification of line segments with numbers was not a part of Greek mathematics.
which is translated as “area”, and explains it this way: “A cubit area is called when a square plot has each side of one cubit.” The tile of Metrica shows Heron’s concern with techniques for actually calculating areas; he even gives a numerical procedure for computing approximate square roots. He also has no problem multiplying four lengths and then taking the square root to get an area. But that answer was a number, not a geometric length. The identification of line segments with numbers was not a part of Greek mathematics.