Area-invariant pedal-like curves derived from the ellipse

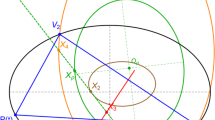
Abstract

We study six pedal-like curves associated with the ellipse which are area-invariant for pedal points lying on one of two shapes: (i) a circle concentric with the ellipse, or (ii) the ellipse boundary itself. Case (i) is a corollary of properties of Steiner’s Curvature Centroid (Krümmungs-Schwerpunkt), proved in 1825. For case (ii) we prove area invariance algebraically. Explicit expressions for all invariant areas are also provided. Finally, we generalize the results for a class of smooth curves.

Appendices

Appendix A: Evolutoids

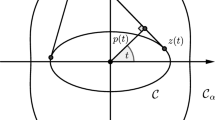
Some of the results in this section appear in Aguilar-Arteaga (2015); Jerónimo-Castro (2014). Consider a plane curve ${\mathcal {C}}(t)=[x(t),y(t)]$ defined by a support function h, see Eq. (4).

The family of lines passing through $P(t)=[x(t),y(t)]$ making a constant angle $\theta$ with $(x^\prime (t),y^\prime (t))$ is given by:

$$\begin{aligned} {\mathcal {L}}_{\theta }(t):&\cos (\theta -t) \,x - \sin (\theta -t)\, y - h(t) \cos \theta + h'(t) \sin \theta = 0 \end{aligned}$$

Let ${\mathcal {C}}_\theta (t)=(x_\theta ,y_\theta )$ denote the envelope of ${\mathcal {L}}_\theta (t)$. This will be given by:

$$\begin{aligned} x_{\theta }(t)=&\,\frac{1}{2} \left( \cos \left( t-2\,\theta \right) + \,\cos t \right) h \left( t \right) -h'(t)\sin t +\frac{1}{2} \left( \cos \left( t-2\,\theta \right) - \,\cos t \right) h'' \left( t \right) \\ y_{\theta }(t)=&\,\frac{1}{2} \left( \sin \left( t-2\,\theta \right) + \,\sin t \right) h(t) +h'(t)\cos t +\frac{1}{2} \left( \sin \left( t-2\,\theta \right) - \,\sin t \right) h'' (t) \end{aligned}$$

Note that ${\mathcal {C}}_{\pi /2}$ is the evolute of ${\mathcal {C}}$. Let $h_{\theta }(t)=h(t-\theta )\cos \theta +h'(t-\theta )\sin \theta$. Changing variables $t=t-\theta$ it follows that the envelope is given by

$$\begin{aligned} x_{\theta }(t-\theta )=&\,h_{\theta }(t)\cos t-h_{\theta }'(t)\sin t\\ y_{\theta }(t-\theta )=&\,h_{\theta }(t)\sin t+h_{\theta }'(t)\cos t \end{aligned}$$

Let S(.) denote the signed area of a curve. Then

$$\begin{aligned} S({\mathcal {C}})=&\,\frac{1}{2} \int _0^{2\pi }( h(t)^2-h'(t)^2) dt\\ S({\mathcal {C}}_{\pi /2})=&\,\frac{1}{2} \int _0^{2\pi }( h'(t)^2-h''(t)^2) dt \end{aligned}$$

Proposition 8

$S({\mathcal {C}}_\theta )$ is given by

$$\begin{aligned} S({\mathcal {C}}_\theta )= S({\mathcal {C}})\cos ^2\theta +S({\mathcal {C}}_{\pi /2})\sin ^2\theta \end{aligned}$$

Proof

The signed area of the evolute ${\mathcal {C}}_{\pi /2}$ is negative in general, and zero if ${\mathcal {C}}$ is a circle. Integrating Eq. 2 by parts and simplifying it yields the claim. $\square$

Let L(.) denote the perimeter of a curve.

Proposition 9

For small $\theta$, $L({\mathcal {C}}_{\theta }$) is given by:

$$\begin{aligned}L({\mathcal {C}}_{\theta } )=L({\mathcal {C}})\cos { \theta } \end{aligned}$$

Proof

Let T, N define the tangent and normal axis of the Frenet frame. From Giblin and Warder (2014) we have that

$$\begin{aligned} {\mathcal {C}}_{\theta }(s)={\mathcal {C}}(s)+\frac{\cos \theta \sin \theta }{k(s)}T(s)+\frac{ \sin ^2\theta }{k(s)}N(s).\end{aligned}$$

Differentiating the above and using Frenet equations $T'={k}N$ and $N'=-{k}T$, it follows that

$$\begin{aligned} {\mathcal {C}}_{\theta }'(s)=\frac{ k(s) ^{2}\cos {\theta } - k'(s)\sin {\theta }}{ k(s) ^{2}} \left( N(s) \sin {\theta }+T(s) \cos {\theta } \right) \end{aligned}$$

Therefore,

$$\begin{aligned} |{\mathcal {C}}_{\theta }'(s)|= \left| \cos \theta -\frac{k'(s)}{k(s)^2}\sin \theta \right| .\end{aligned}$$

For small $\theta$ it follows that

$$\begin{aligned} |{\mathcal {C}}_{\theta }'(s)|= \cos \theta -\frac{k'(s)}{k(s)^2}\sin \theta .\end{aligned}$$

Integration leads to the result stated. $\square$

Appendix B: Table of symbols

See Table 1.

Table 1 Symbols used