Identifying a polytope by its fibre polytopes

Abstract

It is shown that a full-dimensional polytope P is uniquely determined by its r-dimensional fibre polytopes when $r \ge 2$. Further, if $r \ge 4$ and the r-dimensional fibre polytopes are zonotopes, then P itself must be a zonotope.

1 Introduction

Fibre polytopes were devised by Billera and Sturmfels (1992) (see also Billera and Sturmfels (1994)), generalizing the notion of secondary polytopes introduced by Gel’fand et al. (1990). The purpose of these constructions was to describe how different subdivisions of a projected convex polytope arise from the faces of the original. In McMullen (2004), answering a question of  McDonald (2002), we modified the original definition in order to allow mixed fibre polytopes. It is the definition of fibre polytope given there that we adopt here.

It is a well-known fact that a d-dimensional polytope P can be recovered from its orthogonal projections on r-dimensional subspaces when $r \ge 1$; the basic reason is that the support functional of P is given by the support functionals of these projections. Perhaps closer in spirit to what we do here is the solution of Hammer’s X-ray problem in Gardner and McMullen (1980); see also Gardner (2006) for a wider picture. What we shall show is that something analogous happens with fibre polytopes. More precisely, if P is a full-dimensional polytope in the d-dimensional euclidean space V then, when $2 \le r < d$ is fixed, knowing the fibre polytopes $\mathop {\mathrm {fib}}(P;L)$ for each r-dimensional linear subspace L of V determines P uniquely.

It is known that a fibre polytope of a zonotope is a zonotope; see [McMullen (2003), Theorem 14.1]. We shall also show a kind of converse: if $r \ge 4$ and the r-dimensional fibre polytopes of P are zonotopes, then P itself is a zonotope.

In outline, the rest of the paper is as follows. In Sect. 2, we define fibre polytopes and discuss some of their basic properties. In Sect. 3, we look at a special case, which gives us some insight into the general problem. In Sect. 4, we show how to recover enough of the normal fan of a polytope from those of its fibre polytopes. In Sect. 5, we apply this result to establish the main claim of the paper. Section 6 treats the special case of zonotopes. We then make some additional comments in Sect. 7.

2 Fibre polytopes

The setting until Sect. 7 is a d-dimensional euclidean space V. If $\mathcal {G}_r = \mathcal {G}_r(V)$ denotes the Grassmannian of r-dimensional linear subspaces of V and $L \in \mathcal {G}_r$, then we have a short exact sequence

$$\begin{aligned} O \longrightarrow L {\mathop {\longrightarrow }\limits ^{\varPhi }} V {\mathop {\longrightarrow }\limits ^{\varPsi }} M \longrightarrow O, \end{aligned}$$

with $\varPhi$ the isometric injection of L in V and $\varPsi$ the orthogonal projection of V on $M = L^\perp$. We shall not distinguish between spaces and their duals, so that the dual exact sequence is

$$\begin{aligned} O \longleftarrow L {\mathop {\longleftarrow }\limits ^{\varPhi ^*}} V {\mathop {\longleftarrow }\limits ^{\varPsi ^*}} M \longleftarrow O, \end{aligned}$$

with the rôles of injection and projection reversed. We find it convenient to write $s := d - r$.

Following [McMullen (2004), Section 2], if P is a (convex) polytope in V, then we define its fibre polytope in L by

$$\begin{aligned} \mathop {\mathrm {fib}}(P;L) = \mathop {\mathrm {fib}}(P;\varPhi ) := \int _{\varPsi P} \, \bigl ((P - z) \cap L\bigr ) dz; \end{aligned}$$

(1)

we use the two notations interchangeably, depending on where we wish to place the emphasis (in McMullen (2004) there is an equivalent formulation in terms of support functionals). A consequence of the definition is [McMullen (2004), (2.2)], namely, if $t \in V$, then

$$\begin{aligned} \mathop {\mathrm {fib}}(P + t;\varPhi ) = \mathop {\mathrm {fib}}(P;\varPhi ) + \mathop {\mathrm {vol}}\nolimits _s(\varPsi P)(\varPhi ^*t) \end{aligned}$$

(2)

In the present context, we shall demand that P itself be full-dimensional unless we say otherwise, because the fibre polytope construction can degenerate on lower-dimensional polytopes (it always produces $\{o\}$ if $\dim P < d-r$).

We define N(F, P) to be the cone of outer normal vectors to a polytope P at a face F. The normal fan $\mathcal {N}(P)$ of P is the complex consisting of its normal cones N(F, P). An important fact from [McMullen (2004), Section 4] is

Proposition 2.1

The normal fan of $\mathop {\mathrm {fib}}(P;\varPhi )$ is the common refinement of the fan induced by the projection of the normal fan of P under $\varPhi ^*$:

$$\begin{aligned} \mathcal {N}(\mathop {\mathrm {fib}}(P;\varPhi )) = \bigwedge \varPhi ^*\mathcal {N}(P). \end{aligned}$$

Indeed, each point $u \in L$ determines a (unique) cone in $\mathcal {N}(\mathop {\mathrm {fib}}(P;\varPhi ))$, given by

$$\begin{aligned} \bigcap \{\varPhi ^*C \mid C \in \mathcal {N}(P) \text { and } u \in \mathop {\mathrm {relint}}\varPhi ^*C\}. \end{aligned}$$

In [McMullen (2004), Propositions 5.1 and 5.2], we showed how to find the vertices and edges of $\mathop {\mathrm {fib}}(P;L)$; we repeat those results here. We first need to define the scaling factor $\kappa (F,\varPhi ^*)$ for a face F of P. If X is a k-dimensional subspace of V and B is a unit k-cube in X, let $\mu (X) := \mathop {\mathrm {vol}}\nolimits _k(\varPhi ^*B)$. Note that $\mu (X) = 0$ if $\varPhi ^*$ is singular on X, and in particular if $k > r$. We then define

$$\begin{aligned} \kappa (F,\varPhi ^*) := \mu \bigl (\mathop {\mathrm {lin}} N(F,P)\bigr ), \end{aligned}$$

(3)

with $\mathop {\mathrm {lin}} N(F,P)$ denoting the linear hull of N(F, P). (In McMullen (2004), an alternative definition is given in terms of the projection $\varPsi F$ of F on M, but the equivalent one given here is simpler.) If $u \in \mathop {\mathrm {relint}} N(F,P)$, then we say that F is the face of P in direction u.

For vertices, writing

$$\begin{aligned} m_s(F) := \int _F x\,dx \end{aligned}$$

for the moment vector of an s-face F of P (the measure is s-dimensional measure in $\mathop {\mathrm {lin}} F$), we have

Proposition 2.2

If $u \in L$ is a general direction vector, then the vertex of $\mathop {\mathrm {fib}}(P;\varPhi )$ in direction u is

$$\begin{aligned} \sum _{\mathop {\mathrm {int}}(\varPhi ^*N(F,P)) \ni u} \, \kappa (F,\varPhi ^*)\varPhi ^*m_s(F). \end{aligned}$$

The formula for edge-lengths is very similar.

Proposition 2.3

If $u \in L$ is a direction vector lying in the relative interior of a cone of the normal fan of $\mathop {\mathrm {fib}}(P;\varPhi )$ of codimension exactly 1, then the edge of $\mathop {\mathrm {fib}}(P;\varPhi )$ in direction u has length

$$\begin{aligned} \sum _{\mathop {\mathrm {relint}}(\varPhi ^*N(F,P)) \ni u} \, \kappa (F,\varPhi ^*)\mathop {\mathrm {vol}}\nolimits _{s+1}(F). \end{aligned}$$

3 A special case

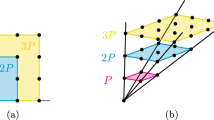
Before we introduce the machinery that we employ generally, we first look at the case $r = 2$ which is easy to treat and, at the same time, is of interest beyond the main topic of the paper.

When $P \in \mathcal {P}(V)$ is full-dimensional, Proposition 2.3 tells us that the edges of the fibre polygon $\mathop {\mathrm {fib}}(P;L)$ in the plane $L \in \mathcal {G}_2(V)$ arise from the facets (faces of codimension 1) of P. Indeed, if the facet $F_i$ of P has unit outer normal vector $u_i$ and corresponding area $\alpha _i$ for $i = 1,\ldots ,n$, then we write $a_i := \alpha _iu_i$, and call $A := (a_1,\ldots ,a_n)$ the area vector array of P. Observe that A is equilibrated, in that $a_1 + \cdots + a_n = o$. At this point, it is worth recalling Minkowski’s existence and uniqueness theorem (see, for instance, [Schneider (2014), Theorems 8.1.1, 8.2.1])

Proposition 3.1

An equilibrated set A that spans V is the area vector array of a full-dimensional polytope $P \in \mathcal {P}(V)$, which is unique up to translation.

Bearing in mind Proposition 3, we can see that the area vector array of $\mathop {\mathrm {fib}}(P,L)$ is just $\varPhi ^*A = (\varPhi ^*a_1,\ldots ,\varPhi ^*a_n)$, with the understanding that, if two or more $\varPhi ^*a_j$ are positive multiples of each other, then they are replaced in $\varPhi ^*A$ by their sum (in other words, the same convention applies as for the Blaschke addition $\#$ – see [Schneider (2014) ,p. 459]); naturally, a vector $a_i \in A$ such that $\varPhi ^*a_i = o$ makes no contributuion. If L is in general position relative to P, then such coincidences will not occur.

We now vary L, and keep track of how just one $\varPhi ^*a_j$ moves. Since $\varPhi ^*a_j$ is the image of $a_j$ under orthogonal projection on L, we see that the vectors $\varPhi ^*a_j$ trace out a sphere in V with diameter $[o,a_j]$ (the triangle with vertices $o,a_j,\varPhi ^*a_j$ is right-angled at $\varPhi ^*a_j$). Moreover, in fact, any open subset of $\mathcal {G}_2$ provides enough information to reconstruct this sphere. In other words, we can recover the original area vector array A from those of the fibre polygons.

Appealing to Proposition 3.1 shows that we have specified P up to translation; in particular, we know $\mathop {\mathrm {vol}}\nolimits _s(\varPsi P)$ for each given $L \in \mathcal {G}_r$. But finally we can identify P completely, because (2) provides enough information to fix P in its translation class.

Remark 3.2

It is worth making a further comment about this case. Bearing in mind that Blaschke addition really acts on translation classes of polytopes, we can see that the fibre polytope mapping induces a homomorphism from $(\mathcal {P}(V),\#)$ to $(\mathcal {P}(L),\#)$; note that Blaschke and Minkowski addition almost coincide in the planar case. It extends to lower-dimensional polytopes in $\mathcal {P}(V)$; it produces line segments (possibly degenerate) from those of codimension 1, and just $\{o\}$ for those of codimension 2 or more. As well, of course, it was at the core of the definition of mixed fibre polytopes in McMullen (2004) that the mapping $P \mapsto \mathop {\mathrm {fib}}(P;L)$ is also a valuation.

4 Recovering the normal fan

Proposition 2.1 tells us what the normal fan of the fibre polytope $\mathop {\mathrm {fib}}(P;\varPhi )$ is. The first stage in the general case is to show how to recover enough of the original normal fan $\mathcal {N} := \mathcal {N}(P)$ from the fans $\mathcal {N}(\mathop {\mathrm {fib}}(P;\varPhi )\bigr )$. We begin with the fairly obvious

$$\begin{aligned} C = \bigcap \left\{ L^\perp + \varPhi ^*C \mid L \in \mathcal {G}_r \right\} , \end{aligned}$$

(4)

if C is a cone in V of dimension at most r (we write $L^\perp$ instead of M, to make the connexion between $\varPhi$ and L more clear). If $C \in \mathcal {N}$, the problem in recovering C lies in the fact that it will be refined in L through being intersected with the images of other cones of $\mathcal {N}$. A crucial fact is that the projections $\varPhi ^*C$ move continously with $L \in \mathcal {G}_r$.

As we have seen, the cones in $\mathcal {N}\bigl (\mathop {\mathrm {fib}}(P;L)\bigr )$ arise as intersections of cones $\varPhi ^*C$ whose relative interiors have common points. But if neither $C_1$ nor $C_2$ is a face of the other, then there is some hyperplane H in V that separates them and meets them only in $C_1 \cap C_2$. If M is any s-subspace of H, then the projection $\varPhi ^*$ with kernel M is such that $\mathop {\mathrm {relint}}\varPhi ^*C_1 \cap \mathop {\mathrm {relint}}\varPhi ^*C_2 = \emptyset$. In other words, while such pairs of cones $C_1,C_2$ can contribute to cones in $\mathcal {N}\bigl (\mathop {\mathrm {fib}}(P;L)\bigr )$ for some subspaces L, they will not for others.

The procedure is thus to reconstruct the cones $C \in \mathcal {N}$ by increasing dimension. We begin with those of dimension 1 (normal cones to facets of P), which are particularly straightforward to single out in the way described, because their projections must survive in all fans $\mathcal {N}\bigl (\mathop {\mathrm {fib}}(P;L)\bigr )$. We then move on to those of dimension 2, which must have edges among those of the known 1-dimensional cones, and trace their projections to see which survive—possibly refined—into the $\mathcal {N}\bigl (\mathop {\mathrm {fib}}(P;L)\bigr )$. In general, once we have identified the family $\mathcal {N}_{k-1}$ of $(k-1)$-cones in $\mathcal {N}$, the potential cones in $\mathcal {N}_k$ must have facets among those in $\mathcal {N}_{k-1}$; we then look among them to see which are identified by their projections as genuinely belonging to $\mathcal {N}$, and so survive for every $L \in \mathcal {G}_r$. What we have shown is

Theorem 4.1

The $(r - 1)$-skeleton of the normal fan $\mathcal {N}(P)$ is determined by the family $\bigl \{\mathcal {N}\bigl (\mathop {\mathrm {fib}}(P;L)\bigr ) \mid L \in \mathcal {G}_r(V)\bigr \}$ of normal fans of the fibre polytopes of P.

Remark 4.2

There is not quite enough information to reconstruct the r-skeleton, because r-cones cannot be distinguished by their projections. However, the $(r - 1)$-skeleton is all that we shall need.

5 General polytopes

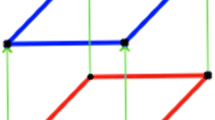
Proposition 2.3 tells us that the edges of a fibre polytope $\mathop {\mathrm {fib}}(P;\varPhi )$ arise from the $(s+1)$-faces F of P alone; however, at this stage, all that we know is that their lengths are sums of terms arising from different such faces F. We have shown in Sect. 4 how to reconstruct the $(r-1)$-skeleton of the normal fan $\mathcal {N}(P)$ from the normal fans $\mathcal {N}(\mathop {\mathrm {fib}}(P;\varPhi ))$; in particular, this yields enough of the strong isomorphism class of P (with faces determined by their normal cones – see, for instance, [Schneider (2014) ,p. 109]), namely, the linear subspaces $F_\Vert$ parallel to the k-faces $F \le P$ with $k > s$. Moreover, if $k \ge s+2$ and G is a k-face of P, then we also know the outer normal vector u(F, G) to G at each of its $(k-1)$-faces F.

The normal cone N(F, P) to F spans the subspace $F_\perp := \mathop {\mathrm {lin}} N(F,P)$ othogonal to $F_\Vert$. If $F,F'$ are two $(s+1)$-faces of P, then there are two possibilities. Either $F_\perp \cup {F'}_\perp$ spans V, or $H := \mathop {\mathrm {lin}}\bigl (F_\perp \cup {F'}_\perp \bigr )$ is a proper subspace of V. In the first case, $\varPhi ^*F_\perp \ne \varPhi ^*{F'}_\perp$ because these $(r-1)$-dimensional images span L. For the second case, if the kernel $M = \ker \varPhi ^*$ does not lie in H, then again $\varPhi ^*F_\perp \ne \varPhi ^*{F'}_\perp$. In neither case, therefore, can the images under $\varPhi ^*$ of the normal cones N(F, P) and $N(F',P)$ overlap, and hence F and $F'$ cannot contribute to the same edge of $\mathop {\mathrm {fib}}(P;L)$ (compare Proposition 2.3). (In saying that two cones $C_1,C_2$ overlap we mean that $\mathop {\mathrm {lin}} C_1 = \mathop {\mathrm {lin}} C_2$ and that $\mathop {\mathrm {relint}} C_1 \cap \mathop {\mathrm {relint}} C_2 \ne \emptyset$.) Since there are only finitely many proper subspaces of V spanned by pairs of normal cones to $(s+1)$-faces of P, we deduce

Lemma 5.1

For all but a set of subspaces $L \in \mathcal {G}_r$ of measure 0, each edge of $\mathop {\mathrm {fib}}(P;L)$ arises from a single $(s+1)$-face of P.

We now employ Proposition 2.3. If $L \in \mathcal {G}_r$ is a general subspace as in Lemma 5.1, then each $(s+1)$-face F of P contributes a single edge of $\mathop {\mathrm {fib}}(P;L)$ of length $\kappa (F,\varPhi ^*)\mathop {\mathrm {vol}}\nolimits _{s+1}F$. Since we now know the subspace $F_\Vert$, we then know the scaling factor $\kappa (F,\varPhi ^*)$, and hence we know $\mathop {\mathrm {vol}}\nolimits _{s+1}F$.

Finally, we appeal to Proposition 3.1 in increasing dimensions. For each $(s+2)$-face G of P, we have found the unit outer normals to G at its $(s+1)$-faces and the volumes of these faces. In other words, we have the area vector array of G, and hence we know G up to translation and, in particular, $\mathop {\mathrm {vol}}\nolimits _{s+2}G$. Carrying on the procedure eventually yields P itself, up to translation.

Finally, exactly as in Sect. 3, applying (2) for varying $L \in \mathcal {G}_r$ enables us to identify P in its translation class. In other words, we have proved

Theorem 5.2

If $2 \le r < d$, then a full-dimensional polytope P in a d-dimensional euclidean space V is uniquely determined by its fibre polytopes $\mathop {\mathrm {fib}}(P;L)$ with $L \in \mathcal {G}_r(V)$.

Remark 5.3

If we want to use slightly more technical language, we can say that the mapping from $\mathcal {P}(V)$ to $\mathcal {P}(V) \otimes \mathcal {G}_r(V)$ given by $P \mapsto \mathop {\mathrm {fib}}(P;L) \otimes L$ is injective on the sub-family of full-dimensional polytopes.

Remark 5.4

While it is not clear that the analogue of the result of Section 3 will hold, in that any large enough subset of $\mathcal {G}_r$ will suffice to reconstruct P, one should expect that to be the case.

6 Zonotopes

The following result was proved in McMullen (2003) on the level of strong isomorphism; here, we look at it in the metrical context.

Theorem 6.1

If $Z \in \mathcal {P}(V)$ is a zonotope, then a fibre polytope $\mathop {\mathrm {fib}}(Z;L)$ is a zonotope.

Proof

In fact, we need only pay attention to the (centrally symmetric) $(s+2)$-faces G of Z. Each 2-face of $\mathop {\mathrm {fib}}(Z;L)$ is a sum of centrally symmetric images of such faces G and line segments, and hence is centrally symmetric; this ensures that $\mathop {\mathrm {fib}}(Z;L)$ is a zonotope (see [Schneider (2014), Theorem 3.5.2]).

We also need a different characterization of a zonotope, which comes from McMullen (1970).

Proposition 6.2

If $2 \le k \le d - 2$ and all the k-faces of a d-polytope P are centrally symmetric, then all the faces of P are centrally symmetric, so that P is a zonotope.

We now show

Theorem 6.3

If $4 \le r < d$ and the fibre polytopes $\mathop {\mathrm {fib}}(P;L)$ of the full-dimensional $P \in \mathcal {P}(V)$ are zonotopes for each $L \in \mathcal {G}_r(V)$, then P is a zonotope.

Proof

A characteristic property of a zonotope Z is the fact that its normal cones N(G, Z) fit together to form complete subspaces of V. Moreover, the faces G corresponding to such subspaces are translates of each other and so, in particular, have the same volume of the appropriate dimension.

To reverse this, consider the varying fibre polytopes $\mathop {\mathrm {fib}}(P;L)$. If each is a zonotope, when we lift the normal fans $\mathcal {N}\bigl (\mathop {\mathrm {fib}}(P;L)\bigr )$ back up to $\mathcal {N}(P)$ the $(r - 1)$-dimensional cones N(F, P) (normal to $(s+1)$-faces F) again fall into subspaces, with each F having the same $(s+1)$-volume because $\kappa (F,\varPhi ^*)$ is the same. We now follow the proof of Theorem 5.2.

If $G \le P$ is a typical $(s+2)$-face, then its $(s+1)$-faces fall into parallel and opposite pairs with the same volume; again, this information comes from what we know of $\mathcal {N}(P)$. Since $s = d - r \ge 1$ by assumption, so that $s + 2 \ge 3$, we can appeal to Proposition 3.1 again to see that G must be centrally symmetric. The argument really begins with the case $r = 2$, when we simply have $G = P$. If $r = 3$, all we can deduce is that P is a polytope with centrally symmetric facets; by the Aleksandrov-Shephard theorem (Aleksandrov (1933), Shephard (1967) see McMullen (1976) for a shorter proof), it follows that P is itself centrally symmetric. (This should be obvious as well from the central symmetry of the fibre polytopes.)

Finally, if $r \ge 4$, in which case $3 \le s + 2 \le d - 2$, then we have a d-polytope P, all of whose $(s+2)$-faces are centrally symmetric. Now Proposition 6.2 implies that P is a zonotope, as claimed.

Remark 6.4

The example of the 4-dimensional regular 24-cell Q, say, shows that we cannot obtain anything stronger when $r = 3$. The facets of Q are regular octahedra. Thus the facets of any 3-dimensional fibre polytope of Q are sums of fibre polygons of octahedra and fibre polytopes of triangles, which are line segments. In other words, every fibre polyhedron $\mathop {\mathrm {fib}}(Q;L)$ has centrally symmetric facets, and so is a zonotope; however, Q itself is not a zonotope.

7 Final remarks

Our approach actually allows us to work in vector spaces over a more general field $\mathbb {F}$ than the real numbers $\mathbb {R}$. We need to compare fibre polytopes as we vary the subspace L in the Grassmannian $\mathcal {G}_r(V)$, and for this we must have something like a euclidean structure on V; hence $\mathbb {F}$ should be square-root-closed. (In this context, observe that the fibre polytope construction only needs Riemann integration.) In many respects, the most appropriate field for convex polytope theory is that of the real algebraic numbers.

One of the referees further observed that we could even take $\mathbb {F} = \mathbb {Q}$ (the rational numbers), apply the fibre polytope construction to lattice polytopes, and blow up any resulting fibre polytope $\mathop {\mathrm {fib}}(P;L)$ by a factor that only depends on the rational subspace L to make it a lattice polytope (the same factor must be applied, whatever $\mathop {\mathrm {fib}}(P;L)$ may be). Reversing this known scaling recovers each original fibre polytope $\mathop {\mathrm {fib}}(P;L)$, and for varying L these will still provide enough information to identify the original polytope P.