Abstract
Motivated by the search for reduced polytopes, we consider the following question: For which polytopes exists a vertex-facet assignment, that is, a matching between vertices and non-incident facets, so that the matching covers either all vertices, or all facets? We provide general conditions for the existence of such an assignment. We conclude that such exist for all simple and simplicial polytopes, as well as all polytopes of dimension \(d\le 6\). We construct counterexample in all dimensions \(d\ge 7\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Background and motivation
The content of the present paper is motivated by the study of reduced convex bodies as introduced by Heil (1978). A convex body is said to be reduced if no proper convex subset has the same minimum width as the body, i.e., the same minimum distance between parallel supporting hyperplanes. This notion is relevant, as the extremal bodies in several geometric minimization problems are necessarily reduced (e.g. in Pál’s problem; Heil 1978). More information on reduced convex bodies in Euclidean space can be found in the survey (Lassak and Martini 2011).
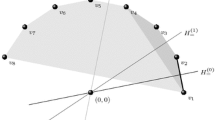
One may attempt to find polytopal minimizers, called reduced polytopes. While the existence of reduced polytopes is clear in the Euclidean plane (e.g. a regular triangle), the only known examples in higher dimensions were obtained in González Merino et al. (2018)—a single family of 3-dimensional polyhedra (see Fig. 1).
A key concept in the study of reduced polytopes consists of the different notions of antipodality of faces. For example, the authors of Averkov and Martini (2008, Theorem 4) obtained the following necessary condition for a polytope \(P\subset \mathbb {R}^d\) to be reduced: for every vertex \(v\in \mathcal {F}_0(P)\) there is an antipodal facet \(F\in \mathcal {F}_{d-1}(P)\) in the following sense:
-
(i)
P admits parallel hyperplanes supported at v and F respectively,
-
(ii)
the distance of the point of F closest to v is the minimum width of P, and
-
(iii)
the point of F closest to v is in the relative interior of F.
It is an immediate consequence of this result, that a reduced polytope admits an injective map from its vertices to non-incident facets.
This latter notion can be seen as a form of combinatorial antipodality and is the main topic of the present paper. We investigate, whether this property can be used to narrow down the search for combinatorial types of polytopes that may admit a reduced realization. It will be convenient to work with the following notion:
Definition 1
A vertex-facet assignment of a polytope P is a matching of non-incident vertex-facet pairs, that covers all vertices or all facets (or both).
This notion works well with polytope duality: clearly, a polytope P has a vertex-facet assignment if and only if P or its dual \({P}^{\Delta }\) (or both) admit an injective map from vertices to non-incident facets. Furthermore, it allows the straightforward application of graph-theoretic methods (via the vertex-facet graph in Sect. 3), in particular, of Hall’s marriage theorem (Theorem 3).
As an application of the latter, in Sect. 4 we obtain sufficient and necessary conditions for the existence of vertex-facet assignments in terms of the f-vectors of P and its faces. These main results read as follows:
Theorem 6
The polytope P has a vertex-facet assignment if and only if
for all faces \(\sigma \in \mathcal {F}(P)\).
Here, \({P}^{\Delta }\) denotes the dual polytope, and \({\sigma }^{\Delta }\) the dual face to \(\sigma \in \mathcal {F}(P)\). This notation is further explained in Sect. 2.
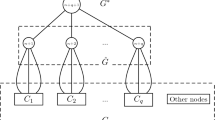
Schematic representation of the face lattice \(\mathcal {F}(P)\) of P, with the relevant sub-lattices and subsets highlighted. The symbol \(\sigma \) denotes a face \(\sigma \in \mathcal {F}(P)\). The upside-down labels indicate that the respective elements belong to the dual polytope and the respective lattices have inverted lattice order
Theorem 7
Suppose that for every face \(\sigma \in \mathcal {F}(P)\) the following holds: \(\sigma \) or \({\sigma }^{\Delta }\) (or both) have at least as many facets as vertices. Then P has a vertex-facet assignment.
It is a corollary of the second theorem that simple/simplicial polytopes always admit vertex-facets assignments (Corollary 9), as do polytopes in dimension \(d\le 6\) (Corollary 8).
In Sect. 5 we construct polytopes without vertex-facets assignments in every dimension \(d\ge 7\) using the free join construction (Theorem 11).
2 A word on notation
Throughout this paper, let \(P\subset \mathbb {R}^d\) be a full-dimensional convex polytope, that is, P is the convex hull of finitely many points, and \({{\,\mathrm{aff}\,}}(P)=\mathbb {R}^d\). Let \(\mathcal {F}(P)\) denote the face lattice of P, and \(\mathcal {F}_\delta (P)\subseteq \mathcal {F}(P)\) the subset of faces of dimension \(\delta \).
Our results are primarily combinatorial, and for the most part, we can identify P with its face lattice \(\mathcal {F}(P)\). Similarly, each face \(\sigma \in \mathcal {F}(P)\) is identified with the sub-lattice
The dual polytope \({P}^{\Delta }\) and, for each \(\sigma \in \mathcal {F}(P)\), the dual face \({\sigma }^{\Delta }\), shall be defined solely by their face lattices: the lattice \(\mathcal {F}({P}^{\Delta })\) is defined on the same set as \(\mathcal {F}(P)\), but with inverted lattice order. The face lattice of \({\sigma }^{\Delta }\) is
also with inverted lattice order. Consider Fig. 2 for a visualization of the placement of these sub-lattices in \(\mathcal {F}(P)\).
It is important to distinguish between \(\sigma \in \mathcal {F}(P)\) as a face of P, and \(\sigma \) as a polytope itself, since \({\sigma }^{\Delta }\) will refer to the dual polytope or the dual face, depending on the chosen interpretation. Similarly, \(\mathcal {F}({\sigma }^{\Delta })\) will refer to distinct sub-lattices of \(\mathcal {F}(P)\) depending on the interpretation. To avoid confusion, we therefore use the following convention: lower-case greek letters like \(\sigma ,\tau ,\ldots \) do always denote faces of P, hence \({\sigma }^{\Delta }, {\tau }^{\Delta }, \ldots \) do always denote dual faces. If other symbols are used to denote faces, this is explicitly mentioned in the respective place (this will only happen in Sect. 5 in the proof of Theorem 11).
Naturally, \(\mathcal {F}_0(P)\) refers to the set of vertices of P, and \(\mathcal {F}_0(\sigma )\subseteq \mathcal {F}_0(P)\) refers to the set of those vertices of P, which are contained in the face \(\sigma \in \mathcal {F}(P)\). The notation \(\mathcal {F}_0({P}^{\Delta })\) is an alternative way to address the set of facets \(\mathcal {F}_{d-1}(P)\) of P. While slightly unusual, we will use this notation in Theorem 6 (and the proof of Theorem 7), to highlight the symmetry of the statement under polytope duality. Similarly, \(\mathcal {F}_0({\sigma }^{\Delta })\subseteq \mathcal {F}_0({P}^{\Delta })\) can be used to conveniently denote the set of those facets of P that contain the face \(\sigma \in \mathcal {F}(P)\).
The cardinality of any of the sets defined above is denoted with \(f_\delta (\,\cdot \,):=\left|\mathcal {F}_\delta (\,\cdot \,)\right|\).
3 Graph-theoretic formulation
To any polytope \(P\subset \mathbb {R}^d\), we assign a bipartite graph as follows:
Definition 2
The vertex-facet graph G(P) of P is the bipartite graph  whose partition classes are (disjoint copies of) the vertices \(V_1=\mathcal {F}_0(P)\) and the facets \(V_2=\mathcal {F}_{d-1}(P)\) of P. A vertex \(v\in \mathcal {F}_0(P)\) and a facet \(F\in \mathcal {F}_{d-1}(P)\) are adjacent in G if and only if they are non-incident in P.
whose partition classes are (disjoint copies of) the vertices \(V_1=\mathcal {F}_0(P)\) and the facets \(V_2=\mathcal {F}_{d-1}(P)\) of P. A vertex \(v\in \mathcal {F}_0(P)\) and a facet \(F\in \mathcal {F}_{d-1}(P)\) are adjacent in G if and only if they are non-incident in P.
To avoid confusion with the terminology of polytopes, the elements of  of G(P) shall be called nodes (instead of vertices).
of G(P) shall be called nodes (instead of vertices).
A matching \(M\subseteq G(P)\) is a 1-regular subgraph. A matching M covers \(\mathcal {F}_0(P)\) (resp. \(\mathcal {F}_{d-1}(P)\)), if every vertex in \(\mathcal {F}_0(P)\) (resp. \(\mathcal {F}_{d-1}(P)\)) is incident to an edge in M.
A vertex-facet assignment of P is a matching in the vertex-facet graph that covers either \(\mathcal {F}_0(P)\) or \(\mathcal {F}_{d-1}(P)\). Hall’s marriage theorem (Diestel 2017, Theorem 2.1.2) is a classical result that gives a necessary and sufficient condition for the existence of a matchings of a bipartite graph  that covers, say, \(V_1\).
that covers, say, \(V_1\).
Theorem 3
The bipartite graph  possesses a matching that covers \(V_1\) if and only if \(\left|S\right|\le \left|N_G(S)\right|\) for all \(S\subseteq V_1\).
possesses a matching that covers \(V_1\) if and only if \(\left|S\right|\le \left|N_G(S)\right|\) for all \(S\subseteq V_1\).
Here, \(N_G(S)\) denotes the set neighbors of vertices in S. The condition \(\left|S\right|\le \left|N_G(S)\right|\) for all \(S\subseteq V_1\) in Theorem 3 is called Hall condition.
4 Existence in low dimensions
The existence of vertex-facet assignments is trivial for \(d\in \{1,2\}\). By applying Hall’s marriage theorem (Theorem 3) to the vertex-facet graph G(P) (Definition 2), we are able to show that there are no counterexamples up to dimension 6 (Corollary 8). Furthermore, simple/simplicial polytopes have vertex-facet assignments in every dimension (Corollary 9).
4.1 The case \(f_0(P)\ge f_{d-1}(P)\)
In this section, we assume that P has at least as many vertices as facets. We therefore try to match vertices and facets in G(P) in such a way that all facets are covered.
If \(S\subseteq \mathcal {F}_{d-1}(P)\) is a set of facets, there exists a nice geometric interpretation of the non-neighborhood \(\mathcal {F}_0(P)\setminus N_{G(P)}(S)\).
Proposition 4
The non-neighborhood of a set \(\{F_1,\ldots ,F_k\}\subseteq \mathcal {F}_{d-1}(P)\) of facets consists of the vertices of the face \(F_1\cap \cdots \cap F_k\), i.e.,
Proof A vertex is in the non-neighborhood of \(\{F_1,\ldots , F_k\}\) if and only if it (considered as a node in G(P)) is not adjacent to any of the \(F_i\). Since adjacency in G(P) means non-incidence in P, these are exactly the vertices incident to all the \(F_i\), that is, contained in the face \(F_1\cap \cdots \cap F_k\). The vertices of P that are contained in the face \(F_1\cap \cdots \cap F_k\) are exactly the vertices of this face.
Together with Hall’s marriage theorem (Theorem 3) we immediately obtain
Corollary 5
A polytope P with \(f_0(P)\ge f_{d-1}(P)\) has a vertex-facet assignment if and only if for all \(\{F_1,\ldots , F_k\}\subseteq \mathcal {F}_{d-1}(P)\) the following holds:
4.2 The general case
We now drop the assumption \(f_0(P)\ge f_{d-1}(P)\). The result of Corollary 5 can be nicely symmetrized:
Theorem 6
P has a vertex-facet assignment if and only if
for all faces \(\sigma \in \mathcal {F}(P)\).
Note that we wrote \(f_0({P}^{\Delta })\) to denote the number of facets of P, and \(f_0({\sigma }^{\Delta })\) to denote the number of those facets that contain \(\sigma \). This notation emphasizes the invariance of the result under polytope duality, i.e., it holds for P if and only if it holds for \({P}^{\Delta }\).
Proof of Theorem 6
We can assume \(f_0(P)\ge f_0 ({P}^{\Delta })\), as otherwise we could prove the statement for \({P}^{\Delta }\) instead. Under this assumption, (3) becomes
Assume (4) holds for all faces of P. Choose facets \(F_1,\ldots ,F_k\in \mathcal {F}_{d-1}(P)\). The face \(\sigma :=F_1\cap \cdots \cap F_k\) is contained in at least k facets, i.e., \(f_0({\sigma }^{\Delta })\ge k\). We conclude
Corollary 5 then yields the existence of a vertex-facet assignment.
Now conversely, assume there is a vertex-facet assignment. Let \(\sigma \in \mathcal {F}(P)\) be a face of P. Consider the set \(\{F_1,\ldots ,F_k\}:=\mathcal {F}_0({\sigma }^{\Delta })\) of facets that contain \(\sigma \). Then \(\sigma =F_1\cap \cdots \cap F_k\) and \(f_0({\sigma }^{\Delta })=k\). Since P has a vertex-facet assignment, there holds (2) in Corollary 5, and therefore
This proves (4). \(\square \)
We conclude a second sufficient condition, which is more convenient to apply to a large class of polytopes.
Theorem 7
Suppose that for every face \(\sigma \in \mathcal {F}(P)\) holds: \(\sigma \) or \({\sigma }^{\Delta }\) (or both) have at least as many facets as vertices. Then P has a vertex-facet assignment.
Proof Choose some arbitrary face \(\sigma \in \mathcal {F}(P)\). We show that \(\sigma \) satisfies (3). Theorem 6 then proves the existence of a vertex-facets assignment.
Suppose \(\sigma \) has at least as many facets as vertices, or in formulas, \((*)\, k\ge f_0(\sigma )\), where k denotes the number of facets of \(\sigma \). Each facet of \(\sigma \) can be written as \(\sigma \cap F\) with some \(F\in \mathcal {F}_0({P}^{\Delta })\setminus \mathcal {F}_0({\sigma }^{\Delta })\) (i.e., F is a facet of P that does not contain \(\sigma \)). It follows \((**)\,k\le f_0({P}^{\Delta })-f_0({\sigma }^{\Delta })\), and we conclude (3) via
On the other hand, if not \(\sigma \), but only its dual face \({\sigma }^{\Delta }\) has at least as many facets as vertices, we can apply the above reasoning to \({\sigma }^{\Delta }\) as a face of \({P}^{\Delta }\), which yields
As \({P}^{\Delta \Delta }=P\) and \({\sigma }^{\Delta \Delta }=\sigma \), this is equivalent to (3) for \(\sigma \).
An immediate consequence of Theorem 7 is the existence of vertex-facet assignments for polytopes up to dimension 6.
Corollary 8
Every polytope \(P\subset \mathbb {R}^d\) of dimension \(d\le 6\) possesses a vertex-facet assignment.
Proof If P is of dimension \(d \le 6\), then for every face \(\sigma \in \mathcal {F}(P)\) we have
Polytopes of dimension \(\le 2\) have the same number of vertices and facets. Theorem 7 then proves the existence.
Therefore, the counterexamples can only occur in dimension 7 or higher. Each 7-dimensional counterexample must have a 3-face \(\sigma \in \mathcal {F}(P)\) with \(f_0(\sigma )+f_0({\sigma }^{\Delta })> \max \{f_0(P),f_0({P}^{\Delta })\}\). We are going to construct such polytopes in the next section.
Another consequence is the existence of vertex-facet assignments for polytopes with only self-dual facets, e.g. simplicial polytopes:
Corollary 9
Simple/simplicial polytopes have vertex-facet assignments.
5 Counterexamples in high dimensions
In this section, we construct polytopes without vertex-facet assignments for any dimension \(d\ge 7\). These “counterexamples” are based on the free join construction.
Construction 10
Given polytopes \(P_i\subset \mathbb {R}^{d_i},i\in \{1,2\}\), their free join \(P_1\bowtie P_2\) is defined as the convex hull of copies of \(P_1\) and \(P_2\) that are embedded into skew affine subspaces of \(\mathbb {R}^{\smash {d_1+d_2+1}}\). Let us call these copies \(\bar{P}_1\) and \(\bar{P}_2\).
The faces of the free join can be given in terms of the faces of \(P_1\) and \(P_2\). Clearly, \(\bar{P}_1\) and \(\bar{P}_2\) are faces of the free join. More generally, for each face \(\sigma \in \mathcal {F}(P_i)\), the corresponding face \(\bar{\sigma }\) of \(\bar{P}_i\) is a face of \(P_1\bowtie P_2\) as well. All other faces of the free join are of the following form: for any two faces \(\sigma _1\in \mathcal {F}(P_1),\sigma _2\in \mathcal {F}(P_2)\), the convex hull \(\sigma _1\bowtie \sigma _2:={{\,\mathrm{conv}\,}}(\bar{\sigma }_1\cup \bar{\sigma }_2)\) is a face of \(P_1\bowtie P_2\).
The number of vertices and facets of the free join are given as follows:
This is clear for the vertices. The facets of \(P_1\bowtie P_2\) are \(P_1\bowtie F,F\in \mathcal {F}_{d-1}(P_2)\) and \(F\bowtie P_2,F\in \mathcal {F}_{d-1}(P_1)\). For details regarding the free join and its properties, consider Tiwary and Elbassioni (2014, Corollary 2).
Theorem 11
Let \(P_1\subset \mathbb {R}^{d_1}\) and \(P_2\subset \mathbb {R}^{d_2}\) be polytopes with
Then \(P_1\bowtie P_2\) does not have a vertex-facet assignment.
Proof Let \(P:=P_1\bowtie P_2\). The face \(\bar{P}_1\in \mathcal {F}(P)\) has \(f_0(P_1)\) vertices and is contained in the \(f_{d-1}(P_2)\) facets \(P_1\bowtie F\) with \(F\in \mathcal {F}_{d-1}(P_2)\). We check that \(\bar{P}_1\) violates condition (3) (in the following, \({\bar{P}_1}^{\Delta }\) shall denotes a dual face in P, rather than the dual polytope of \(\bar{P}_1\)):
Then, P has no vertex-facet assignment by Theorem 6.
The conditions \(f_0(P_1) > f_{d-1}(P_1)\) and \(f_0(P_2) < f_{d-1}(P_2)\) cannot be satisfied for polytopes in dimension \(\le 2\), which is the reason for the fact that this construction only yields counterexamples in dimensions \(\ge 3+3+1=7\).
Example 12
We list some explicit counterexamples for \(d\ge 7\).
-
(i)
Counterexamples exist in all dimensions \(d\ge 7\). Choose \(d_1,d_2\ge 3\) with \(d_1+d_2+1=d\) and polytopes \(P_i\subset \mathbb {R}^{d_i},i\in \{1,2\}\), so that \(P_1\) has more vertices than facets (e.g. the \(d_1\)-cube), and \(P_2\) has more facets than vertices (e.g. the \(d_2\)-dimensional cross-polytope). Then \(P_1\bowtie P_2\) has no vertex-facet assignment by Theorem 11.
-
(ii)
One might think that in self-dual polytopes the duality map \(v\mapsto {v}^{\Delta }\) (dual face to the vertex v) somehow induces an injective map from vertices to non-incident facets, hence, that a self-dual polytope always has a vertex-facets assignment. But surprisingly, there are self-dual polytopes without vertex-facet assignments in dimension \(d=2j+1,j\ge 3\). Let \(P_1\subset \mathbb {R}^j\) be a polytope with more vertices than facets (e.g. the j-cube) and \(P_2:={P}^{\Delta }_1\) its dual. The free join \(P_1\bowtie P_2\) then is a self-dual d-dimensional polytope [see Tiwary and Elbassioni (2014, Corollary 2)] without vertex-facet assignment (by Theorem 11).
6 Open problems and related questions
Several related questions might be asked, for example, about the nature of further counterexamples. Are there other counterexamples for \(d=7\) besides the free joins? We suspect that such can be constructed by taking the convex hull of a free join and a point. In general, what other ways are there to characterize polytopes without vertex-facet assignments?
Günter Ziegler brought up the following naturally related problem (personal communication):
Problem 13
Given a polytope \(P\subset \mathbb {R}^d\) with \(f_0(P)\le f_{d-1}(P)\). Does there exist an injective map from vertices to incident facets?
The answer to this seems comparatively easy and was already suggested by Ziegler himself: No. Even more, a polytope can have arbitrarily many more facets than vertices while still not having such an assignment. The following construction is based on an idea of Ziegler and uses the connected sum operation [see Ziegler (1995, Example 8.41)].
Example 14
Take the 3-cube \(Q\subset \mathbb {R}^3\) and let v be one of its vertices. The other seven vertices are incident to a total number of only six facets, hence an injective map from vertices to incident facets cannot exist. One could argue that this is due to \(f_0(Q)>f_{d-1}(Q)\). However, one can modify Q around v without invalidating the current reasoning (see Fig. 3). Cut off the vertex v, and obtain a new triangular facet that is not incident to any of the other seven vertices. Choose a simplicial 3-polytope \(P\subset \mathbb {R}^3\) with sufficiently many more facets than vertices and “glue it” (in the sense of the connected sum) to that triangular face. The new polytope \(Q':=P\# Q\) satisfies \(f_0(Q')\ll f_{d-1}(Q')\) while still not having an injective map from vertices to incident facets.
References
Averkov, G., Martini, H.: On reduced polytopes and antipodality. Adv. Geom. 8(4), 615–626 (2008). https://doi.org/10.1515/ADVGEOM.2008.037
Diestel, R.: Graph Theory, 5th edn. Graduate Texts in Mathematics, vol. 173. Springer, Berlin (2017). https://doi.org/10.1007/978-3-662-53622-3
González Merino, B., Jahn, T., Polyanskii, A., Wachsmuth, G.: Hunting for reduced polytopes. Discrete Comput. Geom. 60(3), 801–808 (2018). https://doi.org/10.1007/s00454-018-9982-3
Heil, E.: Kleinste konvexe Körper gegebener Dicke, Preprint 453, TU Darmstadt (1978)
Lassak, M., Martini, H.: Reduced convex bodies in Euclidean space—a survey. Expo Math. 29(2), 204–219 (2011). https://doi.org/10.1016/j.exmath.2011.01.006
Tiwary, H.R., Elbassioni, K.: Self-duality of polytopes and its relations to vertex enumeration and graph isomorphism. Graphs Combin. 30(3), 729–742 (2014). https://doi.org/10.1007/s00373-013-1299-7
Ziegler, G.M.: Lectures on Polytopes, Graduate Texts in Mathematics, vol. 152. Springer, New York (1995). https://doi.org/10.1007/978-1-4613-8431-1
Acknowledgements
Open Access funding provided by Projekt DEAL. Thomas Jahn would like to acknowledge support by the DFG Ul-403/2-1. Martin Winter gratefully acknowledges the support by the funding of the European Union and the Free State of Saxony (ESF).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jahn, T., Winter, M. Vertex-facet assignments for polytopes. Beitr Algebra Geom 62, 55–63 (2021). https://doi.org/10.1007/s13366-020-00504-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13366-020-00504-9